基于近邻传播聚类元胞自动机模型的武汉城市扩散和聚合过程同步模拟

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2021-12-29

何青松^,¹, 谭荣辉², 杨俊^,³

1.华中科技大学公共管理学院,武汉 430074

2.天津大学管理与经济学部公共管理学院,天津 300072

3.东北大学江河建筑学院,沈阳 110004

Synchronized simulation of urban diffusional and aggregational process based on the affinity propagation cellular automata: A case study of Wuhan city

HE Qingsong^,¹, TAN Ronghui², YANG Jun^,³

1. College of Public Administration, Huazhong University of Science & Technology, Wuhan 430079, China

2. College of Management and Economics, Tianjin University, Tianjin 300072, China

3. Jangho Architecture, Northeastern University, Shenyang 110004, China

通讯作者: 杨俊(1978-), 男, 湖北孝昌人, 教授, 博士生导师, 主要从事城市遥感应用研究。E-mail: yangjun8@mail.neu.edu.cn

收稿日期:2020-10-13修回日期:2021-06-6

基金资助:

国家自然科学基金项目(42001334)

Received:2020-10-13Revised:2021-06-6

Fund supported:

National Natural Science Foundation of China(42001334)

作者简介 About authors
何青松(1990-), 男, 安徽肥西人, 博士, 副教授, 硕士生导师, 主要从事城市增长模拟、地理过程建模研究。E-mail: baihualin2013@163.com

摘要
元胞自动机（CA）作为城市时空动态模拟应用最广泛的模型,可以有效模拟填充式和边缘式城市扩张过程,但是在飞地式扩张模拟方面稍显不足。本文提出一种改进CA模型—APCA,在传统CA基础上利用近邻传播聚类（AP）搜寻城市扩散增长的“种子点”,实现城市增长扩散过程和聚合过程的同步模拟。以武汉市为研究区域,使用APCA模拟其在2005—2025年间城市扩张的时空过程。结果显示：① APCA在设置“种子点”数量为1~8个时模拟总体精度均高于Logistics-CA,当“种子点”数量为6时,模拟新增部分精度最高,达到0.5217;② 2015—2025年武汉市飞地型增长面积约为8.67 km²,占新增城市用地总面积比例为6.30%;③ 武汉市1995—2025年间“先扩散后聚合”的城市扩张过程符合城市增长相位理论。APCA在一定程度上了完善了传统二维平面CA框架,将城市扩张模拟维度由面维扩展到点维,为准确展现城市用地空间扩展规律提供参考。
关键词： 元胞自动机;AP聚类;扩散增长;武汉市

Abstract

Cellular automata (CA) has been widely recognized as an effective approach in the simulation of spatiotemporal dynamics of metropolitan areas, particularly for infilling and edge urban expansion processes. However, the traditional Logistics-CA has its severe drawbacks in simulating outlying expansion, since it evolves primarily according to the status of a set of neighboring cells, failing to identify other potential seeds that could also stimulate urban expansion in a significant way. This paper develops an advanced CA, called APCA, by using Affinity Propagation (AP) to comprehensively search for urban expansion seed points, as well as by realizing a synchronous simulation of diffusional and aggregational processes of urban cell. This paper uses the data of Wuhan, the largest provincial capital in central China, to validate the effectiveness of APCA. By simulating Wuhan's urban expansion dynamics between 1995 and 2025, the APCA (1) identifies that the total areas of outlying expansion amount to 8.67 km², accounting for 6.30% of added urban land of the city; and (2) successfully simulates a process of "first diffusion and then aggregation" in Wuhan, which is in harmony with the Phase Theory of urban expansion. Compared with the traditional Logistics-CA, the overall accuracy of APCA remains higher regardless of the number of seed points as long as they are within 1-8, while the accuracy of APCA reaches its highest (0.5217) when the seed point is set as 6. The APCA contributes to the two-dimensional CA framework by expanding surface-dimension simulation to point-dimension simulation, and thereby facilitates effective and accurate simulations of urban expansion patterns.

Keywords：cellular automata;affinity propagation;diffusional urban expansion;Wuhan

PDF (4362KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex 收藏本文
本文引用格式
何青松, 谭荣辉, 杨俊. 基于近邻传播聚类元胞自动机模型的武汉城市扩散和聚合过程同步模拟. 地理学报, 2021, 76(10): 2522-2535 doi:10.11821/dlxb202110013
HE Qingsong, TAN Ronghui, YANG Jun. Synchronized simulation of urban diffusional and aggregational process based on the affinity propagation cellular automata: A case study of Wuhan city. Acta Geographica Sinice, 2021, 76(10): 2522-2535 doi:10.11821/dlxb202110013

1 引言

元胞自动机（Cellular Automata, CA）,是一种时空离散的动力学系统,由冯诺依曼于20世纪50年代使用计算机模拟生命游戏时创造^[1],其基本运行流程是对于初始状态,各元胞单元被分配一个初始状态,下一时间点元胞新的状态基于一定的规则（一般是一个数学函数）及其附近元胞集合的状态决定^[2]。自Tobler第一次将CA应用于地理过程建模以来,因其使用简单的规则,并且可以轻松地与高分辨率影像以及地理信息系统集成,而在模拟城市增长方面展现了巨大的潜力^[3,4],并形成了多个变种CA,例如针对不规则图斑模拟的矢量CA^[5,6],面向城市三维演变的3DCA等^[7,8]。

在基于CA的城市扩张建模中,非城市元胞的下一个状态一般由3个因素决定：邻域的属性（周边是否有足够多的城市元胞）、地理条件（空间邻近、地形限制等）以及未知的随机误差干扰^[9]。不同的****往往基于上述3个因素设计不同的元胞转换规则以判断非城市元胞的状态是否发生改变^{[2, 10-12]}。然而,由于大多数传统CA认为新增城市用地仅可能发生在现有城市用地的周边,即非城市元胞的邻域里必须有足够数量的城市元胞才可能在未来转变为城市元胞,因此它们在执行过程中无法准确模拟出城市的不同发展阶段^{[8, 13]}。实际上城市增长在空间上的变化过程具有确定的扩散和聚合的阶段过程^[13,14,15]。扩散是指新增城市用地主要位于已有建成区周围,呈相离状态;而聚合指城市发展到一定阶段,原有城市斑块之间的空隙或者边缘逐渐被新增城市用地填充,城市斑块间开始融合。这两个过程不断重复造成了城市空间不断向外扩张^[16]。为定量表达上述过程,****又进一步地将这两个过程归纳总结为填充式扩张、边缘式扩张和飞地式扩张^{[15, 17]}。填充扩张的特点是新增长城市斑块填补了原有城市斑块内部的空缺;边缘增长是指新增城市斑块沿着原有城市斑块边缘生长;飞地增长则是指新增城市斑块与原有城市斑块之间没有共同的边界,呈现相离状态^{[16, 18-19]}。对应到城市的发展过程中,在城市发展的初期阶段,原有城市中心图斑周边逐渐出现一些新的城市增长中心（“种子点”）,这个过程叫做扩散;随着城市的发展,大量新增城市用地发生在现有城市斑块边缘,使得现有斑块不断变大,形成边缘式扩张;随着过程的持续深入,城市形态逐渐成熟,新增城市用地斑块将此前较为破碎的城市用地零星斑块逐渐聚合在一起或者填充已有城市斑块的空隙,这个过程被称为填充^{[13, 16]}。

传统CA可以有效地模拟城市增长的聚合过程,但是却难以捕捉城市增长的扩散过程^[13]。究其原因,CA模拟过程只能沿着现有城市元胞邻域进行演化,而无法获知扩散增长的“种子点”在哪里。有极少数****开始尝试改进传统CA来模拟飞地型扩张,Clarke提出了一种称为SLEUTH（Slope-Landuse-Exclusion-Urban Extent-Transportation-Hillshade）的改进型CA模型,可以随机选择新生成的点来产生外延扩展^[20],但是城市的扩散并不是完全随机的,它是多种驱动力共同作用的结果^[13],因而SLEUTH可能无法模拟真实的城市扩散情景。Liu等提出了基于景观扩张指数（Landscape Expansion Index, LEI）的城市增长模型LEI-CA^[14],其中LEI用于识别城市扩张类型,并建立扩张类型案例库,基于案例推理技术寻找CA在迭代过程中每个非城市元胞参数与案例库中最匹配的案例,并将该案例的扩张类型赋予待决定非城市元胞,进而能对包括飞地型扩张在内的多种城市扩张类型进行模拟。但是该模型无法给出不同扩张类型的具体数量,此外LEI-CA模型中不同扩张类型的空间增长过程也不清楚^[13]。Liu等提出了SMDUGP（Simulation Model of Different Urban Growth Pattern）模型用于模拟城市形态演变的扩散和聚合过程^[13],SMDUGP基本思路是基于回归结果划分不同扩张类型扩张备选区域,然后考虑邻域因素,分别构建了邻接型和飞地型扩张备选区域内元胞状态转换规则,并集成到元胞自动机模型中,得到针对不同类型区域的模拟方法。

SLEUTH、LEI-CA和SMDUGP为扩展CA在城市扩散增长模拟领域应用做出了有益尝试,然而,LEI-CA和SMDUGP都无法判断扩散增长的“种子点”在哪里;SLEUTH提出使用“种子点”模拟扩散增长,但是“种子点”的选取是随机的,可能无法模拟真实的城市扩散情景。近邻传播算法（Affinity Propagation, AP）亦有翻译为吸引子传播算法、信任力传播算法等,是2007年发表在Science杂志上的一种新的聚类算法^[21]。AP相较于K-Mean、DBSCAN等常用的聚类方法,可以为每个类都找到最具代表性的样本,即聚类中心,且聚类中心点是数据集合中实际存在的点,因此可以将这个聚类中心理解为需要寻找的飞地型增长“种子点”。本文认为“种子点”和聚类中心可以类比的原因在于它们都是各自聚类内最重要的个体,其中飞地增长围绕“种子点”向外延展扩张,而聚类中心是一组样本中最具类特征的个体。将基于AP聚类识别出来的聚类中心作为“种子点”,并结合CA,能够同步模拟城市扩散和聚合过程。

基于上述总结,本文提出了一种实现城市3种扩张类型同步模拟的APCA（Affinity Propagation Cellular Automata）模型,选取湖北省武汉市为研究区,验证模型的有效性。武汉市因为众多河流湖泊等自然条件限制,城市形态的连续性增长在一定程度上受阻,存在着一定数量的扩散型增长,即飞地型增长。飞地斑块与原有城市用地之间的空隙作为未来城市扩张发生的主要空间,对塑造未来城市形态至关重要,因而准确模拟飞地扩张斑块的格局与过程,能够帮助决策者更好地制定未来城市空间布局优化方案。通过本文希望回答：① 城市扩散增长的“种子点”如何确定?② 2005—2025年间武汉市城市扩张过程是否符合先扩散再聚合的特征?

2 研究方法

2.1 近邻传播聚类算法简介

AP算法的基本思想是将所有样本作为网络的节点,在节点之间进行信息交换,经过多次迭代后,将出现若干个聚类中心（Exemplar）,这个中心即作为每类的代表^[21,22]。AP算法首先计算两两节点之间的相似程度,并构成相似度矩阵。相似度通常可以按照两个点之间的“距离”度量,本文中候选区内非城市元胞可以映射为上文中的节点,则元胞i和元胞j的相似度计算公式为：

（1）

s (i, j) = \frac{1}{(1 + \sqrt[]{\overset{q}{\sum_{p = 1}} {(V_{ip} - V_{jp})}^{2}})}

式中：s(i, j)表示元胞i和元胞j的相似程度;V_ip、V_jp分别表示第i个和第j个元胞的第p个属性值;q为属性的数量。

AP聚类中有两个关键概念：吸引度r(i, j)和归属度a(i, j)^[21],前者描述了元胞k作为元胞i的聚类中心的适合程度,后者刻画了元胞i选择元胞k作为其聚类中心的归属程度^[22]。两个值通过迭代的方式不断更新,更新公式为：

（2）

R_{t + 1} (i, k) = (1 - γ) \times R_{t + 1} (i, k) + γ \times R_{t} (i, k)

其中, （3）

R_{t + 1} (i, k) = \{\begin{array}{l} S (i, k) - \max_{j \neq k} \{A_{t} (i, j) + R_{t} (i, j)\}, 若 i \neq k \\ S (i, k) - \max_{j \neq k} \{S (i, j)\}, 若 i = k \end{array}

（4）

A_{t + 1} (i, k) = (1 - γ) \times A_{t + 1} (i, k) + γ \times A_{t} (i, k)

其中, （5）

A_{t + 1} (i, k) = \{\begin{array}{l} \min \{0, R_{t + 1} (k, k) + \sum^{} \max \{0, R_{t + 1} (j, k)\}\}, 若 i \neq k \\ \sum^{} \max \{0, R_{t + 1} (j, k)\}, 若 i = k \end{array}

式中：R_t₊₁(i, k)和A_t₊₁(i, k)分别表示新一次迭代的R_t (i, j)和A_t (i, k);R_t (i, j)和A_t (i, k)则分别代表上一次迭代时的对应值;γ为阻尼系数,用于算法收敛,默认值为0.5。r(i, k)加a(i, k)越大,则元胞k点作为聚类中心的可能性就越大,并且元胞i点隶属于以元胞k点为聚类中心的聚类的可能性也越大。AP算法可以基于Python调用Sklearn库包提供的sklearn.cluster.AffinityPropagation函数实现。

2.2 近邻传播聚类元胞自动机流程

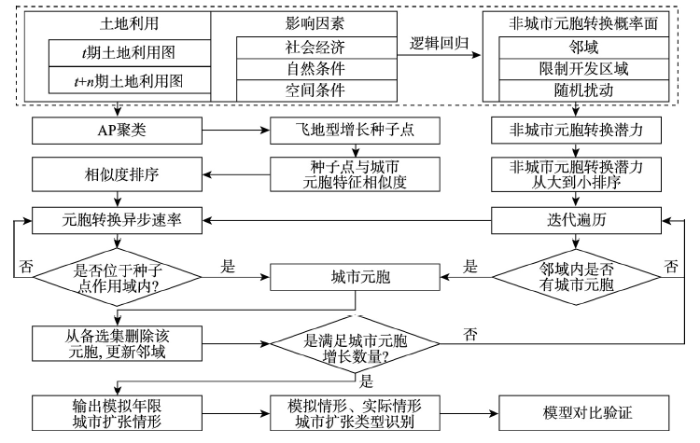
APCA与Logistic-CA（后文称之为TCA）的不同在于APCA迭代过程中会自动决定新增元胞的类型是飞地型还是邻接型（边缘型和填充型的统称）。它将AP确定的聚类中心作为扩散型增长的“种子点”,在“种子点”周围增长不受满足邻域内一定数量的城市元胞要求限制;另一方面原有城市斑块周边或者空隙内的增长过程在本文中被称为邻接增长,需要满足邻域限制。APCA总体思路是使用AP在非城市元胞集合中寻找一定数量的聚类中心作为扩散型增长的“种子点”,并依照“种子点”与原有城市元胞的相似程度设计“异步迭代”的策略,使得相似度更高的“种子点”周围能更快的形成新的城市元胞;对于邻接型增长则基于一种排序元胞自动机的策略,使得转变潜力高的非城市元胞优先发生状态转变。APCA的总体流程图如图1所示。具体方案流程包括：

图1

新窗口打开|下载原图ZIP|生成PPT
图1APCA总体流程图

Fig. 1Flowchart of APCA

（1）确定模拟的开始基期,提取出所有的非城市用地（编码0）和城市用地（编码1）。使用逻辑回归计算每个非城市元胞转向城市元胞的概率^[23]。参考以往研究以及结合研究区实际^{[8, 13]},选取的影响因素包括：社会经济因素（GDP密度、人口密度）、自然条件（高程）和空间临近条件（距市政府距离、距商业中心距离、距主干道距离、距地铁距离、距原有城市用地距离）共3类8个变量。在基期到新期的一定时期内元胞状态发生改变和未发生改变的两组集合中分别采集一定数量的样本,其中基期是非城市用地,新期为城市用地的样本Y = 1;基期是非城市用地,新期仍然是非城市用地的样本Y = 0。使用逻辑回归获得各个变量的系数,则一个非城市用地城市元胞转为城市用地城市元胞的概率为：

（6）

P = \frac{\exp (w_{0} + \sum_{1}^{n} w_{i} x_{i})}{1 + \exp (w_{0} + \sum_{1}^{n} w_{i} x_{i})}

式中：P为非城市用地城市元胞转为城市用地城市元胞的概率;w₀是逻辑回归结果常数项;x_i和w_i分别是第i个变量值以及回归结果系数;n是变量个数,在这里n = 8。

（2）提取出所有的非城市用地城市元胞,按照上一步逻辑回归模型中使用的8个变量外加计算的元胞转换概率值P,共9个变量作为描述该元胞的属性值。使用AP识别出非城市用地元胞的聚类中心。由于聚类中心的数量可能过多且部分距离现有城市过远,因此需要对这些聚类中心做进一步地筛选。通过计算现有城市元胞各个属性的平均值,假设形成新的平均值元胞NC,依次对所有聚类中心元胞与NC同样按照公式（1）进行相似性度量,选取具有最高相似值的前m个聚类中心作为潜在“种子点”。对于这些潜在的“种子点”,本文通过设置一种“异步迭代”机制控制“种子点”周围生成城市元胞的速率,具体思路是：① 依据公式（7）计算每个非城市元胞转向城市元胞的转换潜力：

（7）

T = P (i) \times con (i) \times Ω (i) \times RA

式中：T代表元胞最终的转换潜力,其值范围为[0, 1];con(i)代表限制性因素,其值为0或者1,本文中规定生态红线以及水域范围内元胞禁止转换为城市用地;RA代表随机误差;

Ω (i)

代表3×3邻域内城市元胞占比。

② 对潜力值大到小排列后开始迭代,设置如下规则：如果该非城市元胞邻域内有城市元胞,则该非城市元胞转城市元胞;同时判断：如果当前迭代次数与当前“种子点”按照与NC相似度从大到小排序的位次相除余数为0且当前非城市元胞转换潜力超过一定阈值,那么该“种子点”周围可以生成城市元胞,且从中心向外增长。

2.3 城市扩张类型识别

城市扩张类型有多种定义和描述方法,主要的城市扩张类型可归结为3种：填充型、边缘型和飞地型,其他扩张类型可看作这3种基本类型在不同程度上的组合结果^[24]。其中填充式扩张是指在已形成的城市区域中,进行空隙填充;外延式扩张是指城市用地扩展发生在城市的边缘部分,可理解为“摊大饼”式扩展;跳跃式扩张是指新增城市用地和已有城市区域在空间上没有连接。

按照最常用的新增城市斑块与原有城市斑块共同边或缓冲区关系可以确定每个新增城市斑块的扩张类型^[24,25,26]。参考刘小平等^[27]定义的景观扩张指数（LEI）,如果新增城市用地斑块缓冲区与已有城市用地斑块不相交,则是飞地式扩张;如果新增城市斑块缓冲区与已有城市斑块相交,则分别计算缓冲区与原有城市斑块以及空白区域的相交面积,按照下式识别类型^[27]。

（8）

LEI = \frac{A_{o}}{A_{o} + A_{v}} \times 100

式中：LEI是新增城市斑块的景观扩张指数;A_o是新增城市斑块的缓冲区与原有城市斑块的相交面积;A_v是缓冲区与空白区域的相交面积。刘小平等^[27]通过比较1~5 m与10~30 m的缓冲距离下的LEI值,发现缓冲距离小的LEI值更稳定,并最终推荐使用1 m作为缓冲区的大小。因此本文按照此缓冲区设置,界定当LEI ≤ 5时,则新增城市斑块为飞地式扩张;5 < LEI < 50则新增城市斑块是边缘式扩张;当LEI ≥ 50则为填充式扩张。

3 研究区及数据

武汉市位于江汉平原东部,是湖北省省会,地处29°58′N~31°22′N、113°41′E~115°05′E间。世界第三长河长江及其最大支流汉江将武汉城区一分为三,形成三镇鼎力局面。武汉众多大江大湖的自然条件限制了城市建成区的连片发展,部分新增城市用地会以飞地的形式出现。据研究,在1995—2005历史时期内,武汉市飞地型增长面积占比甚至达到48.58%^[16],因此,忽视扩散型增长过程无法充分了解武汉市城市扩张的特征。

武汉市历年的城市用地从影像中解译提取,用于解译的影像来源于中国科学院地理科学与资源研究所制作的全国土地利用/覆盖数据库（National Land-Use/Cover Database of China, NLUD-C）,共包含5期数据：1995年、2000年、2005年、2010年以及2015年,其空间分辨率为30 m,用地类型包括耕地、林地、草地、水域、建设用地以及未利用地。NLUD-C基于Landsat TM影像以及中巴资源卫星影像数据制作,目视解译、几何校正、实地调查以及大量辅助信息被应用于数据的制作以及更新过程中。Lai等通过全国范围的样本抽取验证,证实NLUD-C分类精度达到了90%以上,因而可以认为分类数据准确可信^[28]。根据武汉市2035年规划,城市建成区面积将在2025年前继续保持增长,2025之后保持稳定。因此以2025年作为期限,根据1995年、2000年、2005年、2010年以及2015年5个时间点建成区面积,按照外推法,可以得到建成区面积与年份的线性关系为Y = -24331.2+12.3334Year（R²= 0.92）,据此推算2025年的城市建成区面积约为643.94 km²。

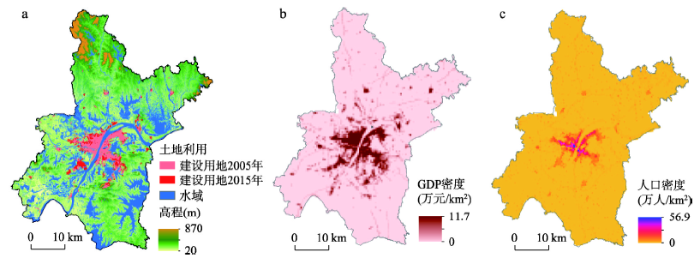
其他的数据还包括研究区2005年、2015年的1 km格网GDP密度数据和人口密度分布数据LandScan,前者来源于国家科技基础条件平台——国家地球系统科学数据中心（http://www.geodata.cn）,后者来自于美国橡树岭国家实验室（http://web.ornl.gov/sci/landscan/）。从武汉市自然资源与规划局收集了研究区的重要的基础地理数据,如主干道、地铁站、商业中心、DEM等。武汉市建设用地以及主要社会经济要素分布如图2所示。

图2

新窗口打开|下载原图ZIP|生成PPT
图22015年武汉市建设用地及主要社会经济要素分布

Fig. 2Distribution of construction land and major socioeconomic elements in Wuhan in 2015

4 结果与分析

4.1 模拟结果与验证

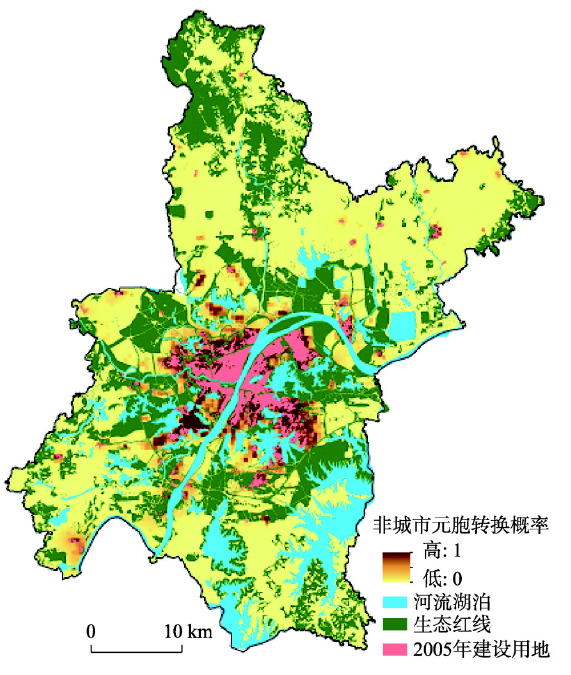
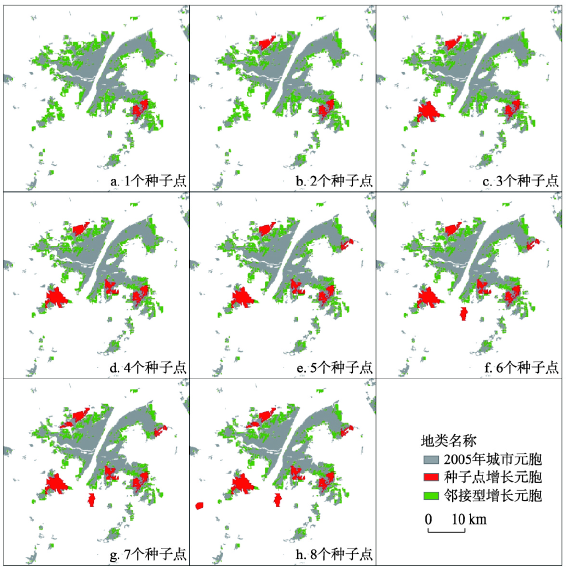
4.1.1 近邻传播聚类元胞自动机模拟结果从实际增长情形看,2005—2015年武汉市新增城市用地斑块1739块,总面积130.50 km²。根据LEI计算结果,共识别出飞地型、边缘型和填充型的斑块数量分别为64、837和838块,面积占比分别为16.68%,39.04%和44.28%。可见这一时间段内武汉市的飞地型面积占比最低,填充型占比最高,城市形态已经相对紧凑。从模拟增长情形看,APCA模拟的基础面是非城市元胞转换概率面,经过多次试验,最终随机选取200个样本（包含100个Y = 0和100个Y = 1）,使用逻辑回归获得了节2.2所提8个变量的权重系数,进而计算了每个非城市元胞的转换概率（图3）。经过多次尝试,设置“种子点”周围非城市元胞转城市元胞的最低转换概率阈值为0.15,分别使用本文提出的APCA模型,模拟不同“种子点”数量下城市用地景观分布。AP首先划分了最优聚类方案和对应的聚类中心（使用轮廓指数评价,具体方法见文献[22]）,在此基础上APCA输出了“种子点”数量为1~8个时的模拟方案（图4）,此时APCA模拟精度均高于TCA。总体上,1~6个点范围内,随着“种子点”数量增加,无论是模拟的新增城市用地还是整体部分（新增城市用地+原有城市用地）精度都越来越高,而超过6个后,随着“种子点”数量继续增加,总体精度呈现下降的趋势（表1）。可见过多或者过少的“种子点”都不利于模拟精度的提高。“种子点”过少,使得围绕“种子点”新增加的城市斑块面积较大,更容易与原有的城市斑块融合,无法获得合适数量的扩散斑块;当“种子点”的数量超过6个之后,城市形态变得过度扩散。基于上述考虑,最终将“种子点”数量定为6个,此时既能保证新增斑块边界相对柔和平滑,也可以让新增城市元胞一定程度的扩散分布。将APCA模拟的2015年城市用地栅格利用ArcGIS工具转换成矢量图斑后,发现从真实2005年到APCA模拟的2015年间,新增城市斑块中飞地型面积占比6.37%,虽然与真实占比存在一定差距,但是就所有斑块按照面积加权求和计算的GLEI而言,两者已经非常接近,模拟与真实的GLEI分别是44.61、45.21,说明APCA能较好的模拟城市局部扩散和整体的紧凑程度。

图3

新窗口打开|下载原图ZIP|生成PPT
图32005年武汉非城市元胞转城市元胞的概率分布

Fig. 3Probability distribution of non-urban cell to urban cell in Wuhan in 2005

图4

新窗口打开|下载原图ZIP|生成PPT
图41~8个“种子点”设置下2005—2015年武汉市新增城市用地模拟情景

Fig. 4Simulation scenarios of newly added construction land from 2005 to 2015 (1-8 seed points)

Tab. 1
表1
表1不同“种子点”数量下APCA模拟新增与整体部分精度值
Tab. 1The accuracy of APCA in the simulation of newly added and overall urban land (1-8 seed points)

种子点数量	1	2	3	4	5	6	7	8
整体部分精度	0.8632	0.8648	0.8724	0.8737	0.8748	0.8753	0.8721	0.8719
新增部分精度	0.4818	0.4866	0.5134	0.5136	0.5207	0.5217	0.5132	0.5015

注：模拟精度=正确分类的元胞数/总元胞数量

新窗口打开|下载CSV

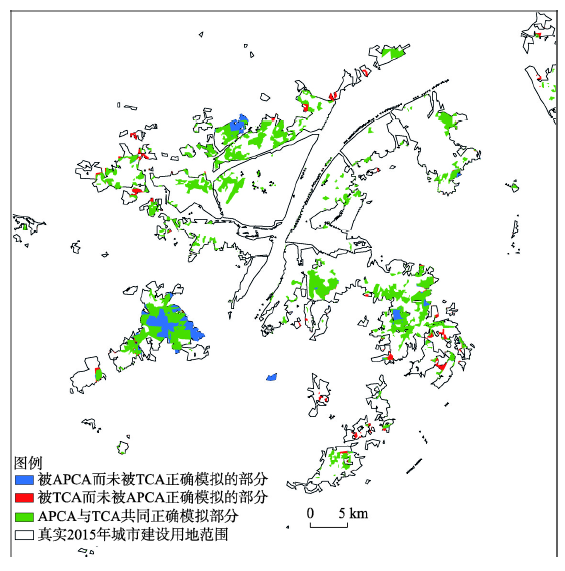
4.1.2 近邻传播聚类元胞自动机与逻辑回归元胞自动机结果对比 TCA可以有效模拟城市边缘式和填充式扩张轨迹,但是难以实现对飞地式增长过程的模拟。TCA模拟的新增城市部分与整体部分模拟精度分别为0.4780和0.8620,且新增城市部分全部是填充现有城市斑块的空隙（填充式扩张,占比51.32%）,或者沿着现有城市斑块往外延展（边缘式扩张,占比48.68%）,无飞地式增长出现。当“种子点”数量在1~8个时候,APCA总体精度均高于TCA。将APCA正确模拟的部分与TCA正确模拟的部分进行空间叠置,其中被APCA正确模拟,但是未被TCA模拟的部分（称为APCANTCA）以及被TCA正确模拟,未被APCA模拟的部分（称为TCANAPCA）如图5所示。TCANAPCA的总面积为4.35 km²,最大斑块面积只有0.32 km²;而APCANTCA的总面积为9.043 km²,超过1 km²的斑块有3个,分别为3.60 km²、1.45 km²和1.09 km²,均是围绕“种子点”形成的斑块,并且延展部分已经与原有斑块进行了融合。可见TCA未考虑“种子点”,空间局部的较大斑块可能无法被有效模拟,这在以下情况中发生的可能性更高：① 非城市元胞与原有斑块之间的距离较远,此时TCA因为邻域限制“不认为”这部分区域可能转换为城市元胞,需要认定一定“种子点”;② 图斑空隙较大,沿着斑块从内向外延展也不能使得图斑融合相通,还需要从附近“种子点”从外向内两个方向的同步增长。

图5

新窗口打开|下载原图ZIP|生成PPT
图5APCA与TCA模拟结果的空间叠置结果

Fig. 5Spatial overlay of APCA and TCA simulation outcomes

4.2 2025年武汉市城市形态预测

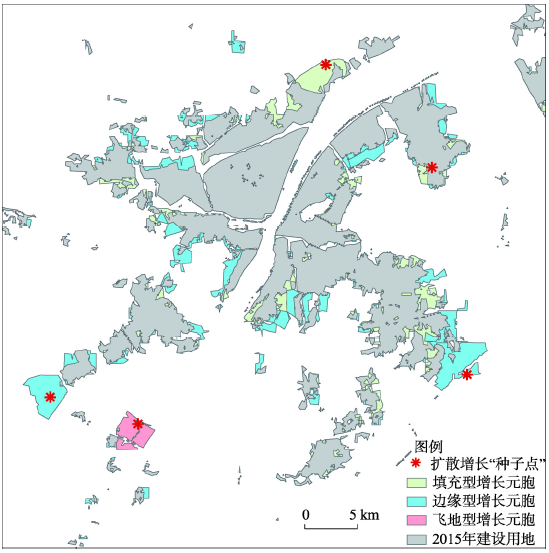
使用APCA在2015年非城市元胞集合内识别出聚类中心11个,它们距离原有城市用地在0.0897~29.6716 km范围内。遵循城市增长模拟时的一般性做法,即城市增长的历史演变规律可以应用于未来城市增长模拟过程^[29]。本文将2015—2025增长模拟的“种子点”数量也设置为6个,在2015年城市用地现状基础上预测模拟了2025年武汉市城市用地空间分布格局（图6）。其中,2015—2025年飞地型增长面积约为8.67 km²,占比为6.30%,较2005—2015年间实际情形下16.68%相应比例明显下降,说明城市形态变得更加紧凑。新增城市用地中,武汉市6个远郊区（江夏、蔡甸、东西湖、新洲区、黄陂、汉南）新增城市总面积为77.25 km²,占比56.15%;7个主城区（武昌、青山、江汉、江岸、汉阳、硚口、洪山）增长总面积为60.32 km²,占比43.85%。洪山区、江夏区和蔡甸区是新增城市面积最多的3个区,分别增加了30.82 km²、29.48 km²和25.58 km²,而江汉区、青山区和武昌区是新增城市面积最小的3个区,分别只增加了0.18 km²,0.41 km²和1.19 km²。统计各个区3种类型的面积占比如表2所示。可以看出,边缘式扩张在洪山、江夏、蔡甸、汉阳、东西湖、硚口、武昌7个区内占比最大,而填充式扩张在江岸、黄陂、汉南、新洲、青山和江汉区占比最大。飞地式扩张只发生在蔡甸和黄陂2个远郊区,说明在2015—2025年时间段内,外延和融合式增长成为主要方式,只有远郊区还存在较少的扩散式增长。

图6

新窗口打开|下载原图ZIP|生成PPT
图62025年武汉市城市景观模拟结果

Fig. 6Simulation results of urban landscape of Wuhan in 2025

Tab. 2
表2
表22015—2025年武汉市13个城区在新增城市用地分类型统计表(%)
Tab. 2Ratios of added construction land by urban growth patterns in 13 districts of Wuhan, 2015-2025 (%)

区名	边缘型占比	填充型占比	飞地型占比
洪山区	67.19	32.81	0.00
江夏区	63.44	36.56	0.00
蔡甸区	63.77	5.74	30.49
汉阳区	80.53	19.47	0.00
江岸区	3.42	96.58	0.00
东西湖区	71.09	28.91	0.00
黄陂区	40.12	41.84	18.04
硚口区	98.99	1.01	0.00
汉南区	47.36	52.64	0.00
新洲区	10.04	89.96	0.00
武昌区	55.43	44.57	0.00
青山区	30.22	69.78	0.00
江汉区	0.00	100.00	0.00

新窗口打开|下载CSV

4.3 城市增长过程

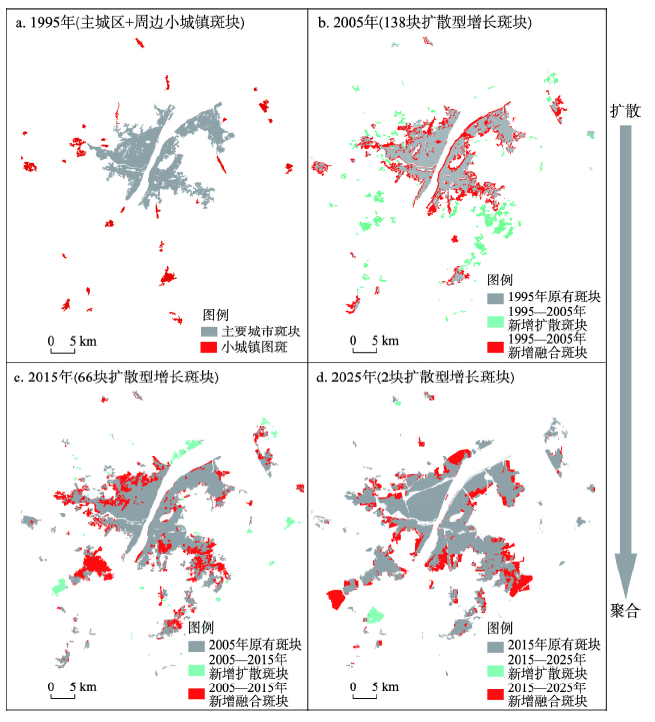
通过对1995—2005年、2005—2015年以及2015—2025年3个时间段武汉市新增城市用地分类型面积占比统计发现：1995年城市建成区主要分布在主城区,在城市扩张的初期阶段（1995—2005年）,城市扩张还存在着大量的扩散过程,飞地型占比（1995—2005）为48.58%,出现了大量城市增长“种子点”;2005—2015年间,实际情形下按照邻接型扩张方式的斑块面积占比显著增加,飞地型增长显著下降,占比为16.68%,而在模拟情况下,飞地型增长占比更低,只有6.37%;由于2015—2025年情形尚未发生,因此无法准确获知这一阶段不同类型斑块的发生情况。但是按照城市增长相位理论^[30],可以预知城市形态相较于前一阶段将更加紧凑。通过APCA预测也发现,这一阶段飞地型占比已经下降到6.30%,邻接型扩张占绝对优势地位,此时城市的形态逐渐由几个大的斑块主导,形态趋于成熟。

通过图7来图解武汉1995—2005年、2005—2015年实际城市发展过程以及2015—2025年的预测过程可以发现武汉市30年的城市扩张轨迹符合城市增长相位理论关于城市发展过程的描述,即存在着从扩散向聚合变化的过程^[26]。① 在1995年初始阶段,城市地区主要由主城区的几个大斑块加上周边一些小的城镇斑块构成。② 1995—2005年间,新增加的融合斑块使得原有的1995年城市斑块同步生长扩张。但同时新增了138块扩散型增长斑块（“种子点”）,且这些斑块与原有城市用地的距离相对较远,平均距离为1670.78 m。③ 2005—2015年武汉市的城市化进程显著加快,新增加了大量的城市用地面积,但是总体上融合扩张已经占据主导地位（83.32%）。但也新增加了66个扩散增加的斑块,此时这些“种子点”斑块与原有城市用地的平均距离已经下降为1374.24 m。斑块之间的融合相对前一时间段已经相对容易。④ 到2025年,城市形态已经发展到非常成熟的水平,原先分散的建成区斑块最终聚合为几个连续的大斑块。只有零星2个新的扩散斑块,且与城市用地斑块的平均距离仅857.65 m,预计未来这些空隙将很容易被新增斑块填充融合,城市形态将更加紧凑。

图7

新窗口打开|下载原图ZIP|生成PPT
图71995—2025年武汉市城市用地增长过程

Fig. 7The expansion process of construction land of Wuhan from 1995 to 2025

5 结论与讨论

5.1 结论

本文选择武汉市为研究案例城市,使用APCA模拟其从2015—2025年间城市空间形态变化。主要结论包括：

（1）相较于TCA,APCA可以在一定程度上模拟武汉市2005—2015年的城市增长中距离城区较远的扩散增长或者原有城区内部空隙较大的融合增长。“种子点”数量在1~8个内,APCA总体精度均高于TCA,且当“种子点”数量为6的时候,APCA模拟的总体精度最高,模拟的整体部分和新增部分精度分别达到0.8753和0.5217。

（2）APCA预测2025年武汉市城市增长情形显示,2015—2025年飞地型增长面积约为8.67 km²,占比为6.30%。③ 武汉市1995—2025年的城市空间形态动态变化过程契合了城市增长先扩散后聚合的基本规律。在武汉市城市发展的早期阶段,市中心附近出现大量扩散扩张,随着时间的推移,这些分散的新城市斑块逐渐聚合,最终所有原先零散分布的城市斑块聚合为几个连续的大的城市斑块,城市形态也趋于成熟。

上述结果说明APCA在模拟复杂城市形态方面相较于TCA具有一定的优势。本文认为APCA的应用场景特别适合于城市增长的加速阶段,此时城市扩张会出现大量的扩散增长情形。例如He等研究发现中国在1995—2005年间有大约18%的城市（65/363）城市增长以飞地扩张为主,主要集中于西藏和东北三省^[16],在这些区域建议使用APCA追踪大量的飞地增长轨迹。另一个典型利用情境是城市自然条件复杂,一定程度阻隔了城市的自然连续增长,形成较为分散的城市结构。这些城市包括：① 地势复杂的山地城市,如重庆、攀枝花、张家界;② 江河湖泊众多的城市,如武汉、鄂州、大庆。除此之外,县域经济发达、存在大量开发区的城市,如苏南地区的苏州、无锡等,在这些城市周边存在大量的飞地工业园区。

5.2 讨论

了解城市空间形态扩张的性质、阶段、趋势,精确模拟其未来发展方向是当前城市可持续发展的重要任务与目标。CA因其使用简单的规则模拟复杂的时空动态过程而得到广泛的应用,但是它难以有效模拟城市扩张的扩散过程。飞地型斑块在形式上具有扩散分布以及小图斑的特点,因而本文将城市新增飞地型扩张的斑块抽象表达为“点”扩张。城市空间扩展的研究目前更侧重于二维平面上横向延展研究,但是由于城市周边区域的非同质性,城市的空间发展不是一个连续的过程^[31],其变化并不能由一个平面所刻画,而是序列的具有内在联系的点、线、面、体及其复合体变化过程的集合。本文提出一种改进CA模型—APCA,它将AP聚类与CA集成在一起,可以帮助识别城市发展的不同扩展类型,并克服传统CA模型在“飞地”扩展模拟中的缺陷,实现对以飞地为代表的城市扩散增长过程和以边缘型填充型为代表的聚合过程的同步模拟。因此,APCA在一定程度完善了二维平面CA框架,将城市增长模拟维度由面维扩展到点维;另一方面,城市扩散增长贯穿整个城市发展过程,但是在初期发生的更加明显,应用APCA有望一定程度改善传统的形态面状延展模拟方法难以较好地反映城市发展初期演变过程的不足。

APCA虽然在城市扩散增长模拟方面展现了一定的优势,但是由AP生成的“种子点”仍然存在较大的随机性。本文首先基于“种子点”与城市元胞的相似性测度对“种子点”进行了初步的筛选,能一定程度降低不合理的“种子点”对模拟结果的影响。但是仍存在以下问题,即当“种子点”离城市较近的时候,新增的元胞容易与原有城市元胞融合,形成融合斑块而非扩散斑块;当“种子点”离城区过远时,模拟情况与真实的城市增长情形相差较远且模型容易生成规则的图斑。在未来研究中作者希望选取不同扩张类型的影响因素,使用逻辑回归、案例推理技术、机器学习等方法预先评估每个非城市元胞转向各个类型元胞的概率,提取出转向飞地型概率高的区域,将落入这些区域的聚类中心作为“种子点”,保证选取的“种子点”能兼顾飞地增长空间特征。

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]

Santé

, García A

, Miranda

, et al. Cellular automata models for the simulation of real-world urban processes: A review and analysis
Landscape and Urban Planning, 2010, 96(2):108-122.

DOI:10.1016/j.landurbplan.2010.03.001 URL [本文引用: 1]

[2]

Feng

Yongjiu

, Yang

Qianqian

, Cui

, et al. Simulation and prediction of urban land use change with spatial autoregressive model based cellular automata
Geography and Geo-Information Science, 2016, 32(5):37-44, 127.

[本文引用: 2]

[ 冯永玖, 杨倩倩, 崔丽, 等. 基于空间自回归CA模型的城市土地利用变化模拟与预测
地理与地理信息科学, 2016, 32(5):37-44, 127.]

[本文引用: 2]

[3]

Yang

Jun

, Xie

Peng

, Xi

Jianchao

, et al. LUCC simulation based on the cellular automata simulation: A case study of Dalian Economic and Technological Development Zone
Acta Geographica Sinica, 2015, 70(3):461-475.

[本文引用: 1]

[ 杨俊, 解鹏, 席建超, 等. 基于元胞自动机模型的土地利用变化模拟: 以大连经济技术开发区为例
地理学报, 2015, 70(3):461-475.]

[本文引用: 1]

[4]

Zhao

, Yang

Jun

, Li

Chuang

, et al. Progress on geographic cellular automata model
Scientia Geographica Sinica, 2016, 36(8):1190-1196.

DOI:10.13249/j.cnki.sgs.2016.08.009 [本文引用: 1]

Cellular Automata (CA) is a kind of spatial discrete dynamic model based on the interaction of micro individual, the inherent parallel computing ability, highly dynamic and spatial concepts and other features, the CA has outstanding advantages in the study of simulated the temporal and spatial dynamics evolution of complex spatial system. To put it simply, CA is not only a discrete system in time, space and state, but also a local grid dynamics model of both spatial interaction and consequence in time, its "bottom-up"research method being applied in various fields such as society, economy and scientific research. constantly.The paper reviewed the development process of cellular automata briefly, expounds the main application fields and study progress of CA in geography, on this basis, from the perspective of the real world geographic entities and the modern urban expansion,analysis the existing problems in the study of CA at present, then for the study trends of CA has carried on the preliminary discussion, The results of the analysis is that the following three aspects will be the focus of future CA research: 1) Use CA model which has irregular cell or controllable neighborhood to simulate the geographic entities of different rules or different neighborhood; 2) In order to overcome the defects of the two dimensional CA model, use three dimensional cellular automata to simulate the three-dimensional expansion of modern urban; 3) For the sake of improvethe accuracy of simulation,use the vector cellular automaton model to simulate the geographic entities.

[ 赵莉, 杨俊, 李闯, 等. 地理元胞自动机模型研究进展
地理科学, 2016, 36(8):1190-1196.]

[本文引用: 1]

[5]

Sun

Yizhong

, Yang

Jing

, Song

Shuying

, et al. Modeling of multilevel vector cellular automata and its simulation of land use change
Acta Geographica Sinica, 2020, 75(10):2164-2179.

DOI:10.11821/dlxb202010009 [本文引用: 1]

Urban planning plays an important guiding role in land use change. The planning at all levels supports and complements each other, and influences the evolution of land-use pattern from top to bottom. Vector cellular automata, which takes irregular geographical entities as its basic units, can express the objective and complicated urban land use structure in a more realistic way, and has become one of the focus in the land use change research. However, when we face urban planning with the characteristics of hierarchical synergy, spatial guidance and controlled conductivity, some key issues are highlighted, such as the establishment of CA hierarchical system, the construction of hierarchical synergy and the acquisition of transition rules. After constructing the multilevel vector CA model, we chose Jiangyin City as the study area and its land use data covering the years 2007, 2012 and 2017 as the basic data to simulate the land use changes from 2012 to 2017. On the basis of multilevel vector cellular automata model, through the comparative analysis between the simulation results and the current situation of land use in 2017, the individual parameters of the model were modified to further improve the feasibility and applicability of the model, and then the urban land use pattern in 2022 was predicted. The simulation results indicated that the development of construction land in Central District has become saturated, while the expansions of construction land in Chengnan District, Chengdongnan District and Chengdong District were obvious. From an overall perspective, there was a tendency to gradually form a three-level urban-rural spatial settlement system "central city area-urban agglomeration-village". Using FoM index, we concluded that the simulation results had great simulation precision and the model had high feasibility and applicability, because the FoM values of the whole city and each district were almost greater than or close to 0.21. This shows that the simulation results are more accurate and the model is more effective in the simulation of land use change based on urban planning.

[ 孙毅中, 杨静, 宋书颖, 等. 多层次矢量元胞自动机建模及土地利用变化模拟
地理学报, 2020, 75(10):2164-2179.]

[本文引用: 1]

[6]

, Laffan

, Pettit

, et al. Land use change simulation and analysis using a vector cellular automata (CA) model: A case study of Ipswich City, Queensland, Australia
Environment and Planning B: Urban Analytics and City Science, 2020, 47(9):1605-1621.

DOI:10.1177/2399808319830971 URL [本文引用: 1]

[7]

Qin

Jing

, Fang

Chuanglin

, Wang

Yang

. The three-dimensional urban growth simulating based on cellular automata
Journal of Geo-Information Science, 2013, 15(5):662-671.

DOI:10.3724/SP.J.1047.2013.00662 URL [本文引用: 1]

[ 秦静, 方创琳, 王洋. 基于元胞自动机的城市三维空间增长仿真模拟
地球信息科学学报, 2013, 15(5):662-671.]

[本文引用: 1]

[8]

He Q

, Liu Y

, Zeng

, et al. Simultaneously simulate vertical and horizontal expansions of a future urban landscape: A case study in Wuhan, Central China
International Journal of Geographical Information Science, 2017, 31(10):1907-1928.

DOI:10.1080/13658816.2017.1338707 URL [本文引用: 3]

[9]

Gao

, Feng Y

, Tong X

, et al. Modeling urban growth using spatially heterogeneous cellular automata models: Comparison of spatial lag, spatial error and GWR
Computers,Environment and Urban Systems, 2020, 81:101459. DOI: 10.1016/j.compenvurbsys.2020.101459.

DOI:10.1016/j.compenvurbsys.2020.101459 URL [本文引用: 1]

[10]

Wang

Haijun

, Xia

Chang

, Zhang

Anqi

, et al. Calibrating urban expansion cellular automata using biogeography-based optimization
Geomatics and Information Science of Wuhan University, 2017, 42(9):1323-1329.

[本文引用: 1]

[ 王海军, 夏畅, 张安琪, 等. 利用生物地理学优化算法获取城市扩展元胞自动机模型参数
武汉大学学报·信息科学版, 2017, 42(9):1323-1329.]

[本文引用: 1]

[11]

Xie

Zhiwen

, Wang

Haijun

, Zhang

Bin

, et al. Urban expansion cellular automata model based on multi-structures convolutional neural networks
Acta Geodaetica et Cartographica Sinica, 2020, 49(3):375-385.

[ 谢志文, 王海军, 张彬, 等. 城市扩展元胞自动机多结构卷积神经网络模型
测绘学报, 2020, 49(3):375-385.]

[12]

Liu

Xiaoping

, Li

Xia

. Retrieving CA nonlinear transition rule from high-dimensional feature space
Acta Geographica Sinica, 2006, 61(6):663-672.

[本文引用: 1]

[ 刘小平, 黎夏. 从高维特征空间中获取元胞自动机的非线性转换规则
地理学报, 2006, 61(6):663-672.]

[本文引用: 1]

[13]

Liu Y

, He Q

, Tan R

, et al. Modeling different urban growth patterns based on the evolution of urban form: A case study from Huangpi, Central China
Applied Geography, 2016, 66:109-118.

DOI:10.1016/j.apgeog.2015.11.012 URL [本文引用: 8]

[14]

Liu X

, Ma

, Li

, et al. Simulating urban growth by integrating landscape expansion index (LEI) and cellular automata
International Journal of Geographical Information Science, 2014, 28(1):148-163.

DOI:10.1080/13658816.2013.831097 URL [本文引用: 2]

[15]

Liu

Xiaoping

, Li

Xia

, Chen

Yimin

, et al. Landscape expansion index and its applications to quantitative analysis of urban expansion
Acta Geographica Sinica, 2009, 64(12):1430-1438.

DOI:10.11821/xb200912003 [本文引用: 2]

Landscape index is an instrument commonly used for quantitative analysis of landscape pattern. However, most of landscape indices are generally focused on simple analysis and description of the geometric features of a landscape patch or pattern, while neglecting information on dynamic changes of landscape pattern. In this paper a new landscape index, i.e., landscape expansion index (LEI), is proposed. In contrast with conventional landscape indices, LEI contains information of the formation processes of landscape pattern, so it can be used to analyze the dynamic changes of two or more temporal phases of landscape pattern, since conventional landscape indices only reflect information for one certain temporal phase of landscape pattern. Landscape expansion index was applied to studies on the urban landscape expansion of Dongguan City, Guangdong, China for the period of 1988-2006, and the results indicate that LEI can perfectly identify the three types of urban expansion, i.e., infilling type, edge-expansion type and outlying type. Additionally, based on an analysis of the LEI changes in the urban expansion processes of Dongguan City, it was found that the rule governing urban expansion of Dongguan City is consistent with the phases theory on urban growth. This study further demonstrates that LEI can be used effectively for a quantitative analysis of the dynamic changes of landscape pattern, and LEI proves to be significant to the studies on landscape pattern and its dynamic changes.

[ 刘小平, 黎夏, 陈逸敏, 等. 景观扩张指数及其在城市扩展分析中的应用
地理学报, 2009, 64(12):1430-1438.]

[本文引用: 2]

[16]

He Q

, Song

, Liu Y

, et al. Diffusion or coalescence? Urban growth pattern and change in 363 Chinese cities from 1995 to 2015
Sustainable Cities and Society, 2017, 35:729-739.

DOI:10.1016/j.scs.2017.08.033 URL [本文引用: 5]

[17]

Yan

, Hu

Shanshan

, Tong

Yan

, et al. Research on modeling for urban expansion pattern recognition based on shared boundary analysis
Geography and Geo-Information Science, 2017, 33(1):78-81, 101, 127.

[本文引用: 1]

[ 俞艳, 胡珊珊, 童艳, 等. 基于公共边测度的城市扩张模式建模研究
地理与地理信息科学, 2017, 33(1):78-81, 101, 127.]

[本文引用: 1]

[18]

Shi Y

, Sun

, Zhu X

, et al. Characterizing growth types and analyzing growth density distribution in response to urban growth patterns in peri-urban areas of Lianyungang City
Landscape and Urban Planning, 2012, 105(4):425-433.

DOI:10.1016/j.landurbplan.2012.01.017 URL [本文引用: 1]

[19]

Cheng

Lan

, Wu

Zhifeng

, Wei

Jianbing

, et al. Spatial identification of built-up land expansion and its significance
Chinese Journal of Ecology, 2009, 28(12):2593-2599.

[本文引用: 1]

[ 程兰, 吴志峰, 魏建兵, 等. 城镇建设用地扩展类型的空间识别及其意义
生态学杂志, 2009, 28(12):2593-2599.]

[本文引用: 1]

[20]

Clarke K

, Hoppen

, Gaydos

. A self-modifying cellular automaton model of historical urbanization in the San Francisco Bay area
Environment and Planning B: Planning and Design, 1997, 24(2):247-261.

DOI:10.1068/b240247 URL [本文引用: 1]

[21]

Frey B

, Dueck

. Clustering by passing messages between data points
Science, 2007, 315(5814):972-976.

DOI:10.1126/science.1136800 URL [本文引用: 3]

[22]

Liu Y

, Tang M

, Wu Z

, et al. Analysis of passenger flow characteristics and their relationship with surrounding urban functional landscape pattern
Transactions in GIS, 2020, 24(6):1602-1629.

DOI:10.1111/tgis.v24.6 URL [本文引用: 3]

[23]

Feng Y

, Liu

, Tong X

. Comparison of metaheuristic cellular automata models: A case study of dynamic land use simulation in the Yangtze River Delta
Computers, Environment and Urban Systems, 2018, 70:138-150.

DOI:10.1016/j.compenvurbsys.2018.03.003 URL [本文引用: 1]

[24]

, Liu M

, Zhang

, et al. The spatiotemporal dynamics of rapid urban growth in the Nanjing metropolitan region of China
Landscape Ecology, 2007, 22(6):925-937.

DOI:10.1007/s10980-007-9079-5 URL [本文引用: 2]

[25]

Jiao L

, Mao L

, Liu Y

. Multi-order Landscape Expansion Index: Characterizing urban expansion dynamics
Landscape and Urban Planning, 2015, 137:30-39.

DOI:10.1016/j.landurbplan.2014.10.023 URL [本文引用: 1]

[26]

Yue

Wenze

, Wang

Ruiliang

, Fan

Beilei

. Spatial patterns analysis of urban expansion in Hangzhou city
Journal of Zhejiang University (Science Edition), 2013, 40(5):596-605.

[本文引用: 2]

[ 岳文泽, 汪锐良, 范蓓蕾. 城市扩张的空间模式研究: 以杭州市为例
浙江大学学报(理学版), 2013, 40(5):596-605.]

[本文引用: 2]

[27]

Liu X

, Li

, Chen Y

, et al. A new landscape index for quantifying urban expansion using multi-temporal remotely sensed data
Landscape Ecology, 2010, 25(5):671-682.

DOI:10.1007/s10980-010-9454-5 URL [本文引用: 3]

[28]

Lai

, Huang X

, Yang

, et al. Carbon emissions from land-use change and management in China between 1990 and 2010
Science Advances, 2016, 2(11):e1601063. DOI: 10.1126/sciadv.1601063.

DOI:10.1126/sciadv.1601063 URL [本文引用: 1]

[29]

Tan R

, Liu Y

, Zhou K

, et al. A game-theory based agent-cellular model for use in urban growth simulation: A case study of the rapidly urbanizing Wuhan area of central China
Computers,Environment and Urban Systems, 2015, 49:15-29.

DOI:10.1016/j.compenvurbsys.2014.09.001 URL [本文引用: 1]

[30]

Duncan

, Sabagh

, Van Arsdol

M D

. Patterns of city growth
American Journal of Sociology, 1962, 67(4):418-429.

DOI:10.1086/223165 URL [本文引用: 1]

[31]

Aguilera

, Valenzuela L

, Botequilha-Leitão

. Landscape metrics in the analysis of urban land use patterns: A case study in a Spanish metropolitan area
Landscape and Urban Planning, 2011, 99(3-4):226-238.

DOI:10.1016/j.landurbplan.2010.10.004 URL [本文引用: 1]