, 方创琳, 黄解军The spatial-temporal characteristics and influencing factors of air pollution in Beijing-Tianjin-Hebei urban agglomeration
LIUHaimeng, FANGChuanglin, HuangJiejun通讯作者:
收稿日期:2017-01-16
修回日期:2017-08-18
网络出版日期:--
版权声明:2018《地理学报》编辑部本文是开放获取期刊文献，在以下情况下可以自由使用：学术研究、学术交流、科研教学等，但不允许用于商业目的.
基金资助:
作者简介:
-->
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (961KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
1 引言
大气污染引发的雾霾对人体健康、气候环境与城市可持续发展影响重大[1,2]。伴随着近年来中国快速城市化和工业化进程,雾霾天气频发,每年大约有120万~160万人因大气污染而过早死亡[3,4],空气质量恶化的经济成本达到每年中国GDP的1%~8%[5,6]。国际癌症研究机构（IARC）在2013年将PM2.5列为人类致癌物[7],PM2.5作为京津冀地区大气污染的首要污染物[8],是造成雾霾天气最重要的“元凶”[9]。京津冀城市群是中国经济核心区和体现国家竞争力的重要区域[10],其协同发展已上升到国家战略,2015年常住人口为1.12亿,占全国的8.14%,GDP总量69312.91亿元,占全国10.24%,但同时该区域也是中国大气污染最集中、最严重的区域[11],2014年和2015年全国空气质量最差的十个城市中京津冀地区分别占8个和7个,且冬季频频出现空气质量指数“爆表”现象（AQI>500）。《京津冀协同发展规划纲要》中指出要在生态环境协同治理方面率先突破,京津冀城市群的大气污染问题成为当前政府、学界、公众和媒体普遍关注的焦点[12,13,14,15]。京津冀城市群大气污染在空间上有什么特征?究竟哪些自然与社会经济因素导致了如此严重的污染?这些因素中,哪些贡献更大?除了本地的贡献,邻近地区的贡献有多显著?这些是本文拟解决的核心问题。针对大气污染影响因素的解析国内外****已有较多研究：对于人类活动相关的社会经济因素,已有的研究表明人口集聚[16,17]、工业生产[18]、煤炭、石油和生物质能源消费[19]、汽车尾气[20]等是大气污染的主要来源;不同的城市化水平[21,22],经济增长速度[23],产业结构[24],能源利用结构和效率[25],土地利用类型[26],交通状况[27],城市形态[28]等对城市空气质量的影响也有所不同。对于自然因素,大量的研究表明气象要素在空气污染中扮演重要角色[29,30,31],包括气温[32]、降水[33]、湿度[34]、气压[32]、风速[35,36]、风向[37]等对大气污染有重要的影响。同时,气候变化[38]、植被覆盖[39]、地形条件[40]、海拔高度[41]等自然环境要素对大气污染物的扩散与集聚有着显著影响。火山爆发、森林火灾等突发性自然影响因素不在本文研究范围。针对这一问题,将京津冀城市群作为案例地区的研究,近几年也开始逐渐增多[42,43,44]。
当前“未来地球（Future Earth）”计划以及可持续性科学（Sustainability Science）都着重强调自然与人文要素的综合集成[45],然而纵观已有研究,很少有****系统的将人文和自然因素纳入污染解析的整体研究框架进行考量,对每个指标进行定量化的分解更是少见[46]。另一方面,已有的研究更多注重时间序列的分析,对于地理空间维度重视不够,忽视了城市群尺度下大气污染的空间依赖性,缺乏对污染物本身以及影响因素的空间溢出效应研究[47,48],模型结果存在偏误。
因此,针对当前研究不足和京津冀城市群雾霾治理的紧迫性,不同于以往单方面注重社会经济因子或自然气象因子的解析,本文从地理学重视区域差异性与依赖性的视角出发,综合运用空间自相关分析和多种空间计量模型,分析了京津冀202个区县PM2.5的时空分异特征,进而创新性地对具体的自然与人文影响因素及其空间溢出效应进行系统的甄别和量化。本研究是京津冀协同发展规划实施的现实需求,对于制定区域和城市大气环境防治政策具有重要指导意义。
2 数据来源与处理
2.1 数据来源说明
本文用PM2.5年均浓度来表征京津冀城市群大气污染程度,京津冀区县尺度历年PM2.5浓度来自于大气成分分析组织（ACAG）[49],该数据融合了遥感监测、模型模拟和站点实测的数据,原始数据为1998-2014年的0.01°×0.01°的栅格数据,精度较高并被广泛使用,网址为：http://fizz.phys.dal.ca/~atmos/martin/?page_id=140。2014年月度PM2.5浓度来自京津冀地区79个空气质量站点的逐日实测数据,原始数据来自青悦开放环境数据中心（https://data.epmap.org）。根据引言中的文献梳理,本文初步选定的自然因素解释变量包括年降水量、年均气温、年均风速、年均相对湿度、植被覆盖度、海拔高度、地形起伏度。气温、降水、相对湿度、平均风速等气象要素数据均来自中国气象数据网（http://data.cma.cn/site）,原始数据为2014年京津冀地区160个气象站点的逐月数据,其中气温、相对湿度、平均风速计算全年的平均值,降水量计算全年总和;基于DEM的Kriging插值方法计算京津冀地区年均气温的栅格分布,运用Ordinary Kriging方法生成相对湿度、年降水量和平均风速的栅格数据。
归一化植被指数（NDVI）是植被生长状态及植被覆盖度最佳指示因子,本文选取京津冀地区7月份的NDVI数据,并剔除水体的影响,以较好反映该年度植被长势最好季节地表的植被覆盖程度。原始数据来自美国国家航空和宇航局（NASA）（http://modis.gsfc.nasa.gov/data/dataprod/mod13.php）。
海拔高度和地形起伏度根据数字高程模型（DEM）计算得到,DEM数据来源于“寒区旱区科学数据中心”（http://westdc.westgis.ac.cn）。
社会经济解释变量包括反映经济发展水平的人均GDP、反映人口集聚水平的人口密度、反映人类生产生活能耗的能源消费指数、反映产业结构的第二产业占GDP比重,其中能源消费指数涵盖了工业生产、日常生活、汽车行驶等的煤炭、石油、生物质等能源类型的消费。研究表明DMSP/OLS夜间灯光数据与能源消费存在显著的线性相关性[50,51],故本文利用DMSP/OLS数据,将行政区域范围内的所有栅格灰度值之和作为衡量该区域能源消费的指标,从而构建能源消费指数来间接反映不同区县的能源消费情况。DMSP/OLS稳定夜间灯光数据来自美国国家海洋和大气管理局（https://www.ngdc.noaa.gov/eog/download.html）。其他社会经济数据来自《2015年中国县域统计年鉴（县市卷）》《北京区域统计年鉴（2015）》《天津统计年鉴（2015）》,以及河北省11个地级市统计年鉴。
2.2 数据预处理
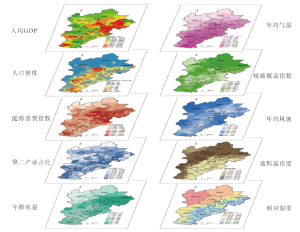
首先,对PM2.5浓度和所有解释变量与202个区县行政单元进行空间匹配。将PM2.5年均浓度、能源消费指数、年降水量、年均气温、年均风速、NDVI、地形起伏度、年均相对湿度的栅格数据在ArcGIS 10.2中进行按照区县行政边界的矢量转化,其中能源消费指数做栅格求和运算,代表能源消费总量,其他变量均取栅格平均值。根据文献综述选取的变量中很可能存在多重共线性问题,为此采用方差膨胀因子(Variance Inflation Factor, VIF)进行所有解释变量的多重共线性分析,发现海拔高度的VIF>7.5,说明其很可能与气温或地形起伏度存在多重共线性,故剔除该变量,将剩余的10个变量作为解释变量纳入模型。表1是所有解释变量的描述性统计、符号预判与空间自相关检验,偏度和峰度计算结果显示大部分变量原始数据不符合正态分布。相关系数是指各个变量与PM2.5的Spearman相关性检验结果,可以看到除了人均GDP、二产比重和年降水量外,其他变量与PM2.5均存在显著的相关性。同时,报告Moran's I的显著性,以辅助研究模型的选择。图1将所有变量进行了地图可视化展示,可以更清晰的看到不同变量在空间上的集聚与分布态势。
Tab. 1
表1
表1解释变量的描述性统计、符号预判与空间自相关检验
Tab. 1Descriptive statistics of explanatory variables and spatial autocorrelation test
| 解释变量 | 缩写 | 符号预判 | 极小值 | 极大值 | 均值 | 标准差 | 偏度 | 峰度 | 相关系数 | Moran's I |
|---|---|---|---|---|---|---|---|---|---|---|
| 人均GDP(元) | GDPPC | - | 4686.7 | 287758.4 | 41853.3 | 36099.1 | 3.3 | 15.1 | 0.04 | 0.36*** |
| 人口密度(人/km2) | people | + | 45.8 | 35154.4 | 2136.1 | 5372.5 | 4.1 | 17.5 | 0.56*** | 0.95*** |
| 能源消费指数 | energy | + | 945.0 | 114412.0 | 17743.3 | 14848.9 | 2.5 | 9.7 | 0.47*** | 0.22*** |
| 第二产业占GDP比重(%) | second | + | 4.2 | 75.4 | 45.5 | 14.9 | -0.5 | -0.1 | 0.01 | 0.30*** |
| 年降水量(mm) | prec | + | 343.1 | 672.1 | 5307.6 | 675.1 | -0.1 | 0.1 | 0.04 | 0.53*** |
| 年均气温(℃) | temp | + | 1.5 | 13.6 | 109.5 | 27.3 | -1.7 | 2.5 | 0.71*** | 0.44*** |
| NDVI | NDVI | - | 2734.6 | 8463.8 | 5641.6 | 1176.1 | 0.1 | -0.2 | -0.54*** | 0.57*** |
| 年均风速(m/s) | wind | - | 1.4 | 2.9 | 20.5 | 2.9 | 0.9 | 0.5 | -0.17** | 0.63*** |
| 地形起伏度 | wavi | - | 1.5 | 311.3 | 54.8 | 74.4 | 1.3 | 0.6 | -0.72*** | 0.41*** |
| 年均相对湿度(%) | RH | - | 47.3 | 67.1 | 58.2 | 3.7 | -0.8 | 0.4 | 0.55*** | 0.55*** |
新窗口打开
显示原图|下载原图ZIP|生成PPT图1自然和人文解释变量的空间分布示意图
-->Fig. 1The spatial distribution diagram of natural and human factors
-->
3 研究方法
3.1 空间自相关分析
根据Tobler地理学第一定律,空间距离越近的事物其属性值之间相关性越大,即空间依赖性越强。经验表明,大气污染在空间上既存在依赖性也存在异质性,为定量测度临近区域大气污染的空间依赖程度,本文选用经典的全局空间自相关指数Moran's I来计算,表达式为[52]：式中：
式中：E（I）表示I的均值;VAR（I）表示I的方差;当Z值为正且显著时,表明存在正的空间自相关,也就是说相似的观测值（高值或低值）趋于空间集聚;当Z值为负且显著时,表明存在负的空间自相关,相似的观测值趋于分散分布;当Z值为0时,观测值呈独立随机分布。
3.2 空间计量模型
空间计量模型可以有效解决线性回归分析无法处理的空间依赖性问题,常用的空间回归模型包括空间滞后模型（SLM）、空间误差模型（SEM）、空间杜宾模型（SDM） 等[53]。当模型的误差项在空间上相关时,即为空间误差模型（SEM）,其表达式如下：式中：Y表示被解释变量,为n×1的向量;X表示解释变量,假设被解释变量共k个,则为（n×k）的矩阵;β表示回归系数,为（k×1）向量;u为随机误差向量;λ为回归残差之间的空间相关性系数;W表示一个（n×n）空间权重矩阵;ε表示随机误差项,通常认为是独立分布的。
当被解释变量间的空间依赖性对模型显得非常关键而导致了空间相关时,即为空间自回归模型,又叫空间滞后模型（Spatial Lag Model, SLM）,公式为：
式中：ρ表示内生交互效应（WY）的系数,其大小反映空间扩散或空间溢出的程度,如果ρ显著,表明被解释变量之间存在一定的空间依赖。
空间杜宾模型（Spatial Durbin Model, SDM）是前两个模型的更一般形式,SLM包含了被解释变量（Y）的内生交互效应,SEM包含了误差项（ε）间的交互效应,而SDM同时包含了内生交互效应（WY）与外生交互效应（WX）[54],公式为：
式中：θ是外生交互效应的系数,当θ = 0时,即为SLM模型,当θ = -ρβ时,即为SEM模型。θ越显著表明解释变量存在的空间交互作用越强,然而仅凭θ不能对是否存在空间溢出效应作出结论。
SLM与SDM均可以估计解释变量的直接效应（direct effects）与间接效应（indirect effects）,但由于SLM具有很大的局限性[55],本文选取SDM进行估计。直接效应是指本地的影响因素对本地雾霾的影响;间接效应,又叫空间溢出效应,可以有两种解释视角,即本地的影响因子对邻近其他区域雾霾的影响或邻近地区的影响因子对本地雾霾的影响。(I-ρW)-1(βk+Wθk)的对角线元素反映直接效应,非对角线元素反映间接效应,这两种效应的显著性检验采用求偏导数矩阵的方法[55]。
本文使用最大似然法（Maximum likelihood, ML）对空间回归模型进行参数估计。空间权重矩阵作为SLM、SEM、SDM运算过程中非常重要的系数矩阵,对结果会产生重要影响,本文首先采用基于距离的K近邻算法（k-nearest neighbors）,取k = 6,来进行模型运算,同时为验证模型结果的稳健性用基于Queen邻接关系和基于欧氏距离倒数的空间权重矩阵做对比验证。不同模型拟合优度的比较采用对数似然比（LR）进行检验。Moran's I的计算通过GS+Version 9完成,空间计量模型使用的原始代码来自Elhorst的空间计量经济Matlab工具箱,地图制作使用ArcGIS 10.3完成。
4 结果分析
4.1 PM2.5浓度分布的时间演变与空间自相关分析
京津冀城市群的大气污染问题由来已久,进入21世纪后呈现爆发式增长。由图2可以清楚地看到,从2000-2014年PM2.5浓度整体呈现越来越高的态势。2000年只有城市建成区范围的零星区域年均浓度超过75 μg/m3,然而到2014年,大约1/3区域的PM2.5浓度超过75 μg/m3。《大气污染防治行动计划》要求,京津冀地区到2017年PM2.5年均浓度要比2013年下降25%,若按照这个治理进度,京津冀地区估计将在2030年左右才能达到35 μg/m3的国家标准[56]。然而就近3年的情况来看,实现该目标显得非常艰巨[57,58]。从空间维度来看,京津冀PM2.5浓度的空间格局整体上呈现东南高、西北低的态势,且近15年没有太大变化。分区域来看,河北的承德市、张家口市以及秦皇岛北部、北京西北部山区等地区PM2.5的浓度相对较低。另外,各个城市建成区的PM2.5浓度相比于周围郊区和农村地区平均高10~20 μg/m3,可见中心城区人类活动对大气污染具有更显著影响。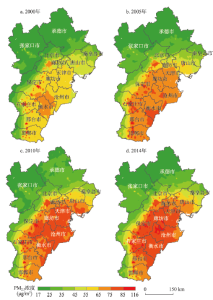
显示原图|下载原图ZIP|生成PPT图2京津冀城市群PM2.5浓度的时空演变
-->Fig. 2Spatial-temporal evolution of PM2.5 concentration in Beijing-Tianjin-Hebei (Jing-Jin-Ji) urban agglomeration
-->
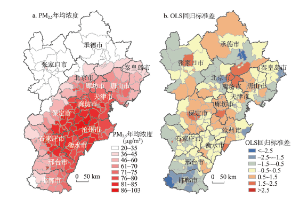
为更清楚的分析京津冀每个区县的大气污染状况,将2014年PM2.5年均浓度的栅格数据按区县行政区划转化为矢量数据,结果如图3a所示。在202个区县中,年均浓度最低的区域为20 μg/m3,年均浓度最高的区域为103 μg/m3;其中空气质量达标的区县（PM2.5<35 μg/m3,图3a中白色区域）只有28个,占总数的13.9%（根据2012年中国发布的《环境空气质量指数（AQI）技术规定》,PM2.5年均浓度不超过35 μg/m3,空气质量达标）;有92个区县PM2.5浓度大于75 μg/m3,空气质量为污染等级。若按照世界卫生组织（WHO）的标准,PM2.5年均浓度应小于10 μg/m3才能对人体健康不产生危害,则没有一个区县达标。另外,图4是依据空气质量检测站点实测数据整理的京津冀地区13个城市PM2.5浓度的月度变化曲线,可以看到邢台、保定、石家庄整体处于曲线簇上方,污染相对更严重,张家口、承德、秦皇岛基本一直处于曲线簇的下方,污染相对较轻。整个曲线簇呈明显的“U”型,即大气污染在一年的前三个和后三个月份要比中间的月份严重。换句话说,京津冀城市群的大气污染秋冬季要比春夏季更为严重。
显示原图|下载原图ZIP|生成PPT图3京津冀城市群2014年PM2.5浓度分布与OLS回归标准差
-->Fig. 3PM2.5 concentration distribution in Jing-Jin-Ji urban agglomeration in 2014 and standard deviation of OLS estimation
-->
显示原图|下载原图ZIP|生成PPT图4京津冀城市群13个城市PM2.5浓度的月度变化
-->Fig. 4The PM2.5 concentration monthly change of 13 cities in Jing-Jin-Ji urban agglomeration
-->
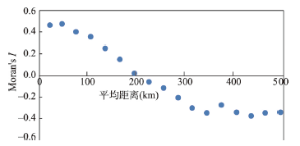
基于欧氏距离倒数（Inverse distance）的空间权重矩阵,计算区县尺度2014年PM2.5年均浓度的Moran's I值为0.477,且Z值为17.22（>2.58）,即PM2.5浓度存在显著的正向空间自相关性,说明京津冀城市群地区大气污染的空间分布并非随机状态,而是呈现显著的空间集聚性。进一步,图5展示了基于欧氏距离的PM2.5各向同性空间自相关分析,X轴代表城市群内部两两城市间的平均距离,Y轴代表每个城市对的平均Moran's I值。可以清晰的看到,两城市间的平均距离在200 km以内时,大气污染有显著的正向交互影响,并且这种影响随着距离的缩短而增强。
显示原图|下载原图ZIP|生成PPT图5基于距离的PM2.5各向同性Moran's I 值
-->Fig. 5Distance correlation of PM2.5 by calculating Moran's I
-->
4.2 回归结果比较与影响因素解析
为了对解释变量进行初步预判并与空间计量模型进行比较,本文首先使用普通最小二乘法（OLS）进行模型估计。以2014年PM2.5年均浓度为被解释变量,以各个自然和人文因素为解释变量做回归分析。为使数据更符合正态分布并消除模型异方差性,在回归分析前对方程的两边同时做对数处理。结果如表2所示,OLS1、OLS2是分别仅对人文要素和自然要素做回归,OLS3是综合所有要素的回归,单纯从拟合效果来看,通过对比对数似然值（Log likelihood）、调整后的拟合优度（Adjusted R2）,发现模型OLS3的估计效果最好,单纯用社会经济变量和单纯用自然环境变量做回归,拟合优度分别为0.564和0.895,而综合人文与自然因素后的回归拟合优度达到0.929,再次验证了大气污染是由自然与人文双重因素导致。然而,一方面被解释变量PM2.5存在显著的空间自相关性;另一方面对模型OLS3的回归标准差进行空间自相关分析（图3b）,其Global Moran's I为0.231,Z值为11.23（>2.58）,在0.01水平上也非常显著。因此,本研究若用普通OLS方法对非独立性样本数据进行估计,不符合线性回归模型的基本假设,结果会产生严重的偏误。Tab. 2
表2
表2OLS、SLM、SEM与SDM的估计结果比较
Tab. 2Estimation results of OLS, SLM, SEM and SDM
| 变量 | OLS1 | OLS2 | OLS3 | SLM | SEM | SDM |
|---|---|---|---|---|---|---|
| CONSTANT | 1.612*** | 3.893*** | 3.468*** | 2.477*** | 0.069*** | 2.413*** |
| lnGDPPC | -0.129*** | -0.009 | -0.006 | -0.004 | 0.001 | |
| lnpeople | 0.278*** | 0.026** | 0.035*** | 0.064*** | 0.074*** | |
| lnenergy | 0.313*** | 0.036* | 0.045** | 0.047** | 0.058*** | |
| lnsecond | 0.259*** | 0.064*** | 0.051*** | 0.049** | 0.036** | |
| lnprec | 0.189** | 0.198** | 0.123* | 0.122 | 0.016 | |
| lntemp | 0.533*** | 0.479*** | 0.187*** | 0.337*** | 0.232*** | |
| lnNDVI | -0.325*** | -0.31*** | -0.161*** | -0.072* | -0.151** | |
| lnwind | -0.262*** | -0.245*** | -0.233*** | -0.219** | -0.321*** | |
| lnwavi | -0.096*** | -0.098*** | -0.071*** | -0.081*** | -0.048*** | |
| lnRH | -0.002 | -0.004 | -0.129 | 0.548* | -0.212 | |
| W×lnPM2.5 | 0.511*** | 0.569*** | ||||
| W×μ | 0.776*** | |||||
| W×lnGDPPC | 0.013 | |||||
| W×lnpeople | -0.068*** | |||||
| W×lnenergy | 0.033** | |||||
| W×lnsecond | -0.008 | |||||
| W×lnprec | 0.092 | |||||
| W×lntemp | -0.109 | |||||
| W×lnNDVI | -0.161** | |||||
| W×lnwind | 0.209 | |||||
| W×lnwavi | -0.032** | |||||
| W×lnRH | 0.109 | |||||
| R2 | 0.564 | 0.895 | 0.929 | 0.963 | 0.961 | 0.9713 |
| Adjusted R2 | 0.555 | 0.822 | 0.926 | 0.961 | 0.958 | 0.968 |
| Loglikelihood | 57.620 | 146.250 | 188.311 | 225.653 | 222.181 | 255.733 |
新窗口打开
基于上述分析,本文更适合采用空间回归模型。然而仅对比LM(lag)和LM(error),以及Robust LM(lag)和Robust LM(error),4个参数均在0.01水平上显著,很难判断究竟空间滞后模型（SLM）、空间误差模型（SEM）和空间杜宾模型（SDM）选择哪一个更合适。另外,通过表1中的Moran's I计算和检验,表明解释变量均存在显著的空间自相关性,模型选择应考虑解释变量之间的外生交互效应。因此,谨慎起见本研究运用最大似然估计（Maximum likelihood estimation, ML）对三种模型均代入数据进行了计算。
对表2中三类空间回归模型估计结果进行分析。首先,通过对比Log likelihood、Adjusted R2,可以明显发现三个模型中,SDM模型的拟合效果最好,SLM模型略好于SEM模型。W×lnPM2.5在1%水平下显著,SLM和SDM中的估计值分别达到0.511和0.569,说明被解释变量PM2.5存在很强的空间上的内生交互效应,在控制住其他解释变量的前提下,邻近地区的PM2.5每升高1%,将导致本地PM2.5至少升高0.5%,区域间大气污染的扩散与传输导致本地的PM2.5受邻近区域影响显著。SEM模型结果显示W×μ在1%水平下显著,即回归模型误差项之间也存在空间上的交互效应,说明可能存在遗漏的解释变量并且这些变量也存在空间上的交互作用。对每个解释变量的显著性进行分析：人口密度、能源消费、第二产业比重、年均气温对PM2.5浓度均存在正向的显著影响;植被覆盖指数、风速、地形起伏度对PM2.5浓度均存在负向的显著影响;降水和相对湿度仅在一个模型中在10%水平下有显著性;人均GDP在三个模型中均不显著。另外,进一步用基于Queen邻接关系和基于欧氏距离倒数的空间权重矩阵对SLM、SEM、SDM三个模型进行了计算,结果表明各解释变量显著性及显著程度没有明显变化,说明本文构建的模型具有良好的稳健性。
4.3 直接效应与空间溢出效应分析
表2中同时给出了表征外生交互效应（WX）的系数估计,可以看到W×lnpeople,W×lnenergy,W×lnNDVI和W×lnwavi都表现出很高的显著性。因此,为了深入剖析这种空间上的交互影响,本文进一步给出SDM模型的直接效应与间接效应的结果（表3）。根据自然和人文解释变量的显著性和弹性系数,可以大致比较不同解释变量的贡献程度。其中,对本地大气污染的直接效应贡献强度排序是：年均风速#>年均气温>人口密度>地形起伏度#>二产占比>能源消费>植被覆盖度#（“#”代表负向效应）,而人均GDP、年降水量和相对湿度对PM2.5没有显著的直接效应的影响。可见,城市本地的风速、气温、地形、植被覆盖等自然要素对本地的大气污染有着直接的显著影响,城市自身的人口密度、能源消费与第二产业占比的增加会直接加重当地大气污染。表3中解释变量的空间溢出效应影响排序大致是：植被覆盖度#>地形起伏度#>能源消费>人口密度#（“#”代表负向效应）。这表明,邻近的其他区县的植被覆盖度与地形起伏度对本地的大气污染有负向消减作用,邻近区县的能源消费会加重本地的大气污染。有意思的是邻近地区的人口集聚度高了反而对本地的大气污染有负向作用,可能的原因是京津冀地区人口一直在往大城市集聚,进而降低了周围小城市的环境承载压力。此外,人均GDP、第二产业占比、年降水量、年均气温、年均风速以及相对湿度对PM2.5均不存在显著的空间溢出效应。Tab. 3
表3
表3SDM的直接效应与间接效应估计
Tab. 3The direct effect and indirect effect of SDM
| 解释变量 | 直接效应 | t-统计量 | 间接效应 | t-统计量 |
|---|---|---|---|---|
| lnGDPPC | 0.003 | 0.256 | 0.031 | 0.665 |
| lnpeople | 0.071*** | 7.194 | -0.055* | -1.650 |
| lnenergy | 0.022** | 1.698 | 0.079** | 2.304 |
| lnsecond | 0.039** | 2.433 | 0.030 | 0.455 |
| lnprec | 0.036 | 0.263 | 0.212 | 0.767 |
| lntemp | 0.234*** | 5.346 | 0.050 | 0.429 |
| lnNDVI | -0.081* | -1.668 | -0.416*** | -3.196 |
| lnwind | -0.319*** | -3.266 | 0.055 | 0.301 |
| lnwavi | -0.058*** | -6.242 | -0.129*** | -5.738 |
| lnRH | -0.211 | -0.567 | -0.033 | -0.056 |
新窗口打开
5 结论与讨论
5.1 主要结论
本文通过分析京津冀大气污染的时空特征,系统甄别可能对大气污染产生影响的自然与社会经济因素,运用三种空间计量模型,创新性的定量解析了不同的自然与人文因素对京津冀城市群区县尺度PM2.5的贡献程度以及空间溢出效应,主要结论包括：（1）2000-2014年京津冀城市群PM2.5浓度整体呈上升趋势,空间上呈现东南高、西北低的态势。2014年空气质量达标的区县仅占总数的13.9%,大气污染月度曲线呈明显的“U”型,季节上呈秋冬高、春夏低的特点。城市建成区PM2.5浓度相比于周围郊区和农村平均高10~20 μg/m3。
（2）PM2.5浓度在区县尺度上存在显著的空间自相关性和空间异质性,表明大气污染在城市群尺度的区域性和集聚性特征明显,两个城市间大气污染的正向交互影响范围平均可达到200 km,区域间大气污染的扩散与传输导致本地的PM2.5受邻近区域影响显著,邻近地区的PM2.5每升高1%,将导致本地PM2.5至少升高0.5%。
（3）空间回归模型尤其是空间杜宾模型对于本研究的拟和效果最好,模型中同时存在内生和外生交互作用。社会经济内因对PM2.5浓度主要是正向影响,自然外因中除了年均气温外,对PM2.5浓度主要是负向影响。各种因素不仅对本地大气污染有直接效应,很多因素对邻近地区亦存在空间溢出效应。
（4）影响因素中对本地大气污染的直接效应贡献强度依次是：年均风速>年均气温>人口密度>地形起伏度>第二产业占比>能源消费>植被覆盖度,人均GDP、年降水量和年均相对湿度对PM2.5没有显著的直接效应的影响;对邻近地区大气污染具有空间溢出效应的影响因素排序是：植被覆盖度>地形起伏度>能源消费>人口密度,而人均GDP、第二产业占比、年降水量、年均气温、风速以及年均相对湿度对PM2.5均不存在显著的空间溢出效应。
5.2 讨论
（1）大气污染由自然外因与人为内因共同作用,京津冀本地污染物排放强度大是雾霾天气高发的根本内因,风速、风向、气温、植被、山脉阻隔等自然条件是京津冀雾霾集聚与扩散的外在因素。然而究竟是哪一方面占主导,由于在不同区域大气污染的主导因素相差很大,很难给出一个绝对的答案。透过本文的定量分析,虽然数值上看自然因素的显著性略大,然而自然因素的很多弹性系数是“缺乏弹性”的,比如地形起伏度、植被覆盖度、年均气温等很难有大的变动,因此虽然人文因素的弹性系数小,但变量的实际弹性更好。换句话说,面对显著的自然影响因素我们不能仅仅“等风来”,更多的是找到针对性的适应策略,例如产业与居住区位优化、城市风道设计、绿带合理布局等;对于人文因素则可以制定有效的调控策略,包括能源和产业结构调整、道路网优化和新车标准升级、超载人口与污染产业疏解、排污监管力度加强等。（2）本文结果显示人均GDP、年降水量和相对湿度对PM2.5没有显著的直接效应的影响,这与部分****的研究结论有所不同。对于经济发展与大气污染的关系,相关研究表明两者符合环境库兹涅兹曲线呈“倒U”型,但也有的呈“U”“N”“倒N”等演变形 态[59,60,61],而京津冀地区这种关系有待进一步检验;降水和相对湿度在“日”尺度上对PM2.5有一定影响[62,63],而在本文时间尺度为“年”的时候,这两个变量的影响显著性不高。在不同时间尺度（日、月、年）和不同空间尺度（街区、城市、区域）下,大气湿度、降水、风速、地形等因素对于大气污染的影响机理会有所不同[64,65,66],在分析大气污染驱动因素以及治理策略时也要充分考虑时空的尺度效应。
（3）大气污染存在明显的跨区域传播特性,即污染物本身具有空间溢出效应[67]。本文的贡献在于发现,植被覆盖、地形、能源消费以及人口集聚状态对大气污染的影响也有显著的空间溢出效应。此外,相关研究表明来自区域外的跨城市群输送对京津冀PM2.5浓度贡献也达到了20%~35%[39, 68]。因此,在制定大气污染防治措施时要重视城市群内部以及城市群与周边区域的交互影响,加强区域间的联防联控与合作治理,建立区域间生态补偿机制,创新排污监管与问责模式,在城市群规划中注重环保规划与环境立法[43, 69-70]。
（4）2015年环保部牵头完成了京津冀重点城市的大气颗粒物源解析工作,其中北京的首要污染来源是机动车,石家庄是燃煤,天津是扬尘[71]。该项工作可以追溯到污染颗粒物的源头,有利于提出针对性防控政策;然而,存在化学成分解析不完全,排放源不确定和“丢失”等缺点[72],且没有考虑气象、植被、气候、地形等关键自然要素对空气质量的影响。本文可以作为政府环保部门污染物源解析工作的有益补充,通过“自上而下”的方法论途径,细化到区县尺度对空气质量的自然和人文影响因素进行较全面甄别和量化,进而明确大气污染防治重点领域,为地方政府提供决策参考。
The authors have declared that no competing interests exist.
