0 引言
【研究意义】叶面积指数（leaf area index,LAI）可综合表述为单位土地面积上作物叶片的叶面积总和[1,2],是地表植被生态系统中重要的理化参数之一,不仅与作物蒸腾作用、光合作用、呼吸作用、地表净初级生产力等密切相关,且常被用作评价作物长势、指导田间管理及预测产量的重要依据[3,4,5]。因此,及时、准确监测作物LAI具有重要的研究意义。【前人研究进展】近年来,遥感技术的快速发展使快速、无损地获取大面积作物LAI成为可能,对于其模型方法国内外已有大量探索。宋开山等[6]基于植被指数建立大豆LAI估算模型时,发现归一化差值植被指数（normalized difference vegetation index,NDVI）在LAI大于3.5时,出现了饱和现象。GITELSON等[7]则通过对植被指数NDVI进行改进,提出了宽动态植被指数（wide dynamic range vegetation index,WDRVI）,可以解决饱和性问题。李鑫川等[8]提出分段选择敏感植被指数OSAVI（LAI≤3）+TGDVI（LAI>3）,在解决饱和性问题的同时能够提高LAI预测精度。LIANG等[9]认为优化土壤调节植被指数（OSAVI）能够降低土壤背景影响,进而提高LAI估算精度。LIU等[10]指出利用增强型植被指数（EVI）反演LAI具有较高的估算精度。随着作物LAI遥感反演研究的深入,一些研究者尝试利用机器学习算法提高LAI估算精度。如利用神经网络法、支持向量机法可提高冬小麦LAI反演精度[11,12,13]。【本研究切入点】尽管这些机器学习算法能够提高反演精度,但是在反演时需要大量的训练样本,且极易出现过拟合问题。随机森林算法是一种基于统计学的机器学习算法,能高效处理大数据集,具有极强的拟合能力且不会产生过拟合现象,具有很好的抗噪性能[14],适合解决作物LAI的反演问题。但是,大多研究者利用随机森林算法进行作物参数反演时,直接将各种植被指数作为输入因子,缺乏对输入因子的预先优选[14,15]。鉴于不同植被指数在抗饱和能力、降低或消除土壤背景影响等方面各有特点,有必要对RF模型的输入因子进行优选,以提高RF模型的估算精度。【拟解决的关键问题】本研究基于冬小麦4个关键生育期（拔节期、挑旗期、开花期及灌浆期）的地面高光谱和LAI实测数据,将相关系数分析（correlation coefficient,r）和袋外数据（out-of-bag data,OOB）重要性分析与随机森林算法（random forest,RF）相结合,构建了|r|-RF和OOB-RF两种LAI估算模型,并进行了验证和对比分析,然后将所建LAI反演模型用于低空无人机获取的高光谱影像,进一步检验所建模型的适用性和可靠性。1 材料与方法
1.1 试验设计
本研究于北京市昌平区小汤山国家精准农业示范基地（116.44°E,40.18°N）开展冬小麦试验,2014年10月上旬播种,2015年6月下旬收获。研究区属北温带半湿润大陆性季风气候,平均海拔约为36 m,年平均气温13.3—14.1℃。通过考虑作物品种、施氮水平、水分供给水平等因素,共设置16种不同处理,其中,作物品种为中麦175、京9843;氮素处理为N1：0,N2：91.065 kg N·hm-2,N3：182.13 kg N·hm-2,N4：273.195 kg N·hm-2;水分处理为雨养、正常水和两倍正常水。每种处理重复3次,共48个小区,每个小区的种植面积为48 m2。其他田间管理按照当地正常水平进行。1.2 数据获取
本研究于2015年冬小麦拔节期（4月13日）、挑旗期（4月26日）、开花期（5月14日）及灌浆期（5月25日）4个关键生育期分别采集了作物冠层高光谱反射率数据和LAI数据。其中,地面观测的非成像高光谱数据和LAI数据用于冬小麦LAI估算模型的建立与验证,其中总样本量70%用于建模（n=128）,剩余30%用于验证（n=64）;无人机遥感获取的成像高光谱数据用于进一步分析检验所建模型对于无人机低空遥感平台的适用性和可靠性。1.2.1 冬小麦LAI测定 在每个试验小区选取具有代表性的20个冬小麦植株作为样本,立刻装入密封袋带回基地实验室,将样本茎叶分离后,利用美国生产的CI-203型激光叶面积仪测定样本叶片叶面积,然后结合田间群体密度调查数据得到冬小麦冠层叶面积指数。4个生育期共获取192个冬小麦叶面积指数样本数据（表1）。
Table 1
表1
表1研究区样本叶面积指数描述统计
Table 1Descriptive statistics of sample leaf area index in study area
| 生育期 Period | 采样小区个数 Sample area | 最小值 Min. | 最大值 Max. | 平均值 Mean | 标准差 Standard deviation |
|---|---|---|---|---|---|
| 拔节期 Jointing | 48 | 1.698 | 5.871 | 3.623 | 0.137 |
| 挑旗期 Flag | 48 | 1.298 | 6.807 | 4.108 | 0.208 |
| 开花期 Flowering | 48 | 1.241 | 5.886 | 3.295 | 0.173 |
| 灌浆期 Grain filling | 48 | 0.352 | 3.815 | 1.586 | 0.128 |
新窗口打开
1.2.2 冬小麦冠层高光谱数据获取 冬小麦地面非成像冠层反射光谱采用美国ASD Field SpecFR Pro 2500光谱辐射仪测定,光谱范围350—2 500 nm,采样间隔为1 nm。测量时天气晴朗,北京时间为10：00—14：00。观测时探头始终垂直向下且距离地面约1.0 m,探头视场角25°。在每个试验小区选定的具有代表性的冬小麦样方采集10条记录,取平均值作为该小区的冠层光谱反射率,每次测量前后均立刻进行标准白板校正。
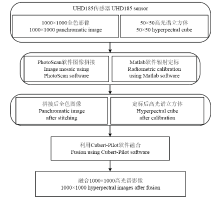
于2015年4月28日（挑旗期）开展了无人机成像高光谱数据观测。飞行平台为RICOPTE（Riegl,Hom,Austria）八旋翼无人机,搭载德国公司生产的UHD185成像光谱仪获取高光谱影像。UHD185成像光谱仪的光谱范围为450—950 nm,光谱采样间隔4 nm,光谱分辨率8 nm,包含125个通道,具有可见-近红外波段全画幅高光谱成像的优点。50 m航高下,焦距17 mm的UHD185可同时获取50×50像素的高光谱影像和1 000×1 000像素的全色影像,即21 cm空间分辨率的高光谱像元和1 cm空间分辨率的灰度像元。无人机高光谱影像处理过程如图1。
显示原图|下载原图ZIP|生成PPT图1无人机高光谱影像处理过程
-->Fig. 1Processing of high spectral image by UHD185 sensor mounted on UAV platform
-->
1.3 光谱指数
光谱指数是由不同波段的反射率以一定代数形式组合而成的一种参数[9],它可削弱环境背景对冠层光谱的干扰,比单波段具有更好的灵敏性。基于重采样的地面非成像光谱数据,根据前人研究结果,选取文献中常用的14个LAI光谱估算指数进行分析（表2）。Table 2
表2
表2本文采用的光谱指数
Table 2Spectral index in this study
| 光谱指数（原始出处文献） Spectral index（Original provenance） | 计算公式 Formula | 用于估算LAI参考文献 References using to estimate LAI |
|---|---|---|
| 归一化植被指数（PENUELAS等[16]） Normalized difference vegetation index NDVI | $\frac{\mathop{R}_{800}-\mathop{R}_{680}}{\mathop{R}_{800}+\mathop{R}_{680}}$ | TANAKA等[28] |
| 比值植被指数（HATFIELD等[17]） Ratio vegetation index RVI | $\frac{\mathop{R}_{800}}{\mathop{R}_{680}}$ | 任哲等[29] |
| 差值植被指数（SHIBAYAMA等[18]） Difference vegetation index DVI | $\mathop{R}_{800}-\mathop{R}_{680}$ | 夏天等[11] |
| 优化土壤调节植被指（RONDEAUX等[19]） Optimized soil adjusted vegetation index OSAVI | $\frac{\left( 1+0.16 \right)\times \left( \mathop{R}_{800}-\mathop{R}_{670} \right)}{\mathop{R}_{800}+\mathop{R}_{670}+0.16}$ | LIANG等[9] |
| 归一化绿度植被指数（BARET等[20]） Green normalized difference vegetation index GNDVI | $\frac{\mathop{R}_{750}-\mathop{R}_{550}}{\mathop{R}_{750}+\mathop{R}_{550}}$ | LELONG等[30] |
| 绿波段指数（GITELSON等[21]） Green ratio vegetation index GRVI | $\frac{\mathop{R}_{800}}{\mathop{R}_{550}}-1$ | 夏天等[11] |
| 改进土壤调整指数（QI等[22]） Modified soil-adjusted vegetation index MSAVI | $\frac{1}{2}\times [2\times \mathop{R}_{800}+1-\sqrt{\mathop{\left( 2\times \mathop{R}_{800}+1 \right)}^{2}-8\times \left( \mathop{R}_{800}-\mathop{R}_{670} \right)}]$ | TANAKA等[28] |
| 红边归一化指数（GITELSON等[23]） Red edge normalized index NDVI705 | $\frac{\mathop{R}_{550}-\mathop{R}_{705}}{\mathop{R}_{550}+\mathop{R}_{705}}$ | 贺佳等[1] |
| 调节型叶绿素吸收比率指（HABOUDANE等[24]） Modified chlorophyll absorption ratio index 2 MCARI2 | $\frac{1.5\times [2.5\times \left( \mathop{R}_{800}-\mathop{R}_{670} \right)-1.3\times \left( \mathop{R}_{800}-\mathop{R}_{550} \right)]}{\sqrt{\mathop{\left( 2\times \mathop{R}_{800}+1 \right)}^{2}-\left( 6\times \mathop{R}_{800}-5\times \sqrt{\mathop{R}_{670}} \right)-0.5}}$ | POTITHE等[31] |
| 调节型三角植被指数（BROGE等[25]） Modified triangular vegetation index MTVII | $1.2\times [1.2\times \left( \mathop{R}_{800}\text{-}\mathop{R}_{550} \right)2.5\times \left( \mathop{R}_{670}\text{-}\mathop{R}_{550} \right)]$ | POTITHE等[31] |
| 增强型植被指数（HUETE等[26]） Enhanced vegetation index EVI | $2.5\times \frac{\mathop{R}_{860}-\mathop{R}_{645}}{1+\mathop{R}_{860}+6\times \mathop{R}_{645}-7.5\times \mathop{R}_{470}}$ | LIU等[10] |
| 宽动态指数（GITELSON等[7]） Wide dynamic range vegetation index WDRVI | $\frac{a\times \mathop{R}_{800}-\mathop{R}_{670}}{a\times \mathop{R}_{800}+\mathop{R}_{670}}$ | TANAKA等[28] |
| 归一化差异光谱指（LI等[27]） Normalized difference spectral index NDSI(i, j) | $\frac{\mathop{R}_{i}-\mathop{R}_{j}}{\mathop{R}_{i}+\mathop{R}_{j}}$ | INOUE等[32] |
| 比值型光谱指数（LI等[27]） Ratio spectral index RSI(i, j) | $\frac{\mathop{R}_{\text{i}}}{\mathop{R}_{j}}$ | INOUE等[32] |
新窗口打开
1.4 数据分析方法
1.4.1 相关系数分析 相关系数是描述两个具备相关性的数据之间密切程度的指标。本研究中,r可以衡量光谱指数与冬小麦LAI之间的相关密切程度,r绝对值越接近于1,光谱指数与LAI之间的关系越密切,反之亦然。1.4.2 袋外数据集重要性分析 随机森林算法RF是由BREIMAN[33]于2001年提出,是一个树型分类器的集合。它通过利用Bootstrap方法,从原始样本集S中进行k次有放回的简单随机抽样,形成训练样本集。在使用Bootstrap对S进行抽样时,每个样本未被抽取的概率p为(1-1/n)n。当n足够大时,p=0.368,表明原始样本集S中大约37%的样本不会出现在训练样本集中,这些未被抽中的样本称为袋外数据（out of bag,OOB）。利用这部分样本进行模型性能的估计称为OOB估计,其原理是随输入因子的改变会产生估算误差,RF算法可以给出每个变量的OOB变量的误差,根据估算误差计算此输入因子的重要性,重要性值越大,表明光谱指数对LAI估算越重要。
1.4.3 建模方法 对表2中的14个光谱指数利用随机森林算法进行LAI回归分析,将14个光谱指数按照相关性、OOB重要性从大到小进行排序;其次,根据相关性和OOB重要性分析结果,第一次仅用排序第一的光谱指数建模,第二次用排序位于前两个的光谱指数建模,第n次用排序位于前n个的光谱指数建模(1≤n≤14);然后,依据调整后的决定系数确定冬小麦LAI估算模型的最佳自变量个数,进而构建两种冬小麦LAI估算模型|r|-RF和OOB-RF。本研究基于MATLAB程序代码进行随机森林回归拟合,其中决策树的数量和分割节点的个数是非常重要的2个参数,本文构建了500棵决策树,分割变量为3。随后,利用地面独立数据集对两种模型进行验证;最后,将所建LAI反演模型应用于低空无人机获取的高光谱影像,开展冬小麦LAI遥感反演和效用检验。
1.5 精度验证
1.5.1 决定系数 决定系数（coefficient of determination,R2）被用来表示模拟值与实测值的拟合效果,R2越接近于1,表明模型拟合精度越高,其计算公式为：${{R}^{2}}=1\text{-}\frac{RSS}{TSS}$ （1）
式中,总离差平方和TSS=$\Sigma _{i=1}^{n}{{({{y}_{i}}-\bar{y})}^{2}}$,残差平方和RSS=$\Sigma _{i=1}^{n}{{({{y}_{i}}-{{\hat{y}}_{i}})}^{2}}$,yi表示测量值,$\bar{y}$表示测量值的平均值,${{\hat{y}}_{i}}$表示预测值,n表示样本个数。
1.5.2 调整R2 在多元回归中,若模型增加一个自变量,即使这个自变量在统计上不显著,R2也会变大。这是因为增加自变量时,会使残差平方和减少,从而使R2变大。因此,在多元回归中,为避免增加自变量而高估R2,通常用调整R2(Adj.R2)来评价拟合效果,因为调整R2同时考虑了样本量（n）和回归中自变量的个数（k）的影响,使得调整R2的值不会由于回归中自变量个数的增加而越来越接近于1。其计算公式为：
$Adj.{{R}^{2}}=1\text{-}\frac{{RSS}/{\left( n\text{-}k\text{-}1 \right)}\;}{{TSS}/{\left( n\text{-}1 \right)}\;}$ （2）
式中,k为自变量的个数。
1.5.3 均方根误差 均方根误差（root mean square error,RMSE）反映了模拟值与实测值的偏离程度,其值越小,表示估算模型的拟合精度越高。其计算公式为：
$RMSE=\sqrt{\frac{\sum\nolimits_{i=1}^{n}{\left( {{y}_{i}}-{{{\hat{y}}}_{i}} \right)}}{n}}$ （3）
2 结果
2.1 ASD和UHD 185数据的光谱响应分析
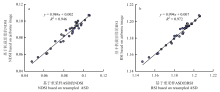
为了将基于地面ASD构建的优选模型应用于无人机高光谱影像上,本研究对ASD光谱数据和无人机搭载的UHD 185数据进行了光谱响应差异分析。对地面ASD光谱数据进行重采样,对UHD185光谱数据进行标准白板定标,使二者的采样间隔和光谱分辨率保持一致。由图2可以看出,两者呈现高度正相关,R2均在0.99以上;由图3可知,基于两种光谱计算的两种植被指数的相关性R2均在0.94以上。综合上述分析,定标后的UHD185和重采样的ASD在462—830 nm范围的光谱反射率比较一致,偏差小于1%。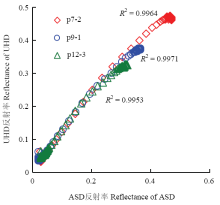
显示原图|下载原图ZIP|生成PPT图2随机3个小区的ASD与UHD185在462—830 nm范围内的光谱反射率相关性分析
-->Fig. 2Spectral response analysis of ASD and UHD 185 data in the range of 462-830 nm about any three plots
-->
显示原图|下载原图ZIP|生成PPT图3基于ASD与UHD185计算的NDSI和RSI的相关性
-->Fig. 3Correlation between NDSI and RSI based on ASD and UHD 185
-->
2.2 光谱指数与冬小麦LAI相关性分析
利用不同试验处理下冬小麦拔节期、挑旗期、开花期和灌浆期等多个生育期的光谱指数与LAI数据进行相关性分析,样本量n=128（表3）。结果表明,本文分析选用的文献中用于估算LAI的光谱指数均与LAI具有较强的相关性,|r|均在0.65以上,并且均达到极显著水平（P<0.01）,其中RVI与LAI的相关系数最高,r=0.886,相关性最小的是MTVII,相关性为0.666。同时,本文分析了450—950 nm波段范围内任意两个波段组合得到的归一化差值光谱指数NDSI和比值型光谱指数RSI与LAI的相关性（图4）。结果表明,494 nm与718 nm组合的NDSI（R494,R718）、490 nm与610 nm组合的RSI（R490,R610）与LAI的相关性比较强,相关系数r分别为0.854,0.893。
显示原图|下载原图ZIP|生成PPT图4LAI与光谱指数的决定系数 a：LAI与NDSI（Ri,Rj）的决定系数;b：LAI与RSI（Ri,Rj）的决定系数
-->Fig. 4Coefficient of determination between LAI and spectral index a: Coefficient of determination between LAI and NDSI (Ri, Rj); b: Coefficient of determination between LAI and RSI (Ri, Rj)
-->
Table 3
表3
表3光谱指数与冬小麦LAI相关性分析及排序（n=128）
Table 3Correlation analysis and ordination between spectral index and winter wheat LAI (n=128)
| 序号 Number | 光谱指数 Spectral index | 相关系数绝对值|r| Absolute value of correlation coefficient | r| | 序号 Number | 光谱指数 Spectral index | 相关系数绝对值|r| Absolute value of correlation coefficient | r| | |
|---|---|---|---|---|---|---|
| 1 | RSI(R490,R610) | 0.893** | 8 | MCARI2 | 0.781** | |
| 2 | RVI | 0.886** | 9 | NDVI | 0.772** | |
| 3 | NDSI(R494,R718) | 0.854** | 10 | OSAVI | 0.767** | |
| 4 | GRVI | 0.848** | 11 | MSAVI | 0.756** | |
| 5 | WDRVI | 0.827** | 12 | EVI | 0.755** | |
| 6 | NDVI705 | 0.820** | 13 | DVI | 0.690** | |
| 7 | GNDVI | 0.813** | 14 | MTVII | 0.666** |
新窗口打开
2.3 光谱指数与冬小麦LAI的OOB重要性分析
本文利用冬小麦拔节期、挑旗期、开花期和灌浆期数据,对光谱指数和LAI进行OOB重要性分析,重要性越大说明光谱指数在RF建模中发挥的作用越大。由表4可知,重要性大于10的光谱指数有10个,小于10的光谱指数有4个,其中重要性最大的是NDSI（R494,R718）,其值为58.683,重要性最小的是MTVII,其值为2.993。与表3结果相比,GRVI、RVI和NDVI的排序发生了较大变化,GRVI从第四变成了第九,RVI从第二变成了第五,NDVI从第九变成了第四,这是由于相关系数主要从每个光谱指数与冬小麦LAI之间是否相关以及相关程度大小的角度考虑,而袋外数据重要性分析则侧重输入每个光谱指数自变量对冬小麦LAI因变量所造成的估算误差,根据估算误差计算此光谱指数的重要性。Table 4
表4
表4光谱指数与冬小麦LAI的OOB重要性分析及排序（n=128）
Table 4Importance analysis and ordination between spectral index and winter wheat LAI (n=128)
| 序号 Number | 光谱指数 Spectral index | 重要性 Importance | 序号 Number | 光谱指数 Spectral index | 重要性 Importance | |
|---|---|---|---|---|---|---|
| 1 | NDSI(R494,R718) | 58.683 | 8 | MCARI2 | 18.905 | |
| 2 | RSI(R490,R610) | 53.539 | 9 | GRVI | 17.669 | |
| 3 | WDRVI | 42.305 | 10 | OSAVI | 12.585 | |
| 4 | NDVI | 39.809 | 11 | MSAVI | 8.819 | |
| 5 | RVI | 30.860 | 12 | EVI | 5.130 | |
| 6 | NDVI705 | 27.967 | 13 | DVI | 3.887 | |
| 7 | GNDVI | 19.536 | 14 | MTVII | 2.993 |
新窗口打开
2.4 冬小麦LAI光谱估算模型|r|-RF和OOB-RF的构建
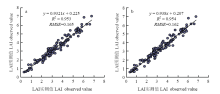
在上述分析的基础上,按照|r|、OOB大小排序依次增加光谱指数的个数作为输入因子进行RF回归建模分析,其调整R2见图5。结果表明,|r|-RF和OOB-RF估算模型的调整R2的总体变化趋势均为先增加后减少。基于|r|-RF建模,输入因子为RSI（R490,R610）、RVI、NDSI（R494,R718）、GRVI、WDRVI 5个光谱指数时,建模的调整R2最高（图5-a）。基于OOB-RF建模,输入因子为RSI（R490,R610）、NDSI（R494,R718）2个光谱指数时,建模的调整R2最高（图5-b）。这表明|r|-RF模型和OOB-RF模型分别以相关性|r|前5强、OOB重要性前2强的光谱指数作为自变量时所建模型效果最佳,其建模结果如图6所示。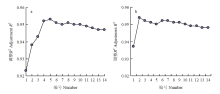
显示原图|下载原图ZIP|生成PPT图5|r|-RF和OOB-RF模型估算结果对比 a：|r|-RF模型 |r|-RF model;b：OOB-RF模型 OOB-RF model
-->Fig. 5Comparison of estimated LAI of winter wheat by RF models
-->
显示原图|下载原图ZIP|生成PPT图6基于RF的LAI预测值与实测值拟合关系 a：|r|-RF模型 |r|-RF model;b：OOB-RF模型 OOB-RF model
-->Fig. 6Relationship between predicted value and measured value based on RF
-->
2.5 冬小麦LAI光谱估算模型|r|-RF、OOB-RF的验证
利用不同试验处理下冬小麦拔节期、挑旗期、开花期和灌浆期等多个生育期的光谱指数与LAI数据（n=64）,分别对所建|r|-RF和OOB-RF估算模型进行验证,结果如图7所示。总体上来看,两种模型的估算精度R2均达到0.8以上,相比较而言,OOB-RF模型的估算精度更高,且OOB-RF模型仅需要两个自变量输入,比|r|-RF模型的输入自变量个数（即5个）要少,更适于应用。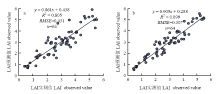
显示原图|下载原图ZIP|生成PPT图7基于 |r|-RF、OOB-RF模型的冬小麦LAI估算值与实测值的拟合关系 a：|r|-RF模型 |r|-RF model;b：OOB-RF模型 OOB-RF model
-->Fig. 7Fitting relationship between LAI estimation value and measured value of winter wheat based on |r|-RF and OOB-RF model
-->
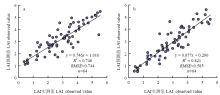
为了对OOB-RF模型进一步评价,本文还采用支持向量机（support vector machine,SVM）与之对比分析,发现|r|-SVM模型以相关性从大到小排序前7的光谱指数作为自变量建模时效果最佳,OOB-SVM模型采用重要性从大到小排序前6的光谱指数作为自变量建模时效果最佳,并且二者的验证精度分别为R2=0.746、RMSE=0.744（图8-a）和R2=0.821、RMSE=0.585（图8-b）。综合上述分析,OOB-RF模型的估算精度更高,且需要的自变量最少。
显示原图|下载原图ZIP|生成PPT图8冬小麦LAI估算模型|r|-SVM、OOB-SVM的检验 a：|r|-SVM模型 |r|-SVM model;b：OOB-SVM模型 OOB-SVM model
-->Fig. 8Validation of estimated LAI of winter wheat by SVM models
-->
2.6 基于OOB-RF模型和无人机高光谱影像的冬小麦LAI反演
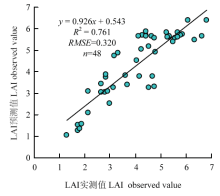
在上述研究的基础上,本文进而利用OOB-RF模型和挑旗期无人机高光谱影像开展了冬小麦LAI遥感监测（图9）。同时利用地面同步采集的实测数据进行了精度检验,每个小区LAI地面实测值与无人机高光谱遥感估算值的拟合关系如图10。无人机遥感监测的冬小麦LAI值（1.02—6.41）与地面实测值（1.29—6.81）比较一致,决定系数R2为0.761,RMSE为0.320,精度较高,表明利用OOB-RF模型可用于低空无人机高光谱遥感影像提取冬小麦LAI信息。
显示原图|下载原图ZIP|生成PPT图9基于无人机影像的冬小麦挑旗期LAI分布图
-->Fig. 9LAI distribution of winter wheat at flag leaf period based on UAV image
-->
显示原图|下载原图ZIP|生成PPT图10基于无人机影像的冬小麦LAI预测值与实测值关系
-->Fig. 10Relationship between estimated and measured of winter wheat LAI based on UAV image
-->
3 讨论
传统的统计分析方法大多基于单一植被指数构建作物LAI估算模型,但单一植被指数所包含的信息易存在饱和现象[6],而选用过多的植被指数则有可能产生过拟合现象[34]。随机森林算法是一种统计学习方法,对数据集的适应能力强,相对其他算法有着很大的优势,它具有很好的抗噪性能和极强的拟合能力但不会产生过拟合现象[33]。但是,大多研究者利用随机森林算法进行作物参数反演时,直接将各种植被指数作为输入因子,缺乏对输入因子进行预先优选[14,15]。鉴于不同植被指数在抗饱和能力、降低或消除土壤背景影响等方面各有特点,因此,将相关系数分析和袋外数据重要性分析与随机森林算法相结合,优选模型输入光谱指数并确定最佳自变量个数显得尤为重要。本文|r|-RF模型以相关性从大到小排序前5强的光谱指数作为自变量建模时效果最佳,OOB-RF模型采用重要性从大到小排序前2强的光谱指数作为自变量建模时效果最佳,并且OOB-RF模型精度高于|r|-RF模型。通过与支持向量机（SVM）对比分析,发现OOB-RF模型的估算精度更高,且需要的自变量较少,这得益于RF算法引入了两个随机性（一个随机性是指每棵树的每个节点是随机产生的,另一个随机性是指每个节点的分割变量是由随机选取的少数变量产生的）,使其具有较强的容噪能力,也不易产生过度拟合现象;而SVR算法的核心问题是确定核函数和相关参数,由于存在核函数和惩罚因子等参数选择的问题,其应用受到了一定限制[12, 35]。本研究构建的LAI估算模型精度高于传统回归模型法[8,9,10]的精度,原因可能在于随机森林算法是基于统计学的机器学习算法,具有容噪能力强、处理大数据集效率高、不易过度拟合、对结果具有可解释性等优点,适合解决LAI反演问题。对于BP神经网络方法而言,该方法较传统回归模型法在进行冬小麦LAI反演时,虽然模型的反演精度有了大幅提高,但还存在一些不足。比如反演时需要大样本训练集（一般认为样本数n>50即为大样本训练集）,且极易出现过度拟合问题;另外,计算量很大,导致其应用能力受限[11, 36]。本文构建的LAI估算模型精度较高,这是由于不同植被指数各有特点,预先进行RF模型输入因子的优选,有助于提高RF模型的估算精度,这与岳继博等[37]的研究结果一致。本文进一步将所构建的OOB-RF模型应用于无人机遥感平台。与地面验证结果（图7-b）相比,无人机平台估算精度（图10）稍有降低,原因可能有以下几个方面。首先,OOB-RF模型是基于地面ASD光谱数据建立的,尽管本文和前人[38,39]研究均表明无人机搭载UHD185与地面ASD所测的光谱反射率比较一致,且已有文献把基于地面ASD构建的模型应用于无人机影像上[40],但二者之间差异还可能会对无人机平台验证精度产生影响;其次,地面ASD观测范围较小（1 m×1 m代表性样方内）,且与LAI采样数据匹配性较强,而无人机遥感监测的LAI值是整个试验小区的均值,鉴于同一小区作物不那么绝对均匀一致,也会影响无人机遥感平台的验证精度;另外,无人机飞行试验(4月28日)与地面测量（4月26日）存在时间差,也会对模型验证精度产生影响。不过,整体来讲,基于无人机遥感平台估算的冬小麦LAI精度较高,这表明本文所构建的OOB-RF模型精度和适用性较强,可基于低空无人机高光谱影像提取高精度的冬小麦LAI信息。
4 结论
本研究基于不同试验处理（品种、氮肥、水分供给等）、不同生育期（拔节期、挑旗期、开花期、灌浆期等）的冬小麦冠层光谱和LAI数据,将随机森林算法与相关性分析、袋外数据重要性分析相结合,构建了冬小麦LAI遥感估算模型。结果表明,|r|-RF、OOB-RF模型分别采用按照相关性和重要性优选的5个和2个光谱指数作为自变量时模型效果最佳。利用独立数据集对两种LAI估算模型进行了验证,|r|-RF、OOB-RF模型验证决定系数（R2）分别为0.805、0.899,均方根误差（RMSE）分别为0.431、0.307,表明OOB-RF模型的估算精度更高一些;与文献已有模型方法相比,亦具有较好的精度。在此基础上,本文进而基于无人机高光谱影像数据,利用OOB-RF模型提取了试验区冬小麦挑旗期的LAI,估算值与地面实测值比较一致,二者拟合方程的决定系数R2为0.761,RMSE为0.320,估算值范围（1.02—6.41）与地面实际情况（1.29—6.81）亦比较相符,表明本文所建的OOB-RF冬小麦LAI估算模型的精度和适用性较强,可用于低空无人机高光谱遥感平台获取高精度的作物LAI信息。（责任编辑 杨鑫浩）
The authors have declared that no competing interests exist.
