0 引言
【研究意义】及时、准确地获取区域农作物种植面积信息对掌握农业动态、制定合理的农业政策至关重要[1,2,3,4,5]。遥感技术具有客观、及时、高效等优势,在粮食作物种植面积监测中得到了广泛应用[6,7,8,9,10,11,12,13]。然而在中国开展大尺度的业务测量中,由于作物种植地块破碎、结构复杂[14],同时受限于遥感影像空间分辨率等因素,“混合像元”和“同物异谱、异物同谱”现象异常突出,作物遥感识别结果精度不高,基于遥感像元直接统计的方式得到的区域作物面积存在较大偏差,无法得到业务应用部门的认可[15]。因此,遥感与空间抽样相结合的调查方式是获取区域作物种植面积的切实可行方案[16,17,18,19,20]。该方法集成遥感对作物分布表达的空间优势,结合遥感识别出的作物分布构建代表性强、不重不漏的抽样框,以遥感识别结果构建定量指标作为分层指标和估计辅助量进行作物面积推断,可优化空间分布样本,同时能大幅降低外业调查成本,提高作物面积的抽样调查效率[21]。分层抽样是一种高效的抽样方法[22],分层指标是决定分层抽样效率的关键,直接决定抽选样本的质量和代表性,进而影响作物种植面积的空间抽样效率和总体推断精度[23,24,25]。【前人研究进展】一些国家实施系列的农作物种植面积和产量调查的重大应用计划中多采用以面积规模作为分层标志。如美国的LACIE计划（large area crop inventory experiment）、CDL计划（cropland data layer）、欧盟MARS计划（monitoring agriculture with remote sensing）、LUCAS计划（land cover/use statistics）[26,27,28]等。此外,一些研究也采用面积规模指标作为分层指标进行空间抽样,推断区域作物种植面积。PRADHAN[29]采用航拍照片统计抽样单元内作物面积构建分层指标,开发了一套地理信息系统用于伊朗哈马丹省的作物面积抽样调查,达到了较高的抽样精度;SHARMA等[30]将抽样框内各种作物种植面积规模的比例作为分层指标,进行了多次抽样的反推试验,验证该指标的有效性。陈仲新等[31]以中国各县冬小麦的种植面积作为分层指标,得到中国冬小麦种植面积变化预测;张锦水等[32]以耕地地块内目标作物的遥感识别面积作为分层指标,估算北京市冬小麦种植面积;焦险峰等[33]基于上一年的各区棉花播种面积为分层指标,外推估算得到新疆全省的棉花播种变化情况。传统的遥感结合空间抽样的技术体系中,多采用面积规模为分层指标进行抽样与推断,这种指标缺少对遥感识别结果分类误差的表达,由于遥感识别的作物空间分布在空间上的误差是不均一的,因此会对样本的代表性产生一定的影响。目前已有研究对遥感分类误差表达的分层指标设计研究进行了突破。比如胡潭高等[23]引入破碎度作为分层指标,该指标对抽样框平均分类误差有着良好反映,但该指标受到抽样单元尺度的影响;谭建光等[24]基于混合像元、同期作物等影响因素定义了结构规模指标,并验证了该指标的有效性;SUN等[25]提出了混合熵分层指标,该指标基于分类器输出的后验概率表达了抽样框内混合像元造成的分类误差,在估计精度和CV值方面都有较好的表现。【本研究切入点】不同于传统的遥感识别作物面积规模指标,本研究提出了一种新的基于遥感分类误差面积进行设计的分层指标——误差校正面积（Scorrect）,定量刻画遥感分类的误差程度,支撑遥感抽样方案设计,提高作物种植面积遥感抽样效率。【拟解决的关键问题】本研究以通州区和大兴区的冬小麦为例,进行抽样方案设计,设计误差校正面积指标,并与传统的面积规模指标进行相关性、抽样总体方差、平均相对误差、CV值的对比性分析,验证误差校正面积指标在遥感结合空间抽样调查方法的可行性与优势。1 材料与方法
1.1 研究区域概况
研究区为北京市通州区和大兴区,如图1-A所示,区域内耕地地块相对破碎、种植结构较为复杂。近些年,该区域在大力发展都市型现代化农业,其中果园、休闲农业占有较大比例;该区域与主城区毗邻,部分区域城市化水平较高,尤其是大兴区的新机场、亦庄开发区、市政府搬迁等建设,导致耕地大量减少和建设用地大幅增加。这造成了研究区内冬小麦种植结构复杂、地块细碎并不连续,这给利用遥感进行冬小麦分类造成了困难,无法保证较高的识别精度。因此,通州区和大兴区作为研究区能够代表中国大部分地区的农业种植现状,破碎的地块特征在遥感影像上造成大量的混合像元,对开展本文研究具有很好的代表性。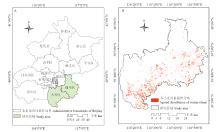
显示原图|下载原图ZIP|生成PPT图1研究区概况（A）与2015年冬小麦真值分布图（B）
-->Fig. 1Overview of the study area (A) and spatial distribution of winter wheat in Tongzhou and Daxing district of Beijing in 2015 (B)
-->
1.2 试验数据
1.2.1 数据准备与预处理 表1列出了本文研究中的数据资料。结合冬小麦的物候特征,本文选择具有较强植被光谱信息的冬小麦返青、起身期（获取时间2015年4月4日）的GF-1号影像数据（分辨率16 m,传感器为WFV相机）作为分类原始影像数据,该影像质量较好。使用ENVI软件对该数据进行正射校正、几何配准、FLAASH大气校正等操作,其中参数设置中大气模型为Sub-Arctic Summer,气溶胶模型选择Rural,将数据投影转换至横轴墨卡托投影（transverse mercator）,将其他数据一致转化为该投影坐标系。耕地地块由2014年该区域的航片数据（分辨率0.4m）为底图进行数字化获取。根据GF-1号影像数据结合地面样方数据与目视解译,对耕地地块进行划分、标定得到冬小麦的空间分布作为真值,用于计算辅助变量相关系数和抽样面积反推精度评价（图1-B）。Table 1
表1
表1试验数据集
Table 1Experimental dataset
| 数据名称 Data name | 数据格式 Data format | 分辨率 Resolution | 处理方法 Treatment | 作用 Function | |
|---|---|---|---|---|---|
| 基础地理信息数据 Base geographic data | 北京市区县行政边界 The districts boundary of Beijing | 矢量数据Shapefile | — | 大气校正、几何配准 Atmospheric correction, geometric registration | 确定研究区域 Define the study area |
| 耕地地块 Farmland parcel data | 辅助冬小麦识别和构建抽样框 Support wheat mapping and construct the sampling framework | ||||
| 冬小麦真值分布地块 Spatial distribution of winter wheat | 提供冬小麦真实面积及分布 Provide the spatial distribution of winter wheat, and the acreage | ||||
| 地面样方 Ground samples | 作为真值数据支撑目视解译 Reference as true value | ||||
| 遥感影像数据 Remote sensing image data | GF-1（2015-04-04） | 栅格数据 GeoTiff | 16 m | 遥感识别分类数据源 The data source of remote sensing classification |
新窗口打开
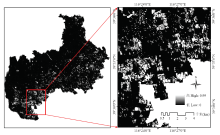
1.2.2 冬小麦遥感识别分类 遥感分类提取的冬小麦空间分布是构建分层抽样分层标志和进行区域面估计的基础。本文采用支持向量机（support vector machine,SVM）方法进行冬小麦分类[34]。首先,选择训练样本数据,根据冬小麦典型的光谱信息结合野外实测数据,确定分为冬小麦、其他植被、裸地、水体、建筑、道路6种地物类型,每个类别选取出约170个像元作为样本;然后,将训练样本输入到SVM分类器中对影像进行分类,得到初步土地覆盖分类结果。考虑到冬小麦种植在耕地范围内,利用耕地地块数据将初步土地覆盖分类结果进行切割,进一步提取得到耕地内的冬小麦分类结果;最后,利用目视解译方法修正冬小麦识别明显错误的图斑,得到冬小麦遥感识别分类结果数据。同时,输出SVM分类器的冬小麦归属概率数据层,如图2所示,用于进一步冬小麦识别分类误差的定义。
显示原图|下载原图ZIP|生成PPT图2SVM分类器输出冬小麦归属概率
-->Fig. 2The classification probability of winter wheat by using SVM classifier
-->
1.3 研究流程
整个试验研究共分为4个部分,分别为数据准备、遥感分类误差分层指标设计、抽样设计和结果分析。具体流程如图3所示。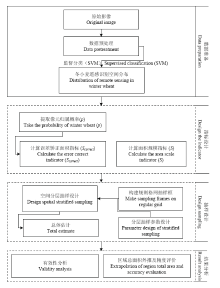
显示原图|下载原图ZIP|生成PPT图3技术流程图
-->Fig. 3Flow chart of technology
-->
1.4 分类误差校正面积指标设计
由于“混合像元”和“同物异谱、异物同谱”现象的存在,分类结果产生错入、错出误差。本研究基于遥感冬小麦识别分类结果,首先,从像元尺度对误差面积进行表达。以一定的规则确定分类结果像元的错入、错出、分类正确的方向,并计算其对应的“错入误差面积”、“错出误差面积”、“分类正确像元误差面积”;然后,在抽样单元尺度上,统计单元内所有像元的错入、错出和分类正确像元的误差面积,用于对冬小麦面积规模（S）进行校正,校正后的结果即为误差校正面积（Scorrect）指标。具体设计过程如下：1.4.1 像元尺度误差面积表达 以分类结果像元为窗口中心像元,构建一个w×w的窗口（本文w取5）,如图4所示,用于判断该像元的错出、错入、分类正确方向并计算误差面积。
显示原图|下载原图ZIP|生成PPT图4构建窗口计算像元误差面积示例
（a）原始影像;（b）冬小麦归属概率;（c）构建窗口过程示意图
-->Fig. 4An example to calculate a pixel's error area in a sample unit by the window
(a) Original image; (b) The classification probability of winter wheat; (c) The diagram of window construction
-->
错入误差面积：对于分类结果为冬小麦的像元,定义错入误差面积有两个情况：①$\frac{n}{N}$≠1;②$\frac{n}{N}$=1且p≤0.8,此时可定义该像元的错入误差面积：
Serror+=-Spixel×(1-p) （1）
式中,n为窗口内遥感识别的冬小麦像元总个数,N为窗口内可容纳的像元总个数（N=5×5=25）,Spixel表示每个像元的面积,p表示该像元的冬小麦归属概率。
错出误差面积：对于分类结果为其他地物的像元,当$\frac{n}{N} \ne 0$时（即$n \ne 0$）,可定义该像元的错出误差面积：
Serror-= Spixel×p （2）
分类正确像元误差面积：定义分类正确的像元有两种情况：
i对分类结果为冬小麦的像元,当$\frac{n}{N}$=1,且p>0.8,则认为该分类结果正确,没有分类误差,即错入
误差面积为0,即
Serror+=0 （3）
ii对分类结果为非冬小麦的像元,当n = 0,则认为该分类结果正确,没有分类错误,即错出误差面积为0,即
Serror-=0 （4）
1.4.2 抽样单元尺度校正面积计算 在抽样单元上定义分类结果的误差校正面积指标。对于每个抽样单元,定义这一尺度上的误差校正面积：
Scorrect=S+∑Serror-+∑Serror+ （5）
式中,Scorrect表示抽样单元的误差校正面积;S为抽样单元冬小麦的面积规模;∑Serror-表示抽样单元内所有像元的错出像元误差面积;∑Serror+表示该抽样单元内所有像元的错入像元误差面积。
1.5 空间抽样方案设计
1.5.1 抽样框构建 考虑到误差校正面积指标可能与抽样格网的尺度相关,因此本文构建边长为90 m、120 m、150 m、180 m、210 m、240 m、270 m、300 m的规则正方形格网为抽样框。基于研究区冬小麦遥感分类结果,以抽样单元内有冬小麦种植面积为条件,在各个尺寸的抽样框中去除不满足总体入样条件的单元。1.5.2 分层方法 考虑到费用与精度之间的平衡,本试验将抽样方案中分层层数设置为6层[35,36]。分层界限的确定采用累计等值频率平方根方法,该方法是由戴仑纽斯（DALENIUS）与霍杰斯（HODGES）提出的一种最优确定分层抽样的快速近似法[37]。
1.5.3 样本分配与样本抽选 样本容量n及其在各层数量的分配是分层抽样效率的关键之一[35,36]。为控制变量与研究方便起见,本研究样本总量为n=200,在这一抽样样本量的前提下,分析指标S和Scorrect 指标在不同尺度抽样单元下对抽样效率的影响。在样本量一定的情况下,为达到目标估计量标准差最小的目的,采用内曼样本分配原则分配各层样本量：
nh=n×$\left( \frac{{{N}_{h}}{{S}_{h}}}{\sum\limits_{h=1}^{L}{{{N}_{h}}{{S}_{h}}}} \right)$ （6）
式中,nh为分层抽样中第h层的样本量,h = 1,2,…,L;L为分层抽样层数;Nh为第h层的容量;Sh 为第h层的标准差,其中L= 6。
样本抽选方法确定为不放回简单随机抽样,对每层样本进行抽取。
1.5.4 面积推断与误差估计 本文采用回归估计进行区域面积的推断,在每种尺寸抽样框下设置100次重复试验。当辅助变量与目标量具有高度的线性相时,回归估计是有效的[38]。推断公式为：
${{\hat{Y}}_{lr}}$=$\sum\limits_{h=1}^{L}{{{N}_{h}}}$[${{\bar{y}}_{h}}$+βh]($\bar{X}$-$\bar{x}$) （7）
其中由样本计算的回归系数βh计算公式如下：
βh=$\frac{{{S}_{xy}}}{S_{x}^{2}}$=$\frac{\sum\limits_{i=1}^{{{n}_{h}}}{({{x}_{hi}}-{{{\bar{x}}}_{h}})({{y}_{hi}}-{{{\bar{y}}}_{h}})}}{\sum\limits_{i=1}^{{{n}_{h}}}{{{({{x}_{hi}}-{{{\bar{x}}}_{h}})}^{2}}}}$ （8）
式中,${{\bar{y}}_{h}}$为第h层样本的均值,yhi为第h层内第i个样本单元取值,$\bar{X}$为辅助变量总体均值,Nh为第h层总单位数,${{\bar{x}}_{h}}$表示第h层的辅助变量均值,$\bar{x}$为辅助变量样本均值,xhi为第h层内第i个样本单元对应辅助变量取值。其中辅助变量分别为面积规模（S）和本文所提出指标Scorrect。
本文选择外推总体平均相对误差$\bar{r}$、总体总值估计量的变异系数CV值这两个指标,定量评价总体精度和稳定性,计算公式为：
$\bar{r}$=$\frac{1}{m}\sum\limits_{k=1}^{m}{\left| \frac{{{{\hat{Y}}}_{k}}-Y}{Y} \right|}$×100% （9）
CV($\hat{Y}$)=$\frac{\sqrt{V(\hat{Y})}}{{\bar{\hat{Y}}}}$×100% （10）
式中,${{\hat{Y}}_{k}}$为第k次试验的区域冬小麦种植面积估计量,Y为区域冬小麦种植面积真值总量,在抽样框下对区域冬小麦面积真值直接统计得到,k = 1,2,…,m,m为试验次数,本研究m取100,$\bar{\hat{Y}}$为m次试验下区域冬小麦种植面积估计量的均值。
2 结果
2.1 指标有效性分析
为了探究所提指标对分类错误像元的校正效果,选取分类结果中两个典型的存在错出误差5-A、错入误差5-B的区域进行对比和分析。其中5-（d）、5-（h）分别为错出、错入像元误差典型区域的误差分布,取值范围为[-1, 1],其中错出像元误差显示为正值,错出程度越高则其灰度值越高,错入像元误差显示为负值,错入程度越高则灰度值越低。图5-（a）中具有较强植被光谱特征的地物为冬小麦,对比5-（a）、5-（b）、5-（c）可知分类结果5-（c）框1中存在分类误差,为冬小麦错出误差,即本该分为冬小麦的像元被分为其他地物类型。框内的3个错出像元经过像元误差面积计算后得到5-（d）图所示结果,显示为错出像元误差面积,对该3个像元可达到误差校正的效果。对比图5-（a）、5-（e）可知,5-（e）中框2内地物特征与冬小麦有一定差距,且其与周边地物不连续,未呈耕地的规则块状分布,由5-（f）可知,该地物并不是目标地物冬小麦。但SVM分类器将其分类为冬小麦,所以该处产生冬小麦错入现象。经过像元误差面积计算后得到结果图5-（h）,框2内显示主要为冬小麦错入像元误差面积,达到较好的误差校正效果。
显示原图|下载原图ZIP|生成PPT图5校正错出误差典型区域（A）与校正错入误差典型区域（B）
（a）,（e）：原始影像;（b）,（f）：冬小麦真值分布;（c）,（g）：遥感冬小麦识别分类结果;（d）,（h）：误差面积分布
-->Fig. 5Typical corrected region for pixel with error of omission and typical corrected region for pixel with error of commission
(a), (e): Original image; (b), (f): True value’s distribution for winter wheat; (c), (g): The classification of Winter Wheat; (d), (h): The distribution of error area
-->
通过以上典型区域原始影像、目标真值分布、遥感分类结果图、分类错误像元误差面积分布图的对比,表明像元误差分布与实际情况相符,指标能综合周边地物特征、冬小麦类别归属概率高低等因素对分类错误像元进行校正。从像元尺度上验证了本文提出的指标对于冬小麦分类结果的错出、错入像元误差的有效表达,可达到较好的校正效果。
再从两种指标相关性的角度对指标进行有效性分析。作为分层指标,根据戴伦纽斯的观点,判断其适用性关键在于目标变量是否与辅助变量存在较好的相关关系[38]。将根据冬小麦遥感识别面积结果统计得到的面积规模指标与误差校正面积分别与冬小麦分布真值进行相关系数计算,结果如表2所示。在试验格网下,误差校正面积和面积规模与真值的相关系数都大于0.7,两个指标均与真值高度相关,说明它们作为分层指标都是适用的。误差校正面积的相关系数相较于面积规模略有提高,呈现稳定且更高的相关性,这是由于遥感影像冬小麦识别过程中不可避免地产生误差,所以每个抽样单元内的冬小麦分类结果存在错入、错出像元,而这些误差像元的空间分布不是均一的,造成了面积规模与真值之间的偏差,影响了两者相关性。而误差指标与真值相关性更高,说明其在数值上更接近真值,表明该指标具有较好的校正误差面积的效果。
Table 2
表2
表2两种指标的相关系数
Table 2Correlation coefficient of two indicators
| 格网尺寸 Grid size (m2) | 误差校正面积指标 Scorrec | 面积规模指标 S |
|---|---|---|
| 90×90 | 0.7370 | 0.7368 |
| 120×120 | 0.7877 | 0.7874 |
| 150×150 | 0.8107 | 0.8101 |
| 180×180 | 0.8282 | 0.8276 |
| 210×210 | 0.8467 | 0.8459 |
| 240×240 | 0.8536 | 0.8527 |
| 270×270 | 0.8672 | 0.8664 |
| 300×300 | 0.8715 | 0.8705 |
新窗口打开
2.2 总量面积推断及精度评价
依照抽样方案方法进行试验,在各尺寸格网抽样框下分别进行了100次重复试验后,得到冬小麦种植总面积的区域抽样外推结果以及相应的总体方差、平均相对误差、变异系数等（表3）。Table 3
表3
表3区域冬小麦种植面积总体估计结果
Table 3The result of total estimation for study area’s winter wheat
| 序号 No. | 格网尺寸 Grid size (m2) | 总体容量 Overall capacity | 抽样比 Sampling ratio | 多次抽样反推总面积方差 Multiple sampling variance (×1013) | 平均相对误差 Average relative error (%) | 总体变异系数CV值 CV value(%) | |||
|---|---|---|---|---|---|---|---|---|---|
| 面积规模 S | 误差纠正面积 Scorrect | 面积规模 S | 误差纠正面积 Scorrect | 面积规模 S | 误差纠正面积 Scorrect | ||||
| 1 | 90 | 28774 | 0.7% | 2.12 | 1.70 | 4.97 | 4.37 | 6.09 | 5.45 |
| 2 | 120 | 19460 | 1.0% | 2.05 | 1.41 | 4.87 | 4.21 | 5.98 | 5.24 |
| 3 | 150 | 14475 | 1.4% | 2.18 | 1.59 | 5.02 | 4.44 | 6.35 | 5.41 |
| 4 | 180 | 11456 | 1.7% | 2.36 | 1.92 | 5.24 | 4.83 | 6.52 | 5.87 |
| 5 | 210 | 9475 | 2.1% | 3.11 | 2.41 | 5.98 | 5.30 | 7.47 | 6.50 |
| 6 | 240 | 7955 | 2.5% | 2.94 | 2.13 | 5.54 | 5.00 | 7.17 | 6.15 |
| 7 | 270 | 6935 | 2.9% | 2.86 | 2.24 | 5.6 | 4.86 | 7.06 | 6.24 |
| 8 | 300 | 5982 | 3.3% | 2.28 | 1.79 | 5.21 | 4.60 | 6.35 | 5.64 |
新窗口打开
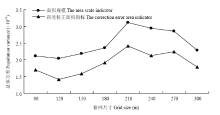
图6为试验结果绘制得到的总体方差随格网尺寸变化的对比图。两种指标的总体方差变化趋势基本一致,都随着抽样单元尺寸的增大总体方差先增加后减少。格网尺寸小于210 m时,两种指标总体方差均随着抽样单元尺寸的增大而不断变大,这可能是由于两种指标本质上是面积数值大小,根据方差的计算公式可知,方差大小不仅取决于总体的波动情况,还同时与总体数值大小相关,所以随着单元尺寸的增加,单个抽样单元内像元面积增大,两种指标的方差随之成倍增大。随着抽样单元边长的继续增大总体方差开始减少,原因可能是由于两种指标与目标真值的相关性不断增大,推断估算面积的精度也不断增大,提高了总体方差的稳定性,导致了总体方差的回落及减少。以误差校正面积作为分层指标,进行多次推断得到的结果的总体方差变化范围为1.70×1013—2.41×1013;面积规模的总体方差变化范围为2.05×1013—3.11×1013,误差校正面积的总体方差总低于面积规模,这表明在一定尺寸格网内,误差校正面积要始终比面积规模在推断稳定性方面更有优势。
显示原图|下载原图ZIP|生成PPT图6两种指标下冬小麦种植面积推断的总体方差
-->Fig. 6The population variance for results of two indicators
-->
图7为使用两种指标经过100次抽样反推总面积计算结果,包括平均相对误差值 $\bar{r}$、总体变异系数CV值的对比。平均相对误差 $\bar{r}$是反映抽样精度的指标, $\bar{r}$越小则精度越高。如图7-A所示,两种指标经多次试验后得到的 $\bar{r}$都随格网尺寸的变化先小幅度增大后减小,总体趋势较为平稳。采用面积规模得到的 $\bar{r}$>在4.87%—5.98%,而误差校正面积得到的 $\bar{r}$在4.21%—5.00%,且始终小于面积规模,即能稳定提高近1%的精度。CV值可以进一步评价多次推断的稳定性,其数值越大则结果越不稳定。CV值与方差的区别在于CV值反映稳定性且一定程度上消除了作物面积规模的影响,因此其变化幅度小于方差的变化幅度,更符合实际抽样结果。图7-B显示两指标的CV值在数值变化上差异不大,总体上呈现先增后减的趋势,误差校正面积的CV值在试验格网下始终低于面积规模的CV值,且能稳定减少近0.8%,这表明采用误差校正面积指标作为分层指标进行抽样可以提高其推断结果的稳定性。
显示原图|下载原图ZIP|生成PPT图7两种指标推断结果平均相对误差（A）和CV值（B）比较
-->Fig. 7A contrastive study of average relative error (A) and CV value (B) for results of two indicators
-->
综上,在90—300 m尺寸格网下,较传统面积规模分层指标,采用误差校正面积作为分层指标进行区域冬小麦种植面积推断能达到更小的抽样误差、更稳定的抽样结果,精度能稳定提高近1%,CV值能降低0.8%。
3 讨论
本文提出并设计了抽样分层指标——遥感分类误差校正面积（Scorrect）,以通州区和大兴区为研究区,以冬小麦为例,采取一定的空间分层抽样方案,进行冬小麦区域总量面积反推及精度评价。试验结果表明该指标较面积规模指标在外推精度、推断稳定性等方面更具有优势,并验证了其作为分层标志的适用性、有效性。本研究提出的指标是从校正冬小麦分类误差面积的角度出发进行设计的,可表达分类结果中存在的误差并对其进行校正。对比其他可表达遥感分类误差的分层指标,误差校正面积具有一定的优势,如胡潭高[23]引入的破碎度指标,其适用性受到抽样单元尺度的影响,在种植结构破碎区域,小尺寸抽样格网下表现较好,但大尺寸下表现不如面积规模。而误差校正面积指标本质上是对经校正后的面积规模的描述,对抽样单元尺度并不敏感,在试验任何格网尺寸下,相关性、推断精度、稳定性均表现较好。因此在抽样单元尺度方面,该指标的适用性更广。不管是破碎度、谭建光[24]提出的结构规模,还是SUN[25]提出的混合熵,其设计思想对于今后指标改进很有参考意义,此外还可考虑多时相影像、周边像元逻辑关系等多种因素综合优化指标。
本试验是基于一定的抽样方案进行的,相应的分层层数、抽样比、抽样方法、总体估计方式等方案是根据经验或出于一定目的而设定的。在今后的研究中,可在误差校正面积进行分层抽样时,讨论不同抽样比、不同抽样方法、不同估计方式等因素的影响;研究更大范围、更多数量的不同尺寸抽样框下,采用该指标得到的各项参数的变化;对比其他分层指标等与该指标的优劣性。同时,可研究该指标在其他农作物（如玉米、水稻等）种植面积调查中的适用性;此外,可将该指标应用于林业调查、土地利用监测等方面,提高本指标的推广性,以期能在遥感误差解析研究、统计技术中的遥感应用研究等方面有一定的推动意义,为北京乃至其他区域的遥感空间抽样调查提供试验支持,为优化农作物种植面积调查方式提供参考依据。
4 结论
4.1 通过在像元尺度对遥感识别典型的错出、错入区域进行对比和分析,验证了误差校正面积指标对冬小麦分类结果的错入、错出像元误差的有效表达,有较好的校正效果,从而改善分类结果。在试验中90—300 m的格网下,误差校正后面积与目标真值的相关系数始终大于面积规模的相关系数,且数值大于0.7,可保证其与真值较高且稳定的相关性,验证了该指标作为分层指标的有效性。4.2 以误差校正面积为分层指标进行多次面积外推得到的总体方差、总体变异系数CV值、平均相对误差 $\bar{r}$总是小于由面积规模指标试验得到相应数值。使用误差校正面积能稳定提高近1%的精度,能稳定降低近0.8%的CV值,提高了抽样估算结果的稳定性。
4.3 本文提出的误差校正面积指标的适用性、有效性得到了验证,该指标可较为明显提高种植面积抽样调查精度、保证外推的稳定性,可以达到提高抽样效率的目的,选择该指标相较于面积规模指标有利于分层抽样的进行,更具有优势。
The authors have declared that no competing interests exist.
