0 引言
【研究意义】土壤有机质（soil organic matter,SOM）的高低是衡量土壤肥力的重要指标,快速、准确地监测SOM对于土壤资源调查、精准农业、土壤数字化制图具有重要意义[1-2]。近年来,土壤近地传感（proximal soil sensing,PSS）凭借方便快捷、无破坏、信息量大等优点,被广泛应用于估算土壤肥力关键参数,成为国际土壤科学研究的热点[3-5],****们针对不同的土壤类型,在稳定的观测条件下,建立了较为完善的Vis-NIR光谱估算土壤属性的理论体系[6-7]。然而,在田间无论是采用静态原位观测还是实时动态观测,土壤含水量（soil moisture,SM）、温度、土壤表面粗糙度等因素均会对土壤Vis-NIR光谱采集产生影响。其中,SM变化对Vis-NIR光谱观测结果造成严重干扰,甚至会掩盖SOM的光谱吸收特征,导致直接利用田间土壤Vis-NIR光谱数据估算SOM的精度较低[8-9]。因此,非常有必要消除SM变化对Vis-NIR光谱的影响以提高SOM估算精度。【前人研究进展】****们通过SM梯度试验揭示了土壤Vis-NIR光谱对SM变化的响应规律,基于光谱分类、光谱转换、参数正交化等数学算法定量消除SM变化过程中土壤Vis-NIR光谱造成的影响,从而较好地提高了田间土壤属性的估测精度。WU等[10]发现800—1 400 nm、1 600—1 700 nm、2 100—2 200 nm、2 300—2 500 nm波段的一阶微分光谱数据受SM变化影响较弱,选择这四个波段区域的波段建立估算模型,有利于提升土壤属性的预测精度,然而,SM梯度试验表明,SM在全波段区域对土壤Vis-NIR光谱造成影响,而且随着SM的增加,光谱反射率的降低是非线性的。NOCITA[11]、王超等[12]利用1 800 nm和2 119 nm处的光谱反射率计算归一化土壤湿度指数（normalized soil moisture index,NSMI）表征光谱对不同SM的响应程度,根据NSMI将湿土样本进行光谱分类,逐类单独建模,较好地实现了土壤属性的预测,但这种方法未能有效消除SM变化对土壤光谱的影响。JI[13]、陈奕云等[14]运用光谱转换算法中的直接标准化法（direct standardization,DS）对湿土光谱进行校正,校正后的光谱数据可以用来预测土壤属性,该算法为全波段进行校正,在光谱曲线较为相似时,易导致过度校正的问题。MINASNY等[15]采用EPO定量化消除SM对Vis-NIR光谱的影响,用处理后的Vis-NIR光谱数据建立了更高精度的土壤有机碳的估算模型;陈红艳等[16]采用奇异值分解（singular value decomposition,SVD）提取土壤水分对应的光谱信息,构建消除土壤水分因素的修正系数,实现对湿土光谱的校正。近年来,研究者对EPO算法消除SM的研究呈上升趋势。EPO算法是建立在土壤水分与待估土壤属性之间相互独立的前提下,即仅基于受SM变化影响的光谱数据进行校正处理,通过简化分析条件,实现SM变化对土壤光谱影响的消除,这忽视了因变量（待估土壤属性的浓度矩阵）与自变量（受SM影响的光谱矩阵）的相互影响,难以模拟土壤水分、待估土壤属性、土壤光谱三个要素的相互作用关系[15]。基于矩阵正交理论的正交信号校正（orthogonal signal correction,OSC）算法对光谱矩阵和浓度矩阵进行正交处理,在此基础上再滤除光谱矩阵中因SM变化引起的噪声偏移,保留与SOM矩阵有关的信息,可以有效地提高估算模型的预测精度[17-18]。【本研究切入点】本研究采集江汉平原公安县和潜江市的土壤样本,在室内设计SM梯度试验,模拟SM、SOM和土壤Vis-NIR光谱的互作用过程,获取9个SM梯度（0%—36%）的Vis-NIR光谱数据,定量表达SM变化对土壤Vis-NIR光谱数据的影响,尝试将EPO、OSC应用于校正不同SM梯度的光谱数据,对比二者校正后的模型精度。【拟解决的关键问题】本研究开发OSC的权重转换矩阵和载荷转换矩阵,定向消除光谱中受水分影响的信息,建立具有更高鲁棒性的SOM光谱估算模型,为今后田间实时动态监测土壤养分信息提供理论支撑。1 材料与方法
1.1 土样采集、制备与样本集划分
2010—2015年,以江汉平原的公安县和潜江市为采样区域,分多次采集深度为0—20 cm的土壤样品共234份,其中,2010年、2011年、2012年在公安县分别采集土样23份、16份、22份,2015年在潜江市采集土样173份。每次采样后,及时处理土样,清除土样中小砾石、表层枯枝落叶、动物残体等外来侵入物,将土样带回实验室进行风干、研磨、过2 mm筛等处理后,将土样分为两份,一份装入玻璃广口瓶中封存,用于测定Vis-NIR光谱数据;另一份继续过60目筛后采用重铬酸钾容量法-外加热法测定 SOM含量[19]。所有批次的样本用于建立样品库。建模集（S0）：从样品库中,随机选取122份作为S0。这些样本采集自江汉平原的公安县和潜江市,土壤类型主要为潮土。
训练集（S1）和验证集（S2）：从样品库中,选取采集自潜江市竹根滩镇的潮土样本95份,其土壤母质为石灰质近代河流冲积物,土壤表层质地以砂质壤土为主;按照SOM的大小,升序排列,间隔2个或3个样本挑选出60份土样作为S1,剩余35份土样作为S2。
1.2 土壤含水量试验设计
本文采用土壤质量含水量作为SM,设计9个SM梯度（0%、4%、8%、12%、16%、20%、24%、28%、32%）对S1和S2的土样进行9个SM梯度的光谱观测试验,研究SM变化对土壤Vis-NIR光谱的影响。每份土样称取150 g烘干土（SM为0%）,放置于直径7.5 cm、深度5 cm规格的圆柱形黑盒中,进行光谱测量,得到干土光谱数据（干土样本）;以每个土样增加4%的SM为标准,用喷雾器均匀喷洒6 g水,而后迅速密封以防水分蒸发;静置8 h使水分在土壤中扩散均匀,测量湿土光谱数据,立即重新称重以计算实际SM（质量含水量）;重复加水步骤,直至完成试验。尽管土壤样本内部不同深度的土壤水分存在较小差异,但这种微小变异不会对光谱数据的测量造成明显的影响,因此忽略不计。湿土特指SM梯度为0%以外的8个SM梯度样本。1.3 光谱数据采集及预处理
土壤Vis-NIR光谱反射率采用ASD Field Spec3地物光谱仪测定,该仪器由美国Analytical Spectral Devices公司生产,波谱范围为350—2 500 nm,采样间隔为1.4 nm（350—1 000 nm）和2 nm（1 000—2 500 nm）。光谱测量在暗室内进行,光源为能够提供平行光线的50 W卤素灯,入射角度（A）为30°,到土样表面中心点的距离（L）为50 cm;采用5°视场角光纤探头,垂直于土样表面且垂足位于土样表面中心点,到土样表面距离（H）为15 cm[20]。测试之前,先对仪器进行标准白板校正,每个土样测量4个方向（转动3次,每次90°）,每个方向上保存5条光谱曲线,共20条,作算术平均后得到土样实际的反射光谱数据。S0共获取122条光谱数据（122个样本）,S1共获取540条光谱数据（60个样本,9个SM梯度）,S2共获取315条光谱数据（35个样本,9个SM梯度）。
利用ViewSpec Pro软件导出原始土壤光谱数据;剔除土壤光谱数据中在噪声较大、信噪比低的边缘波段（350—399 nm,2 400—2 500 nm）,保留400— 2 400 nm的光谱数据;对光谱数据进行10 nm重采样平均,降低冗余度;选用Savitzky-Golay 11点滤波平滑法（多项式阶数为2）对重采样数据进行平滑去噪[21],得到分析和建模的光谱数据。
1.4 EPO、OSC消除SM对Vis-NIR光谱数据影响
EPO在去除外部环境参数方面效果显著,为消除SM的影响提供了新途径。EPO算法首先确定受SM影响的光谱区域,再将所有的光谱投影到与受SM影响相正交的空间上,从而实现SM影响因素的去除。EPO具体运算过程可参见文献[22-23]。鉴于篇幅,本文仅将EPO-PLSR模型结果与OSC-PLSR模型结果进行对比。OSC由WOLDS提出,其基本思想是将光谱矩阵与因变量矩阵（浓度矩阵）进行正交计算,滤除光谱矩阵中因外部参数（SM）变化而引起的差异信息,保留光谱中与因变量有关的有用信息,能有效消除光谱中的与因变量无关的外部噪声,可以保证校正模型的稳健性。因此,该方法能够定量表达SOM-SM-土壤光谱数据三者之间的关系,经OSC处理后,可以获取不含SM噪声且与SOM密切相关的光谱数据。在实际应用OSC时,需要调节正交模型的因子（components,c）,即决定有多少个主成分参与信号的滤波,使处理后的光谱数据建模精度稳定在较高水平。OSC具体运算过程可参见文献[17-18]。
首先对S1光谱矩阵进行主成分分析,获取得分矩阵t并对t进行均值中心化记为\(\overline{t}\),结果记为T,即：
T=t-\(\overline{t}\) （1）
然后正交于土壤有机质（y,经过均值中心化处
理）,结果记为T⊥,即：
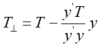
对T进行均值中心化记为\(\overline{T}\),将TI与\(\overline{T}\)相加,得
出t*,即：
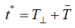
利用t*计算S1的载荷矩阵w,即：
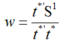
并进行归一化处理,结果记为s,即：
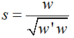
计算新的得分矩阵tnew,即：
tnew=S1s （6）
重复计算上述步骤（1）—（6）直到t*趋于稳定为止。t*描述了光谱矩阵S1与有机质矩阵y的正交信息。选择一定的因子数目,利用t*建立PLSR,模型的回归系数计算如下：
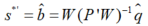
式中,W是包含一定因子数目的权重矩阵,P是包含一定因子数目的权重矩阵,\(\hat{q}\)是包含一定因子数目的回归系数向量（描述的是t*与一定因子数目PLSR模型的每个得分向量之间的内部关系）。
重新计算得分t**,即：
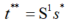
计算S1的载荷矩阵p,即：
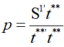
最后,得到去除的无关信息S1OSC,即：
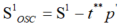
应用于S2验证集时,先利用S*计算S2数据集光谱的得分e,即：
e=S2s* （11）
再利用上述计算得到的载荷p,计算新的光谱（S2*）,即：
S2*=S2-ep’ （12）
1.5 光谱数据主成分分析与光谱相关系数
本文采用主成分分析（principal component analysis,PCA）对光谱数据进行降维,保留方差大、包含信息量多的组分,舍弃信息量少的组分。经PCA变换后的各组分之间相互正交、互不相关,消除光谱波长变量之间的多重共线性,用较低的变量维度、更多地表达光谱数据的向量特征。PCA的计算采用非线性迭代偏最小二乘算法（nonlinear iterative partial least squares,NIPALS）,计算步骤简单,运算速度快[24]。本文利用光谱相关系数作为OSC处理前后光谱向量之间相似性的定量判断标准,判断的基本准则为“相关系数值越接近1,相似性越高”[25]。光谱相关系数测度的计算公式如下：
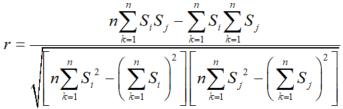
式中,Si、Sj分别为第i个和第j个SM梯度样本的第k个波长变量的数值,n为光谱波长变量总数（n=201）,r为第i个和第j个SM梯度样本之间的光谱相关系数。
1.6 构建SM消除模型
EPO：首先,利用S1开发EPO转换矩阵P,将其应用于处理S0、S2中各个样本的光谱数据,构建S0的转换样本集S0*和S2的转换样本集S2*;然后,利用S0建立PLSR模型（S0的122个样本的光谱数据为自变量,SOM数据为因变量）,利用S0*建立EPO-PLSR模型（S0*的122个样本的光谱数据为自变量,SOM数据为因变量）;最后,将S2的35个样本的315条光谱数据和S2*的35个样本的315条光谱数据分别输入PLSR模型和EPO-PLSR模型预测SOM。OSC：首先,利用S1开发OSC的权重矩阵、载荷矩阵,将其应用于处理S0、S2中各个样本的光谱数据,构建S0的转换样本集S0*和S2的转换样本集S2*;然后,利用S0*建立OSC-PLSR模型（S0*的122个样本的光谱数据为自变量,SOM数据为因变量）;最后,将S2*的35个样本的315条光谱数据输入OSC-PLSR模型预测SOM。
对比PLSR模型与EPO-PLSR、OSC-PLSR模型的预测精度,检验SM的消除效果;对比EPO-PLSR模型与OSC-PLSR模型的预测精度,优选出最佳的估算模型。
1.7 估算模型的建立与验证
本文重点是研究OSC算法消除SM对土壤Vis-NIR光谱影响,选择EPO算法作为对照,实证土壤Vis-NIR光谱通过OSC算法处理后能够有效提升SOM含量的估算精度,但是,限于文章篇幅,在建立估算模型时仅选用了目前较为成熟的线性PLSR方法进行建模、预测。PLSR是一种多变量统计分析方法,同时考虑了分解自变量光谱矩阵和目标因变量SOM矩阵的影响,将数据压缩与回归拟合相结合,使建立的模型具有更好的稳健性,并能有效地解决自变量之间的多重共线性。本文中所有PLSR模型均采用Leave-one-out交叉验证法来确定回归模型中最佳因子数,防止过拟合的发生。模型精度检验选取建模决定系数R2cal、交叉验证决定系数R2cv、预测决定系数R2pre、交叉验证均方根误差RMSEcv、预测均方根误差RMSEpre、RPD值、1:1线等7个参数衡量。R2cal、R2cv、R2pre越接近于1,说明模型的稳定性越好、拟合程度越高。RMSEcv、RMSEpre越小模型估算预测能力越好。RPD是预测样本标准差与预测均方根误差RMSEpre的比值,判断模型的预测能力,RPD<1.4时,模型无法对样品进行预测,模型不可用;1.4≤RPD<2时,认为模型效果一般,可以用来对样品进行粗略评估,模型可用;RPD≥2时,模型具有极好的预测能力,模型较好[26]。1:1线用于检验实测值、预测值所构成的散点偏离y=x线的程度。
本文中的数据处理、PLSR建模在Matlab R2012a（The Mathworks Inc.,USA）软件环境下完成,图形绘制在Matlab R2012a和Origin 2016软件进行。
2 结果
2.1 SOM统计分析
对3个样本集（S0,S1和S2）的SOM进行描述性统计分析（表1）,S0样本的SOM变化范围为9.17—27.92 g·kg-1,S1为9.56—26.55 g·kg-1,S2为9.86—21.85 g·kg-1;与S1、S2相比,S0的标准差和变异系数较大,适合作为模型的建模集。Table 1
表1
表13个样本集（S0,S1和S2）的SOM描述性统计分析
Table 1Summary statistics characteristics of the SOM for the three different subsets (S0, S1 and S2)
| 3个样本集 Three independent data-sets | 样本数 Number of samples | 范围 Range (g·kg-1) | 平均值 Mean (g·kg-1) | 标准差 Standard deviation (g·kg-1) | 变异系数 Coefficient of variation (%) |
|---|---|---|---|---|---|
| S0 | 122 | 9.17—27.92 | 17.52 | 3.99 | 22.76 |
| S1 | 60 | 9.56—26.55 | 17.52 | 3.06 | 17.46 |
| S2 | 35 | 9.86—21.85 | 17.19 | 3.01 | 17.54 |
新窗口打开
2.2 OSC-PLSR模型参数确定
OSC-PLSR模型中有两个参数需要确定：OSC滤波因子个数c和PLSR最佳因子数k。采用S1开发OSC的权重矩阵、载荷矩阵,以模型中的R2cv值最大、RMSEcv值最小作为确定最佳参数组合的标准。PLSR因子数k优化取值范围为1—20,当因子数k≥13,R2cv和RMSEcv的变化趋于稳定,说明后续PLSR因子对模型贡献率较小,因此k取13;滤波因子个数（c）的优化取值范围为1—5,当c=4时,在5个滤波因子中,可以获得最大的R2cv值（0.74）和最小的RMSEcv值（1.58 g·kg-1）（图1）。因此,确定OSC的c=4,PLSR的k=13。
显示原图|下载原图ZIP|生成PPT图1不同OSC滤波因子（c）与PLSR因子数（k）估算S1土壤有机质的R2cv（A）、RMSEcv（B）
-->Fig. 1R2cv (A) and RMSEcv (B) in the estimation of SOM using the OSC for S1 with different numbers of OSC filter factors (c) and PLSR factors (k)
-->
2.3 OSC处理前、后对不同SM梯度的土壤光谱反射率的影响
在全波段（400—2 400 nm）区域范围内,虽然S2样本集不同SM梯度的平均光谱反射率曲线形态特征较为相似,但是,随着SM增加,土壤光谱反射率呈现非线性降低的趋势,当SM<16%时,SM变化对土壤光谱反射率变化的影响相对较大,当SM≥16%时,SM变化对土壤光谱反射率变化的影响逐渐减弱,土壤光谱反射率降低速率趋缓;可见光（400—800 nm）波段范围内光谱反射率差异较小,近红外（800—2 400 nm）波段范围内土壤光谱反射率随SM的绝对变化量明显大于可见光波段,表明SM对土壤近红外波段光谱反射率的影响作用强于可见光波段。不同SM梯度的湿土平均光谱反射率在1 450 nm和1 940 nm附近存在剧烈的反射率变化,随着SM的增加,1 450 nm和1 940 nm附近的水分吸收谷的吸收深度、吸收面积不断变大（图2-A）。然而,经OSC处理后的S2*样本集各SM梯度的平均光谱反射率曲线的变化较为一致（图2-B）,呈现出明显的相似性,光谱曲线之间的差异微小,有效地降低了SM对光谱反射率的影响,将受SM影响显著的1 450 nm和1 940 nm的差异几乎消除。
显示原图|下载原图ZIP|生成PPT图2S2样本集不同SM梯度的OSC处理前（A）、后（B）的平均光谱反射率
DG为干土。下同
-->Fig. 2The average of soil spectra for different SM levels before OSC (A), after OSC (B) from S2 data-sets
DG represent dry ground. The same as below
-->
2.4 基于PCA得分与光谱相关系数对比OSC消除SM变化影响的效果
对OSC处理前的S2样本集和OSC处理后的S2*样本集的光谱数据分别进行均值中心化（mean centre）,再利用PCA方法计算样本的第一和第二主成分得分作为横坐标和纵坐标,在二维空间的坐标系中以样本点的形式表征湿土光谱数据的差异（图3）。OSC处理前,S2的样本点相对分散,湿土样本点与干土样本点的距离较远,反映了干土、湿土样本之间光谱数据相似性很差;不同SM梯度的湿土样本点分布范围的重叠程度极低,表明同一土样在不同SM梯度采集的土壤Vis-NIR光谱数据具有明显的差异性（图3-A）。OSC处理后,S2*的样本点分布范围的重合程度极高,反映出干土和湿土样本的光谱数据已经具有很高的相似性,表明OSC可以有效地消除因SM变化引起的光谱差异（图3-B）。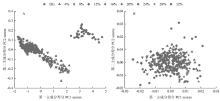
显示原图|下载原图ZIP|生成PPT图3OSC处理前（A）、后（B）的S2样本集第一、二个主成分得分图
-->Fig. 3Scores of the first and second principal components for S2 data-sets before OSC (A), after OSC (B)
-->
计算S2样本集和S2*样本集不同SM梯度两两之间的光谱相关系数（图4）。OSC处理前,S2样本之间的光谱相关系数变化较大（0.63—1）,干土与各SM梯度湿土之间的光谱相关系数随着SM的增大而不断减小,以干土与32%之间的相关系数最低（0.63）最为明显,表明不同SM梯度之间的样本光谱数据的相似性较差（图4-A）。OSC处理后,S2*样本之间的光谱相关系数变化较小（0.95—1）,干土与湿土样本之间光谱数据相似性很高,进一步表明OSC可以消除SM变化对光谱反射率的影响（图4-B）。
显示原图|下载原图ZIP|生成PPT图4OSC处理前（A）、后（B）的S2样本集不同SM梯度的光谱相关系数
-->Fig. 4Spectral correlation coefficients from S2 data-sets for different SM levels before OSC (A), after OSC (B)
-->
2.5 PLSR、EPO-PLSR、OSC-PLSR模型的建立
PLSR、EPO-PLSR、OSC-PLSR模型的R2cal均较好（表2）。PLSR模型的R2cv为0.57,S2的验证平均R2pre、RPD分别为0.34、1.18,验证集9个梯度的R2pre、RMSEpre、RPD的标准差变化较大,说明模型在不同SM梯度下的稳定性差,无法实现SOM在不同SM梯度的有效估算。EPO-PLSR模型的R2cv为0.65（表2）,S2*的验证平均R2pre、RPD分别为0.69、1.80,平均RPD>1.4,模型效果一般,可以用来对SOM进行粗略评估;相比PLSR模型（未进行SM消除）,平均RPD提升了0.62。但验证集9个梯度的R2pre、RMSEpre、RPD的标准差变化较大,模型在不同SM梯度下的稳定性较差。
Table 2
表2
表2OSC前、后的干土模型（S0建模）验证S2的土壤有机质预测结果
Table 2Prediction of SOM before OSC, after OSC for S2 calibrated by dry ground models (dataset from S0)
| 方法 Method | 建模集 Calibration sets (S0) | 预测集Prediction sets (S2) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 平均值Mean value | 标准差Standard deviation | ||||||||||
| R2cal | R2cv | RMSEcv (g·kg-1) | R2pre | RMSEpre (g·kg-1) | RPD | R2pre | RMSEpre (g·kg-1) | RPD | |||
| PLSR | 0.75 | 0.57 | 2.61 | 0.34 | 2.58 | 1.18 | 0.09 | 0.26 | 0.11 | ||
| EPO-PLSR | 0.80 | 0.65 | 2.37 | 0.69 | 1.70 | 1.80 | 0.08 | 0.21 | 0.27 | ||
| OSC-PLSR | 0.82 | 0.66 | 2.24 | 0.72 | 1.60 | 1.89 | 0.02 | 0.05 | 0.06 | ||
新窗口打开
经OSC处理后（表2）,OSC-PLSR模型的R2cv为0.66,S2*的验证平均R2pre、RPD分别0.72、1.89,模型精度一般。相比OSC处理前,平均RMSEpre降低了0.98,模型从不可用级别提高到可用级别;不同SM梯度之间的R2pre、RMSEpre、RPD的标准差均小于0.1,模型在不同SM梯度下的性能稳定、预测能力较好,表明OSC-PLSR模型能有效降低SM变化对光谱的影响,实现SOM在未知SM情况下的粗略估算。
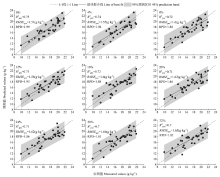
在5%显著性水平,计算得到95%预测区间,对OSC-PLSR模型在不同SM梯度下的实测值和预测值进行精度检验（图5）。S2*样本集中不同SM梯度的湿土光谱数据输入OSC-PLSR模型,获得的SOM预测精度均较好,总体上,随着SM的增加,模型验证精度略有降低,但R2pre均大于0.7,不同SM梯度的SOM最佳拟合线与1:1线偏离较小,模型解释能力均较好。
显示原图|下载原图ZIP|生成PPT图5OSC-PLSR模型的S2*样本集土壤有机质实测值与预测值散点图
-->Fig. 5Scatter plots between measured and predicted values of SOM using OSC-PLSR method for S2*data-sets
-->
3 讨论
由于C-H、O-H、C=O基团的合频和倍频振动吸收而引起的直接光谱响应,为采用光谱技术定量估算SOM提供了可能[27-28]。然而,由于受土壤水分的强烈干扰,利用在田间未知SM状况下观测的Vis-NIR光谱数据所建立的SOM估算模型的精度低于在实验室内观测的烘干土样的Vis-NIR光谱数据建立的估算模型精度;反之,在室内可控条件下,由于难以模拟田间随机条件,构建的估算模型又难以应用于田间SOM预测。因此,本文设计了SM梯度试验,一方面采用同一土壤类型的样本,经过磨碎、过筛等步骤,消除了土壤颗粒组成、土壤质地等因素不同而产生的影响,实现条件控制;另一方面通过室内设计多梯度SM实验,模拟外部环境参数变化对土壤Vis-NIR光谱的影响,揭示土壤Vis-NIR光谱的对SM变化的响应规律,为定量消除SM变化对土壤Vis-NIR光谱的影响提供基础数据。本文利用S0样本集及其经OSC处理后的S0*样本集分别建立PLSR模型和OSC-PLSR模型,分别利用S2和S2*的光谱数据对两个估算模型进行验证。结果显示,PLSR模型的不同SM梯度的湿土的验证效果均较差,表明SM变化严重影响光谱观测,亦是导致SOM预测精度下降重要因素;OSC-PLSR模型用任意SM梯度验证均得到较好的效果,这表明OSC有效降低了因SM变化引起的光谱曲线的偏移差异,使湿土与干土样本之间的光谱曲线更为相似,使得在干土条件下建立的SOM光谱反演模型可以运用于不同SM梯度的SOM的光谱预测[29]。9个SM梯度的验证平均RPD为1.89,说明校正后的OSC-PLSR模型受SM影响微弱,可以对未知SM的土样的SOM进行粗略估算。BARBOZA等[30]研究采用分段直接标准化（PDS）和OSC两种方法对饮料中的酒精含量在4个温度梯度下模型进行温度校正,发现OSC要略优于PDS算法。本文引入OSC,用于消除SM变化对土壤Vis-NIR光谱影响的研究中,取得了较为理想的效果。但采用OSC时需要注意调节正交模型的因子个数c,确定最佳因子数,这是OSC-PLSR模型保持较高精度的关键[31]。
目前,许多不同尺度土壤光谱数据库（soil spectra library,SSL）已经建立,如VISCARRA ROSSEL等[32]描述的全球尺度SSL、史舟等[33]描述的国家尺度SSL、ZENG等[34]描述的区域尺度SSL、于雷[35]描述的局部尺度SSL。在这些SSL中,土壤样本经过风干、磨碎、过筛等室内处理工作,获取了丰富的先验知识信息（土壤烘干光谱数据、土壤理化性质数据、土样空间分布数据等）,可以建立精度较高的多元校正模型。但是,直接将田间观测的光谱数据输入基于室内稳定环境下建立的光谱估算模型,会导致预测精度较低[36]。本研究采用干土样本建模、湿土样本验证的研究思路,为将来充分利用已有的大样本土壤光谱数据库提供理论参考,避免重复采样、分析与建模,节省人力、物力、财力等资源,可有效降低建模成本。今后,可将OSC-PLSR模型应用于田间未知SM状况下Vis-NIR光谱技术动态监测SOM工作中。
相比EPO-PLSR模型,OSC-PLSR模型精度的平均R2pre提升了0.03,平均RPD提升了0.09,二者的模型精度相当。这可能是由于在本研究中,S1、S2样本集的SOM变幅范围均较小,变异系数分别为17.46%、17.54%,样品多样性较窄。此外,本试验的样本加湿方式采用的是土样表层正向梯度喷洒加水,水分多集中于土壤表层,会导致SM在垂直方向难以分布均匀,尤其是在低SM梯度下,进而可能会影响SM消减的模型效果。LIU等[37]采用底部盛水的样本加湿方式（容器底部含有小孔）,该方法可以允许土样充分的吸收SM,在样本内部产生更均匀的SM分布。在后续的研究中,需要对SM梯度试验设计进一步优化。
4 结论
4.1
随着土壤含水量（SM）的增加,土壤光谱反射率呈非线性降低趋势,SM变化对红外波段反射率的影响强于可见光波段,在1 450 nm和1 940 nm附近受SM变化影响最为明显。4.2
OSC处理前,不同SM梯度下的光谱数据PCA得分样本点相对分散,干土样本与湿土样本之间的光谱相关系数相对较小,说明SM变化严重影响土壤Vis-NIR光谱观测结果;OSC处理后,干土与湿土的PCA得分样本点分布范围的重合程度极高,样本之间的光谱相关系数接近1,表明OSC有效地消除了SM变化对光谱数据的影响,使干土和湿土样本的光谱数据具有很高的相似性。4.3
OSC中正交因子参数c的确定对模型精度有一定的影响,在实际应用中需要注意优化调节。本研究中,c取4即可。4.4
OSC-PLSR模型在9个SM梯度验证,得到的平均R2pre、RPD分别为0.72、1.89,不同SM梯度之间的R2pre、RMSEpre、RPD的标准差均小于0.1,校正后的OSC-PLSR模型受SM影响的较小,模型性能稳定,可以较好地估测SOM。这为田间未知SM状况下快速监测土壤肥力信息提供了理论参考。The authors have declared that no competing interests exist.
