0 引言
【研究意义】McCarthy指出,在地理学研究中,不能期望在某一个尺度上研究得出的结论能适用于其他尺度,尺度上的每一个变化都会引出新的问题,没有理由假设在某一个尺度上的关联在其他尺度上仍然存在[1]。不同的自然现象有不同的最佳观测距离和尺度,需要适当的距离和比例尺,才能得到有效完整的观察[2]。遥感是多尺度下土壤数字制图研究中被广泛利用的预测工具[3]。然而,此数据展现出的多种分辨率影响着决策者利用此数据的方式[4]。遥感数据通常呈现出一定的尺度依赖性,并以独立的像元作为分析的基本单元。因此,遥感数据的尺度分析直接涉及空间分辨率[5]。依靠尺度效应,****尝试测量或者模拟下垫面过程,即不同的分辨率可能在捕捉期望中的变异性研究中,拥有不同的效能[6]。环境变量空间尺度分析与栅格分辨率和领域分析(窗口大小的选择)有关。【前人研究进展】目前已有很多****调查分析栅格大小对土壤属性的影响[7-8],以及与既定尺度下生物物理过程的相互作用关系[9-10],多数研究中选择窗口的大小为3×3,其他窗口尺度并未考察。此外,部分****也证明领域大小的选择的重要性以及其对土壤-景观关系的影响。统计模型是预测土壤属性空间变异性研究中的常用方法。特定土壤属性和环境变量的定量描述可以丰富本地的土壤-景观知识库。多数统计模型建立的前提是假设土壤-环境变量之间呈线性相关。然而,土壤属性空间变异性与潜在环境变量之间的关系异常复杂,以线性假设恐难精确拟合二者之间的关系。借助现有遥感数据派生出的环境变量,利用多元统计分析技术,已对土壤有机质、纹理分析、土壤深度等属性进行了初步的探索[7-9]。而在土壤盐度这一领域并未有相关研究。即便是在分布最为广泛的干旱区,如新疆,也未曾涉及。新疆维吾尔自治区堪称干旱区盐碱土博物馆,分布范围广,种类多样,作为西北最大的农业用地储备区,快速精确地评估本地土壤盐度则有利于本地水资源管理、农业用地规划和防止土壤盐渍化的扩张和反复。新疆灌区盐渍化土地面积占灌区总面积的比例高达32.07%[11],多数城市和县级地区都有分布。整体而言,以天山为界,南疆地区比北疆地区严重。盐渍化土地主要分布在该区洪积扇中下部,绿洲-荒漠交错带,新开垦地区或老灌区内部的弃耕地[12]。放眼未来,随着人口的增加,人类活动将不断加剧,及时升级土壤环境数据(物理化学、生物、生态水文等)的需求相比从前更为强烈[13]。新疆天然的地理环境,加之水土资源的不合理利用,势必会造成更多的土地面临土壤盐渍化问题。另外,干旱区生态环境脆弱,准确高效地诊断本地土壤盐度对于评估土壤健康和优化管理尤为重要。相对于传统技术而言,遥感数据因其覆盖面积广,寻访周期快,且非侵入土壤等优势得以广泛应用。【本研究切入点】目前,借助遥感光谱探测土壤盐度的方式主要有两种。首先,在植被覆盖度较低(植被覆盖度小于15%)或盐渍化较为严重的裸土地区,可利用遥感原始波段光谱直接测量其土壤光谱信息[14-15],并与土壤盐分进行关联,定量获取其盐度值。基于目前已有研究关于地面光谱所总结的理论基础,许多****尝试借助盐分敏感波段,建立相关盐度指数定量描述土壤盐度信息。其次,盐渍化土壤因其盐分含量超过正常阈值进而影响到植被的生理参数,在不同像元尺度上表现为,植被类型丰富度、植被出现频率、植被盖度降低的趋势。鉴于此发现,诸多研究****利用植被指数间接推理土壤中的盐分含量[16-17]。而上述研究多在单一尺度上(如运用最为广泛的Landsat数据,30 m分辨率)进行,并未综合考察不同尺度下土壤盐度-环境景观之间的响应关系。【拟解决的关键问题】本研究以渭干河-库车河绿洲为例,利用线性和非线性曲线拟合模型,分析不同尺度下土壤盐度-环境变量之间的响应关系,以期找出最佳的敏感尺度,提高基于遥感推理土壤盐度的精度。1 研究区概况
渭干河-库车河绿洲(41°06′—41°40′N,82°10′—83°50′E)位于塔里木盆地北麓中段。典型的温带大陆性干旱气候,日平均温度变化剧烈(夏天最高温度超过40℃),年平均降水量67.5 mm。由于极端的气候,地质环境和不合理的农业管理的影响,导致本地土壤盐渍化现象普遍。自然条件下植被覆盖度较低,优势植被群落包括芦苇(Phragimites australis),柽柳(Tamarix ramosissima),骆驼刺(Allhagi sparisifolia),花花柴(Karelina caspica)和盐爪爪(Kalidium gracile)。严重的地区出现盐壳风化现象(Salt efflorescence)。相比阜北地区和玛纳斯河绿洲而言,该地区盐渍化现象更为典型和严重。2 数据与方法
2.1 数据
2.1.1 采样数据 本研究使用的样本采样时间为2015年7月10—17日,样本量为87个,每个样点采集5个样本进行混合。研究团队自2005年至今对渭干河-库车河绿洲进行多次采样(每年至少一次),本次样点布局充分考虑到研究区的土地利用方式和不同盐度土壤的分布格局。样本覆盖以下几种土地利用类型:农业用地、盐土、荒漠、低覆盖草地、中等覆盖草地、灌丛。每个样点采集5个样本,覆盖面积范围为30—250 m2。查阅新疆各个典型绿洲关于土壤盐分的空间变程后发现,自相关距离在1.14—27.45 km。而本研究最小分辨率为1 km,小于上述区间。所以,可以认定1 km以内的土壤盐度是相对同质的,或者变异性较小。土样采集深度为:0—10、10—20、20—40和40—60 cm。土样去除杂质,经过2 mm筛后,以20 g土样中加入100 mL蒸馏水进行充分混合,待过滤后,利用土壤溶液电导率仪(Merck Millipore, Billerica, MA, USA)测量土壤溶液电导率(ms·cm-1)。2.1.2 遥感数据 为了更好的拟合图像数据与地面实测土壤盐度数据,且减少大气对最终结果的影响,研究利用遥感软件ENVI5.1(ITT VIS, 2014)中的FLAASH(Fast Line-of-Sight Atmospheric Analysis of Spectral Hypercubes)模块对原始数据进行大气校正。模型中的主要参数包括大气模式(设定为中纬度夏天(Mid-Latitude Summer)),气溶胶模式(选择乡村(Rural))。最终将辐射率转化为地表反射率,为计算指数提供相对精确的数据支持。本文使用的遥感数据为Landsat 8 OLI,影像获取时间为2015年7月15日,行列号为145/31。
2.2 方法
2.2.1 环境变量 因地理环境的不同,借助遥感数据构建的各种指数在其研究区表现出对土壤盐度的高敏感性,在其他地区是否依然能够保持这种特性还有待商榷。目前已有多个植被和盐度指数被应用到世界各地测试间接推理土壤盐度的潜力,其中植被指数包括NDVI[18]、EVI[19]、GARI[20]、CRSI[20]、COSRI[21]、GDVI[22]、SAVI[23]、TGDVI[24]、ENDVI[17]、EEVI[17],盐度指数包括SI-T[25]、S2[26]、SI2[27]、SI3[27]、NDSI[28]。然而,仅BRUNNER等[18]利用NDVI 在新疆的博斯腾湖地区评价过土壤盐度,其他指数均较少应用到新疆地区。而探寻指数与土壤盐度之间的定量关系,对于识别潜在的土壤盐渍化土地以及制定相关利用措施有重要意义。另外,研究还选用了图像变换衍生因子(主成分分析和缨帽变换)和土壤湿度指数。其中后者,即归一化红外指数(即湿度指数)(Normalized Difference Infrared Index, NDII),不仅与冠层湿度有关,还与盐度有关,原因在于融合了Landsat TM的第五波段信息。其他非植被指数类环境协同变量,主成分分析(Principal Component Analysis, PCA)的前三个波段(PCA1、PCA2、PCA3)占整体信息的90%以上和缨帽变换(Tasseled Cap, TC)。TC变换将陆地表面的信息转化成若干个主题指数,如亮度(Tasseled Cap Brightness, BRI),植被绿度(Tasseled Cap Green, GRE)和土壤湿度(Tasseled Cap Wet, WET)信息。其中亮度指数可近似作为土壤反照率或者反射率的相关指示因子。
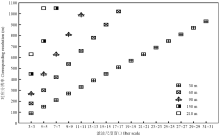
2.2.2 尺度变换 本文主要基于升尺度方法研究不同像元分辨率对土壤盐分-植被指数之间关系的影响。研究将采用两种方法进行升尺度变换。一是利用ENVI 5.1中的重采样模块(RESIZE DATA)将30 m的反射率数据进行重采样,重采样方法选择最邻近(Nearest Neighbor)算法,此方法相对于双线性内插法(Bilinear)和三次卷积内插法(Cubic Convolution)而言,更接近真实值。最终将30 m的原始反射率数据依次重采样成60、90、150、 210、270、330、390、 450、510、630、690、750、810、870、930和1 000 m,将重采样后的反射率数据分别计算2.2.1节中提及的指数和衍生因子,如此共计产生374个环境变量。二是借助GRASS 7.1 的r.param.scale尺度转换模块,按照n×n移动窗口分别计算3×3,5×5,7×7,…,31×31多个领域滤波,窗口大小为奇数,数值间隔为2,具体计算方法详见图1。纹理计算中,初步选择了5种原始分辨率,分别是30、60、90、150和210 m,纹理尺度窗口则选择了(3×3)—(31×31)共计15个级别,如此则对应33个尺度(分辨率)(图1)。每种分辨率下都是优先进行原始反射率数据的纹理计算,之后所形成的新波段数据再计算文中选择的22个指数和主题因子(2.2.1),由此共计获取726个环境变量。
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图1原始分辨率经过滤后对应的空间分辨率
-->Fig. 1Schematic of sampling grid illustrating the grid resolution-neighborhood extent combinations used in this study
-->
2.2.3 统计分析 采用线性和非线性相关性方式检验和分析土壤盐分指数和植被指数对土壤盐度的敏感性,具体包括线性模型、对数模型、逆模型、二次函数、立方函数、复合函数、幂函数、S函数、增长函数、指数函数、逻辑模型。
为了评价上述函数的拟合精度,研究引用决定系数R2和显著性检验(Sig.) (2-tailed),定量评估每个指数与不同深度土壤盐度之间的敏感性。其中Sig.<0.05为显著性,Sig.<0.01为极度显著。数据分析和检验均在SPSS 22.0中的曲线拟合函数完成。
3 结果
3.1 土壤盐度统计分析
根据实验统计结果,表1显示了各层数据的基本分布信息。以表层土壤盐度值为例,根据美国盐度实验室的等级划分(非盐渍化:0—2 ms·cm-1;轻度盐渍化:2—4 ms·cm-1;中度盐渍化:4—8 ms·cm-1;重度盐渍化:8—16 ms·cm-1;极度盐渍化:>16 ms·cm-1),从非盐渍化至极度盐渍化排列,样本所占比例依次为16.00%、6.90%、19.50%、17.20%和40.40%,样本土壤已涵盖各个等级。自上而下观察土壤剖面的盐度均值,25%分位数(将各层盐度值由小到大依次排列,87个样本中1/4处的数值即25%分位数),中值(50%)和75%分位数的分布发现,25%分位数的盐度值已是中度盐渍化,剖面盐度呈显表聚态势,以此判定该区土壤盐渍化情况较为严重且普遍。此外,由实测数据得知(数据表未显示),阴离子C1-的平均含量明显高于SO42-和CO32-的含量。原因在于,易溶性盐类上行过程中,氯化物表聚性最为强烈,硫酸盐次之,碳酸盐最弱。由此可得出,此时该绿洲土壤盐类主要以氯化物为主,同时还伴有少量的硫酸盐-氯化物类。Table 1
表1
表1研究区土壤电导率统计分布特征
Table 1Basic statistical characteristics of soil salinity in the study area
| 土层深度 Soil layer(cm) | 最小值 Min (ms·cm-1) | 最大值 Max (ms·cm-1) | 平均值 Mean (ms·cm-1) | 25% | 50% | 75% | 标准差 Standard deviation |
|---|---|---|---|---|---|---|---|
| 0-10 | 0.27 | 143.10 | 21.54 | 4.09 | 11.84 | 22.90 | 29.00 |
| 10-20 | 0.15 | 127.00 | 8.53 | 2.81 | 5.32 | 11.76 | 14.35 |
| 20-40 | 0.09 | 183.50 | 8.29 | 2.26 | 4.51 | 10.22 | 20.02 |
| 40-60 | 0.12 | 139.40 | 6.62 | 1.31 | 4.52 | 7.30 | 15.41 |
新窗口打开
3.2 尺度变换对土壤盐度-环境变量的影响
图2—9显示了本研究所选环境变量在多个尺度下(栅格重采样和领域滤波)解析土壤盐度(不同土壤深度)变异性。需要说明的是,图中所有的横坐标为不同尺度环境变量,即不同尺度下的植被指数、盐度指数及其他衍生因子。因数量较多,在此仅以数字表达,排列顺序则按照30—1 000 m依次排开,变量顺序不变。另外,绘制的解释力图中,研究只选择了显著性Sig.<0.01的变量,其他指数则未参与显示。由图2—5可知,参与计算的11个模型中,有6个模型拟合精度相对较高,包括逻辑模型,成长模型,复合模型,指数模型,S模型和幂函数。同时,前4个模型最大拟合精度要高于后2个模型,此规律适用于除20—40 cm深度之外的其他土层。图6—9中,横坐标的变量排列顺序为30 m的3×3至31×31,随后为60 m的3×3至17×17,如此依次排开,变量顺序则不变。除了表层复合模型缺席之外,上述6个模型都能够捕捉到各层土壤盐度-环境变量之间的响应关系,且响应尺度较多。总体而言,0—10 cm、10—20 cm两个土层处,30、60、90、150和210 m等5个原始分辨率计算的指数拟合精度要高于其领域滤波计算的指数,且随滤波尺度增大而降低,但不绝对。20—40和40—60 cm两个土层的拟合结果与上述两个土层比较,规律不明显。 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图2不同尺度环境变量(栅格重采样模式)对0—10 cm土层盐度的解释力
-->Fig. 2Relationship between different scales of environment variables (grid resolution)and soil salinity (0-10 cm)
-->
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图3不同尺度环境变量(栅格重采样模式)对10—20 cm土层盐度的解释力
-->Fig. 3Relationship between different scales of environment variables (grid resolution) and soil salinity (10-20cm)
-->
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图4不同尺度环境变量(栅格重采样模式)对20—40 cm土层盐度的解释力
-->Fig. 4Relationship between different scales of environment variables (grid resolution) and soil salinity (20-40 cm)
-->
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图5不同尺度环境变量(栅格重采样模式)对土壤盐度(40—60 cm)的解释力
-->Fig. 5Relationship between different scales of environment variables (grid resolution)and soil salinity(40-60 cm)
-->
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图6不同尺度环境变量(领域滤波)对(0—10 cm)土壤盐度的解释力
-->Fig. 6Relationship between different scales of environment variables (neighborhood extent) and soil salinity (0-10 cm)
-->
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图7不同尺度环境变量(领域滤波)对(10—20 cm)层盐度的解释力
-->Fig. 7Relationship between different scales of environment variables (neighborhood extent) and soil salinity (10-20 cm)
-->
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图8不同尺度环境变量(领域滤波)对(20—40 cm)土层盐度的解释力
-->Fig. 8Relationship between different scales of environment variables (neighborhood extent) and soil salinity(20-40 cm)
-->
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图9不同尺度环境变量(领域滤波)对(40—60 cm)土层盐度的解释力
-->Fig. 9Relationship between different scales of environment variables (neighborhood extent) and soil salinity (40-60 cm)
-->
3.3 不同深度最佳响应尺度和变量
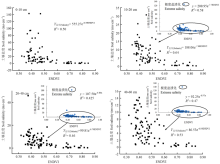
表2总结了两种栅格模式下拟合精度数值和模型参数,并列出各层盐度拟合精度最优尺度和模型。栅格栅格重采样模式中,空间分辨率为30 m下的变量集相对更为敏感。同时,0—40 cm深度的最佳敏感指数皆为扩展性植被指数ENDVI,而40—60 cm处则为植被指数TGDVI。10—20 cm处拟合精度最高,R2=0.46,最低值为R2=0.35 (20—40 cm)。领域滤波模式下,拟合精度最高的尺度为180 m(领域滤波为3×3),响应变量则全为扩展性植被指数ENDVI。最大解释力出现于10—20 cm处,与栅格重采样模式结果相似,能够解释58.10%的盐度变异性,最小值则出现在20—40 cm处,解释力为42.5%。在分析上述两种模式下最优土壤盐度-ENDVI散点图拟合关系时发现(图10和图11),当去除极端案例时,拟合精度会进一步提升(研究区极端盐渍化的覆盖面积相对较少,去除极端案例后的拟合精度更为贴合实际情况)。栅格模式下,10—20和40—60 cm处R2分别提升至47.90%和43.20%。领域滤波模式下,10—20、20—40和40—60 cm处R2分别提升至64.39%、46.21%和52.60%。
Table 2
表2
表2不同深度土壤盐度-植被指数的最佳拟合模型
Table 2The best fit model of soil salinity-vegetation index at different depths
| 尺度转换 Scale transformation | 土层深度 Depth (cm) | 最佳响应尺度 Response scale | 模型类型 Model type | R2 | 模型公式 Function |
|---|---|---|---|---|---|
| 栅格重采样 Grid resolution | 0-10 | 30 m | 成长模型 Growth | 0.43 | Y =exp(3.35-5.55×ENDVI) |
| 指数模型 Exponential | Y =28.45e(-5.55×ENDVI) | ||||
| 10-20 | 成长模型 Growth | 0.46 | Y =exp(2.56-4.93×ENDVI) | ||
| 指数模型 Exponential | Y =12.94e(-4.93×ENDVI) | ||||
| 20-40 | 成长模型 Growth | 0.35 | Y =exp(2.225-4.043×ENDVI) | ||
| 指数模型 Exponential | Y =9.25e(-4.40×ENDVI) | ||||
| 40-60 | 成长模型 Growth | 0.40 | Y =7.77exp(-7.04×TGDVI) | ||
| 指数模型 Exponential | Y =7.68e(-1471.41×TGDVI) | ||||
| 领域滤波 Neighborhood extent | 0-10 | 180 m (3×3) | 指数模型 Exponential | 0.50 | Y =555.47e(-8.391×ENDVI) |
| 成长模型 Growth | Y =exp(6.32-8.391×ENDVI) | ||||
| 10-20 | 指数模型 Exponential | 0.58 | Y =200.95e-7.74×ENDVI | ||
| 成长模型 Growth | Y =exp(5.42-7.91×ENDVI) | ||||
| 20-40 | 指数模型 Exponential | 0.43 | Y =107.50e-6.85×ENDVI | ||
| 成长模型 Growth | Y =exp(4.68-6.85×ENDVI) | ||||
| 40-60 | 指数模型 Exponential | 0.47 | Y =92.25e-6.97×ENDVI | ||
| 成长模型 Growth | Y =exp(4.52-697×ENDVI) |
新窗口打开
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图10去除极端案例下不同深度处土壤盐度-ENDVI/TGDVI的拟合关系(栅格重采样模式)
-->Fig. 10Different depths of soil salinity-ENDVI/TGDVI fitting relationship in grid resampling mode under the removal of extreme cases
-->
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图11去除极端案例下不同深度处土壤盐度-ENDVI的拟合关系(领域滤波模式)
-->Fig. 11Different depths of soil salinity-ENDVI fitting relationship in neighborhood extent mode under the removal of extreme cases
-->
4 讨论
随着空间分辨率的降低,两种模式下的土壤盐度-环境变量拟合精度随之降低。MULLER和van NIEKERK在其研究中对比了多种分辨率下(Rapideye, IRS, SPOT6/7, CBERS4, SENTINEL-2, ASTER)植被指数与土壤盐度之间的响应关系发现,随着分辨率的降低R2值依次降低(0.22—0.66)[29]。本文中的领域滤波模式下以表层盐度拟合关系为例,30 m的滤波由3×3至31×31依次计算,发现拟合精度同样依次降低。但也不绝对,如180 m的 3×3尺度,响应关系明显提升,这与研究区的地理特征和土壤属性的空间变异性有关。整体而言,随着土层深度的增加,该趋势则不明显。由此看来,空间分辨率对拟合精度的影响较为明显。若只用30 m大小的像元去捕捉盐分-地表景观之间的关系,可能会忽视由于尺度影响带来的不确定性。不同传感器获取的固定像元面积就是描述地表景观变异的最佳尺度吗?目前多数研究的地面覆盖的采样面积以像元大小为标准。但土壤属性的空间变异性与地表像元代表的光谱变异性不是一一对应的,这就需要进行研究,到底多大的像元或者空间尺度(由此产生的地表反射率,植被指数,植被覆盖度等特性)可以描述盐分空间的变异性,这就是本文的主题。尺度效应问题同样受到其他****的关注,黄彦等[30]对国内外基于遥感获取植被理化参数因尺度效应产生的原因和空间异质性进行了综述。分析众多文献后发现,当多种地表覆被类型同时出现在单位像元内时,即混合像元现象,会发生尺度效应,由此带来的异质性是产生尺度效应的主要因素。不同的像元(尺度)内的地表景观结构异质性,因分辨率的大小不同程度影响着土壤-植被之间的关系,同时伴随着一定的不确定性。本研究结果显示,像元分辨率180 m是观测本地土壤盐分-植被变化的最优尺度。当研究区发生变化,地表异质性随之改变时,上述尺度还是否是适宜的观测尺度还需要进一步研究。但给予的启发是,基于遥感描述上述关系时,应尝试多种尺度。由郝金标等[31]的研究可以看出,水盐变化导致植被的类型、盖度、频率发生一定的规律性变化。在干旱区,异型性下垫面非常普遍,单位像元下的地表覆被类型各有不同。当地下水位及土壤中的水盐,符合干旱区植被最佳生存环境时,单位面积下的植被类型较为丰富,且类型多样,盖度也会相应增加,此时的异质性也随之加大,而生态水位下降时,生存环境变得苛刻,适应的植被类型减少,即便存在,也多半是耐旱性植被。此时的空间异质性出现下降趋势,地表植被类型单一。裸露的土壤面积加大,异质性的主导因子则转为土壤类型,或者地表土壤的物化属性,涉及地表粗糙度,土壤湿度,土壤颜色等特征。那么针对此问题,单一的尺度未必能很好地诠释不同尺度下由于下垫面异质性而改变的土壤-植被间的关系。
参与计算的各种指数涉及下垫面的相关属性,包括植被覆盖度、土壤湿度、地上植被生物量、土壤亮度、土壤反照率、土壤温度等,但以ENDVI为代表的植被指数响应关系最佳,相对而言,并成明显的负相关关系。其原因可能在于,ENDVI除了NIR和RED波段之外,第三方波段信息的加入,增加了其预测土壤盐度的效能。首先,短波红外的引入增加了植被的信息维度;其次,可见光波段之间和短波红外波段之间呈高度相关性;最后,NIR与可见光和短波红外之间相关性较低[31]。另外,2 100—2 300 nm区具有丰富的植被信息,可以更好地反映植被覆盖度和生长状况[15]。此外,目前该指数在黄河口区效果良好,R2值为0.53(n=113)。本研究结果,以表层为例,在考虑极端案例的情况下,R2值为0.43(栅格重采样)和0.49(领域滤波),样本量为87个,而在不考虑极端案例时,n=86,10—60 cm各土层拟合关系中,R2值都有提升,但领域滤波模式更为明显(R2=0.64)。与前人在该区(渭干河流域)研究对比发现,DING等[32]在构建盐度模型时,综合考虑变量SI(salinity index, SI)和NDVI,拟合精度R2=0.43(n=68),但需要注意的是,该研究中使用时的是EM38大地电导率仪测得的表观电导率,而非饱和溶液电导率值,二者的相关性为R2值为0.663(湿季,7—8月)[31]。对此,需要进一步研究ENDVI与表观电导率之间的关系。
研究结果显示,与线性关系相比,非线性关系更能够表达土壤盐度-植被之间的定量关系。这与MULLER 和 van NIEKERK[29]的研究结果相似,在其研究中显示,土壤盐度与EVI(6 m)之间最佳拟合模型为复合模型,属于非线性模式。FERNÁNDEZ- BUCES 等在其研究中利用构建的联合光谱响应指数(combined spectral response index,COSRI)[21],即NDVI改进型指数(NDVI(B1+B2)/(B3+B4)),与饱和溶液电导率ECe(ms·cm-1)拟合后发现,二者呈现非线性关系(y=348.10e-18.37x,R2=0.83),同NDVI相比,拟合关系更好,但其与盐度之间的非线性关系并没有改变。该指数在本文中并未使用,但在一定程度上说明了上述非线性关系的存在。在查阅相关文献资料后发现,新疆地区的土壤盐分变化与植被物种丰富程度、物种多样性、植被分布频率之间关系较为复杂。郝金标等[31]在其研究中指出,土壤盐分变化与植被物种丰富程度之间呈非线性关系,与物种多样性之间呈线性关系,与植被分布频率之间因植被类型差异即有线性又有非线性关系存在。此外,石瑞花等[33]以新疆焉耆盆地为研究区,分析该地天然植被与地下水关系后发现,乔木、灌木、草本盖度因土壤盐分以及地下水矿化度的变化表现出一定的规律性特征,且皆成指数负相关关系。鱼腾飞等[34]研究中提到,胡杨的平均密度与水溶性盐分含量的关系并非呈线性关系。通过分析上述结果,发现植被盖度或者频率与土壤盐分之间多以负相关出现,并呈非线性关系。上述关系可能与地下水分布关系密切,而地下水位和矿化度之间又呈指数负相关。在渭干河-库车河绿洲地区,当地下水位小于3 m时,地下水的矿化度增加趋势明显。3 m有可能就是盐分聚集速率的分界线,当地下水位大于3 m时的积盐速率要小于地下水位少于3 m的地区。此外,因干旱区,降水稀少,蒸发强烈,多数自然植被依靠地下水位生存。不同植被的出现都与地下水的临界水位有关。张丽等[35]以生态适宜性理论为基础,根据塔里木河干流流域典型植物的随机抽样调查资料,建立了干旱区几种典型植物生长与地下水位关系的对数正态分布模型。由建立的模型得出干旱区典型植物的最适地下水位、适宜地下水位区间及其对环境因子的忍耐度。结论表明,塔里木河干流流域中的几种代表性植被的最适宜的地下水位为1—3 m,而整个干旱区的适宜性生态水位2—4 m。在上述水位范围内的植被长势良好,而地下水位大于4 m时,则植被长势受水分亏缺,或受土壤盐渍化的影响,植被的多样性、盖度和频率都会降低。
本研究以目前应用最为广泛的Landsat数据为依托研究尺度对土壤盐度-环境变量拟合关系的影响,其空间分辨率为30 m,而随着传感器分辨率的不断提升,如worldview-2数据(9个波段,多光谱空间分辨率为2 m,全色波段为0.5 m),为下一步的研究提供新的数据源。本文中栅格重采样的步长为30 m(像元逐个加入),以此计算的多种重采样数据可能存在漏选的尺度,进而随之计算的拟合关系不能精确刻画土壤盐度-环境变量之间动态耦合趋势。高空间分辨率的加入缩短了步长,为改进拟合精度提供了可能性。
5 结论
本文基于遥感分析干旱区绿洲灌区土壤盐度最优预测尺度,初步得出以下结论。即,领域滤波模式和空间重采样模式相比,易于提高土壤盐度-环境变量之间的响应关系。在采用的众多指示因子中,以扩展的归一化植被指数(ENDVI)表现最佳。此外,适于描述本地土壤盐度-环境变量关系的最佳观测尺度为180 m,领域窗口大小为3×3。需要注意的是,因地理环境的差异性,应多尝试几种尺度,以便更好地了解本地的土壤-景观之间的响应关系。The authors have declared that no competing interests exist.
