周萌^,, 韩晓旭, 郑恒彪, 程涛, 田永超, 朱艳, 曹卫星, 姚霞^,南京农业大学/国家信息农业工程技术中心,南京 210095

Remote Sensing Estimation of Cotton Biomass Based on Parametric and Nonparametric Methods by Using Hyperspectral Reflectance

ZHOU Meng^,, HAN XiaoXu, ZHENG HengBiao, CHENG Tao, TIAN YongChao, ZHU Yan, CAO WeiXing, YAO Xia^,Nanjing Agricultural University/National Engineering and Technology Center for Information Agriculture, Nanjing 210095

通讯作者: 姚霞,E-mail： yaoxia@njau.edu.cn

责任编辑: 杨鑫浩
收稿日期:2020-11-25接受日期:2021-02-28

基金资助:

江苏省重点研发计划(BE 2019383) 国家重点研发计划(2019YFE011721) 新疆兵团重大科技项目(2018AA00403) 江苏省“333工程”

Received:2020-11-25Accepted:2021-02-28
作者简介 About authors
周萌,E-mail： 2017101176@njau.edu.cn。










摘要
【目的】利用高光谱遥感数据快速、无损地估算棉花生物量,评估参数化与非参数化方法在棉花上的表现差异。【方法】本研究以4个棉花品种在2个年份(2004和2005年)的试验资料为基础,将2年数据分别进行建模和验证,采用参数化算法(植被指数法、连续小波变换)与非参数化算法(偏最小二乘回归、随机森林、人工神经网络、回归树、袋装树和增强树、支持向量机和高斯过程回归)分别构建吐絮前和吐絮后的生物量估算模型。【结果】近红外与红边波段仍然是棉花生物量遥感监测中最有效的波段区间。参数化方法运算简单,效率高,其中,CI_{red edge}证明是棉花生物量估算上表现最好的植被指数,具有较高的独立验证结果(吐絮前：RMSE=27.23 g·m^-2;吐絮后：RMSE=48.81 g·m^-2)。基于连续小波变换的方法缓解了植被指数的低估现象,尤其是吐絮后(吐絮前：RMSE=31.54 g·m^-2;吐絮后：RMSE=37.57 g·m^-2);在非参数化法中,随机森林是棉花生物量估算的最优算法(吐絮前：RMSE=20.48 g·m^-2;吐絮后：RMSE=30.28 g·m^-2)。吐絮后的估算精度都显著低于吐絮前,表明两类算法的估算精度都受到棉絮的影响。【结论】本研究评估了基于参数化和非参数化算法构建的棉花生物量估算模型,证明了非参数化方法可以作为棉花生物量无损监测的重要研究方法,该结论也为棉花其他生长参数的估测提供了技术支撑。
关键词： 生物量;高光谱;植被指数;连续小波变换;机器学习;棉花

Abstract
【Objective】The aim of this experiment was to use hyperspectral remote sensing data to estimate cotton biomass quickly and non-destructively, and to assess the performance differences between parameterized and non-parametric algorithms on cotton. 【Method】This experiment was based on the dataset of four cotton varieties in two years (2004 and 2005), and the two-year data were modeled and verified respectively. The biomass estimation models in different periods (before and after boll opening) were built by utilizing parameterized algorithms, including vegetation index method and continuous wavelet transform, and non-parameterized algorithms, including partial least squares regression, random forest, artificial neural network, regression tree, bag tree and enhanced tree, support vector machine and Gaussian process regression, respectively. 【Result】Near-infrared and red edge bands were still the most effective bands in monitoring cotton biomass of remote sensing. The parameterized method was simple, efficient and accurate. Among the parametric methods, CI_{red edge} was proved to be the best vegetation index for cotton biomass estimation with high independent verification results (before boll opening: RMSE=27.23 g·m^-2; after boll opening: RMSE=48.81 g·m ^-2). The result based on continuous wavelet transform alleviated the underestimation phenomenon of vegetation index, especially after boll opening (before boll opening: RMSE=31.54 g·m ^-2; after boll opening: RMSE=37.57 g·m ^-2). Among the non-parametric methods, the random forest was the best algorithm for cotton biomass estimation (before boll opening: RMSE=20.48 g·m ^-2; after boll opening: RMSE=30.28 g·m ^-2). The estimation accuracy of the two types of algorithms was affected by cotton wool, and the estimation accuracy after boll opening was significantly lower than before boll opening. 【Conclusion】In this study, the cotton biomass estimation models based on parameterized and non-parameterized algorithms were evaluated, and it was proved that the non-parameterized algorithm had high inversion accuracy and could be used as an important method for non-destructive monitoring of cotton biomass.
Keywords：biomass;hyperspectral;vegetation index;continuous wavelet;machine learning;cotton


PDF (1022KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
周萌, 韩晓旭, 郑恒彪, 程涛, 田永超, 朱艳, 曹卫星, 姚霞. 基于参数化和非参数化法的棉花生物量高光谱遥感估算. 中国农业科学, 2021, 54(20): 4299-4311 doi:10.3864/j.issn.0578-1752.2021.20.005
ZHOU Meng, HAN XiaoXu, ZHENG HengBiao, CHENG Tao, TIAN YongChao, ZHU Yan, CAO WeiXing, YAO Xia. Remote Sensing Estimation of Cotton Biomass Based on Parametric and Nonparametric Methods by Using Hyperspectral Reflectance. Scientia Acricultura Sinica, 2021, 54(20): 4299-4311 doi:10.3864/j.issn.0578-1752.2021.20.005


开放科学（资源服务）标识码（OSID）：

0 引言

【研究意义】棉花是世界上重要的经济作物之一,棉花生产中及时、准确地监测植株长势状况,对棉花的生长诊断和精确管理具有重要指导意义。棉花地上部生物量是反映棉花长势状况的一个重要指标,在准确估测作物产量和品质方面具有重要作用^[1]。【前人研究进展】近年来,遥感无损估测技术的发展为作物生长估测提供了新的方法和手段,在作物长势估测、营养诊断和产量估测等方面均呈现出良好的应用前景^[2]。高光谱遥感具有数据信息丰富、光谱分辨率高和无损监测的特点,通过光谱特征的提取与分析,可获得对作物生长参数、化学组分信息等敏感的波段信息,进而与作物长势和理化参数建立联系进行监测与反演^[3]。总之,高光谱遥感技术在农业领域上发挥了重要作用。在利用高光谱遥感估测作物生物量的研究中,基于经验性模型方法是最方便有效的方法,主要分为参数化算法和非参数化算法两大类,其中最常见的植被指数法就是参数化算法的一种。由于植物叶片在可见光红光波段有很强的吸收特性,在近红外波段有很强的反射特性,因此由可见光波段和近红外波段的线性或非线性组合而成的植被指数蕴含着大量的植被信息,已经广泛应用于作物地上部生物量高光谱估测研究^[4,5,6]。但是,植被指数在估算作物生长参数方面会存在饱和问题,植被指数模型在生物量估算时往往造成较大误差^[6,7,8]。小波变换（wavelet transform,WT）作为另一种参数化算法,可以利用丰富的小波基函数从信号中提取有效信息。该变换分为离散小波变换（discrete wavelet transform,DWT）和连续小波变换（continuous wavelet transformation,CWT）,DWT在分析高光谱数据时在解析输出参数中存在困难,同时CWT可以准确地用于提取光谱特征,已成功用于农作物分类、叶面积指数和叶绿素含量的估算等^[9,10,11]。因此,本研究选用了CWT 对棉花冠层高光谱曲线进行变换。已有研究证明了最佳CWT模型在估算小麦冠层叶片生物量上比最佳的植被指数模型更准确,并且比较了提取的最佳小波系数在不同品种、不同生长阶段和不同地点的表现,证实了CWT用高光谱数据估算冠层叶片生物量的高度稳定性^[12]。但是CWT估测生物量在棉花上的表现还需要进一步探索。由于冠层光谱受到不同环境、不同时期下生长环境的复杂影响,光谱信息和生理生化参数之间的关系不是简单的线性关系,基于植被指数和小波系数构建的估算模型没有体现出其他因素的影响,从而导致准确性、普适性和鲁棒性较低,因此基于非参数化的机器学习算法逐渐受到重视。非参数化算法不同于参数化算法的地方在于它通常基于完整的光谱集进行建模,能够充分利用光谱信息。其次,参数模型可以用数学表达式表示出来,非参数化模型却不能明确表达。近年来,越来越多的研究通过非参数化算法建立作物的遥感估测模型,其中随机森林（random forest,RF）对高光谱遥感数据的应用效果较好。例如,作物叶绿素含量、叶面积指数、氮素含量以及产量都利用RF获得了较高的反演精度^{[13,14,15,16]}。人工神经网络（artificial neural networks,ANN）同样也是一种实时高效的机器学习算法,研究表明基于BP神经网络（back-propagation neural networks,BPNN）的方法相对于高光谱植被指数回归模型能够显著提高小麦生物量的反演精度,尤其是对于比值植被指数（ratio vegetation index, RVI）,T值提高的幅度达99.8%^[17]。除此之外,支持向量机（support vector machine,SVM）、偏最小二乘法（partial least-squares regression,PLSR）与回归树（regression trees,RT）等算法也流行于作物生长参数遥感估算研究中^[18,19,20]。在棉花作物上,随机森林算法是预测SPAD和土壤含水率的最优反演模型^[21,22],支持向量机和神经网络算法被证实在预测棉花产量时优于多元线性回归模型^[23],BP神经网络建立的棉花冠层等效水厚度模型具有更好的建模效果和预测精度,优于支持向量机^[24]。然而其他非参数化算法在估算棉花生长参数上的应用鲜有报道。【本研究切入点】虽然这些算法都能够达到实时反演农作物生长参数的目的,但是对于棉花生物量的高光谱估算研究,至今为止,仍旧没有系统地研究对比与验证不同算法之间的表现差异。并且与小麦、水稻不同的是,棉花在吐絮后冠层结构发生较大变化,建立准确的棉花吐絮前和吐絮后的生物量模型具有潜在的研究价值。【拟解决的关键问题】本研究以不同年份、品种和施氮水平的棉花田间试验数据和冠层高光谱反射率数据为基础,通过分析高光谱反射率与不同品种棉花的生物量的相关性,提取棉花生物量的敏感波段;采用参数化以及非参数化算法,分别构建棉花生物量的遥感估算模型,全面评估比较不同方法的估算结果;探究棉花花絮对棉花生物量估算的影响,比较分析吐絮前与吐絮后的反演结果,为基于高光谱遥感的棉花生长监测和精确管理提供理论依据和技术支持。

1 材料与方法

1.1 试验设计

试验1：2004年在南京农业大学江浦试验站进行。前茬作物为大豆,土壤为重黏土。供试棉花品种为中棉29（杂交棉）和苏棉12（常规棉）,4月16日播种,5月21日移栽。设4个施氮水平,N₀（不施N）,N₁（150 kg·hm^-2纯氮）,N₂（300 kg·hm^-2纯氮）,N₃（450 kg·hm^-2纯氮）,氮种肥﹕第1次花铃肥﹕第2次花铃肥=2﹕5﹕3。试验为两因素随机裂区排列,氮肥为主区,品种为副区,各3次重复。小区面积为30 m²（6 m×5 m）,等行距种植,杂交棉的行、株距为0.75m×0.40m,常规棉的行、株距为0.75 m×0.27 m,移栽密度分别为杂交棉3.3×10⁴株/hm²,常规棉4.95×10⁴株/hm²。同时各处理配施P₂O₅ 225 kg·hm^-2,K₂O 450 kg·hm^-2;磷、钾运筹为种肥占50%,第1花铃肥占50%。全生育期化学调控,其他管理措施按高产要求进行。

试验2：2005年在江苏省淮安市宝应湖农场进行。前茬作物为大豆,土壤为黄棕壤土。供试品种为科棉1号（杂交棉）、美棉33B（杂交棉）,4月26播种,5月25移栽。设3个施氮水平,N₀（不施N）,N₁（240 kg·hm^-2纯氮）,N₂（480 kg·hm^-2纯氮）,氮肥运筹为基肥50%、盛蕾初花期施肥50%。试验为两因素随机裂区排列,氮肥为主区,品种为副区,各3次重复。小区面积为41.04 m²（7.6 m×5.4 m）,等行距种植,行、株距为0.90 m×0.30 m,移栽密度为3.75×10⁴ 株/hm²。同时各处理配P₂O₅ 150 kg·hm^-2,KCL 225 kg·hm^-2,均作为基肥施入。全生育期化学调控,其他管理措施按高产要求进行。

1.2 数据获取

1.2.1 冠层高光谱反射率 本研究采用美国ASD公司生产的FieldSpec Pro FR^TM光谱仪定期测定不同小区的冠层光谱反射率。光谱仪的波段范围为350— 2 500 nm,其中350—1 000 nm光谱采样间隔（波段宽）为1.4 nm,光谱分辨率为3 nm,1 000—2 500 nm光谱采样间隔（波段宽）为2 nm,光谱分辨率为10 nm。测量时探头垂直向下,距离冠层垂直高度约1 m,于棉花封行后开始测试,选择在晴朗无云或少云的天气进行,测量时间为10：00—14：00（太阳高度角大于45º）。每次采集目标光谱前后都进行参考板校正。每小区重复测定5次,取平均值作为该小区的光谱测量值。

1.2.2 生物量 与光谱测量同步,每次每小区取代表性植株2株,将棉花植株按器官进行分离,分为叶、茎、铃,将器官分离后的样品放置在烘干器内,调整其温度为105℃进行30 min的杀青工作,再将烘干器温度调至80 ℃下烘干至恒重,分别称取烘干之后的棉花各器官干物重,最后各器官加起来得到地上部生物量,2年试验季实测的生物量数据汇总如表1所示。

Table 1
表1
表12个试验季棉花生物量实测数据总结
Table 1Summary of cotton biomass measured data in two experiments

试验 Experiment	样点数 Number of samples	生物量Biomass (g·m-2)
		最低值Min	平均值Mean	最大值Max
试验1 Experiment 1	100	14.4	50.9	140.9
试验2 Experiment 2	80	20.0	95.5	155.2

新窗口打开|下载CSV

1.3 研究方法

1.3.1 参数化的生物量估算方法

1.3.1.1 植被指数法 植被指数的构建能够增强植被生理生化反应对冠层反射率的敏感程度,本文在已有研究的基础上,利用高光谱波段计算了14种在生物量估算方面应用较广泛且效果较好的植被指数,如表2所示。分析植被指数与棉花生物量的相关关系,筛选出对棉花生物量敏感的最佳植被指数,然后分别建立最佳植被指数的遥感估算模型。

Table 2
表2
表2高光谱植被指数计算方法
Table 2Algorithm of different hyperspectral vegetation indices

植被指数 Vegetation index	名称 Name	公式 Formula	文献 Reference
DI	差值指数 Difference index	R800 -R550	[26]
DVI	差值植被指数 Difference vegetation index	R800 -R680	[27]
RVI	比值植被指数 Ratio vegetation index	R787/R765	[5]
SRPI	简单比值色素指数 Simple ratio pigment index	R430 /R680	[28]
NPCI	叶绿素归一化植被指数 Chlorophyll normalized vegetation index	(R680-R430)/(R680+R430)	[29]
MTCI	中分辨率陆地叶绿素成像指数 MERIS terrestrial chlorophyll index	(R750-R710)/(R710-R680)	[30]
DATT	DATT	(R800-R720)/( R800 -R680)	[31]
CIred edge	红边叶绿素指数 Red edge chlorophyll index	(R800 /R720)- 1	[32]
NDVI	归一化植被指数 Normalized vegetation index	(R780-R670)/(R780-R670)	[33]
GNDVI	绿色归一化植被指数 Green normalized vegetation index	(R801-R550)/(R800+R550)	[34]
EVI	增强型植被指数 Enhanced vegetation index	2.5×(RNIR /RRED )/(RNIR+6.0×RRED-7.5×RBLUE+1)	[35]
OSAVI	优化土壤调整植被指数 Optimized soil-adjusted vegetation index	1.16×(RNIR-RRED)/(RNIR+RRED+0.16)	[36]
PRI	光化学植被指数 Physiological reflectance index	(R531-R570)/(R530+R570)	[37]
TVI	三角形植被指数 Triangle vegetation index	0.5×[120×(R750-R550)-200×(R670-R550)]	[38]

新窗口打开|下载CSV

1.3.1.2 连续小波变换 CWT通过小波基函数将高光谱数据分解成不同尺度上的一系列的小波系数,其变换公式如下：

（1）$WF(a,b)\le \text{f};{{\psi }_{(a,b)}}\ge \int_{-\infty }^{+\infty }{\text{f(t)}}{{\psi }_{\text{a,b}}}(\text{t})\text{dt}$
（2）$\text{ }{{\text{ }\!\!\psi\!\!\text{ }}_{\text{(a,b)}}}\text{ (t)=}\frac{1}{\sqrt{\text{a}}}\text{ }\!\!\psi\!\!\text{ (}\frac{\text{t-b}}{\text{a}}\text{)}$
式中,f（t）是棉花冠层高光谱反射率数据,t为波段;ψ_a,b（t）为小波基函数,a为尺度因子,本研究中的尺度为3、4、5、6,b为平移因子。WF（a, b）为小波系数,也称为小波特征（Wavelet feature）。

CWT将一维棉花高光谱反射率数据转换为不同尺度的二维小波系数,通过与棉花生物量进行相关分析,进而建立生物量反演模型。

1.3.2 非参数化的生物量估算方法 非参数模型对于总体的分布不做任何假设,只是知道总体是一个随机变量,只有在给定一些样本的条件下,能够依据非参数统计的方法进行推断。非参数算法可以分为线性和非线性回归方法,后者通常也称为机器学习回归算法。在这项研究中,使用了8种非参数算法对棉花生物量进行估算,分别是偏最小二乘回归（partial least-squares regression,PLSR）、随机森林（random forest,RF）、人工神经网络（artificial neutral networks,ANN）、回归树（regression trees,RT）,袋装树（bagging trees,BaT）和增强树（boosting trees,BoT）、支持向量机（support vector machine,SVM）和高斯过程回归（gaussian processes regressions,GPR）。其中,PLSR为线性回归方法,其他都为非线性回归,表3参照VERRELST等^[25]对这些算法进行了全面描述。以上算法的输入量均为获取的冠层高光谱和生物量实测值数据,共计样本数为180个。

Table 3
表3
表3非参数化算法
Table 3Non-parametric algorithm

算法 Algorithms	核心算法 Core algorithm	文献 Reference
PLSR	Matrix inversion	[39]
RF	Bootstraping	[40]
ANN	Levenberg-Marquardt algorithm	[41]
RT	Sorting & grouping	[42]
BaT	Bootstrap aggregation (bagging) + RT	[43]
BoT	Least squares boosting + RT	[44]
SVM	Bayesian statistical inference	[20]
GPR	Bayesian statistical inference	[45]

新窗口打开|下载CSV

1.4 模型校准与验证

为确保模型的稳定性和适用性,将2个年份的数据样本分开采取独立验证的方法,第1年的样本数据用于建模,而第2年的样本用于模型验证。本研究采用决定系数（R²）以及均方根误差（root mean square error, RMSE）作为模型预测精度的评价标准（公式3—4）。其中,R²越接近于1,RMSE越小,表明模型的预测精度和稳定性越高。

（3）$R^{2}=1-\frac{\sum_{i=1}^{n}(y_{i}-x_{i})^{2}}{\sum_{i=1}^{n}(y_{i}-\overline{y}_{i})^{2}}$
（4）$RMSE=\sqrt{\frac{1}{n} \sum_{i=1}^{n}(x_{i}-y_{i})^{2}}$
式中,x_i和y_i分别是基于不同模型的生物量预测值和实测的生物量值。

2 结果

2.1 高光谱反射率与棉花生物量的相关性分析

图1展示了4个不同棉花品种分别在吐絮前与吐絮后各波段的光谱反射率与生物量的相关系数曲线。由于植被光谱在可见光和近红外波段内具有植被的独特特性,能够区别于其他地物,所以本结果只展示了此范围内的相关关系图。

图1

新窗口打开|下载原图ZIP|生成PPT
图1不同棉花品种在不同生育时期的光谱反射率与生物量的相关系数

Fig. 1The correlation coefficient between spectral reflectance and biomass of different cotton varieties at different phenological stages



从图中可以看出,光谱反射率与生物量的相关性在吐絮期前后表现出较大差异,总体上吐絮前的相关性优于吐絮后,吐絮前最大负相关系数和最大正相关系数分别为-0.61、0.78,吐絮后分别为-0.43、0.60。吐絮前,在490 nm之前的光谱范围内,所有品种棉花的冠层反射率与生物量都呈现正相关关系。在490 nm至730 nm光谱范围内,高光谱反射率与生物量呈显著负相关关系,都在红边波段范围内的相关性最强,相关关系最大达0.61;在波段730 nm以后,反射率与生物量继续呈正相关关系,相关系数基本平稳在0.5以上。吐絮后,蓝波段和绿波段范围内的相关关系增强,红波段以及红边处的负相关关系减弱,美棉与中棉甚至降低到0。在720 nm以后,4个棉花品种在吐絮期后的高光谱反射率对生物量的敏感性较一致,相关系数稳定在0.4左右。

由此可见,高光谱反射率在可见光500—670 nm内与生物量呈负相关,而在近红外680—1 300 nm呈正相关,其中以绿光波段600 nm附近、红边波段700 nm附近和近红外波段800—1 100 nm范围内与棉花生物量的相关性最高,因此选择此范围内波段为特征波段,进而构建的植被指数可以更灵敏地探测棉花生物量信息。另外,受棉花冠层结构影响,吐絮前后的高光谱信息对生物量的敏感性存在差异。

2.2 棉花生物量估算模型的构建和验证

2.2.1 基于植被指数法的棉花生物量估算模型 根据高光谱反射率与棉花生物量的相关性规律,选择了14种由以上敏感波段组合的植被指数进行相关性分析,2004年各植被指数与不同时期棉花生物量之间的相关关系如表4所示。吐絮前,除DVI和TVI没有达到0.05显著水平外,其他植被指数都达到0.01极显著水平,与吐絮前棉花生物量相关性最高的植被指数为GNDVI,相关系数达0.67,其次是DATT和CI_{red edge}（相关系数分别为0.63和0.59）。吐絮后,除RVI外其余植被指数都达到0.05显著水平,此时期与生物量相关系数最高达0.55,整体相关性水平较吐絮前低,DATT、CI_{red edge}和GNDVI 3种植被指数仍然在吐絮后表现最好（相关系数分别为0.55、0.55和0.53）。此外,在整个生育期中,除NPCI与生物量存在负相关关系外,其余植被指数都为正相关关系。图2选取了相关系数最高的植被指数分别建立与生物量之间的关系,可以看出植被指数在生物量较高水平下,尤其在吐絮后,呈现饱和现象。

Table 4
表4
表4各植被指数与棉花生物量之间的相关关系
Table 4Correlation between vegetation indices and cotton biomass

植被指数 Vegetation index	相关系数 Correlation coefficient			植被指数 Vegetation index	相关系数 Correlation coefficient
	吐絮前 Before boll opening	吐絮后 After boll opening			吐絮前 Before boll opening	吐絮后 After boll opening
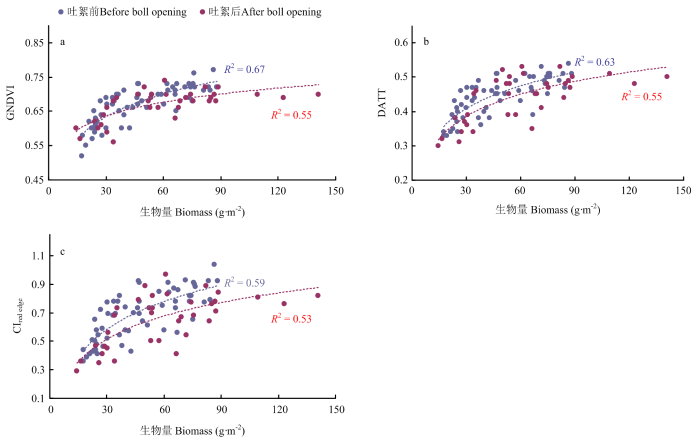
GNDVI	0.67**	0.55**		PRI	0.23**	0.28*
DATT	0.63**	0.55**		RVI	0.26**	0.03
CIred edge	0.59**	0.53**		EVI	0.15**	0.30**
MTCI	0.56**	0.50**		OSAVI	0.18**	0.33**
SRPI	0.34**	0.43**		DI	0.13**	0.16**
NPCI	-0.34**	-0.42**		DVI	0.07	0.14*
NDVI	0.29**	0.36**		TVI	0.04	0.10*

*和**分别表示在0.05和0.01水平上显著
*, ** indicate significant difference at 0.05 and 0.01 levels, respectively

新窗口打开|下载CSV

图2

新窗口打开|下载原图ZIP|生成PPT
图2最佳植被指数与棉花生物量的散点图

a：GNDVI,b：DATT,c：CI_{red edge},蓝色虚线和红色虚线分别是吐絮前和吐絮后数据点的最佳拟合函数
Fig. 2Cotton biomass plotted against best vegetation index

a: GNDVI, b: DATT, c: CI_{red edge}, the blue dotted line and red dotted line are the best-fit function of the data points before and after boll opening, respectively


选取GNDVI、DATT和CI_{red edge}分别用于构建棉花生物量吐絮前后的遥感估算回归模型,并用2005年份的棉花实测数据对模型进行验证,通过分析实测值与预测值的 R² 和 RMSE 评价估算模型的可靠性,不同生育时期验证结果如图3所示。基于CI_{red edge}的模型验证结果最优,吐絮前后的生物量预测值与实测值间的RMSE分别为27.23、48.81 g·m^-2。从植被指数估算棉花生物量的结果来看,吐絮前的预测精度远远优于吐絮后,并且植被指数反演的全生育期生物量较实测值都存在低估现象。

图3

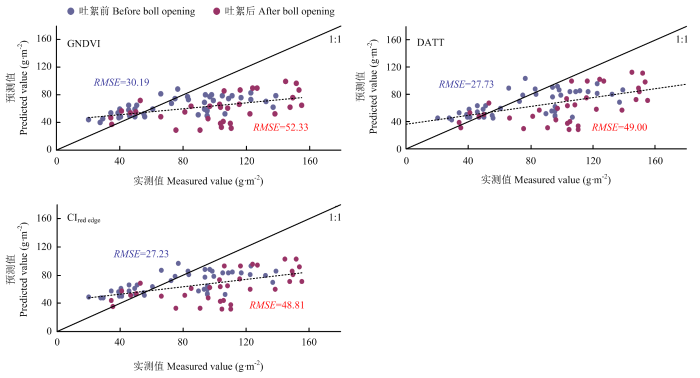新窗口打开|下载原图ZIP|生成PPT
图3最佳植被指数估测棉花生物量的全生育期预测值与实测值比较

Fig. 3Comparison of the predicted value and the measured value of the best vegetation index monitoring cotton biomass for the whole senson



2.2.2 基于连续小波变换的棉花生物量估算模型 图4为CWT处理后不同小波特征与全生育期棉花生物量的相关系数图,红色部分代表相关性强（相关系数大于0.3）的区域。由于植被生物量与可见光和短波近红外波段光谱密切相关,本研究得出的长波近红外未存在红色区域,因此图3仅显示出350 —1 350 nm范围内小波特征与生物量的相关系数图。从图中可以看出,当尺度为3时,与生物量相关性最高的小波特征所在的敏感波段集中在476—482、570、710—721和1 201—1 203 nm处;当尺度为4时,主要集中在713—722 nm和1 201—1 212 nm处;当尺度为5时,主要集中在586—595 nm和714—724 nm处;当尺度为6时,主要集中在715—727 nm和1 065—1 117 nm处。在720 nm附近,基于4种尺度的小波特征都与生物量的相关性显著,可见720 nm处的红边区域在基于连续小波变换估算棉花生物量中是可靠性较高的光谱波段。另外,小波特征WF（6,1 100）附近存在较宽的敏感波段范围,证明1 100 nm处连续波段分解的小波系数在棉花生物量估算中较稳定。

图4

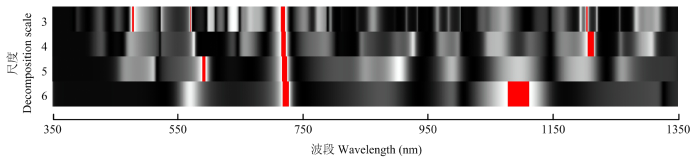新窗口打开|下载原图ZIP|生成PPT
图4CWT小波特征与棉花生物量的相关系数

Fig. 4Correlation coefficient between CWT wavelet features and cotton biomass



分别选取各尺度中相关系数最高的小波特征作为自变量,建立吐絮前后的棉花生物量估算模型并且进行验证,建模与验证结果如表5所示。基于不同时期4种不同尺度建立的模型都为指数函数,决定系数都随尺度的增加而升高,尺度为6时模型的拟合效果最好,吐絮前后的R²分别达到0.59和0.55。基于4种尺度得到的小波特征建立的回归模型在吐絮前均具有较高的验证精度,决定系数R²均在0.55以上,RMSE在31.54—38.43 g·m^-2之间。基于小波变换法的生物量估算在吐絮后的验证精度略低于前期（RMSE在36.49—48.41 g·m^-2之间）。

Table 5
表5
表5基于CWT不同尺度的棉花生物量估算模型
Table 5Cotton biomass monitoring model based on different scales of CWT

时期 Stage	波段 Band (nm)	尺度 Scale	模型 model	决定系数 Coefficient of determination (R2)	验证 Validation
					R2	RMSE (g·m-2)
吐絮前 Before boll opening	1202	3	y = 11.96e-197.80x	0.41**	0.57	38.43
	1209	4	y = 11.11e-68.73x	0.48**	0.63	31.54
	720	5	y = 60.34e-3.52x	0.58**	0.59	34.56
	722	6	y=44.45e-4.19x	0.59**	0.58	36.47
吐絮后 After boll opening	1202	3	y = 8.63e-259.6x	0.40**	0.50	36.49
	1209	4	y = 9.40e-78.69x	0.40**	0.48	37.57
	720	5	y = 78.25e-3.49x	0.46**	0.55	48.41
	722	6	y=53.43e-4.80x	0.55**	0.54	39.50

新窗口打开|下载CSV

对比不同尺度的验证结果,尺度为4建立的模型反演后的RMSE在全生育期中最低（RMSE在吐絮前后分别为31.54 g·m^-2和37.57 g·m^-2）（图5）。值得一提的是,与植被指数结果相比,基于CWT的棉花生物量估算的低估现象在吐絮后都得到了明显改善。

图5

新窗口打开|下载原图ZIP|生成PPT
图5最佳小波特征估算棉花生物量的全生育期预测值与实测值比较

Fig. 5Comparison of the predicted value and the measured value of the best wavelet features for monitoring cotton biomass for the whole season



2.2.3 基于非参数建模算法的棉花生物量估算模型 在这项研究中,一共使用了8种非参数建模算法来估算棉花的生物量（表6）。在吐絮前,从建模结果看,BoT的建模精度最高（R²=0.96,RMSE=3.56 g·m^-2）,可以高度模拟高光谱数据与棉花生物量之间的关系。除PLSR和RF外,所有算法建模精度都保持在较高水平,R²在0.72—0.94范围内,RMSE始终低于10 g·m^-2。从预测结果看,虽然RF的建模表现不如其他算法,但是在预测棉花生物量方面表现最佳,R²和RMSE都保持在首位（R²=0.53,RMSE=20.48 g·m^-2）。其次GPR和PLSR也表现出较好的预测精度,RMSE分别为29.16 g·m^-2和30.28 g·m^-2。非参数建模算法在吐絮前的生物量预测值与实测值间的RMSE均在50 g·m^-2以下。在吐絮后,以上算法的建模与验证精度整体都显著下降,BoT的建模精度和RF的验证精度仍然最高（BoT：R²=0.91,RMSE=7.73 g·m^-2,RF：R²=0.65,RMSE= 30.28 g·m^-2）。除PLSR的预测集RMSE在30.59 g·m^-2较低水平,其他算法都在50 g·m^-2附近,最高达54.53 g·m^-2。

Table 6
表6
表6基于非参数建模算法的棉花生物量估测模型的建模集和预测集结果
Table 6Calibration and validation results of estimation models for cotton biomass based on non-parametric modeling algorithms

方法 Methods	吐絮前Before boll opening				吐絮后After boll opening
	建模集Modeling		预测集Predicting		建模集Modeling		预测集Predicting
	R2	RMSE (g·m-2)	R2	RMSE(g·m-2)	R2	RMSE (g·m-2)	R2	RMSE (g·m-2)
RF	0.76	11.14	0.53	20.48	0.57	16.43	0.65	30.28
SVM	0.84	7.47	0.44	33.55	0.67	14.61	0.54	44.25
GPR	0.85	7.28	0.38	29.16	0.38	19.49	0.39	53.84
BaT	0.72	9.30	0.24	39.92	0.41	17.89	0.35	51.61
BoT	0.96	3.56	0.22	39.71	0.91	7.73	0.36	51.38
RT	0.94	5.06	0.30	40.99	0.90	9.32	0.42	54.53
PLSR	0.43	15.91	0.13	30.28	0.35	23.79	0.19	30.59
ANN	0.83	9.76	0.57	38.09	0.69	23.41	0.42	51.99

新窗口打开|下载CSV

仅比较8种算法的整体预测结果,无论在吐絮前还是吐絮后,RF在这项研究中表现最好。图6选取RF算法,展示了它在棉花生物量估算中的结果。与植被指数法和连续小波变换法相比,RF的低估现象最轻微,估算结果也最靠近于1﹕1线。吐絮前的生物量预测值与实测值间的RMSE在所有方法中最低,为20.48 g·m^-2,吐絮后也表现出最优的估算结果,RMSE为30.28 g·m^-2。

图6

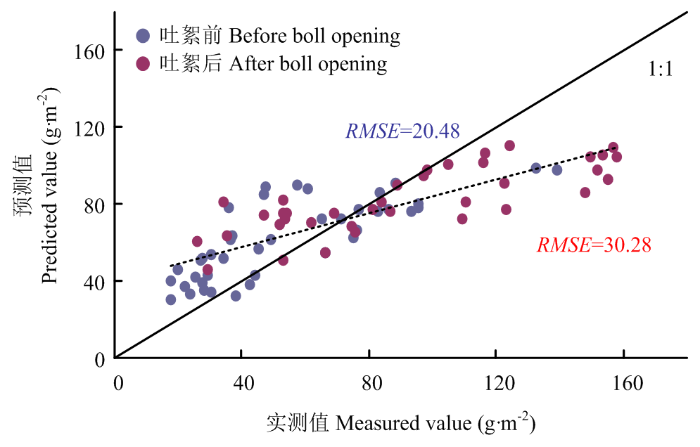新窗口打开|下载原图ZIP|生成PPT
图6RF估算棉花生物量的预测值与实测值比较

Fig. 6Comparison of the predicted value and the measured value of cotton biomass with RF

3 讨论

3.1 植被指数法估算棉花生物量的能力

高光谱遥感因其高光谱分辨率的特点在作物生长监测中具有较大的优势,因此本研究通过高光谱数据探究了不同算法估算棉花生物量的能力。植被指数法被广泛运用于地表植被调查和研究,由于植被在400—700 nm波段范围内的反射光谱主要受叶绿素及叶片的细胞排列方式的影响,近红外波段720—1 100 nm又对冠层结构反应敏感,利用这些波段反射光谱组合产生的大量植被指数可有效用于植被的生长监测研究,本试验就是基于这些植被指数来对棉花生物量进行反演研究的。结果显示DATT和CI_{red edge}的估算效果最好,DATT是由红边波段720nm、红光波段680nm和近红外波段800 nm 3个波段建立的植被指数,被证明是有效评估叶绿素含量的新指标^[31],CI_{red edge}是由红边波段720nm和近红外波段800 nm 2个波段建立的植被指数,与叶面积指数密切相关,二者同样适用于生物量的光谱估算。由此可见,近红外波段与红边波段是生物量研究中最敏感的光谱信息,同时也是对已有文献中研究结果的补充和验证^[46,47]。

在生物量的监测中,光学植被指数能够增强绿色植被的光谱贡献,同时最小化土壤背景、传感器和大气带来的影响,但是光谱指数在高冠层覆盖下的生长后期会存在饱和现象。同时在本研究中,植被指数法在估算棉花生物量呈现出的低估现象可能还受到棉花结构的影响。植被指数反映的是植被覆盖度的生长状况,随绿色植被生物量的增加而迅速增大。但是棉花在进入吐絮期后,白色棉絮渐渐显露出来,冠层结构发生变化,导致吐絮前后冠层反射率产生较大差异,地上部生物量增加的同时植被指数却因棉絮受到影响,会导致低估现象的出现。本研究结果中,造成吐絮后的验证精度大大低于吐絮前精度的原因也在于此。因此,植被指数法估算棉花生物量仍具有一定的局限性。

3.2 连续小波变换估算棉花生物量的能力

CWT作为一种光谱数据处理方法可以很好地挖掘微弱且有效的光谱信息,在作物生长参数反演中具有重要意义。利用CWT对高光谱连续分解后,小波特征与生物量相关性最高的波段仍稳定分布在近红外与红边波段,以小波特征WF（6,722）的相关系数最高,与植被指数的结论相似。与基于CWT进行小麦生物量监测研究的不同之处在于,WF（8,1197）是小麦生物量监测最有效的小波特征,此波段为水、纤维素、淀粉和木质素的吸收波段,位于LAI敏感的近红外区域,与生物量高度相关^[12]。在小麦叶面积指数的研究中,小波特征WF（6,1006）最敏感,与叶面积指数的相关系数变化范围为0.84—0.91。位于红边和近红外区间的小波特征WF（11,717）和WF（8,759）是监测小麦叶绿素含量的首选^[48,49]。综合前人研究,对小麦和棉花生化参数敏感的最佳小波特征分布全部集中在700—1 250 nm的光谱区间内,1 300 nm后的小波特征在冠层的表现较差,连续小波变换尺度多以低尺度10附近最佳。

由于CWT本身利用多尺度分解特性获取生物量的吸收特征的物理学意义,并且小波特征在整个生育期的生物量建模中都未出现饱和现象,因此基于CWT的反演结果缓解了吐絮期后植被指数反演存在的低估现象,有广泛的应用前景,但是反演精度有待进一步提高。

3.3 非参数化算法估算棉花生物量的潜力

众所周知,植被冠层光谱特征受到多种生理生化因素的共同影响^[50],参数化回归方法仅利用单一因素建模不能很好地处理混杂因素,非参数化方法能够模拟因变量与多种因素的复杂关系,因此多数非参数化方法的性能更好。并且与前2种参数化法相比,非参数化方法最大的优势还在于它能够充分利用所有光谱信息,不会遗漏有效信息。这项研究的结果表明,BoT的建模精度R²在0.9以上,证明出BoT强大的学习能力,但是验证结果却一般。其他算法也表现出验证精度低于建模精度的结果。实际上,不同的机器学习方法需要不同数量的最佳训练数据才能得出最优的估计结果。在这项研究中,特征维度远大于样本数,可能样本数据量不足以满足各算法的要求,导致预测精度较低。另外,大多非参数化算法会引入优化核函数的变量,变量的不确定性会导致系统性的误差从而影响算法的精度。因此今后在基于非参数化算法进行监测作物生长研究中,应加入系统验证模块,可能会出现更令人满意的估算结果。

在非参数算法中,RF方法是最准确、最稳定的方法。RF不仅能够高速高效地处理大型数据集,有较强的抗噪音能力,而且拥有对所有特征变量的重要性进行排名的能力。如今,机器学习算法用来遥感监测与反演已炙手可热,选择合适的算法进行研究有利于作物生长参数遥感估算精度的提高。因此在今后的研究中,建议将RF作为一种可靠的农作物生物量估算技术,提高RF算法在农业遥感监测中的应用价值。

4 结论

生物学产量（生物量-地上部干物重）是构成作物经济产量的基础,实时了解棉花生物量信息至关重要。在本研究中,基于近地面获取的高光谱数据,应用参数化和非参数化方法构建了一系列估算不同时期的棉花生物量模型。结果表明,参数化方法中,连续小波变换法的表现较好（吐絮前：RMSE=31.54 g·m^-2;吐絮后：RMSE=37.57 g·m^-2）,非参数化法中,随机森林是棉花生物量估算的最优算法（吐絮前：RMSE=20.48 g·m^-2;吐絮后：RMSE=30.28 g·m^-2）。所有算法中,棉花生物量估算都或多或少受到花絮的影响,表现为吐絮后的反演精度明显低于吐絮前。花絮直接影响冠层高光谱数据,因此在吐絮后应先消除花絮的影响再进行建模反演,或者利用花絮的光谱特异性,甚至采用图像特征进一步探究估测棉花生物量的新方法。本研究评估了上述2种方法在棉花生物量估算中的性能,为基于高光谱遥感的棉花长势监测与精确管理提供理论依据和技术支撑。

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[6] CHENG T, SONG R Z, LI D, ZHOU K, ZHENG H B, YAO X, TIAN Y C, CAO W X, ZHU Y. Spectroscopic estimation of biomass in canopy components of paddy rice using dry matter and chlorophyll indices
Remote Sensing, 2017, 9(4):319-333.
DOI:10.3390/rs9040319URL [本文引用: 2]

[7] TIAN Y C, YAO X, YANG J, CAO W X, HANNAWAY D B, ZHU Y. Assessing newly developed and published vegetation indices for estimating rice leaf nitrogen concentration with ground- and space-based hyperspectral reflectance
Field Crops Research, 2011, 120(2):299-310.
DOI:10.1016/j.fcr.2010.11.002URL [本文引用: 1]

[8] ZHU Y, TIAN Y C, YAO X, LIU X J, CAO W X. Analysis of common canopy reflectance spectra for indicating leaf nitrogen concentrations in wheat and rice
Plant Production Science, 2007, 10(4):400-411.
DOI:10.1626/pps.10.400URL [本文引用: 1]

[9] CHENG T, RIVARD B, SÁNCHEZ-AZOFEIFA A G, FÉRET J B, JACQUEMOUD S, USTIN S L. Deriving leaf mass per area (LMA) from foliar reflectance across a variety of plant species using continuous wavelet analysis
ISPRS Journal of Photogrammetry and Remote Sensing, 2014, 87:28-38.
DOI:10.1016/j.isprsjprs.2013.10.009URL [本文引用: 1]

[10] CHENG T, RIVARD B, SÁNCHEZ-AZOFEIFA A. Spectroscopic determination of leaf water content using continuous wavelet analysis
Remote Sensing of Environment, 2010, 115(2):659-670.
DOI:10.1016/j.rse.2010.11.001URL [本文引用: 1]

[11] KOGER C H, BRUCE L M, SHAW D R, REDDY K N. Wavelet analysis of hyperspectral reflectance data for detecting pitted morningglory (Ipomoea lacunosa) in soybean (Glycine max)
Remote Sensing of Environment, 2003, 86(1):108-119.
DOI:10.1016/S0034-4257(03)00071-3URL [本文引用: 1]

[12] YAO X, SI H Y, CHENG T, JIA M, CHEN Q, TIAN Y C, ZHU Y, CAO W X, CHEN C Y, CAI J Y. Hyperspectral estimation of canopy leaf biomass phenotype per ground area using a continuous wavelet analysis in wheat
Frontiers in Plant Science, 2018, 9:1360.
DOI:10.3389/fpls.2018.01360URL [本文引用: 2]

[13] 李旭青, 刘湘南, 刘美玲, 吴伶. 水稻冠层氮素含量光谱反演的随机森林算法及区域应用
遥感学报, 2014, 18(4):923-945.
[本文引用: 1]

LI X Q, LIU X N, LIU M L, WU L. Random forest algorithm and regional applications of spectral inversion model for estimating canopy nitrogen concentration in rice
National Remote Sensing Bulletin, 2014, 18(4):923-945. (in Chinese)
[本文引用: 1]

[14] 张春兰, 杨贵军, 李贺丽, 汤伏全, 刘畅, 张丽妍. 基于随机森林算法的冬小麦叶面积指数遥感反演研究
中国农业科学, 2018, 51(5):855-867.
[本文引用: 1]

ZHANG C L, YANG G J, LI H L, TANG F Q, LIU C, ZHANG L Y. Remote sensing inversion of leaf area index of winter wheat based on random forest algorithm
Scientia Agricultura Sinica, 2018, 51(5):855-867. (in Chinese)
[本文引用: 1]

[15] 王念一, 于丰华, 许童羽, 杜文, 郭忠辉, 张国圣. 基于机器学习的粳稻叶片叶绿素含量高光谱反演建模
浙江农业学报, 2020, 32(2):359-366.
[本文引用: 1]

[1] 杨国正, 王德鹏, 聂以春, 张献龙. 钾肥用量对棉花生物量和产量的影响
作物学报, 2013, 39(5):905-911.
[本文引用: 1]

YANG G Z, WANG D P, NIE Y C, ZHANG X L. Effect of potassium application rate on cotton (Gossypium hirsutum L.) biomass and yield
Acta Agronomica Sinica, 2013, 39(5):905-911. (in Chinese)
[本文引用: 1]

[15] WANG N Y, YU F H, XU T Y, DU W, GUO Z H, ZHANG G S. Hyperspectral retrieval modelling for chlorophyll contents of japonica-rice leaves based on machine learning
Acta Agriculturae Zhejiangensis, 2020, 32(2):359-366. (in Chinese)
[本文引用: 1]

[16] 陶惠林, 冯海宽, 杨贵军, 杨小冬, 苗梦珂, 吴智超, 翟丽婷. 基于无人机数码影像和高光谱数据的冬小麦产量估算对比
农业工程学报, 2019, 35(23):111-118.
[本文引用: 1]

[2] 赵春江. 农业遥感研究与应用进展
农业机械学报, 2014, 45(12):277-293.
[本文引用: 1]

ZHAO C J. Advances of research and application in remote sensing for agriculture
Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(12):277-293. (in Chinese)
[本文引用: 1]

[16] TAO H L, FENG H K, YANG G J, YANG X D, MIAO M K, WU Z C, ZHAI L T. Comparison of winter wheat yields estimated with UAV digital image and hyperspectral data
Transactions of the Chinese Society of Agricultural Engineering, 2019, 35(23):111-118. (in Chinese)
[本文引用: 1]

[17] 王大成, 王纪华, 靳宁, 王芊, 李存军, 黄敬峰, 王渊, 黄芳. 用神经网络和高光谱植被指数估算小麦生物量
农业工程学报, 2008, 24(S2):196-201.
[本文引用: 1]

[3] 祁亚琴, 王登伟, 陈冠文, 黄春燕, 段震宇, 陈燕, 袁杰, 杨坤. 基于高光谱数据提取作物冠层特征信息的研究进展
棉花学报, 2005, 17(6):371-375.
[本文引用: 1]

QI Y Q, WANG D W, CHEN G W, HUANG C Y, DUAN Z Y, CHEN Y, YUAN J, YANG K. Research of crop canopy characteristic information by using hyperspectral remote sensing data
Cotton Science, 2005, 17(6):371-375. (in Chinese)
[本文引用: 1]

[17] WANG D C, WANG J H, JIN N, WANG Q, LI C J, HUANG J F, WANG Y, HUANG F. ANN-based wheat biomass estimation using canopy hyperspectral vegetation indices
Transactions of the Chinese Society of Agricultural Engineering, 2008, 24(S2):196-201. (in Chinese)
[本文引用: 1]

[18] 吕杰, 汪康宁, 李崇贵, 史晓亮. 基于高光谱遥感的玉米叶绿素含量估测模型
中国矿业大学学报, 2016, 45(2):405-410.
[本文引用: 1]

[4] 黄春燕, 王登伟, 曹连莆, 张煜星, 任丽彤, 程诚. 棉花地上鲜生物量的高光谱估算模型研究
农业工程学报, 2007, 23(3):131-135.
[本文引用: 1]

HUANG C Y, WANG D W, CAO L P, ZHANG Y X, REN L T, CHENG C. Models for estimating cotton aboveground fresh biomass using hyperspectral data
Transactions of the Chinese Society of Agricultural Engineering, 2007, 23(3):131-135. (in Chinese)
[本文引用: 1]

[18] LÜ J, WANG K N, LI C G, SHI X L. Estimation models of corn chlorophyll content based on proximal hyperspectral remote sensing
Journal of China University of Mining and Technology, 2016, 45(2):405-410. (in Chinese)
[本文引用: 1]

[19] QI X M, ZHANG L D, DU X L, SONG Z J, XU S Y. Quantitative analysis using NIR by building PLS-BP model
Spectroscopy and Spectral Analysis, 2003, 23(5):870-872.
[本文引用: 1]

[20] YANG X H, HUANG J F, WU Y P, WANG J W, WANG P, WANG X M, HUETE A R. Estimating biophysical parameters of rice with remote sensing data using support vector machines
Science China Life Sciences, 2011, 54(3):272-281.
DOI:10.1007/s11427-011-4135-4URL [本文引用: 1]

[21] 唐普恩, 丁建丽, 葛翔宇, 张振华. 基于Sentinel-2A 影像干旱区棉花叶片 SPAD 数字制图
生态学报, 2020, 40(22):8326-8335.
[本文引用: 1]

[5] 安海波, 李斐, 赵萌莉, 刘亚俊. 基于优化光谱指数的牧草生物量估算
光谱学与光谱分析, 2015, 35(11):3155-3160.
[本文引用: 1]

AN H B, LI F, ZHAO M L, LIU Y J. Optimized spectral indices based estimation of forage grass biomass
Spectroscopy and Spectral Analysis, 2015, 35(11):3155-3160. (in Chinese)
[本文引用: 1]

[21] TANG P E, DING J L, GE X Y, ZHANG Z H. SPAD digital mapping of cotton leaves in arid area based on Sentinel-2A image
Acta Ecologica Sinica, 2020, 40(22):8326-8335. (in Chinese)
[本文引用: 1]

[22] 陈硕博. 无人机多光谱遥感反演棉花光合参数与水分的模型研究
[D]. 陕西: 西北农林科技大学, 2019.
[本文引用: 1]

CHEN S B. Modeling of cotton photosynthetic parameters and water content retrieval by multi-spectral remote sensing of UAV
[D]. Shaanxi: Northwest Agriculture and Forestry University, 2019. (in Chinese)
[本文引用: 1]

[23] 顾生浩. 棉花功能结构模型建立与新疆棉花产量预测
[D]. 北京: 中国农业大学, 2018.
[本文引用: 1]

GU S H. A functional-structural model of cotton and prediction of cotton yield in Xinjiang
[D]. Beijing: China Agricultural University, 2018. (in Chinese)
[本文引用: 1]

[24] 马岩川. 基于高光谱遥感的棉花冠层水氮参数估算
[D]. 北京: 中国农业科学院, 2020.
[本文引用: 1]

MA Y C. Estimation of water and nitrogen parameters of cotton at canopy scale based on hyperspectral remote sensing
[D]. Beijing: Chinese Academy of Agricultural Sciences, 2020. (in Chinese)
[本文引用: 1]

[25] VERRELST J, RIVERA J P, VEROUSTRAETE F, MUNOZ-MARI J, CLEVERS J G P W, CAMPS-VALLS G, MORENO J. Experimental Sentinel-2 LAI estimation using parametric, non-parametric and physical retrieval methods-A comparison
ISPRS Journal of Photogrammetry and Remote Sensing, 2015, 108:260-272.
DOI:10.1016/j.isprsjprs.2015.04.013URL [本文引用: 1]

[26] BUSCHMANN C, NAGEL E. In vivo spectroscopy and internal optics of leaves as basis for remote sensing of vegetation
International Journal of Remote Sensing, 1993, 14(4):711-722.
DOI:10.1080/01431169308904370URL

[27] JORDAN C F. Derivation of leaf-area index from quality of light on the forest floor
Ecology, 1969, 50(4):663-666.
DOI:10.2307/1936256URL

[28] PENUELAS J, GAMON J A, FREDEEN A L, MERINO J, FIELD C B. Reflectance indices associated with physiological changes in nitrogen- and water-limited sunflower leaves
Remote Sensing of Environment, 1994, 48(2):135-146.
DOI:10.1016/0034-4257(94)90136-8URL

[29] BARNES J D, BALAGUER L, MANRIQUE E, ELVIRA S, DAVISON A W. A reappraisal of the use of DMSO for the extraction and determination of chlorophylls A and B in lichens and higher plants
Environmental and Experimental Botany, 1992, 32(2):85-100.
DOI:10.1016/0098-8472(92)90034-YURL

[30] DASH J, CURRAN P J. Evaluation of the MERIS terrestrial chlorophyll index
International Journal of Remote Sensing, 2004, 25(23):5403-5413.
DOI:10.1080/0143116042000274015URL

[31] DATT B. Visible/near infrared reflectance and chlorophyll content in Eucalyptus leaves
International Journal of Remote Sensing, 2010, 20(14):2741-2759.
DOI:10.1080/014311699211778URL [本文引用: 1]

[32] GITELSON A A, GRITZ Y R, MERZLYAK M N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves
Journal of Plant Physiology, 2003, 160(3):271-282.
DOI:10.1078/0176-1617-00887URL

[33] MA B L, MORRISON M J, DWYER L M. Canopy light reflectance and field greenness to assess nitrogen fertilization and yield of maize
Agronomy Journal, 1996, 88(6):915-920.
DOI:10.2134/agronj1996.00021962003600060011xURL

[34] GITELSON A A, KAUFMAN Y J, MERZLYAK M N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS
Remote Sensing of Environment, 1996, 58(3):289-298.
DOI:10.1016/S0034-4257(96)00072-7URL

[35] HUETE A, DIDAN K, MIURA T, RODRIGUEZ E P, GAO X, FERREIRA L G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices
Remote Sensing of Environment, 2002, 83(1):195-213.
DOI:10.1016/S0034-4257(02)00096-2URL

[36] RONDEAUX G, STEVEN M, BARET F. Optimization of soil- adjusted vegetation indices
Remote Sensing of Environment, 1996, 55(2):95-107.
DOI:10.1016/0034-4257(95)00186-7URL

[37] GAMON J A, PEÑUELAS J, FIELD C B. A narrow-waveband spectral index that tracks diurnal changes in photosynthetic efficiency
Remote Sensing of Environment, 1992, 41(1):35-44.
DOI:10.1016/0034-4257(92)90059-SURL

[38] BROGE N H, LEBLANC E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density
Remote Sensing of Environment, 2001, 76(2):156-172.
DOI:10.1016/S0034-4257(00)00197-8URL

[39] KOWALSKI B R, GELADI P. Partial least-squares regression: A tutorial
Analytica Chimica Acta, 1986, 185(1):1-17.
DOI:10.1016/0003-2670(86)80028-9URL

[40] BALAGUER L. Random forests
Machine Learning, 2001, 45:5-32.
DOI:10.1023/A:1010933404324URL

[41] FARIFTEH J, MEER F V D, ATZBERGER C, CARRANZA E J M. Quantitative analysis of salt-affected soil reflectance spectra: A comparison of two adaptive methods (PLSR and ANN)
Remote Sensing of Environment, 2007, 110(1):59-78.
DOI:10.1016/j.rse.2007.02.005URL

[42] BREIMAN L I, FRIEDMAN J H, OLSHEN R A, STONE C J. Classification and regression trees
Encyclopedia of Ecology, 2015, 57(3):582-588.


[43] BREIMAN L. Bagging predictors
Machine Learning, 1996, 24(2):123-140.


[44] FRIEDMAN J, HASTIE T, TIBSHIRANI R. Additive logistic regression: A statistical view of boosting
The Annals of Statistics, 2000, 28(2):337-407.


[45] RASMUSSEN C E, WILLIAMS C K L. Gaussian processes for machine learning [M]. New York: MIT Press, 2006.


[46] ZHENG H B, CHENG T, ZHOU M, LI D, YAO X, TIAN Y C, CAO W X, ZHU Y. Improved estimation of rice aboveground biomass combining textural and spectral analysis of UAV imagery
Precision Agriculture, 2019, 20(3):611-629.
DOI:10.1007/s11119-018-9600-7URL [本文引用: 1]

[47] GITELSON A A, ANDRÉS V, ARKEBAUER T J, RUNDQUIST D C, GALINA K, BRYAN L. Remote estimation of leaf area index and green leaf biomass in maize canopies
Geophysical Research Letters, 2003, 30(5):335-343.
[本文引用: 1]

[48] WANG H F, HUO Z G, ZHOU G S, LIAO Q H, FENG H K, WU L. Estimating leaf SPAD values of freeze-damaged winter wheat using continuous wavelet analysis
Plant Physiology and Biochemistry, 2016, 98:39-45.
DOI:10.1016/j.plaphy.2015.10.032URL [本文引用: 1]

[49] LI D, TIAN L, WAN Z F, JIA M, CHENG T. Assessment of unified models for estimating leaf chlorophyll content across directional- hemispherical reflectance and bidirectional reflectance spectra
Remote Sensing of Environment, 2019, 231:111240.
DOI:10.1016/j.rse.2019.111240URL [本文引用: 1]

[50] ASNER G P. Biophysical and biochemical sources of variability in canopy reflectance
Remote Sensing of Environment, 1998, 64(3):234-253.
DOI:10.1016/S0034-4257(98)00014-5URL [本文引用: 1]