费帅鹏^,1,2, 禹小龙², 兰铭², 李雷², 夏先春², 何中虎^2,3, 肖永贵^,21河南理工大学测绘与国土信息工程学院,河南焦作 454003
²中国农业科学院作物科学研究所,北京 100081
³CIMMYT中国办事处,北京 100081

Research on Winter Wheat Yield Estimation Based on Hyperspectral Remote Sensing and Ensemble Learning Method

FEI ShuaiPeng^,1,2, YU XiaoLong², LAN Ming², LI Lei², XIA XianChun², HE ZhongHu^2,3, XIAO YongGui^{,2 1}School of Surveying and Land Information Engineering, Henan Polytechnic University, Jiaozuo 454003, Henan
²Institute of Crop Sciences, Chinese Academy of Agricultural Sciences, Beijing 100081
³CIMMYT-China Office, c/o CAAS, Beijing 100081

通讯作者: 肖永贵,E-mail： xiaoyonggui@caas.cn

责任编辑: 杨鑫浩
收稿日期:2020-11-18接受日期:2021-04-8

基金资助:

国家自然科学基金(31671691)

Received:2020-11-18Accepted:2021-04-8
作者简介 About authors
费帅鹏,E-mail： feishuaipeng@163.com。









摘要
【目的】利用2种灌溉处理下不同发育阶段的冬小麦冠层高光谱信息,通过机器学习方法对小麦籽粒产量进行估测精度研究,明确产量最佳估测模型,对于育种工作有着重要应用价值。【方法】以黄淮麦区207个主栽小麦品种为材料,于2018—2019和2019—2020年度连续2个生长季在河南省新乡基地的正常灌溉和节水处理下种植,并调查开花期、灌浆前期和灌浆中期的冠层高光谱数据,分别以6种机器学习方法和集成方法建立光谱指数产量估测模型。【结果】2种灌溉处理下,3个生育期各光谱指数均与产量呈极显著相关（P<0.0001）,且表现出较高的遗传力（0.61-0.85）,主要受遗传因素控制。在正常灌溉处理下,与传统机器学习方法表现最佳的模型相比,集成学习方法在3个生育期的平均决定系数(R²) 分别由0.610、0.611和0.640提高至0.649、0.612和0.675,平均均方根误差 (RMSE) 分别降低至0.607、0.612和0.593 t·hm^-2;节水处理下,3个生育期的平均R²分别由0.461、0.408和0.452提高至0.467、0.433和0.498,平均RMSE分别降低至0.519、0.559和0.504 t·hm^-2。【结论】利用集成方法将不同模型估测结果进行结合,能够有效地提高产量估测精度,2种灌溉处理下均在灌浆中期估测精度最佳,可为冬小麦育种工作中产量估测提供参考。
关键词： 冬小麦;产量;高光谱;集成方法;机器学习

Abstract
【Objective】Using the hyperspectral data of winter wheat canopy at different development stages under two irrigation treatments, the estimation accuracy of wheat grain yield was studied by machine learning method, and the best yield estimation model was defined, which had the important application value for crop breeding. 【Method】 A total of 207 widely-grown wheat varieties in the Yellow and Huai Valleys Winter Wheat Zone (YHVWWZ) of China were planted under full irrigation and limited irrigation treatments in Xinxiang, Henan province during two consecutive growing seasons of 2018-2019 and 2019-2020, the canopy hyperspectral was investigated at three growth stages after flowering, and six machine learning methods and ensemble methods were adopted to establish yield prediction model by using spectral index as input features.【Result】 The spectral indices at each growth stage were significantly correlated with yield (P<0.0001) under both the two irrigation treatments, and also showed high heritability (0.61-0.85) across all the three growth stages under both the irrigation treatment, which were mainly controlled by genetic factors. Under the full irrigation treatment, compared with the model with the best performance of traditional machine learning methods, the average coefficient of determination (R²) of ensemble learning method in the three growth stages increased from 0.610, 0.611 and 0.640 to 0.649, 0.612 and 0.675, respectively, and the average root mean square error (RMSE) decreased to 0.607, 0.612 and 0.593 t·hm^-2, respectively; Under the limited irrigation treatment, the average R² increased from 0.461, 0.408 and 0.452 to 0.467, 0.433 and 0.498, respectively, and the average RMSE decreased to 0.519, 0.559 and 0.504 t·hm ^-2, respectively.【Conclusion】Combining the prediction results of different models with the ensemble learning method could effectively improve the yield estimation accuracy, and the mid grain filling achieved the best prediction accuracy under both the two irrigation treatments. Overall, this study could provide the reference for yield estimation in winter wheat breeding.
Keywords：winter wheat;grain yield;hyperspectral;ensemble method;machine learning


PDF (552KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
费帅鹏, 禹小龙, 兰铭, 李雷, 夏先春, 何中虎, 肖永贵. 基于高光谱遥感和集成学习方法的冬小麦产量估测研究[J]. 中国农业科学, 2021, 54(16): 3417-3427 doi:10.3864/j.issn.0578-1752.2021.16.005
FEI ShuaiPeng, YU XiaoLong, LAN Ming, LI Lei, XIA XianChun, HE ZhongHu, XIAO YongGui. Research on Winter Wheat Yield Estimation Based on Hyperspectral Remote Sensing and Ensemble Learning Method[J]. Scientia Acricultura Sinica, 2021, 54(16): 3417-3427 doi:10.3864/j.issn.0578-1752.2021.16.005


开放科学（资源服务）标识码（OSID）：

0 引言

【研究意义】在育种工作中,需要在多个生长环境下对大量品种和高代品系进行评价。产量作为主要指标^[1],可通过作物早期的生理性状进行评估,而传统方法在调查性状时效率低下且具有破坏性^[2]。利用冠层光谱信息对冬小麦产量进行无损估测并明确最佳估测时期和模型,对于提高育种工作效率和保障国家粮食安全具有重要意义。【前人研究进展】基于冠层光谱反射率构造的光谱指数与作物生长状况之间存在显著相关性,已被广泛应用于作物产量的评估^[3,4],且将多个光谱指数作为输入特征表现出了比单个光谱指数更高的估测精度^[5,6]。高光谱遥感具有分辨率高、波段连续性强和光谱信息量大等特点^[7],基于不同波长范围光谱反射率构造的光谱指数能够提供较高的作物参数反演精度,同时高光谱数据的巨大容积性和多样性将导致“大数据”问题^[2],即需要先进的算法对其进行解析以生成生理参数评估模型。凭借优异的特征提取能力和数据推断能力,机器学习算法在与高光谱数据结合构建高维作物参数反演模型上受到了研究人员的重视^[8],随机森林^[9]（random forest,RF）、支持向量机^[10]（support vector machine,SVM）、人工神经网络^[11]（artificial neural network,ANN）等算法已被应用于作物生物量^[12]、叶面积指数^[13]、叶绿素含量^[8],叶片含水量^[14],产量^[2]等参数的评估,表现出了较高的估测精度和鲁棒性。近年来,集成学习以其优异的模型性能被广泛关注^[15],Stacking是一种使用“学习法”的多模型集成方法,由Breiman于1992年提出^[16],通过次级模型对多个初级模型的输出预测值再次训练,从而将不同模型解析数据的能力进行结合,使用多元线性回归（multiple linear regression, MLR）作为次级模型,集成效果较佳^[17]。Stacking集成通常能得到比单一模型更高的估测精度,对异常值和噪声具有较好的容忍度,对高光谱遥感等高维度数据进行训练时效果显著,已在森林变化监测,植物光合能力估测等遥感领域得到应用^[18,19]。【本研究切入点】多数研究在构造作物产量估测模型时仅使用单一算法,在特定环境或生长阶段具有优异表现的算法在应用到其他生长条件时,较难得到最佳的产量估测效果。模型集成方法在冬小麦产量评估中的应用较少,考虑到不同算法在解析数据时的异质性,研究基于Stacking的多模型集成,有助于提高冬小麦产量估测模型的估测精度和泛化能力。【拟解决的关键问题】本研究使用冬小麦开花期与灌浆前、中期冠层高光谱数据,构造了多个光谱指数,以SVM、RF、ANN、高斯过程^[20]（gaussian process,GP）、岭回归^[21]（ridge regression,RR）和MLR作为初级模型,分别构建正常灌溉处理和节水处理下多个生育期的产量估测模型,并以MLR作为次级模型对初级模型输出预测结果进行再次训练和测试,以期获取一种具有较高估测精度的作物产量评估方法。

1 材料与方法

1.1 试验材料与设计

本研究选用黄淮麦区主要栽培品种207份,分别于2018—2019年和2019—2020年2个生长季种植于中国农业科学院作物科学研究所新乡实验基地（113°51’E,35°18’N）。设置正常灌溉（越冬水、拔节水、灌浆水）和节水（越冬水）2种处理,每次灌溉灌水量约为2 250—2 700 m³·hm^-2。试验采用随机区组设计,2次重复,小区长3 m,宽1.4 m,行距为20 cm,小区面积为4.2 m²。为保证小区产量的可靠性,出苗后对缺苗断垅处采取移栽方式进行处理,确保苗全苗匀。田间管理按照当地丰产田标准进行,并防治病虫害及杂草。

1.2 高光谱数据获取

本研究采用美国 ASD Field Spec3高光谱辐射仪实施冠层光谱测量,波长范围为 350—2 500 nm,采样间隔为1.4 nm（350—1 000 nm）和2 nm（1 000—2 500 nm）,重采样间隔为 1 nm,视场角为25°。在小麦开花期（Zadok 65）、灌浆前期（Zadok 73）和灌浆中期（Zadok 85）采集冠层高光谱数据。在晴朗、无云且光照条件较好时（北京时间10：00—14：00）对所有小区进行冠层光谱采集,采集时将探头垂直向下置于冠层上方1 m处。在每个小区对分布均匀的4个点进行测量,每个点测量10次,取平均值作为该小区的冠层光谱反射率,每采集10个小区,使用漫反射标准白板进行反射率校正。成熟后,使用小区联合收割机（Wintersteiger Classic）进行收获,对每个小区单独装袋,晾晒后籽粒含水量约12.5% 时进行称重测定产量。

1.3 光谱指数计算

光谱指数是由不同波段的反射率以代数形式组合成的一种参数,可降低条件背景对光谱反射率数据的干扰,比单波段具有更好的灵敏性^[22]。本研究选择用于估测产量的光谱指数如表1所示。

Table 1
表1
表1本研究选用的光谱指数
Table 1Spectral indices used in this study

光谱指数 Spectral index	名称 Name	公式 Formula
NDVI[23]	归一化光谱指数 Normalized difference vegetation index	$\frac{R_{800}-R_{670}}{R_{800}+R_{670}}$
MCARI[24]	修正叶绿素吸收比指数 Modified chlorophyll absorption ratio index	$\left[\left(R_{702}-R_{671}\right)-0.2\left(R_{702}-R_{549}\right)\right] \times \frac{R_{702}}{R_{671}}$
NDRE[25]	归一化红边光谱指数 Normalized difference red edge	$\frac{R_{790}-R_{720}}{R_{790}+R_{720}}$
GNDVI[26]	绿色归一化光谱指数 Green normalized difference vegetation index	$\frac{R_{750}-R_{550}}{R_{750}+R_{550}}$
MSR[23]	修正红边比值指数 Modified simple ratio index	$\frac{R_{750} / R_{705}-1}{\sqrt{R_{750} / R_{705}+1}}$
NDRSR[27]	归一化红边简单比值指数 Normalized difference red-edge simple ratio	$\frac{R_{872}-R_{712}}{R_{872}+R_{712}}$
MTVI[28]	修正三角光谱指数 Modified triangular vegetation index	1.2[1.2(R800-R500)-2.6(R670-R550)]
MTCI2[29]	MERIS陆地叶绿素指数2 MERIS terrestrial chlorophyll index 2	$\frac{R_{754}-R_{709}}{R_{709}+R_{681}}$
MNDVI[30]	修正归一化光谱指数 Modified normalized difference vegetation index	$\frac{R_{750}-R_{705}}{R_{750}+R_{705}-2 R_{445}}$
RDVI[31]	重归一化光谱指数 Renormalized difference vegetation index	$\frac{R_{800}-R_{670}}{\sqrt{R_{800}+R_{670}}}$
VDI[32]	植被干指数 Vegetation dry index	$\frac{R_{970}-R_{900}}{R_{970}+R_{900}}$
CI[33]	叶绿素指数 Chlorophyll index	(R749-R720)-(R701-R672)
VREI[34]	沃格尔曼红边指数 Vogelmann red edge index	$\frac{R_{742}}{R_{722}}$
ARVI[35]	大气抗性光谱指数 Atmospherically resistant vegetation index	$\frac{R_{872}-\left[R_{661}-\left(R_{488}-R_{661}\right)\right]}{R_{872}+\left[R_{661}-\left(R_{488}-R_{661}\right)\right]}$
NDMI[36]	归一化物质指数 Normalized difference matter index	$\frac{R_{1649}-R_{1792}}{R_{1649}+R_{1792}}$

新窗口打开|下载CSV

1.4 Stacking 集成方法

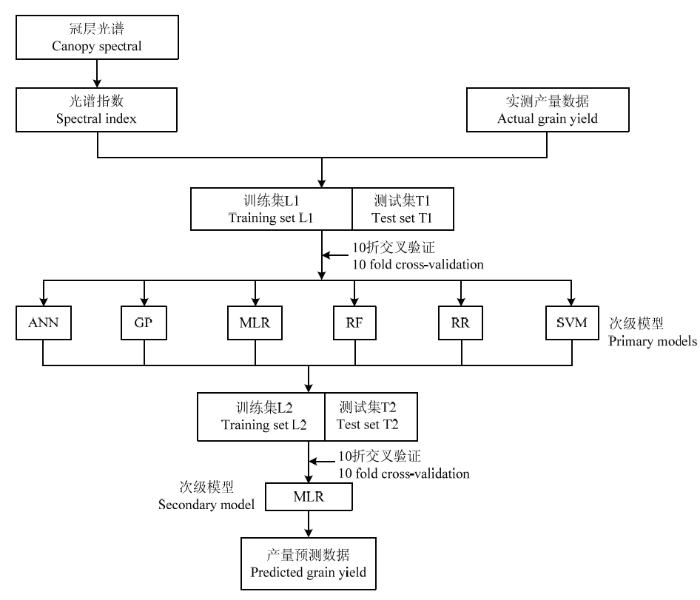
Stacking 集成方法如图1所示,首先从与原始数据中训练出多种类型的初级模型,然后将初级模型的输出当作次级模型的输入,原始数据的响应变量仍被当作次级模型的响应变量,最后对数据进行再次训练。若直接使用初级模型的训练集来产生次级训练集,则存在过拟合的风险,通常利用交叉验证的方式用训练初级模型未使用的样本来产生次级模型的训练样本^[37],具体步骤如下^[38]：

图1

新窗口打开|下载原图ZIP|生成PPT
图1使用Stacking集成方法建立产量估测模型流程图

Fig. 1Flow chart for establishing grain yield estimation model based on Stacking method



（1）将原始数据划分为训练集L1和测试集T1。

（2）将训练集随机划分为 K份样本量相等的子集,初级模型将其中 1 份作为K折测试集,其余K-1 份作为K折训练集,此过程迭代K次,即为K折交叉验证。利用 K折训练集训练每个初级模型,并对 K 折测试集进行估测,将各初级模型在K折测试集上的估测结果进行结合,构成样本外估测值矩阵（out-of- sample predictions matrix, OSPM）,作为次级模型的训练集L2。

（3）每个初级模型对原始测试集T1进行K次估测,并对其求平均作为次级模型的测试集T2。

（4）在次级模型中仍利用K折交叉验证进行训练和测试,输出K次测试结果并求平均作为最终输出估测值。

本研究将各个生育期的原始数据以4﹕1的比例划分为训练集与测试集,此划分方式迭代20次以减少偶然因素的影响。在每次划分后以ANN、GP、MLR、RF、RR和SVM为初级模型,以MLR为次级模型并使用10折交叉验证法进行训练和测试。对原始数据进行训练集和测试集的20次划分后,各初级模型与次级模型均在测试集上产生200次测试,以此200次测试产生的决定系数R²和均方根误差RMSE的平均值作为精度评价指标,对每种模型的适用性能进行评价,同一灌溉处理下不同生育期均采用相同的10折交叉验证划分方式。

1.5 数据统计分析

利用R语言（v 4.0.2）实现了光谱指数计算、相关性分析和产量估测模型构造。结合QTL IciMapping软件计算2种灌溉处理下各光谱指数及产量2年间的最佳线性无偏估计值（best linear unbiased estimates,BLUE）和遗传力（heritability,H²）。

2 结果

2.1 光谱指数分析

2年间冬小麦开花期、灌浆前期和灌浆中期光谱指数的BLUE值与产量BLUE值相关性分析表明（表2—3）,2种灌溉处理下各生育期全部光谱指数均与产量呈极显著相关（P<0.0001）。正常灌溉处理下,灌浆中期（|r|=0.61—0.73）光谱指数与产量的相关系数绝对值高于开花期（|r|=0.45—0.72）和灌浆前期（|r|=0.43—0.67）。节水处理下各光谱指数与产量的相关性低于正常灌溉处理,开花期、灌浆前期和灌浆中期光谱指数与产量的相关系数绝对值（|r|）范围分别为0.44—0.57、0.41—0.61和0.49—0.58。各光谱指数在2种灌溉处理下各生育期均表现出了较高的遗传力（0.61—0.85）,主要受遗传因素调控。综上,建立产量估测模型时使用全部15个光谱指数作为各模型的输入特征。

Table 2
表2
表2正常灌溉处理下光谱指数与产量相关性分析和光谱指数遗传力
Table 2Correlation analysis of spectral index and grain yield under full irrigation treatment, spectral index heritability

光谱指数 Spectral index	开花期Flowering		灌浆前期Early grain filling		灌浆中期Mid grain filling
	|r|	H2	|r|	H2	|r|	H2
NDVI	0.50***	0.83	0.53***	0.75	0.66***	0.74
MCARI	0.61***	0.85	0.65***	0.85	0.69***	0.82
NDRE	0.71***	0.81	0.65***	0.79	0.72***	0.78
GNDVI	0.68***	0.82	0.63***	0.78	0.71***	0.77
MSR	0.65***	0.80	0.62***	0.76	0.70***	0.76
NDRSR	0.72***	0.82	0.67***	0.79	0.73***	0.79
MTVI	0.59***	0.77	0.60***	0.73	0.63***	0.75
MTCI2	0.63***	0.83	0.59***	0.80	0.68***	0.80
MNDVI	0.62***	0.83	0.63***	0.76	0.69***	0.83
RDVI	0.60***	0.77	0.62***	0.77	0.66***	0.78
VDI	0.45***	0.84	0.43***	0.80	0.62***	0.83
CI	0.61***	0.82	0.59***	0.79	0.64***	0.81
VREI	0.69***	0.81	0.65***	0.75	0.72***	0.76
ARVI	0.52***	0.79	0.54***	0.73	0.65***	0.73
NDMI	0.53***	0.80	0.56***	0.63	0.61***	0.77

***表示在P<0.0001 水平下显著。下同
*** indicates significant at P <0.0001. The same as below

新窗口打开|下载CSV

Table 3
表3
表3节水处理下光谱指数与产量相关性分析和光谱指数遗传力
Table 3Correlation analysis of spectral index and grain yield under limited irrigation treatment, spectral index heritability

光谱指数 Spectral index	开花期 Flowering		灌浆前期 Early grain filling		灌浆中期 Mid grain filling
	|r|	H2	|r|	H2	|r|	H2
NDVI	0.48***	0.63	0.42***	0.69	0.53***	0.65
MCARI	0.57***	0.64	0.49***	0.70	0.56***	0.68
NDRE	0.56***	0.67	0.48***	0.78	0.55***	0.73
GNDVI	0.54***	0.66	0.41***	0.73	0.54***	0.71
MSR	0.55***	0.65	0.43***	0.74	0.52***	0.69
NDRSR	0.57***	0.68	0.49***	0.79	0.55***	0.73
MTVI	0.45***	0.64	0.46***	0.68	0.49***	0.68
MTCI2	0.50***	0.62	0.45***	0.71	0.50***	0.66
MNDVI	0.52***	0.64	0.49***	0.67	0.51***	0.71
RDVI	0.49***	0.66	0.47***	0.65	0.50***	0.67
VDI	0.59***	0.69	0.61***	0.68	0.58***	0.73
CI	0.48***	0.64	0.49***	0.74	0.52***	0.74
VREI	0.55***	0.68	0.48***	0.68	0.52***	0.69
ARVI	0.49***	0.61	0.42***	0.71	0.51***	0.68
NDMI	0.44***	0.73	0.49***	0.66	0.50***	0.72

新窗口打开|下载CSV

2.2 冬小麦产量估测模型精度分析

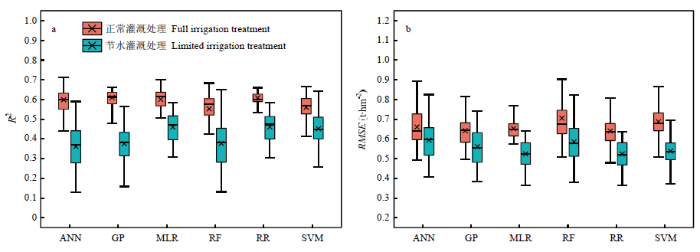
将15个光谱指数作为输入特征构造冬小麦产量估测模型。开花期各初级模型在测试集上产生的R²和RMSE的分布如图2所示,结果表明正常灌溉处理下 RF与SVM模型估测精度较低,ANN、GP、MLR和RR模型平均R²相近且较高,其中GP模型估测精度最高,平均R²为0.610,RMSE为0.643 t·hm^-2;节水处理下,RR模型的估测精度最高,平均R²为0.461,平均RMSE为0.524 t·hm^-2。

图2

新窗口打开|下载原图ZIP|生成PPT
图2开花期6种初级模型交叉验证过程在测试集上R²（a）和 RMSE（b）分布

Fig. 2The R² (a) and RMSE (b) distribution on the test set during cross-validation of six primary models at flowering



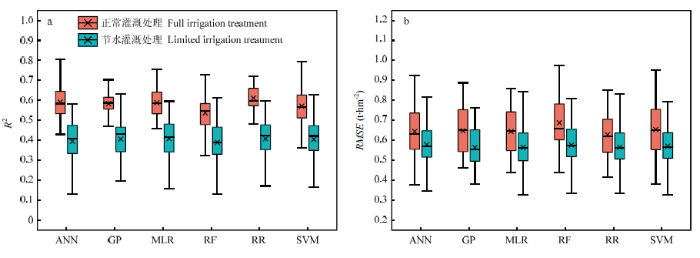
在灌浆前期（图3）,正常灌溉处理下 RF模型估测精度较低,ANN、GP、MLR、RR和SVM模型估测精度相近,其中RR模型估测精度最高,平均R²为0.611,RMSE为0.638 t·hm^-2;节水处理下,6种模型的平均R²相差较小,其中MLR的估测精度最高,平均R²为0.408,平均RMSE为0.564 t·hm^-2。

图3

新窗口打开|下载原图ZIP|生成PPT
图3灌浆前期6种初级模型交叉验证过程在测试集上R²（a）和RMSE（b）分布

Fig. 3The R² (a) and RMSE (b) distribution on the test set during cross-validation of six primary models at early grain filling



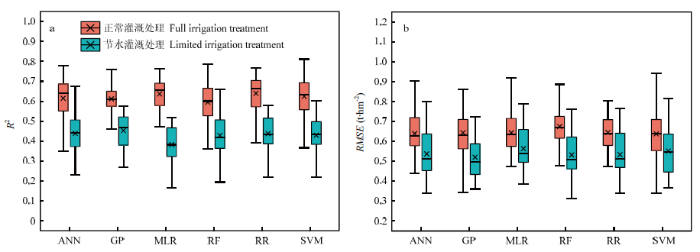
在灌浆中期（图4）,正常灌溉处理下各模型估测精度均高于开花期与灌浆前期,除RF外各模型的平均R²均大于0.6,其中RR模型的估测精度最高,平均R²为0.640,平均RMSE为0.645 t·hm^-2;节水处理下GP模型的估测精度最高,平均R²为0.452,平均RMSE为0.519 t·hm^-2。

图4

新窗口打开|下载原图ZIP|生成PPT
图4灌浆中期6种初级模型交叉验证过程在测试集上R²（a）和RMSE（b）分布

Fig. 4The R² (a) and RMSE (b) distribution on the test set during cross-validation of six primary models at mid grain filling

2.3 集成学习方法估测精度分析

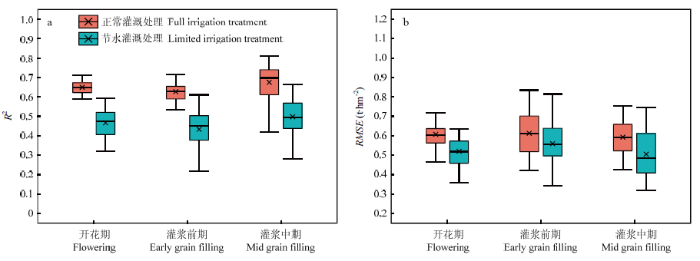
在2种灌溉处理下,以MLR作为次级模型,将各初级模型输出的估测产量作为输入特征建立产量估测模型。结果表明（图5）, 在正常灌溉处理下,开花期的平均R²由初级模型中估测精度最高的0.610（GP）提升至0.649,平均RMSE降至0.607 t·hm^-2;灌浆前期的平均R²由初级模型中估测精度最高的0.611（RR）提升至0.627,平均RMSE降至0.612 t·hm^-2;灌浆中期的平均R²由初级模型中估测精度最高的0.640（RR）提升至0.675,平均RMSE降至0.593 t·hm^-2。在节水处理下,开花期的模型估测精度提升效果微弱,平均R²由初级模型中估测精度最高的0.461（RR）提升至0.467,平均RMSE为0.519 t·hm^-2;灌浆前期的平均R²由初级模型中估测精度最高的0.408（MLR）提升至0.433,平均RMSE降至0.559 t·hm^-2;灌浆中期的平均R²由初级模型中估测精度最高的0.452（GP）提升至0.498,平均RMSE降至0.504 t·hm^-2。次级模型的产量估测精度分析表明,Stacking集成方法能够将各算法解析数据的能力进行结合以获得兼具稳定性和精确性的模型,从而提高产量估测精度,提升育种工作效率。

图5

新窗口打开|下载原图ZIP|生成PPT
图5次级模型交叉验证过程在测试集上R²（a）和RMSE（b）分布

Fig. 5R² (a) and RMSE (b) distribution on the test set during cross-validation of secondary model

2.4 初级模型系数分析

对初级模型对应输出产量估测值在次级模型（MLR）交叉验证过程中拟合方程的回归系数进行分析（表4）,较高的系数表示在次级模型训练过程中所占权重较大。在正常灌溉处理下,开花期模型集成性能在较大程度上取决于MLR和RR,平均系数分别为6.13和1.91;RR、ANN和SVM模型在灌浆前期模型训练中所占权重较大,平均系数分别为0.61、0.43和0.42;在灌浆中期,MLR、RR和SVM模型平均系数较高,分别为4.51、4.32和2.34。在节水处理下,开花期RR、SVM和GP模型平均系数分别为3.47、2.43和2.10,所占权重较大;RR和GP模型在灌浆前期模型训练中所占权重较大,平均系数分别为4.06和0.77;在灌浆中期,RR、ANN和GP模型平均系数较高,分别为3.28、0.93和0.86。回归系数分析结果表明次级模型在不同的建模条件下对各个初级模型的输出估测值进行合理的权重分配,以将各初级模型解析不同类型数据的优势结合,从而得到更高的估测精度。

Table 4
表4
表4次级模型建模过程各模型系数平均值
Table 4The average coefficients of each primary learner in the modeling of the secondary learner

模型 Model	正常灌溉处理 Full irrigation treatment			节水处理 Limited irrigation treatment
	开花期 Flowering	灌浆前期 Early grain filling	灌浆中期 Mid grain filling	开花期 Flowering	灌浆前期 Early grain filling	灌浆中期 Mid grain filling
ANN	-4.53	0.43	-0.59	-4.10	-2.81	0.93
GP	0.24	0.26	-1.85	2.10	0.77	0.86
MLR	1.91	-0.19	4.51	-2.14	-0.14	-2.02
RF	0.84	-0.30	-7.30	-0.47	0.02	-0.37
RR	6.13	0.61	4.32	3.20	4.06	3.28
SVM	-3.41	0.42	2.34	2.43	-0.56	-1.59

新窗口打开|下载CSV

3 讨论

地面空间异质性随作物的生长发育而发生变化,导致不同生长阶段的冠层光谱指数与产量相关性大小有所差异^[39]。开花期和灌浆期与冬小麦产量三要素中的穗粒数和千粒重紧密相关,这2个时期的光谱指数在先前的研究中具有较高的产量估测精度^[1,3],常被视为产量估测的理想时期。

作物冠层结构在不同的生长阶段、营养条件和品种之间均存在差异,也会导致冠层光谱反射率的变化^[40],而研究人员构建作物产量估测模型时大都选择单一算法,单一算法在解析不同数据时模型性能有所差异,使其较难在不同的建模条件下均得到最优的产量估测效果。Stacking是一种集成学习方法,对数据的适应能力较强,相对单一算法具有较强的抗噪性能和拟合能力。本研究通过Stacking方法将6种算法结合,构建了产量估测集成模型,结果表明集成学习方法的估测精度在2种灌溉处理下不同生育期均明显优于传统机器学习方法。本文和前人研究表明Stacking方法能够在植物表型评估中提升模型性能,FENG等^[15]将大量光谱指数作为输入特征对苜蓿产量进行评估,将模型集成后R²在各条件下均能得到不同程度的提升。FU等^[18]使用350— 2 500 nm波长范围的全部波段反射率作为Stacking方法输入特征,对烟叶光合作用能力进行评估,集成模型的提升效果明显,参数V_c,maxh和J_max的估测精度（R²）分别提升0.10和0.08。此外,FENG等^[41]有关大气PM2.5评估的研究显示,Stacking方法的精度提升效果与初级模型的数量成正比,在进一步的作物产量估测研究中可增加初级模型的数量以获取更高的模型精度。

充分性和多样性是Stacking方法选择初级模型的2个主要原则^[42]。首先,集成方法结合了单一模型的估测值,致使每个初级模型的性能将会影响最终集成结果,故每个初级模型都应具有良好的估测能力^[15]。其次,模型之间也应具有差异性,某些算法对冬小麦产量的真实假设通常不在当前选用模型所计算的假设空间内,使用此模型对数据进行学习时将会无效,而不同类型的算法考虑的假设空间也会有所差异^[37],将多种回归算法通过Stacking方法集成后,相应的假设空间会在一定程度上扩大,从而得到更好的近似。本研究中正常灌溉处理下开花期与灌浆中期及节水处理下灌浆中期对初级模型进行集成后,估测精度提升明显,R² 均能提高0.03以上,其余情况提升效果微弱,在此情况下对数据进行训练时,各模型假设空间类似或重叠,与VAN等^[43]得出的结论相近,即某些建模条件下Stacking方法集成结果估测精度“渐近等价”于表现最佳的初级模型。

本研究发现,产量估测模型在正常灌溉处理下的R²较高,节水处理下R²较低。分析可能原因：（1）冬小麦受到水分胁迫时,冠层面积较小,群体覆盖率低,导致冠层光谱反射率易受到土壤背景干扰,影响高光谱数据精度^[44];（2）水分亏缺导致节水处理下冬小麦衰老速率增加,致使灌浆时间缩短,使得最终产量降低^[4],而收获过程中由于人为因素和机器因素等影响,每个小区会损失部分产量,此部分误差对节水处理下各小区产量的影响大于正常灌溉处理,导致节水处理下产量估测精度低于灌溉处理。因此,建议在做不同品种产量估测模型精度提升研究时,品种应在正常适宜灌溉处理下充分进行产量试验,并保证产量收获精度,提升模型优化。

4 结论

选取性能优异的算法精准估测小麦产量对于提升育种工作效率具有重要意义。本研究表明,使用Stacking集成方法能够获得比单一算法更高的产量估测精度。在正常灌溉处理下,3个生育期的平均R²分别提高至0.649、0.627和0.675,平均RMSE降至0.607、0.612和0.593 t·hm^-2。节水处理下,3个生育期平均R²分别提高至0.467、0.433和0.498,平均RMSE降至0.519、0.559和0.504 t·hm^-2。不同的灌溉处理和发育阶段对产量估测精度均有影响,使用模型集成方法在正常灌溉处理下,灌浆中期得到最佳估测精度,可作为一种新的方法在育种工作中对作物产量进行早期评估。

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] HERNANDEZ J, LOBOS G A, MATUS I, DEL POZO A, SILVA P, GALLEGUILLOS M. Using ridge regression models to estimate grain yield from field spectral data in bread wheat (Triticum aestivum L. ) grown under three water regimes
Remote Sensing, 2015, 7(2):2109-2126.
DOI:10.3390/rs70202109URL [本文引用: 2]

[2] MONTESINOS-LÓPEZ O A, MONTESINOS-LÓPEZ A, CROSSA J, DELOS G, CAMPOS , ALVARADO G, SUCHISMITA M, RUTKOSKI J, GONZÁLEZ-PÉREZ L, BURGUEÑO J. Predicting grain yield using canopy hyperspectral reflectance in wheat breeding data
Plant Methods, 2017, 13:4.
DOI:10.1186/s13007-016-0154-2URL [本文引用: 3]

[3] HASSAN M A, YANG M, RASHEED A, YANG G, REYNOLDS M, XIA X, XIAO Y, HE Z. A rapid monitoring of NDVI across the wheat growth cycle for grain yield prediction using a multi-spectral UAV platform
Plant Science, 2019, 282:95-103.
DOI:10.1016/j.plantsci.2018.10.022URL [本文引用: 2]

[4] HASSAN M A, YANG M, RASHEED A, JIN X, XIA X, XIAO Y, HE Z. Time-series multispectral indices from unmanned aerial vehicle imagery reveal senescence rate in bread wheat
Remote Sensing, 2018, 10(6):809.
DOI:10.3390/rs10060809URL [本文引用: 2]

[5] GITELSON A A, PENG Y, ARKEBAUER T J, SCHEPERS J. Relationships between gross primary production, green LAI, and canopy chlorophyll content in maize: Implications for remote sensing of primary production
Remote Sensing of Environment, 2014, 144:65-72.
DOI:10.1016/j.rse.2014.01.004URL [本文引用: 1]

[6] BOLTON D K, FRIEDL M A. Forecasting crop yield using remotely sensed vegetation indices and crop phenology metrics
Agricultural & Forest Meteorology, 2013, 173:74-84.
[本文引用: 1]

[7] 李岚涛, 李静, 明金, 汪善勤, 任涛, 鲁剑巍. 冬油菜叶面积指数高光谱监测最佳波宽与有效波段研究
农业机械学报, 2018, 49(2):156-165.
[本文引用: 1]

LI L T, LI J, MING J, WANG S Q, REN T, LU J W. Selection optimization of hyperspectral bandwidth and effective wavelength for predicting leaf areaindex in winter oilseed rape
Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(2):156-165. (in Chinese)
[本文引用: 1]

[8] SHAH S H, ANGEL Y, HOUBORG R, ALI S, MCCABE M F. A random forest machine learning approach for the retrieval of leaf chlorophyll content in wheat
Remote Sensing, 2019, 11:920.
DOI:10.3390/rs11080920URL [本文引用: 2]

[9] BREIMANL. Random forests
Machine Learning, 2001, 45:5-32.
DOI:10.1023/A:1010933404324URL [本文引用: 1]

[10] SAIN, STEPHAN R. The nature of statistical learning theory
Technometrics, 1996, 38:409.
[本文引用: 1]

[11] BRADLEY J B. Neural networks: A comprehensive foundation
Information Processing & Management, 1995, 31:786.
DOI:10.1016/0306-4573(95)90003-9URL [本文引用: 1]

[12] WANG L, ZHOU X, ZHU X, DONG Z, GUO W. Estimation of biomass in wheat using random forest regression algorithm and remote sensing data
The Crop Journal, 2016, 4:212-219.
DOI:10.1016/j.cj.2016.01.008URL [本文引用: 1]

[13] YUAN H, YANG G, LI C, WANG Y, LIU J, YU H, FENG H, XU B, ZHAO X, YANG X. Retrieving soybean leaf area index from unmanned aerial vehicle hyperspectral remote sensing: Analysis of RF, ANN, and SVM regression models
Remote Sensing, 2017, 9:309.
DOI:10.3390/rs9040309URL [本文引用: 1]

[14] JIN X, XU X, SONG X, LI Z, WANG J, GUO W. Estimation of leaf water content in winter wheat using grey relational analysis-partial least squares modeling with hyperspectral data
Agronomy Journal, 2013, 105:1385-1392.
DOI:10.2134/agronj2013.0088URL [本文引用: 1]

[15] FENG L, ZHANG Z, MA Y, DU Q, WILLIAMS P, DREWRY J, LUCK B. Alfalfa yield prediction using UAV-based hyperspectral imagery and ensemble learning
Remote Sensing, 2020, 12(12):2028.
DOI:10.3390/rs12122028URL [本文引用: 3]

[16] WOLPERT D H. Stacked generalization
Neural Networks, 1992, 5:241-259.
DOI:10.1016/S0893-6080(05)80023-1URL [本文引用: 1]

[17] TING K M, WITTEN I H. Issues in stacked generalization
Journal of Artificial Intelligence Research, 1999, 10:271-289.
DOI:10.1613/jair.594URL [本文引用: 1]

[18] FU P, MEACHAM-HENSOLD K, GUAN K, BERNACCHI C J. Hyperspectral leaf reflectance as proxy for photosynthetic capacities: An ensemble approach based on multiple machine learning algorithms
Frontiers in Plant Science, 2019, 10.
[本文引用: 2]

[19] HEALEY S P, COHEN W B, YANG Z, KENNETH BREWER C, BROOKS E B, GORELICK N, HERNANDEZ A J, HUANG C, JOSEPH HUGHES M, KENNEDY R E, LOVELAND T R, MOISEN G G, SCHROEDER T A, STEHMAN S V, VOGELMANN J E, WOODCOCK C E, YANG L, ZHU Z. Mapping forest change using stacked generalization: An ensemble approach
Remote Sensing of Environment, 2018, 204:717-728.
DOI:10.1016/j.rse.2017.09.029URL [本文引用: 1]

[20] WILLIAMSCK, RASMUSSENCE. Gaussian processes for machine learning. Cambridge, CA: MIT Press, 2006.
[本文引用: 1]

[21] MCDONALD G C. Ridge regression
Wiley Interdisciplinary Reviews Computational Statistics, 2009, 1:93-100.
DOI:10.1002/wics.v1:1URL [本文引用: 1]

[22] LIANG L, DI L P, ZHANG L P, DENG M X, QIN Z H, ZHAO S H, LIN H. Estimation of crop LAI using hyperspectral vegetation indices and a hybrid inversion method
Remote Sensing of Environment, 2015, 165:123-134.
DOI:10.1016/j.rse.2015.04.032URL [本文引用: 1]

[23] SIMS D A, GAMON J A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages
Remote Sensing of Environment, 2002, 81(2/3):337-354.
DOI:10.1016/S0034-4257(02)00010-XURL [本文引用: 2]

[24] DAUGHTRY C S T, WALTHALL C L, KIM M S, DE COLSTOUN E B, MCMURTREY J E. Estimating corn leaf chlorophyll concentration from leaf and canopy reflectance
Remote Sensing of Environment, 2000, 74:229-239.
DOI:10.1016/S0034-4257(00)00113-9URL [本文引用: 1]

[25] RODRIGUEZ D, FITZGERALD G J, BELFORD R, CHRISTENSEN L K. Detection of nitrogen deficiency in wheat from spectral reflectance indices and basic crop eco-physiological concepts
Australian Journal of Agricultural Research, 2006, 57:781-789.
DOI:10.1071/AR05361URL [本文引用: 1]

[26] GITELSON A A, KAUFMAN Y J, MERZLYAK M N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS
Remote Sensing of Environment, 1996, 58:289-298.
DOI:10.1016/S0034-4257(96)00072-7URL [本文引用: 1]

[27] GITELSON A A, VINA A, CIGANDA V, RUNDQUIST D C, ARKEBAUER T J. Remote estimation of canopy chlorophyll content in crops
Geophysical Research Letters, 2005, 32:1-4.
[本文引用: 1]

[28] HABOUDANE D, MILLER J R, PATTEY E, ZARCO-TEJADA P J, STRACHAN I B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture
Remote Sensing of Environment, 2004, 90:337-352.
DOI:10.1016/j.rse.2003.12.013URL [本文引用: 1]

[29] DASH J, CURRAN P J. Evaluation of the meris terrestrial chlorophyll index (MTCI)
Advances in Space Research, 2007, 39:100-104.
DOI:10.1016/j.asr.2006.02.034URL [本文引用: 1]

[30] SIMS D A, GAMON J A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages
Remote Sensing of Environment, 2002, 81:337-354.
DOI:10.1016/S0034-4257(02)00010-XURL [本文引用: 1]

[31] ROUJEAN J L, BREON F M. Estimating PAR absorbed by vegetation from bidirectional reflectance measurements
Remote Sensing of Environment, 1995, 51:375-384.
DOI:10.1016/0034-4257(94)00114-3URL [本文引用: 1]

[32] PENUELAS J, FILELLA I, BIEL C S, SERRANO L, SAVE R. The Reflectance at the 950-970 Nm region as an indicator of plant water status
International Journal of Remote Sensing, 1993, 14(10):1887-1905.
DOI:10.1080/01431169308954010URL [本文引用: 1]

[33] GUPTA R K, VIJAYAN D, PRASAD T S. New hyperspectral vegetation characterization parameters
Advances in Space Research, 2001, 28(1):201-206.
DOI:10.1016/S0273-1177(01)00346-5URL [本文引用: 1]

[34] VOGELMANN J, ROCK B, MOSS D. Red edge spectral measurements from sugar maple leaves
Remote Sensing. 1993, 14:1563-1575.
[本文引用: 1]

[35] KAUFMAN Y J, TANRE D. Atmospherically resistant vegetation index (ARVI) for eos-modis
IEEE Transactions on Geoscience and Remote Sensing, 1992, 30:261-270.
DOI:10.1109/36.134076URL [本文引用: 1]

[36] WANG L, HUNT E R, JR, QU J J, HAO X, DAUGHTRY C S T. Towards estimation of canopy foliar biomass with spectral reflectance measurements
Remote Sensing of Environment, 2011, 115(3):836-840.
DOI:10.1016/j.rse.2010.11.011URL [本文引用: 1]

[37] 周志华. 机器学习.第一版. 北京: 清华大学出版社, 2016: 181-182.
[本文引用: 2]

ZHOU Z H. Machine Learning.1st edition. Beijing: Tsinghua University Press, 2016: 181-182. (in Chinese)
[本文引用: 2]

[38] 邓威, 郭钇秀, 李勇, 朱亮, 刘定国. 基于特征选择和Stacking集成学习的配电网网损估测
电力系统保护与控制, 2020, 48:108-115.
[本文引用: 1]

DENG W, GUO Y X, LI Y, ZHU L, LIU D G. Power losses prediction based on feature selection and Stacking integrated learning
Power System Protection and Control, 2020, 48:108-115. (in Chinese)
[本文引用: 1]

[39] JULIANE B, ANDREAS B, SIMON B, JANIS B, SILAS E, GEORG B. Estimating biomass of barley using crop surface models (CSMs) derived from UAV-Based RGB imaging
Remote Sensing, 2014, 6(11):10395-10412.
DOI:10.3390/rs61110395URL [本文引用: 1]

[40] ZOU X C, MOTTUS M. Sensitivity of common vegetation indices to the canopy structure of field crops
Remote Sensing, 2017, 9:994.
DOI:10.3390/rs9100994URL [本文引用: 1]

[41] FENG L, LI Y, WANG Y, DU Q. Estimating hourly and continuous ground-level PM2.5 concentrations using an ensemble learning algorithm: The ST-Stacking model
Atmospheric Environment, 2020, 223:117242.
DOI:10.1016/j.atmosenv.2019.117242URL [本文引用: 1]

[42] FRAME J, MERRILEES D W. The effect of tractor wheel passes on herbage production from diploid and tetraploid ryegrass swards
Grass and Forage Science, 1996, 51:13-20.
DOI:10.1111/gfs.1996.51.issue-1URL [本文引用: 1]

[43] VAN D L, M J, POLLEY E C, HUBBARDAE. Super learner
Statistical Applications in Genetics & Molecular Biology, 2007, 6(1):25.
[本文引用: 1]

[44] 陈智芳, 宋妮, 王景雷, 孙景生. 基于高光谱遥感的冬小麦叶水势估测模型
中国农业科学, 2017, 50(5):871-880.
[本文引用: 1]

CHEN Z F, SONG N, WANG J L, SUN J S. Leaf water potential estimating models of winter wheat based on hyperspectral remote sensing
Scientia Agricultura Sinica, 2017, 50(5):871-880. (in Chinese)
[本文引用: 1]