作为一种可靠性分析和风险管理技术，故障模式和影响分析(Failure Mode and Effects Analysis，FMEA)方法已被广泛应用于汽车、制造和化工等各个领域^[1-3]。传统FMEA方法的具体步骤可总结为：先利用1~10的量化数值来评估风险因子发生率(Occurrence，O)、严重性(Severity，S)和难测度(Detection，D)的临界等级，然后，确定由O、S和D相乘得到的风险优先级数(Risk Priority Number，RPN)，最后依据RPN值来度量潜在故障模式的风险优先级顺序^[4]。尽管传统FMEA方法具有易用性、多功能性等优点，但仍然存在许多缺陷^[5-7]，本文主要关注的缺点有：①量化的精确数值无法准确地描述专家提供的真实故障评估信息；② 3个风险因子被赋予相同权重，忽略风险因子之间的相对重要性；③RPN计算公式缺乏全面的科学依据，导致RPN值对风险因子变化非常敏感，并且易出现故障模式具有相同RPN值难以判断风险顺序的情况。
为了准确真实地描述专家故障评估信息，许多****将模糊集理论引入传统FMEA方法中。耿秀丽和邱华清^[8]提出了基于犹豫模糊集的FMEA风险评估方法；Liu等^[9]和王睿等^[10]用直觉模糊集表征专家故障评估信息；Wang等^[11]运用梯形模糊软集描述专家评估信息的不确定性。然而，在故障风险评估过程中，由于决策环境的不确定性和复杂性以及人类认知的固有模糊性，专家更倾向于用诸如“很低、低、一般、高、很高”定性的语言术语(Linguistic Term Set，LTS)表示故障风险评估^[12-13]。此外，专家时常会由于自身经验、能力和知识的缺乏，在多个语言术语之间犹豫不决，Rodriguez等^[14]提出的犹豫模糊语言术语集(Hesitant Fuzzy Linguistic Term Set，HFLTS)允许决策者用多个不同的语言术语表达评估信息，但每个语言术语的权重都是相等，忽略了专家对不同语言术语的偏好程度。为了改善这种情况，Pang等^[15]在HFLTS基础上通过对每个语言术语增加概率开发了概率语言术语集(Probabilistic Linguistic Term Sets，PLTS)，有效地避免了偏好信息的丢失，提高了语言信息表达的灵活性。另外，FMEA作为一种群体决策行为，通常由一组跨职能、多学科的专家团队执行^[12]。考虑到FMEA团队专家通常来自不同的领域，可能在知识结构和实践经验方面存在差异，专家在给出语言评价信息时，可能会选择不同粒度的语言术语集。因此，多粒度PLTS能很好地解决专家风险评估信息的不确定性和多样性问题。
为了避免传统FMEA方法忽略了风险因子相对重要性的缺陷，主观赋权法、客观赋权法和综合赋权法被用于确定风险因子权重。其中，主观赋权法一般有层次分析法(Analytical Hierarchy Process，AHP)^[16]和德尔菲法^[17]等，近年来，最优最劣法(Best-Worst Method，BWM)^[18]由于能保证专家判断信息一致性和需要更少的比较数据等特点受到广泛关注。此外，熵权法^[5]、最大偏差法^[13]等通常用于推导客观风险因子权重。将主观赋权法和客观赋权法结合的综合赋权法，不仅能克服主观赋权法依赖专家经验判断的缺点，还能充分考虑评估信息本身的客观因素，并且可根据专家对评估信息的确定程度调整主客观权重比例，具有较强的灵活性和实用性^[10]。
FMEA方法中故障模式的风险优先级问题实质上是多属性决策(Multiple Criteria Decision Making，MCDM)问题^[12-13]。因此，许多MCDM方法已被用于改进传统FMEA方法，其中包括灰色关联分析^[6]、逼近于理想解的排序技术(Technique for Order Preference by Similarity to an Ideal Solution，TOPSIS)^[5]、复杂比例评估法(Complex Proportional Assessment，COPRAS)^[13]、多属性边界逼近区域比较法(Multi-Attribute Border Approximation area Comparison，MABAC)^[19]。Brans等^[20]提出的偏好顺序结构评估法(Preference Ranking Organization Method for Enrichment Evaluations，PROMETHEE)是一种基于两两比较方案优序关系的MCDM方法，相比于其他方法，其不需要对指标值进行规范化处理，合理避免了数据处理中产生信息偏差^[18]，而且充分考虑了决策者偏好存在的客观事实，使得评价结果更具有说服力。
综上所述，本文提出一种多粒度概率语言环境下基于PROMETHEE的改进FMEA方法。该方法采用多粒度PLTS适应了不同知识背景和经验水平的专家的表达习惯，并利用基于二元语义粒度转换函数为引入工具的语言计算模型融合FMEA团队多粒度风险评估信息；考虑专家主观经验知识和故障评估客观信息两方面因素，运用BWM和熵权法结合的综合赋权法确定风险因子权重；将PLTS的可能度公式作为优先函数计算故障模式两两比较的优劣程度，然后基于PL-PROMETHEE对故障模式进行风险排序。最后，以托盘交换架故障风险评估分析为例验证了本文方法的有效性和适用性。
1 基础知识 1.1 概率语言术语集 定义1^[15]??设一个语言术语集为S={s_α|α=0, 1，…, 2τ}，其中，τ为正整数，为了描述专家评估时的犹豫和不确定性，定义一个PLTS为

(1)

式中：L^(l)(p^(l))为概率信息为p^(l)的语言术语L^(l)；#L(p)为所有L(p)中包含的语言术语的个数。

1.1.1 PLTS的标准化 PLTS中的值表示专家关于所有可能的语言术语的概率分布信息。当时，专家给出的评估信息是不完整的概率分布，则需要对PLTS进行标准化。
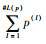
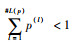
定义2^[15]??若PLTS中，则标准化的PLTS L(p)定义为

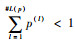
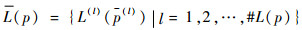(2)

式中：。令r^(l)为语言术语L^(l)的下标，则PLTS内所有元素按照r^(l)p^(l)的值升序排列，若PLTS内含具有相等r^(l)p^(l)值的元素，则元素按照r^(l)的值升序排列。
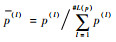
定义3^[15]??设L₁(p)={L₁^(l)(p₁^(l))l=1, 2, …, # L₁(p)}和L₂(p)={ L₂^(l)(p₂^(l))l=1, 2, …, # L₂(p)是2个不同概率语言术语集，如果#L₁(p)>#L₂(p)，则将#L₁(p)-#L₂(p)个语言术语添加到中L₂(p)，其中添加的语言术语是L₂(p)中最小的语言术语，且其概率为0，使得L₁(p)和中L₂(p)包含的语言术语的个数相等。

1.1.2 PLTS的聚合 定义4^[21]??由Q位来自不同专业领域的专家E=(q=1, 2, …, Q)，其权重向量为[λ₁, λ₂, …, λ_Q]^T且。第q位专家给出的PLTS为L^(q)(p)={L_α^(q)(p_α^(q))L_α^(q)∈S}(q=1, 2, …, Q)，则专家组集体评估的综合PLTS为

(3)

式中：v_α^(q)为L^(q)(p)中语言术语L_α^(q)的权重，即

(4)

1.1.3 基于可能度的PTLSs排序 定义5^[22]??对L₁(p)和L₂(p)任意2个PTLS，r_i^(l)(i=1, 2)是L_i^(l)(i=1, 2)的下标，则L₁(p)不小于L₂(p)的可能度定义为

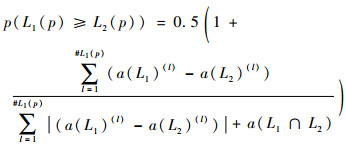(5)

式中：a(L_i)^(l)=r_i^(l)p_i^(l)(i=1, 2)；a(L₁∩L₂)为L₁(p)和L₂(p)的交叉区域。
1.2 二元语义不同粒度转换函数 二元语义的定义、运算和逆运算参见文献[23]，下面简述基于二元语义表示的不同粒度转换函数。
定义6^[23]??设含有T_m个不同粒度语言评价集为S={S^T₁, S^T₂, …, S^T_m}，其S^T_k={s_α^T_k|α=0, 1, …, T_k-1}表示粒度为T_k(T_k为奇数)的第k层语言评价集。对于形式为(s_α, θ)的二元语义，其中，θ为符号转移值，定义转换函数ξ实现不同层级之间的语言变量集合的映射：S^T_k→S^T′_k，则有

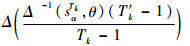(6)

1.3 二元语义转换PLTS 定义7??设S={s_α|α=0, 1，…, 2τ}是一个语言术语集，Ω是S的所有概率语言术语集评估的集合，定义转换函数F将二元语义(s_α, θ)转换为其等价的PLTS：

(7)

式中：t为Δ^-1(s_α, θ)的整数部分，且β=Δ^-1(s_α, θ)-t。
对于定义7，给出定理1。
定理1??设S={s_α|α=0, 1，…, 2τ}是一个语言术语集，二元语义(s_α, θ)的等价PLTS为

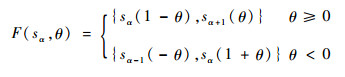(8)

证明??如果θ≥0，Δ^-1(s_α, θ)≥α，则t=α且β=Δ^-1(s_α, θ)-t=α+θ-α=θ，运用式(7)得到，F(s_α, θ)={s_α(1－θ), s_α+1(θ)}；如果θ < 0，Δ^-1(s_α, θ) < α，则t=α-1且β=Δ^-1(s_α, θ)-t=α+θ-α+1=1+θ，运用式(7)得，F(s_α, θ)={s_α－1(－θ), s_α(1+θ)}。????证毕
2 改进FMEA方法 为解决传统FMEA模型的缺陷，本文提出了一种多粒度概率语言环境下基于PROMETHEE的改进FMEA方法，该方法主要包括3阶段:①基于多粒度PLTS的故障模式风险评估；②利用综合权重法结合由BWM和熵权法确定的风险因子主客观权重；③基于PL-PROMETHEE的故障模式优先级排序。改进FMEA方法框架流程图如图 1所示。

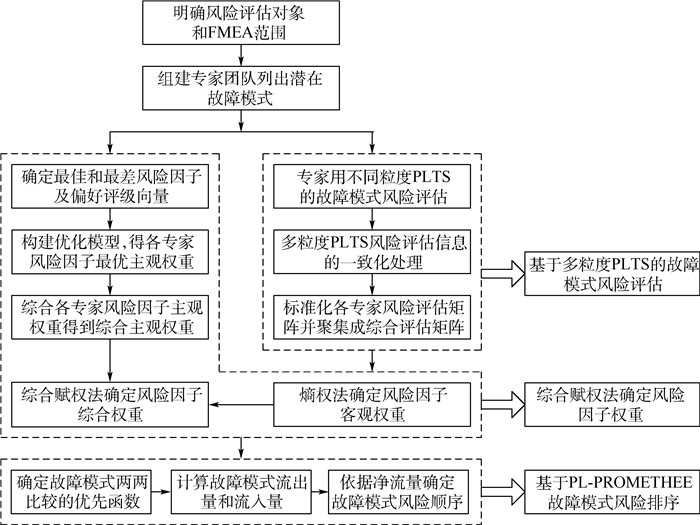图 1 改进FMEA方法框架流程图 Fig. 1 Flowchart of improved FMEA method

图选项

2.1 基于多粒度PLTS的故障模式风险评估 在故障模式风险评估前，拥有相关背景知识和专业经验的FMEA团队需确定风险评估对象、FME范围和识别对象潜在故障模式。

2.1.1 专家采用不同粒度PLTS对故障模式进行风险评估 设FMEA团队中有Q位来自不同专业领域的专家E_q(q=1, 2, …, Q)，每个专家被分配专家权重λ_q≥0(q=1, 2, …, Q)，FMEA团队专家可以根据个人背景和偏好，选用不同粒度语言术语集S={S^T₁，S^T₂，…, S^T_m}来表达自己观点，假设专家E_q使用基于S^T_k={s_α^T_k|α=0, 1, …, T_k-1}的PLTS来提供故障评估信息，则该专家对关于风险因子RF_j(j=1, 2, …, n)下潜在故障模式FM_i(i=1, 2, …, m)的评估矩阵为

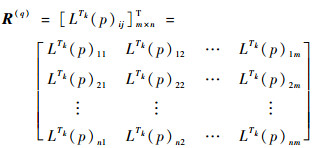(9)

2.1.2 多粒度PLTS的一致化 由于FMEA专家知识背景和经验水平差异，专家在对同一方案进行评价时可能会选择不同粒度的语言评价集，具有提供精确信息能力的专家使用更精细的语言术语集，相反，专家可能选择粗粒度语言术语集^[24]。为了对专家的不同粒度评估信息进行集结，首先将多粒度的评价集一致化，即从中选择一种粒度的评价集作为基本语言评价集，将评价集转换为基本语言评价集的形式^[25]。
本文提出一种基于二元语义转换函数为引入工具的语言计算模型实现多粒度PLTS间的转换。
定义8??设S^T_k={s_α^T_k|α=0, 1, …, T_k-1}，S^T′_k={s_t^T′_k|t=0, 1, …, T_k′-1}是2个不同粒度语言评价集，为了将基于S^T_k的PLTS L^T_k(p)={L_α^T_k(p_α^T_k)L_α^T_k∈S^T_k}转变为基于S^T′_k的PLTS L_k^T′(p)，可将中语言术语L_α^T_k增添符号转移值0变成二元语义(s_α^T_k, 0)，接着根据定理1把由式(6)导出的二元语义转换成等价PLTS L_α^T′_k(p)为

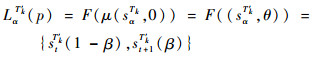(10)

式中：t为α(T′_k-1)/(T_k-1)的整数部分，且β=α(T′_k-1)/(T_k-1)-t。
考虑到PLTS各个元素上与L_α^T_k对应的概率p_i^T_k，可将其视为对应L_α^T′_k(p)的权重。最后通过式(3)和式(4)聚集得到L^T′_k(p)。

2.1.3 专家故障评估信息的聚集 基于定义2和定义3，对个体故障评估矩阵R^(q)=[L^T_k(p)_ij]_m×n^T标准化处理，结合专家权重，由式(3)和式(4)聚集专家故障评估矩阵得群体故障评估矩阵R=[L^T_k(p)_ij]_m×n^T。
2.2 综合赋权法确定风险因子权重
2.2.1 BWM确定风险因子主观权重 BWM与AHP类似，也是基于成对比较的思想，但并不是任意准则两两比较，而是构造一种结构化的比较方式^[18]。BWM确定风险因子主观权重具体操作步骤如下：
步骤1??专家确定最佳风险因子RF_B^(q)和最差风险因子RF_W^(q)。
步骤2??专家利用1~9标度打分, 确定最佳风险因子相比其他风险因子的偏好程度, 构建比较向量A_B^(q)={ a_B1^(q), a_B2^(q), …, a_Bn^(q)}，其中a_Bj^(q)为最佳风险因子与第j个风险因子相比的偏好程度，显然，a_BB=1。同理，确定其他风险因子相比于最差风险因子的偏好程度, 构建比较向量A_W^(q)={a_1W^(q), a_2W^(q), …, a_nW^(q)}，其中a_jW^(q)为第j个风险因子与最差风险因子相比的偏好程度。
步骤3??为求取专家最优风险因子主观权重{w₁^s(q), w₂^s(q), …, w_n^s(q)}，构建优化模型：

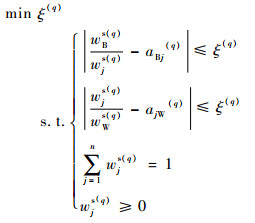(11)

式中：ξ(q)为专家E^q比较结果一致性的误差；w_B^s(q)、w_W^s(q)和w_j^s(q)分别为专家E_q决定的最佳风险因子、最差风险因子和第j个风险因子的主观权重。
步骤4??一致性检查，BWM利用一致性比率CR来检查比较矩阵的一致性：

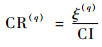(12)

式中：CI为一致性指数(见表 1)。一致性比率CR反映了比较的一致性水平，CR值接近0表明比较更接近一致性，通常，CR值小于0.5足以表明BWM的可靠性和有效^[26]。
表 1 一致性指数 Table 1 Consistency index

aBW	CI
1	0
2	0.44
3	1.00
4	1.63
5	2.30
6	3.00
7	3.73
8	4.47
9	5.23

表选项






步骤5??求解式(11)中的模型获得各个专家最优风险因子主观权重，最终通过使用加权平均算子集聚生成风险因子主观权重{w₁^s，w₂^s…，w_n^s}。

2.2.2 熵权法确定风险因子客观权重 熵权法通过计算传递给决策者信息量的多少来确定其权重的大小，熵越小含有的信息量越大，熵越大信息量越小，是一种常见的求取客观属性权重的方法^[5]。本文采用文献[27]提出的一种PLTS环境下的熵权法求解风险因子客观权重，基本步骤如下：
步骤1??将群体故障评估矩阵R=[L^T_k(p)_ij]_m×n^T转换为得分函数矩阵R′=[L^T_k(p)_ij′]_m×n^T，其中L^T_k(p)_ij′= /# L(p)。
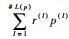
步骤2??计算各风险因子熵值，第j个风险因子熵值为

(13)

步骤3??计算各风险因子客观权重，第j个风险因子客观权重为

(14)

2.2.3 风险因子主观权重和客观权重综合 综合BWM和熵权法导出的主观和客观权重，每个风险因子的综合权重可以计算为

(15)

式中：γ为主观权重系数，反映专家主观判断在风险因子权重中占有的比例，取值范围为[0, 1]。
2.3 基于PL-PROMETHEE的故障模式风险排序 PROMETHEE是一种利用流出量及流入量判断各方案优先程度的MCDM方法。本文在风险因子综合权重w_j={w₁, w₂, …, w_n}确定的情况下，将PROMETHEE拓展到PLTS语言环境下以解决传统FMEA方法中故障模式的风险优先级问题。基于PL-PROMETHEE的故障模式风险排序方法步骤如下：
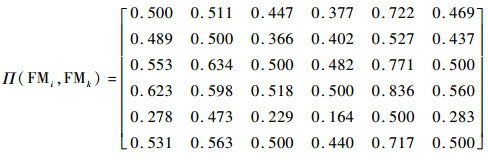
步骤1??计算风险因子RF_j(j=1, 2, …, n)下故障模式FM_i对于FM_k(i, k=1, 2, …, m)的优先函数Π(FM_i, FM_k)为

(16)

步骤2??计算每个故障模式的流出量Φ⁺(FM_i)和流入量Φ^－(FM_i)为

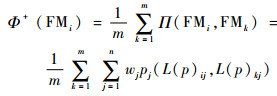(17)

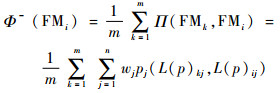(18)

步骤3??计算净流量Φ(FM_i)为

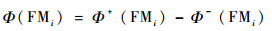(19)

步骤4??根据净流量的值进行故障模式风险排序。
3 案例分析 托盘交换架是加工中心的关键功能部件，其主要功能是实现机床加工时将已加工件与待加工毛坯进行位置交换，从而实现将待加工毛坯送入到加工位置，并对其自动定位。本文以国产某卧式加工中心的托盘交换架为评估对象，FMEA团队由3位分别来自维修、制造、研发部门的专家(E₁、E₂、E₃)组成，专家的权重λ分别为0.2、0.4、0.4。FMEA团队依据数控转台功能结构特点和实践经验识别出托盘交换架的6个潜在故障模式：油缸漏油(FM₁)、旋转减速瞬间振动和噪声(FM₂)、交换速度过快或过慢(FM₃)、升降不到位(FM₄)、旋转到位时晃动(FM₅)、旋转不到位(FM₆)。
3.1 基于多粒度PLTS的故障模式的风险评估 3位专家根据自身专业背景和经验水平选用不同粒度PLTS对各个故障模式关于风险因子O、S和D进行故障评价：E₁选用5粒度的语言术语集S⁵；E₂和E₃选用7粒度的语言术语集S⁷，上述语言术语集等级语言变量为S⁵={s₀⁵:低, s₁⁵:稍低, s₂⁵:中等, s₃⁵:稍高, s₄⁵:高}，S⁷={s₀⁷:很低, s₁⁷:低, s₂⁷:稍低, s₃⁷:中等, s₄⁷:稍高, s₅⁷:高, s₆⁷:很高}。
收集3位专家对6个故障模式评估信息，并汇总于表 2中。
表 2 3位专家提供的概率语言评估信息 Table 2 Probabilistic linguistic evaluation information provided by three experts

Eq	RFj	FM1	FM2	FM3	FM4	FM5	FM6
E1	O	{s25(0.8)}	{s35(0.8), s45(0.2)}	{s25(0.8)}	{s25(0.8), s35(0.2)}	{s15(0.5), s25(0.5)}	{s15(0.4), s25(0.6)}
	S	{s25(0.5), s35(0.5)}	{s25(0.4), s35(0.4)}	{s35(0.4), s45(0.6)}	{s35(0.5), s45(0.5)}	{s25(0.4), s35(0.6)}	{s35(0.8)}
	D	{s35(0.5), s45(0.5)}	{s05(0.6), s15(0.4)}	{s25(1)}	{s45(0.8)}	{s15(0.2), s25(0.8))}	{s45(1)}
E2	O	{s37(0.2), s47(0.8)}	{s47(0.5), s57(0.5)}	{s37(0.8), s47(0.2)}	{s37(0.8), s47(0.2)}	{s27(0.75), s37(0.25)}	{s17(0.4), s27(0.6)}
	S	{s37(0.25), s47(0.75)}	{s37(0.2), s47(0.6), s57(0.2)}	{s47(0.5), s57(0.5)}	{s47(0.4), s57(0.4)}	{s37(0.8), s47(0.2)}	{s47(0.5), s57(0.5)}
	D	{s47(0.25), s57(0.5), s67(0.25)}	{s07(0.25), s17(0.75)}	{s27(0.2), s37(0.8)}	{s57(0.8), s67(0.2)}	{s17(0.25), s27(0.5), s37(0.25)}	{s57(0.75), s67(0.25)}
E3	O	{s37(0.8), s47(0.2)}	{s47(0.2), s57(0.2), s67(0.6)}	{s37(0.2), s47(0.8)}	{s37(0.8), s47(0.2)}	{s17(0.4), s27(0.6)}	{s27(0.4), s37(0.4)}
	S	{s37(0.25), s47(0.75)}	{s37(0.8), s47(0.2)}	{s57(0.6), s67(0.2)}	{s47(0.8)}	{s37(0.25), s47(0.5), s57(0.25)}	{s47(0.5), s57(0.5)}
	D	{s47(0.6), s57(0.2)}	{s17(0.6), s27(0.4)}	{s27(0.75), s37(0.25)}	{s57(0.8), s67(0.2)}	{s37(0.8)}	{s57(0.2), s67(0.8)}

表选项






选择S⁷作为基本语言评价集，将E₁提供的评估信息R⁽¹⁾=[L⁵(p)_ij]_6×3^T转化为[L⁷(p)_ij]_6×3^T，如表 3所示，其中以L⁵(p)₁₂={s₂⁵(0.5), s₃⁵(0.5)}为例，首先利用式(10)计算L⁵(p)₁₂中每个语言术语对应的等效PLTS分别为：L₂⁷(p)={s₃⁵(1)}, L₃⁷(p)={s₄⁷(0.5), s₅⁷(0.5)}, 其概率权重分别为[0.5, 0.5]^T，最后运用式(3)和式(4)聚集得到L⁷(p)₁₂={s₃⁷(0.5), s₄⁷(0.25), s₅⁷(0.25)}。
表 3 一致化处理后的专家3故障模式评估信息 Table 3 Unified E'₃ s evaluation information of each failure mode

RFj	FM1	FM2	FM3	FM4	FM5	FM6
O	{s37(0.8)}	{s47(0.4), s57(0.4), s67(0.2)}	{s37(0.8)}	{s37(0.8), s47(0.1), s57(0.1)}	{s17(0.25), s27(0.25), s37(0.5)}	{s17(0.2), s27(0.2), s37(0.6)}
S	{s37(0.5), s47(0.25), s57(0.25)}	{s37(0.4), s47(0.2), s57(0.2)}	{s47(0.2), s57(0.2), s67(0.6)}	{s47(0.25), s57(0.25), s67(0.5)}	{s37(0.4), s47(0.3), s57(0.3)}	{s47(0.4), s57(0.4)}
D	{s47(0.25), s57(0.25), s67(0.5)}	{s07(0.6), s17(0.2), s27(0.2)}	{s37(1)}	{s67(0.8)}	{s17(0.1), s27(0.1), s35(0.8)}	{s67(1)}

表选项






分别对3位专家评估信息进行标准化处理，结合专家权重λ={0.2, 0.4, 0.4}，并根据式(3)和式(4)聚集各专家故障评估矩阵得群体故障评估矩阵R=[L⁷(p)_ij]_6×3^T，如表 4所示。
表 4 群体故障评估矩阵 Table 4 Group failure evaluation matrix

RFj	FM1	FM2	FM3	FM4	FM5	FM6
O	{s37(0), s47(0.4), s37(0.6)}	{s47(0.16), s57(0.36), s67(0.48)}	{s37(0), s47(0.4), s37(0.6)}	{s57(0.02), s47(0.18), s37(0.8)}	{s17(0.21), s37(0.2), s27(0.59)}	{s17(0.2), s27(0.48), s37(0.32)}
S	{s57(0.05), s37(0.3), s47(0.65)}	{s57(0.13), s47(0.37), s37(0.5)}	{s47(0.24), s67(0.22), s57(0.54)}	{s67(0.1), s57(0.25), s47(0.65)}	{s57(0.16), s47(0.34), s37(0.5)}	{s47(0), s47(0.5), s57(0.5)}
D	{s67(0.2), s57(0.35), s47(0.45)}	{s07(0.22), s27(0.2), s17(0.58)}	{s27(0), s27(0.38), s37(0.62)}	{s57(0), s67(0.36), s57(0.64)}	{s17(0.12), s27(0.22), s37(0.66)}	{s57(0), s57(0.38), s67(0.62)}

表选项






3.2 风险因子权重确定 根据FMEA团队专家的判断，确定每个团队专家的最佳和最差风险因子的偏好评级向量，如表 5和表 6所示，并依据式(11)，构建风险因子优化模型。通过使用加权平均算子，聚合FMEA团队专家得到的风险因子主观权重及其权重λ={0.2, 0.4, 0.4}，获得风险因子的合成主观权重w_j^S={0.341, 0.486, 0.173}。推导结果如表 7所示。
表 5 最佳标准的风险因子评级向量 Table 5 Preference rating vectors for the best risk factor

Eq	RFB	O	S	D
E1	S	2	1	8
E2	S	9	1	3
E3	O	1	3	8

表选项






表 6 最差标准的风险因子评级向量 Table 6 Preference rating vectors for the worst risk factor

Eq	RFW	O	S	D
E1	D	2	8	1
E2	O	1	7	4
E3	D	7	3	1

表选项






表 7 风险因子主观权重 Table 7 Subjective weights of risk factor

Eq	O	S	D	CR
E1	0.246	0.663	0.091	0.157
E2	0.078	0.622	0.300	0.191
E3	0.652	0.261	0.087	0.112
wjS	0.341	0.486	0.173

表选项






将群体决策矩阵R=[L⁷(p)_ij]_6×3^T转化为得分函数矩阵R′=[L⁷(p)′_ij]_6×3^T，利用式(13)和式(14)，得到风险因子熵值H_j={-0.47 8, -1.556, -1.292}和客观权重w_j^O={0.234, 0.404, 0.362}。利用式(15)，其中将γ设定为0.5，对主观和客观权重聚合得到风险因子综合权重为w_j={0.287, 0.445, 0.368}。
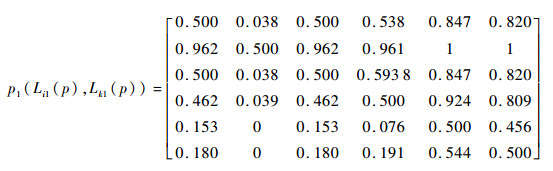
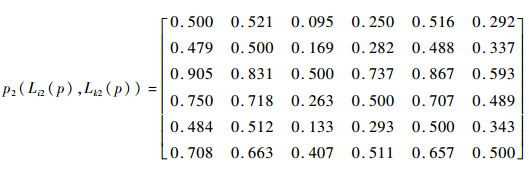
3.3 基于PL-PROMETHEE的故障模式风险排序 通过式(5)计算各风险因子下故障模式间的可能度p_j(L(p)_ij, L(p)_kj)，并根据式(16)确定故障模式两两比较的优先函数Π(FM_i, FM_k)。利用式(17)和式(18)，计算故障模式的流出量Φ⁺(FM_i)、流入量Φ^-(FM_i)和净流量Φ(FM_i)分别为
Φ⁺(FM_i)={3.025, 2.722, 3.440, 3.636, 1.927, 3.250)；Φ^－(FM_i)={2.975, 3.278, 2.560, 2.364, 4.073, 2.750}；Φ(FM_i)={0.050, －0.556, 0.880, 1.272, －2.146, 0.500}
最终，由净流量的值确定的故障模式风险排序为：FM₄>FM₃>FM₆>FM₁>FM₂>FM₅。其中，FM₄作为风险最高故障模式，应赋予最高级别风险优先度而被重点关注，FM₃风险次之，最低风险故障模式为FM₅。




3.4 灵敏度与对比分析 风险因子的综合权重很大程度上取决于主观权重系数γ，且γ是在[0, 1]中变化的调整参数，在本文案例中设置为0.5。为验证γ对风险优先级排序的影响，取γ不同值的情况时6种失效模式的风险等级排序结果如图 2所示。

图 2 参数γ的敏感度分析 Fig. 2 Sensitivity analysis on parameter γ

图选项

由图 2可知，当γ≤0.8时，故障模式的等级顺序几乎不受γ值的影响，这说明这些故障模式在专家主观判断和评估信息客观因素两方面具有相同的重要性；当γ>0.8时，FM₂和FM₃风险排名提高，相应FM₆和FM₄风险排名下降，意味着在本文案例中采用偏主观的风险因子权重对故障模式的风险排序有一定影响。基于以上分析，在现实的FMEA风险评估过程中，需要根据风险评估实际情景和专家对评估信息确定程度来合理确定适当的γ值。
为验证本文所提方法的合理性和有效性，将本文提出的PL-PROMETHEE方法与传统FMEA法、文献[15]提出的PL-TOPSIS方法和文献[8]提出的HFL-PROMETHEE方法作对比分析。将4种方法得出的故障模式风险排序结果汇总于表 8中。其中PL-TOPSIS方法和HFL-PROMETHEE方法沿用本文风险因子综合权重，与本文方法不同的是：PL-TOPSIS方法将TOPSIS拓展到概率语言环境下确定故障模式风险排序顺序，而HFL-PROMETHEE方法则采用犹豫模糊语言集HFLTS评估故障风险信息。
表 8 不同方法故障模式风险排序比较 Table 8 Risk ranking comparison of failure modes by different methods

故障模式	传统FMEA						PL-TOPSIS[15]			HFL-PROMETHEE[8]			PL-PROMETHEE
	O	S	D	RPN	排序		CI(FMi)	排序		Φ(FMi)	排序		Φ(FMi)	排序
FM1	5	6	7	210	3		-0.743	4		0.176	3		0.050	4
FM2	8	4	6	192	4		-0.962	5		-0.440	5		-0.556	5
FM3	6	8	4	192	4		-0.556	3		0.368	2		0.879	2
FM4	5	6	9	270	1		0	1		2.017	1		1.272	1
FM5	3	6	5	90	5		-1.368	6		-2.167	6		-2.146	6
FM6	4	7	9	252	2		-0.353	2		0.045	4		0.500	3

表选项






由表 8可知，虽然4种方法获得的故障模式排序结果不完全相同，但都将FM₄和FM₅分别确定为最高和最低故障模式，一定程度上验证了本文方法的有效性。此外，图 3描绘了4种方法排序数据归一化处理后故障模式间排序相对偏差量，其中，PL-PROMETHEE曲线波动幅度最大，意味着本文方法在故障模式中的辨别度高于其他3种方法。

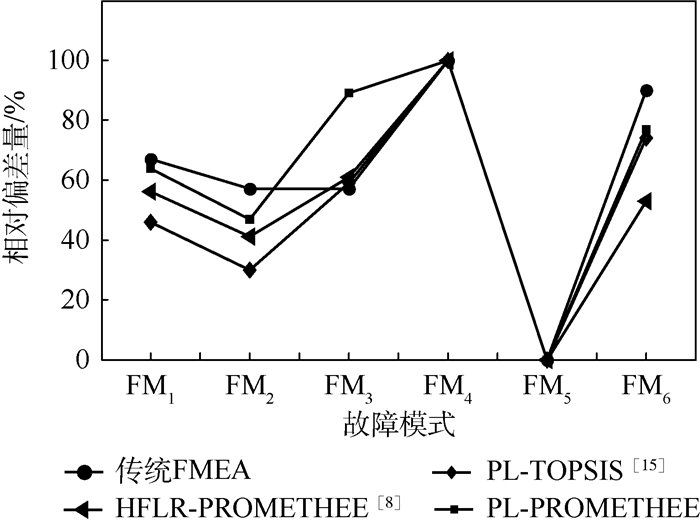图 3 不同方法故障模式间相对偏差量 Fig. 3 Relative deviations between failure modes by different methods

图选项

另一方面，本文方法故障模式排序顺序与传统FMEA方法之间差距较为明显，即FM₄和FM₅排序相同，其余故障模式排序均不同；对比于PL-TOPSIS排序结果，仅FM₃和FM₆的风险等级发生了互换；与HFL-PROMETHEE故障模式排序顺序相比，则在FM₆和FM₁的排序顺序发生互换。导致这些差异可能原因为:①对比传统FMEA方法采用清晰的数字和HFL-PROMETHEE采用的HFLTS，本文使用PLTS使专家能够更准确，更接近实际情况提供风险评估。②传统FMEA方法中风险因子具有同等重要性，然而，本文采用综合赋权法来识别风险因子权重，充分融合了主客观权重方法的优势。③PL-TOPSIS使用TOPSIS来获得故障模式的风险等级，TOPSIS具有决策补偿性，一个指标下的高评价值能弥补其他指标下的低评价值，相比之下，PROMETHEE基于方案间的两两比较得出最终的排序结果, 决策相对结果更加准确。
4 结论 本文提出了一种多粒度概率语言环境下基于PROMETHEE的改进FMEA方法，以改善传统FMEA方法的缺陷，提高其科学性和有效性。所提的方法特点如下:
1) 用多粒度PLTS评估故障模式风险，不仅能满足不同知识背景和经验水平的专家的表达习惯，而且还能解决专家评估信息表达模糊和信息丢失的问题。相比于传统FMEA方法，更真实地刻画了专家评估信息的多样性和不确定性。
2) 运用BWM和熵权法结合的综合赋权法区分风险因子的相对重要性，克服了主观赋权法或客观赋权法单方面的缺陷，并且通过设置主观权重系数调整主客观权重比例，可以有效地适用于各种不同现实情况。
3) 基于PL-PROMETHEE对故障模式进行风险排序，避免了决策补偿性对故障模式评价结果的影响，充分考虑了决策者偏好存在的客观事实，在实际应用中更具广泛性。
尽管本文方法为故障风险评估提供了一种有效实用的工具，但仍有一些问题需要在未来研究中加以解决。首先，FMEA团队成员不同的风险态度可能直接影响最终故障模式风险排序结果，因此，未来可以将专家风险态度作为影响风险评估的重要因素。其次，在未来研究中可以确定未考虑的其他风险因子，以更全面反映故障模式风险。最后，本文方法可用于应对其他更复杂的风险分析问题，以进一步验证其适用性和有效性。

参考文献

[1]	CERTA A, ENEA M, GALANTE G M, et al. ELECTRE TRI based approach to the failure modes classification on the basis of risk parameters:An alternative to the risk priority number[J]. Computers & Industrial Engineering, 2017, 108: 100-110.
[2]	LO H, LIOU J, HUANG C, et al. A novel failure mode and effect analysis model for machine tool risk analysis[J]. Reliability Engineering and System Safety, 2019, 183: 173-183. DOI:10.1016/j.ress.2018.11.018
[3]	LIU H C, YOU J X, CHEN S, et al. An integrated failure mode and effect analysis approach for accurate risk assessment under uncertainty[J]. IIE Transactions, 2016, 48(11): 1027-1042. DOI:10.1080/0740817X.2016.1172742
[4]	HUANG J, LI Z, LIU H C. New approach for failure mode and effect analysis using linguistic distribution assessments and TODIM method[J]. Reliability Engineering and System Safety, 2017, 167: 302-309. DOI:10.1016/j.ress.2017.06.014
[5]	杜晗恒, 彭翀. 基于模糊TOPSIS的FMEA方法[J]. 北京航空航天大学学报, 2016, 42(2): 368-374. DU H H, PENG C. Failure mode and effects analysis method based on fuzzy TOPSIS[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(2): 368-374. (in Chinese)
[6]	SAKTHIVEL G, IKUA B W. Failure mode and effect analysis using fuzzy analytic hierarchy process and GRA TOPSIS in manufacturing industry[J]. International Journal of Productivity and Quality Management, 2017, 22(4): 466-484. DOI:10.1504/IJPQM.2017.087864
[7]	WANG W Z, LIU X W, CHEN X Q, et al. Risk assessment based on hybrid FMEA framework by considering decision maker's psychological behavior character[J]. Computers & Industrial Engineering, 2019, 136: 516-527.
[8]	耿秀丽, 邱华清. 基于犹豫模糊PROMETHEE Ⅱ的设计方案群决策方法[J]. 计算机应用研究, 2018, 35(10): 3020-3024. GENG X L, QIU H Q. Group decision-making method of design concept based on hesitant fuzzy PROMETHEEⅡ[J]. Application Research of Computers, 2018, 35(10): 3020-3024. DOI:10.3969/j.issn.1001-3695.2018.10.032 (in Chinese)
[9]	LIU H C, YOU J X, DUAN C Y, et al. An integrated approach for failure mode and effect analysis under interval-valued intuitionistic fuzzy environment[J]. International Journal of Production Economics, 2019, 207: 163-172. DOI:10.1016/j.ijpe.2017.03.008
[10]	王睿, 朱江洪, 李延来. 基于直觉模糊MULTIMOORA的改进FMEA风险评估方法[J]. 计算机集成制造系统, 2018, 24(2): 290-301. WANG R, ZHU J H, LI Y L. Improved FMEA method for risk evaluation based on intuitionistic fuzzy MULTIMOORA[J]. Computer Integrated Manufacturing Systems, 2018, 24(2): 290-301. (in Chinese)
[11]	WANG Z L, YOU J X, LIU H C, et al. Failure mode and effect analysis using soft set theory and COPRAS method[J]. International Journal of Computational Intelligence Systems, 2017, 10(1): 1002-1015. DOI:10.2991/ijcis.2017.10.1.67
[12]	LIU H C, LI Z, SONG W, et al. Failure mode and effect analysis using cloud model theory and PROMETHEE method[J]. IEEE Transactions on Reliability, 2017, 66(4): 1058-1072. DOI:10.1109/TR.2017.2754642
[13]	NIE R X, TIAN Z P, WANG X K, et al. Risk evaluation by FMEA of supercritical water gasification system using multi-granular linguistic distribution assessment[J]. Knowledge-Based Systems, 2018, 162: 185-201. DOI:10.1016/j.knosys.2018.05.030
[14]	RODRIGUEZ R M, MARTíNEZ L, HERRERA F. Hesitant fuzzy linguistic term sets for decision making[J]. IEEE Transactions on Fuzzy Systems, 2012, 20(1): 109-119. DOI:10.1109/TFUZZ.2011.2170076
[15]	PANG Q, WANG H, XU Z. Probabilistic linguistic term sets in multi-attribute group decision making[J]. Information Sciences, 2016, 369: 128-143. DOI:10.1016/j.ins.2016.06.021
[16]	YANG Z, WANG J. Use of fuzzy risk assessment in FMEA of offshore engineering systems[J]. Ocean Engineering, 2015, 95: 195-204. DOI:10.1016/j.oceaneng.2014.11.037
[17]	ZHOU Y, XIA J, ZHONG Y, et al. An improved FMEA method based on the linguistic weighted geometric operator and fuzzy priority[J]. Quality Engineering, 2016, 28(4): 491-498. DOI:10.1080/08982112.2015.1132320
[18]	REZAEI J. Best-worst multi-criteria decision-making method[J]. Omega, 2015, 53: 49-57. DOI:10.1016/j.omega.2014.11.009
[19]	DRAGAN P, GORAN C. The selection of transport and handling resources in logistics centers using multi-attributive border approximation area comparison (MABAC)[J]. Expert Systems with Applications, 2015, 42(6): 3016-3028. DOI:10.1016/j.eswa.2014.11.057
[20]	BRANS J P, VINCKE P, MARESCHAl B. How to select and how to rank projects:The PROMETHEE method[J]. European Journal of Operational Research, 1986, 24(2): 228-238. DOI:10.1016/0377-2217(86)90044-5
[21]	WU X, LIAO H. An approach to quality function deployment based on probabilistic linguistic term sets and ORESTE method for multi-expert multi-criteria decision making[J]. Information Fusion, 2018, 43: 13-26. DOI:10.1016/j.inffus.2017.11.008
[22]	LIU P D, LI Y. The PROMTHEE Ⅱ method based on probabilistic linguistic information and their application to decision making[J]. Informatica, 2018, 29(2): 303-320. DOI:10.15388/Informatica.2018.169
[23]	张震, 郭崇慧. 基于相对熵的多粒度不确定语言型群决策方法[J]. 大连理工大学学报, 2012, 52(6): 921-927. ZHANG Z, GUO C H. A multi-granularity uncertain linguistic group decision-making method based on relative entropy[J]. Journal of Dalian University of Technology, 2012, 52(6): 921-927. (in Chinese)
[24]	ZHANG Z, GUO C, MARTíNEZ L. Managing multi-granular linguistic distribution assessments in large-scale multi-attribute group decision making[J]. IEEE Transactions on Systems Man & Cybernetics Systems, 2017, 47(11): 3063-3076.
[25]	张发明, 袁宇翔, 梁龙武. 多粒度不确定语言变量的多属性群决策方法及应用[J]. 系统管理学报, 2017, 26(6): 64-73. ZHANG F M, YUAN Y X, LIANG L W. Multi-attribute group-decision-making with multi-granularity uncertain linguistic variables and its application[J]. Journal of Systems & Management, 2017, 26(6): 64-73. (in Chinese)
[26]	CHITSAZ N, AZARNIVAND A. Water scarcity management in arid regions based on an extended multiple criteria technique[J]. Water Resources Management, 2017, 31(1): 233-250. DOI:10.1007/s11269-016-1521-5
[27]	LIU P, YOU X. Probabilistic linguistic TODIM approach for multiple attribute decision-making[J]. Granular Computing, 2017(12): 1-10.