信噪比估计传统算法主要分为基于最大似然(Maximum Likelihood,ML)估计法、统计量估计法、谱分析(Spectrum Analysis, SA)估计法等。文献[2]提出了基于ML的高斯信道下低偏差信噪比估计算法;文献[3]结合期望值最大化技术与ML技术,研究了SIMO(Single-Input-Multiple-Output)系统下高维度调制信号的信噪比估计方法,扩大了ML类算法的适用范围。ML估计法理论上估计效果最接近克拉美罗下界(Gramer-Rao Lower Bound, CRLB),但在低信噪比情况下性能很差,且运算量较大。基于统计量估计法中分隔符号矩算法由美国喷气推进实验室提出,已用于美国航空航天局(NASA)的深层空间研究中[4];文献[5]研究了基于接收信号高阶统计量的改进二阶四阶矩(M2M4)算法;文献[6]进一步研究了该类算法在SIMO系统中的性能。基于统计量估计法计算简单,但需要数据足够多,并且随着调制阶数的增加,高信噪比情况下估计误差较大。文献[7]利用移动信道的功率谱特性,提出了一种基于SA的平均信噪比估计算法;文献[8]利用功率谱提出一种无需先验信息的快速信噪比盲估计算法。该类算法计算量小,但估计精度相对较低。
深度学习(deep learning)近年来在图像/视频处理、自然语言处理等领域发展迅速,但在通信信号领域的研究却刚刚起步。其中,文献[9]将卷积神经网络(Convolutional Neural Networks, CNN)应用到通信信号的调制方式自动分类(Automatic Modulation Classification, AMC)问题中,取得较好的效果;文献[10]提出了一种融合深度神经网络的结构,在该问题中得到了更高的分类准确率;文献[11]使用深度学习算法,考虑载波频率偏移、符号率和多径衰落的影响,实现了对无线电通信信号的分类;文献[12]提出了将一维信号转化为类似图像的二维矩阵,使用二维CNN网络实现信号分类。
目前,深度学习算法尚未在通信信号信噪比估计问题得到应用,其主要难点在于:①网络层面:传统的网络结构提取通信信号特征的能力有限;②数据层面:缺少无人机通信信号公开的数据集。
针对以上问题,本文根据无人机数据链信号的特点,提出一种CNN与长短时记忆(Long Short Term Memory, LSTM)网络结合的估计算法。通过结合仿真数据与实测数据,构建了无人机通信信号数据集,利用该数据集对网络模型进行训练。使用CNN-LSTM网络对分割后的信号进行特征提取,得到特征向量,最终通过全连接层融合特征并计算信噪比估计值。通过测试,验证了本文算法可以很好地估计无人机数据链信号的信噪比。
1 CNN与LSTM网络适用性分析 在信噪比估计问题中,传统算法普遍根据待测信号自身的特点进行估计,而没有用到其他信号的数据。深度神经网络则是在经过大量信号数据的训练后,自动提取待测信号的深度特征,并将特征学习融入到了建立模型的过程中,减小单一信号计算带来的误差,提高估计精度。因此,在数据样本充足的情况下,深度学习算法可以更好地实现对信噪比的估计。
CNN模型[13]可以提取数据在空间结构上的关系,在图像识别[14]等领域有着出色的表现。CNN网络通过共享局部视野,减少了神经网络参数的数量,并且通过权值共享使运算量降低。本文将分割后的波形数据作为CNN模型的输入,每个卷积层的输出经过非线性激活后作为下一个卷积层的输入,利用多个卷积层堆叠的形式来更深入地描述信号的空间属性。
时间属性对信号数据尤为重要,虽然CNN网络可以很好地提取空间特征,但无法模拟时间序列的变化,因此需要利用LSTM模型时序地实现网络中的信息传递,循环提取特征,反复学习并生成新特征。由于待测无人机数据链序列普遍较长,LSTM网络则可以解决处理长序列时会发生的梯度爆炸或者梯度消失[15-16]问题。
综上所述,CNN和LSTM网络分别在空间和时间2个不同的维度对无人机数据链信号进行特征提取,可以发掘不同信噪比的信号之间深层次的差别。因此,本文选择CNN-LSTM网络结构来解决信噪比估计问题。
2 信噪比估计算法 无人机数据链信号具有信道空间特殊,信道时间动态化等特点,针对这些特点,本节给出了基于CNN-LSTM网络的信噪比估计算法,网络模型如图 1所示。
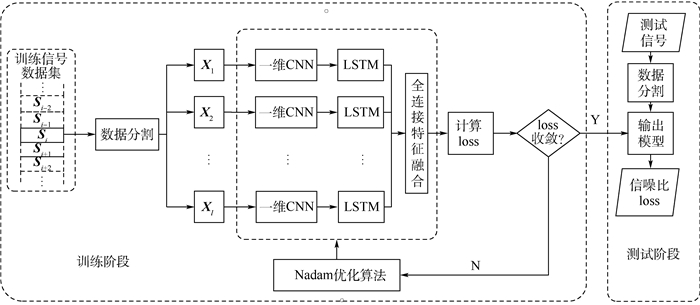 |
| 图 1 基于CNN-LSTM信噪比估计网络框架 Fig. 1 Network framework of SNR estimation based on CNN-LSTM |
| 图选项 |
本模型采用3层CNN网络刻画信号之间的深层次差异,每个卷积层的卷积核尺寸都是不同的,通过多次特征提取可以得到更多有效特征,这种方式减少了学习参数,简化了最终特征图的结构,便于网络之间融合。融合模型的剩余部分采用LSTM网络来学习并记忆信号数据时序特征,在数据链信号信噪比估计的问题上,本文LSTM将每一个数据点作为一个时间步,将CNN网络的输出特征图输入至LSTM网络,最终的输出结果表征信号的时序关联特征。
在训练阶段,首先把一条长序列的信号数据分割成短序列,对每一段短序列使用一维CNN网络提取特征,将生成的特征序列输入至LSTM网络进一步提取特征,最终在全连接层将每一段短序列的特征融合,输出损失函数loss,通过优化算法迭代优化网络模型,继续训练下一条数据,直到loss收敛,将模型参数保存,训练结束。本文采用的优化算法是文献[17]提出的Nadam算法,在Adam算法的基础上加入了Nesterov加速梯度[18],既可以防止振荡与局部极值的出现,又可以自适应地更新学习率。与其他算法相比,可以得到更快的收敛速度与更好的收敛效果。
在测试阶段,对测试信号进行同样的分割处理,将处理后的数据输入至已经训练好的网络模型中,最终输出得到信噪比估计值与loss值,测试得到的loss值可以直观地反映模型的训练效果。
2.1 数据分割 本文所提算法需要对训练集中的信号逐条进行训练,将训练集信号数据表示为
 | (1) |
式中:Si为训练信号序列。
训练集标签表示为
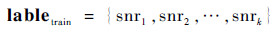 | (2) |
式中:snri为信噪比真值。
在使用LSTM模型提取特征时,遗忘门会读取当前输入信息与上一时刻状态,通过sigmoid函数输出一个0到1之间的数值到当前细胞状态中,这就不可避免地造成信息丢失。一些****研究人员尝试着改变LSTM的门结构来解决这个问题,但普遍没有取得预期效果。文献[19]分析总结了超过一万种LSTM的变体结构,最终得到的结论是相比于标准LSTM结构,没有任何一种变体结构可以有大幅度的改进。因此研究的重点转移到了对数据本身的处理,如归一化、时频域转换等。文献[19]指出分割信号数据可以一定程度地提升神经网络效果,并给出了基于分割窗的信号数据分割算法,信号分割窗长度L为其中的关键参数。适当的数据分割可以将一个长序列分解为几段短序列,减少在处理长序列时LSTM网络遗忘门对重要信息的丢失程度。
本文选择对每一条信号进行数据分割,把长序列分解为若干等长的短序列,分别保存在不同的数组中。设第i条输入信号的原始序列为
 | (3) |
分割过程如图 2所示。
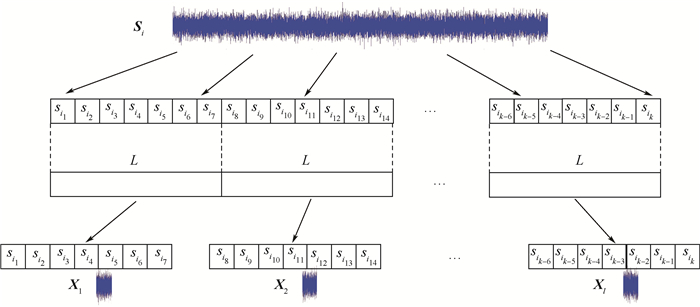 |
| 图 2 基于分割窗的信号数据分割算法示意图 Fig. 2 Schematic diagram of signal data segmentation algorithm based on split window |
| 图选项 |
该条信号的标签为lablei=snri,分割窗口的长度为L。经过分割后的信号表示为
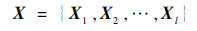 | (4) |
 | (5) |
2.2 CNN网络特征提取 将分割后的信号数据输入至图 3所示网络结构中,利用CNN网络对X的每个子集分别进行特征提取。本文使用的一维CNN网络采取3个卷积层级联的结构,由于相比于二维图像数据,一维信号数据结构简单、卷积运算时计算量小,因此没有在卷积层之间加入池化层,避免了关键信息的损失。
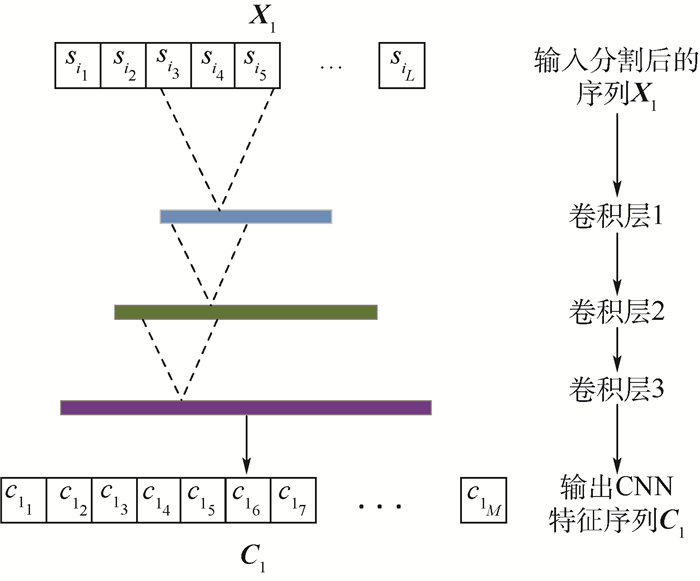 |
| 图 3 CNN网络运算流程图 Fig. 3 Operation flowchart of convolution network |
| 图选项 |
输入信号以图 3中的X1为例:
 | (6) |
设定卷积层1的卷积核大小为a*1,卷积层2的卷积核大小为b*1,卷积层3的卷积核大小为c*1,卷积计算过程如图 3所示。
输入序列按照式(7)进行计算:
 | (7) |
式中:x为输入序列;hik为第i个一维数据在第k层进行卷积运算后的值;fa为激活函数,如tanh和sigmoid等;Wk为该层的权重值;bk为对应的偏置值。最终CNN网络输出的特征序列为
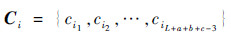 | (8) |
2.3 LSTM网络特征进一步提取 将CNN网络输出的特征序列输入至LSTM网络中,该网络由(L+a+b+c-3)个同构LSTM细胞构成,每个细胞单元按照时间顺序连接。
经过LSTM网络后输出的特征序列表示为
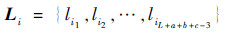 | (9) |
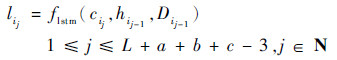 | (10) |
式中:flstm为LSTM细胞前向计算方法;cij、hij-1和Dij-1分别为当前细胞的输入、前一个细胞的输出与前一个细胞的状态。
2.4 全连接层特征融合 对于X中每一段信号Xi(1≤i≤l),经过CNN网络与LSTM网络之后都会输出一段特征序列Li(1≤i≤l),将这些特征序列按照时间顺序排列,得到一个维度为[l(L+a+b+c-3), 1]的向量f。
在全连接网络中本文选择2个全连接层级联的方式,经过全连接网络计算后,最终输出矩阵为R1×1,该矩阵的数值即为信噪比估计值pi。选用均方误差(Mean Square Error, MSE)作为训练准确程度的衡量标准,因此损失函数loss可定义为
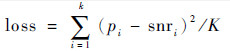 | (11) |
式中:K为批尺寸(batch_size)的值。
在深度神经网络结构已经确定的情况下,可以将网络表示为
 | (12) |
式中:W为网络的权重矩阵;B为网络的偏置矩阵。首先对网络中各个节点的参数进行初始化,设初始参数分别为W0和B0,经过一次训练后,以W为例,Nadam优化函数对损失函数进行优化,按照式(13)~式(17)计算并更新网络参数W:
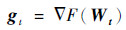 | (13) |
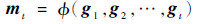 | (14) |
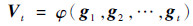 | (15) |
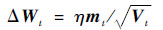 | (16) |
 | (17) |
式中:F为目标函数;η为初始学习率;m和V分别为对梯度的一阶矩估计与二阶矩估计;?和φ分别为计算梯度一阶矩与二阶矩的函数。
为了达到最小化loss值的目的,每次训练完成后,网络参数W与B都会更新,当loss最终收敛时,将网络模型的参数W′与B′保存。
3 实验验证 本节建立了一个包含信噪比等信息的无人机通信信号数据集,并且对第2节所提出的基于CNN-LSTM的信噪比估计算法进行实验验证。
3.1 实验准备 在进行实验之前,需要对数据集、对比模型、评价模型指标以及实验平台的软硬件环境进行详细的描述。
3.1.1 无人机通信信号数据集建立 目前,尚无公开可用的通信信号数据集,因此本文基于真实的地理环境,结合无人机信号的特点,通过仿真与实测相结合的方式生成信号数据。
数据集属性如表 1所示。
表 1 通信信号数据集属性 Table 1 Attributes of communication signal data set
| 序号 | 字段名 | 定义 |
| 1 | 编号 | 数据样本的顺序 |
| 2 | SNR | 信噪比 |
| 3 | 调制类型 | 信息和载波结合的方式 |
| 4 | 载波频率 | 通信信号的工作频段 |
| 5 | 样本数 | 样本总共的条数 |
| 6 | 信号长度 | 信号的序列长度 |
| 7 | 码元速率 | 信道中码元传输的速率 |
表选项
编号:按照生成信号的顺序定义了信号数据样本的编号。
SNR:有效信号功率与噪声功率的比值,本数据集的信噪比范围为-10~20 dB。
调制类型:常用的无人机通信信号调制方式共有4种:2PSK、4PSK、8PSK和16QAM。
载波频率:按照工信部颁布的无人机通信使用频段:840.5~845、1 430~1 444和2 408~2 440 MHz。
样本数:数据集中样本总条数,本数据集包含10 000条数据,其中仿真8 000条,实测2 000条。
信号长度:每条信号的序列长度,本数据集中单条信号长度为2 000个点。
码元速率:单位时间内通过信道的码元个数,本数据集里码元速率的范围在5 000~20 000。
3.1.2 对比算法 本文将基于CNN-LSTM网络的信噪比估计算法与以下5种算法进行对比实验,其中ML、MLM4、SA为传统估计算法,基于CNN和LSTM的深度学习为单一网络结构的估计算法。
1) ML估计算法
信噪比的ML估计算法基于ML估计理论。将接收端的复信号分解为同相分量与正交分量,分别得到有效信号的同相正交分量联合概率分布函数与噪声的同相正交分量联合概率分布函数,进而求得有效信号与噪声的功率估计值。利用ML理论的重要性质:2个参量比值的估计等于2个参量估计值的比值,可以求得信噪比估计值。
2) M2M4估计算法
M2M4估计算法主要利用了信号的能量与信号矩的关系,在统计的基础上计算出接收信号的二四阶矩,利用信号与噪声的独立性计算出信号的功率和噪声的功率,从而计算出信噪比估计值。
3) SA估计算法
SA估计算法是将时域信号转换到频域进行处理。首先利用傅里叶变换以及周期图法得到含噪信号的功率谱,然后计算信号的起止频率,功率谱分割为有效信号部分与噪声部分,最后,分别计算每一部分的功率谱值,可计算得到信噪比估计值。
4) 基于CNN的深度学习估计算法
将CNN-LSTM网络结构中LSTM部分去除,单独使用CNN网络提取信号特征,生成的特征序列直接输入至全连接层进行融合,信号数据处理方法不变,训练与测试流程不变。
5) 基于LSTM的深度学习估计算法
将CNN-LSTM网络结构中CNN部分去除,单独使用LSTM网络提取信号特征,生成的特征序列直接输入至全连接层进行融合,信号数据处理方法不变,训练与测试流程不变。
3.1.3 模型评价指标 对于不同信噪比估计算法,估计精度是评价算法优劣的最重要的指标。参考损失函数loss,本文选择MSE作为估计精度的衡量标准。MSE计算公式可表示为
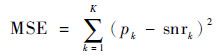 | (18) |
式中:snrk为第k条信号的标签,即信噪比真值;pk为该信号经过网络计算出的信噪比的估计值;K为一次测试信号的总条数。通过计算测试集的MSE,可以准确直观地评价模型的精度。
3.1.4 实验平台及软硬件环境 本实验所使用的计算机配置如下:处理器为英特尔酷睿i7-8700K;CPU频率为3.7 GHz;内存16 GB;GPU为Nvidia TITAN-XP,显存12 GB;操作系统为ubuntu18.04;程序设计语言为Python+MATLAB;集成开发环境为Pycharm Community Edition 2018.8.2与MATLAB 2017b。
3.2 实验结果 在实验验证阶段,从测试数据集中选取8 000条信号作为训练集,剩余2 000条信号作为测试集。使用训练集对2.1节所提出的深度网络进行训练,训练参数如下:分割窗口长度L取400,训练步数steps取30 000,初始学习率η取0.005。
测试集信号属性与训练集相同,共有2 000条信号,信噪比范围在-10~20 dB,调制类型包含2PSK、4PSK、8PSK和16QAM这4种,载波频率分布在840.5~845、1 430~1 444和2 408~2 440 MHz间,码元速率分布在5 000~20 000,每条信号长度为2 000个点。
分别使用本文所提算法与ML、M2M4、SA这3种传统估计算法对测试集进行验证,并且将误差结果与CRLB作对比。为了便于观察,实验生成的误差结果MSE均以对数形式表达。由图 4所示的比较结果可以看出,本文算法的估计精度在各个信噪比的情况下均优于传统估计算法,估计效果最接近CRLB,证明了相比传统估计算法,深度学习的估计算法可以更有效地提升信噪比估计精度。
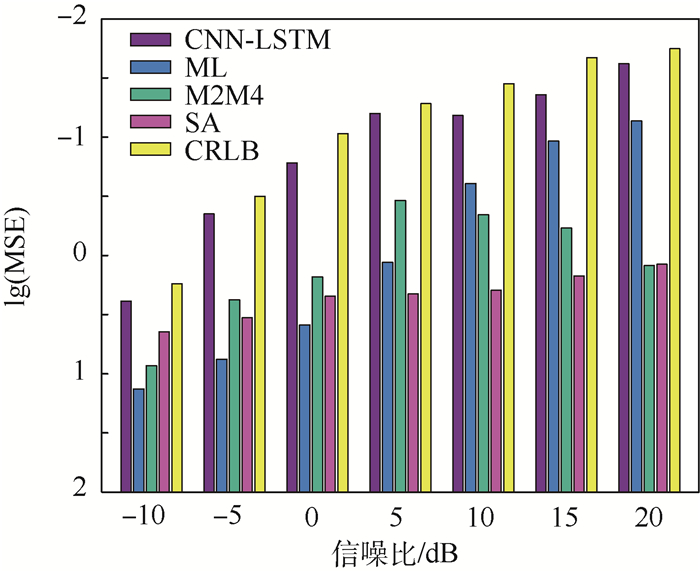 |
| 图 4 不同估计算法精度对比 Fig. 4 Comparison of accuracy between CNN-LSTM network and traditional algorithms |
| 图选项 |
为了验证CNN-LSTM网络结构的收敛性,本文将CNN-LSTM网络结构替换为单独的CNN网络与单独的LSTM网络,分别以相同的训练参数进行训练。训练参数如下:分割窗口长度L取400,训练步数steps取30 000,初始学习率η取0.005。将每一次训练的loss值保存,图 5展示了loss随训练步数变化的趋势,可以看出:LSTM网络收敛速度较慢;CNN网络则在收敛过程中振荡比较严重;CNN-LSTM网络无论在收敛速度还是收敛精度上均优于其他2种网络。
 |
| 图 5 不同网络结构的训练损失变化对比 Fig. 5 Comparison of training loss change with different network structures |
| 图选项 |
在估计精度对比方面,分别使用已经训练好的3种模型对测试集进行实验,同样将误差结果MSE以对数形式表达,结果如图 6所示。由图 6可以发现,CNN-LSTM网络预测精度远高于CNN网络,除了在信噪比为15 dB时预测精度与LSTM网络几乎相同,其余信噪比情况效果均好于LSTM网络。
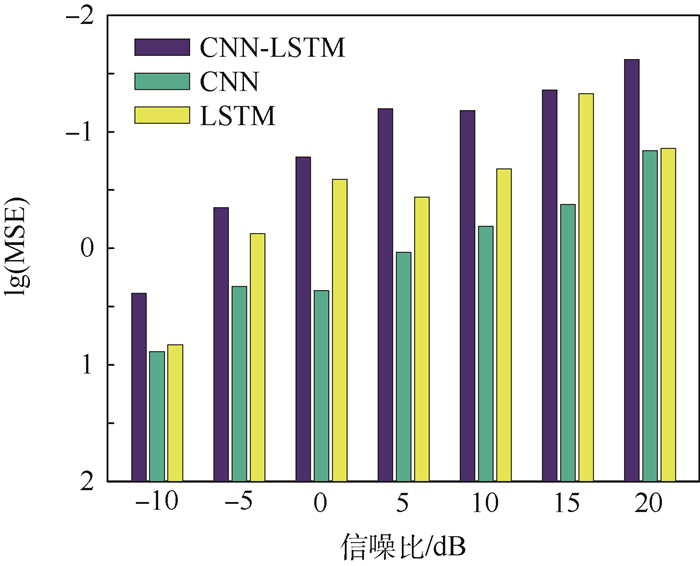 |
| 图 6 不同网络结构的测试精度对比 Fig. 6 Comparison of test accuracy with different network structures |
| 图选项 |
为了验证码元速率对网络估计性能的影响,在测试集中将码元速率为5 000、10 000、15 000、20 000的信号分别提取出来构建测试子集,将每个测试子集的信号输入至已训练好的CNN-LSTM网络中进行验证,结果如图 7所示。由图 7可以发现,在信噪比相同时,网络对不同码元速率的信号估计精度差异很小,因此说明码元速率对于网络估计效果影响较小。
 |
| 图 7 不同码元速率的测试精度对比 Fig. 7 Comparison of test accuracy with different symbol transmission rates |
| 图选项 |
为了进一步验证分割窗长度L对网络估计性能的影响,将不使用数据分割的网络与分割窗长度分别取1 000、500、400、200、100的网络进行对比实验。
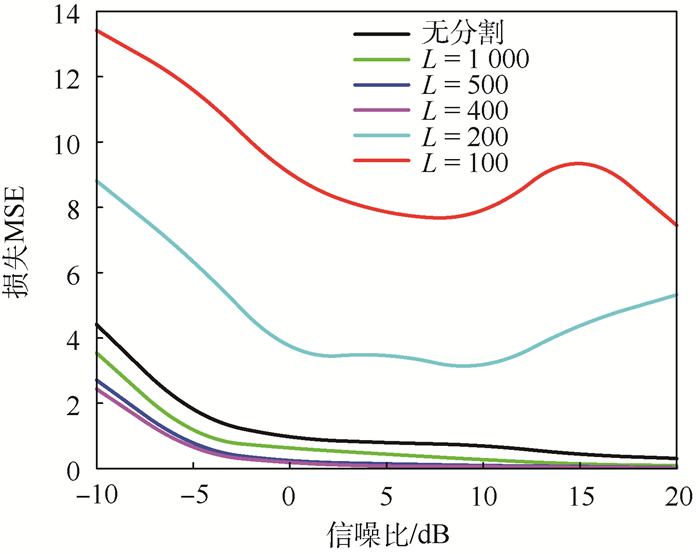
以相同的训练参数分别训练每个网络并保存模型,训练步数steps取30 000,初始学习率η取0.005,测试结果如表 2所示。观察可得当信噪比为-10~15 dB的情况下,L取400时MSE值最低;信噪比为20 dB的情况下,L取500时MSE值为0.021,稍低于L取400时的0.023。将表 2中数据表示在图 8中,可以发现:分割窗长度L>400时,相比与未经数据分割的模型,估计精度随L值的减小而提高;L=400时,性能最佳;当L值继续减小,估计性能急剧下降,图 8中L为200与100时误差非常大。
表 2 不同分割窗长度实验结果对比 Table 2 Comparison of experimental results of different split window lengths
| 分割窗长度 | 损失MSE | ||||||
| SNR=-10dB | SNR=-5dB | SNR=0dB | SNR=5dB | SNR=10dB | SNR=15dB | SNR=20dB | |
| 无分割 | 4.417 | 1.542 | 0.911 | 0.796 | 0.726 | 0.423 | 0.315 |
| 1000 | 3.547 | 0.896 | 0.624 | 0.441 | 0.272 | 0.137 | 0.095 |
| 500 | 2.716 | 0.562 | 0.211 | 0.146 | 0.092 | 0.063 | 0.021 |
| 400 | 2.436 | 0.446 | 0.165 | 0.063 | 0.065 | 0.043 | 0.023 |
| 200 | 8.811 | 6.428 | 3.347 | 3.574 | 2.916 | 4.467 | 5.324 |
| 100 | 13.424 | 11.756 | 8.815 | 7.741 | 7.629 | 9.945 | 7.453 |
| 注:最小MSE值由下划线标记。 | |||||||
表选项
 |
| 图 8 不同分割窗长度对测试精度的影响 Fig. 8 Effect of split window length on test accuracy |
| 图选项 |
综上所述,深度神经网络利用大量数据训练并建立模型,减少了单一测试信号计算带来的误差,因此整体表现优于传统算法;CNN和LSTM网络分别在空间和时间2个不同的维度对无人机数据链信号进行特征提取,具有更强的特征提取能力,可以发掘信号间更深层次的差异,所以融合网络模型的训练收敛速度估计精度均高于单一网络模型;LSTM网络在处理长序列时,每个单元会利用遗忘门将部分信息丢弃,如果序列过长,后面单元的遗忘门会丢弃一些前面序列的重要信息,造成了部分特征丢失,而适当的数据分割可以减小单次通过网络序列的长度,减少了特征的丢失,所以序列分割会使估计精度有一定的提升。但如果分割窗长度太短,深度网络无法对每一部分过短的序列提取特征,造成了更多的信息丢失,因此会出现估计性能急剧下降的现象。
4 结论 本文基于CNN-LSTM深度神经网络,提出了一种无人机信号的信噪比估计算法,并根据实际地理环境信息建立了无人机通信信号数据集。通过分析和实验结果表明:
1) 与传统估计算法相比,深度神经网络在无人机通信信号信噪比估计方面整体性能更优。
2) CNN-LSTM网络模型比单一的CNN网络或LSTM网络提取特征能力更强,得到的模型估计精度更高。
3) 在一定范围内,信号分割窗长度越小,CNN-LSTM网络的性能越好;然而如果分割窗长度太小,网络性能急剧下降。
本文使用的数据分割算法能够提升深度神经网络的性能,但目前数据分割算法是将长序列分成几段等长的短序列,如何更科学地分割信号数据,根据不同信号的特点将其分割成若干段长度不同的短序列,进而进一步提高估计精度,则是下一步需要深入研究的工作。
参考文献
| [1] | 张文秋, 丁文锐, 刘春辉. 一种无人机数据链信道选择和功率控制方法[J]. 北京航空航天大学学报, 2017, 43(3): 583-591. ZHANG W Q, DING W R, LIU C H. A channel selection and power control method for UAV data link[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(3): 583-591. (in Chinese) |
| [2] | PAULUZZI D R, BEAUCIEU N C. A comparison of SNR estimation techniques for the AWGN channel[J]. IEEE Transactions on Communications, 2000, 48(10): 1681-1691. DOI:10.1109/26.871393 |
| [3] | BOUJELBEN M A, BELLILI F.EM algorithm for non-data-aided SNR estimation of linearly-modulated signals over SIMO channels[C]//Lobal Telecommunications Conference.Piscataway, NJ: IEEE Press, 2009: 4464-4469. |
| [4] | XIAO H F, SHI Y Q, SU W, et al.An investigation of non-data-aided SNR estimation techniques for analog modulation signals[C]//IEEE Sarnoff Symposium.Piscataway, NJ: IEEE Press, 2010: 351-355. |
| [5] | áLVAREZ-DíAZ M, LóPEZ-VALCARCE R, MOSQUERA C. SNR estimation for multilevel constellations using higher-order moments[J]. IEEE Transactions on Signal Processing, 2010, 58(3): 1515-1526. DOI:10.1109/TSP.2009.2036069 |
| [6] | STEPHENNE A, BELLILI F, AFFES S. Moment-based SNR estimation over linearly-modulated wireless SIMO channels[J]. IEEE Transactions on Wireless Communications, 2010, 9(2): 714-722. DOI:10.1109/TWC.2010.02.081719 |
| [7] | 华惊宇, 黄清, 滑翰, 等. 一种移动环境下的信噪比估计算法及其在多普勒频移估计中的应用[J]. 通信学报, 2005, 26(5): 135-140. HUA J Y, HUANG Q, HUA H, et al. A SNR estimation algorithm in mobile environment and its application in Doppler shift estimation[J]. Transactions of Communications, 2005, 26(5): 135-140. (in Chinese) |
| [8] | 彭耿, 黄知涛, 陆凤波, 等. 中频通信信号信噪比的快速盲估计[J]. 电子与信息学报, 2010, 32(1): 102-106. PENG G, HUANG Z T, LU F B, et al. Fast blind estimation of signal-to-noise ratio of IF communication signals[J]. Journal of Electronics & Information Technology, 2010, 32(1): 102-106. (in Chinese) |
| [9] | O'SHEA T J, HOYDIS J. An introduction to deep learning for the physical layer[J]. IEEE Transactions on Cognitive Communications & Networking, 2017, 3(4): 563-575. |
| [10] | ZHANG D N, DING W R, ZHANG B C, et al. Automatic modulation classification based on deep learning for unmanned aerial vehicles[J]. Sensors, 2018, 18(3): 924-939. DOI:10.3390/s18030924 |
| [11] | O'SHEA T J, ROY T, CLANCY T C. Over the air deep learning based radio signal classification[J]. IEEE Journal of Selected Topics in Signal Processing, 2017, 12(1): 168-179. |
| [12] | O'SHEA T J, CORGAN J, CLANCY T C.Convolutional radio modulation recognition networks[C]//International Conference on Engineering Applications of Neural Networks.Berlin: Springer, 2016: 213-226. |
| [13] | LéCUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324. DOI:10.1109/5.726791 |
| [14] | SUN Y, WANG X, TANG X.Hybrid deep learning for face verification[C]//IEEE International Conference on Computer Vision.Piscataway, NJ: IEEE Press, 2013: 1489-1496. |
| [15] | SAK H, SENIOR A, BEAUFAYS F.Long short-term memory based recurrent neural network architectures for large vocabulary speech recognition[C]//15th Annual Conference of the International Speech Communication Association, 2014: 338-342. |
| [16] | GHOSH S, VINYALS O, STROPE B, et al.Contextual LSTM (CLSTM) models for large scale NLP tasks[EB/OL].(2016-05-31)[2018-10-15].https://www.researchgate.net/publication/301857393_Contextual_LSTM_CLSTM_models_for_Large_scale_NLP_tasks. |
| [17] | WANG J, CAO Z W.Chinese text sentiment analysis using LSTM Network based on L2 and Nadam[C]//IEEE International Conference on Communication Technology.Piscataway, NJ: IEEE Press, 2017: 1891-1895. |
| [18] | JOZEFOWICZ R, ZAREMBA W, SUTSKEVER I.An empirical exploration of recurrent network architectures[C]//Proceeding of the 32nd International Conference on Machine Learning, 2015, 37: 2342-2350. |
| [19] | GREFF K, SRIVASTAVA R K, KOUTNíK J, et al. LSTM:A search space odyssey[J]. IEEE Transactions on Neural Networks & Learning Systems, 2015, 28(10): 2222-2232. |
