现有测试性验证方案通常依据相关国内外军用标准[2-4]来制定。文献[5]分析总结了国内外军用标准中给出的测试性验证方法缺乏普适性和可操作性,指出应该制定测试性验证专用标准。文献[6]对比分析了正态分布、二项分布等模型的优缺点及其适用性,同时表明二项分布模型较之其他模型的优势。以上方法及标准确定的测试性验证方案往往需要较大的故障样本量和较长的试验周期,工程应用中难以实现。为此国内外研究****考虑如何将测试性验证前的先验信息应用到测试性验证方法中,以达到降低故障样本量、缩短验证周期的问题。文献[7-8]提出了一种基于研制阶段的成败型数据的等效折合方法,重新确定了测试性验证试验方案,较之传统验证方案明显降低故障样本量。文献[9]综合考虑了弃真和采伪2类风险损失,提出了基于Bayes理论的测试性验证试验方案。以上研究中需采用的先验信息均来源于整机系统自身的历史试验数据,但由于装备系统复杂导致验证组织困难、费用高昂,所以整机系统自身的先验信息缺乏,现阶段基于装备整机系统测试性先验信息的测试性验证方法适用性不强,针对此问题,研究人员关注到构成整机系统的分系统或单机包含大量先验信息,通过这些先验信息可以确定整个系统的测试性先验水平,进而确定基于分系统先验信息的测试性验证试验方法。文献[10]以故障检测率为指标提出了利用研制阶段分系统先验信息,并基于Bayes最大后验风险准则给出了制定系统测试性验证方案的新方法。文献[11]在传统Bayes评估方法的基础上建立了综合利用历史试验信息和现场试验数据等先验信息的测试性Bayes评估模型,较之经典评估方法给出较高置信度的测试性评估结论。文献[12]提出了基于验前信息的复杂设备的Bayes测试性验证试验方法,先将各先验信息进行融合,再建立成败型装备测试性验证试验方案的Bayes决策模型,通过实例证明,该方案较之经典方案能减少故障样本量。以上研究中虽然考虑了先验信息,但仍存在对先验信息处理的有效性和局限性,降低使用可信度。
随着现代工业、科技水平的迅猛发展,武器装备系统结构越来越复杂,按照测试性设计与分析需求可划分为系统、分系统、外场可更换单元(LRU)、内场可更换单元(SRU)、模块、子模块、元件和故障模式等不同层级[13],在实际工程应用中,各层级单元的先验信息是多样的且容易获得[14],并且是从下层逐步向上层表征的,充分运用各层级所包含的先验信息。本文提出了一种三维Bayes网络测试性验证模型,旨在根据复杂装备系统层次划分原则,用层次化和模块化方法构建Bayes网络。同时基于复杂系统所确定的三维网络结构,提出三维Bayes网络的条件概率学习方法,实现对Bayes网络的概率赋值,并结合给出的G/M-H算法验证其能充分融合各层级先验信息,以及能有效减少故障样本量。
1 三维Bayes网络测试性验证模型 1.1 传统Bayes网络模型 Bayes网络模型作为不确定性信息和知识的处理工具[15],遵循经典Bayes概率理论,使用统一的联合分布作为知识表示形式,同时利用结构中存在的条件独立性有效解决确定联合概率分布的组合爆炸难题(NP-hard问题)。传统Bayes网络模型定义如下。
定义1??Bayes网络。一个Bayes网络可以表示为B=〈G, P〉,其中包含网络结构G和条件概率P两部分。
1) G=〈V, E〉表示有向无环图(Directed Acyclic Graph,DAG),其中V表示节点集合,V中的元素代表变量,E表示有向边的集合,代表变量间的关联关系。
2) P表示条件概率分布(Conditional Probability Distribution,CPD)。Bayes网络中每一个节点都包含一个条件概率分布,通过条件概率分布的注释,可以在模型中表达局部条件的依赖性。假设Bayes网络中节点集合V={X1, X2, …, Xn},对每个节点Xi及其父节点pa(Xi)均对应一个条件概率分布表(随机变量为离散情形)或条件概率分布函数(随机变量为连续情形),以离散情形为例:
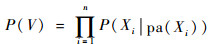 | (1) |
而Bayes网络参数学习是指从样本数据中估计条件概率P(Xi|pa(Xi))。
Bayes网络的建立一般分为3个步骤:①根据问题域的特点和经验,确定网络节点及其取值状态;②根据经验或通过数据学习确定网络结构;③根据经验或数据学习为每个节点确定条件概率分布。
根据以上传统Bayes网络定义及Bayes网络建立步骤,若采用传统Bayes网络构建测试性验证模型,在网络结构方面,由于武器装备系统复杂的结构,会增加构建Bayes网络模型的复杂度,同时会导致所建立的Bayes网络结构的准确性无法保证;在条件概率方面,由于所建立的Bayes网络模型不能充分反映出武器装备各层次结构中蕴含的条件独立性,从而增加概率推理计算的复杂度。因此,对于复杂装备系统而言,采用传统Bayes方法构建测试性验证模型无法保证构建模型网络结构的准确性,同时也无法降低推理的复杂度。
结合定义1中Bayes网络建立原则和步骤,并根据装备纵向结构和横向结构层次化划分的特征,同时考虑问题域中包含的先验知识未能充分利用,给出一种三维Bayes网络测试性模型的定义,旨在充分运用复杂系统的纵向结构信息和横向结构信息,以及各结构中各组成单元所蕴含的先验信息。
1.2 模型建立 在给出三维Bayes网络测试性验证模型定义前,首先给出组成网络模型的几个基本要素。
定义2??层次节点。将构成三维Bayes网络的节点变量称之为层次节点,记为Nx,y,zi,其中x、y、z表示三维Bayes网络的三维坐标,且x, y, z∈N,同时i=Ⅰ, Ⅱ, Ⅲ表示层次节点的3种类型,具体解释如下:
1) x轴表示层次划分维,y轴表示输入因子维,z轴表示层级划分维。z轴所表示的层级划分数由系统纵向结构(即复杂武器装备系统层级划分)所决定,若z=0, 1, …, n,则层级划分数为n+1;x轴所表示的层次划分数由系统横向结构(即复杂武器装备各层级单元自身逻辑关联的层次划分)所决定,若x=0, 1, …, m,则层次划分数为m+1;y轴所表示的输入因子数由系统纵向结构和横向结构共同决定(即确定同一层级同一层次所包含的层次节点数)。
2) i=Ⅰ时,表示层次节点Nx, y, zI无父节点;i=Ⅱ时,表示层次节点Nx, y, zⅡ仅有上层父节点;i=Ⅲ时,表示层次节点Nx, y, zⅢ至少具有本层父节点。
根据定义2,进一步可以得到:所有层次节点的集合记为H={Nx, y, zi|x, y, z∈N},构成三维Bayes网络的所有网络节点;则每一层的层次节点的集合记为H|z=l(l∈N且0≤l≤n),表示z=l时层次节点的集合,并约定H|z=0所在平面为第1层,H|z=l所在平面为第l+1层。
定义3??层级。将三维Bayes网络任一层所包含的层次节点集、有向边集、层次节点输入集和层次节点输出集构成的四元组称之为层级,记为Hz+1:Hz+1=〈H|z, E, AI, AO〉,具体解释如下:
1) 给定z时,Hz+1表示第z+1层级,H|z则表示给定z时层次节点的集合,构成第z+1层级的层次节点集合。
2) E表示Hz+1中有向边的集合,记为Hz+1:E,对于H|z中任意2个层次节点Nx1, y1, zi和Nx2, y2, zi,若存在Nx1, y1, zi指向Nx2, y2, zi的有向边,表示为Nx1, y1, zi→Nx2, y2, zi,则类比于定义1,称Nx1, y1, zi为Nx2, y2, zi的父层次节点。
3) AI表示Hz+1中层次节点集H|z的nz+1个输入组成的集合,记为AI=
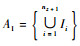
4) AO表示Hz+1中层次节点集H|z的mz+1个输出组成的集合,记为AO=
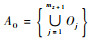
根据定义3,进一步可以得到:
1) 若一些层次节点组成的集合Hx+1?H|z在Hz+1中无父层次节点,即在该层级不存在其他层次节点指向该集合中任意一个层次节点,则集合Hx+1称为Hz+1层级中第1层次节点集,并约定符号H1|x=0表示Hz+1层级的第1层次节点集。进一步,Hx+1|x表示随x的取值变化反映Hz+1层级的层次划分数及相应层次的层次节点集,且Hx+1|x=h表示pa(Hx+1|x=h+1)\pa(Hx+1|x=h)的层次节点集合,即保证Hx+1|x=h去掉其下层所有层次节点之后无父层次节点。
2) 为规范化表示,选取Hz+1层级中第Hx+1|x层次中任一节点Nx, y, zi∈(Hz+1:Hx+1|x),将每一层级每一层次所选节点构成集合,并令y=0:

定义4??输入模块。将所有层级中AI所包含变量的值域的集合称之为输入模块,记为:IM=
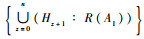
定义5??输出模块。将所有层级中AO所包含变量的值域的集合称之为输出模块,记为:
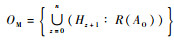
定义6??数据处理模块。将三维Bayes网络中所有层级内数据处理单元DIz+1和相邻层级间数据处理单元DBz+1→z+2的集合称之为数据处理模块,记为:DM=
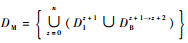
1) 层级内数据处理单元DIz+1用来处理本层输入Hz+1:R(AI)信息并存储。
2) 相邻层级间数据处理单元DBz+1→z+2用来处理第z+1层输出Hz+1:R(AO)信息,并传递给上层输入模块。
定义7??层级间有向边集。将所有相邻层级间层次节点之间的有向边构成的集合称之为层级间有向边集,记为E→,并记符号Nx, y, zi|E→表示与层次节点Nx, y, zi有层级间有向边连接的层次节点集。
E→是连接各层级使网络形成有向无环图的关键因素,由复杂装备系统的层级划分所确定,同时表明了网络的信息流向。
由定义2~定义7,结合传统Bayes网络的定义,可以得到三维Bayes网络模型的定义如下。
定义8??三维Bayes网络模型。一个三维Bayes网络模型包含层次节点、层级、输入模块、输出模块、数据处理模块、层级有向边集及条件概率分布,表示为

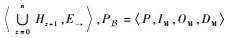
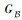
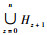
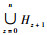
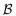
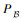
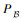
至此,依据复杂装备系统的纵向和横向层次性结构完成了三维Bayes网络测试性验证模型的构建。
2 融合先验信息的推理方法 2.1 先验信息的处理原则 对于复杂系统而言,大量可信的先验信息是保证融合推理可信度的重要保证。当前可用于测试性验证的先验信息具备多层级、多阶段及多来源的特点,从层级上可划分为单元级、SRU级、LRU级、分系统级及系统级信息,从阶段上可划分为摸底试验信息和增长试验信息等,从来源上可划分为实物试验信息、专家经验信息及虚拟试验信息等。充分利用这些先验信息,能很大程度上弥补当前复杂装备系统实物试验信息的不足,在确保装备质量和控制装备成本的前提条件下,能有效降低测试性验证所需故障样本量。
上述多层级、多阶段及多来源的先验信息从信息类型上总体可划分为3类:成败型信息、点估计型信息及区间估计型信息,导致先验信息的形式不一,不利于先验信息的融合处理。针对该问题,结合测试性验证的特性,通过对先验信息进行一定方式的折合,转化为统一的信息类型——成败型数据(N′, F′)进行表示。当前对于不同类型的先验信息的折合处理方式有大量文献进行了研究,本文主要研究模型建立及推理,对于先验信息处理不再赘述,具体折合方案参见文献[14]进行的相关研究,后续数据均采用文献[14]所述方法进行了相应处理,确保先验信息的合理有效性,增加后续融合推理的可信度。
2.2 三维Bayes网络的融合推理算法 考虑到三维Bayes网络的结构确定是依据复杂装备的结构特性所决定的,在对装备层级进行划分时通过系统纵向结构及横向结构进行确定,故结构学习是基于装备FMECA进行分析。下面主要推导三维Bayes网络的概率学习方法。
2.2.1 层级内三维Bayes网络的概率学习方法 1) 对于层次节点Nx, y, zI,由于其无父层次节点,仅含自身先验,直接将其先验信息转化为先验分布,一般取为贝塔分布Beta(α, β)(二项分布的共轭先验分布)。
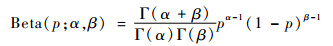 | (2) |
式中:p为故障检测率(Fault Detect Rate,FDR);α、β称为超参数。
结合节点的成败型测试性试验数据X=(N′, F′),根据Bayes理论,可以得到FDR的后验分布π(p|X)为
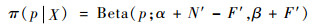 | (3) |
2) 对于层次节点Nx, y, zⅢ,由于其至少具有本层父层次节点,考虑仅含有本层父层次节点的情形。用pa(Nx, y, zⅢ)表示层次节点Nx, y, zⅢ所有父节点的集合,则P(Nx, y, zⅢ|pa(Nx, y, zⅢ))表示层次节点Nx, y, zⅢ在给定其父节点集合时的条件概率分布,且有
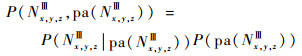 | (4) |
基于式(4),P(pa(Nx, y, zⅢ))仍可以递归分解,一旦获得其联合概率分布,则任一节点的边缘概率分布可以表示为
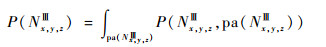 | (5) |
2.2.2 层级间三维Bayes网络的概率学习方法 1) 对于层次节点Nx, y, zⅡ,由于其仅有上层级父层次节点,按照规范化表示则层次节点Nx, y, zⅡ必位于第Hz+1层级第1层次上,即x=0。与2.2.1节相似,为求得层次节点Nx, y, zⅡ的边缘概率密度分布,需首先求取式(6)的联合概率分布:
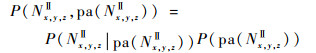 | (6) |
式中:P(Nx, y, zⅡ|pa(Nx, y, zⅡ))的分布获取取决于上层与之有有向边连接的层次节点集Nx, y, zⅡ|E→的输出集Hz+2:R(AO)|(Nx, y, zⅡ|E→);P(pa(Nx, y, zⅡ))的分布则取决于层次节点Nx, y, zⅡ的自身先验信息输入Beta(α, β)所共同决定。进而通过联合概率分布能够逐步确定层次节点Nx, y, zⅡ的边缘概率分布。
2) 对于层次节点Nx, y, zⅢ,考虑既有上层父层次节点又有本层父层次节点时,为求取层次节点Nx, y, zⅢ的条件概率分布,则需求取式(7)所示联合概率分布:
 | (7) |
式中:P(pa(Hz+2:Nx, y, zⅢ))取决于上层与之有有向边连接的层次节点集Nx, y, zⅢ|E→的输出集Hz+2:R(AO)|(Nx, y, zⅢ|E→);P(pa(Hz+1:Nx, y, zⅢ))取决于层次节点Nx, y, zⅢ的自身先验输入集;P(Nx, y, zⅢ|pa(Hz+1:Nx, y, zⅢ), pa(Hz+2:Nx, y, zⅢ))则由上述共同所确定。
至此,即给出了三维Bayes网络的概率学习方法,使模型能够融合先验信息进行推理。
3 案例分析 3.1 模型建立 以某型导弹飞控系统为研究对象,纵向结构包括6个LRU模块:电缆网络、总线网络、弹上计算机、惯测组合、舵等效器及综合控制器。考虑简单情形,在此假设6个LRU模块之间无相互影响。其中,惯测组合包括3个SRU模块:线加速度测量组合、角速度测量组合和二次电源。弹上计算机包括2个SRU模块:信息处理电路及弹机供电。实际上,与综合控制器横向具备信号交互的部件较多,加上考虑LRU模块间无相互影响,现仅考虑地面测试设备对综合控制器的影响,故根据以上对某型导弹飞控系统纵向和横向结构划分,飞控系统的三维Bayes网络模型如图 1所示。
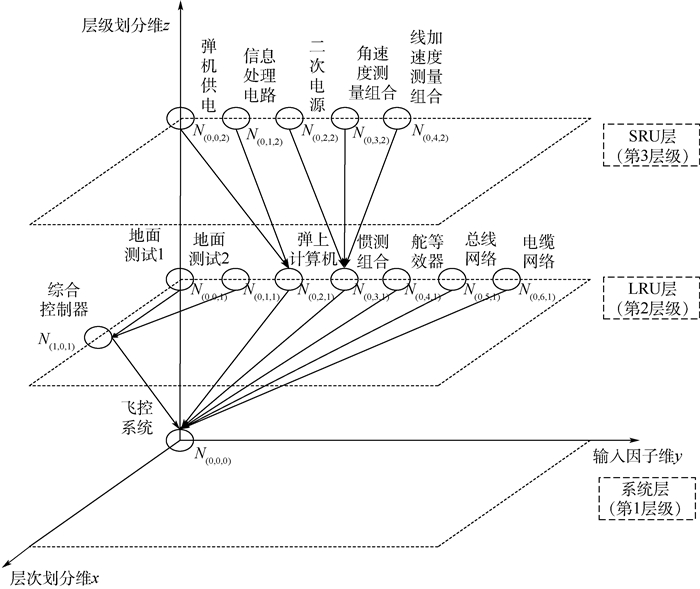 |
| 图 1 飞控系统三维Bayes网络模型 Fig. 1 Three-dimensional Bayes network model of flight control system |
| 图选项 |
在飞控系统开展系统级测试性验证试验前,每个LRU和SRU都开展了相应的摸底试验,这些试验产生的数据都可以作为三维Bayes网络的先验信息。以各LRU和SRU的测试性实物试验数据作为三维Bayes网络模型的先验信息,通过给出的三维Bayes网络的融合推理算法对LRU级和SRU级的试验数据进行融合,得到系统测试性指标——FDR的后验分布并进行试验方案的制定。系统级的故障检测试验数据如表 1所示,各LRU和SRU的故障检测试验数据如表 2和表 3所示,LRU层级中综合控制器横向联系地面测试设备测试试验数据如表 4所示。
表 1 系统实物试验数据 Table 1 Physical test data of system
| 参数 | 故障样本量 | 失败次数 |
| 数值 | 10 | 1 |
表选项
表 2 LRU实物试验数据 Table 2 Physical test data of LRU
| LRU模块 | 故障样本量 | 失败次数 |
| 电缆网络 | 5 | 0 |
| 总线网络 | 3 | 1 |
| 弹上计算机 | 9 | 1 |
| 惯测组合 | 14 | 2 |
| 舵等效器 | 8 | 1 |
| 综合控制器 | 4 | 1 |
表选项
表 3 SRU实物试验数据 Table 3 Physical test data of SRU
| SRU模块 | 故障样本量 | 失败次数 |
| 线加速度测量组合 | 5 | 1 |
| 角速度测量组合 | 5 | 1 |
| 二次电源 | 4 | 0 |
| 信息处理电路 | 2 | 0 |
| 弹机供电 | 2 | 0 |
表选项
表 4 综合控制器检测试验数据 Table 4 Detection test data of integrated controller
| 综合控制器 | 故障样本量 | 失败次数 |
| 地面测试1 | 4 | 0 |
| 地面测试2 | 4 | 0 |
表选项
结合表 1~表 4数据,假设每个部件的试验故障数目服从Bionmial(mi, pi),mi为每个部件所进行的试验次数,pi为相应的成功检测概率,并假设所有不具备父层次节点的pi来自一个具有参数Kε和K(1-ε)的Beta分布,即
 | (8) |
式中:ε为pi的先验均值,由于pi的先验方差为ε(1-ε)/(K+1),故K决定了Beta先验分布的分散性,其中K和ε为随机变量。
3.2 模型推理及分析
3.2.1 模型推理 系统测试性指标FDR后验分布的确定步骤流程如下:
步骤1??领域专家结合自身经验对各状态进行打分评定,确定三维Bayes网络各节点变量的条件概率表(Conditional Probability Table, CPT)。假定层次节点Nx, y, zi=k(k=0, 1),对应层次节点故障不可检测和可检测2种状态,故系统(层次节点N(0, 0, 0))的测试性指标FDR可表示为P(N(0, 0, 0)=1)(其他节点FDR可类似表示),由三维Bayes网络的定义:
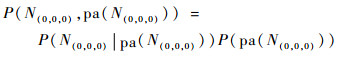 | (9) |
式中:pa(N(0, 0, 0))表示N(1, 0, 1)、N(0, 2, 1)、N(0, 3, 1)、N(0, 4, 1),N(0, 5, 1),N(0, 6, 1)六个层次节点,且它们相互独立,故P(pa(N(0, 0, 0))可以根据自身先验信息及其上层级父层次节点输出集获得,为了得到联合概率分布,除需确定P(N(0, 0, 0)|pa(N(0, 0, 0)))外,P(N(1, 0, 1)|pa(N(1, 0, 1)))、P(N(0, 2, 1)|pa(N(0, 2, 1)))和P(N(0, 3, 1)|pa(N(0, 3, 1)))亦需确定。领域专家结合自身经验及通过打分评定,给出各状态的条件概率分布如表 5所示。表中:可检测部件数表示相应层次节点取值为1的个数;R1~R14表明相应概率的先验分布为均匀分布。基于此便可实现三维Bayes网络的概率推理。
表 5 各状态条件概率 Table 5 Conditional probability of each state
| 可检测部件数 | 层次节点 | ||
| N(0, 0, 0) | N(1, 0, 1)/N(0, 2, 1) | N(0, 3, 1) | |
| 0 | R1:U(0, 0.2) | R8:U(0, 0.2) | R11:U(0, 0.2) |
| 1 | R2:U(0.1, 0.3) | R9:U(0.6, 0.8) | R12:U(0.4, 0.6) |
| 2 | R3:U(0.3, 0.5) | R10:U(0.8, 1) | R13:U(0.7, 0.9) |
| 3 | R4:U(0.5, 0.6) | R14:U(0.9, 1) | |
| 4 | R5:U(0.6, 0.8) | ||
| 5 | R6:U(0.8, 0.9) | ||
| 6 | R7:U(0.9, 1) | ||
表选项
步骤2??三维Bayes网络层级内信息融合推理。由于本例仅LRU层级存在层级内信息融合,即第二层级DI2数据处理单元对N(0, 0, 1)、N(0, 1, 1)及N(1, 0, 1)进行概率推理,将融合后的信息更新后赋予层次节点N(1, 0, 1)的输出模块;相应更新三维Bayes网络的输入模块AI。基于二项似然函数和式(4),可以得到联合后验密度为
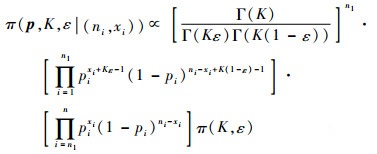 | (10) |
式中:p=(p1, p2, …, pn);ni和xi分别为各单元故障样本量和故障成功检测次数;n为层次节点总数,这里n=3;n1为符合Beta(Kε, K(1-ε))分布的层次节点数,这里n1=2,为参数ε和K的联合先验分布。假设K~Gamma(α′, λ),ε~Beta(a, b),故联合后验分布为
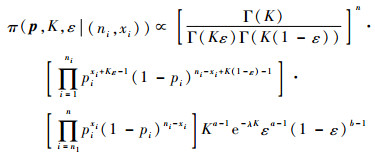 | (11) |
为了求解上述模型,结合M-H算法和Gibbs抽样的MCMC方法(G/M-H算法),求解这一局部层次模型。G/M-H算法具体过程如下:
1) 选取初值j=0,α=15,λ=1,a=8,b=2,K(0)=α′/λ,ε(0)=a/(a+b)。
2) 当i=1, 2, …, n1时,产生:pi(j)~Beta(xi+K(j-1)ε(j-1), ni-xi+K(j-1)(1-ε(j-1)))。根据表 5和三维Bayes网络融合推理算法更新相关pi(i=n1, n1+1, …, n)的样本值,并从分布N(0, 1)中抽取z,并使K*=K(j-1)exp(z)。同时计算
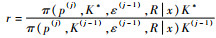
3) 生成ε*~Beta(K(j)p, K(j)(1-p)),p=
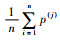
4) 求取各条件分布中各概率分布参数R1~R14的后验分布。令R=(R1, R2, …, R14),首先从分布U(0, 0.2)中产生R1*,更新R, 计算r=
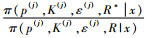
5) 令j=j+1,并回到步骤2)。
通过以上G/M-H算法可以得到层次节点N(1, 0, 1)参数的后验分布,将其储存于三维Bayes网络的输入模块以进行下一步计算。
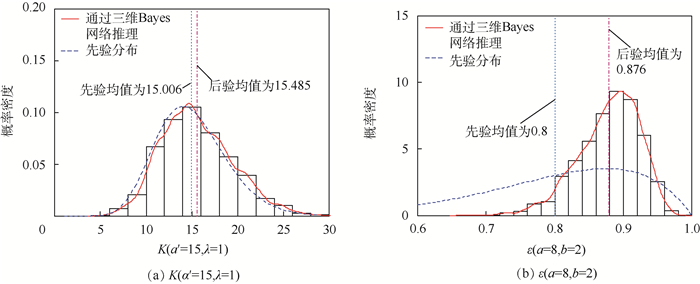
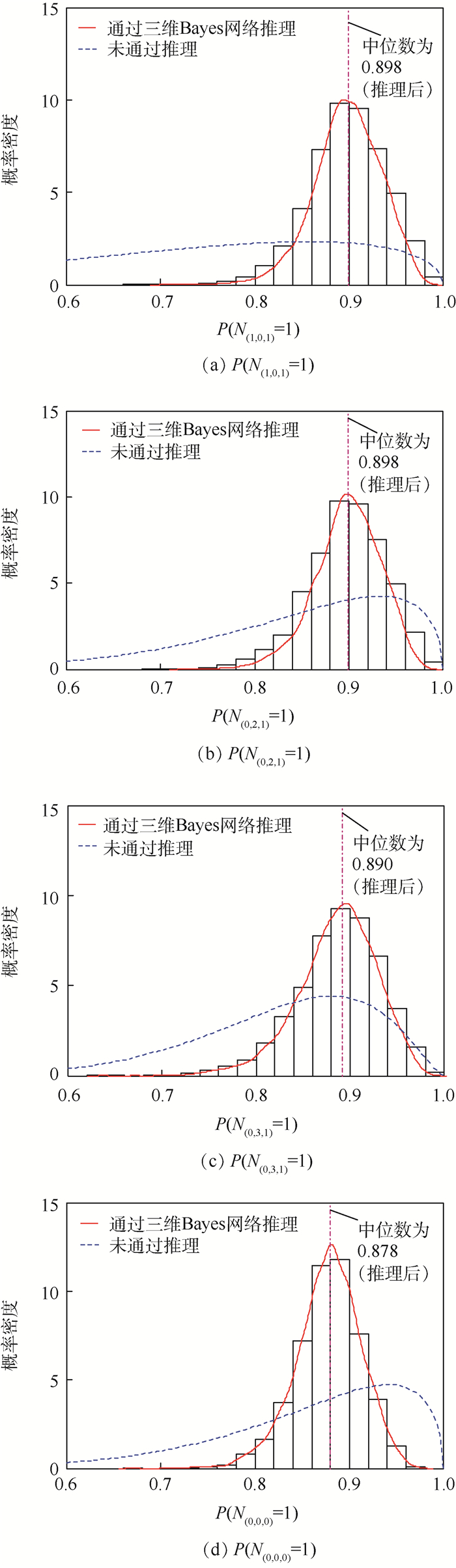
步骤3??三维Bayes网络层级内信息融合。基于自顶向下的逐步融合,首先考虑SRU层向LRU层融合,即层级间数据处理模块DB2→3处理N(0, 0, 2)、N(0, 1, 2)和N(0, 2, 1)的融合及N(0, 2, 2)、N(0, 3, 2)、N(0, 4, 2)和N(0, 3, 1)的融合,同样利用步骤2中给出的G/M-H算法实现求解,求解完成更新相应的输入模块,并通过层级间数据处理模块DB1→2处理LRU层到系统层的数据处理。采用同样的算法实现求解,所得结果如表 6所示,给出了三维Bayes网络概率推理过程中参数K、ε及各节点故障检测率P(N(0, 0, 0)=1)、P(N(1, 0, 1)=1)、P(N(0, 2, 1)=1)和P(N(0, 3, 1)=1)的后验分布相关指标值。图 2给出了参数K、ε的先验和后验概率密度函数曲线,图 3则给出了通过三维Bayes网络推理及未通过推理的后验概率密度分布曲线。
表 6 相关参数后验分布 Table 6 Posterior distribution of related parameters
| 参数 | 均值 | 标准差 | 分位数 | ||||
| 2.5% | 5% | 50% | 95% | 97.5% | |||
| K | 15.485 | 3.790 | 9.339 | 10.033 | 15.091 | 22.294 | 24.108 |
| ε | 0.876 | 0.046 | 0.770 | 0.791 | 0.881 | 0.944 | 0.952 |
| P(N(0, 2, 1)=1) | 0.896 | 0.043 | 0.801 | 0.823 | 0.898 | 0.961 | 0.970 |
| P(N(0, 3, 1)=1) | 0.886 | 0.046 | 0.782 | 0.804 | 0.890 | 0.955 | 0.964 |
| P(N(1, 0, 1)=1) | 0.897 | 0.041 | 0.808 | 0.827 | 0.898 | 0.961 | 0.970 |
| P(N(0, 0, 0)=1) | 0.876 | 0.036 | 0.799 | 0.814 | 0.878 | 0.931 | 0.941 |
表选项
 |
| 图 2 先验-后验概率密度函数对比 Fig. 2 Comparison of prior-posterior probability density function |
| 图选项 |
 |
| 图 3 不同层次节点后验概率密度函数对比 Fig. 3 Comparison of posterior probability density function at different hierarchical nodes |
| 图选项 |
3.2.2 融合推理结果分析 通过三维Bayes网络融合推理计算,由图 2(a)可以得到,参数K的边缘后验分布较之先验分布差距不明显,且先验均值和后验均值十分接近,这意味着数据包含的信息不多,以致于后验分布并未发生较大的改变。ε的先验均值为0.8,计算得到后验均值集中在0.876附近,由图 2(b)可见,边缘后验分布和其先验分布的形状差距较明显,说明确定的联合概率分布对其后验分布的影响很大,且其后验分布密度曲线表明对参数ε的置信度提高,其90%置信区间为[0.791, 0.944]。
图 3给出了层次节点N(1, 0, 1)、N(0, 2, 1)、N(0, 3, 1)及N(0, 0, 0)测试性指标FDR是否通过三维Bayes网络融合推理的后验分布概率密度曲线的对比情况,并于图中标识出通过三维Bayes网络融合推理后的各层次节点FDR后验中位数作为指标参照。可以看出,有无三维Bayes网络推理后验分布密度曲线对比差距明显,经过融合推理得到的各层次节点FDR后验概率密度估计准确度更高,这一点亦可以从表 6中各节点的95%置信度区间及后验分布均值得到,而无三维Bayes网络融合推理由于节点先验假定为无信息先验及实际样本量较小,导致后验分布趋势均较平缓。这正是由于层次节点N(1, 0, 1)、N(0, 2, 1)、N(0, 3, 1)及N(0, 0, 0)测试性试验信息缺乏所导致,如若不采用不同层级不同层次节点的先验信息进行融合,所能利用的信息是极少的。
飞控系统(N(0, 0, 0))FDR指标的后验中位数为0.878,其90%置信区间为[0.814, 0.931],其后验中位数和相应置信度取决于6个LRU的先验信息,如果能给出更为精确的先验信息或者继续增加系统实验数据,便能得到更为精确的关于FDR的指标,给出合理的评估结论。进一步,LRU的信息由其下一层次的SRU或者处于同一层级的子层次节点给出。例如,以惯测组合(N(0, 3, 1))为例,其均值为0.886,90%置信区间为[0.804, 0.955],其取决于层次节点N(0, 2, 2)、N(0, 3, 2)、N(0, 4, 2)及其自身先验信息,若所包含的先验能更好地支撑其FDR指标,则所得到的后验均值能相应提高。
3.3 故障样本量确定及分析
3.3.1 基于后验分布的故障样本量确定方法 本文通过三维Bayes网络已经得到层次节点N(0, 0, 0)的FDR后验分布,同时基于Bayes后验风险准则确定故障样本量的方法[16]不能直接采用,若以后验分布π(p|X)取代π(p),则更能体现出p≥p0|X时生产方对装备拒收的接受程度及p≤p1|X时使用方对装备接收的支持程度,故重新定义生产方后验风险为
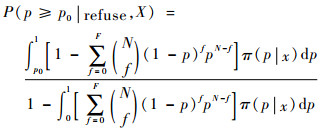 | (12) |
定义使用方后验风险为
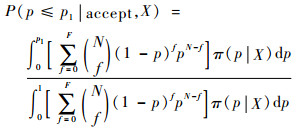 | (13) |
为得到测试性验证故障样本量,则需满足:
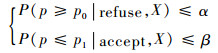 | (14) |
基于后验分布确定故障样本量的算法的具体实施流程如图 4所示,利用该算法即可求得满足式(14)的最小故障样本量方案。
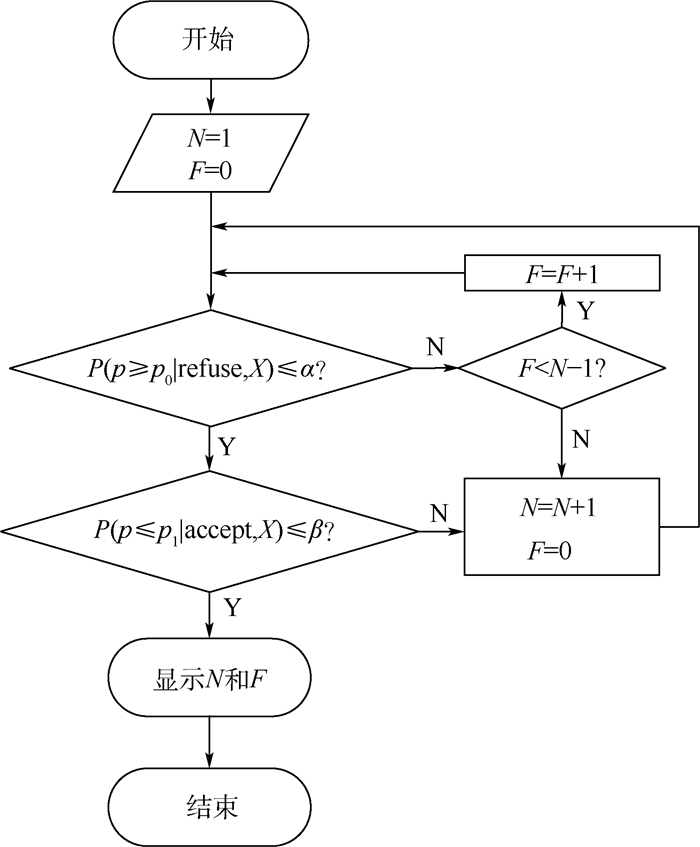 |
| 图 4 基于后验分布确定故障样本量算法实施流程 Fig. 4 Algorithm implementation process for determining fault sample size based on posterior distribution |
| 图选项 |
3.3.2 故障样本量确定方法的比较分析 通过3.3.1节所述三维Bayes网络测试性验证模型融合推理可以得到顶层测试性指标FDR的后验分布满足:
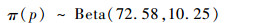 | (15) |
以系统的FDR值为验证对象,生产方和使用方确定的FDR指标和风险要求为:生产方要求值p0=0.95,使用方要求值p1=0.90,生产方风险α=0.1,使用方风险β=0.1。
1) 由文献[16]中经典风险准则可得,在双方要求值和双方风险要求下的测试性方案为(187, 13),生产方和使用方实际风险分别为0.098和0.087。
2) 考虑节点先验信息不足的原因,以本文方法所得到的顶层测试性指标FDR替代传统Bayes验证方法中的先验分布,根据文献[12]中传统Bayes测试性验证故障样本量确定方法,得到的最小故障样本量及最大允许失败数为(n, c)=(81, 6),生产方和使用方实际风险分别为0.097和0.096。
3) 通过三维Bayes网络推理后生成的系统FDR后验样本分布,结合上述给出的基于后验分布的故障样本量确定方法,得到本文最小故障样本量方案为(59, 0),同时得到的实际生产方风险P(p≥p0|refuse,X)=0.008 4,实际使用方风险为P(p≤p1|accept,X)=0.099 7。
由此可见,较之经典风险准则得到的故障样本量(187, 13),以及传统Bayes测试性验证故障样本量确定方法所确定的故障样本量(81, 6),在相同双方风险的情况下,基于三维Bayes网络测试性模型推理确定的故障样本量得到有效降低。同时,本文方法得到的实际生产方风险为P(p≥p0|refuse,X)=0.008 4,较之经典方法和传统Bayes方法所得明显降低,这是由于P(N(0, 0, 0)=1)的95%置信区间为[0.804, 0.955],而生产方要求值p0=0.95位于区间末端,故使得落入P(p≥p0|refuse,X)的样本数较少,因此生产方风险P(p≥p0|accept,X)会明显减小。
4 结论 本文针对现有测试性工程中未能有效考虑复杂装备系统的系统结构特征,且基于装备整机系统测试性先验信息的测试性验证方法难以适用,基于分系统测试性先验信息的测试性验证方法不能有效地处理先验信息,导致结果可信度不高的问题,通过对FMEA分析,确定装备纵向结构和横向结构,据此提出了一种面向复杂系统的三维Bayes网络测试性验证模型,旨在充分运用装备各层级结构中所蕴含的条件独立性和先验信息。一方面有效降低构建Bayes网络模型的复杂度,另一方面通过给出的三维Bayes网络推理算法逐步由底层单元数据通过模型逐步向上融合得到顶层数据,给出系统FDR后验分布,并通过后验分布结合基于后验分布的故障样本量确定方法,确定系统故障样本量。因此本文模型在工程上具备可行性,且具备以下优点:
1) 三维Bayes网络测试性验证模型充分考虑了复杂装备系统的系统结构特征,通过层次节点反映实际复杂装备结构之间的内在联系。
2) 三维Bayes网络测试性验证模型能充分利用Bayes网络概率推理的优点,并能充分融合各层次节点所存在的先验信息,使得系统FDR后验分布结果具备更高的可信度,同时由于基于后验分布的故障样本量确定方法能结合系统测试性数据增加装备测试,未通过生产方对装备拒收的接受程度以及装备测试通过使用方对装备接收的支持程度,故一方面能使得所确定的故障样本量较之经典测试性验证方案以及传统Bayes测试性验证方案有效减少,另一方面由于系统FDR后验分布结果可信度的提高进而保证所确定的故障样本量亦具备更高的可信度。
参考文献
| [1] | 石君友. 测试性设计分析与验证[M]. 长沙: 国防工业出版社, 2011. SHI J Y. Testability design analysis and verification[M]. Chang-sha: National Defense Industry Press, 2011. (in Chinese) |
| [2] | U.S.Department of Defense.Military standard testability program for electronic systems and equipments: MIL-STD-2165A[S].Washington, D.C.: U.S.Department of Defense, 1993. |
| [3] | 中国人民解放军总装备部.装备测试性工作通用要求: GJB 2547A-2012[S].北京: 总装备部军标出版发行部, 2012. General Armament of PLA.General requirement for materiel testability program: GJB 2547A-2012[S].Beijing: General Armament Department Military Standards Publication and Distribution Department, 2012(in Chinese). |
| [4] | U.S.Department of Defense.Maintainability verification/demonstration/evaluation: MIL-STD-471A-1973[S].Washington, D.C.: U.S.Department of Defense, 1973. |
| [5] | 石君友, 纪超, 李海伟. 测试性验证技术与应用现状分析[J]. 测控技术, 2012, 31(5): 29-32. SHI J Y, JI C, LI H W. Analysis of testability verification technology and application status[J]. Measurement & Control Technology, 2012, 31(5): 29-32. DOI:10.3969/j.issn.1000-8829.2012.05.007 (in Chinese) |
| [6] | 田仲, 石君友. 现有测试性验证方法分析与建议[J]. 质量与可靠性, 2006(2): 47-51. TIAN Z, SHI J Y. Analysis and recommendations of existing testability verification methods[J]. Quality and Reliablity, 2006(2): 47-51. (in Chinese) |
| [7] | 李天梅, 邱静, 刘冠军. 利用研制阶段试验数据制定测试性验证试验方案新方法[J]. 机械工程学报, 2009, 45(8): 52-57. LI T M, QIU J, LIU G J. New methodology for determining testability integrated test scheme with test data in the development stages[J]. Journal of Mechanical Engineering, 2009, 45(8): 52-57. (in Chinese) |
| [8] | 李天梅, 邱静, 刘冠军. 基于Bayes变动统计理论的测试性外场统计验证方法[J]. 航空学报, 2010, 31(2): 335-341. LI T M, QIU J, LIU G J. Research on testability field statistics verification based on Bayes inference theory of dynamic population[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(2): 335-341. (in Chinese) |
| [9] | 邓露, 许爱强, 李文海, 等. 基于Bayesian理论的测试性验证试验方案[J]. 南京理工大学学报(自然科学版), 2014, 38(6): 775-780. DENG L, XU A Q, LI W H, et al. Testability demonstration test scheme based on Bayesian theory[J]. Journal of Nanjing University of Science and Technology, 2014, 38(6): 775-780. DOI:10.3969/j.issn.1005-9830.2014.06.012 (in Chinese) |
| [10] | 王敏, 杨江平, 卢雷, 等. 利用分系统数据制定整机测试性验证试验方案[J]. 现代防御技术, 2015, 43(5): 213-217. WANG M, YANG J P, LU L, et al. Determining testability demonstration test scheme with subsystem data[J]. Modern Defence Technology, 2015, 43(5): 213-217. DOI:10.3969/j.issn.1009-086x.2015.05.034 (in Chinese) |
| [11] | 常春贺, 杨江平, 胡亮. 基于Bayes理论的复杂装备测试性评估方法[J]. 火力指挥与控制, 2012, 37(11): 173-176. CHANG C H, YANG J P, HU L. Study on testability evaluation method for complex equipment based on Bayes theory[J]. Fire Control & Command Control, 2012, 37(11): 173-176. (in Chinese) |
| [12] | 张西山, 黄考利, 闫鹏程, 等. 基于验前信息的测试性验证试验方案确定方法[J]. 北京航空航天大学学报, 2015, 41(8): 1505-1512. ZHANG X S, HUANG K L, YAN P C, et al. Method of confirming testability verification test scheme based on prior information[J]. Journal of Beijing University of Aeronautics and Astronantics, 2015, 41(8): 1505-1512. (in Chinese) |
| [13] | 郑应荣.系统级层次化测试性建模与分析[D].哈尔滨: 哈尔滨工业大学, 2014. ZHENG Y R.Testablity modeling and analysis of hierarchical system[D].Harbin: Harbin Institute of Technology, 2014(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D591285 |
| [14] | 王京, 李天梅, 何华锋, 等. 多源测试性综合数据等效折合模型与方法研究[J]. 兵工学报, 2017, 38(1): 151-159. WANG J, LI T M, HE H F, et al. Research on multi-source data equivalent methods for testability integrated evaluation[J]. Acta Armamentarii, 2017, 38(1): 151-159. DOI:10.3969/j.issn.1000-1093.2017.01.020 (in Chinese) |
| [15] | 刘钰, 韩峰, 闫凯, 等. 基于贝叶斯网络的分层系统可靠性分析[J]. 航空动力学报, 2016, 31(6): 1385-1392. LIU Y, HAN F, YAN K, et al. Reliability analysis of hierarchical systems based on Bayesian network[J]. Journal of Aerospace Power, 2016, 31(6): 1385-1392. (in Chinese) |
| [16] | 王超.虚实结合的测试性试验与综合评估技术[D].长沙: 国防科学技术大学, 2014. WANG C.Testability test and integrated evaluation technology with virtual-physical test[D].Changsha: National University of Defense Technology, 2014(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-90002-1016922110.htm |
