路径规划问题主要是根据出行者的需求,在给定的数字道路地图中根据OD信息规划出一条最优路径,从而节省驾驶员旅行费用,优化的标准包含行车距离最短、旅行时间最短、通行费用最低等[1]。近几年国内外在该领域已取得多项显著成果,并推动了新型智能交通技术的应用[2]。
在国内,向冬梅和陈树辉[3]通过管理空间数据与拓扑网络,研究最优寻路策略,提出了面向动态路径规划优化新方法。李露蓉等[4]基于优化蚁群算法构建了面向动态路径规划的模型, 达到了控制网络中车流量合理分配的目的,特别在大规模动态交通网络应用中效果更为显著。刘微等[5]建立了基于卡尔曼滤波理论的行程时间多步预测模型,综合利用实时数据、行程时间多步预测数据及历史数据优化实时路径导航算法,与传统方法对比取得了更优的规划效果。周明秀等[6]在传统蚁群算法的基础上提出了改进距离启发因子以增加目标节点对下一节点的影响,从而提高全局搜索能力,避免陷于局部最优解的同时提高了收敛速度。周申培等[7]基于路阻函数建立了道路状况的数学模型,利用传统媒体(交通广播电台路况信息收集渠道),获取实时道路交通状况,采用定量分析法将道路信息车流量代入路阻函数计算得到当前状态下道路实际通行时间,提供更优质的路径规划功能。
在国外,Sen等[8]针对传统路径规划方法缺乏考虑出行者对行程时间变化的容忍性的因素,建立了一个基于旅行时间均值和方差的多目标规划模型,为出行者提供诸如旅行时间变化可能最小的路线,以满足更多实际需求。Wu和Nie[9]基于随机优势理论提出了一种基于冒险行为建模的统一路径选择方法,根据出行者的实际需求和偏好,分别计算适合它们的保守或激进的路线,从而最大化地满足各方需求。Xing和Zhou[10]提出了一种基于抽样的方法,以多天的旅行时间观测值动态构建代理目标函数,使用次梯度算法减少最优性间隙来迭代地提高规划路线质量。Chen等[11]同样研究了路径规划系统中预测行程时间的可靠性,使用多标准最短路径方法确定起点和终点之间可靠的最短路径,确保所提供的路线可靠性较高。Backfrieder等[12]面向网联汽车系统设计了一个运输网络中智能线路动态规划方法,以预测阻塞最小算法为基础向驾驶员提供路线建议,并通过动态微观交通仿真证明了其在真实场景中的有效性。
从上述文献中可以看出,先进的路径规划系统需依靠海量实时交通数据实现[13]。但目前相关研究成果中所用的数据主要通过车辆行驶轨迹、手机信令和检测器等来源间接获取,与真实场景存在一定的偏差,导致计算精度和实时性仍存在不足[14];同时,传统路径规划系统在计算路段路阻权值时,通常不考虑车辆在灯控信号影响下转向所花时间。而在实际城市道路环境中,受交通信号控制影响,路阻存在明显差异性[15]。
随着先进车路协同技术应用,新型路径规划系统可获取更丰富的车辆行驶数据[16-17]。因此,本文从传统路径规划问题出发,面向车路协同系统(Cooperative Vehicle Infrastructure System, CVIS)提出了一种考虑交通信号控制影响的网联车辆通过城市交叉口行程时间计算方法,并基于此方法提出了分阶段的区域最优路径决策方法,为车路协同系统中路径规划问题提供了技术支持和理论依据。
1 车路协同环境下路径决策系统 车路协同技术通过网联车辆与路侧智能设备之间的无线信息交互实现了多源数据的直接获取,从而代替传统方法中无法获取或只能间接计算得到的一些数据源,且数据实时性高,为需要大量数据支持的动态路径规划引入了新的思路,以下分别从场景、特征和策略3个角度就本文所述的路径决策系统进行描述。
1.1 路径决策场景 本文所研究的实时路径决策方法基于车路协同系统实现。远程服务端用于汇总区域内的实时路网信息并提供最优路径规划服务,网联车辆上安装的智能车载终端(On Board Unit, OBU)与路侧终端(Road Side Unit, RSU)之间建立V2X网络通信,车载终端根据车辆总线和传感器信息向路侧终端上报所要求的统计数据,同时向远程服务端发送路径规划请求;路侧终端根据同时段内上报数据来计算各车道的行程时间,上报远程服务端,并根据行程时间和所采集的信号机控制信息实时向车载终端返回所需信息和指令,在该场景下,每一个交叉口的路侧设备都承担着该路网节点与相邻节点间的数据汇总与分析功能,比传统的后台数据处理方法具有更强的灵活性和实时性。
1.2 路径决策特征 传统动态路径规划方法以行程时间为路阻权值来寻找行程时间最短的路线方案。由于交通运行状态的时变性,路阻权值的浮动性很大,传统方法多采用一定时间内的平均值当做短时预测量来表示路阻权值,但时间采样间隔过大时将导致规划的实时性降低,而采样间隔过小时又无法保证规划精度。特别对于城市道路来说,由于交通信号的影响,车辆的行程时间不随交通波的移动而连续变化,很可能因为相位切换而导致行程时间突增,这种周期性的变化规律使得平均值的算法存在一定误差。因此,需要在保证精度的情况下,将采样时间间隔降低至一个周期内,甚至精准预测每一辆车的行程时间和抵达停止线时将遇到的灯控信号,车路协同系统为该方法的实现提供了可能。
本文所述车路协同环境下路径决策方法在传统方法预测行程时间的基础上进一步预测可能在交叉口处的灯控事件,特征结构如图 1所示,即车辆根据与路侧智能设备间的数据和指令交互计算其行驶至停止线所需的时间并判断抵达停止线前将遇到的信号灯灯色,由此计算该相位因为交通信号控制所产生的时间路阻值,从而得到整条道路上每一辆车的精确路阻预测值。
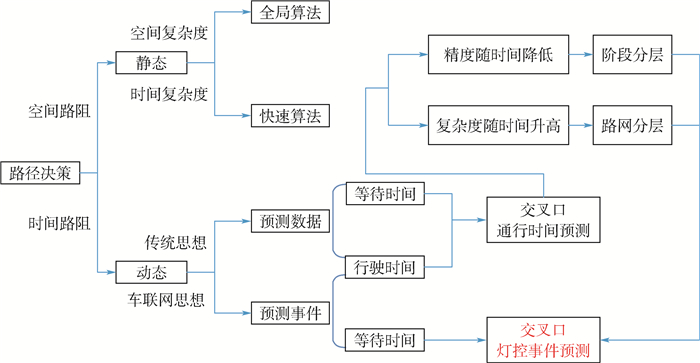 |
| 图 1 车路协同系统下路径决策方法特征 Fig. 1 Characteristics of path decision method in CVIS |
| 图选项 |
综上可以看出,车路协同环境下的路径决策方法对比传统方法具有以下优势:①考虑所处相位可能遇到的信号灯控事件;②考虑因为不同转向的行程时间差异;③在微观视角下对行程时间进行预测,具有高实时性特点。
1.3 路径决策策略 为提高路径决策精度,传统方法针对每一辆车的行程时间和事件进行预测,但某一个交叉口的事件预测出现偏差时,将导致后续事件预测结果均无法成立,因此很难适用于途经交叉口数目过多的长路线,即使是在一个小区域内进行规划,也会因为计算复杂度过高而不适用。由此本文参考图 1中传统方法为降低运算复杂度、提高可靠度而提出的路网分层分级思想,确定了基本分阶段的区域路网最优规划方法。过程示意如图 2所示,主要步骤如下:
 |
| 图 2 车路协同系统下路径决策方法策略 Fig. 2 Strategy of path decision method in CVIS |
| 图选项 |
步骤1??车载终端首先向远程服务端发送路径规划请求和OD信息,如图 2中O、D点所示。
步骤2??远程服务端根据OD信息和路网状态计算全局最优路径,选取行程时间最小的2条路线作为备选,如图 2中黄色和蓝色路线所示。
步骤3??寻找2条路线中重合的路段(或节点),记为公众路段,如图 2中绿色线段所示,由此得到节点1与节点2、节点3与讫点D之间2个待选路线段(2个阶段)。
步骤4??将规划路线发送给车载终端,由车载终端按照指定路线行驶,直至车载终端根据GPS数据和V2X交互信息判断车辆在下一个路口将进入待选路线段(节点1至节点2)。
步骤5??车载终端向远程服务端发送区域最优路线规划指令,远程服务端根据路侧终端实时数据分别计算2条待选路线在考虑转向和灯控信息影响下的行程时间,选择二者中行程时间最小的一条路线提供给车载终端。
步骤6??车辆驶离节点2后,以节点2为起点重新计算到D点的最优路径,并重复步骤2~步骤6的过程,直至车辆到达讫点D。
该策略的核心思想是:利用车路协同技术所提供的路侧信号机控制数据和V2X网络的通信手段,对全局算法所提供的多条行程时间相近的路线提供一个考虑信号控制的精细化比较,并逐步得到全程的最优行驶路线。
2 基于车路协同的路径决策方法 基于1.3节所述路径决策策略,建立高效车路通信体系,在考虑交通信号情况下建立新型路阻值计算方法,根据区域路网拓扑分阶段得出最优路径。
2.1 基于车路协同的动态数据交互方法 为了确定各转向车道各自的路阻值,需要确保用于计算行程时间的动态车辆数据源根据车辆实际驶出方向进行区分,为此划定了路段与交叉口分界线,以停止线前禁止换道实线开始处为分界点,如图 3所示。根据该划分方法,车辆在进入交叉口区域后,其转向方向也同时确定,最终统计的车辆行驶数据将经由V2X网络上传至路侧终端,并记录于指定转向的数据集中。
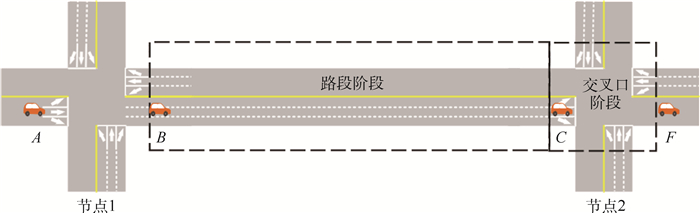 |
| 图 3 两阶段通信流程划分 Fig. 3 Division of two-phase communication process |
| 图选项 |
位于节点附近的路侧终端会与附近行驶中的网联车辆建立V2X通信,并广播交叉口区域的定位范围,网联车辆根据自身GPS数据判断是否驶入/驶离交叉区域,从而根据约定在指定时刻上传所需数据。车辆在每一条道路的行驶过程中,有图 3中A、B、C、F四个关键位置节点。点A表示车辆尚未驶入本条道路,此时车辆中记录的行车数据仍归属于上游路段;点B表示车辆刚刚驶离上游节点的交叉口区域,已完成与上一路侧终端的数据交互流程,开始重新记录行驶数据;点C表示车辆从路段区域驶入交叉口区域,此时车辆通知路侧终端准备接收车辆数据,路侧终端记录车辆ID并记录在数据库中;点F表示车辆驶离交叉口区域,将向路侧终端发送点B至点F间的车辆行驶数据,用于路侧终端计算实时路阻值,并开始记录统计下一条道路的车辆数据。
在该车路协同系统中,路侧终端固定于交叉口附近,在路阻计算之前,其主要功能有3项:
1) 数据汇总。有线连接信号机读取信号控制数据, 并通过V2X网络汇总驶过交叉口的车辆行驶数据。
2) 数据分拣。根据车辆驶入(图 3中点C)和驶离(图 3中点F)交叉口区域时的位置向量判断车辆转向,从而确定数据归属。
3) 数据清洗。根据静态道路特征和动态车辆数据过滤掉异常数据,如车辆行驶距离远大于道路长度等。
车载终端根据路侧终端的指令读取行驶数据并按照要求计算后上传,这些数据是为了路阻值计算,每个转向对应的路段会对应记录一组数据,最终路侧终端汇总的数据如表 1所示。
表 1 车载及路侧单元采集数据 Table 1 Data collected in OBU and RSU
| 数据类型 | 数据含义 |
| 平均行驶速度v | 一定时间内该路段上所有车辆的平均行驶速度 |
| 平均排队车辆数N | 一定时间内该路段上每个周期平均排队车辆数 |
| 信号控制周期C | 该交叉口对应信号控制周期 |
| 相位绿灯起始时间Ps | 在信号周期中该路段所处相位绿灯起亮时间 |
| 相位绿灯持续时间Pd | 在信号周期中该路段所处相位绿灯持续时间 |
| 当前所处时间c | 目前已处于信号控制的第几秒 |
表选项
其中,道路里程为常量调查数据,信号控制相关信息由路侧终端连接信号机获取,速度与排队车辆数信息由路侧终端根据上报的车辆数据计算得到,根据实际需求和客观条件可调整计算间隔。
2.2 车路协同系统下路阻计算方法 本文系统中的路阻值是一个微观变量,特指对于任意一辆即将进入路段的车辆(图 3中点B),预测其驶离(图 3中点F)前方交叉口时所需经历的行程时间,因此,对于自由驶入的车流中的每一辆车,其路阻值均不同。
图 4为一组6辆网联汽车驶入某一路段的轨迹。图中:横轴为时间轴,长度为下游交叉口的一个信号控制周期,纵轴表示该条路段的长度L,绿色轨迹表示匀速行驶过程,黄色轨迹表示加减速行驶过程,红色轨迹表示停车过程。可以看出,6辆车的行驶速度相近,由于信号控制和排队的影响,路阻值有较大差异。
 |
| 图 4 路阻计算中的3种情形 Fig. 4 Road resistance calculation in 3 situations |
| 图选项 |
定义下游交叉口信号控制周期为C,以红灯起亮时间为第0 s,任意一个相位红灯时间为TRX,绿灯时间为TGX,X=L, S, R,表示左、直、右3种转向情况。则当右转不受控时有TRR=0,对于两相位控制交叉口,有TRL=TRS, TGL=TGS,为了提高方法的容错率,将信号控制中黄灯时间一律计入红灯时间,则有
 | (1) |
记车辆在ciX时刻进入路段,以路段平均行驶速度v到达路口时,信号控制周期所处的时间为coX,当全程无排队或减速情形发生时(右转),可得
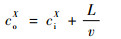 | (2) |
当coX < TRX时,车辆必然遇上红灯停车;当coX>TRX时,因为有排队车辆消散过程,则对照图 4可分为3种情形:有停车情形(1、2、3号车)、无停车有减速情形(4号车)和匀速行驶情形(5、6号车),分别记为情形1、情形2和情形3。
暂不考虑二次排队的情形,记排队消散时间为T1X,排队消散后仍对后车存在影响的时间为T2X,排队消散后对后车没有影响的时间为T3X,则有
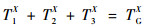 | (3) |
由此,有如下计算路阻值的3种分类讨论情况:
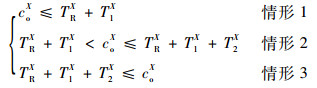 | (4) |
为了确定T1X和T2X的值,需要判断路口车辆排队数,考虑到无突发情形下交通运行状态的连续性,该值在本文系统中由路侧终端根据上2个信号控制周期的平均排队车辆数计算得到,记为N。
在T1X持续时间内,排队车辆经过排队和驶离交叉口2个过程,记所需要的时间分别为TxX和TpX,有
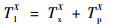 | (5) |
取车辆加速度为a,约定车辆排队时车间距为dp,跟驰时车间距为dg,车辆长度为dl,则最大排队车辆数为N的队列,根据运动学公式有排队消散时间TxX的计算式为
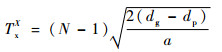 | (6) |
经过此时间后,最后一辆排队车辆开始加速直至达到路段平均行驶速度v,根据实际排队长度可能有2种情况。当2a(N-1)(dp+dl)≤v2时,车辆加速通过交叉口,通过交叉口所需时间TpX为
 | (7) |
当2a(N-1)(dp+dl)>v2时,车辆先加速后匀速通过交叉口,通过交叉口所需时间TpX为
 | (8) |
由此根据实际情况可算出在当前预测排队长度下的T1X值。
在T2X阶段内,车辆不会在路段中停车,但由于前方车辆仍处于未启动或缓慢加速过程中需要减速,记某一车辆为该条车道的第N+1辆车,临界情况下,其速度将在减速过程中趋于0,而后再加速行驶,则T2X的持续时间可看作为该车辆因减速行为而导致的时间延误,考虑加减速过程为匀变速运动,则有变速过程中平均速度为0.5 v,最大延误时间T2X为
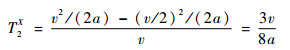 | (9) |
由此可由式(4),根据T1X、T2X值判断对于任意时刻ciX进入路段后车辆的行驶状态。
当前方路口行驶方向不为右转时,路口可能存在排队情况,记排队长度为S,有
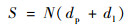 | (10) |
记ci1X、ci2X、ci3X分别为车辆到达路口时,信号灯所处时间cXo=TXR+T1X、cXo=TXR+T1X+T2X和cXo=TXR+T1X+T2X+T3X的驶入时间分界点,考虑车辆在行驶过程中的匀速及减速过程,可得
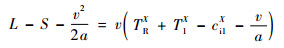 | (11) |
 | (12) |
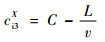 | (13) |
即对于一个完整的信号控制周期C而言,当上游路口驶入时间ciX在ci1X、ci2X之间时,车辆在路口将遇到情形2,在ci2X、ci3X之间时,车辆在路口将遇到情形3,其他时间段内将遇到情形1。
分别计算对于3种情形下进入路段的车辆的具体驶出时间co1X、co2X、co3X,对于没有排队和减速过程的情形3而言,式(2)代表了该情形下的计算方法,对于另2种情况,需要计算出情形2下的具体减速过程和情形1下的具体排队次序n(排队时的序号),分别以车辆驶入时间ciX占该情形下的总持续时间的比重来预测减速时间和排队次序n,则有
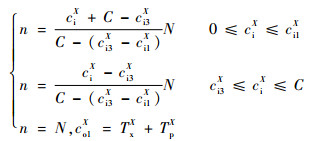 | (14) |
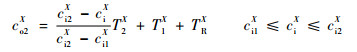 | (15) |
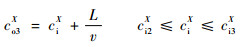 | (16) |
由此可根据车辆在上游驶入时间ciX计算车辆驶出时间coX,则当前路段路阻值Rk为
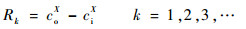 | (17) |
对于途经多交叉口的一整条路线,可通过将上一个路段的计算结果Rk作为输入迭代进下一个路段的求解过程中,如下:
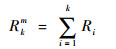 | (18) |
从而计算得出当前完整路线m的路阻值Rkm(m=1, 2, 3, …),实现最终车路协同环境下路阻值计算方法。
2.3 基于阶段划分的最优路径决策方法 1) 建立路径搜索空间
针对实际车路协同系统覆盖的路网区域,选定OD点后可根据实际路网节点建立区域路网模型,如图 5所示。
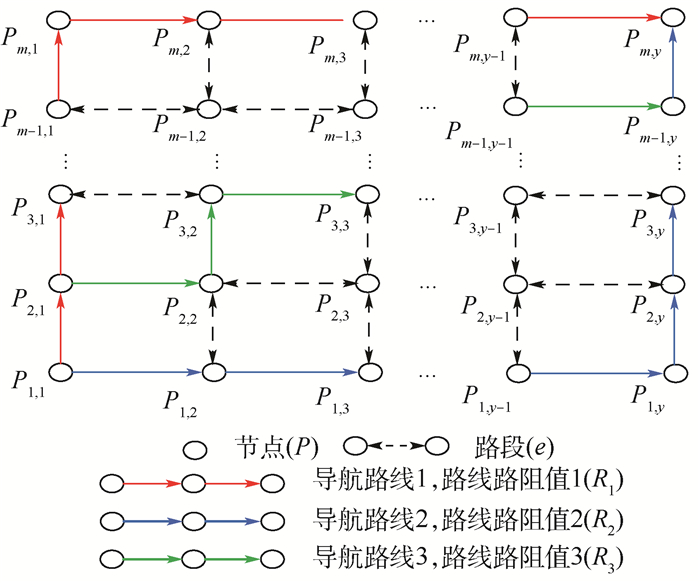 |
| 图 5 车路协同系统下路网模型建立 Fig. 5 Road network model established in CVIS |
| 图选项 |
将路网中的交叉口定义为网络节点,则任意2个交叉口之间的道路表示连接两节点的边,边的权值由路网提供。由此路网可以表示成一个带权有向图G=(P, {E}),P={P1, 1, P1, 2, …, Pm, y}为节点的集合,权值为当前路段路阻值Rk,E={e1, e2, …, em}为边的集合,节点间线段表示当前路段。对图 5所示路网采用遍历模型[18-19]建立路径搜索空间,得到全部路径集Z。
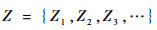 | (19) |
2) 最优路径决策
将式(18)代入路径集合式(19)中,按路阻值排序,最终OD区间内最优路径应当为当前车路协同系统中所有可行路线路阻最小的路线,即
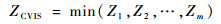 | (20) |
将本文方法应用于实际导航系统中,路网结构以拓扑图的形式存储于远程服务器中,以图 6所示路网为例,每一个节点均记载了区域内各路侧终端所记录汇总的数据。
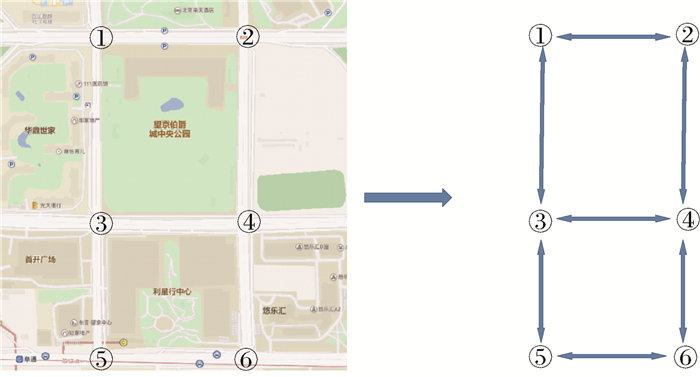 |
| 图 6 路网拓扑结构 Fig. 6 Structure of road network topology |
| 图选项 |
路侧终端记载着与相邻节点间的信息,除去由路网自身特性决定的静态常量信息外,还包括由V2X网络数据计算后得到的动态信息,当路线规划完毕后,得到如图 7所示的重合路段细化路线方案。2个方案如黄线、蓝线所示,OD点相同,约定对于任一路段的表示方式为
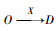

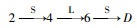
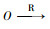
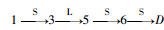
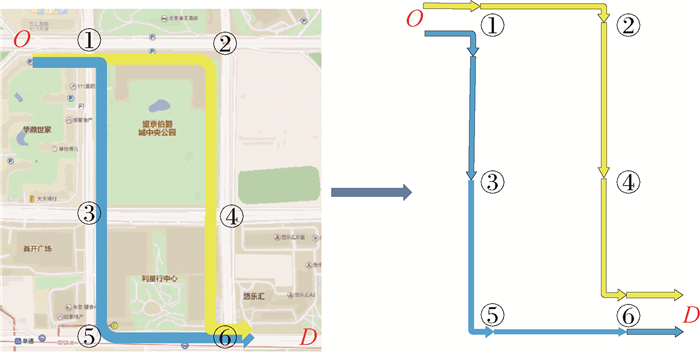 |
| 图 7 细化路线方案 Fig. 7 Route refinement plan |
| 图选项 |
图 8为本文中区域路径优化方法的一个典型流程。图中红色和绿色分别代表红灯和绿灯时间。对于OD相同、里程与绿信比近似的2条路径,方案2的平均行驶速度较低,若只考虑路阻条件,则常规导航系统会推荐方案1为最优,但实际情况下, 由于方案2所选路径在当前时刻下排队时间较少,最终行程优于方案1,体现了这种微观优化方法的优势。
 |
| 图 8 路线优化方案 Fig. 8 Route optimization plan |
| 图选项 |
3 测试验证 3.1 测试环境与方法 为了验证本文方法的有效性,选取北京市望京地区的典型路网区域进行验证。选择OD点为望京地铁站B口至利泽西街与望京西路交叉口西方向出口。本文实验分为06:00—08:00、08:00—10:00、10:00—12:00 3个时段进行,分别由二次开发后的导航系统得到了3次路径规划结果,3次结果均生成了相同的3条路线,如图 9所示,路线详情如表 2所示。
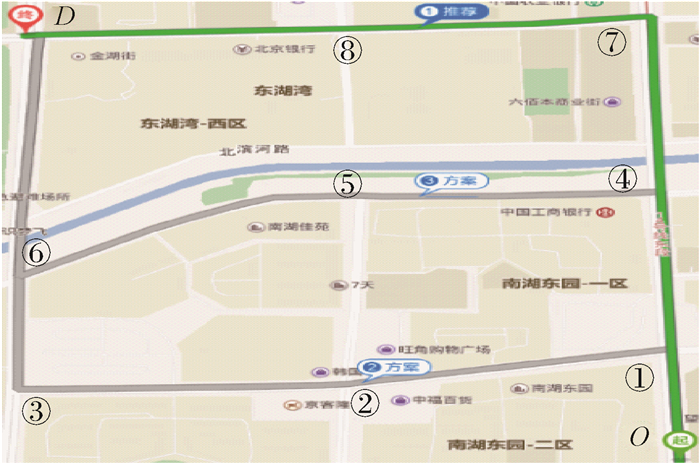 |
| 图 9 实验设计路线方案 Fig. 9 Route plan in experimental design |
| 图选项 |
表 2 实验路线参数 Table 2 Parameters of experimental route
| 路线编号 | 途经灯控交叉口/个 | 行驶里程/km | 预测行程时间/min | 行驶路线 | ||
| 06:00—08:00 | 08:00—10:00 | 10:00—12:00 | ||||
| 路线1 | 5 | 2.0 | 9 | 7 | 6 | 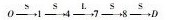 |
| 路线2 | 5 | 2.1 | 10 | 9 | 7 | 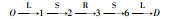 |
| 路线3 | 5 | 2.2 | 10 | 9 | 7 | 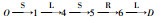 |
表选项
此时常规导航系统默认推荐路线1为最优方案,为了对比本文方法应用后的验证效果,在不同时段下的同一时刻采用浮动车实时记录路线中涉及的所有交叉口交通流状态,将收集到的数据进行对比分析,结果如表 3所示。
表 3 路侧终端采集数据 Table 3 Data collected in RSU
| 路段 | 平均行驶速度v/(km·h-1) | 平均排队车辆数N | 路段长度 L/m | 信号控制 周期C/s | 绿灯起止时 间Ps~Pd/s | |||||
| 06:00—08:00 | 08:00—10:00 | 10:00—12:00 | 06:00—08:00 | 08:00—10:00 | 10:00—12:00 | |||||
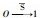 | 24 | 28 | 38 | 15 | 14 | 12 | 431 | 150 | 0~42 | |
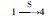 | 26 | 32 | 43 | 9 | 8 | 6 | 374 | 150 | 0~88 | |
 | 22 | 30 | 38 | 7 | 6 | 5 | 415 | 150 | 52~76 | |
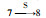 | 20 | 28 | 34 | 6 | 5 | 4 | 368 | 60 | 28~54 | |
 | 21 | 33 | 37 | 9 | 8 | 7 | 443 | 90 | 48~84 | |
 | 20 | 26 | 33 | 9 | 8 | 6 | 431 | 150 | 49~69 | |
 | 15 | 19 | 24 | 8 | 7 | 6 | 418 | 70 | 0~38 | |
 | 14 | 20 | 25 | 0 | 0 | 0 | 422 | 70 | 0~70 | |
 | 16 | 22 | 27 | 7 | 6 | 5 | 387 | 70 | 0~36 | |
 | 12 | 15 | 22 | 9 | 8 | 7 | 430 | 90 | 0~32 | |
 | 24 | 28 | 38 | 15 | 14 | 12 | 431 | 150 | 0~42 | |
 | 18 | 25 | 31 | 11 | 10 | 7 | 374 | 150 | 0~88 | |
 | 12 | 15 | 19 | 10 | 9 | 8 | 381 | 80 | 0~39 | |
 | 13 | 18 | 21 | 0 | 0 | 0 | 502 | 70 | 0~70 | |
 | 12 | 15 | 22 | 9 | 8 | 7 | 430 | 90 | 0~32 | |
表选项
将表 3所记录的数据作为不同时段下实验中3条路线环境参数,根据平均排队车辆数与红灯时间长度的对比关系,设计实验为假定150辆以固定8 s车头时距从O点驶入,根据2.2节中的路阻计算方法,分别计算每辆车选择1、2、3号路线时到达D点的预测行程时间及预测排队次数并以此为评价指标[20-21],其中计算参数如表 4所示。
表 4 路阻计算参数 Table 4 Calculation parameters of road resistance
| 参数 | 典型值 |
| a/(m·s-2) | 3 |
| dl/m | 4.3 |
| dp/m | 0.5 |
| dg/m | 6 |
表选项
3.2 测试结果 针对不同时段下的车辆行驶,最终计算结果如图 10~图 18所示。其中,图 10、图 13、图 16均为预计行程时间计算结果,图 11、图 14、图 17均为预测排队次数计算结果,图 12、图 15、图 18均为本文方法计算所得最优路线与导航软件推荐最优路线的行程时间偏差结果。
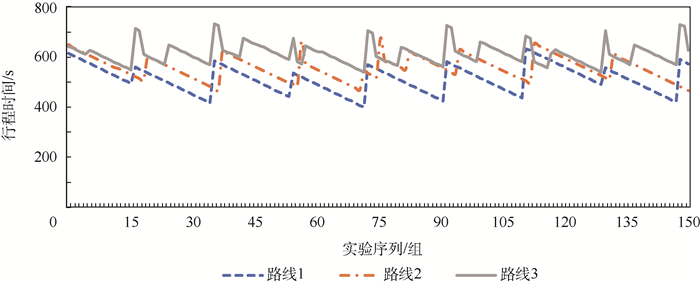 |
| 图 10 06:00—08:00时段行程时间 Fig. 10 Travel time from 06:00 to 08:00 |
| 图选项 |
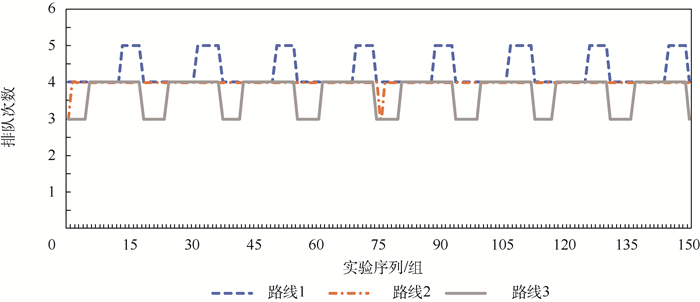 |
| 图 11 06:00—08:00时段排队次数 Fig. 11 Queue number from 06:00 to 08:00 |
| 图选项 |
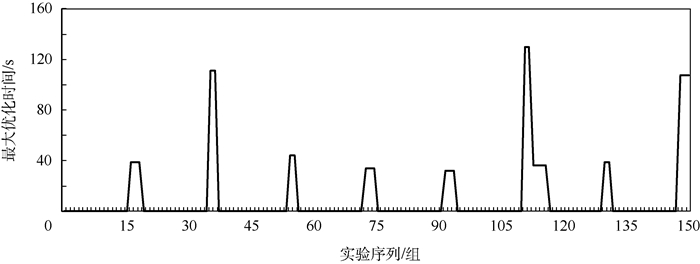 |
| 图 12 06:00—08:00时段最大优化时间 Fig. 12 Maximum optimization time from 06:00 to 08:00 |
| 图选项 |
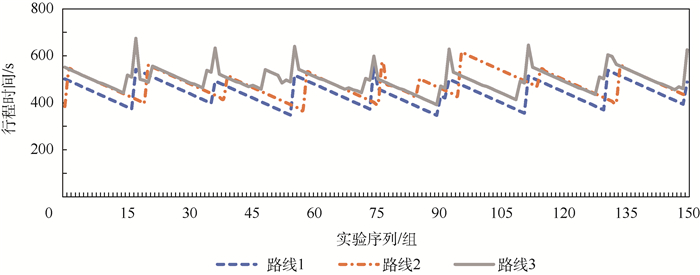 |
| 图 13 08:00—10:00时段行程时间 Fig. 13 Travel time from 08:00 to 10:00 |
| 图选项 |
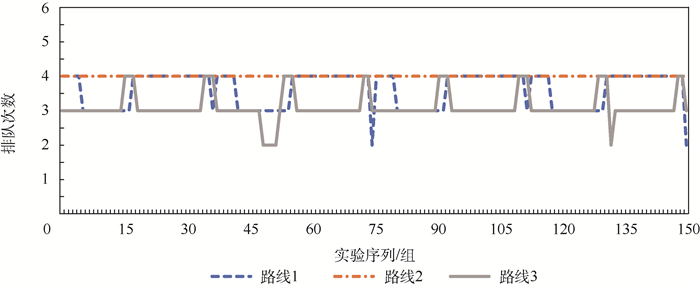 |
| 图 14 08:00—10:00时段排队次数 Fig. 14 Queue number from 08:00 to 10:00 |
| 图选项 |
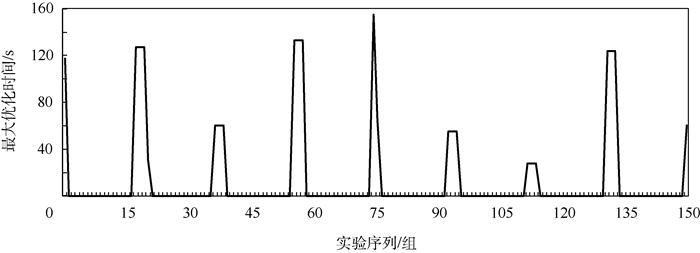 |
| 图 15 08:00—10:00时段最大优化时间 Fig. 15 Maximum optimization time from 08:00 to 10:00 |
| 图选项 |
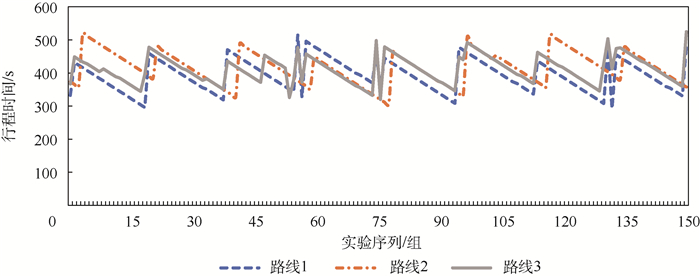 |
| 图 16 10:00—12:00时段行程时间 Fig. 16 Travel time from 10:00 to 12:00 |
| 图选项 |
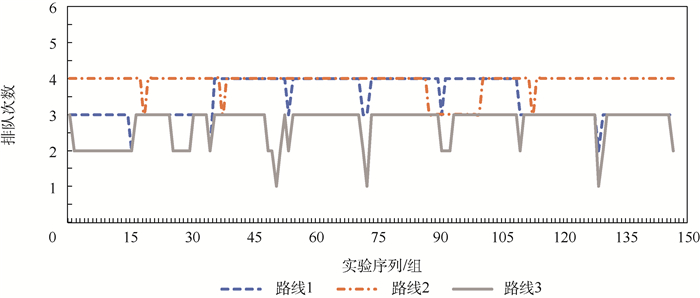 |
| 图 17 10:00—12:00时段排队次数 Fig. 17 Quene number from 10:00 to 12:00 |
| 图选项 |
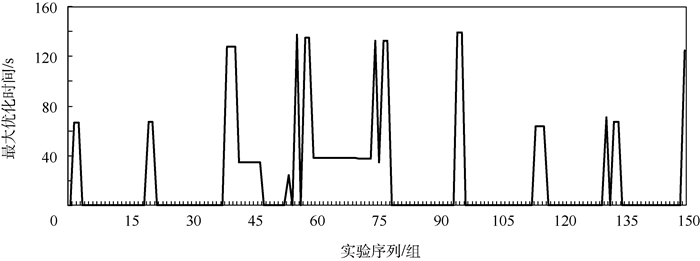 |
| 图 18 10:00—12:00时段最大优化时间 Fig. 18 Maximum optimization time from 10:00 to 12:00 |
| 图选项 |
可以看出,虽然车辆顺序驶入O点,但由于交叉口信号控制的影响,即使是序号相邻的车辆的行程时间也可能有较大差异,这也就导致了最优路线选择上的差异。纵向对比3条路线的预测行程时间可以看到,常规导航系统默认推荐的路线1并不总是预测时间最少的路线。
将上述计算结果进一步整理,结果对比如表 5~表 7所示。可以看出,平峰阶段效果优于高峰阶段;不同时段下,虽然路线1的平均预测指标较其他2条路线更优,但有总数分别为24次、23次及45次情况下路线1并不是最佳选择,即16%、15%及30%的情况下如果按照本文方法进行路线选择可进一步优化行程时间,通过进一步计算,在150组实验过程中,不同时段下,150组数据中,本文方法计算所得最优路线行程时间与导航系统推荐最优路线行程时间差值的平均值, 分别减少了9.52s、13.39s及20.65s, 证明了本文路径决策方法的有效性。
表 5 06:00—08:00路线结果对比 Table 5 Comparison of route results from 06:00 to 08:00
| 路线 | 平均预测 行程时间/s | 平均预测 排队次数 | 平均预测 排队时间/s | 最优路线 次数 |
| 路线1 | 510.54 | 4.28 | 306.61 | 126 |
| 路线2 | 556.37 | 3.99 | 261.19 | 20 |
| 路线3 | 611.48 | 3.69 | 298.61 | 4 |
表选项
表 6 08:00—10:00路线结果对比 Table 6 Comparison of route results from 08:00 to 10:00
| 路线 | 平均预测 行程时间/s | 平均预测排 队次数 | 平均预测 排队时间/s | 最优路线 次数 |
| 路线1 | 440.84 | 3.63 | 236.91 | 127 |
| 路线2 | 478.31 | 4 | 183.13 | 22 |
| 路线3 | 497.64 | 3.11 | 184.77 | 1 |
表选项
表 7 10:00—12:00路线结果对比 Table 7 Comparison of route results from 10:00 to 12:00
| 路线 | 平均预测 行程时间/s | 平均预测 排队次数 | 平均预测 排队时间/s | 最优路线 次数 |
| 路线1 | 392.62 | 3.45 | 188.69 | 105 |
| 路线2 | 416.05 | 3.89 | 120.87 | 23 |
| 路线3 | 411.66 | 2.74 | 98.79 | 22 |
表选项
4 结论 1) 本文重点研究了车路协同环境下新型实时路径决策方法,针对现有方法受限于客观因素只能通过历史或间接数据来预测路阻值的技术不足,通过充分挖掘车路协同系统丰富的实时数据,面向城市道路场景提出了考虑转向信号控制的路径选择优化方法。
2) 在传统路径决策方法的基础上进一步考虑路径搜索空间内可能受灯控影响而产生停车和排队行为,从而根据相关道路实时状态预测任意时刻车辆的行程时间,最后对路径集合内的路阻值重新计算排序得出最优路径。
3) 实验表明,与常规导航系统推荐的最优路线相比,优化后约有20%~30%的车辆实际行程时间将降低,证明了本文方法的可行性。
参考文献
| [1] | 葛艳, 王健, 孟友新, 等. 车辆导航动态路径规划的研究进展[J]. 公路交通科技, 2010, 27(11): 113-117. GE Y, WANG J, MENG Y X, et al. Research progress on dynamic route planning of vehicle navigation[J]. Journal of Highway and Transportation Research and Development, 2010, 27(11): 113-117. DOI:10.3969/j.issn.1002-0268.2010.11.021 (in Chinese) |
| [2] | 孙海鹏, 翟传润, 战兴群, 等. 基于实时交通信息的动态路径规划技术[J]. 微计算机信息, 2007, 23(24): 177-178. SUN H P, ZHAI C R, ZHAN X Q, et al. Dynamic route planning techniques based on real time traffic information[J]. Microcomputer Information, 2007, 23(24): 177-178. DOI:10.3969/j.issn.1008-0570.2007.24.068 (in Chinese) |
| [3] | 向冬梅, 陈树辉. 基于动态交通的最短时间路径规划方法研究[J]. 微计算机信息, 2012, 28(9): 317-319. XIANG D M, CHEN S H. Research on the shortest time path planning based on dynamic traffic[J]. Microcomputer Information, 2012, 28(9): 317-319. (in Chinese) |
| [4] | 李露蓉, 王蕾, 高应波, 等. 基于优化蚁群算法的动态路径规划问题研究[J]. 广西大学学报(自然科学版), 2013, 38(2): 359-367. LI L R, WANG L, GAO Y B, et al. A dynamic path planning model based on the optimal ant colony algorithm[J]. Journal of Guangxi University(Natural Science Edition), 2013, 38(2): 359-367. DOI:10.3969/j.issn.1001-7445.2013.02.018 (in Chinese) |
| [5] | 刘微, 朱征宇, 刘琳, 等. 基于行程时间多步预测的实时路径导航算法[J]. 计算机应用研究, 2013, 30(2): 346-349. LIU W, ZHU Z Y, LIU L, et al. Realtime navigation algorithm based on multistep travel time prediction[J]. Application Research of Computers, 2013, 30(2): 346-349. DOI:10.3969/j.issn.1001-3695.2013.02.006 (in Chinese) |
| [6] | 周明秀, 程科, 汪正霞. 动态路径规划中的改进蚁群算法[J]. 计算机科学, 2013, 40(1): 314-316. ZHOU M X, CHENG K, WANG Z X. Improved ant colony algorithm with planning of dynamic path[J]. Computer Science, 2013, 40(1): 314-316. DOI:10.3969/j.issn.1002-137X.2013.01.073 (in Chinese) |
| [7] | 周申培, 朱泽雨, 吴涛. 基于Android平台的实时路径规划应用开发[J]. 信息通信, 2016(5): 110-112. ZHOU S P, ZHU Z Y, WU T. Real-time path planning application development based on the Android platform[J]. Information & Communications, 2016(5): 110-112. DOI:10.3969/j.issn.1673-1131.2016.05.050 (in Chinese) |
| [8] | SEN S, PILLAI R, JOSHI S, et al. A mean-variance model for route guidance in advanced traveler information systems[J]. Transportation Science, 2001, 35(1): 37-49. DOI:10.1287/trsc.35.1.37.10141 |
| [9] | WU X, NIE Y. Modeling heterogeneous risk-taking behavior in route choice:A stochastic dominance approach[J]. Transportation Research Part A:Policy and Practice, 2011, 45(9): 896-915. DOI:10.1016/j.tra.2011.04.009 |
| [10] | XING T, ZHOU X. Finding the most reliable path with and without link travel time correlation:A Lagrangian substitution based approach[J]. Transportation Research Part B:Methodological, 2011, 45(10): 1660-1679. DOI:10.1016/j.trb.2011.06.004 |
| [11] | CHEN B Y, LAM W H K, SUMALEE A, et al. Finding reliable shortest paths in road networks under uncertainty[J]. Networks and Spatial Economics, 2013, 13(2): 123-148. DOI:10.1007/s11067-012-9175-1 |
| [12] | BACKFRIEDER C, OSTERMAYER G, MECKLENBR?UKER C F. Increased traffic flow through node-based bottleneck prediction and V2X communication[J]. IEEE Transactions on Intelligent Transportation Systems, 2017, 18(2): 349-363. DOI:10.1109/TITS.2016.2573292 |
| [13] | LIU J, WAN J, WANG Q, et al. A survey on position-based routing for vehicular ad hoc networks[J]. Telecommunication Systems, 2016, 62(1): 15-30. DOI:10.1007/s11235-015-9979-7 |
| [14] | ZHU T, SONG Z, WU D, et al. A novel freeway traffic speed estimation model with massive cellular signaling data[J]. International Journal of Web Services Research, 2016, 13(1): 69-87. DOI:10.4018/IJWSR |
| [15] | QIN Q, FENG M, SUN J, et al.Prediction of road resistance based on historical/real-time information and road quality[C]//International Conference on Fuzzy Systems and Knowledge Discovery.Piscataway, NJ: IEEE Press, 2016: 1073-1077. |
| [16] | WANG Z, CHEN Y, CHEN N, et al. The research on control strategy of urban expressway under CVIS[J]. International Journal of Simulation:Systems, Science and Technology, 2016, 16(1): 30-34. |
| [17] | 王庞伟, 余贵珍, 王云鹏, 等. 基于滑模控制的车车协同主动避撞算法[J]. 北京航空航天大学学报, 2014, 40(2): 268-273. WANG P W, YU G Z, WANG Y P, et al. Cooperative active collision avoidance algorithm based on sliding mode control[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(2): 268-273. (in Chinese) |
| [18] | 章权, 温惠英, 孙博.适于配送车辆导航路径规划的遍历模型的改进型粒子群优化算法[D].华南理工大学学报, 2011, 39(8): 110-117. ZHANG Q, WEN H Y, SUN B.Improved particle swarm optimization algorithm of ergodic model for routing planning of delivery vehicle navigation[D].Journal of South China University of Technology, 2011, 39(8): 110-117(in Chinese). |
| [19] | JANCHIV A, BATSAIKHAN D, KIM B S, et al. Time-efficient and complete coverage path planning based on flow networks for multi-robots[J]. International Journal of Control, Automation, and Systems, 2013, 11(2): 369-376. DOI:10.1007/s12555-011-0184-5 |
| [20] | ADLER J L, SATAPATHY G, MANIKONDA V, et al. A multi-agent approach to cooperative traffic management and route guidance[J]. Transportation Research Part B:Methodological, 2005, 39(4): 297-318. DOI:10.1016/j.trb.2004.03.005 |
| [21] | PAZ A, PEETA S. On-line calibration of behavior parameters for behavior-consistent route guidance[J]. Transportation Research Part B:Methodological, 2009, 43(4): 403-421. DOI:10.1016/j.trb.2008.07.007 |
