由于双转子系统的动力特性设计对提高航空发动机结构系统稳健性方面起着重要作用,众多****对其进行了大量的理论和实验研究。早期研究大多是针对双转子耦合特性的验证及振动响应的分析。Childs[5]基于Jeffcott转子建立了双转子-支承结构的力学模型,考虑了陀螺力矩、支承阻尼与非线性等因素,并对叶片丢失激励的振动响应进行了分析;Athre等[6-7]将不平衡激励引入传递矩阵,建立了双转子系统的状态方程,仿真并通过实验验证耦合激励下的不平衡响应的特点;Li等[8]采用了简化传递矩阵法,对带中介轴承挤压油膜阻尼器的双转子发动机的稳态不平衡响应进行了分析,并研究了径向间隙对减振效果的影响。近年来,随着航空发动机的发展需求,双转子系统振动特性优化设计及激励模型等方面的研究也在不断深入。Hylton[9]分析了反向旋转双转子发动机的优点,提出了通过调整中介轴承位置靠近模态节点,使双转子振动响应幅值最小化的观点;Chen和Liao[10-11]利用拉格朗日方程,通过有限元法,建立了考虑基础运动的双转子系统运动方程,其中基础平动相当于只增加外力,而基础转动会带来系统矩阵参数化,对稳态、瞬态响应影响复杂;Yu等[12]通过分析风扇叶片丢失的物理过程,建立了突加不平衡、惯性不对称及叶片机匣碰摩等激励模型,得到突加不平衡对瞬态响应影响最大,碰摩可以抑制响应幅值,而惯性不对称对振动特性影响较小的结论。
上述文献大多针对不同双转子系统激励模型及振动响应振幅进行计算分析。随着航空发动机性能的不断提高,转子系统的负荷逐步加大,支点振动问题越发突出,有必要开展复杂转子系统振动响应尤其是中介轴承支点动载荷优化设计技术的研究。本文通过建立单、双转子系统支点动载荷力学模型,分析了支点动载荷组成成分及其随转子工作状态的变化规律,结合典型双转子系统振动响应的计算分析,提出了通过调整转子弯曲变形弹性线斜率,实现中介支点动载荷的优化设计方法。
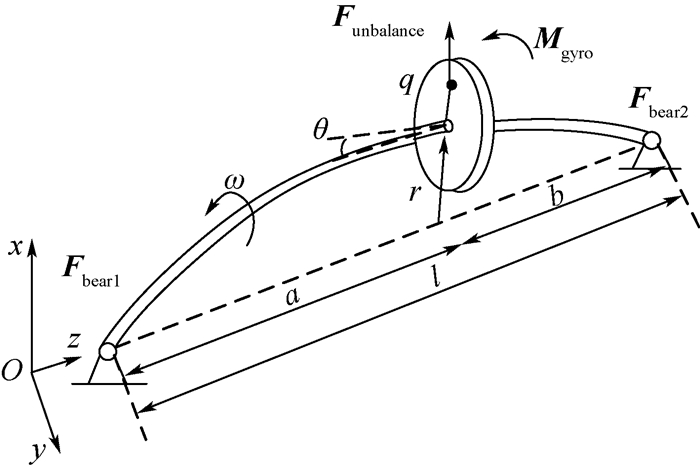
1 转子系统支点动载荷力学模型 1.1 单转子系统 图 1为两端简支单盘转子模型。不平衡量为q的轮盘位于转子中点的一侧,距离两支点为a、b,转速为ω,轮盘的质量、极转动惯量、直径转动惯量分别为m、Jp、Jd,其中,a>b, a=tl, b=(1-t)l,
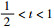
 |
| 图 1 单盘转子模型 Fig. 1 Single disk rotor model |
| 图选项 |
通过拉格朗日方程建立单盘偏置转子的动力学方程,以复数坐标表示转子旋转中轮盘中心的横向位移为r=x+iy,转角为θ=θy-iθx,x、y、θx、θy为系统广义坐标。则系统动能为
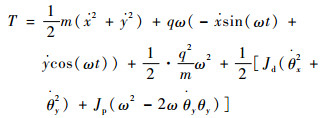 | (1) |
系统势能为
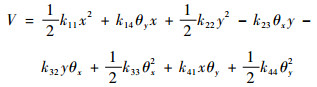 | (2) |
式中:
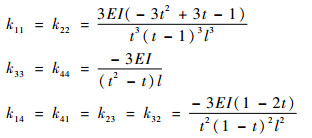 |
其中:EI为截面抗弯刚度。
代入拉格朗日方程,整理得
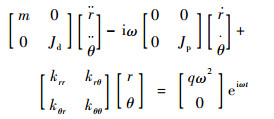 | (3) |
式中:k11=k22=krr, k33=k44=kθθ,k14=k41=k23=k32=krθ=kθr。
设解的形式为
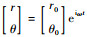
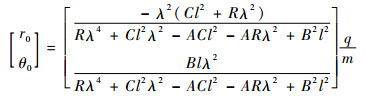 | (4) |
式中:
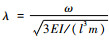
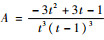
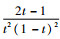
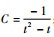
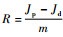
因此,转子受不平衡载荷为
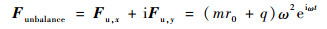 | (5) |
轮盘受陀螺力矩为
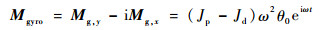 | (6) |
对转子受力分析可知,两支点动载荷Fbear1、Fbear2分别为
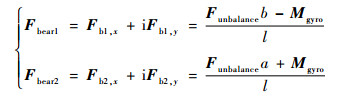 | (7) |
根据式(7)可知,在支点动载荷组成成分中,除了由于质量偏心引起的不平衡载荷项,还包括由于转子弯曲变形引起的轮盘陀螺力矩项。对比1、2两支点动载荷表达式可知,陀螺力矩的存在,会使得各支点动载荷发生显著差异,陀螺力矩成分与不平衡载荷成分同相位会使支点动载荷增大,反相位时会使动载荷减小;此外,动载荷大小还与不平衡量所在位置相关,支点2较支点1轴向靠近不平衡量位置,使得支点2中不平衡载荷成分更大,说明支点动载荷受支点附近不平衡量的影响更敏感。因此在转子动力学设计中,应考虑控制支点附近转子的弯曲变形,减小不平衡量和陀螺力矩对支点动载荷的影响。
1.2 双转子系统 为分析航空发动机双转子系统支点载荷的影响因素,根据双转子结构特征建立如图 2所示的模型,采用有限元法建立系统运动方程[13]。
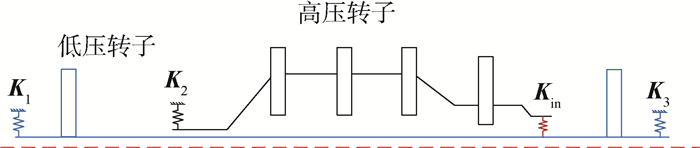 |
| 图 2 双转子系统模型 Fig. 2 Dual-rotor system model |
| 图选项 |
对于轮盘单元,根据拉格朗日方程建立运动方程为
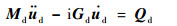 | (8) |
式中:ud为轮盘节点位移列阵;Md为轮盘质量矩阵;Gd为轮盘陀螺矩阵;Qd为轮盘广义力,包括轮盘两端弹性轴的作用力和力矩,以及轮盘质量偏心引起的不平衡力。
同理,对于转轴单元,其运动方程为
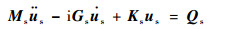 | (9) |
式中:us为转轴节点位移列阵;Ms为转轴质量矩阵;Gs为转轴陀螺矩阵;Ks为转轴刚度矩阵;Qs为转轴广义力,包含相邻轴段的作用力与力矩及不平衡广义力。
对于支承单元,其运动方程为
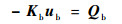 | (10) |
式中:ub为支点位移列阵;Kb为支承刚度矩阵;Qb为广义力,也是支点动载荷。
特别地,对于双转子系统的中介轴承单元,其运动方程为
 | (11) |
式中:Kin为中介支点刚度矩阵;uinh、uinl分别为与中介轴承单元相连的高、低压转子节点位移;Qinh、Qinl分别为中介支点作用于高、低压转子上的广义力,即中介支点动载荷,且Qinh=-Qinl。
组集方程式(8)~式(10),消去各单元相互作用内力,并通过方程式(11)进行高、低压转子的耦合,可以得到双转子系统的振动方程为
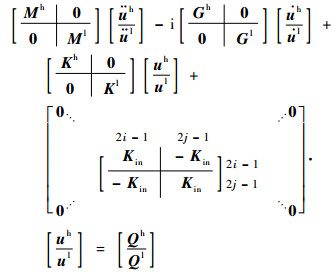 | (12) |
式中:上标h表示高压转子项,上标l表示低压转子项;i、j分别表示与中介支点相连的高、低压转子节点编号;u为节点位移列阵;Q为系统广义力;M为质量矩阵;G为陀螺矩阵;K为刚度矩阵(不包括中介支点)。
方程式(12)进行适当变形,写成弹性力与惯性载荷平衡的形式为
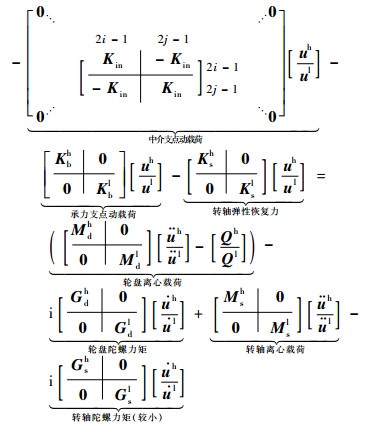 | (13) |
根据式(12)、式(13)可知,双转子系统通过中介轴承进行高、低压转子振动方程的耦合,支点动载荷和转轴弹性恢复力除与高、低压不平衡激励引起的轮盘、转轴的离心载荷平衡外,还要与由于转子弯曲变形产生的轮盘陀螺力矩载荷相平衡(转轴陀螺效应远小于轮盘,略去其影响)。中介支点动载荷同时受高、低压转子的不平衡载荷与陀螺力矩载荷影响,包含高、低压转速成分,载荷变化复杂。
2 复杂转子系统振动响应分析 典型双转子结构系统如图 3所示。风扇1级盘、压气机1级盘、高压涡轮、低压涡轮分别记为fan1、hpc1、hpt、lpt,高压转子采用1-0-1支承方案,低压转子采用1-1-1支承方案,其中4#支点为中介支点,建立有限元模型并进行双转子系统振动响应仿真计算。
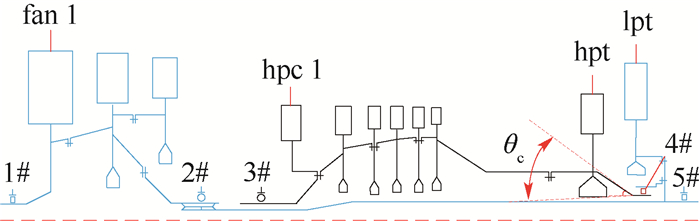 |
| 图 3 典型双转子结构系统示意图 Fig. 3 Schematic of typical dual-rotor structure system |
| 图选项 |
2.1 不同转速下的支点动载荷特点 在给定不同的高、低压转速下(反向旋转),分别在高、低压涡轮处施加50 g·mm不平衡量,计算各支点动载荷随转速变化关系曲线及对应的转子弹性线变形,结果如图 4、图 5所示。
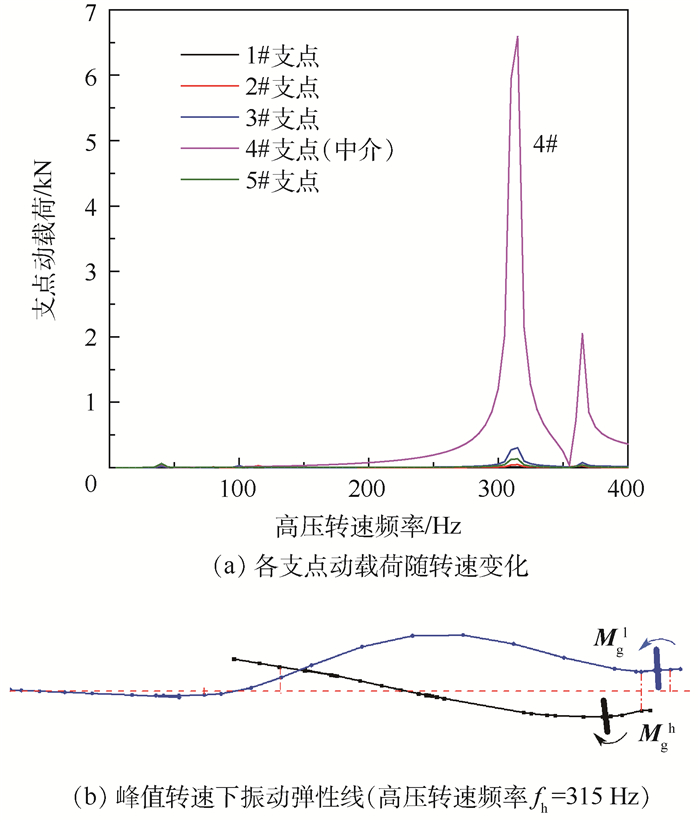 |
| 图 4 高压不平衡激励下的振动响应 Fig. 4 Vibration response under high pressure unbalanced excitation |
| 图选项 |
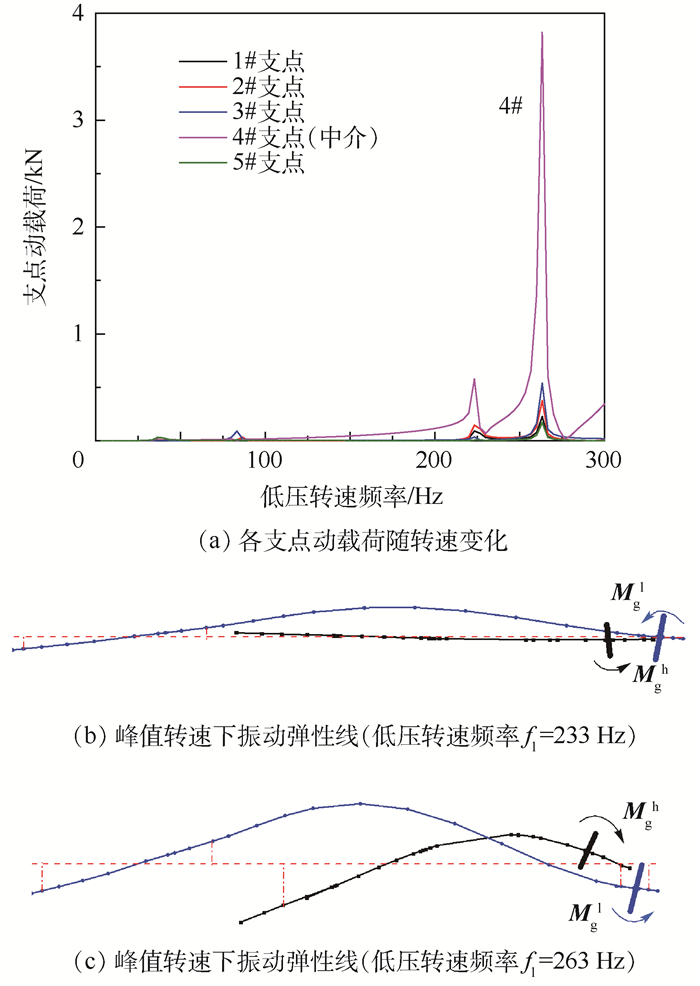 |
| 图 5 低压不平衡激励下的振动响应 Fig. 5 Vibration response under low pressure unbalanced excitation |
| 图选项 |
从图 4、图 5中可知,随转速升高,当转子存在弯曲变形时,无论哪个转子存在不平衡激励,中介支点的动载荷均较其他承力支点显著增大,在峰值转速附近,中介支点动载荷幅值是其他支点的10倍以上。这是因为高转速下,中介支点同时受高、低压转子弯曲变形的影响,高、低压转子不平衡激励均使得反向旋转双转子系统同时存在正、反涡动[14],结合所对应的振动弹性线可知,相应涡轮盘的陀螺效应在中介支点产生的动载荷相互叠加是引起中介支点动载荷显著增大的原因。
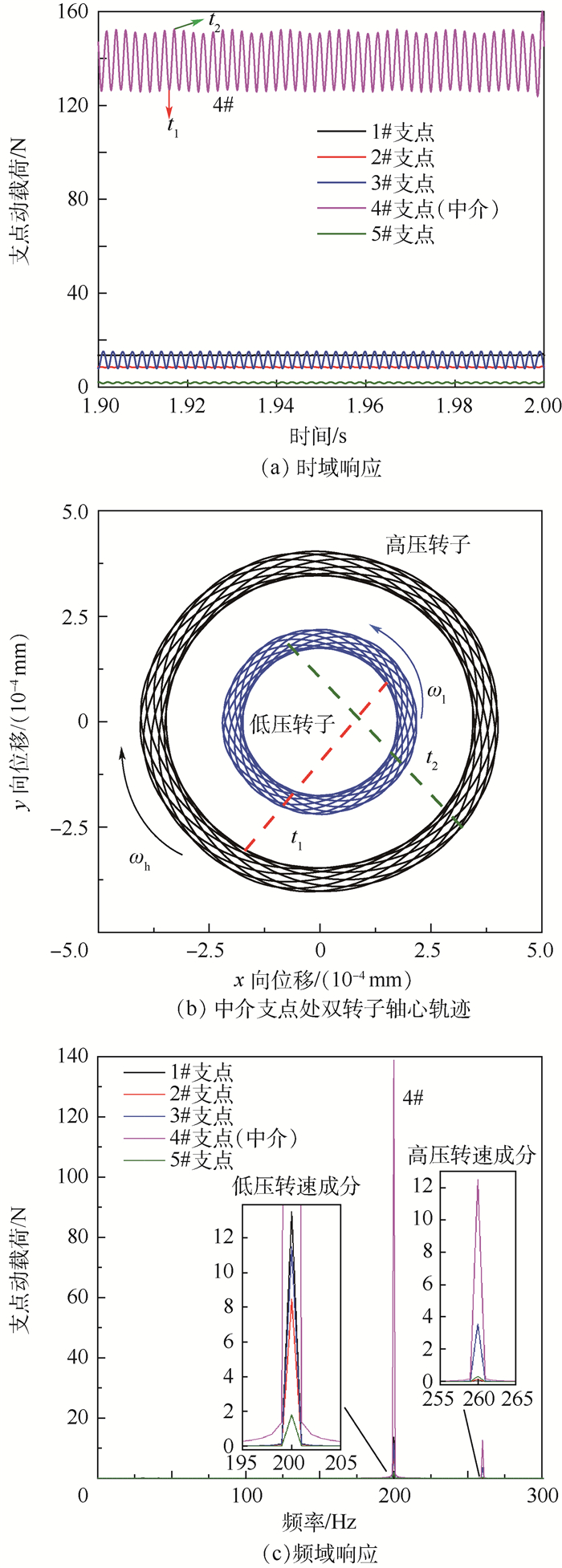
2.2 不平衡量分布对支点动载荷的影响 为分析高转速下不平衡量分布对支点动载荷的影响,在计算中选取最大转速状态,在风扇1级盘、压气机1级盘、高、低压涡轮处施加50 g·mm的不平衡量(同相位),计算复杂不平衡激励下各支点动载荷响应特性,如图 6及表 1、表 2所示。
 |
| 图 6 复杂不平衡激励下支点响应特性 Fig. 6 Response characteristics of bearings under complex unbalanced excitation |
| 图选项 |
表 1 支点动载荷时域数值对比 Table 1 Numerical comparison of bearing dynamic loads in time domain
| 支点编号 | 支点动载荷/N | |
| 均值 | 变化区间 | |
| 1# | 13.5 | 0.2 |
| 2# | 8.5 | 0.4 |
| 3# | 11.8 | 7.3 |
| 4# | 139.1 | 26.6 |
| 5# | 1.85 | 0.7 |
表选项
表 2 支点动载荷频域幅值对比 Table 2 Amplitude comparison of bearing dynamic loads in frequency domain
| 支点编号 | 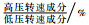 |
| 1# | 0.4 |
| 2# | 1.7 |
| 3# | 15.7 |
| 4# | 9 |
| 5# | 16.7 |
表选项
根据计算结果,中介支点动载荷远大于其他承力支点,并且由于不平衡激励的复杂性,其时域曲线呈现复杂的周期变化,且波动范围较大。通过中介支点处轴心轨迹分析可知,其动载荷大小与双转子的运动状态有关,极小(t1)与极大(t2)值分别发生在两包络线圆环内侧与外侧。此外,对比频域响应中高、低压转速成分可知,1#、2#支点动载荷主要受低压转速影响,基本不受高压转速的影响,3#、4#、5#支点动载荷同时受高、低压转速成分的影响。
为明确高、低压转子不同位置处不平衡激励对不同支点动载荷的影响,寻找敏感位置,以便进行振动响应的优化设计,需进行动载荷的敏感度计算。考虑转子系统不平衡响应是输入激励的多元函数,即
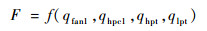 | (14) |
当自变量改变Δqk引起因变量变化ΔF(k分别对应fan1、hpc1、hpt、lpt),则因变量的相对变化与自变量的相对变化之比即敏感度为
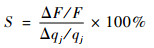 | (15) |
据此定义计算4处不平衡激励对各个支点动载荷影响的敏感度,如图 7所示。
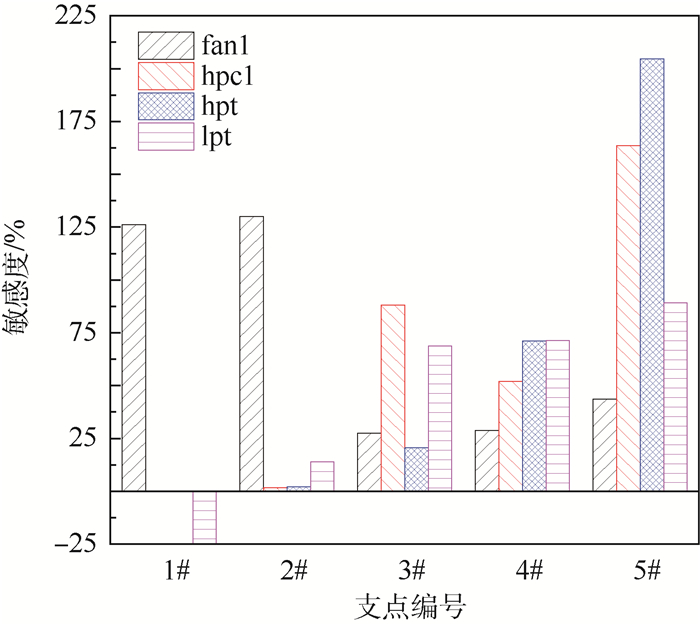 |
| 图 7 支点动载荷对不同位置不平衡激励的敏感度 Fig. 7 Sensitivity of bearing dynamic loads to unbalanced excitation at different locations |
| 图选项 |
敏感度计算结果表明,1#、2#支点动载荷只对低压不平衡敏感,而3#、4#、5#支点动载荷对高、低压不平衡均较敏感,验证了支点动载荷频率成分的分析。而对于动载荷最大的中介支点,其受高、低压涡轮不平衡的影响较大,结合支点动载荷力学模型分析,可知高压涡轮不平衡影响的敏感度高于压气机不平衡,是因为高压涡轮靠近中介支点,同时由于高压涡轮的盘轴连接弯曲刚度弱,系统刚度矩阵中由于不平衡载荷产生的交叉刚度项较小,转子弯曲变形时弹性线的斜率较大,这样,大转动惯量的涡轮盘产生较大陀螺力矩,因而对中介支点动载荷影响更加显著。同理,低压涡轮靠近中介支点,及其陀螺力矩的作用,使得低压涡轮不平衡对中介支点动载荷影响高于风扇不平衡。因此,不平衡激励的分散性对中介支点动载荷影响敏感度有显著差异,在双转子振动响应的优化设计中,应关心对中介支点动载荷影响较大的高、低压涡轮处的结构设计。
3 复杂转子系统振动响应优化设计 从支点动载荷力学模型及复杂双转子系统振动响应仿真计算中,可以看到中介支点动载荷的组成成分及不平衡分布影响敏感度与高、低压转子弯曲变形和运动状态紧密相关。或者说,针对动载荷影响敏感度较高的位置,进行结构优化设计,可以减小高、低压转子弯曲变形,实现中介支点动载荷的有效控制。由此提出基于转子弯曲变形弹性线控制的双转子系统振动响应优化设计方法。由于转子的弯曲变形由转子和支承结构特征共同决定,因此,可以以转轴抗弯刚度分布和支点相对位置为优化参数进行中介支点动载荷的优化设计。
3.1 转子结构抗弯刚度分布优化 由于高压转子弯曲变形及高压涡轮的陀螺力矩对中介支点动载荷影响敏感度较大,在此选取高压涡轮后轴颈局部结构,调整其锥壳角度,即图 3中的θc,分析中介支点动载荷随锥角的变化曲线。由2.2节中敏感度分析可知,高、低压涡轮处不平衡激励对中介支点动载荷影响敏感度较高,故计算中只考虑高、低压不平衡激励的影响。图 8为归一化后的中介支点动载荷均值随高压涡轮后轴颈锥角的变化关系曲线。
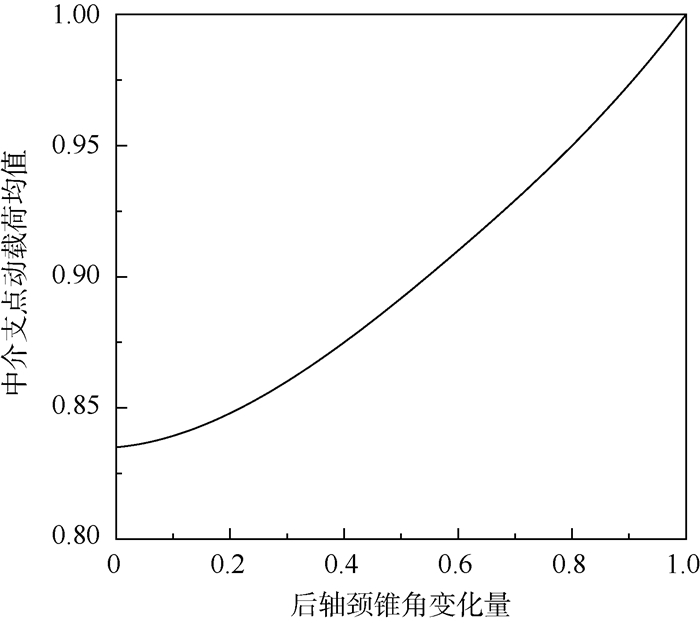 |
| 图 8 后轴颈锥角对中介支点动载荷的影响 Fig. 8 Influence of rear journal cone angle on dynamic loads of inter-shaft bearing |
| 图选项 |
由图 8可知,随着后轴颈锥角的减小,中介支点动载荷均值也发生显著减小,这是因为随着锥角的减小,后轴颈局部结构的弯曲刚度减弱,转子弯曲变形时,后轴颈弯曲曲率增大,而高压涡轮盘处弹性线斜率减小,减弱了涡轮盘陀螺力矩,从而减小了高压转子弯曲变形对中介支点动载荷的影响。通过对弹性线进行分析,可得归一化后涡轮盘处弹性线斜率(最大值)随后轴颈锥角变化关系,如图 9所示。因此,转子结构抗弯刚度的调整,可以实现对转子弯曲变形弹性线斜率的优化,进而实现对中介支点动载荷的有效控制。
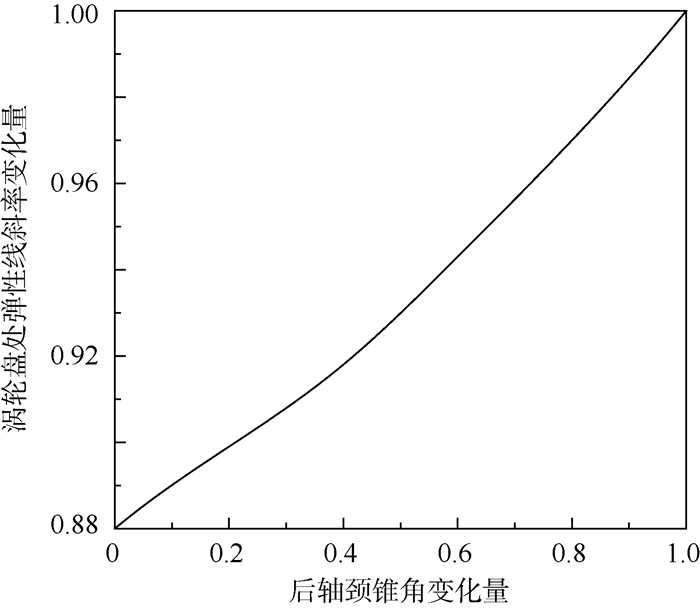 |
| 图 9 后轴颈锥角对涡轮盘处弹性线斜率的影响 Fig. 9 Influence of rear journal cone angle on slope of elastic curve at turbine disk |
| 图选项 |
3.2 中介支点及承力支点位置优化 由于低压涡轮局部变形及陀螺力矩对中介支点动载荷影响也较为敏感,类比转子结构抗弯刚度分布的优化设计可知,对低压转子弯曲变形的弹性线进行控制,也是双转子系统振动响应优化设计的一个方向。而低压转子为多支点的柔性转子,支承特征对其动力特性有重要影响[15-16]。同样地,对于双转子系统,可以考虑采用调整低压转子支承特征的方法来减小中介支点动载荷。
因低压涡轮后支点(5#支点)作为承力支点,用于支承高、低压涡轮转子,该支点的支承特征对高、低压涡轮的局部振动特性有重要影响。为控制低压涡轮局部变形及陀螺力矩对中介支点的影响,改变5#支点的轴向位置,计算中介支点动载荷均值随5#支点轴向位置的变化关系,计算结果归一化如图 10所示。
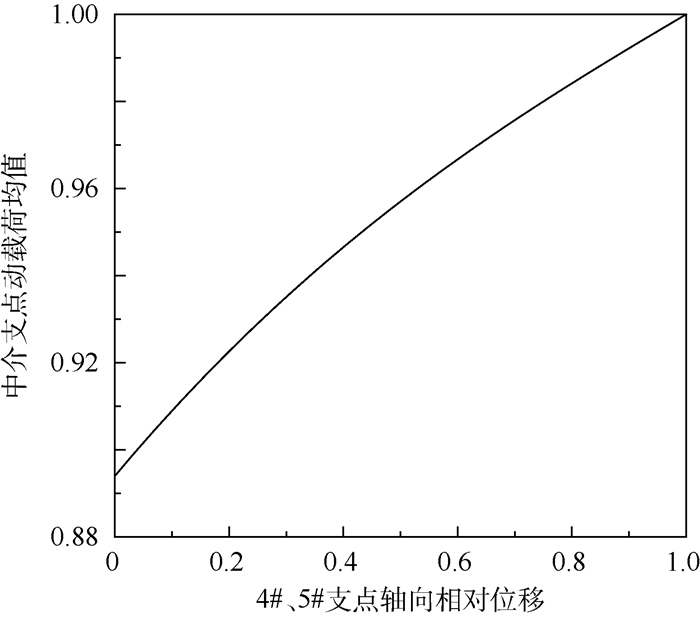 |
| 图 10 中介支点动载荷随5#支点位置变化曲线 Fig. 10 Dynamic loads of inter-shaft bearing changing with position of 5# bearing |
| 图选项 |
由图 10可知,当5#支点靠近4#支点时,中介支点动载荷均值明显降低。这是因为5#支点相当于低压转子弯曲变形的节点,由于支承的约束作用限制了5#支点附近转子弯曲变形,当其靠近中介支点时,可以有效减小中介支点由于低压转子振动引起的动载荷幅值增大。应该指出的是,通过改变支承位置对中介支点附近低压转子弯曲变形进行控制,其实质仍是对转子弯曲变形弹性线的优化设计。另外,这里使5#支点靠近中介支点相当于增大中介支点附近的低压轴弯曲刚度,据此,可以将该支点位置优化的内涵进行扩展,即通过结构设计,增大低压涡轮局部抗弯曲变形能力,可以减小低压涡轮局部振动对中介支点动载荷的影响。
4 结论 本文通过理论与仿真分析,得到主要结论如下:
1) 高速转子系统支点动载荷由不平衡载荷及陀螺力矩载荷组成,不平衡激励的位置及轮盘处的弹性线斜率决定支点动载荷的大小,尤其是复杂双转子系统,其中介支点动载荷同时受高、低压转子的不平衡激励以及轮盘陀螺力矩的影响,载荷成分复杂。
2) 针对典型双转子系统进行振动响应分析,结果表明,随转速升高,当转子出现弯曲变形时,中介支点动载荷远大于其他承力支点,同时,靠近中介支点的高、低压涡轮处的不平衡激励对于中介支点动载荷影响的敏感度较高。通过不平衡分散性的敏感度分析确定了双转子振动响应优化设计的方向。
3) 基于中介支点动载荷敏感度的分析,从转子结构特征与支承结构特征两方面,分别进行高、低压转子振动响应优化设计。研究表明,通过优化转子局部抗弯刚度分布,调整中介支点与承力支点的相对位置,可以改变高、低压转子弯曲变形弹性线的斜率,实现对轮盘陀螺力矩的控制,调节中介支点动载荷大小,从而对复杂转子系统振动响应进行优化设计。
参考文献
| [1] | 洪杰, 于欢, 肖森, 等. 高速柔性转子系统非线性振动响应特征分析[J]. 北京航空航天大学学报, 2018, 44(4): 653-661. HONG J, YU H, XIAO S, et al. Nonlinear vibration response characteristics of high-speed flexible rotor system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(4): 653-661. (in Chinese) |
| [2] | 于欢, 马艳红, 肖森, 等. 高速柔性转子支承松动力学特征及动力特性[J]. 北京航空航天大学学报, 2017, 43(8): 1677-1683. YU H, MA Y H, XIAO S, et al. Mechanical and dynamic characteristics of bearing with looseness on high-speed flexible rotor[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(8): 1677-1683. (in Chinese) |
| [3] | 廖明夫, 刘永泉, 王四季, 等. 中介轴承对双转子振动的影响[J]. 机械科学与技术, 2013, 32(5): 641-646. LIAO M F, LIU Y Q, WANG S J, et al. The vibration features of a twin spool rotor system with an inter-bearing[J]. Mechanical Science and Technology for Aerospace Engineering, 2013, 32(5): 641-646. (in Chinese) |
| [4] | 王俨剀, 廖明夫, 张家豪. 航空发动机中介轴承的动力学减载设计[J]. 航空动力学报, 2017, 32(2): 492-499. WANG Y K, LIAO M F, ZHANG J H. Dynamic load reduction design for inter-shaft bearing of aircraft engine[J]. Journal of Aerospace Power, 2017, 32(2): 492-499. (in Chinese) |
| [5] | CHILDS D W. A modal transient rotor dynamic model for dual-rotor jet engine systems[J]. Journal of Manufacturing Science and Engineering, 1976, 98(3): 876-882. |
| [6] | GUPTA K, ATHRE K, GUPTA K D. Unbalance response of a dual rotor system:Theory and experiment[J]. Journal of Vibration and Acoustics, 1993, 115(4): 427-435. DOI:10.1115/1.2930368 |
| [7] | GUPTA K D, GUPTA K, ATHRE K.Stability analysis of dual rotor system by extended transfer matrix method[C]//ASME 1989 International Gas Turbine and Aeroengine Congress and Exposition.New York: ASME, 1989: V005T13A013. |
| [8] | LI Q, YAN L, HAMILTON J F. Investigation of the steady-state response of a dual-rotor system with intershaft squeeze film damper[J]. Journal of Engineering for Gas Turbines and Power, 1985, 108(4): 613-618. |
| [9] | HYLTON P D.Minimizing dynamic response of counter-rotating engines through optimized node placement[C]//ASME Turbo Expo 2010.New York: ASME, 2010: 25-32. |
| [10] | CHEN X, LIAO M F.Steady-state characteristic of a dual-rotor system with intershaft bearing subjected to mass unbalance and base motions: GT-2018-75215[R].New York: ASME, 2018. |
| [11] | CHEN X, LIAO M F.Transient characteristic of a dual-rotor system with intershaft bearing subjected to mass unbalance and base motions dueing start-up: GT-2018-75227[R].New York: ASME, 2018. |
| [12] | YU P C, ZHANG D Y, MA Y H, et al. Dynamic modeling and vibration characteristics analysis of the aero-engine dual-rotor system with fan blade out[J]. Mechanical Systems and Signal Processing, 2018, 106: 158-175. DOI:10.1016/j.ymssp.2017.12.012 |
| [13] | 钟一谔, 何衍宗, 王正, 等. 转子动力学[M]. 北京: 清华大学出版社, 1984. ZHONG Y E, HE Y Z, WANG Z, et al. Rotor dymamics[M]. Beijing: Tsinghua University Press, 1984. (in Chinese) |
| [14] | 张大义, 刘烨辉, 梁智超, 等. 航空发动机双转子系统临界转速求解方法[J]. 推进技术, 2015, 36(2): 292-298. ZHANG D Y, LIU Y H, LIANG Z C, et al. Prediction for critical speed of double spools system in aero engines[J]. Journal of Propulsion Technology, 2015, 36(2): 292-298. (in Chinese) |
| [15] | 洪杰, 王华, 肖大为, 等. 转子支承动刚度对转子动力特性的影响分析[J]. 航空发动机, 2008, 34(1): 23-27. HONG J, WANG H, XIAO D W, et al. Effects of dynamic stiffness of rotor bearing on rotor dynamic characteristics[J]. Aeroengine, 2008, 34(1): 23-27. DOI:10.3969/j.issn.1672-3147.2008.01.008 (in Chinese) |
| [16] | 马艳红, 何天元, 张大义, 等. 支承刚度非线性转子系统的不平衡响应[J]. 航空动力学报, 2014, 29(7): 1527-1534. MA Y H, HE T Y, ZHANG D Y, et al. Imbalance response of rotor system with nonlinear bearing stiffness[J]. Journal of Aerospace Power, 2014, 29(7): 1527-1534. (in Chinese) |
