无人机导航的状态估计主要使用的是卡尔曼滤波算法[5]。由于无人机的导航系统是一个非线性系统,需要借助非线性滤波算法。目前常用的方法有扩展卡尔曼滤波[6](Extended Kalman Filter,EKF)、无迹卡尔曼滤波(Unscented Kalman Filter,UKF)以及容积卡尔曼滤波(Cubature Kalman Filter,CKF)[7]。其中,EKF是对非线性函数泰勒展开保留一阶项,将其近似为线性函数,再代入标准的卡尔曼滤波算法中,进而完成对非线性系统状态的近似估计。因其具有计算量小、精度高[8]、适应性强的特点,EKF广泛应用于导航系统中[9-12]。已有许多****建立了针对导航的UKF和CKF算法,并对其作出了改进[13-16]。再例如Marina[17]将UKF应用于无人飞行器导航并得到了优于EKF的滤波效果。尽管这些方法对强非线性系统的估计精度高于EKF, 但随之带来的是计算量的显著增加[18],而且在高维系统中不稳定,极易出现滤波发散等问题[19],这在要求快速实时和稳定的导航系统中显得得不偿失。因此,实际的飞行器导航系统中,多使用EKF进行数据融合和状态估计[20-22]。
在无人飞行器导航实际过程中,GPS信号不是时刻保持有效的[23]。例如当无人飞行器驶入森林、荒漠等卫星覆盖不全的地区,GPS信号就会出现异常。此外,GPS的接收端也可能出现短期的故障。由于GPS发生临时中断,导航滤波估计将偏离真实的飞行状态,且当导航系统由故障状态变为正常状态时,基本的EKF算法不能及时作出响应,恢复到正常的滤波状态。也就是说,EKF缺乏对突变状态的快速响应能力。具体的原因是:当系统逐渐进入稳定状态时,滤波的最佳增益矩阵将趋于最小值。在这时,若系统发生突变,滤波器的增益矩阵不会因为残差的增大而增大,也就是说,滤波器丧失了对突变状态的跟踪能力。当系统从突变状态快速趋于稳态时,滤波器的增益矩阵也不会快速的减小。从这个意义上来说,EKF类滤波器是一种开环滤波器。
针对上述问题,本文将强跟踪扩展卡尔曼滤波(STEKF)算法运用到无人飞行器导航系统中,目的是当GPS信号中断又恢复后,导航系统能快速地回到稳态,重新完成对无人飞行器状态的有效估计。针对STEKF在导航系统中应用的弊端,本文对原有的STEKF作出了改进,引入了模糊理论的思想,利用隶属度函数来实现EKF和STEKF的优势互补。
1 标准离散扩展卡尔曼滤波模型 导航系统是一个有时间间断的离散系统,因此这里只讨论离散的扩展卡尔曼滤波流程。设随机的离散非线性系统模型为
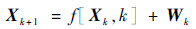 | (1) |
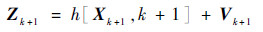 | (2) |
式中:Wk和Vk+1均为彼此不相关的零均值白噪声序列,它们与初始状态不相关, 且
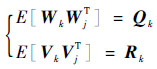 | (3) |
式中:Qk为状态模型噪声协方差阵;Rk为量测模型噪声协方差阵。
在最优滤波值
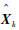
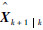
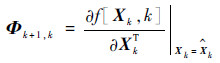 | (4) |
 | (5) |
状态一步预测为
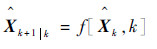 | (6) |
一步预测均方差为
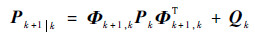 | (7) |
滤波增益为
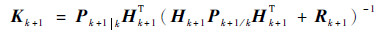 | (8) |
状态估计为
 | (9) |
估计均方差为
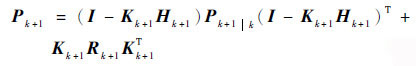 | (10) |
2 针对导航的模糊强跟踪扩展卡尔曼滤波器 2.1 强跟踪滤波器 为了解决导航中存在的GPS信号中断的问题,本文引入强跟踪滤波的思想,将其与标准的扩展卡尔曼滤波结合。使系统在GPS中断恢复后,能够快速地进入稳态。
2.2 含次优渐消因子的扩展卡尔曼滤波器 为了使滤波器具有较强的跟踪性能,一个想法是采用一个随时间变化的因子对过去的数据进行渐消,衰减老数据对当前滤波预测的影响。这可以通过更改协方差阵进而更改增益矩阵来实现。具体做法是,在EKF模型中,对协方差预测矩阵公式:
 |
将其改为
 | (11) |
式中:ωk+1为随时间变化的渐消因子,下面是渐消因子的求取方法:
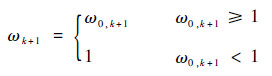 | (12) |
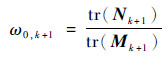 | (13) |
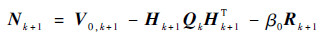 | (14) |
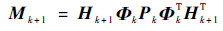 | (15) |
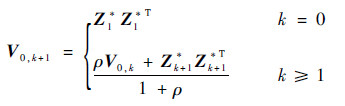 | (16) |
式中:ρ为遗忘因子,一般取ρ=0.95;β0为弱化次优因子,β0≥1。
 | (17) |
2.3 模糊强跟踪扩展卡尔曼滤波器 具有强跟踪特性的扩展卡尔曼滤波器的确有对突变的快速响应能力,但这是以牺牲一定的滤波精度为代价的。因为标准的EKF是在满足最小方差准则的基础上来确定最佳增益矩阵的,如式(7)。而含渐消因子的EKF则对式(7)中的Pk+1k取值做了修改,如式(11)所示,这样计算的最佳增益矩阵Kk+1不满足卡尔曼滤波的基本原则,其精度就有所下降。应用于无人机导航中,以牺牲整体的导航精度换取局部的快速响应,显得得不偿失。
针对此,本文提出一种改进的STEKF算法,目的是在保证滤波精度的同时,提高系统应对快速突变的能力。
改进算法的主体思想是调整协方差预测式(11)中的渐消因子ωk+1。在2.2节的STEKF算法中,无论系统是否发生突变,均采取固定的渐消因子。这样在系统稳定状态时(大部分时候),STEKF具有较低的精度。而本文的改进算法里,将通过比较系统估计残差和期望的关系,来确定最终的渐消因子。
计算当前残差偏离期望残差的比值为
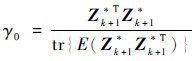 | (18) |
式中:
 | (19) |
E(Zk+1*Zk+1*T)为残差的期望,表达式为
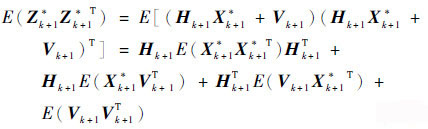 | (20) |
注意到,E(Xk+1*Vk+1T)=E(Vk+1Xk+1*T)=0,E(Xk+1*Xk+1*T)=Pk+1k,E(Vk+1Vk+1T)=Rk+1。所以有
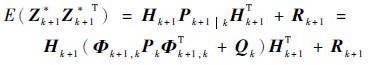 | (21) |
在求得γ0后,令γ1=max{γmin, γ0},γmin>1为临界残差参数,当γ1≤γmin时认为残差较小,GPS量测未发生中断。
设隶属度函数g(γ1)为
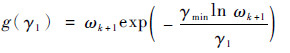 | (22) |
式中:ωk+1为2.2节由标准STEKF算法求得的渐消因子。
则将协方差预测公式(11)变为
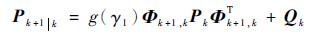 | (23) |
以上就是模糊强跟踪扩展卡尔曼滤波的基本模型。
直观地看,当计算出的残差与期望之比γ0小于门限值γmin时,可以认为此时的估计残差在允许范围内,系统的量测(GPS量测值)未发生突变,此时
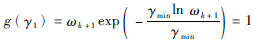
改进算法的优点在于借助了模糊理论中的隶属度函数,对于EKF和STEKF, 没有完全的抛弃一种算法而采用另一种。而是将两者的优势互补。大多数情况下,当系统稳定,GPS量测正常时,更多地借助EKF保证滤波精度,当GPS信号发生故障后,更多地借助STEKF。
为了证明提出的模糊强跟踪扩展卡尔曼滤波能够对系统状态做出有效估计,提出如下假设和定理。
假设1?系统状态模型正确,且由式(6)~式(10)构成的标准扩展卡尔曼滤波器的实际误差均方阵存在有限上界。
定理1?对于由式(6)~式(10)、式(12)~式(17)和式(22)~式(23)构成的模糊强跟踪扩展卡尔曼滤波器,若上述假设成立,改进算法实际的估计误差均方阵为
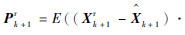
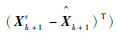
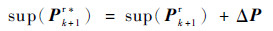 | (24) |
式中:Xk+1r为真实状态;Pk+1r为标准卡尔曼滤波算法的实际误差均方阵;ΔP为改进算法式(23)额外引入的误差均方阵;上标r代表实际误差均方阵。
证明 ?当模型正确时,真实估计误差均方阵为
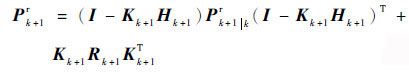 | (25) |
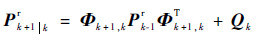 | (26) |
由于模糊渐消函数g(γ1)的存在,式(26)中的滤波增益将产生偏差,Kk+1*=Kk+1+ΔK,且由所设计的模糊规则可知ΔK有界。由于ΔK实际均方差也将偏离原始值:
 | (27) |
将式(25)代入式(27),并注意到
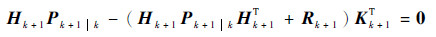 |
因此有
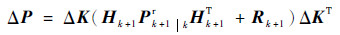 | (28) |
因为ΔK有界,且Pk+1kr和Rk+1为正定矩阵,所以ΔP存在有限上界。????证毕
由上述定理可知,随着迭代过程,本文的模糊强跟踪扩展卡尔曼滤波器的误差将收敛于有限值。
3 仿真实验 本文以无人机INS/GPS组合导航系统来仿真研究本文所提滤波算法的稳定性与适应性。
3.1 无人机导航运动学模型 定义系统的状态向量为
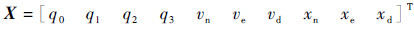 | (29) |
式中:q0、q1、q2和q3为无人机当前时刻的姿态四元数;Vn、Ve和Vd为无人机在导航(地球)坐标系下的速度;xn、xe和xd为相应的位置。
确定状态方程为
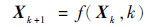 | (30) |
导航状态更新方程包括速度、未知项和姿态3方面,其中姿态更新方程为
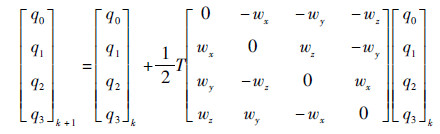 | (31) |
式中:wx、wy和wz 为陀螺仪传感器在当前时刻的读数;T为传感器的采集周期。
相应地,速度更新方程为
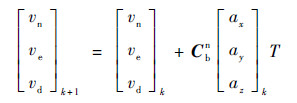 | (32) |
式中:ax、ay和az为加速度计读数;Cbn为载体坐标系向导航坐标系坐标变换的方向余弦矩阵,Cbn=(Cnb)T。
设运载体的航向角为ψ,俯仰角为θ,滚转角为γ,则有
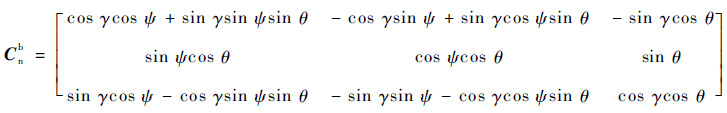 | (33) |
位置更新方程为
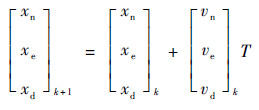 | (34) |
最后,确定系统的观测方程为
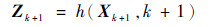 | (35) |
导航系统采用的是INS—GPS组合导航系统,将GPS的量测信息作为系统的观测向量:
 | (36) |
可见系统观测信息就是状态位置信息,则系统观测方程可以写成
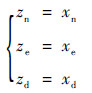 | (37) |
3.2 滤波参数设计 需要注意的是,滤波的效果受2个初值和2个矩阵参数影响,在经过多次调试后,并且为了对比不同滤波方法的性能,本文对不同滤波方法都采用相同的初值和参数。具体取值为
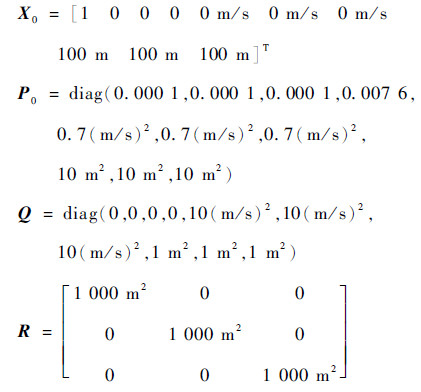 |
用英达软件实现仿真,时间采样周期T=0.02 s。总时长为40 s。仿真过程中GPS量测始终有效,仿真结果如图 1所示。
 |
| 图 1 3种滤波算法结果(东向) Fig. 1 Results of three filtering algorithms (east) |
| 图选项 |
图 1中,将本文改进STEKF算法与文献[24]中的ASTKF算法做对比(文献[24]提出了自适应强跟踪卡尔曼滤波(ASTKF),并将其运用于位置估计中),本文提出的基于模糊理论的强跟踪扩展卡尔曼滤波器能够对飞行状态做出有效估计,且具有较低的跟踪误差,在整个仿真时间内稳定。
下面定量地分析3种滤波算法的精度,导航滤波精度的指标是估计误差的均方根值:
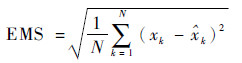 | (38) |
式中:N为仿真采样点数,N=2 000;xk和
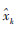
计算出无人机北向、东向、地向的位置误差EMSn、EMSe、EMSd后,则导航滤波误差指标可以表示为
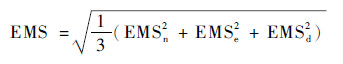 | (39) |
计算得出3种滤波算法的误差如表 1所示。
表 1 3种滤波算法的精度 Table 1 Accuracy of three filtering algorithms
| 算法 | 估计误差均方根值/m |
| EKF | 6.35 |
| ASTKF [24] | 7.54 |
| 本文改进的STEKF | 5.99 |
表选项
可见,相较于文献[24]中ASTKF算法以牺牲一定滤波精度换取强跟踪效果,本文改进的STEKF算法具有更高的滤波精度(甚至优于普通的EKF算法)。
3.3 GPS中断响应测试 给GPS信号人为地加入持续时间为4 s的故障(仿真开始后的10~14 s),在这4 s内,GPS的量测值清零。这段时间内,无人机仅借助惯性导航而进行位置姿态估计,随着时间的推移将产生累计误差。GPS故障解除后,无人机重新利用GPS信号来进行定位,误差会逐渐减小。为了观察系统的恢复情况。比较了不同滤波算法对GPS信号突变的快速响应能力。
图 2为GPS发生中断后,仿真得到的滤波估计轨迹与理论飞行轨迹的路线,可见在GPS故障的这段时间,滤波轨迹发生了偏移。
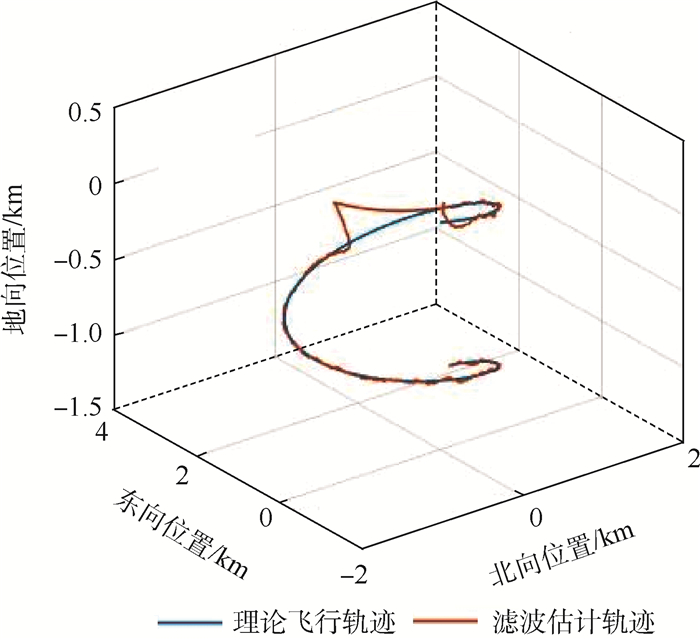 |
| 图 2 飞行轨迹变化 Fig. 2 Flight path variation |
| 图选项 |
图 3为3种滤波算法在北向、东向和地向上滤波误差。可见,在14 s时GPS信号回复到正常后,本文改进的STEKF的滤波算法和[24]文献中ASTKF算法误差能够快速地收敛至零,而普通EKF的滤波则会出现较大幅度的振荡,至少需要3 s左右的时间才能完成对位置的准确估计。
 |
| 图 3 3种滤波算法在北向、东向和地向误差变化 Fig. 3 North, east and ground direction error variation |
| 图选项 |
可以利用估计残差对滤波是否收敛进行检测[4], 根据式(31),认为当估计残差与期望残差之比γ0始终小于3时滤波收敛且进入稳定状态。从GPS中断结束到滤波进入稳态的这段时间,称之为收敛时间。通过仿真,得到不同滤波算法的收敛时间如表 2所示。
表 2 3种滤波算法针对GPS中断收敛速度 Table 2 Convergence speed of three filtering algorithms for GPS interruption
| 算法 | GPS中断恢复后收敛速度/s |
| EKF | 3.84 |
| ASTKF [24] | 0.38 |
| 本文改进的STEKF | 0.25 |
表选项
可见,改进算法相较于普通的EKF算法极大地减小了导航过程中GPS中断恢复后的收敛时间。
综合3.2节和3.3节,可见本文提出的基于模糊理论的强跟踪扩展卡尔曼滤波器在能够快速追踪GPS量测信号的同时,比[24]文献中ASTKF算法具有更高的滤波精度。
4 结论 针对导航系统中存在这GPS信号中断丢失的问题,本文利用模糊理论中的隶属度函数,对基本的强跟踪扩展卡尔曼滤波器作出了改进,主要结论如下:
1) 本文将强跟踪扩展卡尔曼滤波(STEKF)运用到了无人机导航系统中,并对其作出了改进。
2) 改进STEKF算法能够在GPS信号恢复后迅速地进入稳态(0.25 s),而不是逐渐地收敛。
3) 改进STEKF算法保证了导航滤波精度,误差小于普通的EKF算法和[24]文献中的ASTKF算法。
参考文献
| [1] | 李子月, 张林, 陈善秋, 等. 捷联惯性/卫星超紧组合导航技术综述与展望[J]. 系统工程与电子技术, 2016, 38(4): 866-874. LI Z Y, ZHANG L, CHEN S Q, et al. Ultra-tightly coupled SINS/GLASS navigation technology review and prospect[J]. Systems Engineering and Electronics, 2016, 38(4): 866-874. (in Chinese) |
| [2] | 樊云鹏, 杨锁昌. GNSS/INS深组合导航关键技术研究[J]. 飞航导弹, 2017(10): 22-25. FAN Y P, YANG S C. Research on key technologies of GNSS/INS deep integrated navigation[J]. Aerodynamic Missile Journal, 2017(10): 22-25. (in Chinese) |
| [3] | 韩乃龙.高动态惯性/卫星组合导航技术研究[D].南京: 南京理工大学, 2017. HAN N L.Research on high dynamic inertial/satellite integrated navigation technology[D].Nanjing: Nanjing University of Science and Technology, 2017(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10288-1017053559.htm |
| [4] | 王辰熙.多旋翼无人机组合导航技术研究[D].南京: 南京航空航天大学, 2017. WANG C X.Research on integrated navigation technology for multi-rotor unmanned aerial vehicle[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2017(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10287-1017875103.htm |
| [5] | KALMAN R E. A new approach to linear filtering and prediction problems[J]. Journal of Basic Engineering Transactions, 1960, 82(1): 35-45. DOI:10.1115/1.3662552 |
| [6] | BUCY R. Nonlinear filtering theory[J]. IEEE Transactions on Automatic Control, 1965, 10(2): 198. DOI:10.1109/TAC.1965.1098109 |
| [7] | JULIER S, UHLMANN J, DURRANTWHYTE H F. A new method for the nonlinear transformation of means and covariances in filters and estimators[J]. IEEE Transactions on Automatic Control, 2000, 45(3): 477-482. DOI:10.1109/9.847726 |
| [8] | 景丽.基于卡尔曼滤波组合导航算法的计算量与精度分析[D].哈尔滨: 哈尔滨工业大学, 2014. JING L.Analysis of calculation and precision based on Kalman filter combined navigation algorithm[D].Harbin: Harbin Insti-tute of Technology, 2014(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10213-1015979797.htm |
| [9] | PERSSON S M, SHARF I.Invariant momentum-tracking Kalman filter for attitude estimation[C]//2012 IEEE International Conference on Robotics and Automation.Piscataway, NJ: IEEE Press, 2012: 592-598. |
| [10] | TAYLOR C N.An analysis of observability-constrained Kalman filtering for vision-aided navigation[C]//Position Location and Navigation Symposium.Piscataway, NJ: IEEE Press, 2012: 1240-1246. |
| [11] | JIANG Z, ZHOU W, LI H, et al. A new kind of accurate calibration method for robotic kinematic parameters based on the extended Kalman and particle filter algorithm[J]. IEEE Transactions on Industrial Electronics, 2018, 65(4): 3337-3345. DOI:10.1109/TIE.2017.2748058 |
| [12] | DAVARI N, GHOLAMI A. An asynchronous adaptive direct Kalman filter algorithm to improve underwater navigation system performance[J]. IEEE Sensors Journal, 2017, 17(4): 1061-1068. DOI:10.1109/JSEN.2016.2637402 |
| [13] | 李兆铭, 杨文革, 丁丹, 等. 多星对合作目标的分布式协同导航滤波算法[J]. 北京航空航天大学学报, 2018, 44(3): 462-469. LI Z M, YANG W G, DING D, et al. Distributed cooperative navigation filtering algorithm for multi-satellite cooperative targets[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(3): 462-469. (in Chinese) |
| [14] | SUN F, TANG L. Augmented and non-augmented cubature Kalman filter[J]. Journal of Information & Computational Science, 2012, 9(2): 437-450. |
| [15] | 赵曦晶, 刘光斌, 汪立新, 等. 五阶容积卡尔曼滤波算法及其应用[J]. 红外与激光工程, 2015, 44(4): 1377-1381. ZHAO X J, LIU G B, WANG L X, et al. Fifth-order volume Kalman filter algorithm and its application[J]. Infrared and Laser Engineering, 2015, 44(4): 1377-1381. DOI:10.3969/j.issn.1007-2276.2015.04.046 (in Chinese) |
| [16] | 刘旭, 张其善, 杨东凯. 一种用于GPS/DR组合定位的非线性滤波算法[J]. 北京航空航天大学学报, 2007, 33(2): 184-187. LIU X, ZHANG Q S, YANG D K. A nonlinear filtering algorithm for GPS/DR combined positioning[J]. Journal of Beijing University of Aeronautics and Astronantics, 2007, 33(2): 184-187. DOI:10.3969/j.issn.1001-5965.2007.02.013 (in Chinese) |
| [17] | MARINA H G D. UAV attitude estimation using unscented Kalman filter and TRIAD[J]. IEEE Transactions on Industrial Electronics, 2012, 59(11): 4465-4474. DOI:10.1109/TIE.2011.2163913 |
| [18] | GUPTA S D, YU J Y, MALLICK M, et al.Comparison of angle-only filtering algorithms in 3D using EKF, UKF, PF, PFF, and ensemble KF[C]//18th International Conference on Information Fusion.Piscataway, NJ: IEEE Press, 2015: 1649-1656. |
| [19] | CHANG L, HU B, LI A, et al. Transformed unscented Kalman filter[J]. IEEE Transactions on Automatic Control, 2012, 58(1): 252-257. |
| [20] | 薛远奎.小型旋翼无人机姿态融合及导航方法[D].成都: 电子科技大学, 2016. XUE Y K.Attitude fusion and navigation method of small rotorcraft[D].Chengdu: University of Electronic Science and Technology of China, 2016(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10614-1016176273.htm |
| [21] | 王亭亭, 蔡志浩, 王英勋. 无人机室内视觉/惯导组合导航方法[J]. 北京航空航天大学学报, 2018, 44(1): 176-186. WANG T T, CAI Z H, WANG Y X. Indoor vision/INS integrated navigation method for UAV[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(1): 176-186. (in Chinese) |
| [22] | 钱华明, 王迪, 吴永慧. 小视场星敏感器量测延时滤波算法[J]. 北京航空航天大学学报, 2019, 45(2): 234-242. QIAN H M, WANG D, WU Y H. Delayed filtering algorithm for small field of view star sensor measurement[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(2): 234-242. (in Chinese) |
| [23] | 王尔申, 贾超颖, 曲萍萍, 等. 基于混沌粒子群优化的北斗/GPS组合导航选星算法[J]. 北京航空航天大学学报, 2019, 45(2): 259-265. WANG E S, JIA C Y, QU P P, et al. Beidou/GPS integrated navigation star selection algorithm based on chaotic particle swarm optimization[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(2): 259-265. (in Chinese) |
| [24] | LIN C L, CHANG Y M, HUNG C C, et al. Position estimation and smooth tracking with a fuzzy-logic-based adaptive strong tracking Kalman filter for capacitive touch panels[J]. IEEE Transactions on Industrial Electronics, 2015, 62(8): 5097-5108. DOI:10.1109/TIE.2015.2396874 |
