目前,国内外****在航空发动机转子系统动力特性分析和转子-承力结构系统振动特性分析方面进行了诸多研究工作。常见的转子系统振动耦合问题为带中介轴承的双转子系统间的相互激励耦合振动,由于转子具有各自的动力特性,并且在中介轴承处具有复杂横向激振力的交互作用,因此使得双转子系统具有复杂的振动特性。文献[5-9]分别建立了滚动轴承-双转子系统动力学方程,并采用仿真方法求解分析了滚动轴承对转子系统临界转速等动力特性的影响规律。而共用支承-转子结构系统不同于带有中介轴承的双转子系统,在共用承力框架上具有多个轴承支点,分别支承不同转速的转子,因此在振动特性分析中需要进一步考虑承力框架的振动响应特性及其对各个转子振动特性的影响。
文献[10-14]提出了建立航空发动机整机动力学模型的思想和具体方法,考虑转/静子结构之间的振动耦合影响,但仅对转子系统的动力特性进行了计算分析,并未研究承力结构的振动响应。本文针对带有涡轮级间共用承力框架的航空发动机转子系统,提炼出“共用支承-转子”结构系统(RSR system),并建立了动力学方程,对转子系统动力学振动响应耦合特征及其主要力学参数的影响规律进行理论分析和仿真计算。
1 共用支承-转子结构系统振动特征 如图 1所示,典型高推重比涡轴发动机使用涡轮级间共用承力框架支承动力涡轮转子和燃气发生器转子(简称“燃发转子”)的后支点,转子之间存在振动耦合影响。当动力涡轮转子以不同转速旋转时,共用支承结构会产生不同振动响应,即燃气发生器转子后支点位置产生基础振动,会导致燃发转子的临界转速等动力特性发生变化。同样,燃发转子振动对动力涡轮转子产生类似的影响,即2个转子之间存在振动耦合。
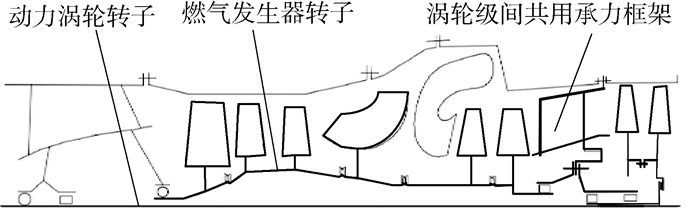 |
| 图 1 高推重比涡轴发动机结构示意图 Fig. 1 Schematic diagram of structure of turbo-shaftengine with high thrust-weight ratio |
| 图选项 |
1.1 振动耦合产生机理 如图 2所示,建立对应的等效动力学模型,其中燃发转子和动力涡轮转子质量分别为m1、m2,燃发转子和动力涡轮转子前后支承刚度分别为k11、k12、k21、k22,并假设转子结构具有横向自由度y1、y2;共用承力框架质量为m3,转动惯量为J3,假设承力结构具有横向自由度y3和角向自由度θ3,横向支承刚度为k3,角向支承刚度为kθ,支点到共用支承的距离分别为l1、l2。其中,图 2 (a)为转/静子联合的整体等效模型,图 2 (b)为转/静子分离的子结构等效模型。
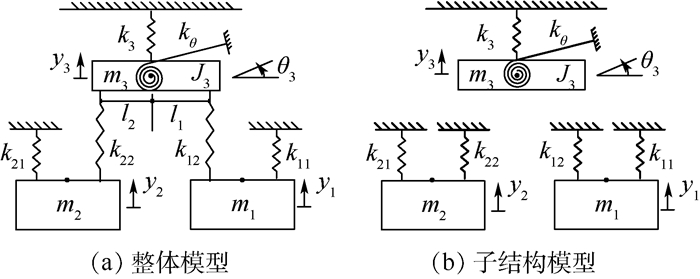 |
| 图 2 考虑共用支承角向自由度的等效动力学模型 Fig. 2 Equivalent dynamic model considering angular degree of shared support |
| 图选项 |
耦合系统动力学方程为
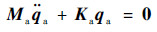 | (1) |
式中:Ma和Ka分别为系统的质量矩阵和刚度矩阵; qa为系统自由度向量。分别表示为
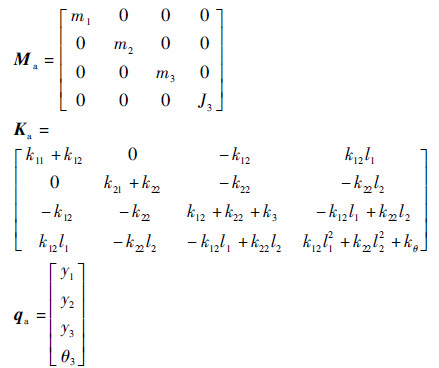 |
对于地面燃气轮机,静子支承刚度和结构质量远大于转子,假设k11=k12=k21=k22=0.01k3,m1=m2=0.01m3,kθ=100k11l12,J3=100m1l12,l1=l2,计算系统的固有频率f1~f4。
耦合模型:
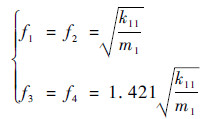 | (2) |
独立模型:
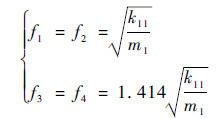 | (3) |
由式(2)和式(3)可知,2种模型计算获得的结果相差很小,固有频率相对误差约为1%。
对于航空发动机,静子支承刚度和结构质量与转子相当,可假设k11=k12=k21=k22=k3,m1=m2=m3,kθ=k11l12,J3=m1l12,l1=l2。
耦合模型:
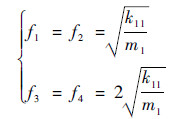 | (4) |
独立模型:
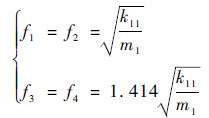 | (5) |
由式(4)和式(5)可知,对于2个转子的固有频率f3和f4,2种模型计算结果相对误差超过40%。
通过上述分析可知,在共用支承-转子结构系统动力特性分析中忽略共用承力框架带来的振动耦合特性影响,将会使计算结果产生较大的误差,需要建立共用支承-转子结构系统动力学模型,才能获得准确的转子系统临界转速和振动响应。
1.2 转子结构系统动力学方程 对于带有共用承力框架的转子结构系统,如图 3所示,建立其动力学模型的基本原理为:使用子结构传递矩阵法[15]分别建立两转子的状态参量方程,并建立共用承力框架在支点动载荷作用下的强迫振动动力学方程,再在支点位置使用平衡方程和协调方程组集转/静子动力学方程,获得共用支承-转子结构系统动力学方程,图中:k6、k7、k8分别为3个支点4#、5#、6#的刚度;M为承力框架质量;m为轴承座质量;下标为M和m的变量分别为对应参数。
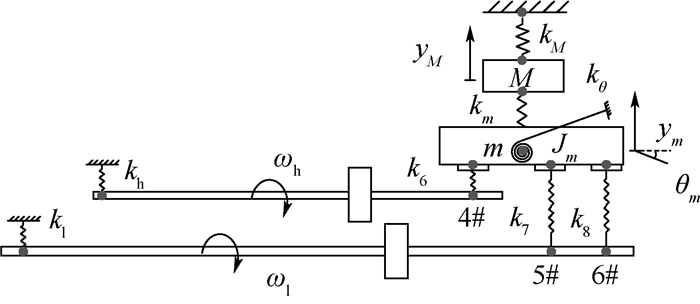 |
| 图 3 共用支承-转子结构系统动力学模型 Fig. 3 Dynamic modeling of RSR system |
| 图选项 |
对于任意两转子结构系统,转子的动力学方程均可写为
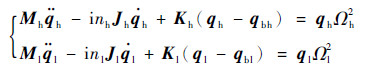 | (6) |
式中:M、J和K分别为转子质量矩阵、陀螺力矩矩阵和刚度矩阵;n为转子转速;qΩ2为转子不平衡激励向量,q为转子状态向量,Ω为转子不平衡量;qb为转子自由度的基础振动;下标h代表燃气发生器转子参数,l代表动力涡轮转子参数。
对于图 3中的动力学模型,假设其各转子前支点均无基础振动,后支点4#、5#、6#上存在基础振动x4s(t)、y4s(t)、x5s(t)、y5s(t)、x6s(t)、y6s(t)。则有
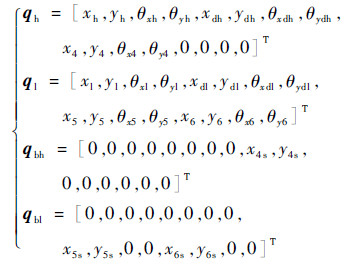 | (7) |
对于共用承力框架,其强迫振动响应动力学方程为
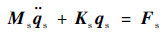 | (8) |
式中:Ms和Ks分别为转子的质量矩阵和刚度矩阵;qs为共用承力框架的自由度向量;Fs为共用承力框架各支点位置的动载荷向量。有
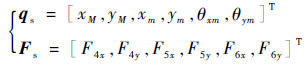 | (9) |
根据4#、5#和6#支点上的平衡方程以及共用承力框架中的位移协调方程:
 | (10) |
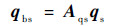 | (11) |
式中:Kb为支点动刚度矩阵;qbs和qbr分别为承力框架和转子结构在4#、5#、6#支点位置的自由度向量;Aqs为承力框架向转子支点位置的自由度变化矩阵。可组集系统振动耦合动力学方程:
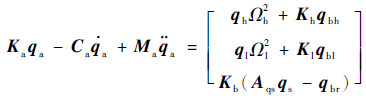 | (12) |
式中:
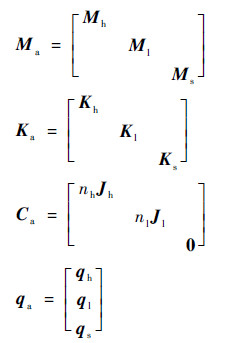 |
将转子支点基础自由度向量向承力框架自由度向量转化:
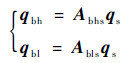 | (13) |
式中:Abhs、Abls均为变换矩阵。可获得共用支承-转子结构系统振动耦合统动力学方程:
 | (14) |
在结构系统中,转/静子结构之间存在刚度耦合项KhAbhs和KlAbls,进而使系统发生振动耦合。
2 共用支承-转子结构系统动力特性耦合影响 在使用涡轮级间共用承力框架的发动机中,转/静子之间存在振动耦合,会影响转子的动力特性,本节将以高推重比涡轴发动机为例,基于有限元仿真方法计算分析转/静子振动耦合对转子系统临界转速和支点动载荷的影响规律。
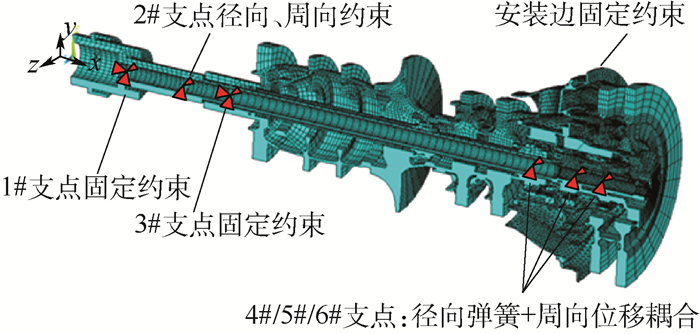
2.1 有限元模型与约束 针对图 1中的涡轴发动机,采用Solid186单元建立共用支承-转子结构系统有限元模型,使用弹簧单元模拟轴承支承,如图 4所示。为避免复杂模型带来的庞大计算量,对结构进行合理简化。忽略连接界面的影响,转/静子连接接触面均采用固结;忽略对整体力学性能影响较小的圆角、小孔等细节因素,提高计算效率。
 |
| 图 4 共用支承-转子结构系统有限元模型 Fig. 4 Finite element model of RSR system |
| 图选项 |
考虑转子系统原有的支承方式,燃发转子和动力涡轮转子前支点(1#和3#)位置弹簧单元的外端进行固定约束,2#支点位置弹簧单元外端施加径向和周向约束。4#、5#、6#支点由涡轮级间共用承力框架支承,使用弹簧单元连接转/静子上的对应节点,并对节点进行周向位移耦合。
2.2 结构系统模态 影响模态、临界转速等固有特性的关键因素主要有2点:转子自身的刚度/质量分布,转子支承的位置和刚度[16]。在带有共用支承结构的转子结构系统中,2个转子通过共用承力框架可发生振动响应的相互影响。通过模态分析计算结构系统的固有频率与相应振型,如图 5~图 7所示。可见,高/低压转子与共用承力框架之间存在振动耦合影响,采用耦合模型计算获得的转子模态频率与单转子模型计算结果有所差异。
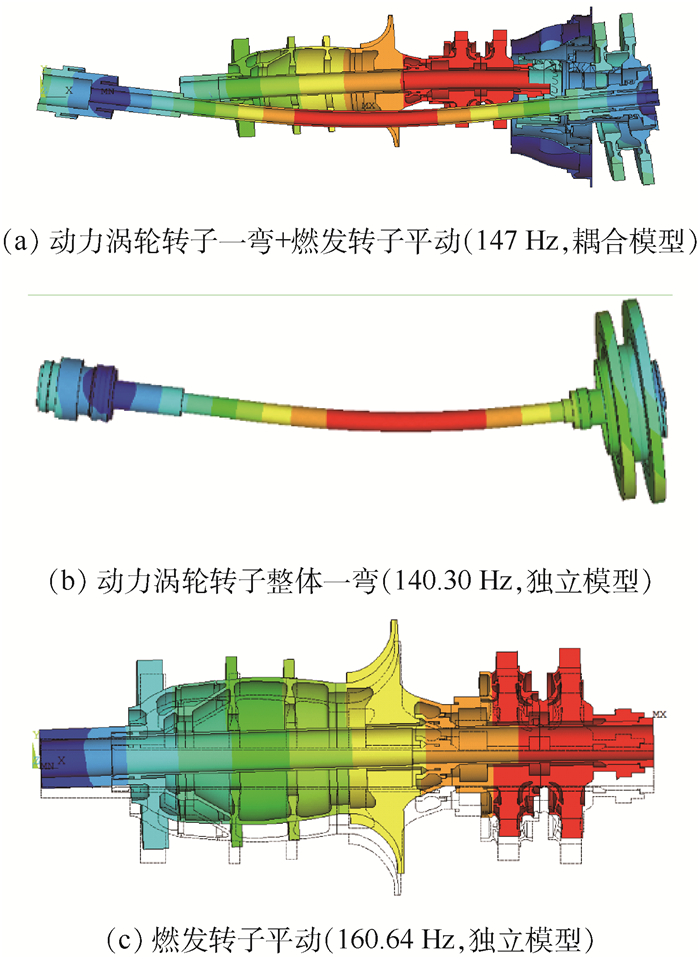 |
| 图 5 共用支承-转子结构系统第1阶耦合模态及其对应的单转子振型 Fig. 5 First-order coupled mode of RSR system and corresponding modes in single-rotor model |
| 图选项 |
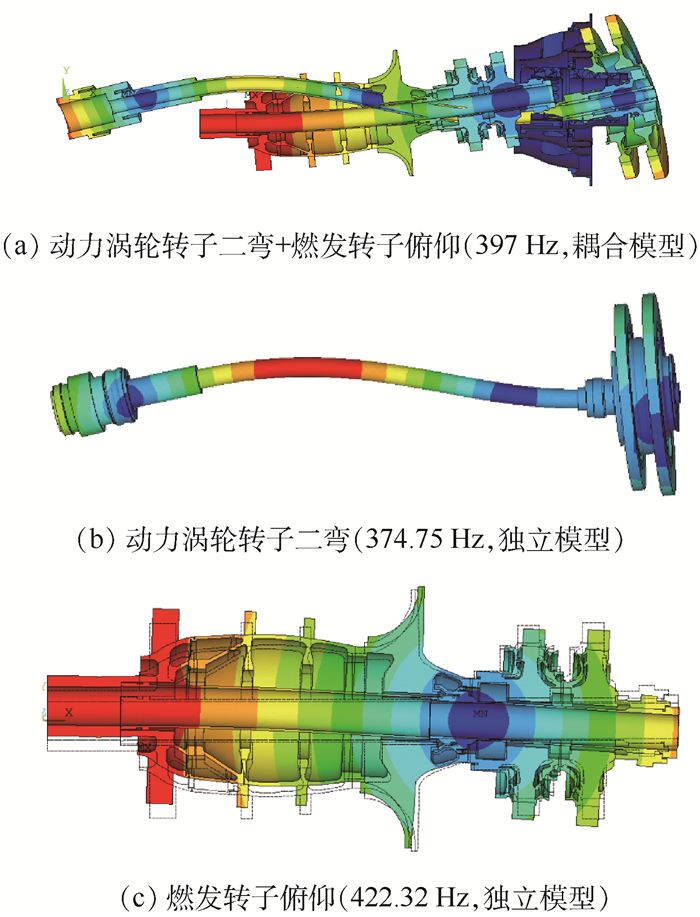 |
| 图 6 共用支承-转子结构系统第2阶耦合模态及其对应的单转子振型 Fig. 6 Second-order coupled mode of RSR system and corresponding modes in single-rotor model |
| 图选项 |
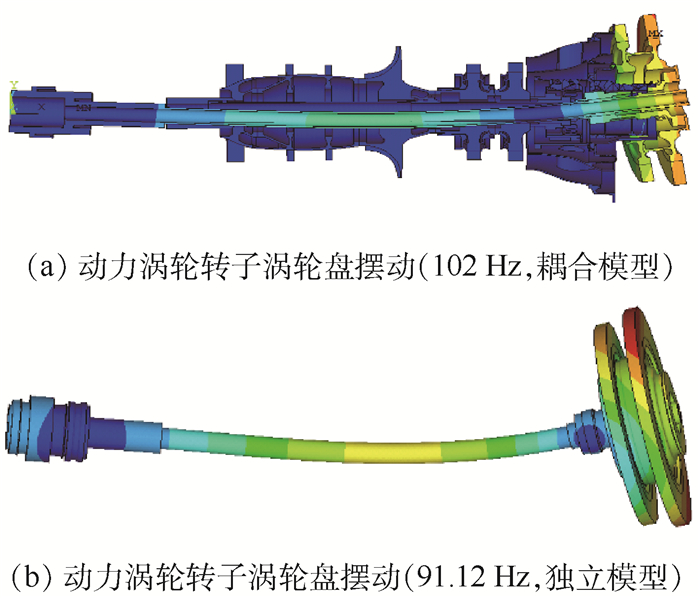 |
| 图 7 共用支承-转子结构系统非耦合模态及其对应的单转子振型 Fig. 7 Non-coupled mode of RSR system and corresponding mode in single-rotor model |
| 图选项 |
当2个转子的模态频率相近时,将在共用支承-转子结构系统中形成新的耦合振型,其模态频率在对应的两转子单独模态频率之间。此外,结构系统中还保留着某些单转子局部模态,但其模态频率相对于单转子模型中计算获得模态频率发生变化。
2.3 结构系统临界转速 由于存在共用承力框架,结构系统的各阶模态可以分别被2个转子单独激起,因此需要考虑某一转子激起的临界转速受另一转子转速变化的影响。以燃气发生器转子为例,确定其临界转速计算的基本步骤为:①给定动力涡轮转子转速nl和燃发转子转速nh;②固定动力涡轮转速,改变燃发转子转速nh,计算不同转速下的系统固有模态并绘制Campbell图,获得在动力涡轮转子转速为nl时燃发转子激起系统共振的临界转速;③改变nl,重复步骤②,计算不同动力涡轮转子转速下的燃发转子激起系统共振的临界转速。同理可计算动力涡轮转子激起系统共振的临界转速。结果如图 8所示。
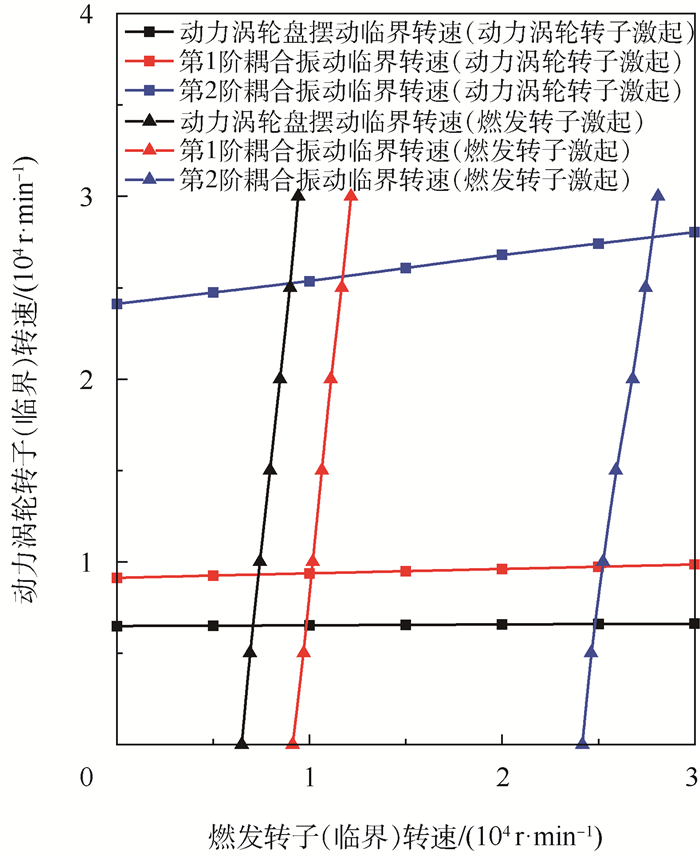 |
| 图 8 共用支承-转子结构系统临界转速 Fig. 8 Critical speed of RSR system |
| 图选项 |
转子系统临界转速取决于转子自身刚度和支点的支承刚度,不同转速下陀螺力矩发生变化进而改变转子自身刚度是转速影响临界转速的主要原因。对于动力涡轮转子激起的动力涡轮盘摆动和系统第1阶耦合振动,燃发转子为平动振型,转子陀螺力矩基本不随转速改变,因此对应的临界转速基本不变;而对于动力涡轮转子激起的第2阶耦合振动,燃发转子为俯仰振型,陀螺力矩受转速影响较大,临界转速变化明显。对于燃发转子激起的各阶共振振型,动力涡轮转子均发生弯曲变形,因此,当动力涡轮转子转速增加时,转子上陀螺力矩增大,转子自身刚度提高,进而导致各阶临界转速均上升。在共用支承-转子结构系统中,当某转子工作转速内存在俯仰或弯曲临界转速时,动力学设计中需要考虑另一转子转速变化对该转子临界转速的影响。
为定量分析振动耦合对共用支承转子系统动力特性的影响,本文引入临界转速敏感系数描述燃发转子激起临界转速随动力涡轮转子转速的变化规律,可表示为
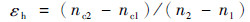 | (15) |
式中:n1、n2分别为计算范围内动力涡轮转子的最小和最大转速; nc1、nc2为相应燃发转子激起的临界转速。
转/静子振动耦合特性受结构系统刚度分布特征影响,因此,临界转速敏感系数应是支点支承刚度的函数。支点支承刚度应是弹性支承结构和承力框架各部件刚度的串联结果,并主要取决于弹性支承的刚度[17],因此,可以在保证承力框架结构特征不变的条件下,仅改变弹性支承刚度(有限元模型中点的弹簧刚度),计算分析燃发转子临界转速敏感系数随4#支点弹性支承刚度的变化规律,结果如图 9所示。随着支承刚度的增加,燃发转子临界转速对动力涡轮转速的敏感度上升。其原因在于,在共用承力框架处振动耦合主要是位移耦合,在共用承力框架振动位移响应相同情况下,支点支承刚度较大时,所产生的动刚度波动幅值更大,对转子-支承系统动力特性影响更为显著。
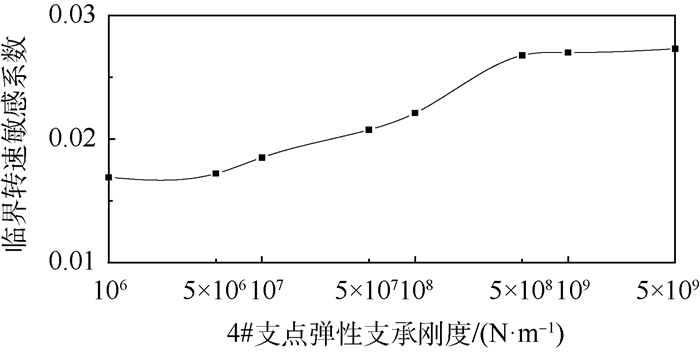 |
| 图 9 燃发转子激起临界转速敏感系数变化曲线 Fig. 9 Variation curve of sensitivity coefficient of critical speed in gas generator rotor |
| 图选项 |
共用支承-转子系统动力特性的耦合影响,还表现为转子-共用支承-转子中任一结构力学特征的改变,会对其他结构动力特性产生影响。同样以4#支点弹性支承刚度变化为例,分析其对结构系统动力特性影响。图 10为燃发转子激起的系统临界转速随4#支点弹性支承刚度的变化曲线。随着支点弹性支承刚度的增加,动力涡轮转子激起的两阶耦合振动临界转速也有所增加。
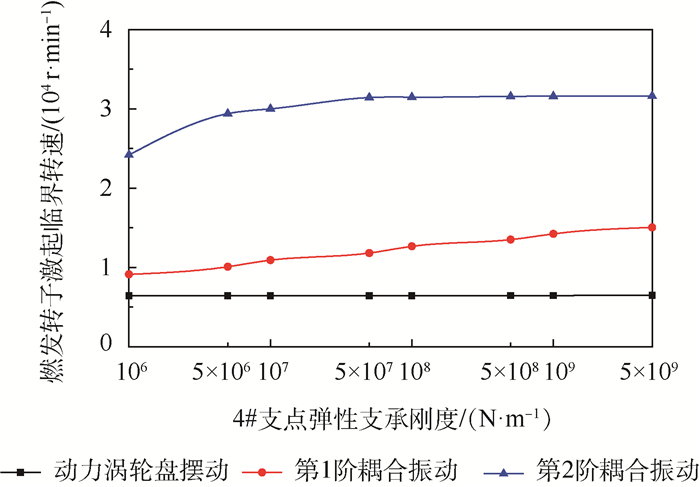 |
| 图 10 支承刚度对临界转速的影响 Fig. 10 Influence of support stiffness to critical speed |
| 图选项 |
在对使用涡轮级间共用承力框架的转子系统进行动力特性分析时,需要考虑转/静子耦合振动的影响。特别是通过调整支承刚度优化转子临界转速时,当转子转速变化时,临界转速以及临界转速对其他转子转速变化的敏感性均会变化。应选取合适的支承刚度,既满足临界转速高于工作转速20%的裕度要求[18],同时对其他转子转速变化敏感度较低。
2.4 支点动载荷 支点动载荷是共用支承-转子结构系统描述转/静子结构间振动耦合的关键参数。在非共振状态,承力框架振动响应主要是支点载荷激励引起,支点载荷增大导致共用支承结构振动水平上升是引起振动耦合的主要原因。支点动载荷频率也是共用支承转子系统重要振动响应特征参数,动载荷大小、频率组成及其占比一定程度可反映不同结构间振动耦合程度。
支点动载荷主要来源于旋转转子不平衡载荷及其陀螺力矩效应。由于制造、装配误差或运行过程中的热变形等因素,转子不可避免地存在不平衡量,转子旋转过程中,不平衡激振力将在支点位置产生动载荷[19]。此外,转子发生弯曲或其上存在陀螺力矩时,支点动载荷将发生变化以平衡转子上的弯矩。
本文计算载荷状态取燃发转子转速50 000 r/min,动力涡轮转子转速30 000 r/min,并在2个转子上分别施加不平衡量,通过有限元仿真计算获得转子系统支点动载荷响应,计算结果如图 11所示。
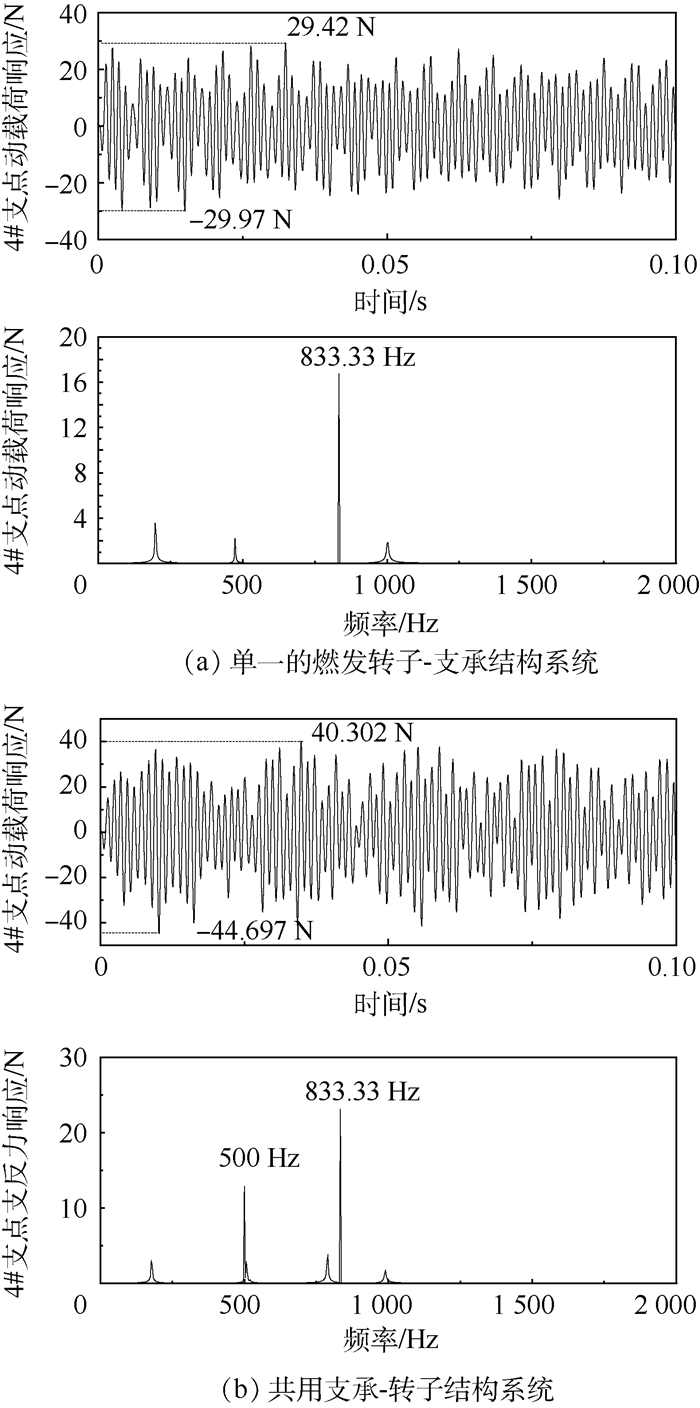 |
| 图 11 不同系统力学模型下支点动载荷响应幅值 Fig. 11 Response amplitude of bearing dynamic load in different mechanical models |
| 图选项 |
在单独的燃发转子-支承结构系统中,动载荷响应频率组成主要为转子自身转速频率(833.33 Hz),计算模型中支点最大载荷值约为30 N。而在共用支承-转子结构系统中,响应频率中除了燃发转子转速频率外,还具有动力涡轮转子转速频率(500 Hz),而支点动载荷最大值可达44.697 N,约为单一转子模型中的1.5倍。分析认为,在共用支承-转子结构系统中,动力涡轮转子不平衡量在5#、6#支点处产生较大的动载荷,并引起共用支承结构的整体振动响应,即在燃发转子后支点处施加基础振动,使得该支点处动载荷响应频率变化,响应幅值增加。
3 共用支承-转子结构振动响应耦合特性 在共用支承-转子结构系统中,振动耦合将同时改变转子动力特性和承力结构振动响应特性。共用承力框架上各支点动刚度、支点之间的机械阻抗、支点到框架安装边的载荷传递系数等振动特性均会发生变化。
3.1 支点动刚度与机械阻抗 引入支点动刚度Ki和支点间机械阻抗Xij:
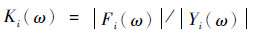 | (16) |
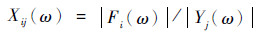 | (17) |
式中:Fi(ω)为第i号支点位置的动载荷,ω为转子角速度; Yi(ω)、Yj(ω)分别为i号、j号支点位置的位移响应。支点动刚度反映了支承结构刚度随转速变化的敏感性[20],支点间机械阻抗反映了共用承力框架各个支点之间的隔振特性。
图 12和图 13分别为采用共用支承-转子结构系统振动耦合模型和单一转子模型时,4#支点动刚度和支点间机械阻抗随激振频率的变化曲线。在共用支承-转子结构系统中,由于各结构间刚度耦合项的存在,提高了支承结构的固有频率以及支点载荷动刚度,增加了共用承力框架的抗变形能力。此外,结构系统中由于考虑了不同子结构固有频率的影响,因此当激振力频率等于承力结构固有频率(达到临界转速,图 12点B、C)或转子结构固有频率(图 12点A)时,共用承力框架均会发生支承刚度突降。
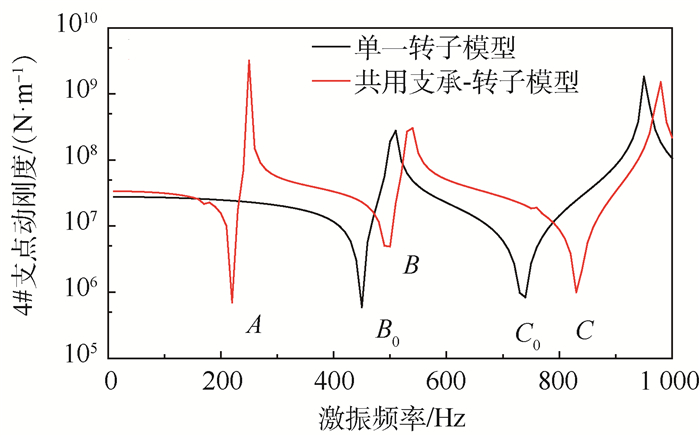 |
| 图 12 不同模型中的支点动刚度曲线 Fig. 12 Curves of dynamic stiffness in different models |
| 图选项 |
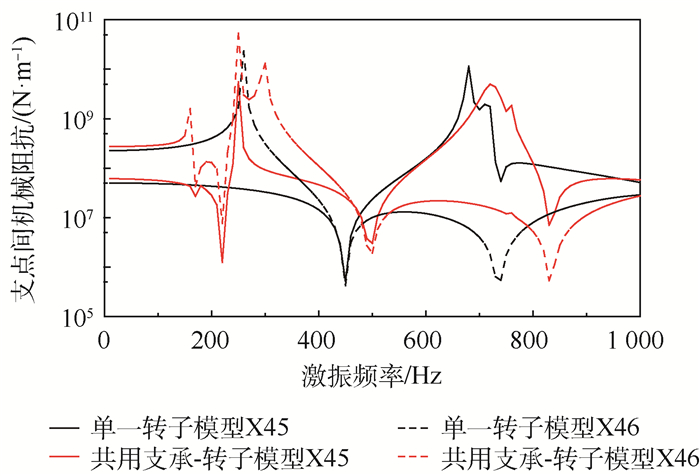 |
| 图 13 不同模型中的机械阻抗曲线 Fig. 13 Curves of mechanical impedance in different models |
| 图选项 |
3.2 载荷传递系数 引入载荷传递系数:
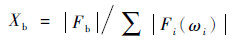 | (18) |
式中:Fi(ωi)为共用承力框架在其所支承的第i号支点位置的动载荷; Fb为承力框架安装边位置的动载荷响应。载荷传递系数反映了转子支点动载荷在共用承力框架中传递特性,若该系数大于1,即表明支点载荷在承力框架中传递时被放大。在动力学设计中,应尽可能降低承力框架的载荷传递系数,增强结构的隔振性[21]。在共用支承-转子结构系统中,由于转子和支承结构的刚度/质量分布特征的影响,使得共用承力框架的载荷传递系数将随转子转速发生变化。
当燃发转子转速为50 000 r/min,动力涡轮转子转速为30 000 r/min时,计算获得共用承力框架在各支点位置和安装边的动载荷响应。再将支点动载荷响应作为激励载荷施加在共用承力框架结构计算模型的相应支点,计算获得安装边动载荷并对比不同模型中框架载荷传递系数,结果如表 1所示。可以发现,考虑转子与支承结构振动耦合特性后,承力框架安装边动载荷和载荷传递系数均会上升。
表 1 动载荷响应与载荷传递系数 Table 1 Dynamics load response and load-transferring coefficient
| 模型 | 支点动载荷幅值/N | 载荷传递系数 | |||
| 4# | 5# | 6# | 安装边 | ||
| 共用支承-转子模型 | 44.69 | 5.98 | 11.73 | 157.11 | 2.52 |
| 单一转子模型 | 44.69 | 5.98 | 11.73 | 107.95 | 1.73 |
表选项
4 结论 本文运用转子动力学理论及仿真计算方法对使用涡轮级间共用承力框架的高推重比涡轴发动机进行转子系统动力特性与承力结构振动特性计算,对共用支承-转子结构系统振动耦合特性进行分析,主要结论如下:
1) 在共用支承转子系统中,2个转子之间存在动力特性的相互影响,主要表现在转子模态热性、弯曲临界转速、临界转速对支点的刚度的敏感度以及支点动载荷等转子动力特性参数均会随其他转子转速变化的改变。共用支承-转子结构模型可以考虑转子与支承结构之间的振动耦合影响,因此使用该模型对共用支承-转子结构系统动力特性进行计算分析更为准确。
2) 由于转子与支承结构之间存在振动耦合特征,各支点位置的动载荷中同时包含2个转子的转速频率,在共用承力结构振动特性设计中需要考虑框架在多点、宽频复杂激励载荷作用下的振动响应特征。依据本文的计算分析结果,支点激振载荷在共用承力框架传递的过程中将发生放大,并且当考虑支承结构之间振动耦合之后,放大效应将进一步增强。因此为保证承力结构安全裕度准确可靠,在其振动特性设计中应采用共用支承-转子结构系统振动耦合模型。
目前,在共用支承-转子结构系统中只分析了转子与共用支承结构振动耦合对转子系统动力特性和共用承力框架振动特性的影响,在工程应用中还需考虑轴承支承阻尼以及在热环境下承力框架对结构系统振动耦合特性的影响。
参考文献
| [1] | SEDA J F. Aircraft engine with inter-turbine engine frame: US6708482[P].2005-04-26. |
| [2] | KUMAR K B, SOMANATH N, SOWA W A.Mid-turbine frame: US8181466[P].2012-05-22. |
| [3] | 马艳红, 曹冲, 李鑫, 等. 涡轴发动机涡轮级间支承结构设计关键技术[J]. 航空发动机, 2014, 40(4): 34-40. MA Y H, CAO C, LI X, et al. Key design technology of mid turbine frame for turbo-shaft engine[J]. Aeroengine, 2014, 40(4): 34-40. (in Chinese) |
| [4] | 洪杰, 马艳红, 张大义. 航空燃气轮机总体结构设计与动力学分析[M]. 北京: 北京航空航天大学出版社, 2014. HONG J, MA Y H, ZHANG D Y. Structare design and dynamic analysis of aviation gas tuwbine[M]. Beijing: Beihang University Press, 2014. (in Chinese) |
| [5] | GUPTA K, GUPTA K D, ATHRE K. Unbalance response of a dual rotor system:Theory and experiment[J]. Journal of Vibration and Acoustics, 1993, 115(4): 427-435. DOI:10.1115/1.2930368 |
| [6] | VILLA C, SINOU J J, THOUVEREZ F. Stability and vibration analysis of a complex flexible rotor bearing system[J]. Communications in Nonlinear Science & Numerical Simulation, 2008, 13(4): 804-821. |
| [7] | CHIANG H W D, HSU C N, TU S H. Rotor-bearing analysis for turbomachinery single-and dual-rotor systems[J]. Journal of Propulsion & Power, 2004, 20(6): 1096-1104. |
| [8] | 邓四二, 付金辉, 王燕霜, 等. 航空发动机滚动轴承-双转子系统动态特性分析[J]. 航空动力学报, 2013, 28(1): 195-204. DENG S E, FU J H, WANG Y S, et al. Analysis on dynamic characteristics of aero-engine rolling bearing/dual-rotor system[J]. Journal of Aerospace Power, 2013, 28(1): 195-204. (in Chinese) |
| [9] | 张大义, 刘烨辉, 梁智超, 等. 航空发动机双转子系统临界转速求解方法[J]. 推进技术, 2015, 36(2): 292-298. ZHANG D Y, LIU Y H, LIANG Z C, et al. Prediction for critical speed of double spools system in aero engines[J]. Journal of Propulsion Technology, 2015, 36(2): 292-298. (in Chinese) |
| [10] | 高金海, 洪杰. 航空发动机整机动力特性建模技术研究[J]. 战术导弹技术, 2006(3): 29-35. GAO J H, HONG J. Study of modeling technique for dynamic characteristics of engine casing[J]. Tactical Missile Technology, 2006(3): 29-35. DOI:10.3969/j.issn.1009-1300.2006.03.007 (in Chinese) |
| [11] | 陈萌, 马艳红, 刘书国, 等. 航空发动机整机有限元模型转子动力学分析[J]. 北京航空航天大学学报, 2007, 33(9): 1013-1016. CHEN M, MA Y H, LIU S G, et al. Rotor-dynamic analysis of whole aero-engine models based on finite element method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(9): 1013-1016. DOI:10.3969/j.issn.1001-5965.2007.09.003 (in Chinese) |
| [12] | 陈果. 双转子航空发动机整机振动建模与分析[J]. 振动工程学报, 2011, 24(6): 619-632. CHEN G. Vibration modeling and analysis for dual-rotor aero-engine[J]. Journal of Vibration Engineering, 2011, 24(6): 619-632. DOI:10.3969/j.issn.1004-4523.2011.06.007 (in Chinese) |
| [13] | 陈果. 航空发动机整机振动耦合动力学模型及其验证[J]. 航空动力学报, 2012, 27(2): 241-254. CHEN G. A coupling dynamic model for whole aero-engine vibration and its verification[J]. Journal of Aerospace Power, 2012, 27(2): 241-254. (in Chinese) |
| [14] | 张大义, 刘烨辉, 洪杰, 等. 航空发动机整机动力学模型建立与振动特性分析[J]. 推进技术, 2015, 36(5): 768-773. ZHANG D Y, LIU Y H, HONG J, et al. Investigation on dynamical modeling and vibration characteristics for aero engine[J]. Journal of Propulsion Technology, 2015, 36(5): 768-773. (in Chinese) |
| [15] | 晏砺堂. 结构系统动力特性分析[M]. 北京: 北京航空航天大学出版社, 1989. YAN L T. Analysis of dynamics characteristics of structural systems[M]. Beijing: Beihang University Press, 1989. (in Chinese) |
| [16] | 顾家柳. 转子动力学[M]. 北京: 国防工业出版社, 1985. GU J L. Rotor dynamics[M]. Beijing: National Defense Industry Press, 1985. (in Chinese) |
| [17] | 洪杰, 王华, 肖大为, 等. 转子支承动刚度对转子动力特性的影响分析[J]. 航空发动机, 2008, 34(1): 23-27. HONG J, WANG H, XIAO D W, et al. Effects of dynamic stiffness of rotor bearing on rotordynamic characteristics[J]. Aeroengine, 2008, 34(1): 23-27. DOI:10.3969/j.issn.1672-3147.2008.01.008 (in Chinese) |
| [18] | 朱梓根. 航空涡轴、涡桨发动机转子系统结构设计准则[M]. 北京: 航空工业出版社, 2000. ZHU Z G. Structure design criteria for rotor system of turbo shaft and turboprop aero-engine[M]. Beijing: Aviation Industry Press, 2000. (in Chinese) |
| [19] | 付才高. 航空发动机设计手册第19册, 转子动力学及整机振动[M]. 北京: 航空工业出版社, 2000. FU C G. Aero-ergine design manual.Volumn 19:Rotor dynamic and vibration[M]. Beijing: Aviation Industry Press, 2000. (in Chinese) |
| [20] | 马艳红, 曹冲, 李鑫, 等. 航空发动机承力系统结构效率评估方法[J]. 航空动力学报, 2016, 31(2): 274-281. MA Y H, CAO C, LI X, et al. Assessment method of structural efficiency on bearing system in aero-engine[J]. Journal of Aerospace Power, 2016, 31(2): 274-281. (in Chinese) |
| [21] | 黄太平. 多转子系统振动的子系统分析方法-阻抗耦合法与分振型综合法[J]. 振动工程学报, 1988, 1(3): 30-40. HUANG T P. Subsystem analysis for multi-rotor system-impedance coupling method and component mode synthesis[J]. Journal of Vibration Engineering, 1988, 1(3): 30-40. (in Chinese) |
