1985年,GPS共视技术正式应用于远距离时间比对[3]。自此以后,国内外****对GNSS共视技术投入了很多精力进行研究,并开展了多次不同基线试验,取得了大量的研究成果[4-7]。由于GNSS共视法的许多试验对试验场地有着十分苛刻的要求,如共视技术长基线试验需要两台接收机相距50 km以上,需要耗费巨大的人力物力。此外,受到天气等各种复杂环境影响,使得试验的可重复性较差。因此,开展GNSS共视信号模拟仿真的研究和测试迫在眉睫,有助于推动GNSS共视接收机算法的研究。GNSS共视信号模拟仿真技术可以在实验室环境中测试不同基线状态下各误差对信号的影响,从而为共视信号接收机的研发与测试提供一个可靠、稳定、准确和易用的仿真环境,以检验其功能和性能指标是否满足研制要求,大大减少了GNSS共视接收机研制测试过程中的成本。
目前,国内外对于卫星导航信号的模拟仿真已经趋于成熟,各类商用软硬件模拟器在科研和工程等领域应用十分广泛。但是,国内外对于GNSS共视信号模拟仿真技术的研究并不完善,可以检索到的相关文献十分稀少,模拟方法和模型设计还在探索之中。本文根据GNSS共视法相关原理,设计了简易可行的基于信道复用方法的GNSS共视信号模拟仿真方法,利用设计的软件进行共视信号仿真和实场测试验证,并对结果进行分析和评估。
1 GNSS共视技术原理 近年来,随着国防和空间技术的发展,对高精度时间传递提出了更高的要求。特别是同步数字体系(Synchronous Digital Hierarchy, SDH)通信网的时间同步,以及空中目标的探测和拦截,对时间传递精度要求达ns量级。在现有的远距离无线时间传递技术中,传递精度较高的方法主要是GNSS共视、GNSS全视(All in View, AV)、双向卫星时间频率比对(Two-Way Satellite Time and Frequency Transfer, TWSTFT)及GPS精确点定位(Precise Point Positioning, PPP)技术等[8]。其中,GNSS共视技术用于测量位于不同地方的2个频率源。与其他时间传递技术相比,共视技术具有设备简单、经济成本低、精度高等优点,并且该方法可应用于具有转发授时信号功能的通信卫星,通信卫星提供授时信号源的同时,也具有广播授时数据的功能[8]。在测量过程中,每个地方各有1个频率源和1台共视接收机。共视接收机测量本地频率源与GNSS信号, 并保存测量结果。经过一段时间的测量后,汇总两地的测量数据, 经数据处理后得到两地频率源的比较结果。
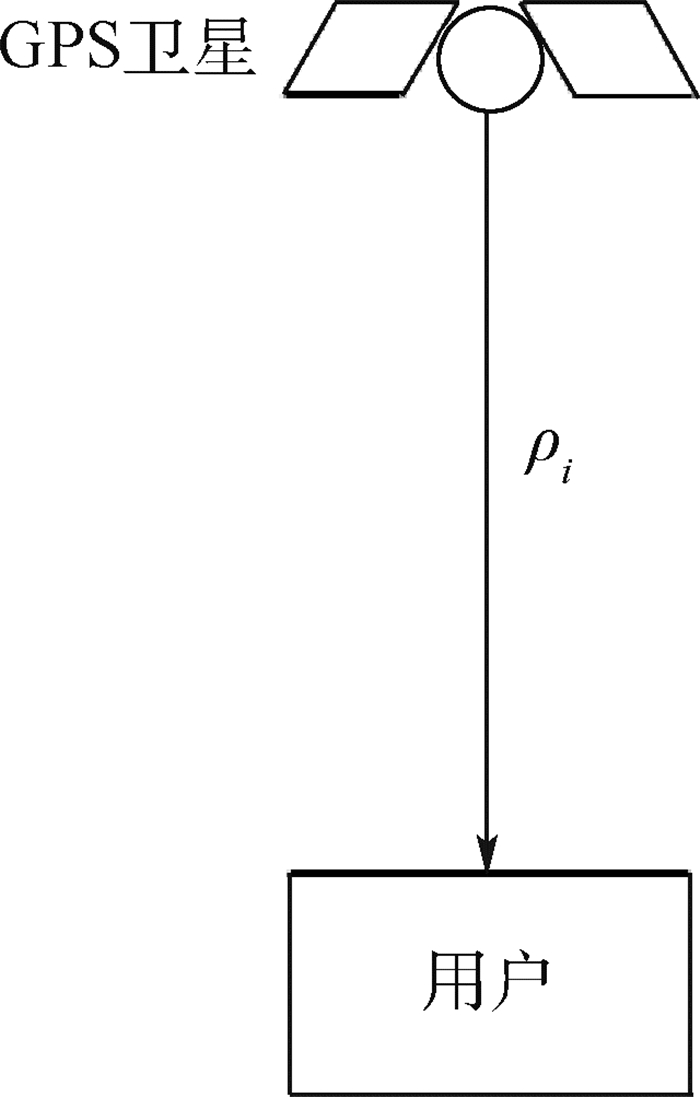
GNSS共视信号是指经由某一颗卫星k发射,两站接收机天线同时接收的两路信号[9],如图 1所示。共视法利用了星钟误差、星历误差、电离层延迟和对流层延迟的空间相关性和时间相关性的特点,对双路输出的信号进行时间比对。星钟误差与用户N到基准站M的距离(基线)无关,可以完全消除。而电离层延迟误差、对流层延迟误差和星历误差与用户N到基准站M的基线长度有关,基线越短,相关性越强,抵消程度越大。从而可消除或部分消除2个接收站之间共有的误差,提高了测量精度。GNSS共视信号可以充分满足零基线、短基线和长基线等条件下比对两地接收站对于授时精度的要求,在国家之间或地域性的时间校正中具有重要的工程应用价值[10]。
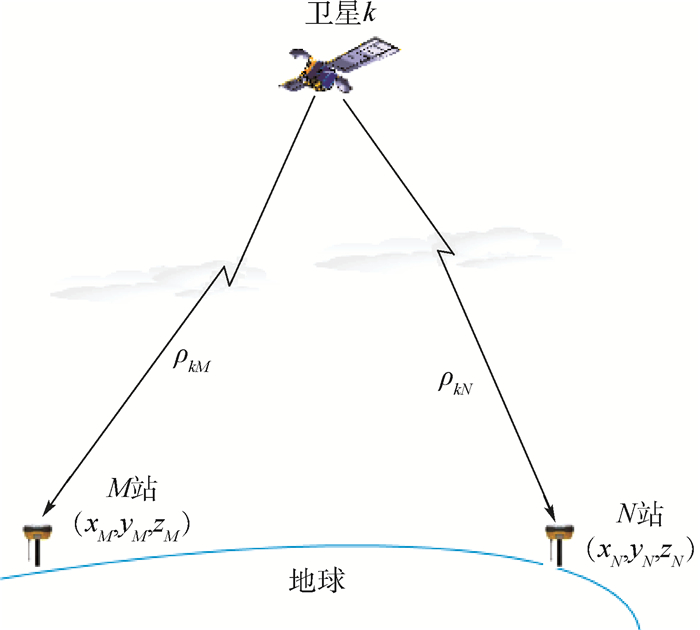 |
| 图 1 GNSS共视信号传播示意图 Fig. 1 Schematic diagram of GNSS CV signal propagation |
| 图选项 |
在时刻t,卫星k到M、N两站的几何距离分别为rkM、rkN,若设卫星k的位置为(x(k), y(k), z(k)), M站接收机位置为(xM, yM, zM),N站接收机位置为(xN, yN, zN),则
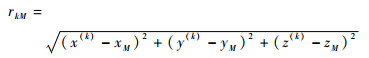 | (1) |
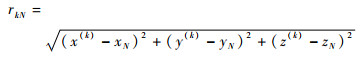 | (2) |
令M、N两站接收机在时刻t观测到卫星k的伪距分别为ρkM和ρkN,那么有
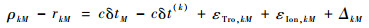 | (3) |
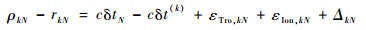 | (4) |
式中:c为光速;δtM和δtN分别为M、N两站的接收机钟差;δt(k)为GNSS系统时间与星钟的偏差;εTro, kM和εTro, kN分别为M、N两站的对流层延迟误差;εIon, kM和εIon, kN分别为M、N两站的电离层延迟误差;ΔkM和ΔkN分别为M、N两站的其他误差。
再对两站观测的结果进行数据通信和计算处理,得到两站接收机时钟的相对偏差为
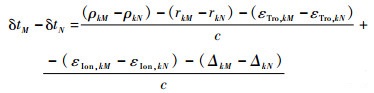 | (5) |
由式(5)容易得出,GNSS共视信号可以完全将系统时间与星钟的偏差δt(k)抵消。当两站距离较短时,GNSS共视信号还可以抵消大部分对流层延迟误差和电离层延迟误差。当两站进行零基线测试时,GNSS共视信号还可以抵消全部对流层延迟误差和电离层延迟误差及其他误差,此时有
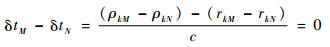 | (6) |
对于GNSS共视接收处理,可以分为3种情况:零基线、短基线和长基线。零基线共钟配置下,信号从卫星到两接收机天线路径中受到传播路径误差的影响相同,两台接收机由相同可见星得到的时差数据的差值反应了系统的性能,其误差主要受两台接收机的内部噪声和时延变化的影响。短基线一般2个共视接收机相距几十公里,相比零基线的情况,信号受空间传播的路径误差影响。长基线则2个共视接收机相距几百公里以上,共视结果受两站钟的影响较大。
2 GNSS共视信号模拟方法设计 2.1 GNSS共视信号模拟 为了对GNSS共视信号进行模拟仿真,必须建立不同基线状态下的GNSS共视信号模型。当前,成熟的软件GNSS直射信号模拟仿真大都基于传统的MATLAB、C/C++语言实现,而GNSS共视信号的模拟仿真则可以在直射信号模拟器的基础上利用信道复用的方法进行实现。
利用GNSS直射信号模拟器来完成GNSS共视信号的模拟仿真,一个很大的不同在于GNSS直射信号模拟器只产生一路信号,在时间传递角度可以作为单向授时,如图 2所示。而模拟GNSS共视信号时,必须仿真产生两路信号,分别到达2个接收机。因此,需要在直射信号模拟器的基础上进行第2路共视信号的信道复用,保证仿真时刻相同,同时模拟仿真出两路信号,分别作为到达接收机M和接收机N的信号,即模拟仿真的共视信号。
 |
| 图 2 单向授时原理示意图 Fig. 2 Schematic diagram of one-way time transfer |
| 图选项 |
在信号产生的过程中,多普勒对卫星信号状态的影响直接反映在延时上,对于载波,已将多普勒加入到频率上,故而在载波表达式上没有在时间上加上延时项。对于数字中频信号,经接收机射频前端(下变频)、滤波、放大之后的模拟中频信号可以表示为[11]
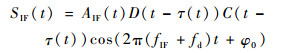 | (7) |
式中:AIF(t)为模拟信号的幅度电平; D(t-τ(t))为调制的导航电文; C(t-τ(t))为伪噪声序列码; τ(t)为伪噪声序列码的信号传播延时; fIF为下变频后的载波频率; fd为多普勒频移; φ0为载波的初始相位。
为满足共视法要求,即要保证信号接收时刻在同一时刻,则再给每个卫星的发射时刻增加一个时间延迟Δt(此Δt可正可负)。则另一路共视信号可以表示为
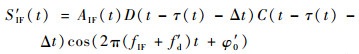 | (8) |
在GNSS共视信号模拟仿真的过程中,首先根据输入参数进行各类导航信息的计算,经过两路通道生成两路信号,在此基础上添加星历误差、电离层延迟、对流层延迟等路径误差,再分别经过采样、量化和编码得到数字中频信号,这样可以送入接收机进行计算处理。GNSS共视信号的模拟仿真流程设计如图 3所示。
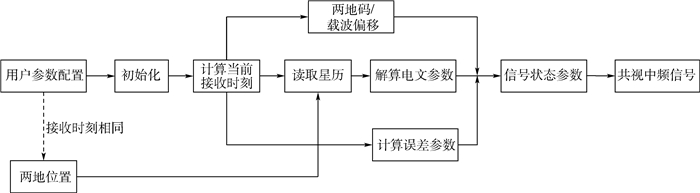 |
| 图 3 GNSS共视信号模拟仿真流程设计框图 Fig. 3 Design block diagram of GNSS CV signal simulation process |
| 图选项 |
2.2 GNSS共视信号误差模拟 对信号传播路径中各类误差的分析和仿真,是信号仿真中必不可少的一部分。GNSS共视法包含星钟误差、星历误差、电离层延迟误差、对流层延迟误差、多普勒频移误差以及相对论效应等误差延迟,具有空间相关性和时间相关性的特点。下面对几种共视场景中常见的误差逐一进行分析。
2.2.1 星钟误差模拟 星钟误差为卫星时钟与GNSS系统时间的差值。卫星钟与GNSS系统时之间的误差控制在1 ms以内。地面监控站对卫星进行监测,测试卫星时钟偏差,用如下二阶多项式对该偏差进行修正[12]:
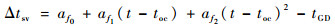 | (9) |
式中:Δtsv为GNSS卫星钟差;toc为由星历文件得到的数据块-1中的参考时间;af0、af1和af2为对应toc时刻的卫星钟校正参数,分别表示时间偏差常值、线性漂移项和老化平方项;tGD为由星历文件得到的群延迟误差。按式(9)修正后,由卫星时钟造成的测距误差小于3 m。
2.2.2 星历误差模拟 卫星轨道近似为圆轨道,计算星历误差可将卫星轨道当作圆轨道处理[13]。在地心地固坐标系下,设t时刻利用广播星历计算的卫星的位置在轨道上点S(xs,ys,zs),卫星的实际位置在S′处,其坐标为(xs′,ys′,zs′)。用户接收机位置坐标为(xu,yu,zu),星历误差引起的用户测距误差与用户位置与有关,可以表示为
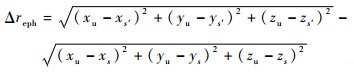 | (10) |
2.2.3 电离层延迟误差模拟 电离层使得无线电波的传播方向、速度、相位、振幅及偏振状态等发生变化。Klobuchar模型[14]是针对地面用户电离层修正而提出的,利用导航电文发布的8个电离层参数αi、βi(i=0, 1, 2, 3)计算电离层延迟误差Δεdion,单位为s。该模型修正精度能达到60%左右。电离层引起的时延误差计算式为
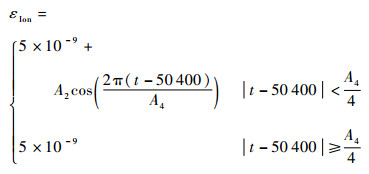 | (11) |
式中:t为接收机至卫星连线与电离层交点处的地方时(取值范围为0~86 400 s);A2为白天电离层延迟余弦曲线的幅度;A4为余弦曲线的周期,单位为s。
2.2.4 对流层延迟误差模拟 从地面向上到40 km为对流层,对流层是非色散介质。对流层延迟一般泛指非电离大气对电磁波的折射,如不修正,对流层在天顶方向的延迟约为2.4 m,仰角为5°时,延迟可达25 m左右。对流层延迟常用Hopfield模型[15]进行计算:
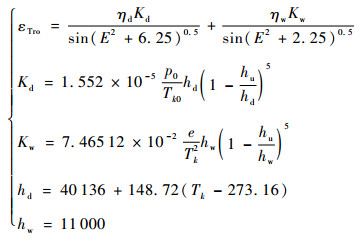 | (12) |
式中:E为卫星相对用户接收机的仰角;ηd和ηw分别为对流层干分量和湿分量修正系数;hu为用户接收机的高度;hd为以海平面为基准的对流层干分量的上限;hw为对流层湿分量上限;e为水气压;p0为测站上大气压力;Tk为测站上的绝对温度;Tk0为标准海平面的绝对温度。
2.2.5 多普勒频移模拟 由于GNSS卫星绕地球运行,接收机与GNSS卫星之间存在着相对运动,使得接收机收到的GNSS卫星信号中存在着多普勒频移[16]。当卫星运行向接收机方向接近时,接收到的频率比发射频率高,这时多普勒频移为负。当卫星运行远离接收机时,接收到的频率比发射频率低,多普勒频移为正。当卫星径向速度为零时,多普勒频移为零。设接收机M的位置坐标点为(xM, yM, zM),接收机N的位置坐标点为(xN, yN, zN)。t时刻卫星的位置为(xs, ys, zs),卫星的速度为(vx, vy, vz),根据卫星与接收机的相对运动,求得多普勒频移fd1、fd2分别为
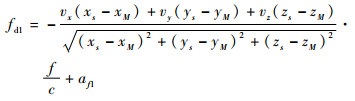 | (13) |
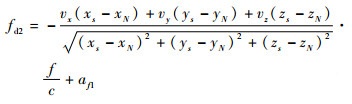 | (14) |
式中:f为载波频率;af1从导航星历电文中得出。
2.2.6 相对论效应误差模拟 由于卫星时钟被安置在高速运动的卫星上,按照爱因斯坦狭义相对论的观点,会产生时间膨胀现象。由于卫星和接收机处于不同的重力势,根据广义相对论观点,同一台时钟放在卫星上和放在地面会产生频差[17]。这2种效应综合起来,使星钟产生的频率偏差Δf=4.449×10-10f。相对论效应引起的时钟偏差为
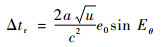 | (15) |
式中:a为卫星椭圆轨道的长半轴; e0为卫星椭圆轨道的偏心率; Eθ为计算历元时刻t的偏近点角,模拟器从星历文件获取该组轨道参数;u为地球引力常量。
3 GNSS共视信号仿真及试验测试 3.1 零基线共视仿真测试 对于零基线的仿真环境,将2个接收机设置为零基线共钟,两地均以UTC(NTSC)标准时间和频率信号为参考输入,同时观测卫星,生成共视信号数据文件。
仿真环境设置接收机1和2的位置均设置为经纬高分别为经度115°E,纬度40°N,高度10 m,频点参数设置为采样频率Fs为16.369 MHz,中频频率IF为3.996 MHz。在各项参数配置完成之后可以开始生成信号状态信息,在仿真软件的对应路径下分别生成共视信号数字中频文件“IF_I_N_1.bin”和“IF_I_N_2.bin”,可以直接由共视接收机进行相关处理。
对产生的共视信号进行定位测试,两路信号的平均定位结果均在39°59′59.993 8″N,114°59′59.885 8″E,高约12.1 m,如图 4所示。每一路信号的处理结果包括东向、北向和天向误差图,二维平面定位结果,以及星空图。定位结果与仿真设置的接收机位置基本一致,定位精度在米级,证明产生的两路共视信号的可靠性。
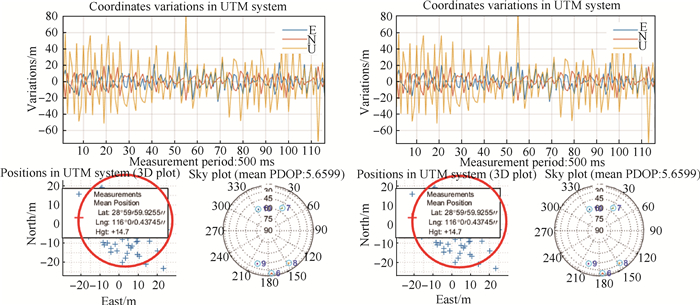 |
| 图 4 零基线两路共视信号处理结果对比 Fig. 4 Comparison of signal processing results between two channels of zero base line |
| 图选项 |
选取产生的共视信号中的8号星进行分析,到达接收机1的直射信号的星历误差为6.938 313,而到达接收机2的星历误差为6.937 971,其差值只有0.000 342,接近于0;对比电离层延迟,到达接收机1的直射信号的电离层延迟为20.038 404,到达接收机2的电离层延迟为20.038 530,差值为0.000 126,也接近于0。同时,两接收机处理得到的星钟误差相同,也证明仿真出的两路共视信号在零基线条件下的正确性。
3.2 短基线共视仿真测试 一般地,短基线的距离范围为两地相距小于50 km。由于经度相差1°,在赤道上距离约为111 km。根据公式:
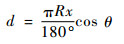 | (16) |
式中:d为基线距离;R为地球半径;x为同一纬度上基线经度差;θ为当地纬度。那么在某纬度线上,经度相差1°的距离差可以求得。
接收机1的位置设置为经纬高分别为经度115°E,纬度40°N,高度10 m;接收机2的经纬高分别为经度115.5°E,纬度40°N,高度10 m,即本次短基线测试将基线设为42.52 km,进行短基线实验。
同样对产生的共视信号进行定位测试,处理结果如图 5所示。
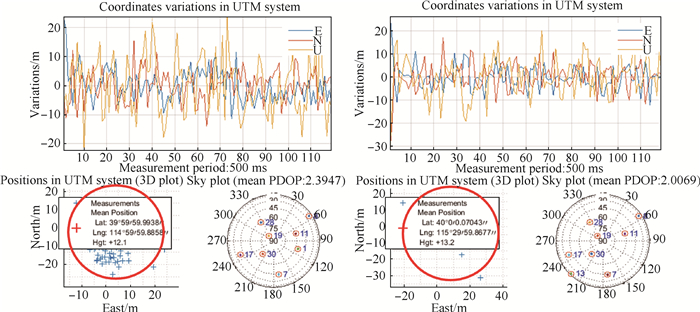 |
| 图 5 短基线两路共视信号处理结果对比 Fig. 5 Comparison of signal processing results between two channels of short base line |
| 图选项 |
1路信号平均定位结果在39°59′59.993 8″N,114°59′59.885 8″E,高约12.1 m。2路信号平均定位结果在40°0′0.070 43″N,115°29′59.867 7″E,高13.2 m附近。定位精度在米级,与仿真条件设置基本吻合。
短基线在同一时间段内两地REFGPS(实际跟踪过程中本地钟与GPS时间之差,以1 ns为单位)测试数据与两地本地卫星钟差差值测试输入如图 6所示。对差值数据求平均可以看出,短基线状态下GNSS共视时间比对测试评估两地本地卫星钟差差值平均值为0.365 ns。而为了进一步验证,可以用均方根值RMS来表示。均方根值也称有效值,对数据进行先平方、再平均、然后开方的计算。均方根值反映的是有效值而不是平均值,其常常具有一定的实际(物理)意义。对于本次测试结果,其RMS精度值为10.74 ns。
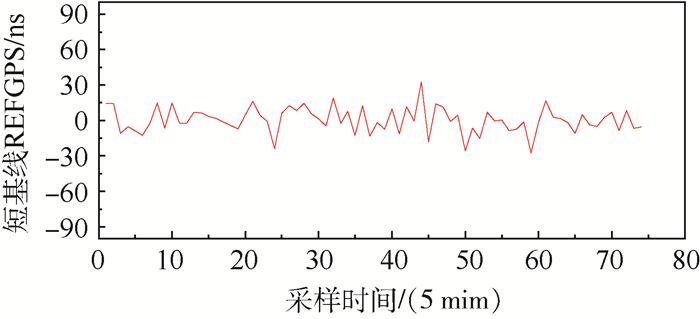 |
| 图 6 短基线两地共视卫星钟差测试对比 Fig. 6 CV clock errors contrast test of short base line between two locations |
| 图选项 |
3.3 长基线共视仿真测试 一般地,长基线的距离范围为两地相距大于50 km,本次长基线仿真测试将基线长度设为1 450 km,比对模拟的共视信号。
接收机1的位置设置为经纬高分别为经度115°E,纬度40°N,高度10 m;接收机2的经纬高分别为经度106°E,纬度30°N,高度20 m,即本次长基线测试将基线长度约为1 450 km,进行长基线实验。
同样对产生的共视信号进行定位测试,处理结果如图 7所示。
 |
| 图 7 长基线两路共视信号处理结果对比 Fig. 7 Comparison of signal processing results between the two channels of long base line |
| 图选项 |
1路信号平均定位结果在40°0′0.053 39″N,114°59′59.833 4″E,高约17.2 m。2路信号平均定位结果在30°0′0.030 64″N,115°59′59.811 3″E,高约26.1 m附近。定位精度在米级,与仿真条件设置基本吻合。
长基线在同一时间段内两地REFGPS测试数据与两地本地卫星钟差差值测试数据如图 8所示,对差值数据求平均可以看出,长基线状态下GNSS共视时间比对测试评估两地本地卫星钟差差值平均值约为4.19 ns,RMS精度值约为12.17 ns。
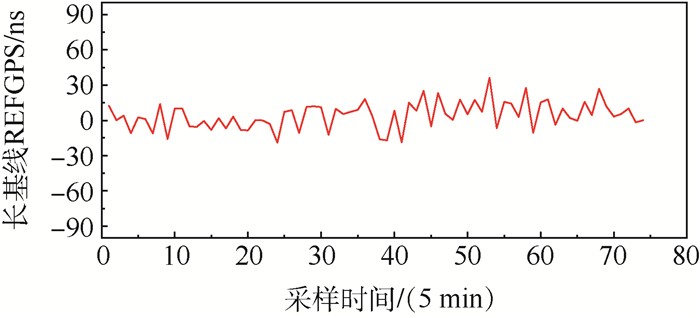 |
| 图 8 长基线两地共视卫星钟差测试对比 Fig. 8 CV clock errors contrast test of long base line between two locations |
| 图选项 |
从3组不同基线共视时间比对结果可以看出:基线越长,共视比对RMS精度值逐渐变差。这也是由于随着基线越长,误差的相关性越弱造成的。
3.4 实场试验测试 为了进一步对设计的GNSS共视信号模拟方法和仿真软件进行验证,进行了一次零基线实场试验。试验场景如图 9所示。
 |
| 图 9 实场试验场景 Fig. 9 Experimental scenario of true environment |
| 图选项 |
实场试验场景位于北京航空航天大学国际学院顶层楼顶,包括天线的架设与授时接收机的时间同步测试,天线视角良好,测试期间可见星数多于10颗,试验通过SR620时间间隔计数器对两台授时型接收机输出的时间信息进行记录并存储。模拟仿真和实测数据结果如图 10所示。其中,模拟仿真数据比对结果两地本地卫星钟差差值平均值约为-0.90 ns,RMS精度值约为10.69 ns。实测结果两地本地卫星钟差差值平均值约为0.79 ns,RMS精度值约为5.11 ns。实测结果与仿真结果一致。
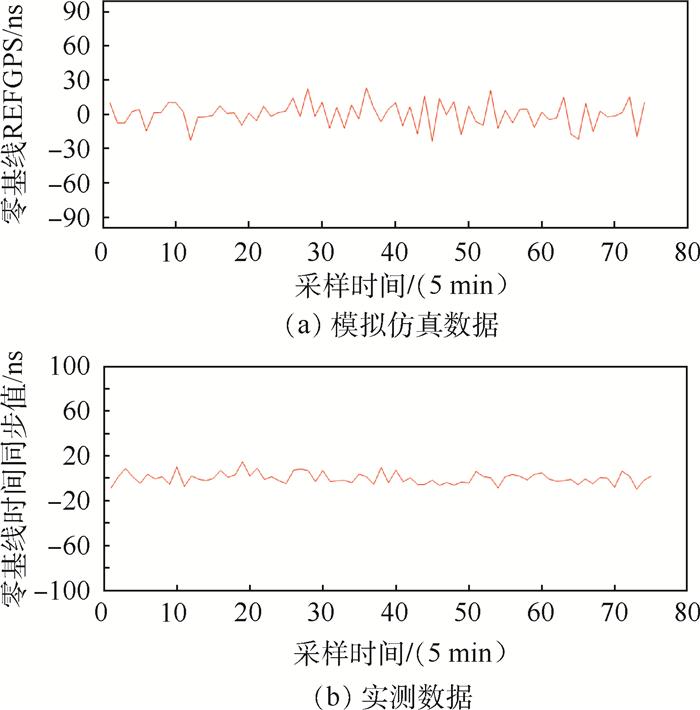 |
| 图 10 模拟仿真和实测数据比对结果 Fig. 10 Comparative result of simulation and experimental data |
| 图选项 |
4 结论 本文在分析GNSS共视技术理论的基础上,基于GNSS直射信号模拟器提出了一种GNSS共视信号模拟方法。根据描述的模拟流程,对不同基线长度进行了仿真测试,并进行了一次零基线实场试验,结果表明:
1) 提出的GNSS共视信号模拟方法基于GNSS直射信号模拟,架构清晰,简单易行。并加入误差的模拟,提高信号模拟精度。模拟的两路共视信号定位精度均达到米级,符合导航信号定位要求。
2) 仿真信号的共视比对结果RMS精度优于12 ns,表明仿真的共视信号符合共视技术要求,可以进行共视法时间传递。
3) 零基线实场数据与仿真数据进行对比,在一定程度上验证了该模拟方法的可行性和有效性;此外,后续考虑进行短基线和长基线的实场实验,对该模拟方法进行进一步的验证。
参考文献
| [1] | ALLAN D, WEISS M.Accurate time and frequency transfer during common-view of a GPS satellite[C]//34th Annual Symposium on Frequency Control.Piscataway, NJ: IEEE Press, 1980: 334-346. |
| [2] | 王彦辉, 秘金钟, 谷守周. 不同基线长度的GPS共视授时算法[J]. 导航定位学报, 2017, 5(4): 41-45. WANG Y H, MI J Z, GU S Z. Algorithm of GPS common-view timing on different baseline lengths[J]. Journal of Navigation Positioning, 2017, 5(4): 41-45. (in Chinese) |
| [3] | DACH R, BEUTLER G, HUGENTOBLER U, et al. Time transfer using GPS carrier phase:Error propagation and results[J]. Journal of Geodesy, 2003, 77(1-2): 1-14. DOI:10.1007/s00190-002-0296-z |
| [4] | 杨旭海.GPS共视时间频率传递应用研究[D].西安: 中国科学院研究生院, 2003: 37-57. YANG X H.Study on the application of time and frequency transfer with GPS common-view[D].Xi'an: Graduate School of Chinese Academy of Sciences, 2003: 37-57(in Chinese). http://xuewen.cnki.net/CDFD-2003112209.nh.html |
| [5] | 许国宏, 韦金辰, 陈国宇. 双星系统高精度共视授时技术[J]. 应用科学, 2007, 34(2): 41-44. XU G H, WEI J C, CHEN G Y. Research on high precision common-view time service of double star systen[J]. Applied Science and Technology, 2007, 34(2): 41-44. (in Chinese) |
| [6] | 高小珣, 高源, 张越, 等. GPS共视法远距离时间频率传递技术研究[J]. 计量科学, 2008, 29(1): 80-83. GAO X X, GAO Y, ZHANG Y, et al. GPS common view method for remote time and frequency transfer[J]. Acta Metrologica Sinica, 2008, 29(1): 80-83. (in Chinese) |
| [7] | 温会锋, 张增强. 基于3σ法的卫星共视时间传递算法设计[J]. 航空计算技术, 2016, 46(3): 98-100. WEN H F, ZHANG Z Q. Satellite common-view time transfer algorithm based on 3σ method[J]. Aeronautical Computing Technique, 2016, 46(3): 98-100. DOI:10.3969/j.issn.1671-654X.2016.03.024 (in Chinese) |
| [8] | 许龙霞.基于共视原理的卫星授时方法[D].西安: 中国科学院大学, 2012: 7-25. XU L X.A new common-view based timing method[D].Xi'an: University of Chinsee Academy of Sciences, 2012: 7-25(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2381502 |
| [9] | 王天.北斗卫星导航系统授时性能评估研究[D].西安: 长安大学, 2014: 15-20. WANG T.Study on the timing performance evaluation of Bei Dou satellite navigation system[D].Xi'an: Chang'an University, 2014: 15-20(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D558111 |
| [10] | 钦伟瑾, 葛玉龙, 韦沛.基于共视模式的GEO载波相位时间传递精度评估[C]//第九届中国卫星导航学术年会, 2018: 73-77. QIN W J, GE Y L, WEI P.Evaluation on precision of GEO time transfer of CV-based[C]//The 9th China Satellite Navigation Conference, 2018: 73-77(in Chinese). |
| [11] | 杨东凯, 张其善. GNSS反射信号处理基础与实践[M]. 北京: 电子工业出版社, 2012. YANG D K, ZHANG Q S. GNSS reflected signal processing:Fundamentals and applications[M]. Beijing: Publishing House of Electronics Industry, 2012. (in Chinese) |
| [12] | ARINC Research Coporation.Navstar GPS spacesegment/navigation user interfaces(Public release version C): ICD-GPS-200[R].Segundo: ARINC Research Coporation, 1993. |
| [13] | 赵军祥.高动态智能GPS卫星信号模拟器软件数学模型研究[D].北京: 北京航空航天大学, 2003. ZHAO J X.The study on mathematical model of high dynamic and intelligent GPS Satellite signal simulator's software[D].Beijing: Beihang University, 2003(in Chinese). |
| [14] | KLOBUCHAR J A.Design and characteristics of the GPS ionospheric time delay algorithm for single frequency users[C]//PLAN'S 86-Position Location & Navigation Symposium.Piscataway, NJ: IEEE Press, 1986: 280-286. |
| [15] | HOPFIELD H S. Tropospheric effect on electromagnetically measured range:Prediction from surface weather data[J]. Radio Science, 2016, 6(3): 357-367. |
| [16] | PíRIZ R, PEIRó B, MERINO M.The Galileo constellation design: A systematic approach[C]//Proceedings of the 18th International Technical Meeting of the Satellite Division of the Institute of Navigation.Manassas: ION, 2005, 1296: 1306. |
| [17] | ROULSTON A, TALBOT N, ZHANG K.An evaluation of various GPS satellite ephemerides[C]//Proceedings of International Technical Meeting of the Institute of Navigation, 2000. |
