随着计算机硬件的发展和网络结构的优化，卷积神经网络(CNN)已成为计算机视觉识别领域的主要学习方法。从最初的LeNet-5^[1]到在ImageNet竞赛^[2]上表现优异的AlexNet^[3]、VGGNet^[4]、GoogleNet^[5]和ResNet^[6]等，各种性能优异的模型被提出并成功应用于计算机视觉领域，例如图像分类^[7]、目标检测^[8]、目标跟踪^[9]以及视频分类^[10]等。
近年来，****提出三输入通道的卷积神经网络模型(三生网络模型)^[11-12]，这种模型通过一种新的三生损失(triplet loss)函数进行度量学习，现已广泛应用于多个领域，例如人脸识别^[13]、场景分类^[14]以及车辆识别^[15]。在高维的嵌入空间中，三生损失能缩短标签相同的样本的间距，并且增大标签不同的样本的间距。与其他单输入通道的深度卷积模型相比^[3-6]，三生网络模型^[11-12]学习到的个体级别上的细粒度特征会更为出色。三生损失与传统的归一化指数损失(softmax loss)相比有两点优势:一是如果类别中只有极少数样本可用于训练，三生损失的效果会比归一化指数损失更好^[12]；二是如果标签数量非常大，则在批量大小相同的情况下，与归一化指数损失相连的全连接层会占用大量的GPU内存，而三生损失只占用较少的内存。
虽然三生网络的优势显而易见，但还面临着收敛慢、难收敛等挑战。Hermans等^[15]认为并不是所有的训练样本都有利于网络训练泛化能力，故给出了挑战性样本(hard samples)的采样方法，选择与原点样本距离最远的正样本和距离最近的负样本作为训练样本，提高网络学习能力。在车辆识别领域，Liu等^[16]认为单一网络结构不足以识别同一车型的不同车辆，提出了一个多任务分支模型来识别车辆，一个网络分支判断车辆是否是同一型号，另一个网络分支识别车辆的实际特征，综合所有情况得到结果。Cheng等^[17]将多通道网络与三生网络结合，学习分析人体部分特征，从而进行任务识别。Zhang等^[18]认为原点样本与正样本的地位相同，在同一三元组样本内，正负样本位置可以互换，意味着正样本也需要远离负样本。Chen等^[19]考虑到同类样本之间距离方差较大，提出了四生网络，在三生损失中加入了限制类内方差的约束项。
除了改进三生损失函数或者优化采样的方法，优化嵌入网络(如图 1所标识的网络)也能提高整体网络性能。Simonyan和Zisserman^[4]用小尺寸卷积核代替大尺寸卷积核，减少了参数量，提高了网络拟合能力，达到了很好的效果。Szegedy等^[5]考虑到网络层数增加会导致参数的增加，提出了Inception网络结构来增加网络的宽度，获取多尺度的特征信息。Huang等^[20]提出一种密集型卷积神经网络，每个卷积层的输入结合了来自前面所有卷积层的输出，鼓励重复使用特征，并且大幅地减少了参数数量。****们普遍认为，网络层数变多，容量变大，前向网络可以表示任何函数。但是随着网络深度增加，网络训练难度增大，网络准确率也降低，网络性能无法提升。He等^[6]提出了ResNet来解决网络退化问题，网络层数达到152层甚至更高。

图 1 三生网络 Fig. 1 Triplet network

图选项

传统神经网络模型目的是将网络训练成一个映射函数，而ResNet将网络训练成残差函数F(x)=H(x)-x，其中x表示输入，H(x)表示输出。相对直接学习原始特征来说，训练残差函数更加简单。目前构建深层网络的方法，一种是通过对浅层网络添加恒等映射层，就能保证网络的深度且不会发生退化，但网络性能无法提高，这与构造深层网络的目的相背。另一种是将网络训练成残差函数，这样也能满足网络深度的要求。即使某一网络层所表示的残差函数F(x)=0 (该网络层做恒等映射)，保证网络准确率不会变低。在实际网络训练学习中，F(x)不会置为0，网络层能够在输入信息中持续且容易地学习到新的特征。所以在残差学习的网络中，在输出F(x)中加入输入特征x，得到H(x)作为下一网络层的输入，解决了因网络加深导致测试误差变大的问题，同时还能保证网络能够进行端对端的训练。
在三生网络中，网络的性能与很多因素相关，首先是如何使用大规模数据有效地训练三生网络模型。例如，某数据库共有M个标签，每个标签有N个样本，共会产生约M²N³个三元组样本，这其中包含大量无效的训练样本，这样的三元组样本会使损失函数变成0，无法进行权重更新，对网络训练没有帮助，花费大量时间成本。所以需要先对训练样本进行筛选，得到合适的三元组样本。然后是嵌入网络的设计，提高神经网络提取特征的能力需要合理构建网络。设计新的网络拓扑结构^{[5-6, 21-22]}，适当增加网络深度，再结合激活函数(Relu)、Dropout^[3]以及批标准化(BN)^[23]等方法，能够减少网络参数量，加强网络泛化能力，提高网络训练速度。
本文首先介绍三生网络结构，并提出了新的三元组预处理方法；然后，介绍改进的损失函数与训练方法；最后，进行实验结果分析和总结。
1 三生网络结构 传统的卷积神经网络通过堆叠网络层(conv)，构建一个深层的架构来提高效果，但网络加深后，层数过多不一定会取得更好的效果，有时反而会导致梯度消失或梯度爆炸，从而引起网络退化的问题。原因在于浅层的网络可以获得学习和更新，而深层的网络几乎没有任何变化，或者深层的网络更新调整太大，使网络无法收敛。一种解决的方法就是在浅层网络上继续添加恒等映射，能保证网络拥有足够深的结构而且不会产生比浅层网络更高的训练误差，但这样的方式并不能保证提高网络的效果。为了加深网络深度、提高网络性能，本文提出了一种新的基于残差学习的三生网络结构。
在残差学习中，H(x)是将每个块(block)的输入x映射成下一个block的输入的函数，训练block去学习H(x)和x的残差，记为F(x)=H(x)-x。block可以明确地表示残差函数F(x)，前一个block输出的特征F(x)与输入的特征x相加后进入到下一个block中作为新的输入。F(x)和H(x)两种函数都能逐渐逼近想要学习的函数，但学习的难易程度有所不同，而且随着网络加深，H(x)容易出现梯度弥散或爆炸的情况。残差学习的目的是忽略主体，突显微小的变化，使网络对输出的变化更敏感。例如：设输入为x=P，输出为H(x)=Q，则残差为

(1)

当输出H(x)的变化量为ε时，H(x)的变化率为，同时F(x)的变化量也是ε，F(x)的变化率为。当Q-P趋于零时，F(x)的变化率将大大高过H(x)的变化率。在网络中输出的变化大多都是细微的，这就能保证Q-P足够小，能够突出微小的变化，因此残差学习对调整网络权重的效果更好。
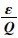
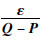
本文设计构建了一个21层的残差学习网络作为嵌入网络，结构如图 2所示。首先将图像x通过如图 2(c)所示的深度卷积神经网络，经过第1个卷积层的卷积操作后，输出特征进入到stage 1，stage 1里包含3个具有相同拓扑结构的block (见图 2(b))。对于由几个卷积层堆叠而成的block，设输入信息为x′，通过block之后得到F(x′)，为了能够让block学习到残差的变化，以一种短路连接(shortcut)的方法，在block的输出F(x′)中加上输入特征信息x′，由此实现了残差学习的结构。若特征F(x′)与x′的维度是匹配的，则直接相加得到y=F(x′)+x′，若维度不匹配，应采用如下计算方式：

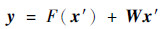(2)

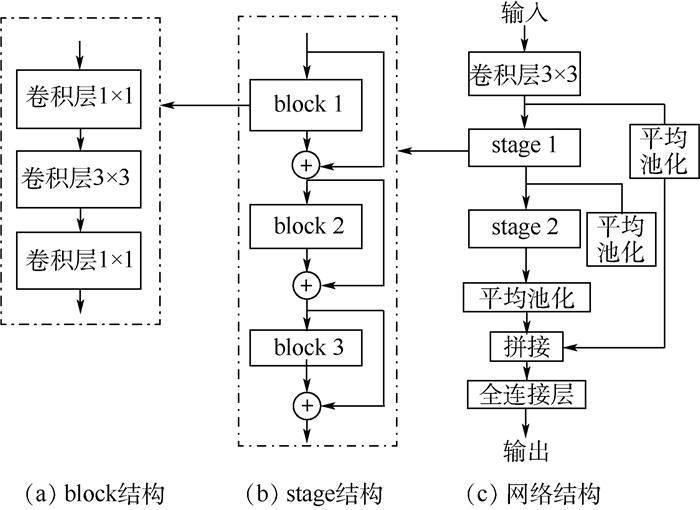图 2 嵌入网络结构 Fig. 2 Embedded network structure

图选项

式中：W为1×1的卷积操作，目的是将x′的维度调整至与F(x′)相同。
如图 2(a)所示，本文网络中每一个block由3个卷积层组成，因为1×1的卷积层可以实现跨通道的信息交互和整合，加强网络模型的表达能力，所以用第1个和第3个1×1的卷积层进行特征信息通道数的维度处理，先提高维度，再降低维度，降低了计算量。第2个卷积层的卷积效果等价于多个并行卷积的卷积层的卷积效果，在ResNeXt^[22]中提到图 3的2种模型是相互等价的。因此本文借助于“分离-变换-合并”的思想，拓宽了网络的宽度，使得特征信息通过升维处理后，进入到各个拓扑结构相同的路径，之后进行聚合变换，最后再通过降维处理进入下一个block。

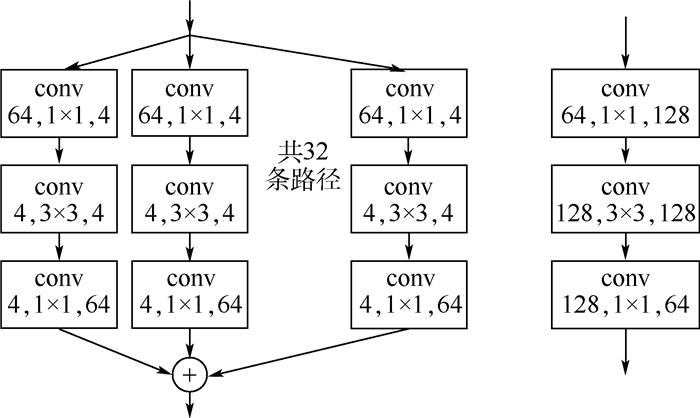图 3 ResNeXt[22]的等价网络结构 Fig. 3 Equivalent network structure of ResNeXt[22]

图选项

本文将第1个3×3的卷积层输出的特征与后2个区输出的特征进行拼接，目的是在全连接层中，最大程度地保留前面主要层的输出信息，将信息特征映射到d维欧氏空间中。本文网络在每一个卷积层后添加批标准化层，把卷积后的每个输出进行标准化，来稳定网络学习，提高训练速度，在第一个3×3的卷积层以及每个block中前2个卷积层后添加激活函数层，防止网络出现梯度消失问题，使网络保持一个稳定收敛的状态。网络配置如表 1所示，表中s为卷积步长，p为边界填充量。
表 1 网络配置 Table 1 Network configuration

区	块	网络层	通道数变化	步长/填充量	池化层
stage1	block1	conv3	3-64	s=1, p=1	avgpool
		conv1	64-512	s=1, p=0
		conv3	512-512	s=2, p=1
		conv1	512-256	s=1, p=0
	block2	conv1	256-512	s=1，p=0
		conv3	512-512	s=1, p=1
		conv1	512-256	s=1, p=0
	block3	conv1	256-512	s=1, p=0
		conv3	512-512	s=1, p=1
		conv1	512-256	s=1, p=0	avgpool
stage2	block1	conv1	256-1 024	s=1, p=0
		conv3	1 024-1 024	s=2，p=1
		conv1	1 024-512	s=1, p=0
	block2	conv1	512-1 024	s=1, p=0
		conv3	1 024-1 024	s=1, p=1
		conv1	1 024-512	s=1, p=0
	block3	conv1	512-1 024	s=1, p=0
		conv3	1 024-1 024	s=1, p=1
		conv1	1 024-512	s=1, p=0	avgpool
		fc-32
注：以32×32RGB图像为例。

表选项






经典的深度卷积网络^[3-6]为了解决多分类问题(n个标签)，固定设置n个输出节点，利用归一化指数损失将神经网络输出层每个节点值变成一个概率值，测试图像x通过前向传播网络，在最后输出层中得到属于各个标签的概率。三生损失函数的目的是让属于同一标签的图像在d维欧氏空间上尽可能地靠近，属于不同标签的图像尽可能地远离，所以在几何层面上，三生网络的输出结果可以理解成投影到d维欧氏空间上的点，各类标签都有各类的聚集区域。标签相同的点的聚集程度高，则说明网络表现优异。
2 基于三生网络的三元组处理 在一个标准的三生网络中(如图 1所示)，输入的3个样本被称为三元组，记作{x_a, x_p, x_n}，其中x_a和x_p分别为原点样本(anchor)和正样本(positive)，二者具有相同的标签；x_n为负样本(negative)，标签与原点样本不同。针对每一个即将输入到网络中的批量，利用上一个批量训练后的网络，获得当前批量的样本x的网络特征表示f(x)，若是初始训练的第1个批量，则利用初始网络来获得f(x)，将f(x)进行d维L₂归一化处理^[24]，满足。三元组通过训练好的网络，其特征表示应满足如下距离不等式：

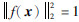
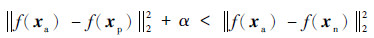(3)

式中：α为间隔常数，表示同类样本间距的最大值与异类样本间距的最小值的差值。若α的值较大，则网络难以收敛；若α的值较小，则网络学习效果较弱，无法区分不同标签样本，本文设定α的值为0.5。
令B表示批量大小，三生损失函数为

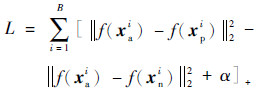(4)

式中:[·]₊表示取正。
显而易见，在所有的三元组训练样本中，存在大量满足式(3)的三元组，称为简单三元组，这些三元组对损失函数没有贡献，因为无效的训练样本导致网络收敛速度变慢，所以需要选择能够提升网络训练的三元组。下面将讨论三元组选择的方法。
为了防止简单三元组对三生网络训练阶段产生干扰，导致网络收敛缓慢，常用的方法是在线挑战性负样本挖掘(OHNM)^{[12, 15]}，旨在选择对训练最有挑战的三元组，抛弃对训练无意义的三元组，避免简单三元组经过网络，节约训练时间。本文提出一种改进的三元组预处理方法，针对大小为B的一个批量，先将批量中的所有训练样本x通过网络后得到B个d维的网络特征表示，定义欧氏距离，计算B个网络特征表示相互之间的距离，再将所有样本x均设为原点样x_a，根据三元组样本的构成，依照原点样本的标签找到与其距离最远的2个正样本x_p和距离最近的2个负样x_n，如图 4所示进行交叉组合，由此可以在线产生4B个三元组。传统的OHNM法只产生B个三元组，而本文改进的方法可以产生数量更多且有效的三元组。本文通过实验，测试选择不同数量的正负样本数量，对比训练时间以及测试效果。由于x_n数量必定远远多于x_p数量，故可以找到距离最近的K(K>2)个负样本x_n，从而扩充有效训练样本量。这种三元组预处理方法可以选择有挑战性的样本使网络加速收敛，且对各类别样本较少的数据集，可以大幅增加有效训练样本，提高网络训练效果。

图 4 三元组选择 Fig. 4 Triplet selection

图选项

3 基于三生网络的损失函数 三生网络是一种通过三生损失函数进行度量学习的模型，使相同标签样本更接近，同时隔开异类标签样本，因此同一标签中的样本可以彼此在d维欧氏空间靠得更近。损失函数的设计决定了其如何指导网络进行训练以及网络性能。经过多次迭代训练后的三生网络，能够将相同标签的样本聚集在d维欧氏空间的某个公共中心点周围，即相同标签的样本应该聚集成簇，而不同标签的样本应该保持相对较远的距离，所以各个标签的样本簇应该有其样本中心点(如图 5所示)。

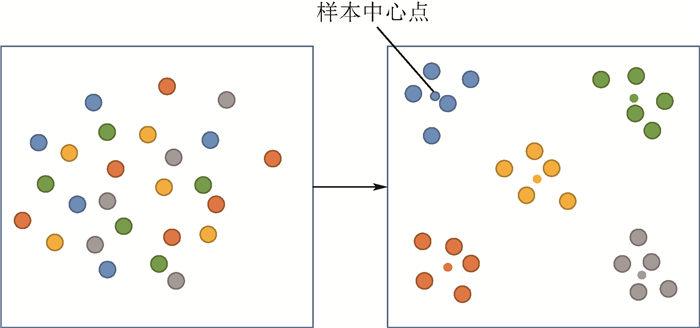图 5 二维欧氏空间样本中心点示例 Fig. 5 2D European space sample center point example

图选项

为了能够进一步促进同类样本聚集且异类样本互斥，考虑在第i次迭代之后，用{c_p, x_p, x_n}代替{x_a, x_p, x_n}作为三元组输入，c_p表示某一标签的样本中心点，即

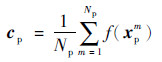式中：N_p为该标签的样本数量，则新的三元组应满足如下距离不等式：

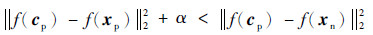记第i次迭代之后的三生损失函数为中心三生损失函数为

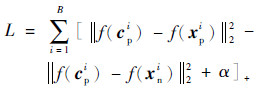这2个不同训练阶段使用的损失函数有着不同的意义，三生损失选择每一个样本作为x_a并搭配x_p和x_n作为输入的三元组，能在训练初始阶段较快地处理位置随机的样本，将相同标签的样本聚集在一起；中心三生损失只选择样本中心点c_p作为原点样本，使聚在一起的同类样本更加靠近c_p，并且排斥异类样本。如果直接使用中心三生损失函数训练网络，得到的特征表示f(x)位置散乱无规律，获得的中心点c_p不具有代表性，会影响网络训练速度，导致收敛缓慢。
4 实验结果与分析 本文实验运行环境：Intel Xeon 2650v4 CPU处理器，Tesla P100 GPU加速卡。本文初始网络使用Kaiming初始化方法，所有的训练均由随机梯度下降法(SGD)完成，固定动量值设定为0.9，权重衰减设定为0.000 5。网络采用学习率逐步衰减的方式，初始学习率设定为0.01，本文网络在迭代50次、150次、225次后，自动将学习率除以10之后继续训练，降低训练损失。本文没有对数据集使用任何数据增强方法。通过网络获得的空间表示向量维数d=32，当d值过低时，全连接层降维幅度过大，容易导致图像信息丢失，影响分类效果；当d值过高时，使得网络参数变多，增加训练和测试时间成本，空间表示向量经过归一化以后，其每一个分量的值变得很小，向量之间的区别度降低，会影响分类效果。此外维度太高会使得二维可视化效果不理想。网络训练结束后，使用嵌入网络对全体训练集提取d维特征之后，计算各类标签的d维样本中心点，再将测试集中的图像通过嵌入网络得到d维向量，计算与各类样本中心点的欧氏距离，距离哪个标签的中心点最近，则测试图像标记成该标签。该验证方法与归一化指数损失的方法不同，前者以距离进行分类预测，后者以概率大小确定预测标签。本文网络与Stochastic Pooling^[25]、Maxout Network^[26]、ResNet^[6]、NIN^[27]、DSN^[28]、CMC^[29]、MLDNN^[30]、DenseNet^[20]、ResNeXt^[22]、AlexNet^[3]、TripletNet^[31]在CIFAR10^[32]、MNIST^[1]和SVHN^[33]3个数据集上比较错误率和计算复杂度。
CIFAR10数据集共有10个标签，包含50 000张尺寸大小为32×32的彩色图像作为训练集和10 000张彩色图像作为验证集。图 6是本文网络与目前性能优异的网络DenseNet-BC^[20]和ResNeXt-29^[22]的训练测试图，网络共迭代310次，每5次测试错误率。ResNeXt选用29层网络层，16×64d的结构达到了3.58%的错误率，这是CIFAR10在无数据增强情况下最好的测试识别效果(如表 2所示)。DenseNet^[20]在同时调用Bottleneck和转化层的情况下(即为DenseNet-BC)达到了5.19%的错误率。本文网络因为在迭代过程中设置自动下调学习率，所以在图 6中可以看到迭代50次后错误率有一次明显的下降。如第3节所述，网络训练后期用{c_p, x_p, x_n}作为三元组输入，目的是让同类标签样本与样本中心点更靠近。在250次迭代训练之后更改样本中心点作为三元组输入，之后每5次迭代训练，重新更新一次各标签样本中心点c_p，所以网络测试错误率能持续降低。本文实验发现，训练后期更改损失函数比不做任何变化情况下，网络在数据集上的错误率能够平均降低0.5%，证明了这种方法是有效的。本文网络与其他网络在CIFAR10数据集的比较如表 2所示，ResNeXt-29系列达到了3.58%的效果，本文网络位列第二，达到了4.28%，DenseNet两个不同版本分别达到了5.19%和5.83%，ResNet达到了6.43%，CMC达到了6.87%，MLDNN达到了8.12%，NIN达到了8.8%，DSN达到了9.69%，AlexNet达到了11%，Maxout Network达到了11.68%，Stochastic Pooling达到了15.13%。值得一提的是，作为三生网络系列中的TripletNet达到了12.90%，本文三生网络错误率比其低了8.62%，因为在网络结构方面，设计了较深的残差学习网络作为嵌入网络，使得三生网络具有很好的特征表示能力；在训练过程中使用正负样本交叉组合采样方法和改变训练的方式，让本文网络在一些数据集上有明显的优势。如表 3所示，在网络学习能力方面，除了ResNet需要迭代60 000次，其余网络均在几百个周期内完成训练，而且本文网络在网络参数较多的情况下，以较少的周期快速完成训练，说明网络的学习能力较强。本文网络结构具有较大规模，所以需要减少网络的计算量，降低计算复杂度。以表 1里stage 1中的block 1为例，第一个卷积层和第3个卷积层的1×1卷积核代替了3×3卷积核，保证其具备升维和降维功能的前提下，网络的计算量由7.5×10⁹次降低至4.0×10⁹次，在时间上减少约47%。

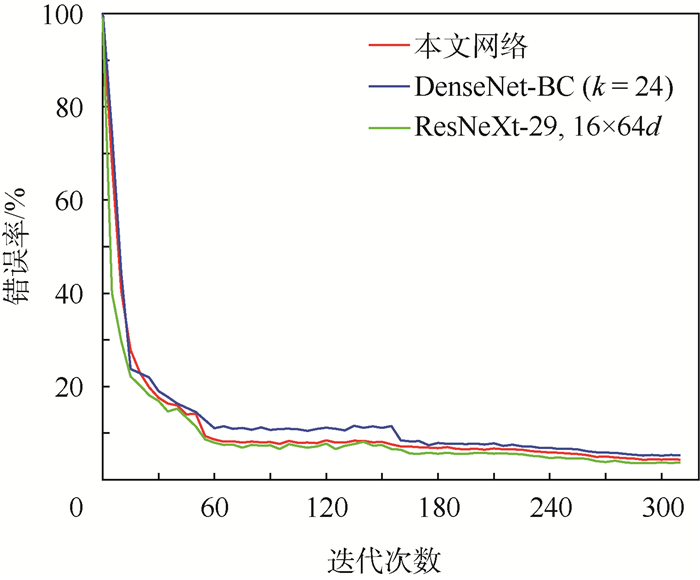图 6 本文网络与DenseNet-BC和ResNeXt-29的CIFAR10测试曲线 Fig. 6 CIFAR10 testing curves of proposed network, DenseNet-BC and ResNeXt-29

图选项

表 2 CIFAR10上的错误率 Table 2 Error rates on CIFAR10

网络	错误率/%
Stochastic Pooling[25]	15.13
TripletNet[31]	12.90
Maxout Network[26]	11.68
AlexNet[3]	11
DSN[28]	9.69
NIN[27]	8.8
MLDNN[30]	8.12
CMC[29]	6.87
ResNet[6]	6.43
DenseNet[20]	5.83
DenseNet-BC[20]	5.19
本文网络	4.28
ResNeXt-29[22]	3.58

表选项






表 3 网络训练迭代次数(CIFAR10) Table 3 Iteration times of network training (CIFAR10)

网络	迭代次数	错误率/%
ResNet[6]	60 000	6.43
Maxout Network[26]	700	11.68
Stochastic Pooling[25]	500	15.13
本文网络	310	4.28
MLDNN[30]	300	8.12
DenseNet-BC[20]	300	5.19
DenseNet[20]	300	5.83
ResNeXt-29[22]	300	3.58
NIN[27]	200	8.8
DSN[28]	110	9.69

表选项






MNIST是手写灰度图像数据集，由60 000张大小为28×28，标签从0到9的训练图像和10 000张测试图像组成。比较结果如表 4所示，可以观察到本文网络要比其他的方法都要好，错误率达到了0.22%，比第2名的CMC要低0.11%，比同属于三生网络的TripletNet要低0.16%。
表 4 MNIST上的错误率 Table 4 Error rates on MNIST

网络	错误率/%
Stochastic Pooling[25]	0.47
Maxout Network[26]	0.47
NIN[27]	0.47
MLDNN[30]	0.42
DSN[28]	0.39
TripletNet[31]	0.38
CMC[29]	0.33
本文网络	0.22

表选项






SVHN数据库与MNIST的相似，由600 000个从Google街景图像中获得32×32彩色门牌图像，标签从0到9。比较结果如表 5所示，最好的结果均来自DenseNet，分别达到了1.59%和1.74%的错误率，第3名CMC达到了1.76%，本文网络仅比CMC低0.05%，达到了1.81%，MLDNN和DSN均达到了1.92%，NIN达到了2.35%，Maxout Network达到了2.67%，Stochastic Pooling达到了2.80%。三生网络TripletNet仅达到了4.63%，本文网络错误率比其低了2.82%。
表 5 SVHN上的错误率 Table 5 Error rates on SVHN

网络	错误率/%
TripletNet[31]	4.63
Stochastic Pooling[25]	2.80
Maxout Network[26]	2.67
NIN[27]	2.35
DSN[28]	1.92
MLDNN[30]	1.92
本文网络	1.81
CMC[29]	1.76
DenseNet-BC[20]	1.74
DenseNet[20]	1.59

表选项






如表 6所示，本文测试4种正负样本组合情况，发现增加有效三元组训练样本，能较为明显地提高网络训练效果，降低错误率。CIFAR10数据集通过4种样本组合方法，有效的三元组训练样本数量分别为5×10⁴、1×10⁵、2×10⁵、3×10⁵，网络训练迭代一次所需的时间如表 6所示，近似等比例增加。本文网络的批量B=50，所以正样本的数量不能过多，避免产生无效的三元组样本，根据GPU的性能，可以适当调节负样本的数量。所以本文三元组预处理方法对样本较少的数据集能增加训练样本以提高网络训练效果。
表 6 样本组合的实验对比(CIFAR10) Table 6 Experimental comparison of sample combination (CIFAR10)

正负样本组合	训练时间/s	错误率/%
1正1负	230	4.74
1正2负	410	4.52
2正2负	750	4.28
2正3负	1190	4.29

表选项






三生损失函数指导网络训练的方式决定了其具有样本聚类的效果，所以在验证数据集时，网络能够将图像映射入d维欧氏空间。本节所示内容已从定量分析角度分析了本文网络的分类效果，下面从定性分析角度认识三生网络的分类效果。
t分布随机邻域嵌入(T-SEN)是一种较为高级的非线性降维算法，基于在领域图上随机游走的概率分布来解释数据内的结构，可以将d维数据映射到2维欧氏空间上实现可视化。本文使用T-SEN将d维特征输出f(x)投影到可视化的二维欧氏空间中，可以通过观察测试集样本二维的分类效果。
图 7为本文网络在CIFAR10数据集上的分类效果，因为本文网络在CIFAR10数据集有4.28%的错误率，所以从图中可以看到，仅有少量样本还无法区分，但已经有明显的整体分布，考虑到数据从d维降至二维，必然会产生一些重叠以及误差，因此从测试样本聚类的角度认为网络分类效果是比较优异的。图 8为本文网络在MNIST数据集上的实验结果，MNIST是手写数字灰度图像，且各标签图像差别明显，所以比较容易训练和测试。在图中聚类效果十分明显，只有极少数的样本被错误分类。图 9为本文网络在SVHN数据集上的实验结果，SVHN是三维彩色数字图像，训练难度比MNIST稍高一点，但训练与测试结果比较优异，在二维可视图中聚类程度高。

图 7 CIFAR10-二维特征表示 Fig. 7 CIFAR10-2D feature representation

图选项

图 8 MNIST-二维特征表示 Fig. 8 MNIST-2D feature representation

图选项

图 9 SVHN-二维特征表示 Fig. 9 SVHN-2D feature representation

图选项

5 结论 1) 本文设计了一个21层的卷积神经网络作为三生网络的嵌入网络。该卷积神经网络连接2个stage，共6个block，利用残差学习的方式，在每个block输出f(x)的基础上加入x防止网络出现退化问题，每个block中采用相同拓扑结构分路的Inception网络结构，最后在全连接层拼接来自第1个卷积层和2个区的输出。
2) 本文提出一个三元组预处理方法，选择与原点样本距离最远的2个正样本和距离最近的2个负样本组成4个三元组作为训练样本，这种正负样本交叉组合可以增加有效的困难训练样本，降低网络训练难度。
3) 在网络训练中，用样本中心点c_p替换原点样本x_a可以让同类样本更加聚集。最后网络在数据集上的训练测试结果显示本文网络对比其他三生网络模型有明显优异的表现，也优于绝大多数基于归一化指数损失的神经网络。
接下来，将利用本文提出的三生网络用于人脸识别、车辆识别等细粒度图像分类的任务。

参考文献

[1]	LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324. DOI:10.1109/5.726791
[2]	RUSSAKOVSKY O, DENG J, SU H, et al. ImageNet large scale visual recognition challenge[J]. International Journal of Computer Vision, 2014, 115(3): 211-252.
[3]	KRIZHEVSKY A, SUTSKEVER I, HINTON G.Imagenet classification with deep convolutional neural networks[C]//International Conference on Neural Information Processing Systems.New York: Curran Associates Inc., 2012: 1097-1105.
[4]	SIMONYAN K, ZISSERMAN A.Very deep convolutional networks for large-scale image recognition[C]//International Conference on Learning Representations, 2015: 1-14.
[5]	SZEGEDY C, LIU W, JIA Y.Going deeper with convolutions[C]//IEEE Conference on Computer Vision and Pattern Recognition.Piscataway, NJ: IEEE Press, 2015: 1-9.
[6]	HE K M, ZHANG X Y, REN S Q, et al.Deep residual learning for image recognition[C]//IEEE Conference on Computer Vision and Pattern Recognition.Piscataway, NJ: IEEE Press, 2016: 770-778.
[7]	SZEGEDY C, VINCENT V, IOFFE S.Rethinking the inception architecture for computer vision[C]//IEEE Conference on Computer Vision and Pattern Recognition.Piscataway, NJ: IEEE Press, 2016: 2818-2826.
[8]	GIRSHICK R, DONAHUE J, DARRELL T, et al.Rich feature hierarchies for accurate object detection and semantic segmentation[C]//IEEE Conference on Computer Vision and Pattern Recognition.Piscataway, NJ: IEEE Press, 2014: 580-587.
[9]	WANG N, YEUNG D Y.Learning a deep compact image representation for visual tracking[C]//International Conference on Neural Information Processing Systems.New York: Curran Associates Inc., 2013: 809-817.
[10]	KARPATHY A, TODERICI G, SHETTY S, et al.Large-scale video classification with convolutional neural networks[C]//IEEE Conference on Computer Vision and Pattern Recognition.Piscataway, NJ: IEEE Press, 2014: 1725-1732.
[11]	KANG B N, KIM K Y, KIM D J.Deep convolutional neural network using triplets of faces, deep ensemble, and score-level fusion for face recognition[C]//IEEE Conference on Computer Vision and Pattern Recognition.Piscataway, NJ: IEEE Press, 2017: 611-618.
[12]	WANG C, LAN X P, ZHANG X.How to train triplet networks with 100K identities?[C]//IEEE Conference on Computer Vision and Pattern Recognition.Piscataway, NJ: IEEE Press, 2017: 1907-1915.
[13]	SCHROFF F, KALENICHENKO D, PHILBIN J.Facenet: A unified embedding for face recognition and clustering[C]//IEEE Conference on Computer Vision and Pattern Recognition.Piscataway, NJ: IEEE Press, 2015: 815-823.
[14]	LIU Y S, HUANG C. Scene classification via triplet networks[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(1): 220-237. DOI:10.1109/JSTARS.2017.2761800
[15]	HERMANS A, BEYER L, LEIBE B.In defense of the triplet loss for person re-identification[EB/OL].(2017-11-21)[2018-12-01].https://arxiv.org/paf/1703.07737.pdf.
[16]	LIU H, TIAN Y, WANG Y, et al.Deep relative distance learning tell the difference between similar vehicles[C]//IEEE Conference on Computer Vision and Pattern Recognition.Piscataway, NJ: IEEE Press, 2016: 2167-2175.
[17]	CHENG D, GONG Y H, ZHOU S P, et al.Person re-identification by multi-channel parts-based CNN with improved triplet loss function[C]//IEEE Conference on Computer Vision and Pattern Recognition.Piscataway, NJ: IEEE Press, 2016: 1335-1344.
[18]	ZHANG S, GONG Y, WANG J.Deep metric learning with improved triplet loss for face clustering in video[C]//Pacific-rim Conference on Advances in Multimedia Information Processing.Berlin: Springer, 2016: 497-508.
[19]	CHEN W, CHEN X, ZHANG J, et al.Beyond triplet loss: A deep quadruplet network for person re-identification[C]//IEEE Conference on Computer Vision and Pattern Recognition.Piscataway, NJ: IEEE Press, 2017: 1320-1329.
[20]	HUANG G, LIU Z, MAATEN L, et al.Densely connected convolutional networks[C]//IEEE Conference on Computer Vision and Pattern Recognition.Piscataway, NJ: IEEE Press, 2017: 2261-2269.
[21]	SZEGEDY C, IOFFE S, VANHOUCKE V, et al.Inception-v4, inception-resnet and the impact of residual connections on learning[C]//AAAI Conference on Artifical Intelligence.Palo Atlo, CA: AAAI Press, 2017: 4278-4284.
[22]	XIE S, GIRSHICK R, DOLLAR P, et al.Aggregated residual transformations for deep neural networks[C]//IEEE Conference on Computer Vision and Pattern Recognition.Piscataway, NJ: IEEE Press, 2017: 5987-5995.
[23]	IOFFE S, SZEGEDY C.Batch normalization: Accelerating deep network training by reducing internal covariate shift[C]//International Conference on Machine Learning.Boston: MIT Press, 2015: 448-456.
[24]	DING S, LIN L, WANG G, et al. Deep feature learning with relative distance comparison for person re-identification[J]. Pattern Recognition, 2015, 48(10): 2993-3003. DOI:10.1016/j.patcog.2015.04.005
[25]	ZEILER M D, FERGUS R.Stochastic pooling for regularization of deep convolutional neural networks[EB/OL].(2013-01-16)[2018-11-25].https://arxiv.org/pdf/1301.3557.pdf.
[26]	GOODFELLOW I J, WARDE-FARLEY D, MIRZA M, et al.Maxout networks[C]//Proceedings of the International Conference on Machine Learning.Boston: MIT Press, 2013: 1319-1327.
[27]	LIN M, CHEN Q, YAN S.Network in network[C]//International Conference on Learning Representations, 2014: 1-10.
[28]	LEE C Y, XIE S N, GALLAGHER P W, et al.Deeply-supervised nets[C]//Proceedings of the International Conference on Artificial Intelligence and Statistics.San Diego, California: PMLR, 2015: 562-570.
[29]	LIAO Z B, CARNEIRO G.Competitive multi-scale convolution[EB/OL].(2015-11-18)[2018-11-10].https://arxiv.org/pdf/1511.05635.pdf.
[30]	XU C Y, LU C Y, LIANG X D, et al. Multi-loss regularized deep neural network[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2016, 26(12): 2273-2283. DOI:10.1109/TCSVT.2015.2477937
[31]	HOFFER E, AILON N.Deep metric learning using triplet network[C]//International Workshop on Similarity-based Pattern Recognition.Berlin: Springer, 2015: 84-92.
[32]	KRIZHEVSKY A, HINTON G.Learning multiple layers of features from tiny images[D].Toronto: University of Toronto, 2009: 32-35.
[33]	NETZER Y, WANG T, COATES A, et al.Reading digits in natural images with unsupervised feature learning[C]//NIPS Workshop on Deep Learning and Unsupervised Feature Learning.New York: Curran Associates Inc., 2011: 1-9.