就目前而言,磨粒图像分割技术的研究主要以铁谱图像为目标对象,大量的分割方法均以磨粒沉积链为主[7-8],而对于以过滤法获取的滤膜谱片图像,则较少有针对性的分割方法。与铁谱磨粒图像不同,滤膜谱片上磨粒的分散度在提取环节已经达到较好的效果,无磨粒沉积链的产生,但受背景复杂程度不一的影响,通常需要在分割过程中借助交互式后处理技术来保证分割效果。交互式处理虽然保证了分割效果,但当样本数量巨大时会严重影响分割效率,使得磨粒智能分析的优势难以完全凸显。
为了保证大量的磨粒样本在分割过程中可以达到分割质量和分割效率的最佳折中,最大化地避免交互式人工分割的参与,本文以滤膜谱片图像为主要对象,尝试提出一种适合大量磨粒图像快速分割的新方法。该方法包括图像梯度修正、分水岭预分割、过分割区域合并3个环节。首先利用形态学重构及自适应H-minima技术对梯度图像进行修正,其次利用分水岭算法对修正后的梯度图像进行一次分割,再结合颜色特征和纹理特征对过分割产生的相似区域进行合并,完成磨粒图像的分割问题。为了保证分割方法的自适应性,设计分割过程涉及的主要参数均可实现动态调整。将本文的分割方法与经典图像分割方法从定性、定量的角度进行测试对比,验证本文方法在分割效果上的优越性,以此来提高磨粒图像的自适应分割需求。
1 分水岭分割 1.1 形态学梯度重构 传统分水岭算法对噪声非常敏感,尤其对于背景及纹理复杂程度不一的磨粒图像而言,更是存在严重的过分割问题。形态学重构是消除图像噪声点的有效方法之一。记f为标记图像,m为掩模图像,se为结构元素,从f重构m的迭代过程定义为
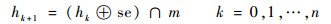 | (1) |
式中: hk为迭代到第k次时的标记图像;h0为初始迭代的标记图像f。式(1)满足hk+1=hk时停止迭代。
本文首先利用形态学重构算法对灰度图像进行处理,以消除背景中的部分噪声点和磨粒的表面纹理在构建梯度图像过程中形成的伪边缘。进行形态学重构工作时,首先结合图像的光源特征,将图像从RGB颜色空间转化到HSV颜色空间,获取V分量图像,其次创建合适的结构元素se,对V分量图像依次进行开重构运算和闭重构运算,获取原图像的形态学重构图像。
使用Sobel边缘算子对重构图像的水平和垂直方向分别进行滤波运算,提取形态学重构图像的梯度图g。图 1为疲劳磨粒的梯度图像提取示例。与对V分量图像直接提取梯度图像相比,基于形态学重构获取的梯度图像在很大程度上减少了图像中的噪声点及强纹理变化,大量的伪边缘获得消除,梯度图像的强弱对比更加明显。
 |
| 图 1 形态学重构梯度图像 Fig. 1 Gradient image after morphological reconstruction |
| 图选项 |
1.2 基于自适应H-minima技术的分水岭分割 受背景及纹理复杂程度不一的影响,基于形态学重构提取的梯度幅值图像仍存在一定数量与目标区域无关的极小值点。为了尽可能消除冗余信息对分水岭分割结果的影响,本文基于H-minima技术[9]对梯度图像进行修正,通过阈值H的设定,消除图像中深度小于H的局部极小值,以达到减少干扰极小值点的目的,从而改善分水岭的过分割问题。基于H-minima技术对梯度图像g进行修正的主要步骤为:利用阈值H对梯度图像进行标记,对标记后的图像采用强制最小运算进一步修正,使得图像的极小值点只出现在被标记的位置上,从而完成梯度图像的修正工作,计算过程如式(2)、式(3)所示。
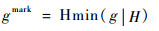 | (2) |
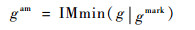 | (3) |
式中:gmark为经过H-minima变化后的标记图像;gam为经过强制最小运算后的修正梯度图像;Hmin(·|·)表示对重构梯度图像g利用H值进行H-minima变换;IMmin(·|·)表示对重构梯度图像利用gmark标记图像进行强制最小运算。
阈值H是控制图像过分割和欠分割程度的关键参数,较大的H值可以消除更多的噪声,但对弱边缘也会产生较大的屏蔽作用。传统的H-minima技术一般都对H值预先进行人为设定,既定的H值无法保证每张图像都达到最优的分割效果。为了保证H-minima技术可以对梯度图像的修正产生正向作用,文献[10]综合考虑了重构梯度图像的均值、局部极大值与局部极小值,提出了一种H参数的计算方法:
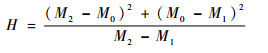 | (4) |
式中:M0、M1和M2分别为重构梯度图像g的均值、局部极小值的均值和局部极大值的均值。
利用式(4)对梯度图像进行修正,发现对于形态各异的磨粒样本而言,此时的H值虽然较好地消除了部分磨粒的强纹理与噪声(见图 2(a)左图),但有些磨粒的弱边缘无法获得准确定位,如图 2(a)右图的磨粒,在图 2(c)中出现了较严重的欠分割现象,说明此时H值偏大,H值的自适应性并未获得完全突显。为了实现磨粒图像的梯度修正,使自适应H值有更好的容错性,在式(4)的基础上对H参数引入了定值修正因子β(0 < β≤1),修正后H参数的计算公式为
 | (5) |
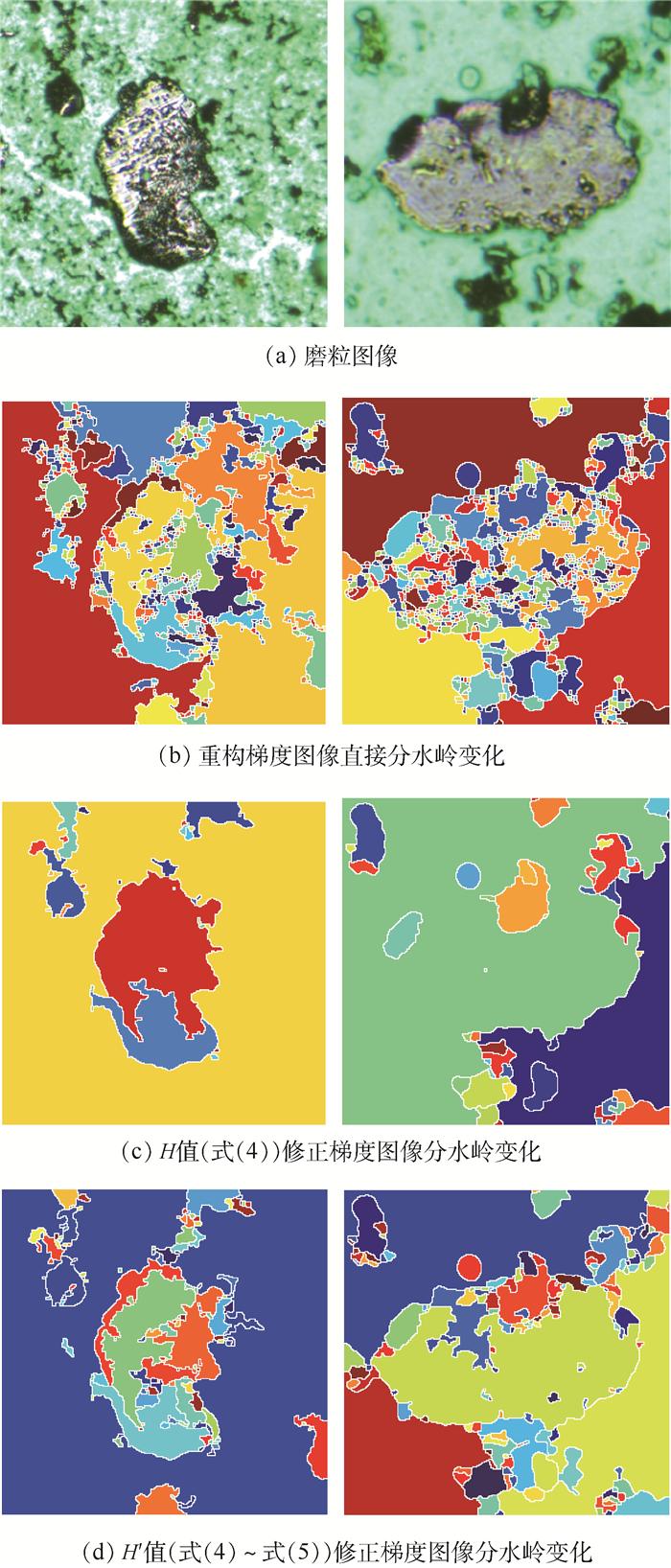 |
| 图 2 梯度修正图像的分水岭变化 Fig. 2 Watershed variation of gradient corrected image |
| 图选项 |
β值的选择主要基于梯度修正图像gam的分水岭变化结果进行定值试验,其确定原则是:尽可能保证每张图像在分水岭分割后形成的任何一个区域都不会同时包括前景部分和背景部分。综合对比试验结果,取修正因子β=0.5,此时分水岭变化可以在强纹理和弱边缘之间取得较好的平衡,分水岭变化结果如图 2(d)所示,记其标记图像为Z,分割线为0。此时,H-minima技术不仅显著改善了分水岭算法的过分割问题,有效抑制了背景中的极小值噪声点,同时也保证了磨粒轮廓的准确定位。对于严重滑动磨粒、滚动疲劳块状磨粒、滚滑磨粒等具有强纹理的磨粒图像,分水岭算法在前景区域上还是会表现一定的过分割现象,但是考虑到磨粒轮廓的完整性,本文采用修正后的H′值来允许少量过分割问题的存在。为了进一步解决前景区域的过分割问题,将分水岭分割后的一次区域作为同质区域,提出基于区域相似性的区域合并规则,以准确提取前景目标。
2 区域合并 2.1 基于Lab空间的颜色直方图特征提取 受磨粒样本获取条件的影响,磨粒图像的前景与背景通常有明显的颜色差异,因此颜色信息是区域合并时首要考虑的指标之一。颜色直方图是最常用的颜色特征表达方法之一,广泛用于图像检索,在特征提取领域具有平移不变、旋转不变、尺度不变的优点[11]。考虑到RGB颜色空间并不符合人眼的视觉感应,为了使计算机对颜色信息的读取与人的主观认识一致,本文主要在Lab颜色空间完成同质区域颜色直方图的提取工作。为了节省计算空间,提高计算效率,本文将L通道、a通道、b通道图像分别压缩至16个颜色等级,获取分水岭分割图像Z中各个区域的颜色值,每个区域各由163=4 096种颜色表示,依次提取各个区域的归一化颜色分布直方图。图 3为图 2(d)左图中区域1与区域39的颜色直方图提取示例。
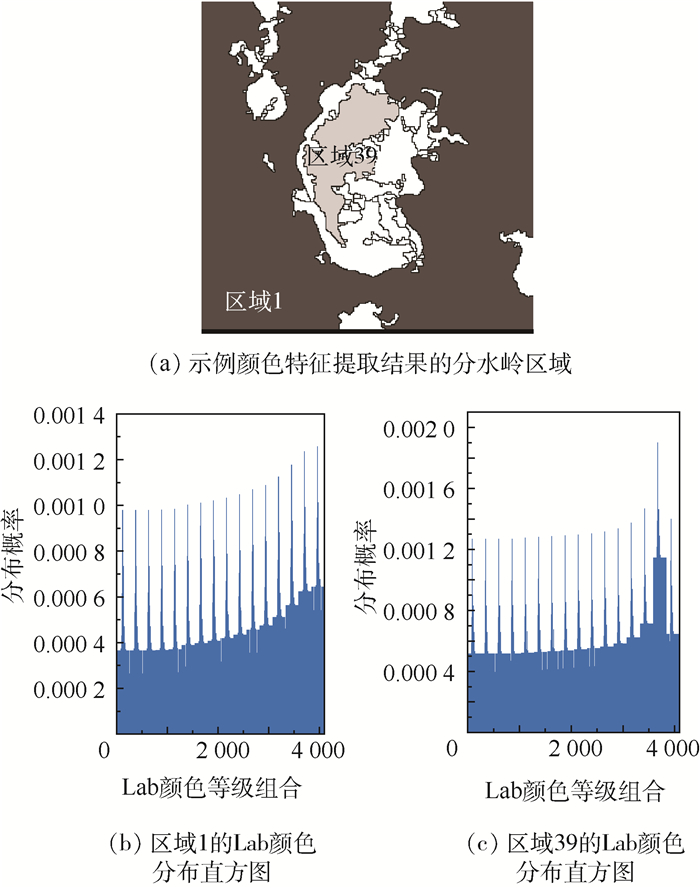 |
| 图 3 分水岭分割区域的颜色直方图提取示例 Fig. 3 An example of color histogram extraction from watershed segmentation regions |
| 图选项 |
2.2 基于LBP的纹理直方图特征提取 由于部分磨粒表面具有显著纹理,这种纹理信息不仅难以在颜色分布直方图上获得体现,还可能造成颜色信息的混淆。为了使合并规则同样适用于纹理变化显著的图像,本文提出基于局部二值模式(LBP)获取同质区域纹理特征的方法,将其作为区域的第2个相似性指标。为了同时满足灰度不变性和旋转不变性,利用半径为R的圆形领域进行LBP算子的提取工作。参考文献[12]获取原图像的LBP图谱,再基于LBP图谱计算分水岭分割后各个区域的纹理统计直方图来标识该区域的纹理信息,并对直方图做归一化处理。
图 4为图 2(d)左图中区域1与区域39的纹理直方图提取示例。在计算LBP图谱时,在半径为2的圆形邻域内确定了8个采样点,提取的纹理值分布在[0, 255]之间。
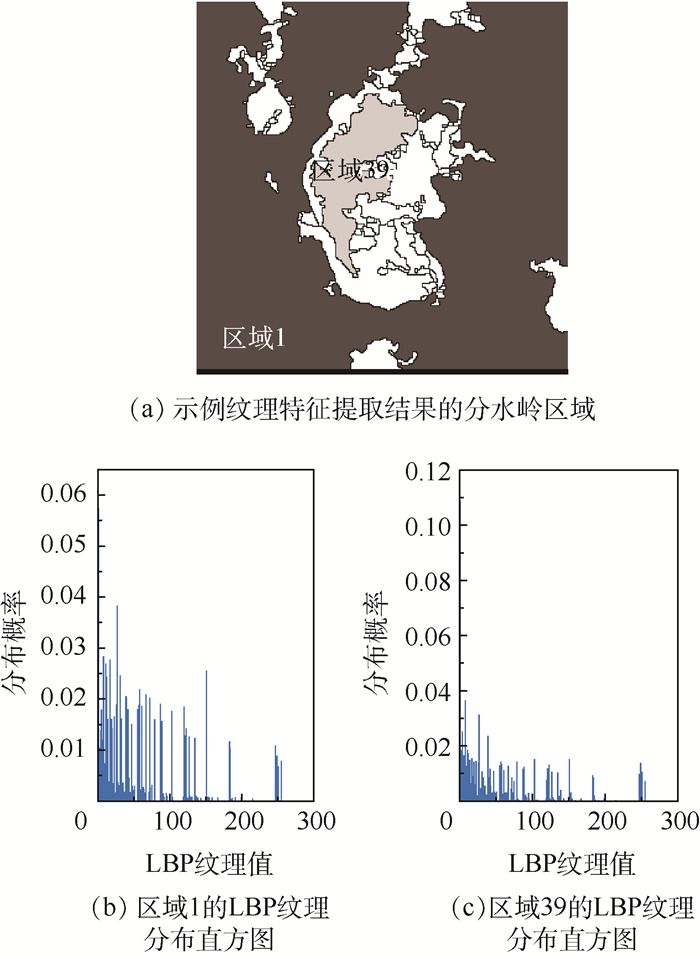 |
| 图 4 分水岭分割区域的纹理直方图提取示例 Fig. 4 An example of texture histogram extraction from watershed segmentation regions |
| 图选项 |
2.3 基于巴氏距离的区域相似性度量 为了判断区域之间的颜色相似性及纹理相似性,基于Bhattacharyya系数来完成直方图的相似性度量。记区域Rm的颜色归一化直方图为ColorHistRm, 纹理归一化直方图为LBPHistRm,则区域Rm与Rn之间的颜色相似度ρcolor和纹理相似度ρLBP分别为
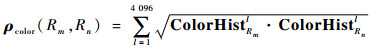 | (6) |
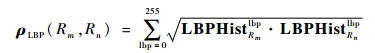 | (7) |
2.4 基于特征综合相似度的分水岭同质区域合并
2.4.1 特征融合 区域相似性综合颜色相似性和纹理相似性进行度量。对于严重滑动磨粒和疲劳磨损磨粒等图像,纹理特征是区分前景与背景的主要因素,颜色特征由于磨粒表面纹理的变化可能呈现无规则性。因此,在计算该类图像的区域相似度时,LBP纹理特征应占有较大的权重,而对于氧化物、切削磨粒的图像,颜色特征比较明显,较大比重的颜色直方图特征可以更好地度量区域之间的相似性。因此,为了提高区域合并规则的自适应性,有必要动态调整颜色指标和纹理指标之间的权重,使得相似度矩阵的建立可以完全结合待处理图像的特点实现自适应调整。由于ρcolor、ρLBP为相似度参数,其数值越大,表示2个区域之间的该类特征越相似,在综合相似度矩阵的构建过程中,该类特征应该占有较大的权重。因此,直接根据各个区域的颜色、纹理相似度的大小按比例分配权重,定义区域Rm与区域Rn之间的综合相似度w为
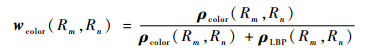 | (8) |
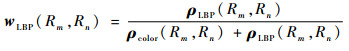 | (9) |
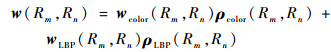 | (10) |
图像的相似度矩阵W为
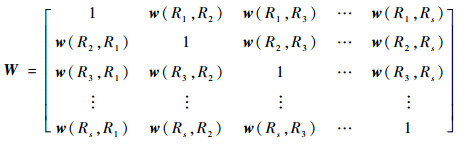 |
2.4.2 种子区域的自动选取与标记 本文主要完成前景区域与背景区域的分割问题,涉及的合并区域目标数为2。为了降低区域合并工作的人工参与度,首先对前景种子区域和背景种子区域进行自动选择与标记,以此作为两大目标区域的基准点,完成区域合并工作。
1) 背景种子区域的选择与标记。本文提出的基于H-minima技术的分水岭算法极大地减少了背景噪声点,使得背景区域的连通性增强,因此,直接将分水岭分割后面积最大的同质区域ssmax定义为背景种子区域Rb。将该区域标记为1,即Z(Rb)=1。
2) 前景种子区域的选择与标记。前景种子区域的标记主要基于邻接区域进行。采用如下方法判断目标区域的邻接区域:追踪目标区域的边缘轮廓,对轮廓外部像素点的标记值进行判断,外部像素点对应的标记值均与目标区域相邻,由此可以获取邻接区域的标记值。
设分水岭算法分割后的同质区域构成的向量集为s,以相邻区域为准,前景种子区域的判断过程为
1) 提取背景区域Rb的邻接区域标记值,记为Rv,v∈s且v≠b,前景种子区域在Rv中进行选择。
2) 依次获取Rv的邻接区域,记为Rvr,r∈s且r≠v,从相似度矩阵W中提取Rv与其邻接区域的相似度值w(Rv, Rr)。
3) 根据相似度w依次计算区域Rv的节点度矩阵D,将矩阵D取最大值时对应的区域标记值v0定义为前景区域种子点,将该区域标记为0。计算过程如下:
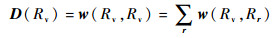 | (11) |
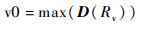 | (12) |
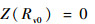 | (13) |
2.4.3 区域合并准则设计 完成背景种子区域和前景种子区域的标记工作后,进行区域的合并。区域Ri(i∈s且i≠b、i≠v0)的合并规则
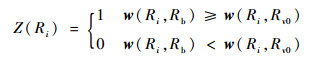 | (14) |
2.4.4 区域合并及形态学后处理 基于合并规则,图 2(d)左侧图像的区域合并结果如图 5(a)所示。结果表明,前景区域与背景区域获得了正确合并,图像分割效果良好。为了消除属于背景区域的分水岭同质区域分割线及边缘细小连接处,在视场下仅保留前景目标,对合并后的图像进行统一形态学后处理,处理流程如图 6所示。基于上述处理过程,即可完成图像的分割工作,最终获得图 5(b)所示的分割图像,其中前景目标用1表示,背景目标用0表示。
 |
| 图 5 区域合并及分割图像示例 Fig. 5 Image example of regional merging and segmentation |
| 图选项 |
 |
| 图 6 区域合并图像的形态学后处理流程 Fig. 6 Post-processing flow of region merging image based on morphology |
| 图选项 |
3 测试及对比分析 3.1 方法流程 对于待分割磨粒图像集F={f1, f2, …, fn},利用本文方法对其进行分割的主要流程如图 7所示。
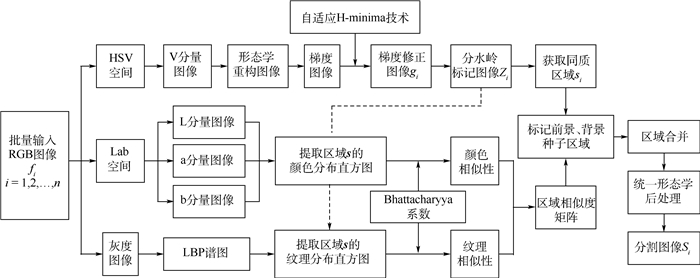 |
| 图 7 本文分割方法流程 Fig. 7 Flowchart of proposed segmentation method |
| 图选项 |
3.2 区域合并规则自适应性测试 为了测试区域自适应合并规则的可行性,验证式(8)~式(10)中特征融合规则在磨粒图像分割方面的优势,将自适应权重合并结果与定值权重的合并结果进行对比分析,分别取任意2个同质区域之间的wcolor=0.5、wLBP=0.5完成特征参数的合并。分析结果表明,对于部分图像,定值权重下会导致磨粒的边缘、内部区域出现错误合并的情况,典型的如图 8(a)所示的磨粒,在定值权重下,左侧磨粒的轮廓出现错误合并,右侧磨粒中较多属于前景的区域都被合并到背景中,而选择自适应权重时,磨粒的区域合并结果更为准确,说明本文提出的区域合并规则有更强的自适应性,能够保证尽可能多类型的磨粒获得更为准确的区域合并结果。
 |
| 图 8 区域合并图像对比测试 Fig. 8 Comparison of region merging image test |
| 图选项 |
3.3 分割结果 为了分析本文方法的效果,随机选择60张磨粒图片进行测试,测试图像包含磨损机理下产生的各类典型磨损磨粒,图像的大小均为300×300。本文的油液磨粒均基于滤膜谱片技术提取,采用铁谱显微镜获取磨粒图像,反射光源选择白色,透射光源选择绿色。测试时的计算机配置为Intel(R) Core(TM) i7-7700 CPU @ 3.60 GHz,8 GB内存,MATLAB 8.4.0环境。在采用本文方法时,形态学重构过程的结构元素选择半径为10的平面圆盘形结构,在半径为2的圆形区域内设置8个采样点以提取区域纹理特征,对区域合并图像进行后处理时,开运算部分选择半径为4的平面圆盘形结构,批量完成图像的分割处理工作。
通过对比试验来进一步验证本文方法的有效性,将其与文献[3, 13-14]提出的分割方法进行性能对比。分别选择典型的球形磨粒、滚滑磨粒、氧化物、疲劳片状磨粒、疲劳块状磨粒、切削磨粒、严重滑动磨粒等的图像来展示分割效果,如图 9(a)所示。图 9(b)~(d)依次为本文方法中H-minima分水岭分割(HWS)、区域合并(HWS-CLB)及最终分割结果。图 9(e)为本文提出的基于H-minima技术的分水岭分割方法(HWS)与蚁群聚类结合的分割结果,蚁群聚类的具体流程参见文献[3]。图 9(f)为基于本文形态学重构图像进行的大津阈值分割结果。图 9(g)为文献[14]提出的彩色图像K-均值聚类算法。
 |
| 图 9 本文方法与其他方法的分割结果对比 Fig. 9 Comparison of segmentation results between proposed method and other methods |
| 图选项 |
3.4 分割效果评价
3.4.1 定性评价 定性地分析不同方法下图像的分割结果,蚁群聚类算法(见图 9(e))对图像表面纹理的变化过于敏感,同质区域在合并过程中并未实现完全聚类,区域合并效果不佳;大津阈值算法(见图 9(f))下虽然使用自适应灰度阈值,部分图像都实现了较好的分割,但还是有部分图像出现过分割问题和欠分割问题,因此难以开展统一的后处理过程来对误分割进行修正;基于彩色图像的K-均值聚类算法(见图 9(g))对图像中的噪声十分敏感,分割效果极不稳定,尤其对纹理明显的严重滑动磨损磨粒图像更是表现出严重的欠分割情况,其对片状磨粒的分割效果虽然较为理想,但难以正确检测出有一定厚度的块状体区域,对这类磨粒出现了明显的分割错误。而采用本文分割方法时,前景区域与背景区域在区域合并过程中进行了较为准确的聚类,分割图像仅在目标磨粒边缘处出现少量的误分割现象,通过一系列既定的形态学后处理,即可以将目标区域完整提取出来,获得完整的分割区域。
3.4.2 定量评价 从分割速度和分割精度2个方面来定量地评价不同的分割算法。图 10为60张测试图像在本文方法及3种对比算法下的分割时间,为了使图像的对比度更加明显,将纵坐标时间以对数形式表示。测试时间表明,蚁群聚类算法由于涉及迭代过程,运算速度明显变慢,单张图像的平均分割时间为88.383 3 s,且分割时间的波动较大,对测试图像的最长分割时间高达586.4 988 s。大津阈值算法与K-均值聚类算法的分割速度均在毫秒级别,平均分割时间依次为0.037 1 s、0.223 7 s,而本文方法的平均分割时间为12.854 0 s,显著少于蚁群聚类算法。
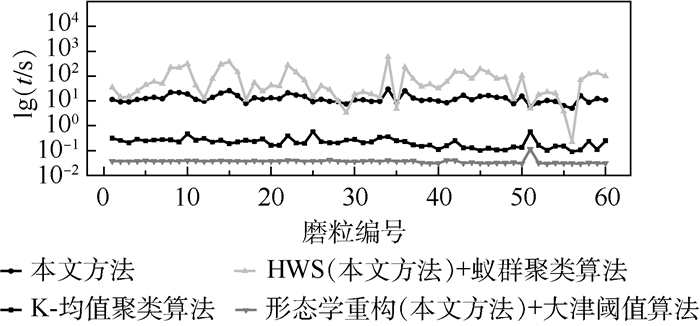 |
| 图 10 不同方法的分割速度对比 Fig. 10 Comparison of segmentation speed among different methods |
| 图选项 |
定性对比及分割时间对比结果表明,在对比算法中,大津阈值算法在分割时间及分割效果方面都是最优的,因此进一步对本文方法与大津阈值算法进行分割准确度的定量比较。获取60张图像的人工分割结果图像作为误差评判基准,选择区域误分割率RMR、边缘分割误差EMR、区域重合度RCD 3个指标来衡量算法的分割结果,将本文方法和大津阈值算法进行比较。三大指标的定义如表 1所示。
表 1 分割精度评价指标的定义 Table 1 Definition of segmentation accuracy evaluation index
| 评价指标 | 表达式 | 取值范围 |
| RMR | RMR=(SRf-SRft)/SRft | (-1, 1) |
| EMR | EMR=(FDRf-FDRft)/FDRft | (-1, 1) |
| RCD | RCD=(SRf∩SRft)/SRft | [0, 1] |
| 注:SRf表示分割图像目标区域的面积,SRft表示参考图像目标区域的面积,FDRf、FDRft分别表示以FAENA法[15]提取的分割目标区域、参考目标区域的边界分形维数。RMR、EMR指标的取值有正有负,正值表示分割过程中对目标区域存在过分割问题,负值表示目标区域分割不完整,其绝对值的大小表示错误分割的具体程度。 | ||
表选项
图 11为分割效果的定量评价结果。可以看出,大津阈值算法的分割速度虽然可以达到毫秒级,但分割结果不够稳定,各个评价指标都呈现非常大的波动,错误分割的情况也无规律可寻,只能通过交互式后处理来进行分割结果的修正,而这种修正在样本数量庞大时是非常费时费力的一项工作。本文方法的误分割率基本控制在10%以内,分割图像无论以区域度量,还是以轮廓度量,都达到了较好的分割效果,说明本文方法在分割速度和分割精度之间取得了最佳折中。
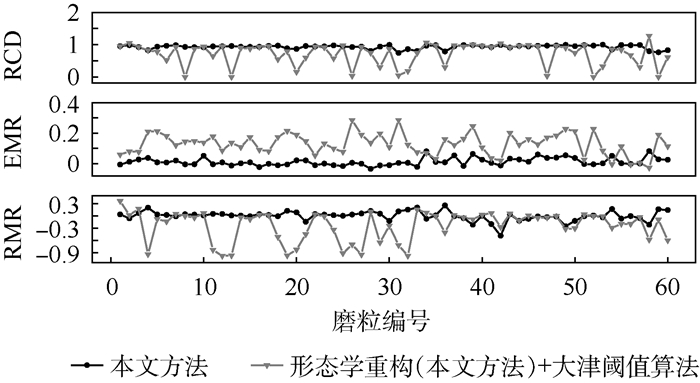 |
| 图 11 不同方法的分割精度指标对比 Fig. 11 Comparison of segmentation accuracy index among different methods |
| 图选项 |
4 结论 1) 本文将分水岭算法与区域相似度合并结合,提出了一种适用于油液磨粒图像快速分割的新方法,适用于典型磨损机理下产生的各类磨粒。与现有的常规分割方法相比,本文方法对单幅图像(大小为300×300)的分割时间在12 s左右,正确分割率达90%以上,在分割速度和分割精度之间取得了最佳折中,是一种自适应程度较高的磨粒图像分割方法。
2) 基于形态学重构和H-minima技术的改进分水岭算法对背景噪声点和纹理变化均具有较强的抑制作用,且在梯度图像修正过程中利用自适应的H′值可以更有效地改善分水岭算法的过分割现象,使得图像仅在强纹理区域出现少量的过分割问题,极大地减少了分水岭分割后产生的同质区域数量。
3) 在区域合并过程中,以颜色特征和纹理特征作为区域量化指标,可以获得具有尺度不变性的特征指标集,通过动态调整颜色相似度指标和纹理相似度指标的权重来获取区域的综合相似度矩阵,并基于此设计合并规则,不仅极大地增强了分割方法的自适应程度,同时保证了分割精度的提高不会以分割时间为代价,实现了自适应分割需求。
4) 以区域相似度矩阵为主,利用邻接区域的相似度节点矩阵可以实现前景、背景种子区域的自动选择,避免了人工标记种子区域的繁琐,保证了区域合并过程的效率和自适应性。
参考文献
| [1] | 金路, 王静秋. 基于形态学算法分割铁谱图像研究[J]. 机械制造与自动化, 2011(3): 10-13. JIN L, WANG J Q. Technical research on ferrography division of morphology[J]. Machine Building & Automation, 2011(3): 10-13. DOI:10.3969/j.issn.1671-5276.2011.03.003 (in Chinese) |
| [2] | 王静秋, 张龙, 王晓雷. 融合颜色聚类和分水岭算法的铁谱图像分割[J]. 中国矿业大学学报, 2013, 42(5): 866-872. WANG J Q, ZHANG L, WANG X L. Ferrographic image segmentation by the method combining k-means clustering and watershed algorithm[J]. Journal of China University of Mining & Technology, 2013, 42(5): 866-872. (in Chinese) |
| [3] | 张龙.蚁群算法在铁谱图像处理中的应用研究[D].南京: 南京航空航天大学, 2013: 31-37. ZHANG L.Application research of ant colony algorithm in ferrography image processing[D].Nanjing: University of Aeronautics and Astronautics, 2013: 31-37(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10287-1014005868.htm |
| [4] | WANG J, YAO P, LIU W, et al. A hybrid method for the segmentation of a ferrograph image using marker-controlled watershed and grey clustering[J]. Tribology Transactions, 2016, 59(3): 513-521. DOI:10.1080/10402004.2015.1091534 |
| [5] | 张云强, 张培林, 王国德. 铁谱图像典型磨粒自动提取方法研究[J]. 计算机工程与应用, 2013, 49(16): 175-178. ZHANG Y Q, ZHANG P L, WANG G D. Research on automatic extraction of wear particles for ferrographic images[J]. Computer Engineering and Applications, 2013, 49(16): 175-178. DOI:10.3778/j.issn.1002-8331.1111-0507 (in Chinese) |
| [6] | 温广瑞, 徐斌, 张志芬, 等. 基于差商的油液监测铁谱图像自适应分割[J]. 光学精密工程, 2017, 25(5): 1322-1330. WEN G R, XU B, ZHANG Z F, et al. Self-adaptive segmentation of oil monitoring ferrographic image based on difference quotient[J]. Optics and Precision Engineering, 2017, 25(5): 1322-1330. (in Chinese) |
| [7] | WU H K, WU T H, PENG Y P, et al. Watershed-based morphological separation of wear debris chains for on-line ferrograph analysis[J]. Tribology Letters, 2014, 53(2): 411-420. DOI:10.1007/s11249-013-0280-1 |
| [8] | WU T, WU H, DU Y, et al. Imaged wear debris separation for on-line monitoring using gray level and integrated morphological features[J]. Wear, 2014, 316(1-2): 19-29. DOI:10.1016/j.wear.2014.04.014 |
| [9] | SOILLE P. Morphological image analysis principles and applications[M]. Berlin: Springer, 1999: 123-140. |
| [10] | 余旺盛, 侯志强, 王朝英, 等. 基于改进滤波和标记提取的分水岭算法[J]. 电子学报, 2011, 39(4): 825-830. YU W S, HOU Z Q, WANG C Y, et al. Watershed algorithm based on modified filter and marker-extraction[J]. Acta Electronica Sinica, 2011, 39(4): 825-830. (in Chinese) |
| [11] | ALI H, LALI M I, NAWAZ M Z, et al. Symptom based automated detection of citrus diseases using color histogram and textural descriptors[J]. Computers and Electronics in Agriculture, 2017, 138. |
| [12] | BACKES A R. LBP maps for improving fractal based texture classification[J]. Neurocomputing, 2017, 266: 1-7. DOI:10.1016/j.neucom.2017.05.020 |
| [13] | 宋国云, 范彦斌. 基于最大类间方差的数字化铁谱图像分割[J]. 佛山科学技术学院学报(自然科学版), 2007, 25(1): 36-39. SONG G Y, FAN Y B. The algorithm for the ferrography image segmentation based on maximum variance between clusters[J]. Journal of Foshan University (Natural Science Edition), 2007, 25(1): 36-39. DOI:10.3969/j.issn.1008-0171.2007.01.009 (in Chinese) |
| [14] | 邱丽娟, 宣征南, 张兴芳. 基于K-means聚类与最大类间方差的磨粒彩色图像分割[J]. 润滑与密封, 2014, 39(12): 101-104. QIU L J, XUAN Z N, ZHANG X F. Debris color image segmentation by K-means clustering and Ostu method[J]. Lubrication Engineering, 2014, 39(12): 101-104. DOI:10.3969/j.issn.0254-0150.2014.12.021 (in Chinese) |
| [15] | 齐福柱.基于分形维数的磨粒识别方法研究[D].大连: 大连海事大学, 2014: 16-18. QI F Z.Based on the fractal dimension of abrasive identification method research[D].Dalian: Dalian Maritime University, 2014: 16-18(in Chinese). http://d.wanfangdata.com.cn/Thesis/Y2583853 |
