在众多的去噪模型中, 基于能量泛函的模型由于具有有效刻画图像结构特征的数学性质, 在近十年来成为国内外研究的热点[1]。其中, Rudin等[2]于1992年提出的全变分(TV)去噪模型(ROF模型)具有开创性, 其是以梯度信息作为图像平滑性的度量来实现图像去噪与修复。由于该模型中的正则项所在的函数空间在广义若当测度意义下, 并不要求函数具有连续性, 因此能有效地保持图像中不具有连续性的边缘结构特征, 从而在图像复原领域内得到了广泛的应用[3], 并推动了基于能量泛函的图像复原模型的发展。然而, ROF模型所依赖的梯度范数在模型中惩罚较小的跃迁信息时, 经常导致图像的光滑渐变区域出现阶梯现象。为此, 近年来基于ROF模型提出了众多的改进模型,如高阶全变分去噪模型[4]、广义全变分去噪模型[5]、加权全变分去噪模型[6]、方向全变分(DTV)去噪模型[7]、边缘自适应DTV去噪模型[8]、分数阶全变分去噪模型[9-10]、零化多项式去噪模型[11]等。上述模型虽然在一定程度上能反映图像的结构特征, 但是由于模型的固有属性导致在数值计算过程中存在下述问题:①x与y方向的微分算子权重是对等的, 并没有考虑图像中结构特征的差异性; ②对于具有方向性的图像, 在数值计算时仅仅利用水平和竖直方向的差分并不能有效刻画图像的方向特征。
为了有效克服上述缺陷, 文献[7]通过耦合旋转算子、各向异性加权算子与差分算子等3类算子提出了DTV去噪模型。随后, 文献[8]提出了具有边缘自适应性的DTV去噪模型。上述2类模型在微分格式上具有方向性和加权性, 因此在去噪过程中能很好地保持图像的方向特征。但是, 这些模型并未考虑图像中的结构性特征, 而这些结构性特征在梯度意义下表现为稀疏性或者跃迁性, 因此对全变分算子进行有效的约束至关重要。为此, 本文提出了一种具有鲁棒性的基于

1 图像去噪模型 令u为初始清晰图像, f为被噪声污染的图像, n为干扰噪声, 则退化图像模型可以表示为
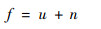 |
图像去噪问题的目的是从退化图像f中有效地复原初始图像u。然而,在此过程中由于部分先验缺信息缺失,直接求解将导致经典的病态问题。有效克服该问题的方法是正则化方法, 下面介绍几类与本文有关的全变分正则化模型。
1.1 ROF模型 为了克服早期模型不能有效保持图像边缘的问题, Rudin等[2]于1992年提出了基于全变分的正则化去噪模型ROF。
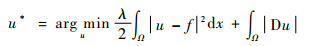 | (1) |
式中:u*为原始图像的估计值; λ为拟合项参数;Ω为图像的积分区域;D为梯度算子。该模型的第一项称为数据拟合项, 确保去噪后的图像能够尽可能逼近原始图像;第二项称为正则项, 用来刻画图像中的先验信息, 可以促使去噪图像具有一定的平滑性。由于模型中的∫Ω|Du|在若当测度意义下可表示为
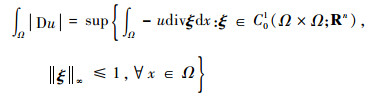 |
式中:ξ=(ξ1, ξ2)T。显然, 定义中不要求u具有连续性, 因此在去噪过程中能有效保持图像边缘。事实上, 该模型的最优性条件[14]含有曲率项,该项本质上对应求解各向异性扩散方程, 扩散过程主要是沿着切线方向, 因此可以保持图像中大的跃迁结构。然而, 在求解过程中, 该模型的差分格式仅仅考虑水平和竖直2个方向, 并不能有效刻画图像中具有方向特征和像素值振荡的情况。
1.2 DTV去噪模型 为了克服ROF模型不能有效描述图像中带有方向性结构特征的缺陷, 文献[7]提出了DTV去噪模型。
 | (2) |
式中:Rθ为旋转矩阵, 用来刻画图像中特征结构方向性,θ为噪声图像f的旋转角度;Λα为尺度矩阵, 用来耦合图像在坐标方向的权重。
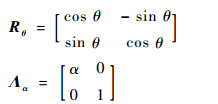 |
经过简单计算,不难得到RθT=R-θ和ΛαT=Λα, α > 1为尺度参数。
1.3 改进的图像去噪模型 由于图像中含有大量的冗余信息, 在一定的算子变换意义下表现为稀疏性, 因此近年来基于
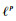
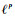
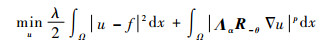 | (3) |
式中:p∈(0, 2)。当0 < p < 1时, 正则项为拟模, 模型式(3)为非凸优化问题;当1≤p < 2时, 正则项为范数, 模型式(3)为凸优化问题。
2 数值方法 本节考虑模型式(3)的求解方法, 其对应的离散形式为
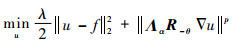 | (4) |
式中:||·||2表示离散意义下的
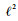
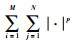
针对式(4)中的梯度算子?u, 采用向前差分格式:
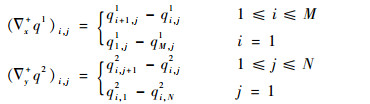 |
其中:q=(q1, q2)。
利用散度定理(div q, u)=-(?u, q), 可知向后差分格式描述为
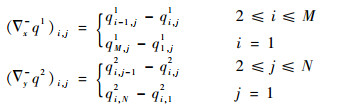 |
上述差分格式可表示为如下五点差分格式,如图 1所示。
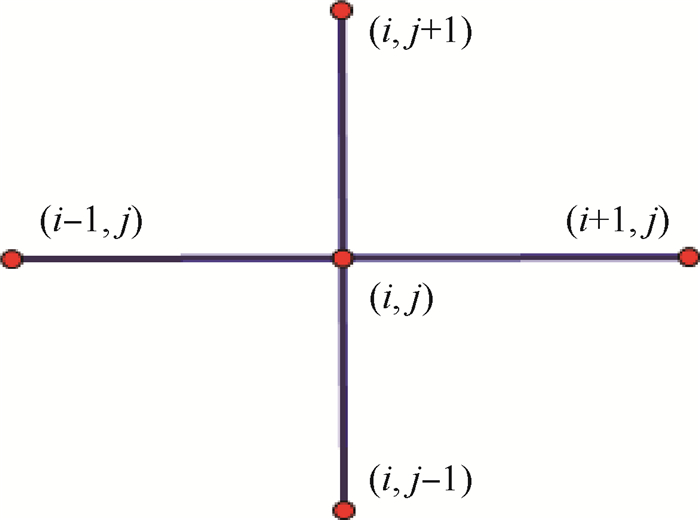 |
| 图 1 五点差分格式 Fig. 1 Five-point difference format |
| 图选项 |
由图 1可以看出,梯度算子仅仅考虑水平方向和垂直方向的差分, 这不能有效描述具有其他方向的差分信息, 因此在具有方向性结构的图像中, 需对?u做旋转变换, 即R-θ?u, 如图 2(b)、(c)所示。另外, 为了更有效反映图像差分的权重, 需要对差分格式做一定的惩罚, 即ΛαR-θ?u, 如图 3所示。
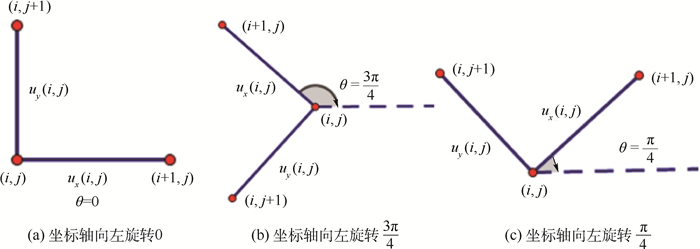 |
| 图 2 两个差分方向取相同权重时的旋转变换 Fig. 2 Rotation transformation when two differential directions take the same weight |
| 图选项 |
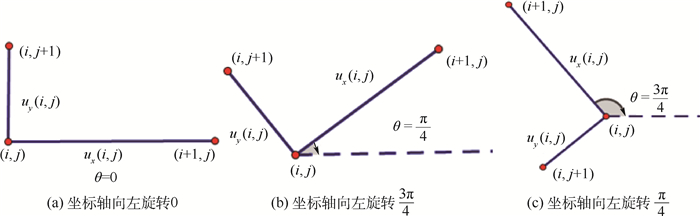 |
| 图 3 两个差分方向取不同权重时的旋转变换 Fig. 3 Rotational transformation when two differential directions take different weights |
| 图选项 |
在式(4)中, 算子Λα、R-θ与?的耦合给数值求解带来巨大的挑战, 求解该问题的有效方法是算子分裂型方法, 如ADMM[12-13]、本原对偶方法[15]、不动点方法[16]及Douglas-Rachford分裂方法[17]等。这些方法的本质是通过引入辅助变量将初始问题转化为几个易于求解的子问题, 因此近年来在图像处理和机器学习等领域得到了广泛的应用。
下面考虑用ADMM求解问题式(4)。令v=?u, w=ΛαR-θv, 则其可转化为如下约束优化问题:
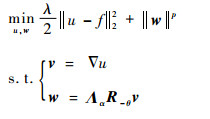 | (5) |
利用增广拉格朗日方法, 问题式(5)可转化为极大极小值问题。
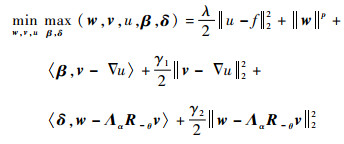 | (6) |
式中:β=(β1, β2)T, δ=(δ1, δ2)T, w=(w1, w2)T, β、δ为拉格朗日乘子;γ1、γ2 > 0为惩罚参数。显然, 鞍点问题式(6)为多变量优化问题, 因此可以利用ADMM求解:
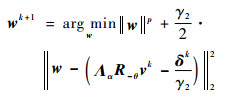 | (7a) |
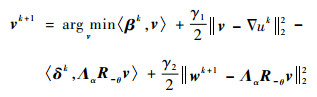 | (7b) |
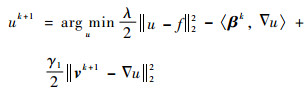 | (7c) |
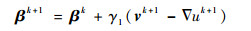 | (7d) |
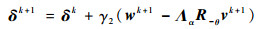 | (7e) |
下面考虑式(7)中各个子问题的具体求解过程。
1) 求解子问题式(7a)
子问题式(7a)为经典的
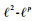
引理1??若对于任何p∈(0, 1)和w∈Y\{(0, 0)T}, 则
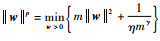
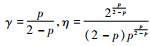
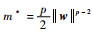
基于引理1, 子问题式(7a)可转化为
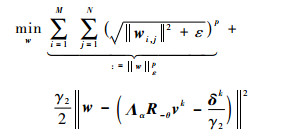 | (8) |
进一步便有
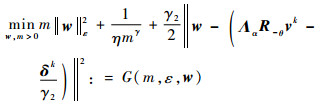 |
式中:γ和η如引理1所述。显然该问题为光滑优化问题, 故可交替求解。
算法1??ADM求解w子问题。
初始化:γ2 > 0,选择w0和ε0初始值。
步骤1??执行下述循环:
 |
式中:ρ∈(0, 1)为约束常数。
步骤2??直到满足终止条件,输出w:=wk+1。
2) 求解子问题式(7b)
子问题式(7b)为光滑凸优化问题, 其最优化条件满足:
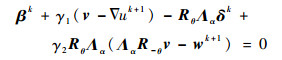 | (9) |
显然, 该问题对应二元线性方程组, 其解可表示为
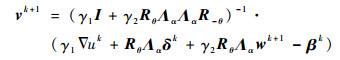 | (10) |
式中:I为单位矩阵。
3) 求解子问题式(7c)
子问题式(7c)依旧为光滑凸优化问题, 其对应的最优性条件为
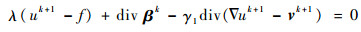 | (11) |
由于本文假设的差分离散格式是循环边界条件, 故用快速傅里叶变换求解:
 | (12) |
式中:F与F-1分别表示傅里叶变换与傅里叶逆变换;Δ为拉普拉斯算子。
综上, 求解问题式(4)的数值算法如下。
算法2??求解问题式(4)。
输入:初始变量v0、β0、δ0和参数λ、α、θ、γ1、γ2,以及最大迭代步数Maxiter和相对误差Rerr。
步骤1??利用算法1及式(10)、式(12)、式(7d)、式(7e)求解(wk+1, vk+1, uk+1, βk+1, δk+1)。
步骤2??若满足终止条件, 算法终止, 输出复原图像u:=uk+1, 否则令k=k+1, 返回步骤1。
3 数值实验 由于本文主要考虑方向性图像, 故选取图 4所示4幅图像作为测试图像, 其中图 4(a)、(b)具有单一的方向特征, 图 4(c)、(d)具有多结构的方向特征。
 |
| 图 4 仿真实验的原始图像 Fig. 4 Original image of simulation experiment |
| 图选项 |
实验中基于MATLAB2017(b)进行仿真实验, 并采用信噪比SNR与结构相似度SSIM来衡量图像去噪的有效性。另外, 若最大迭代次数达到500次或相对误差满足下述条件:
 |
则算法终止。
3.1 参数选取 模型式(4)和算法2中主要存在尺度参数α、旋转角度参数θ、正则化参数λ、指数参数p与罚参数γ1、γ2。在这些参数中, λ为主参数, 其取值严重影响数值结果,若太小, 则图像过度平滑导致边缘模糊; 若太大, 则复原图像趋向于噪声图像, 达不到去噪的目的。有效选取该参数的方法有L曲线方法或广义交叉方法等。然而, 由于本文主要考虑模型的有效性, 因此主要采用经验选取的方法, 即在较大的范围[a, b]中选取一个小区间[c, d]使得图像在区间中取得较好的复原结果。然后令λ=(c+d)/2为最优参数值。针对方向参数θ与尺度参数α, 根据图像特征经验性选取。模型中指数参数p的取值在影响模型凸性的同时也能判断是否惩罚图像结构特征的稀疏性,若p≥1, 则模型为凸性, 算法2可收敛到初始问题式(4)的全局最优解,尤其是若p接近2, 则有效保持图像的光滑区域,若p接近1, 则有效保持图像的边界区域,反之, 若p∈[0, 1), 则此时模型是非凸的, 由于其中的梯度算子为差分形式, 因此利用压缩感知理论, 可知此时保持图像的近似常数区域。实验中主要利用图像的结构特征对p进行试探性选取。若去噪图像具有较高的SNR时, 选取p值为最优值。如图 5所示, 在复原图像4(a)和(b)时通过比较可以发现,选取p=0.6和p=1.8比较合适。针对罚参数γ1与γ2, 实验中也采用经验选取方法, 本文针对不同数据的实验在[0.03,22]之间选取。
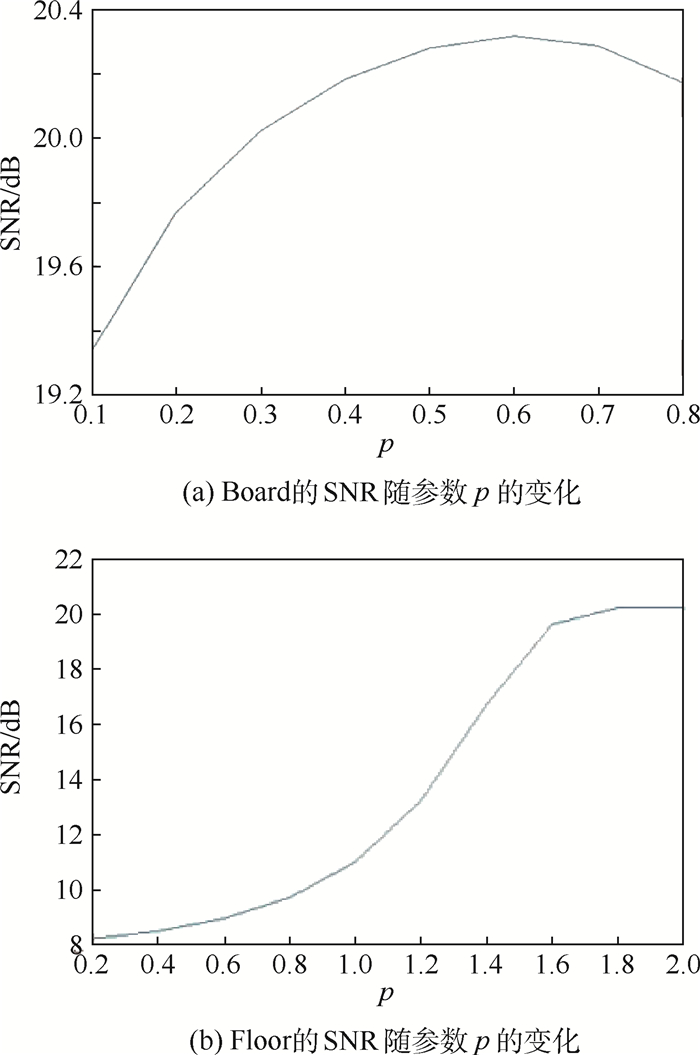 |
| 图 5 DTVP模型去噪过程中SNR随参数p的变化 Fig. 5 Variation of SNR with p during denoising by DTVP model |
| 图选项 |
3.2 实验比较与分析 文献[7]利用半隐式梯度下降法求解, 而该模型可以归类于本文p=1的情况, 因此本文利用ADMM求解, 记为ADMM-DTV, 并与ROF模型和DTV去噪模型进行比较。
本文采用信噪比SNR和结构相似度SSIM客观评价质量指标对各种图像处理结果进行评价,如表 1所示。评价去噪效果时, SNR和SSIM的值越大, 表明去噪效果越好。本文中选取不同的图像分别加入不同强度的噪声(噪声方差σ=0.01、0.05、0.1)进行实验, 表 1总结了不同去噪算法对不同图像实验结果的信噪比SNR和结构相似度SSIM值的比较结果。可以看出, DTV、ADMM-DTV和DTVP去噪模型的SNR明显高于ROF模型, 而且DTVP去噪模型比DTV和ADMM-DTV去噪模型的SNR和SSIM数值都大, 从侧面反映出DTVP去噪模型的去噪效果更好, 不仅可以去除噪声影响, 还可以重建出更多清晰的高频段纹理, 当图像纹理越强时, 去噪性能越优。所加噪声为σ=0.01时, 对于图 4中方向单一的图像(见图 4(a)、(b)),纹理性较弱, 图像存在大面积平滑区域, DTV、ADMM-DTV和DTVP去噪模型去噪获得的SNR高于ROF模型不足1 dB, DTV、ADMM-DTV和DTVP去噪模型之间的SNR不太明显。对于图 1中具有多结构的方向图像(见图 4(c)、(d)), 图像纹理性较强, 因此更能体现模型的优越性, DTVP模型的SNR高于ROF模型1.5 dB左右。
表 1 不同去噪模型去噪后所得的SNR和SSIM比较 Table 1 Comparison of SNR and SSIM obtained after denoising by different denoising models
| 图像 | 模型 | SNR/dB | SSIM | |||||
| σ=0.01 | σ=0.05 | σ=0.1 | σ=0.01 | σ=0.05 | σ=0.1 | |||
| 图 4(a) | ROF | 18.846 5 | 14.873 3 | 13.415 7 | 0.757 9 | 0.461 0 | 0.332 2 | |
| DTV | 19.823 9 | 15.971 4 | 14.301 1 | 0.792 0 | 0.554 5 | 0.428 4 | ||
| ADMM-DTV | 19.896 0 | 16.060 4 | 14.381 1 | 0.796 2 | 0.560 1 | 0.438 9 | ||
| DTVP | 19.923 1 | 16.219 2 | 14.607 0 | 0.800 0 | 0.591 5 | 0.484 1 | ||
| 图 4(b) | ROF | 21.350 5 | 19.210 5 | 18.414 8 | 0.652 1 | 0.511 8 | 0.462 0 | |
| DTV | 21.530 8 | 19.344 0 | 18.478 3 | 0.673 2 | 0.532 0 | 0.483 0 | ||
| ADMM-DTV | 21.804 4 | 19.842 5 | 19.149 4 | 0.682 2 | 0.553 5 | 0.508 3 | ||
| DTVP | 22.024 1 | 20.224 6 | 19.509 4 | 0.701 4 | 0.578 0 | 0.534 2 | ||
| 图 4(c) | ROF | 19.094 0 | 12.534 0 | 09.684 7 | 0.982 6 | 0.922 5 | 0.854 2 | |
| DTV | 19.314 8 | 12.755 5 | 9.880 8 | 0.983 5 | 0.926 2 | 0.860 4 | ||
| ADMM-DTV | 19.537 1 | 12.908 6 | 10.054 3 | 0.984 3 | 0.928 6 | 0.865 5 | ||
| DTVP | 20.251 9 | 13.567 8 | 10.446 6 | 0.986 6 | 0.938 3 | 0.876 1 | ||
| 图 4(d) | ROF | 19.428 8 | 14.903 9 | 13.196 0 | 0.851 0 | 0.642 0 | 0.486 9 | |
| DTV | 20.483 1 | 15.805 8 | 13.887 4 | 0.884 4 | 0.703 9 | 0.573 8 | ||
| ADMM-DTV | 20.699 0 | 16.016 1 | 14.011 2 | 0.889 1 | 0.712 0 | 0.586 4 | ||
| DTVP | 20.925 7 | 16.325 7 | 14.357 3 | 0.896 1 | 0.740 7 | 0.622 7 | ||
表选项
从图 6中的实验结果可以看出, ROF、DTV和ADMM-DTV的残差图像灰度值较大, 且波动较大, 而DTVP的残差图像灰度值较小, 图像偏暗, 波动较小。残差图像灰度值越小,图像去噪效果越好。实验结果表明,DTVP去噪模型去噪的效果明显优于ROF模型和DTV去噪模型, 去噪后的图像纹理信息得到更好地保持。仿真实验中所加噪声为σ=0.05, 尺度参数α=2, 旋转角度参数θ=0.5π, 指数参数p=0.8。
 |
| 图 6 不同去噪模型去噪后的残差图像比较 Fig. 6 Compare residual image after denoising by different denoising models |
| 图选项 |
本文以图 4(b)为例对图像去噪前后的结果进行对比, 如图 7所示。经过ROF、DTV、ADMM-DTV和DTVP去噪实验结果的SNR和SSIM分别为21.350 5 dB、21.530 8 dB、21.804 4 dB、22.024 1 dB、0.652 1、0.673 2、0.682 2和0.701 4。这从定量描述中反映出DTVP算法相比ROF、DTV、ADMM-DTV算法重建效果更佳。另外可以看到DTVP的去噪效果最好, 不仅提高了图像的清晰度, 而且保留了图像的纹理信息。仿真实验中所加噪声σ=0.01,尺度参数α=2.3,旋转角度参数θ=0.75π,指数参数p=1.89。
 |
| 图 7 不同去噪模型去噪后的复原图像比较 Fig. 7 Compare restored images after denoising by different denoising models |
| 图选项 |
本文以图 4(d)为例对图像去噪前后的结果进行对比, 如图 8所示。从处理结果可看出, 噪声基本被抑制, 并且图像的边缘和细节特征也得到保留。可近一步说明, 本文的模型有效地将噪声图像基本恢复到接近于原图。
 |
| 图 8 不同去噪模型去噪后的直方图比较 Fig. 8 Compare histograms after denoising by different denoising models |
| 图选项 |
4 结论 本文通过分析ROF模型和DTV去噪模型, 针对其不足, 提出了正则项基于参数p的自适应模型, 并通过实验证明:
1) 具有全变分去噪模型的优点, 更好地去除平滑区域的噪声, 降低了全变分模型引入的阶梯效应。
2) 具有DTV去噪模型的优点, 同时可以更好地刻画图像的结构信息。
仿真实验表明, 本文提出的正则项基于参数p的自适应方法降噪效果明显优于ROF模型和DTV去噪模型, 在去噪的同时保留了更多的图像细节信息, 去除噪声更充分, 获得更高的峰值信噪比和结构相似度。当图像纹理方向性越明显时, 去噪优越性越明显, 主观视觉效果方面更佳。另外, 实验表明针对方向性明显的图像通常取较大的权重α, 以利于模型对应的偏微分方程沿边界切线方向扩散, 进而达到保持图像边缘的目的, 同时针对该类图像可以有效地判断方向角θ。然而,对于结构比较复杂和噪声较大的图像, 权参数α与方向角θ的判断更具有挑战性。因此, 下一步工作将研究如何结合图像的结构特征建立权重α与方向角θ具有自适应选取性质的图像复原模型。
参考文献
| [1] | CATTE F, LIONS P L, MOREL J M, et al. Image selective smoothing and edge detection by nonlinear diffusion[J]. SIAM Journal on Numerical Analysis, 1992, 29(1): 182-193. DOI:10.1137/0729012 |
| [2] | RUDIN L, OSHER S, FATEMI E. Nonlinear total variation based noise removal algorithms[J]. Physica D:Non-linear Phenomena, 1992, 60(1-4): 259-268. DOI:10.1016/0167-2789(92)90242-F |
| [3] | HOREV I, NADLER B, ARIAS-CASTRO E, et al. Detection of long edges on a computational budget:A sublinear approach[J]. SIAM Journal on Imaging Science, 2015, 8(1): 458-483. DOI:10.1137/140970331 |
| [4] | HU Y, ONGIE G, RAMANI S, et al. Generalized higher degree total variation (HDTV) regularization[J]. IEEE Transactions on Image Processing, 2014, 23(6): 2423-2435. DOI:10.1109/TIP.2014.2315156 |
| [5] | BREDIES K, KUNISCH K, POCK T. Total generalized variation[J]. SIAM Journal on Imaging Science, 2012, 3(3): 492-526. |
| [6] | COLL B, DURAN J, SBERT C. Half-linear regularization for nonconvex image restoration models[J]. Inverse Problem and Imaging, 2015, 9(2): 337-370. DOI:10.3934/ipi |
| [7] | BAYRAM I, KAMASAK M. Directional total variation[J]. IEEE Signal Processing Letters, 2012, 19(12): 781-784. DOI:10.1109/LSP.2012.2220349 |
| [8] | ZHANG H, WANG Y Q. Edge adaptive directional total variation[J]. The Journal of Engineering, 2013, 2013(11): 61-62. DOI:10.1049/joe.2013.0116 |
| [9] | BAI J, FENG X C. Fractiona-order anisotropic diffusion for image denoising[J]. IEEE Transactions on Image Processing, 2007, 16(10): 2492-2502. DOI:10.1109/TIP.2007.904971 |
| [10] | ZHANG J P, CHEN K. A total fraction-order variation model for image restoration with non-honogeneous boundary conditions and its numerical solution[J]. SIAM Journal on Imaging Science, 2015, 8(4): 2487-2518. DOI:10.1137/14097121X |
| [11] | ARCHIBALD R, GELB A, PLATTE R. Image reconstruction from undersampled Fourier data using the polynomial annihilation transform[J]. Journal of Scientific Computing, 2016, 67(2): 432-452. DOI:10.1007/s10915-015-0088-2 |
| [12] | GUO W H, QIN J, YIN W T. A new detail-preserving regularity scheme[J]. SIAM Journal on Imaging Sciences, 2014, 7(2): 1309-1334. DOI:10.1137/120904263 |
| [13] | WANG Q, WU Z H, SUN M J, et al. Single image super-resolution using directional total variation regularization and alternating direction method of multiplier solver[J]. Journal of Electronic Imaging, 2015, 24(2): 023026. DOI:10.1117/1.JEI.24.2.023026 |
| [14] | CHAN T F, ESEDOGLU S. Aspects of total variation regularized L1 function approximation[J]. SIAM Journal on Applied Mathematics, 2005, 65(5): 1817-1837. DOI:10.1137/040604297 |
| [15] | CHAMBOLLE A, POCK T. A first-order primal-dual algorithm for convex problems with applications to imaging[J]. Journal of Mathematical Imaging and Vision, 2011, 40(1): 120-145. DOI:10.1007/s10851-010-0251-1 |
| [16] | YUAN J H, YANG J, SHI D, et al. A continuation fixed-point iterative method on harmonic generations with strong nonlinear optical effects in multi-layer structures[J]. Computational and Applied Mathematics, 2017, 36(1): 805-824. DOI:10.1007/s40314-015-0267-7 |
| [17] | ECKSTEIN J, BERTSEKAS D. On the Douglas-Rachford splitting method and the proximal point algorithm for maximal monotone operators[J]. Mathematical Programming, 1992, A55(3): 293-318. |
| [18] | XU Z B, ZENG J S, WANG Y, et al. L1/2 regularization:Convergence of iterative half thresholding algorithm[J]. IEEE Transactions on Signal Processing, 2014, 69(2): 2317-2329. |
| [19] | CHAN R, LIANG H X.Half-quadratic algorithm for 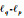 problems with application to problems with application to 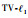 image restoration and compressive sensing[M]//BRUHN A, POCK T, TAI X C.Efficient algorithms for global optimization method in computer vision.Berlin: Springer, 2014: 78-103. image restoration and compressive sensing[M]//BRUHN A, POCK T, TAI X C.Efficient algorithms for global optimization method in computer vision.Berlin: Springer, 2014: 78-103. |
