为了实现AGV的视觉定位,需要事先给AGV提供一张三维“地图”,供AGV搜索匹配,以此完成位姿的求解任务。地图是一种包含环境空间几何信息的结构,有多种表示方法[3]。其中,基于路标的稀疏地图是常用的一种表示法。稀疏地图将环境抽象为一些表示空间三维坐标的3D路标,利用“描述子”对这些3D路标进行区分。视觉传感器根据这些独一无二的描述子对检测到的图像特征点和地图进行匹配,从而实现数据关联,实现位姿的求解。对于3D路标的表示,点特征是最常用的描述方法,如ORB(Oriented fast and Rotabed Brief)特征[4]和SIFT(Scale-Invariant Feature Transform)特征[5]等,另外一些更复杂的几何特征也被用于描述3D路标,如线特征、平面和灭点[6]。
全局定位算法要求在任何位置,都能根据传感器的数据,唯一地、重复地解算出AGV的位姿。这极大地简化了定位策略,然而这通常是困难的[7]。基于视觉的全局定位方式面临噪声和混淆两大问题的挑战。视觉传感器的噪声来自于光照变化、图像抖动和模糊、遮挡等多个方面,极大地影响到3D特征的检测和匹配。混淆即通过视觉无法分辨相似场景(如走廊)[8]。在AGV作业的工业环境中,环境通常是动态变化的(如白天和夜晚光照的变化,托盘的移动等),同时存在大量的相似场景(如货架等),使得采用自然特征构建地图的策略变得困难。一方面动态环境使得难以建立稳定不变的3D路标,另一方面是大量重复的场景给数据关联带来挑战。Wulf等[9]为了克服动态场景的影响,使用仓库天花板的结构和特征作为导航定位依据。但是在智能泊车的应用场景中,AGV需要在上方放置托盘运送汽车,同时AGV自身高度也极低(30 cm左右),很难看到工业环境的天花板。在环境中铺设位置已知、易于识别、不会变化的人工路标,可以辅助机器人的定位,如在激光定位中使用的反光板。然而,在工业应用中,为了能覆盖AGV行驶的所有路径,往往需要设置大量的人工路标,如何准确无误地匹配这些路标是具有挑战性的问题[10]。
本文针对以上问题,考虑AGV车身高度低,上方运载货物的限制,提出了一种新的二维编码点作为人工路标,并以此为基础实现鲁棒的特征匹配,构建了一种稀疏地图,供AGV搜索匹配,实现AGV精确的全局定位。二维编码点设计为方形棋盘格样式,通过黑白色块编码ID信息,作为二维编码点的区分标志;二维编码点作为人工路标铺设于地面,使用单反相机进行拍摄,通过一种分参数块的三维重建方法,实现厂房的大规模地图构建,生成一种稀疏电子地图。实验结果表明,使用本文方法,AGV视觉传感器能准确识别每个编码点的编码信息,并和提供的电子地图鲁棒匹配,完成定位任务,速度和精度都能满足工业应用要求。
1 二维编码点的设计、检测及解码 1.1 二维编码点的设计 工业环境中使用的人工路标要求能够易于识别,同时,如果每个编码点都有自己独一无二的编码信息,可大大简化多幅图像之间的匹配[11]。常用的人工编码点为环状编码点,如图 1(a)所示[12]。此种编码点利用环带编码信息。由于圆形的周期性,解码时需要以每一位为起点进行解码,然后进行选择;同时周期性使得编码容量较小。本文设计一种新的大容量二维编码点,如图 1(b)所示。编码点设计为底色为黑色的正方形,使用时印刷在白色背景上。方形二维编码点仅有4种可能的解码方向,提高了解码效率。编码区域划分为7×7的棋盘格,每一格可为黑色或者白色,分别对应二进制编码0和1。49位二进制数字作为二维编码点的编码结果,为了方便起见,二进制编码结果会映射到从0开始编码的十进制数字。理论上可以有249种编码方式,容量满足工业大规模应用的需求。
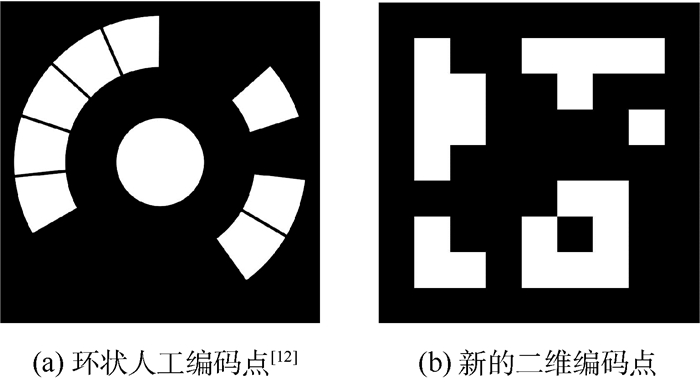 |
| 图 1 编码点 Fig. 1 Coded points |
| 图选项 |
1.2 二维编码点的检测 二维编码点检测的关键是识别编码点的黑色四边形边框。基于此提出了一种四边形区域的检测算法,以提取出二维编码点可能存在的区域。检测算法的流程如下。
1.2.1 图像预处理 图像预处理包括滤除图像噪声和提取显著的图像特征。首先对原始图像(图 2(a))进行平滑处理,使用高斯模板进行滤波,减小噪声带来的影响。然后使用传统的Canny算子[13]检测图像梯度显著变化的点,并对这些点进行连接和聚类,获得图像中的轮廓(图 2(b))。同时对图像进行Harris角点检测[14],获得整幅图像每个像素点的角点响应值(图 2(c))。
 |
| 图 2 二维编码点的检测和识别 Fig. 2 Detection and recognition of two-dimensional coded points |
| 图选项 |
1.2.2 四边形检测 对于四边形的检测基于如下的假设:具有4个顶点的轮廓为四边形。对于每一组轮廓,判断是否为四边形的算法步骤如下:
1) 将轮廓的每个像素扩大至3×3的区域作为图像掩模。
2) 对Harris角点的响应图使用掩模,将掩模以外的区域设置为0(图 2(d))。
3) 寻找全图响应值最大的点,作为一个顶点并记录;并对角点响应图该点处进行非极大值抑制(NMS)。
4) 重复步骤3),直至最大响应值小于一定的阈值。
5) 若记录的顶点数目为4,则判断该轮廓为四边形;否则舍弃该轮廓。
由此可判断该轮廓是否为四边形,如果是四边形,还记录保存了四边形的4个顶点。检测结果中会包含一些凹四边形,如图 2(e)左上角,凹四边形明显不符合二维编码点的透视投影规律,因此对所有检测结果用Graham scan算法[15]进行筛选,保留下仅为凸包的四边形(图 2(f))。
1.3 二维编码点的解码 如图 2(g)所示,解码通过二维平面点的单应变换实现。首先在理想二维编码点上建立坐标系,同时获得所有编码位置的坐标,并将其投影到实际图像中。理想二维编码点的坐标系建立在中心,从左下角开始,按顺时针顺序4个角点坐标设为(-1,-1),(-1,1),(1, 1),(1,-1)。设理想二维编码点角点齐次坐标为X1=(u1, v1, 1)T,角点图像坐标为X2=(u2, v2, 1)T,两者之间的变换关系为
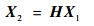 | (1) |
式中:H=(h1, h2, h3)T为3×3的单应矩阵,变换式(1)有
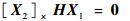 | (2) |
其中:[]×表示向量之间的叉乘。由式(2)得
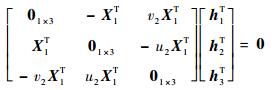 | (3) |
即单应矩阵的求解转换为最小二乘问题AX=0,其中hi表示H矩阵的第i行。对A做奇异值解得A=UDVT取V最后一列,即为单应矩阵H。
得到单应矩阵后,使用单应矩阵把每一位编码投影到图像中得到相应的坐标,根据图像中该像素点的灰度值和阈值,决定该点编码为0还是1对49个位置解码得到最终的二进制编码串,从而实现二维编码点的解码。把解码结果和编码数据库进行对照匹配,获得最终的编码ID。如果在数据库中没有该编码,则舍弃该四边形。为了使识别结果更加鲁棒,在设计二维编码点时应遵循以下原则:
1) 同一编码点一次顺时针旋转90°,可以获得4种不同的编码(没有对称的情况)。为了使二维编码点具有旋转不变性,4种编码点只使用一种,其余编码情况舍弃。同时避免对称的二维编码点设计。
2) 舍弃简单的二维编码点设计,如全黑和全白。
3) 二维编码点编码值之间汉明距离大于一定的阈值,使之易于区分。
二维编码点的最终检测结果包含4个有序角点像素坐标和编码ID,同时可以通过4个角点坐标计算出编码点的中心坐标。因此,结合编码ID,每个二维码可以提供5个特征点用于特征匹配。每个特征点的ID和像素坐标使用散列表存储,匹配通过散列表的查找实现,在速度和准确率上都优于依靠特征描述子的特征匹配方法。
2 全局稀疏地图重建算法 基于上述的特征点匹配方法,提出一种全局稀疏地图的重建算法,流程如图 3所示。重建算法将相机内参数加入到参数列表中,省去了相机标定的过程。
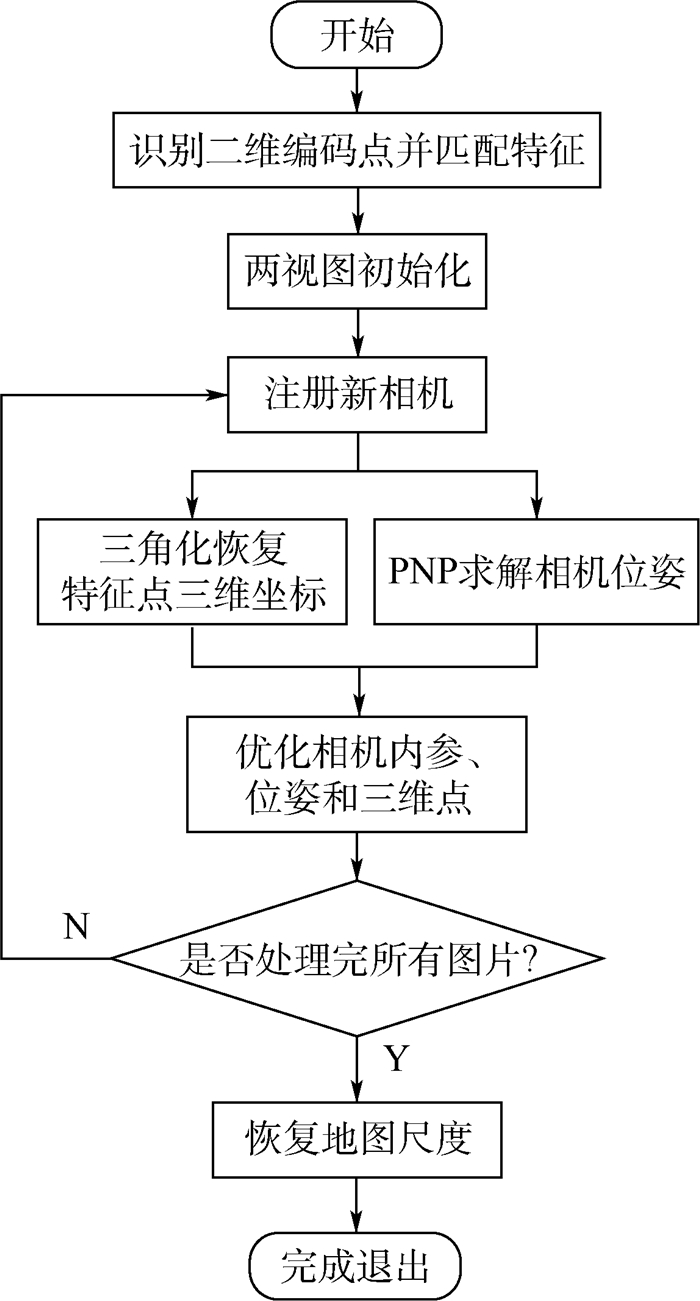 |
| 图 3 全局稀疏地图重建流程图 Fig. 3 Flowchart of global sparse map reconstruction |
| 图选项 |
2.1 基于多模型的两视图初始化 初始化是指由最初两视图建立世界坐标原点和初始三维点的过程,其结果的好坏直接影响随后重建算法的收敛性。初始化必须被谨慎处理,因此同时采用单应矩阵初始化模型和本质矩阵初始化模型[16]。用H表示初始化的平面单应矩阵,E表示初始化的本质矩阵。对于初始化结果,采用如下的评价方式:
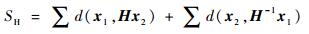 | (4) |
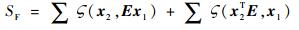 | (5) |
式中:x1和x2为图像中对应点的图像齐次坐标;d(·)为图像像素点之间的欧氏距离;?(·)为点到极线的垂直距离。对于二者的选择,采用如下的经验式:
 | (6) |
若R>0.6,则选择平面单应模型;反之,则选择本质矩阵的初始化模型。由经验值可以看出,因为是在平坦地面铺设的二维编码点,所以更倾向于使用平面单应模型进行初始化。
2.2 分参数块优化地图参数 初始化过后,对于每一帧新到来得图片,使用三角化算法和迭代PNP算法[16],进行新的三维点生成和新相机的注册。值得注意的是,为了在AGV行驶过程中没有盲区,每个二维码提供的特征点都需要记录在电子地图中。因此在三维重建过程中,并不判断新恢复的特征点质量的好坏,也不舍弃任何特征点,对于三维重建结果较差的点,通过优化算法进行优化更新。
三维地图重建的过程中,相机参数并没有被标定,而是被赋予了一定的初值,三维点和相机姿态的初始值也是不准确的,需要不断对相机内参、相机姿态和三维点进行优化。优化的指标通常为重投影误差,即三维点通过相机投影模型投影到图像中的坐标,和拍摄图片中对应点像素观测值的残差。用数学表达式为
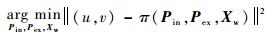 | (7) |
式中:π(·)表示相机的投影模型,采用针孔成像模型;Pin为相机内参数,包括焦距、主点和畸变,拍摄过程中相机内参保持不变;Pex={Ri, ti}i∈?为相机的位姿参数,包括旋转和平移,?为所有的图片集合;Xw={xk, yk, zk}k∈p为所有三维点的坐标,p为所有的三维点集合。对于该问题,待优化参数非常多,在优化求解式(7)的过程中非常容易发散。为了使算法收敛,需要给每个待估计的状态量赋予良好的初值。对于相机外参数Pex,使用迭代PNP算法的结果作为初值;对于三维点Xw,使用三角化的结果作为初值;对于相机内参数Pin,以像素为单位的焦距f由式(8)确定:
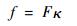 | (8) |
式中:F为相机镜头的焦距;κ为像素有效长度的倒数。相机拍摄画面的宽为w, 高为h,设置主点参数为
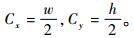
在优化过程中,采用相机位姿参数、机内参数和三维点坐标分块优化的方法来避免算法发散。在两视图初始化过后,首先固定相机的位姿参数进行优化,然后固定相机内参数和三维点坐标,优化相机位姿参数;当新的图片加入地图过后,首先优化相机内参数,然后固定相机内参数,优化相机位姿参数和三维点坐标。每过一段时间,对所有的参数进行一次整体优化。同时,通过固定参数减少参数量,避免算法发散。相机内参数在图片多于一定张数过后,就不再参与优化,而是固定下来,相当于完成了相机的标定。如果相机外参数或三维点参与优化到达一定次数,则不再将其加入优化算法,而是作为最后的测量值保存下来。整个优化算法流程如下,
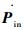
算法1??优化重投影误差算法。
输入:相机内参数Pin,相机外参数Pex,三维点坐标Xw。
输出:参数优化结果。
步骤1??初始化。优化目标函
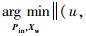
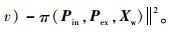
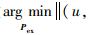
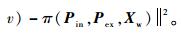
步骤2??注册新相机。优化目标函数
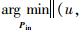
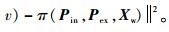
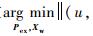
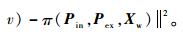
步骤3??若注册新相机数目超过一定阈值,
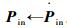
步骤4??若某一相机位姿参数Pexi参与优化次数超过预定次数,则从Pex中剔除。
步骤5??若某一三维点坐标参数Xwi参与优化次数超过预定次数,则从Xw中剔除。
步骤6??若距离上一次全局优化,新注册的相机超过一定数目,进行一次全局优化,优化目标函数为
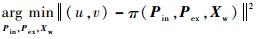
步骤7??返回步骤2,直至所有图片处理完毕。
分参数块优化的策略使得算法对于较差的初始值鲁棒性更强。通过不断剔除参数,避免了参数规模的无限制增长,使得算法更容易收敛。
3 基于稀疏地图的定位技术 AGV的定位通过提取图像中的二维编码点和稀疏地图进行数据关联,求解PNP实现。AGV位姿的解算结果包括航向(和世界坐标系x轴的夹角)和位置(x, y坐标)2部分。如图 4所示,一共有世界坐标系(Ow)、相机坐标系(Oc)和AGV坐标系(Ov) 3个坐标系。世界坐标系的xy平面建立在地平面上;使用激光跟踪仪将AGV坐标系建立在AGV正中心,并使得x轴朝前、z轴垂直向上。Tcw为PNP解算结果,Tcv由事先标定得到。Tab为将b系坐标下的点转换到a系下所使用的变换。
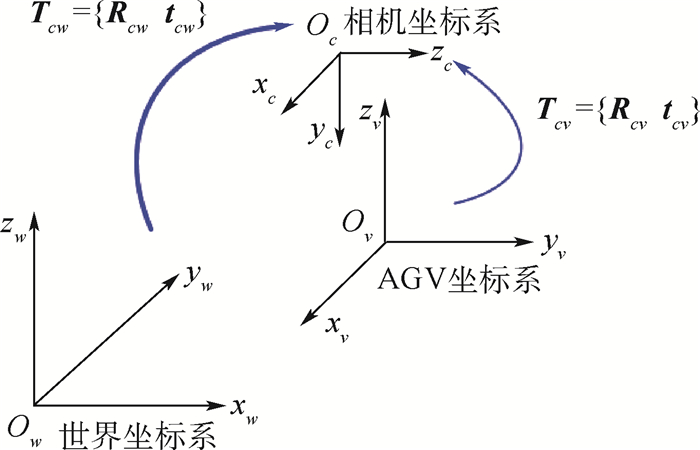 |
| 图 4 坐标系转换关系 Fig. 4 Transformation relationship of coordinate system |
| 图选项 |
由坐标转换关系,推导AGV小车在世界坐标系下的平移和旋转为
 | (9) |
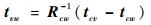 | (10) |
AGV正方向为rv=(1, 0, 0)T,将其转换到世界坐标系下:
 | (11) |
设正航向和世界坐标系x轴的夹角为θ,得到航向角度为
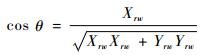 | (12) |
因为世界坐标系xy平面建立在地平面上,取tvw的前两维坐标即为AGV的x坐标和y坐标。
4 实验和实际应用 4.1 大规模地图构建实验 在55 m×15 m的工业环境中以0.2 m的间距铺设二维编码点,共20 671个。为了减少相机噪声带来的影响,提高二维编码点角点提取的精度,使用尼康D810单反拍摄高分辨图片(7 360像素×4 912像素)。相机使用焦距为24 mm镜头,视觉感器有效像素为3 635万,尺寸大小为35.9 mm×24 mm,计算得到相机内参初值fx=fy=4 979.512。设置主点的初始参数为Cx=3 680,Cy=2 456.5。共顺序拍摄540张照片(图 5)。建图采用离线的方式,整个过程需要5 h左右。最后以场地的短边作为参照恢复尺度,并将稀疏地图转换到以0号编码点为原点,xy平面建立在地面,x为场地长边,z轴朝上的坐标系。重建结果如图 6所示。为了评定重建结果,使用地面的二维编码点边长作为参考,二维编码点使用360 dpi(dpi为每英寸点数)的打印机打印,边长的理论值为(28.00±0.07) mm。使用统计方法的评定结果见表 1。随机选取地面上的编码点,用精度为1 mm卷尺进行小、中和大3种尺度的测量,并和重建稀疏地图中相应的距离比较,比较结果如图 7(a)~(c)所示。小、中、大3种尺度的平均误差分别为0.5、5.2、6.7 mm, 误差的标准差分别为0.4、2.1、4.8 mm。
 |
| 图 5 用于重构的原始图像 Fig. 5 Original image for reconstruction |
| 图选项 |
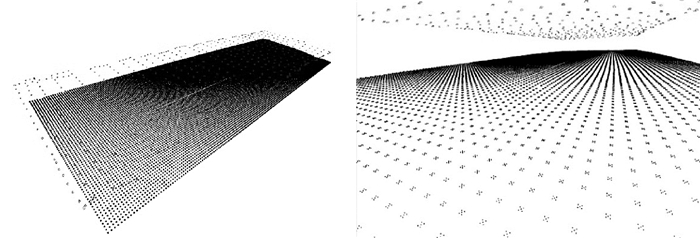 |
| 图 6 用于定位的稀疏地图 Fig. 6 Sparse map for localization |
| 图选项 |
表 1 二维编码点边长重构统计结果 Table 1 Statistical results of two-dimensional code side length reconstitution
| mm | |||
| 参数 | 平均值 | 平均误差 | 标准差 |
| 数值 | 27.98 | 0.05 | 0.08 |
表选项
 |
| 图 7 测量值和重建值结果的对比 Fig. 7 Comparison of measurement and reconstruction results |
| 图选项 |
4.2 AGV定位实验 搭载视觉定位系统的AGV如图 8所示,矩形标注的部分即为视觉定位系统。AGV使用麦克纳姆轮,能在拥挤的工业环境中最大限度地减少转弯半径。车体高度为293 mm,中间部留有720 mm×800 mm的空间,用于安装视觉定位系统。由于高度较低,相机视场较小,因此使用2个相机,其中一个相机作为另一个相机的辅助相机,当主相机视野中没有检测到二维编码点时,使用辅助相机进行检测。该系统选用2个大恒MER-200-20GM-P工业相机,该型号相机帧率为20帧/s,分辨率为1 628像素×1 236像素,使用触发器控制2个相机同时获取图像;在侧面下部安装2个条形光源,减少光照变化带来的影响。
 |
| 图 8 搭载视觉定位系统的AGV Fig. 8 AGV equipped with visual localization system |
| 图选项 |
为了验证该定位方法的可行性,在真实环境中分别对AGV的主要状态进行定位实验。
4.2.1 静态定位实验 AGV的最常见的状态停在某个车位长时间静止。将AGV停在某一车位,并记录x、y和角度的数据,结果如图 9所示。由图 9可知,定位结果稳定且没有漂移。x坐标最大变化范围为0.21 mm,重复定位精度为0.03 mm;y坐标最大变化范围为0.19 mm,重复定位精度为0.01 mm;角度最大变化范围为0.12°,重复定位精度为0.01°。
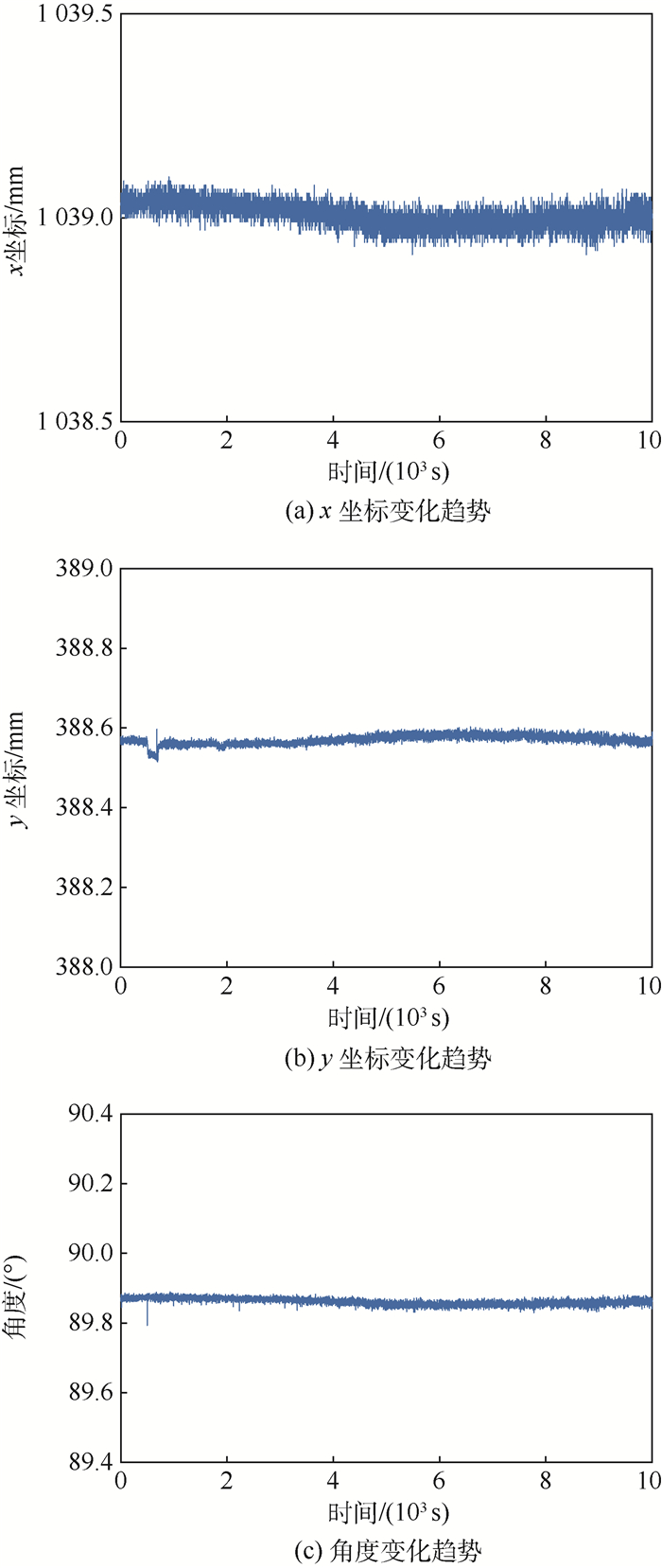 |
| 图 9 静态定位实验 Fig. 9 Experiment of static localization |
| 图选项 |
4.2.2 动态定位实验 使用控制器控制AGV在B201、B104两个车位之间反复行驶。每次使AGV停在B201车位相同的起点,设定路径如下:从B201车位出发,前进6.23 m到达行车道,左转90°前进2.80 m,右转90°前进6.12 m进入B104车位。使用控制器控制AGV在该预定路径行驶,并记录定位系统的输出。记录的10次往返过程中起点和终点的停车定位数据见表 2。x坐标最大变化范围为1.0 mm,重复定位精度为0.3 mm;y坐标数据最大变化范围为0.9 mm,重复定位精度为0.2 mm;角度最大变化范围为0.9°,重复定位精度为0.3°。
表 2 动态定位结果 Table 2 Result of dynamic localization
| 车位 | 测量次数 | x坐标/mm | y坐标/mm | 角度/(°) |
| B201 | 1 | 31 814.1 | 13 511.2 | 89.4 |
| 2 | 31 813.9 | 13 512.1 | 89.5 | |
| 3 | 31 814.0 | 13 512.0 | 89.6 | |
| 4 | 31 813.9 | 13 511.8 | 90.3 | |
| 5 | 31 814.0 | 13 511.7 | 89.4 | |
| 6 | 31 813.8 | 13 511.9 | 89.9 | |
| 7 | 31 814.1 | 13 512.0 | 89.8 | |
| 8 | 31 813.9 | 13 511.9 | 89.8 | |
| 9 | 31 813.9 | 13 511.8 | 89.6 | |
| 10 | 31 813.7 | 13 511.8 | 89.6 | |
| B104 | 1 | 34 600.7 | 1 154.9 | 270.5 |
| 2 | 34 600.7 | 1 154.9 | 270.3 | |
| 3 | 34 601.6 | 1 155.3 | 270.5 | |
| 4 | 34 601.7 | 1 155.2 | 270.8 | |
| 5 | 34 601.3 | 1 155.4 | 271.1 | |
| 6 | 34 601.7 | 1 155.2 | 270.3 | |
| 7 | 34 601.5 | 1 154.9 | 270.8 | |
| 8 | 34 600.9 | 1 154.8 | 270.8 | |
| 9 | 34 600.9 | 1 154.7 | 270.7 | |
| 10 | 34 600.8 | 1 155.1 | 271.2 |
表选项
为了能让AGV每次都准确进入狭窄的车位,需要很高的轨迹重复精度。对于整条行驶路径的重复定位精度,采用KITTI[17]中视觉里程计的评价方式。该方法用于评价2条轨迹之间的相近程度,最后结果用2条轨迹之间的位置误差表示,越小则说明2条轨迹越相近。按照原始方法,设置评价尺度为10 m。对于记录的定位数据进行处理,每一组数据从第10帧开始运动,直到终点停止,共记录951帧数据。记录的4组轨迹如图 10所示,对记录的4组定位数据两两进行比较,获得最终结果见表 3。轨迹重复定位精度(即平均位移误差)为0.082%,轨迹的重复精度很高。
 |
| 图 10 行驶轨迹 Fig. 10 Travelling trajectory |
| 图选项 |
表 3 定位轨迹的误差 Table 3 Error of localization trajectory
| % | ||
| 比较次数 | 位移误差 | 平均位移误差 |
| 1 | 0.071 | 0.082 |
| 2 | 0.084 | |
| 3 | 0.082 | |
| 4 | 0.087 | |
| 5 | 0.082 | |
| 6 | 0.084 | |
表选项
目前采用该方法的定位系统已在工业环境中稳定测试超过一个月。完全满足工业应用的要求。
5 结论 1) 提出了一种新的大容量人工标志点,能在工业环境中大规模布置。并以此为基础,构建了一种可用于AGV视觉定位的稀疏地图。该稀疏地图稳定不变,且匹配策略简单鲁棒。
2) AGV定位时不需要当前状态的先验信息,有效地解决了机器人的“绑架”问题;仅根据当前状态解算AGV位姿,不会出现累积误差,解决了“静态漂移”的问题,同时也保证了定位的重复性非常高。
3) 路线灵活,没有预设轨迹,AGV在全场任何位置均可获得定位信息。
实验和实际应用表明,该方法简单实用,不受环境变化影响,AGV运行频率达20 Hz,停车重复定位精度小于0.5 mm,角度偏差小于0.5°,轨迹平均位移误差小于0.1%,为AGV的视觉定位方法提供了新的思路。
致谢 感谢中国航天科工集团第三研究院北京星航机电装备有限公司对本研究的大力支持。
参考文献
| [1] | 张建鹏, 楼佩煌, 钱晓明, 等. 多窗口实时测距的视觉导引AGV精确定位技术研究[J]. 仪器仪表学报, 2016, 37(6): 1356-1365. ZHANG J P, LOU P H, QIAN X M, et al. Research on precise positioning technology by multi-window and real-time measurement for visual navigation AGV[J]. Chinese Journal of Scientific Instrument, 2016, 37(6): 1356-1365. DOI:10.3969/j.issn.0254-3087.2016.06.020 (in Chinese) |
| [2] | KIM J, CHUNG W. Localization of a mobile robot using a laser range finder in a glass-walled environment[J]. IEEE Transactions on Industrial Electronics, 2016, 63(6): 3616-3627. DOI:10.1109/TIE.2016.2523460 |
| [3] | CESAR C, LUCA C, HENRY C, et al. Past, present, and future of simultaneous localization and mapping:Toward the robust-perception age[J]. IEEE Transactions on Robotics, 2016, 32(6): 1309-1332. DOI:10.1109/TRO.2016.2624754 |
| [4] | RUBLEE E, RABAUD V, KONOLIG K, et al.ORB: An efficient alternative to SIFT or SURF[C]//International Conference on Computer Vision.Piscataway, NJ: IEEE Press, 2012: 2564-2571. https://www.researchgate.net/publication/221111151_ORB_an_efficient_alternative_to_SIFT_or_SURF |
| [5] | LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. DOI:10.1023/B:VISI.0000029664.99615.94 |
| [6] | LU Y, SONG D. Visual navigation using heterogeneous landmarks and unsupervised geometric constraints[J]. IEEE Transactions on Robotics, 2017, 31(3): 736-749. |
| [7] | ROLAND S, ILLAH R N, DAVIDE S, et al. Introduction to sutonomous mobile robots[M]. Cambridge: MIT Press, 2010: 345-346. |
| [8] | 曹天扬, 蔡元浩, 东方明, 等. 结合图像内容匹配的机器人视觉导航定位与全局地图构建系统[J]. 光学精密工程, 2017, 25(8): 2222-2232. CAO T Y, CAI Y H, DONG F M, et al. Robot vision system for keyframe global map establishment and robot localization based on graphic content mathing[J]. Optics and Precision Engineering, 2017, 25(8): 2222-2232. (in Chinese) |
| [9] | WULF O, LECKING D, WAGNER B.Robust self-localization in industrial environments based on 3D ceiling structures[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems.Piscataway, NJ: IEEE Press, 2007: 1530-1534. https://www.researchgate.net/publication/224685066_Robust_Self-Localization_in_Industrial_Environments_Based_on_3D_Ceiling_Structures |
| [10] | DAVIDE R, ROBERTO O, CRISTIAN S, et al.AGV global localization using indistinguishable artificial landmarks[C]//IEEE International Conference on Robotics and Automation.Piscataway, NJ: IEEE Press, 2011: 287-292. https://www.researchgate.net/publication/221076429_AGV_global_localization_using_indistinguishable_artificial_landmarks |
| [11] | 杨剑, 韩建栋, 秦品乐. 视觉测量中可纠错的编码点识别及提取[J]. 光学精密工程, 2012, 20(10): 2293-2299. YANG J, HAN J D, QIN P L. Correcting error on recognition of coded points for photogrammetry[J]. Optics and Precision Engineering, 2012, 20(10): 2293-2299. (in Chinese) |
| [12] | 段康容, 刘先勇. 摄影测量中编码标记点检测算法研究[J]. 传感器与微系统, 2010, 29(8): 74-77. DUAN K R, LIU X Y. Detection algorithm on circular encoded point in photogrammetry[J]. Transducer and Microsystem Technologies, 2010, 29(8): 74-77. DOI:10.3969/j.issn.1000-9787.2010.08.024 (in Chinese) |
| [13] | CANNY J. A computational approach to edge detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1986, PAMI-8(6): 679-698. DOI:10.1109/TPAMI.1986.4767851 |
| [14] | HARRIS C, STEPHENS M.A combined corner and edge detector[C]//Proceedings of the 4th Alvey Vision Conference, 1988: 147-151. |
| [15] | ANDERSON K R. A reevaluation of an efficient algorithm for determining the convex hull of a finite planar set[J]. Information Processing Letters, 1978, 7(1): 53-55. DOI:10.1016/0020-0190(78)90041-8 |
| [16] | RICHARD H, ANDREW Z. Multiple view geometry in computer vision[M]. Cambridge: Cambridge University Press, 2004: 159-173. |
| [17] | ANDREAS G, PHILIP L, RAQUEL U.Are we ready for autonomous driving? The KITTI vision benchmark suite[C]//2012 IEEE Conference on Computer Vision and Pattern Recognition.Piscataway, NJ: IEEE Press, 2012: 3354-3361. https://www.researchgate.net/publication/261861888_Are_we_ready_for_autonomous_driving_The_KITTI_vision_benchmark_suite |
