Alippi等[2]最先对钢轨轮廓及磨耗测量中的图像处理技术进行了系统化研究,综合激光扫描和图像处理技术实现了轮廓光条的提取和重构。Attivissimo等[3]提出了一种用于估计轮轨作用关系的钢轨轮廓测量系统,可用于指导钢轨打磨。Magnus等[4]发明了一种基于给定波长结构光的钢轨磨耗实时测量系统。Liu等[5]提出了一种基于结构光的钢轨磨耗快速测量方法,利用轨腰大小圆拟合圆心实现了轨廓图像对齐。占栋等[6]提出了一种钢轨轮廓全断面高精度动态视觉测量方法,建立了钢轨轮廓视觉测量的全局测量模型。Molleda等[7]提出了一种基于机器视觉的非接触式钢轨轮廓测量系统,并用于钢轨生产质量评价。
在钢轨磨耗测量的过程中,选取准确有效的匹配基准点将系统的钢轨测量轮廓与标准设计轮廓对齐,这一过程称之为轮廓的配准,之后按照钢轨磨耗定义计算相关磨耗值。文献[8]以曲率作为轮廓曲线各线段的形状特征,利用固定的曲率阈值来分割轮廓曲线上的各段圆弧,并选择曲率半径为20 mm的圆弧区段来拟合圆心作为轮廓对齐的匹配基准点,该方法数据处理量小,可以快速有效地完成对磨耗的实时测量,但钢轨的测量轮廓由于系统标定、车体振动及光条中心线提取等过程引入的噪声干扰[9-12],轮廓曲线各区段的实际曲率值并不是固定不变的,仅依靠曲率作为阈值难以对轮廓曲线进行准确分割。
文献[13]采用最近点迭代(Iterative Closest Point,ICP)[14]算法确定轨腰轮廓点从测量坐标系到轨道设计坐标系的几何校正参数,仅采用单一传感器实现了基准测量和磨耗测量,该算法测量重复性高,且实现成本低,为了提高算法效率,将迭代搜索限制在较小的局部区域内进行,但该算法易受轨腰上的噪声数据影响,特别是当轨腰上存在脏污泥土等凸状斑点干扰时,测量精度有较大的损耗,此外若车体发生激烈的晃动,过小的搜索区域容易使迭代求解陷入局部最优,得到错误的校正参数。
本文针对列车运行环境下由于车体晃动、轨腰污损等造成的干扰,提出了一种基于截断残差直方图多项式拟合和动态窗口曲率熵的轨腰小圆弧自动提取方法,并基于提取的2段圆弧区域分别拟合2个圆心作为基准与标准设计轮廓对齐配准,有效克服了动态行车环境下列车晃动及轨腰噪声对磨耗测量造成的影响。
1 钢轨磨耗测量原理 基于结构光的测量技术是当前视觉测量领域的研究重点和热点,已被广泛应用于工业测量的各个领域。该技术主要利用激光发射器生成具有特定形状的光场,与被测物体相交形成三维轮廓断面,经图像传感器采集得到物体的三维点云数据。钢轨磨耗测量是一种典型的结构光测量应用技术,其测量原理如图 1所示。
 |
| 图 1 钢轨磨耗测量原理 Fig. 1 Schematic diagram of rail wear measurement |
| 图选项 |
首先,采用线结构光视觉传感装置扫描钢轨断面生成钢轨的廓形光条图像。然后,对图像进行细化操作,进一步提取光条的中心线。之后,通过坐标变换将2个轮廓半断面合成为1个全断面廓形。具体操作方法是:根据预先标定好的激光摄像组件的参数矩阵,将提取的光条中心线的二维图像坐标转换为三维物理坐标,即得到钢轨截面的真实三维轮廓。最后,分别提取左右两侧轨廓上曲率半径为20 mm的圆弧区域拟合2个圆心作为匹配基准点进行空间配准,将三维钢轨测量轮廓与标准设计轮廓统一到同一空间坐标系下进行比对,计算测量点与对应标准轨上的匹配基准点之间的欧氏距离,得到钢轨轮廓上各点的磨耗值(注:因为轨头在使用过程中存在磨耗,不适合作为配准的基准,而轨腰和轨底状态较稳定,所以选取轨腰和轨底连接处半径为20 mm的圆弧拟合2个圆心作为匹配基准点来进行轨廓对齐)。
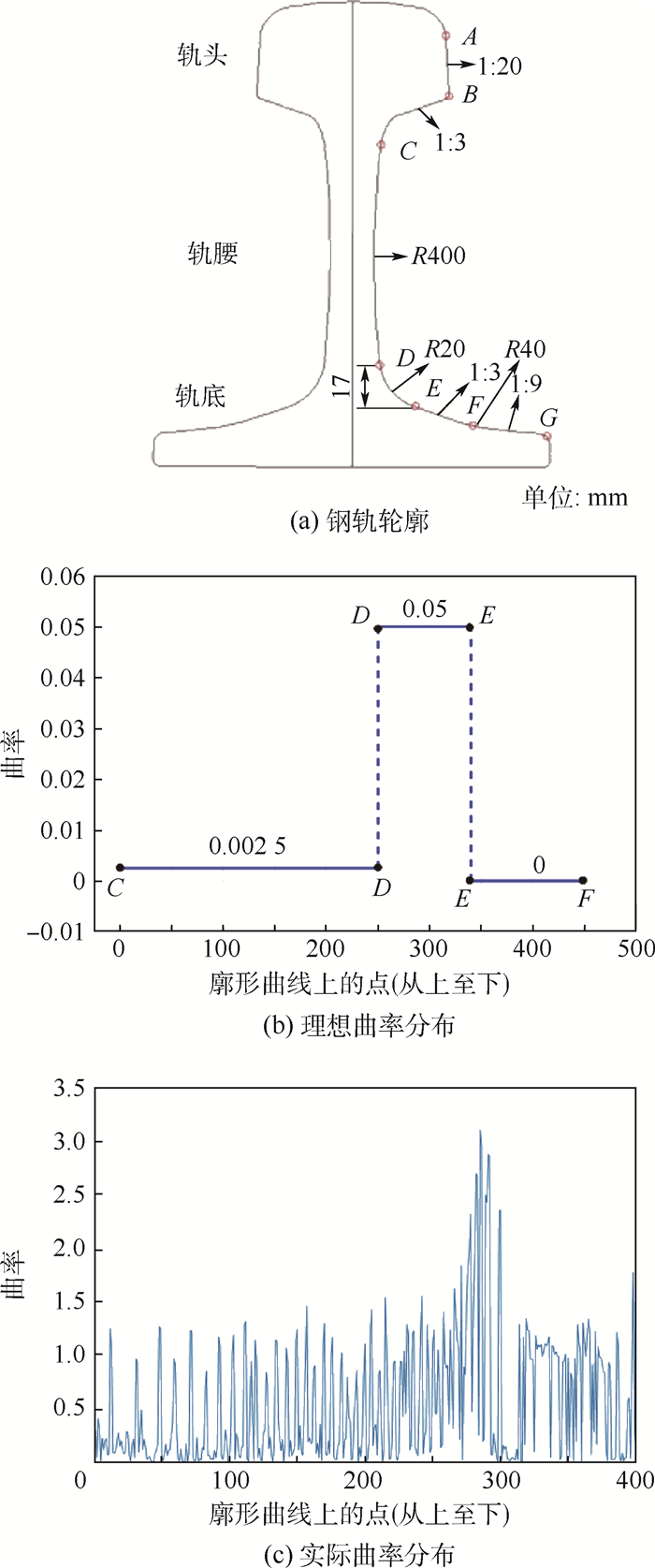
2 钢轨轮廓配准 图 2(a)为标准60 kg/m钢轨的轮廓结构,轮廓曲线由多段直线和圆弧组成。其中,轨腰由一段半径为400 mm的圆弧CD和半径为20 mm的圆弧DE组成。从第1节中的分析已知,轮廓配准的关键在于从轨腰数据中精确地提取小圆区域。曲率能够很好地反映轮廓曲线各区段的形状特征,各区段的曲率分布如图 2(b)所示。理想情况下,从大圆弧CD到小圆弧DE及从小圆弧DE到线段EF的曲率均存在显著的阶跃变化,利用曲率很容易将小圆区域DE提取出来。而列车行车环境下,由于受到随机噪声、标定误差、车体扰动和采集设备自身等诸多因素的影响,实测的轮廓数据中存在大量不确定的噪声干扰(见图 2(c))。因此,依靠固定的曲率值分割小圆是行不通的。
 |
| 图 2 钢轨轮廓结构及各区段曲率分布 Fig. 2 Rail profile structure and curvature distribution in each section |
| 图选项 |
针对这一问题,本文首先对轮廓离散点数据进行多项式拟合,去除噪声干扰;之后基于动态窗口最大曲率熵阈值分割方法提取小圆区域;最后根据小圆区域的数据点拟合小圆圆心作为与对应的标准轨小圆圆心相匹配的基准点,经几何旋转平移后实现与标准轨轮廓的配准。
2.1 基于截断残差直方图多项式拟合的数据预处理 图 3(a)为受噪声干扰的轨廓光条图像,轨腰处的光条亮度和宽度都呈现不均匀的变化,导致提取的光条中心线不够平滑,进一步导致图 3(b)中经坐标变换后得到的空间轮廓点发生与曲率无关的杂乱起伏变化,使得基于曲率特性的小圆区域提取变得非常困难。因此,需要对轨廓数据进行预处理,去除噪声干扰。
 |
| 图 3 轨廓噪声 Fig. 3 Rail profile noise |
| 图选项 |
基于最小二乘法的多项式拟合方法是一种常见的数值逼近方法,可以用来对曲线进行平滑去噪。如果利用多项式对实测的空间轮廓点坐标(xn, yn)进行拟合,则可记为
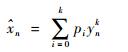 | (1) |
式中:k为多项式阶次;pi为多项式拟合系数;n=1, 2, …, N为空间轮廓点索引,N为参与拟合的总点数(注:xn→yn不满足函数映射关系,而yn→xn满足映射关系,因此这里将yn作为自变量,
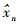
利用最小二乘法求解优化问题:
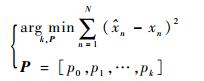 | (2) |
即寻求与轮廓点(xn, yn)距离的平方和误差(SSE)最小的曲线x=f(y),函数f(y)称为拟合函数或最小二乘解。这里,令
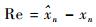
对图 3(b)中所示的轮廓数据分别进行多次拟合,得到的误差统计如表 1所示。
表 1 空间轮廓点多项式拟合误差统计 Table 1 Error statistics of polynomial fitting of spatial profile points
| 拟合阶次 | 平方和误差 | 确定系数 | 均方根误差 |
| 1 | 20 862 | 0.393 4 | 12.34 |
| 2 | 6 516 | 0.807 8 | 6.922 |
| 3 | 1 389 | 0.959 6 | 3.207 |
| 4 | 51.93 | 0.998 5 | 0.623 |
| 5 | 53.07 | 0.998 5 | 0.632 |
| 6 | 67.14 | 0.998 | 0.713 |
| 7 | 79.42 | 0.997 7 | 0.779 |
| 8 | 92.69 | 0.997 3 | 0.844 |
| 9 | 104.8 | 0.997 | 0.901 |
表选项
从表 1中可以看到,当拟合阶次取4时,拟合误差最小。但事实上,由于噪声点的干扰,残差平方和最小不一定意味着最优拟合结果。图 4为4次和6次拟合的轮廓曲线,虽然4次拟合具有更小的数值误差,但6次拟合的曲线穿过了更多的真实轮廓点,且曲线形状与轨腰形状更加吻合。
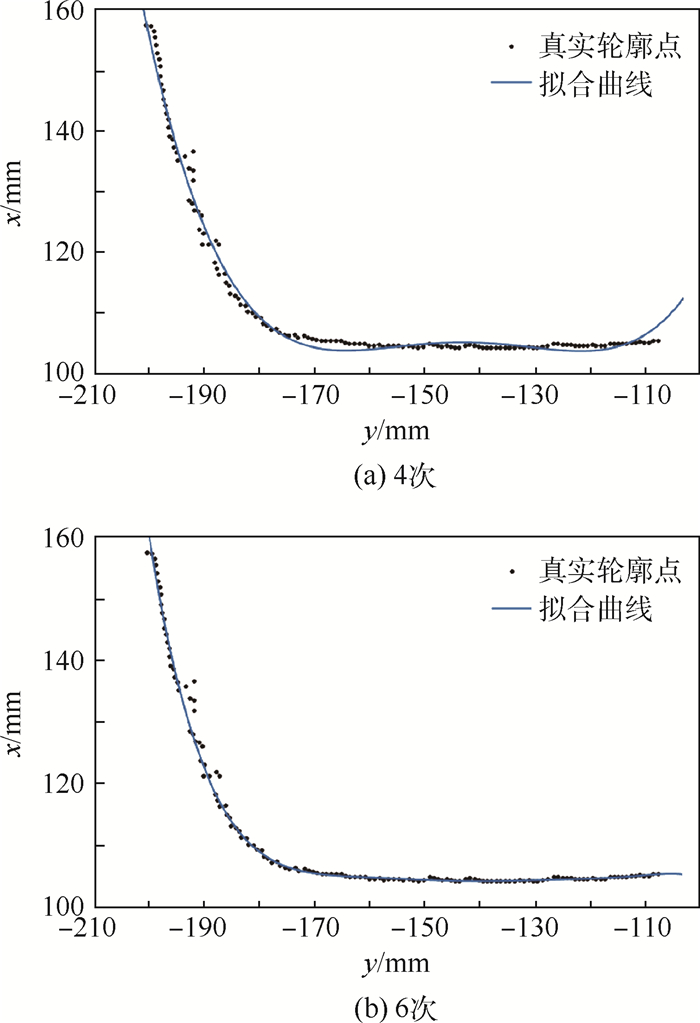 |
| 图 4 不同阶次的轮廓点拟合结果 Fig. 4 Fitting results of profile points with different orders |
| 图选项 |
图 5为图 3(b)的残差统计直方图。可以看到,4次拟合的残差分布近似于均匀分布,轮廓点比较均匀地分布在拟合曲线两侧;而6次拟合的残差分布则近似于正态分布,大部分轮廓点位于或紧贴拟合曲线。自然条件下的测量误差满足正态分布,说明6次拟合的结果更加趋于真实。
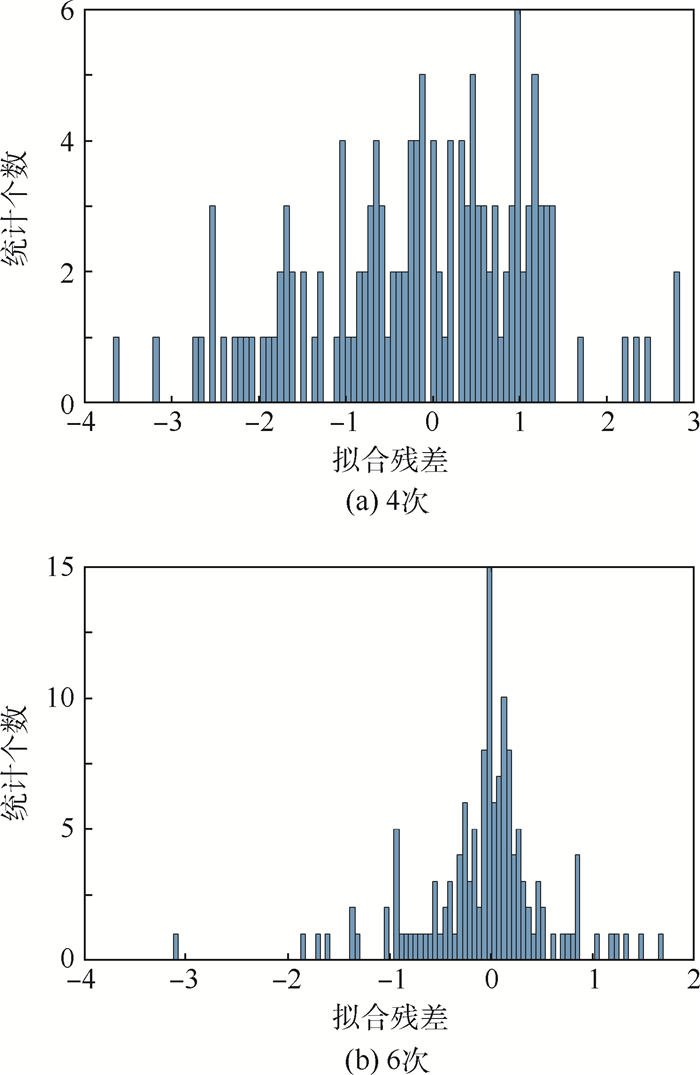 |
| 图 5 残差统计直方图 Fig. 5 Residual statistics histogram |
| 图选项 |
为了得到残差满足正态分布的最优拟合曲线,本文提出了基于截断残差直方图的多项式拟合方法,寻找最优的拟合阶次,使拟合曲线穿过尽可能多的空间轮廓点,降低了噪声对拟合结果的影响。
拟合过程即求解以下优化问题:
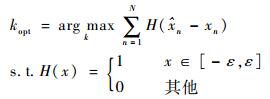 | (3) |
式中:[-ε, ε]为残差截断区间,ε为截断参数,属于经验因子,设置过大易受噪声干扰,而过小又会造成信号损失。理想的ε应使得截断区间内的残差直方图分布接近正态分布,如图 6所示。
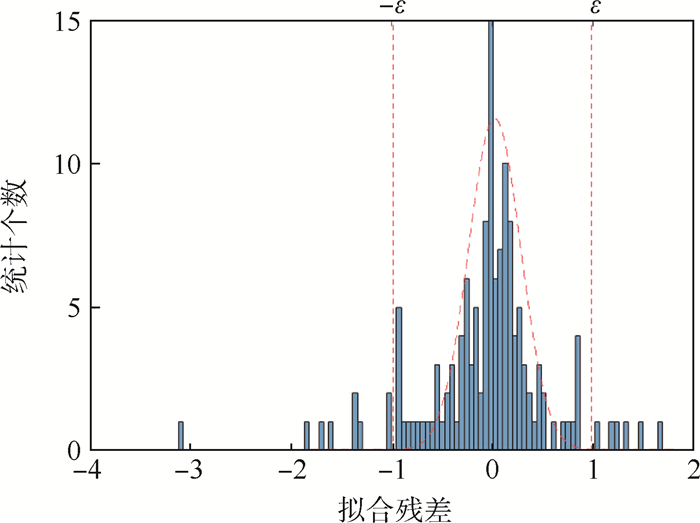 |
| 图 6 截断残差直方图与正态分布 Fig. 6 Truncated residual histogram and normal distribution |
| 图选项 |
2.2 基于动态窗口曲率熵的轨腰小圆弧自动提取方法 图 7为标准轨的轨腰区域数据拟合前后的曲率对比。可以看到,拟合后的轨腰曲率分布较为平滑,有效降低了噪声点干扰。但由于系统成像、光条提取及曲线拟合等过程中存在不可避免的误差,导致拟合后的曲率分布并不符合理想的方波,大圆(图 2(a)中CD段)和小圆(图 2(a)中DE段)区域都存在一定的波动。大圆区域曲率整体比较平稳,而小圆区域变化则较为剧烈。
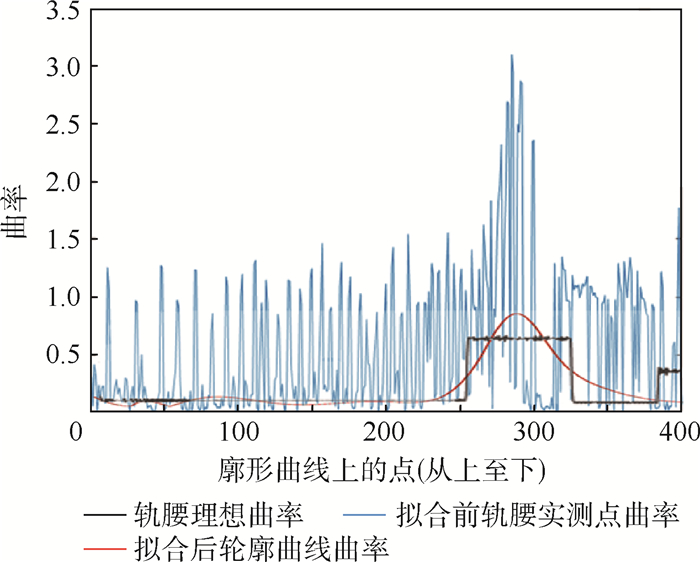 |
| 图 7 标准轨的轨腰轮廓曲率 Fig. 7 Curvature of standard rail waist profile |
| 图选项 |
信息熵由信息论之父香农于1948年提出,用来描述信号的不确定性。某信号的熵值越大,则该信号的无序程度越高。将拟合后的轨廓曲率看作一维信号,记作Sn(n=1, 2, …, N)。从图 7中观察到,大圆区域的信号平稳有序,近似于均匀分布,而小圆区域信号变化剧烈近似于正态分布。因此,通过对整个信号区域{Sn}进行滑窗遍历,寻找曲率熵最大的区域,即可确定小圆区域。具体过程描述如下。
对于拟合曲线方程x=f(y),其上的曲率定义为
 | (4) |
区间(n, n+w)上的曲率概率分布定义为
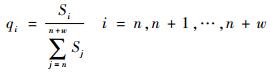 | (5) |
则该区间的曲率熵可记作
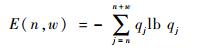 | (6) |
给出了曲率熵的定义后,其随分割点位置和窗口大小的变化分布如图 8所示,小圆分割问题就转换为在曲面上搜索曲率熵值最大的点位置问题。从图 8中可以观察到,较大值的点都集中在某一区域,因此选择合适的起始点有利于提高搜索效率。
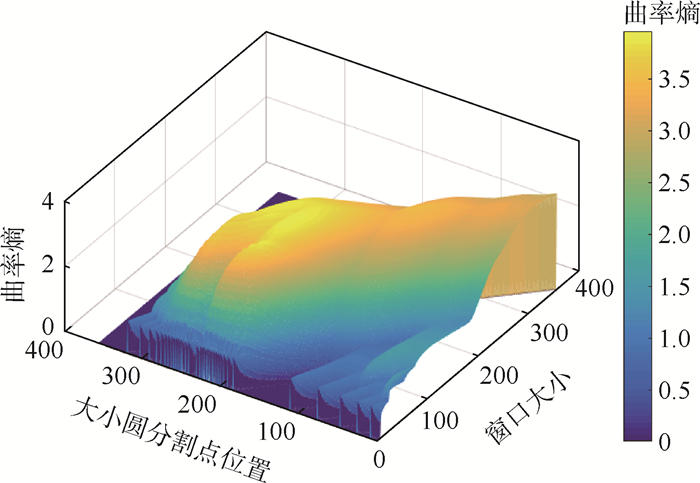 |
| 图 8 曲率熵变化分布 Fig. 8 Variation distribution of curvature entropy |
| 图选项 |
至此,轨腰小圆分割问题可表示为求解如下优化问题:
 | (7) |
图 9为基于动态窗口的最大曲率熵区间搜索过程。由于系统误差的影响,拟合后小圆区域的曲率分布由近似均匀分布(黑色)变为近似正态分布(蓝色),且分布区间变宽,导致由以上算法求得的大小圆分割点与实际有些许偏差。设小圆区域的真实点数为D,则利用式(8)对分割点位置nopt进行修正,第3节中将通过实验分析验证修正后的分割精度和稳定性。
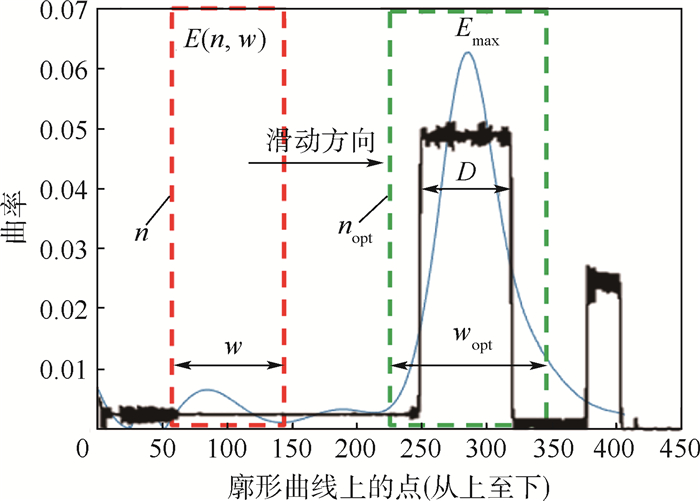 |
| 图 9 基于动态窗口的最大曲率熵区间搜索 Fig. 9 Maximum curvature entropy interval search based on dynamic window |
| 图选项 |
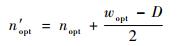 | (8) |
2.3 基于轨腰小圆弧拟合圆心的轮廓对齐配准 众所周知,通过任意2个匹配基准点可以将实测钢轨廓型统一到标准钢轨廓型所在的坐标系下进行重合比对,因为轨头在使用过程中被逐渐磨耗,所以不适合选取匹配基准点,轨腰和轨底不存在磨耗变形现象,所以选取该位置两侧轨腰上小圆弧的圆心作为匹配基准点是比较合理的。
轨腰和轨底结合部为半径20 mm的小圆弧(60 kg/m钢轨为例),理论上所有属于小圆的点到圆心的距离都应为20 mm,所以以轨腰数据点到圆心的距离建立优化目标函数,此距离与20 mm半径的绝对差应取得极小值。
为此,设拟合的小圆圆心为
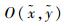
 | (9) |
通过最小二乘法求解min fi(x)得到小圆圆心的最优值。
求得2个小圆圆心后,根据2对点之间的空间匹配关系可以求得几何校正参数,即旋转平移矩阵。将采集图像中的钢轨断面经旋转平移后实现与标准钢轨断面的对齐配准。按照相应磨耗的位置定义,计算采集钢轨垂直磨耗、侧面磨耗位置处坐标与标准位置坐标的差值即可得到钢轨磨耗值。
3 实验与分析 3.1 实验环境及数据 为了验证本文方法的正确性和有效性,针对线下实验室环境和线上行车环境分别进行了误差分析以及重复性精度验证实验,如图 10所示。
 |
| 图 10 实验环境与结构光图像 Fig. 10 Experimental environment and structured light image |
| 图选项 |
实验室静态实验采用60 kg/m的精密加工标准钢轨作为标准测量块,长度为0.2 m。结构光视觉采集前端采用PhotoFocus CMOS面阵相机和2 W近红外线激光器。计算机硬件配置为:Intel 3.0 GHz四核CPU,4 G 1 333 MHz内存。图像分辨率为1 312像素×1 082像素,相机曝光时间设置为0.1 ms。
行车现场动态实验基于车载式轨廓测量系统,分别对3条实际线路各5次测量历史数据进行测量精度重复性对比。测试路段长度为100 m,列车行驶速度约为80 km/h。
3.2 线下静态实验及误差分析 图 11为实测标准轨左右两侧小圆区域的分割及对应圆心拟合结果。利用实测廓形小圆区域的数据点拟合的左右两侧圆心坐标为:OL=(43.97,-169.7),OR=(104.1,-171.2)。如图 12所示,标准设计廓形小圆区域的真实圆心坐标为:
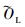
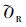
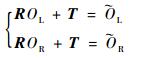 | (10) |
 |
| 图 11 实测标准轨的小圆区域分割及圆心拟合结果 Fig. 11 Results of small circle area segmentation and circle center fitting for actual measurement standard rail |
| 图选项 |
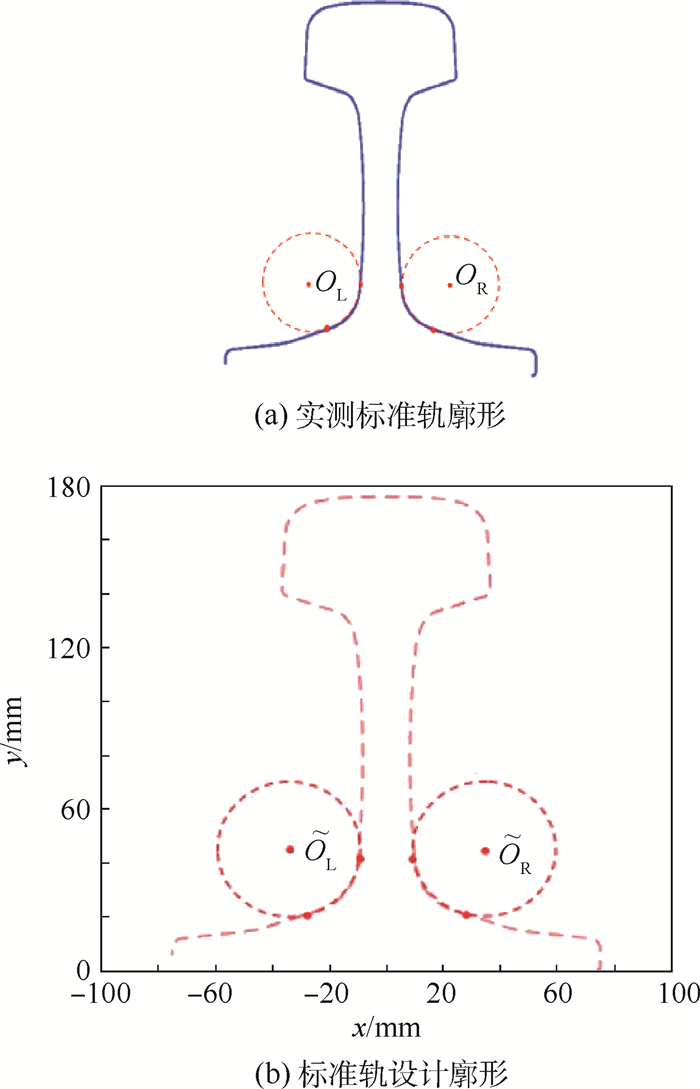 |
| 图 12 基于左右侧小圆圆心的标准轨轮廓对齐 Fig. 12 Alignment of standard rail profile on left and right side of small circle center |
| 图选项 |
求得旋转矩阵R和平移向量T,将实测廓形与标准设计廓形对齐,如图 12所示。
对齐后的轨廓如图 13所示。定义钢轨顶面宽1/3处(距标准工作边)为垂磨点,钢轨踏面下16 mm处为侧磨点。通过对标准轨进行775次重复采集,统计垂磨值和侧磨值的变化来验证测量的系统误差和静态重复性精度。
 |
| 图 13 标准轨廓形对比 Fig. 13 Standard rail profile comparison |
| 图选项 |
图 14为775次静态重复测量的垂磨和侧磨数值统计结果。可以看到,测量最大误差垂磨为0.023 45 mm,侧磨为0.037 01 mm。经统计得到系统测量误差均值,垂磨为0.004 2 mm,侧磨为0.008 4 mm;测量标准差垂磨为0.003 3 mm,侧磨为0.005 9 mm。
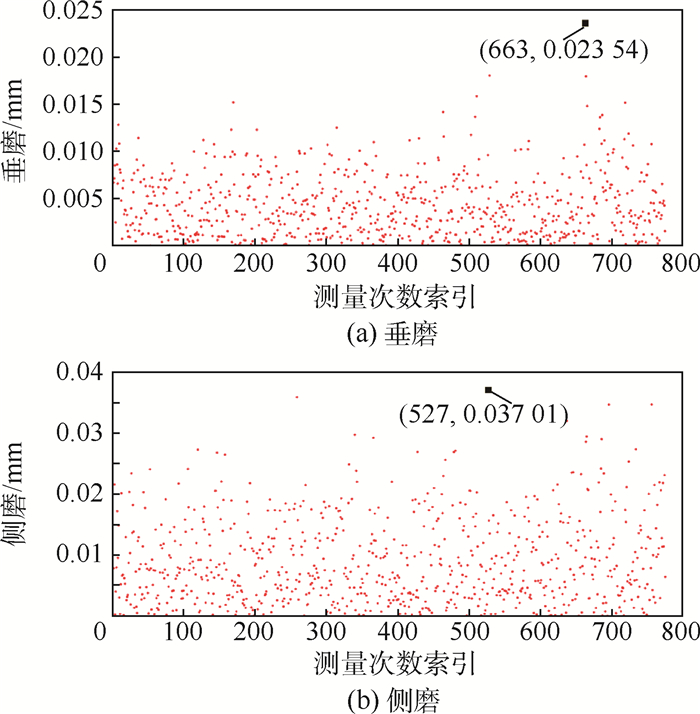 |
| 图 14 系统测量误差及静态重复性精度 Fig. 14 System measurement error and static repeatability accuracy |
| 图选项 |
3.3 线上动态实验及重复性验证 图 15为针对行车现场受噪声干扰轨廓图像的小圆区域分割和圆心拟合结果。可以看出,本文方法具有较强的抗干扰能力,有效克服了噪声的影响。这里,利用拟合小圆的半径统计值来评价分割的稳定性。现场选取100 m长钢轨,每1 m采集4个轨廓断面,共计400个测量断面。小圆半径统计结果如图 16所示,固定的曲率阈值分割方法[8]拟合的小圆半径均值为19.53 mm,标准差为2.304 mm;而本文方法拟合的小圆半径均值为20.05 mm,标准差为0.092 mm。
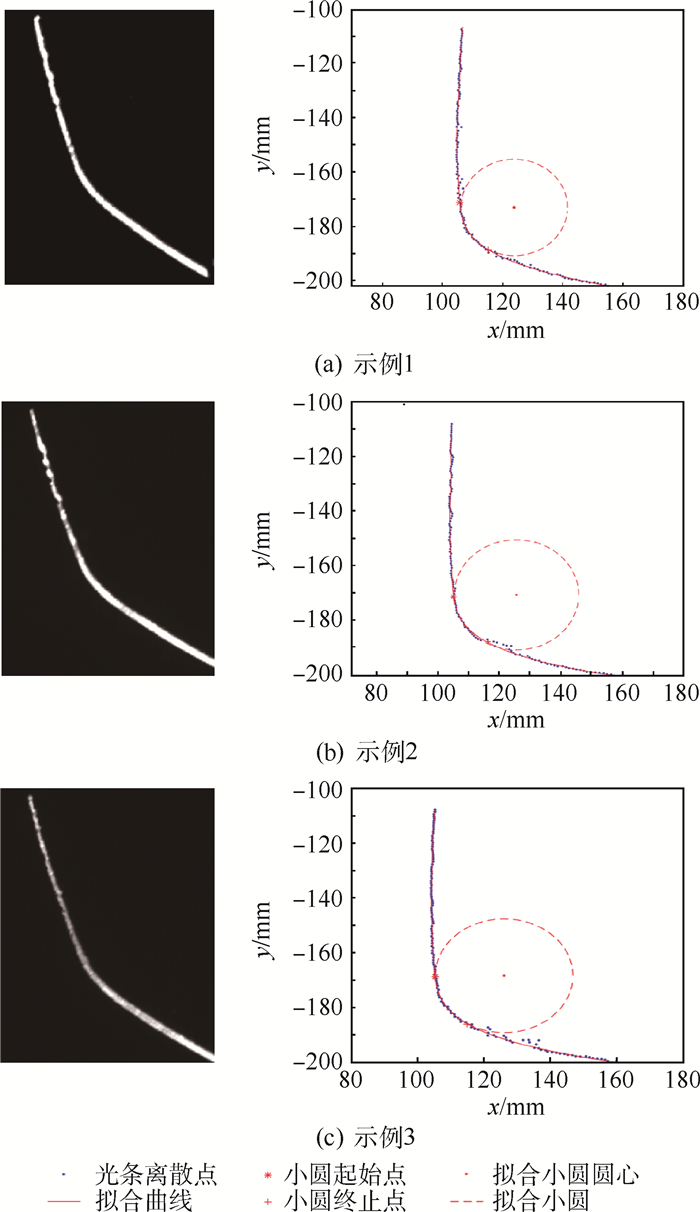 |
| 图 15 噪声干扰轨廓数据的小圆分割和圆心拟合结果 Fig. 15 Small circle segmentation and circle center fitting result of rail profile with noise interference |
| 图选项 |
 |
| 图 16 动态测量中拟合小圆的半径变化 Fig. 16 Radius variation of small fitting circle with dynamic measurement |
| 图选项 |
本文提出的钢轨磨耗测量方法已经应用于几十台轨道检查车或探伤车上。在多条实际线路的运用中表明,该技术测量结果重复性良好,测量精度较高,行车环境下自身重复性精度小于0.2 mm[15]。以左轨垂磨为例,图 17为3条实际线路各取100 m钢轨,分别经5次测量后的钢轨磨耗值波形对比。
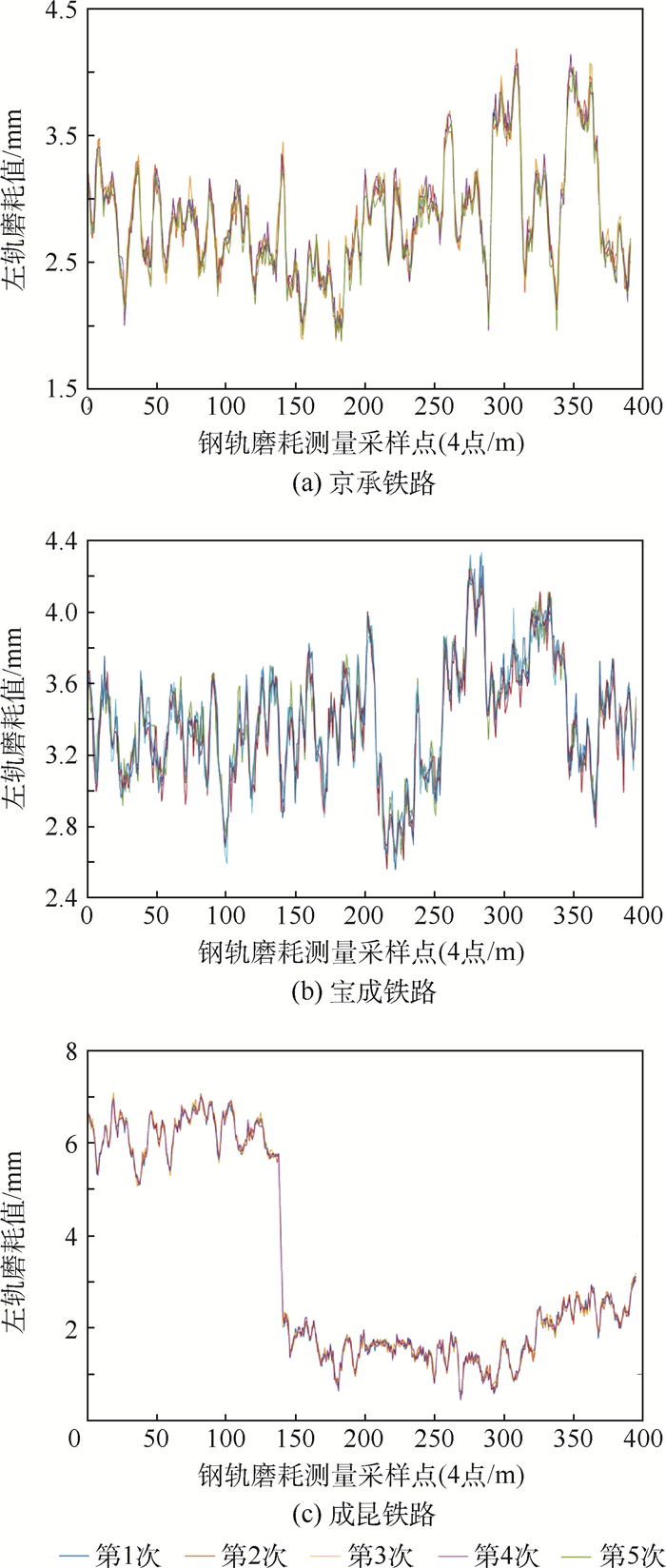 |
| 图 17 钢轨磨耗测量的动态重复性精度 Fig. 17 Dynamic repeatability accuracy of rail wear measurement |
| 图选项 |
4 结论 本文对行车环境下用于钢轨磨耗测量的轨廓自动匹配方法进行了系统化研究。
1) 针对轨腰条纹图像中心点,经坐标变换后得到空间轮廓点数据,并基于截断残差直方图多项式拟合去除噪声干扰。
2) 提出了一种基于动态窗口曲率熵的轨腰小圆弧自动分割方法,经圆弧拟合圆心作为匹配基准点实现实测轮廓与标准设计轮廓的空间配准。
3) 静态实验结果表明本文方法的系统测量误差均值和标准差都控制在0.01 mm之内,具有较小的测量误差和良好的重复性。现场动态测量验证了本文方法在行车环境下的重复性精度,多次测量结果的重复性良好,钢轨磨耗动态测量偏差控制在0.2 mm以内,有效克服了行车环境下晃车及轨腰噪声对磨耗测量造成的影响,满足现场作业的要求。
参考文献
| [1] | 严隽耄. 车辆工程[M]. 北京: 中国铁道出版社, 2009: 240-265. YAN J M. Vehicle engineering[M]. Beijing: China Railway Press, 2009: 240-265. (in Chinese) |
| [2] | ALIPPI C, CASAGRANDE E, SCOTTI F, et al. Composite realtime image processing for railways track profile measurement[J]. IEEE Transactions on Instrumentation and Measurement, 2000, 49(3): 559-564. DOI:10.1109/19.850395 |
| [3] | ATTIVISSIMO F, DANESE A, GIAQUINTO N, et al. A railway measurement system to evaluate the wheel-rail interaction quality[J]. IEEE Transactions on Instrumentation and Measurement, 2007, 56(5): 1583-1589. DOI:10.1109/TIM.2007.903583 |
| [4] | MAGNUS S, MAGNUS D.Rail measurement system: US2009/0073428 A1[P].2009-03-19. |
| [5] | LIU Z, SUN J, WANG H, et al. Simple and fast rail wear mea-surement method based on structured light[J]. Optics and Lasers in Engineering, 2011, 49(11): 1343-1351. DOI:10.1016/j.optlaseng.2011.05.014 |
| [6] | 占栋, 于龙, 肖建, 等. 钢轨轮廓全断面高精度动态视觉测量方法研究[J]. 铁道学报, 2015, 37(9): 96-106. ZHAN D, YU L, XIAO J, et al. Study on high-accuracy vision measurement approach for dynamic inspection of full cross-sectional rail profile[J]. Journal of the China Railway Society, 2015, 37(9): 96-106. (in Chinese) |
| [7] | MOLLEDA J, USAMENTIAGA R, MILLARA A F, et al. A profile measurement system for rail quality assessment during manufacturing[J]. IEEE Transactions on Industry Applications, 2016, 52(3): 2684-2692. DOI:10.1109/TIA.2016.2524459 |
| [8] | 占栋, 于龙, 肖建, 等. 钢轨轮廓全断面检测中轨廓动态匹配方法研究[J]. 铁道学报, 2015, 37(5): 71-77. ZHAN D, YU L, XIAO J, et al. Study on dynamic matching algorithm in inspection of full cross-section of rail profile[J]. Journal of the China Railway Society, 2015, 37(5): 71-77. (in Chinese) |
| [9] | 刘震, 张广军, 魏振忠, 等. 一种高精度线结构光视觉传感器现场标定方法[J]. 光学学报, 2009, 29(11): 3124-3128. LIU Z, ZHANG G J, WEI Z Z, et al. An accurate calibration method for line structured light vision sensor[J]. Acta Optica Sinica, 2009, 29(11): 3124-3128. (in Chinese) |
| [10] | 占栋, 于龙, 邱存勇, 等. 钢轨轮廓测量中的车体振动补偿问题研究[J]. 仪器仪表学报, 2013, 34(7): 1625-1633. ZHAN D, YU L, QIU C Y, et al. Study on vehicle vibration compensation in railway track profile inspection[J]. Chinese Journal of Scientific Instrument, 2013, 34(7): 1625-1633. DOI:10.3969/j.issn.0254-3087.2013.07.027 (in Chinese) |
| [11] | 胡坤, 周富强, 张广军. 一种快速结构光条纹中心亚像素精度提取方法[J]. 仪器仪表学报, 2006, 27(10): 1326-1329. HU K, ZHOU F Q, ZHANG G J. Fast extraction method for sub-pixel center of structured light stripe[J]. Chinese Journal of Scientific Instrument, 2006, 27(10): 1326-1329. DOI:10.3321/j.issn:0254-3087.2006.10.034 (in Chinese) |
| [12] | 贾倩倩, 王伯雄, 罗秀芝. 光切法形貌测量中光条中心的亚像素提取[J]. 光学精密工程, 2010, 18(2): 390-396. JIA Q Q, WANG B X, LUO X Z. Extraction of central positions of light stripe in sub-pixel in 3D surface measurement based on light sectioning method[J]. Optics and Precision Engineering, 2010, 18(2): 390-396. (in Chinese) |
| [13] | 孙军华, 王伟华, 刘震, 等. 基于结构光视觉的钢轨磨耗测量方法[J]. 北京航空航天大学学报, 2010, 36(9): 1026-1029. SUN J H, WANG W H, LIU Z, et al. Rail wear measurement method based on structured-light vision[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(9): 1026-1029. (in Chinese) |
| [14] | BESL P J, MCKAY N D. A method for registration of 3-D shapes[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239-256. DOI:10.1109/34.121791 |
| [15] | 王昊, 王胜春, 潘大海, 等. 车载非接触式钢轨磨耗测量方法研究及应用[J]. 铁道建筑, 2017, 57(12): 97-101. WANG H, WANG S C, PAN D H, et al. Research and application on train-borne non-contact rail wear measurement method[J]. Railway Engineering, 2017, 57(12): 97-101. DOI:10.3969/j.issn.1003-1995.2017.12.26 (in Chinese) |
