随着高超声速飞行器的不断发展,国内外对电离作用下的气动热环境开展了诸多研究。屈程和王江峰[10]研究电离作用对高超声速飞行器在稀薄流中的气动热载荷影响,数值分析了星尘号探测器在不同飞行高度稀薄流绕流流场特性,对比研究探测器驻点和壁面热流分布特性;随着飞行高度增加,电离作用对探测器气动热载荷影响因高空气体逐渐稀薄而不断减弱。Hao等[11]对比研究Gupta模型[12]和Park模型[13] 2种化学反应模型,分别应用于高超声速再入体气动热环境数值模拟;Gupta模型获得的壁面附近电子数密度与试验符合的较好,Park模型获得的电子数密度偏低,但Gupta和Park 2种化学反应模型各自获得的流场热化学非平衡温度分布相似。Lorzel和Mikellides[14]采用Park双温度模型[15]数值研究高超声速钝头锥体在61~81 km高空环境气动热特性,给出壁面电子数密度、离子体质量分数和各类温度沿驻点线分布特性;飞行越高,气体沿驻点线平动-转动温度与振动温度之间的温差增大,各离子体质量分数减小。Massimi等[16]数值计算空间飞行器壁面气动热载荷时考虑了电离作用的影响,给出流场中各离子体质量分布;因头部驻点区域温度高,大多数离子体只出现在头部小区域范围,电离产生的NO+比其他离子体质量分数大。Allouche和Haoui[17]分析了飞行器在不同飞行高度电离环境下空气平动-转动温度变化特性,激波后的高温气体吸收热量出现离解和电离,沿驻点线气体温度不断降低而到达平衡状态,激波后的最大非平衡平动-转动温度减小到热化学平衡温度的距离随着飞行高度的降低而不断减小。Kim等[18]对多种再入飞行器高超声速绕流中的电子能特性进行数值研究,结论指出气体因热化学非平衡作用加剧而电离量增多,电离作用加剧,飞行器气动热环境需要考虑电子能方程影响,对电子温度的可靠预测能为高超声速飞行器热防护系统和通信系统设计提供有效指导。
本文采用Gupta化学反应模型[12]和Park双温度控制模型[15],数值研究电离作用对高超声速飞行器热化学非平衡气动热环境影响。采用5组元(N2,O2,NO,O,N)、7组元(N2,O2,NO,O,N,NO+,e-)和11组元(N2,O2,NO,O,N,N2+,O2+,NO+,O+,N+,e-)热化学反应数值计算飞行器气动热环境,对比研究非电离、弱电离和强电离状态不同气动热环境特性。此外,本文分析了飞行器壁面在不同催化条件下,电离作用对高超声速飞行器气动热和气动力载荷的影响。
1 流动控制方程与数值计算方法 直角坐标系下,由质量、动量和能量守恒构成的高超声速热化学非平衡流动控制方程[19]具体形式如下:
 | (1) |
 | (2) |
 | (3) |
 | (4) |
 | (5) |
式中:i=j时, δij=1;i≠j时,δij=0;ns为混合气体组元总数;nd为混合气体中分子组元总数;ρ、p、τ和wv分别为混合气体密度、压强、切应力和振动能源项;cs、Ds、ws、hs和eve, s分别为混合气体中组元s的质量分数、扩散系数、质量生成率、单位焓和振动-电子能;xi、ui、qi和qv, i分别为i方向上的坐标轴分量、速度分量、平动-转动热流分量和振动热流分量;E和H分别为混合气体总能和总焓。
数值计算采用有限体积法对流动控制方程进行离散。采用HLLC(Harten Lax van Leer Contact)上风差分格式对无黏通量进行离散[20],黏性通量离散采用中心差分格式,限制器选用二阶精度的min mod限制器,时间推进采用欧拉隐式格式。
2 热化学非平衡 2.1 热力学特性 混合气体总能为
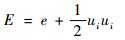 | (6) |
式中:混合气体内能为
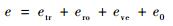 | (7) |
其中:e0为混合气体零点能;ero和etr分别为混合气体平动能和转动能,其定义分别为
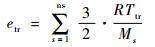 | (8) |
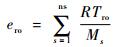 | (9) |
式中:R为摩尔气体常数;Ttr和Tro分别为平动温度和转动温度;Ms为组元s的摩尔质量。
混合气体振动-电子能为
 | (10) |
式中:ev和ee分别为混合气体振动能和电子能,其定义分别为
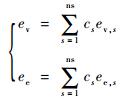 | (11) |
其中:组元s的振动能ev, s和电子能ee, s分别为
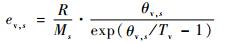 | (12) |
 | (13) |
式中:gi, s和θe, i, s分别为组元s的i能级自由度和特征电子温度;θv, s为组元s的振动特征温度;Tv为混合气体振动温度。对原子或电子组元s,ev, s=0;对电子组元s,ee, s=0。
2.2 化学反应模型 高超声速空气绕流流场,分别采用5组元(N2,O2,NO,O,N)、7组元(N2,O2,NO,O,N,NO+,e-)和11组元(N2,O2,NO,O,N,N2+,O2+,NO+,O+,N+,e-)化学反应对飞行器热化学非平衡气动热环境进行数值计算。选用Gupta化学反应模型[12],如表 1所示。化学反应控制温度采用Park双温度控制模型[15]。
表 1 Gupta化学反应模型 Table 1 Gupta's chemical reaction model
| 序号 | 化学反应式 |
| 1 | N2+ M1?2N+M1 |
| 2 | N2+N?2N+N |
| 3 | O2+M2?2O+M2 |
| 4 | NO+M2?N+O+M2 |
| 5 | N2+O?NO+N |
| 6 | NO+O?O2+N |
| 7 | N+O?NO++e- |
| 8 | O+e-?O++e-+e- |
| 9 | N+e-?N++e-+e- |
| 10 | O+O?O2++e- |
| 11 | O+O2+?O2+O+ |
| 12 | N2+N+?N+N2+ |
| 13 | N+N?N2++e- |
| 14 | O2+N2?NO+NO++e- |
| 15 | NO+M3?NO++e-+M3 |
| 16 | O+NO+?NO+O+ |
| 17 | N2+O+?O+N2+ |
| 18 | N+NO+?NO+N+ |
| 19 | O2+NO+?NO+O2 |
| 20 | O+NO+?O2+N+ |
| 注:M1= N2, O2, O, NO; M2= N2, O2,N, O, NO; M3= N2, O2。 | |
表选项
混合气体中,组元s的质量生成率为
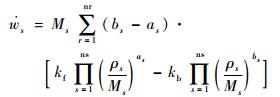 | (14) |
式中:nr为各组元化学反应式总数;as和bs分别为化学反应式中组元s为反应物和生成物时的化学反应计量系数;kf和kb分别为正向和逆向化学反应速率;ρs为组元s的密度。
正向化学反应速率采用Arrhenius公式[14]
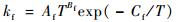 | (15) |
式中:Af、Bf和Cf分别为正向化学反应频率因子、温度指数和活化温度;T为流场气体温度。
逆向化学反应速率可通过化学反应平衡常数Keq[12]确定:
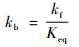 | (16) |
 | (17) |
式中:z =10 000/T;A0、A1、A2、A3和A4为常量系数。
2.3 输运参数 组元s的黏性系数μs和热传导系数κs采用Gupta-Yos拟合函数[12, 19]求取:
 | (18) |
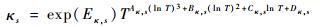 | (19) |
式中:Aμ, s、Bμ, s、Cμ, s和Aκ, s、Bκ, s、Cκ, s、Dκ, s、Eκ, s分别为与组元s黏性和热传导相关的常量。
混合气体的黏性系数μ,热传导系数κ采用Wilke半经验公式[19]计算如下:
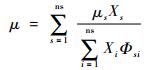 | (20) |
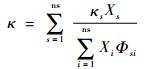 | (21) |
式中:Xs和Φsi分别为组元s的摩尔分数和配分函数。此外,混合气体中各组元的扩散系数Ds通过Fick定理[21]计算确定。
2.4 壁面催化条件 1) 非催化壁面
原子或离子在壁面处无复合反应发生[22],气体各组元在壁面上复合的质量生成率
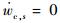
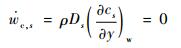 | (22) |
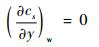 | (23) |
2) 完全催化壁面
原子或离子在壁面处以无穷大速率复合,气体各组元在壁面上的质量分数与远场自由来流中所对应组元的质量分数相同:
 | (24) |
式中:cs, w和cs, ∞分别为组元s在壁面和远场自由来流中的质量分数。
3 数值计算与结果分析 3.1 电离与非电离热化学非平衡气动热环境分析 选用文献[23]中的高超声速绕流半球模型,采用11组元(N2,O2,NO,O,N,N2+,O2+,NO+,O+,N+,e-),32组化学反应式(表 1中化学反应式1~20)和5组元(N2,O2,NO,O,N),17组化学反应式(表 1中化学反应式1~6),分别对考虑电离和非电离的高超声速热化学非平衡气动热环境进行数值对比分析。半球直径d=38.1 mm。自由来流条件:马赫数Ma∞= 12.4,静温T∞=535 K,静压P∞= 178.1 Pa;等温非催化壁面Tw= 300 K。自由来流中组元N2和O2的质量分数分别为cN2= 0.77,cO2=0.23。二维半球模型网格结点数分布为115×105(流向×法向)。
11组元和5组元化学反应获得的半球高超声速热化学非平衡流场平动-转动温度(Tt-r)如图 1所示。理想气体模型流场最大理论温度、5组元和11组元热化学非平衡流场数值计算最大平动-转动温度分别为16 987、13 421和13 028 K。考虑高温热化学反应时,由于热化学反应会消耗大量热能,流场最大气体温度降低。11组元比5组元热化学非平衡流场的最大平动-转动温度略小,这是由于电离反应消耗的热能较少,激波后气动加热产生的热能主要被气体分子离解和化学置换反应所消耗造成。此外,激波离体距离Δ与激波后气体密度密切相关,而11组元和5组元热化学非平衡流场温度分布区别小,激波后气体密度也随之差别不大,使得各自获得的头部激波离体距离差别很小,因此,电离作用对激波离体距离影响较小。
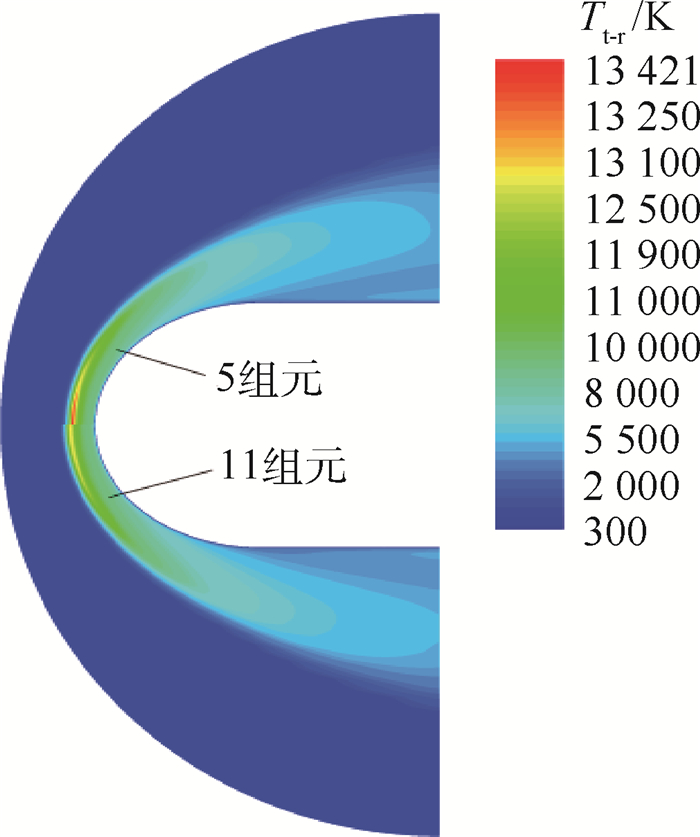 |
| 图 1 11组元与5组元热化学非平衡流场平动-转动温度(Tt-r) Fig. 1 Translational-rotational temperatures (Tt-r) calculated by 11 and 5 species in thermo-chemical non-equilibrium flow fields |
| 图选项 |
图 2给出了不同组元热化学非平衡流场平动-转动温度(Tt-r)和振动温度Tv沿驻点线分布特性。由于11组元化学反应数量较多,消耗的能量也随之增大,流场平动-转动温度和振动温度最大值均比5组元化学反应的要小。但是,11组元化学反应的平动-转动温度与振动温度曲线之间的温度差值及两者所包含的区域面积都要比5组元化学反应的大,进一步说明了采用11组元化学反应的热化学非平衡特性要比5组元化学反应的剧烈。
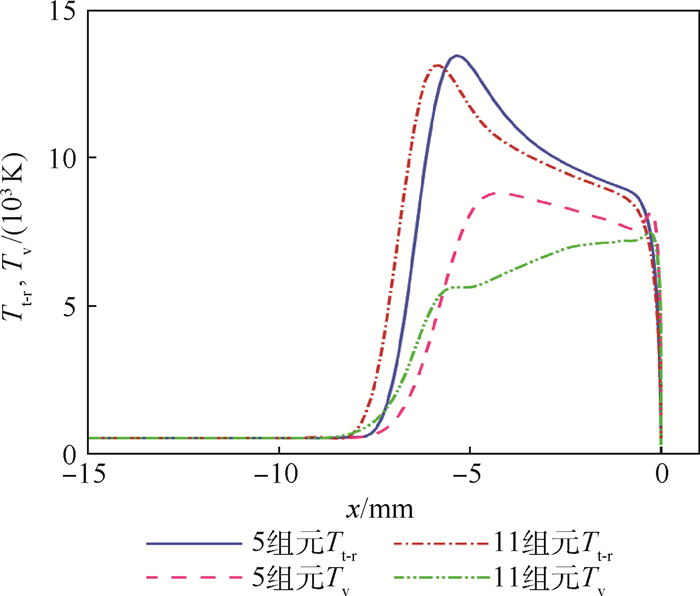 |
| 图 2 11组元与5组元热化学反应不同温度沿驻点线分布 Fig. 2 Distribution of different temperatures calculated by 11 and 5 species thermo-chemical reactions along stagnation point line |
| 图选项 |
图 3给出了流场各中性组元沿驻点线的质量分数c分布。图 3(a)中,因O2离解温度比N2的低,O2在激波后的高温环境中几乎全部离解为O。激波后气体温度沿驻点线降低,直至壁面附近低温区域才有部分O2生成。图 3(b)中,因电离作用会使得中性组元数量减少,11组元化学反应生成的NO、O和N最大质量分数均要比5组元化学反应中相应组元的最大质量分数略小些,其中,5组元化学反应生成的O质量分数最大。
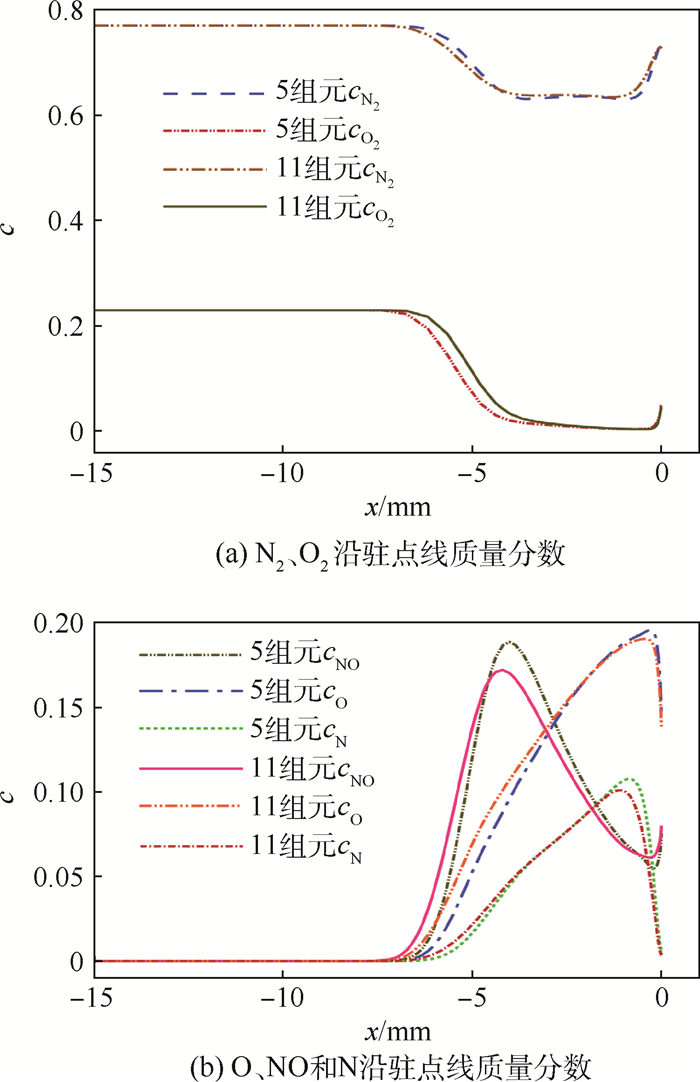 |
| 图 3 不同中性组元沿驻点线质量分数 Fig. 3 Mass fractions of different neutral species along stagnation point line |
| 图选项 |
图 4分别给出了半球壁面压强Pw和热流密度q沿球面周角θ分布特性。图 4(a)中,11组元和5组元化学反应的壁面压强分布曲线几乎重合。中性粒子在高温下电离变成离子体并生成电子,而由电子引起的流场压强变化非常弱,因此,电离作用对壁面气动力载荷影响很小。图 4(b)中,驻点热流密度实验值约为6.51×106 W/m2,11组元和5组元化学反应数值计算的驻点热流密度与实验值相对误差分别为1.6%和20.3%。未考虑电离作用的5组元化学反应获得的壁面热流密度整体过于偏大,而11组元化学反应获得的壁面热流密度分布与实验结果符合的很好。由于激波后高温环境下的电离反应会消耗气动加热作用产生的热能,11组元化学反应比未考虑电离反应的5组元化学反应获得的流场最大温度低,因而两者各自获得的壁面热流密度差别较大。因此,电离作用对高超声速热化学非平衡环境气动热载荷比对气动力载荷的影响大。
 |
| 图 4 11组元与5组元化学反应壁面压强与热流密度对比 Fig. 4 Comparison of wall pressures and heat fluxes calculated by 11 and 5 species chemical reactions |
| 图选项 |
3.2 不同电离状态热化学非平衡气动热环境分析 分别采用7组元(N2,O2,NO,O,N,NO+,e-),18组化学反应式(表 1中化学反应式1~7)和11组元(N2,O2,NO,O,N,N2+,O2+,NO+,O+,N+,e-),32组化学反应式,对第3节的半球模型[23]在不同电离状态下的气动热环境数值分析。
图 5为半球在不同电离状态下的流场平动-转动温度。7组元热化学非平衡状态和11组元热化学平衡状态(简称11组元平衡)的流场最大平动-转温度分别为13 261和10 871 K。7组元热化学非平衡状态只考虑一个电离反应式:N+O?NO++ e-,该电离消耗的能量较少,气体电离强度较弱,7组元热化学非平衡流场平动-转动温度较大。11组元32组化学反应式比7组元18组化学反应式数量多,而且在11组元热化学平衡状态下,为使各化学反应都能充分进行,所需消耗的热能更多,气体电离强度要比11组元热化学非平衡状态大。因此,从7组元、11组元热化学非平衡到11组元热化学平衡状态,随着电离作用不断增强,能量消耗增大,因而半球高超声速流场最大平动-转动温度也依次减小。
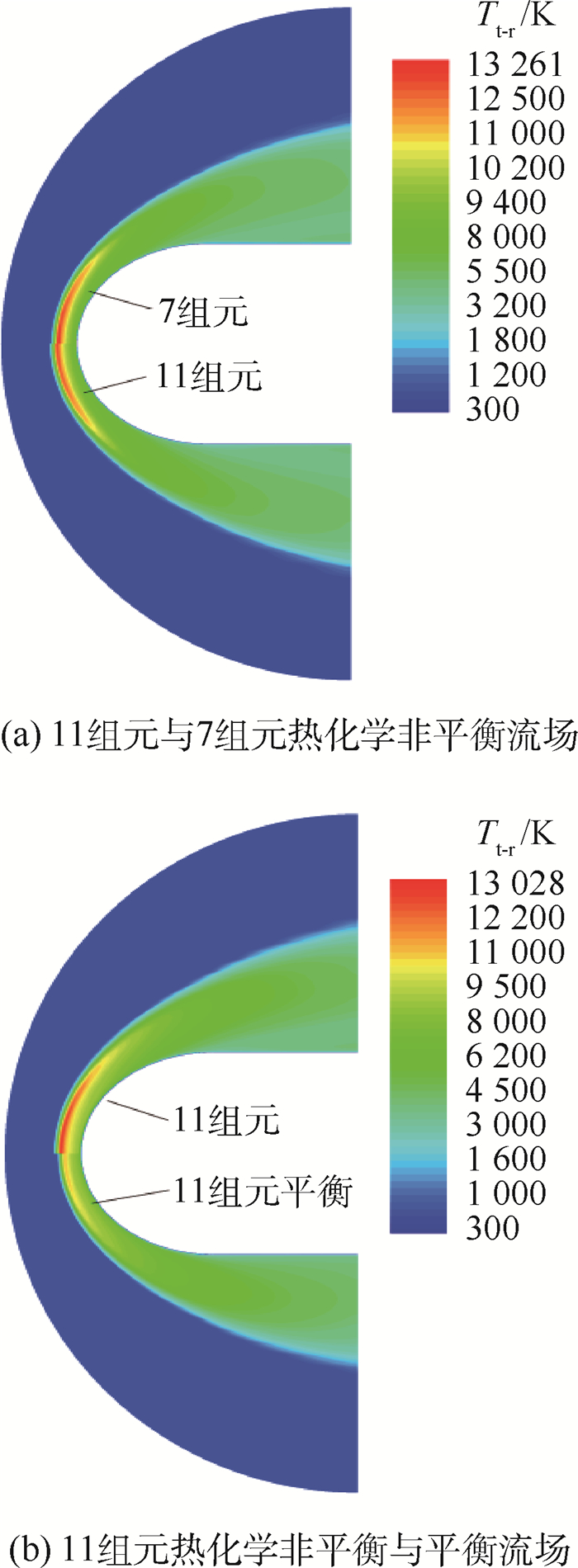 |
| 图 5 不同电离状态下流场平动-转动温度 Fig. 5 Translational-rotational temperatures in different ionization flow fields |
| 图选项 |
图 6为不同电离状态下的流场平动-转动温度、振动温度和平衡温度Teq沿驻点线分布特性。11组元热化学平衡状态,正向和逆向化学反应充分进行而达到平衡,使其流场平衡温度介于7组元和11组元热化学非平衡流场平动-转动温度与振动温度之间。7组元18组化学反应式虽然也考虑了高温电离作用,但远比11组元32组化学反应式数量少,热能消耗也少,因此7组元热化学非平衡流场平动-转动温度和振动温度都较大。
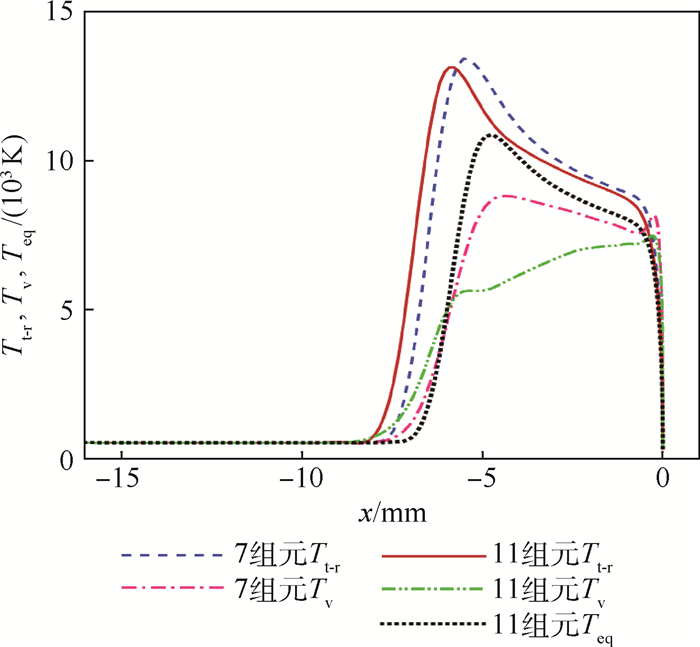 |
| 图 6 不同电离状态下各种温度沿驻点线分布 Fig. 6 Distribution of different temperatures calculated in different ionization conditions along stagnation point line |
| 图选项 |
图 7和图 8分别给出了7组元和11组元热化学非平衡流场中NO+和e-摩尔分数XNO+和Xe-分布。NO+和e-主要出现在头部驻点附近小区域。7组元热化学非平衡流场中的NO+和e-最大摩尔分数相比11组元均过于偏低。7组元化学反应中,因只考虑了N+O?NO++e-生成NO+和e-,此外,生成N比生成O所需的温度要高,N和O生成量差别较大,流场中NO+和e-生成量也随之较少。11组元32组化学反应式考虑到其他更多化学反应式生成NO+和e-,它们才是生成NO+和e-的主要来源。因此,数值计算高超声速热化学非平衡气动热环境时,采用7组元18组化学反应式获得的NO+和e-生成量远低于11组元32组化学反应式生成量;7组元化学反应不能对高超声速飞行器壁面周围电子或离子体分布特性进行有效预测。
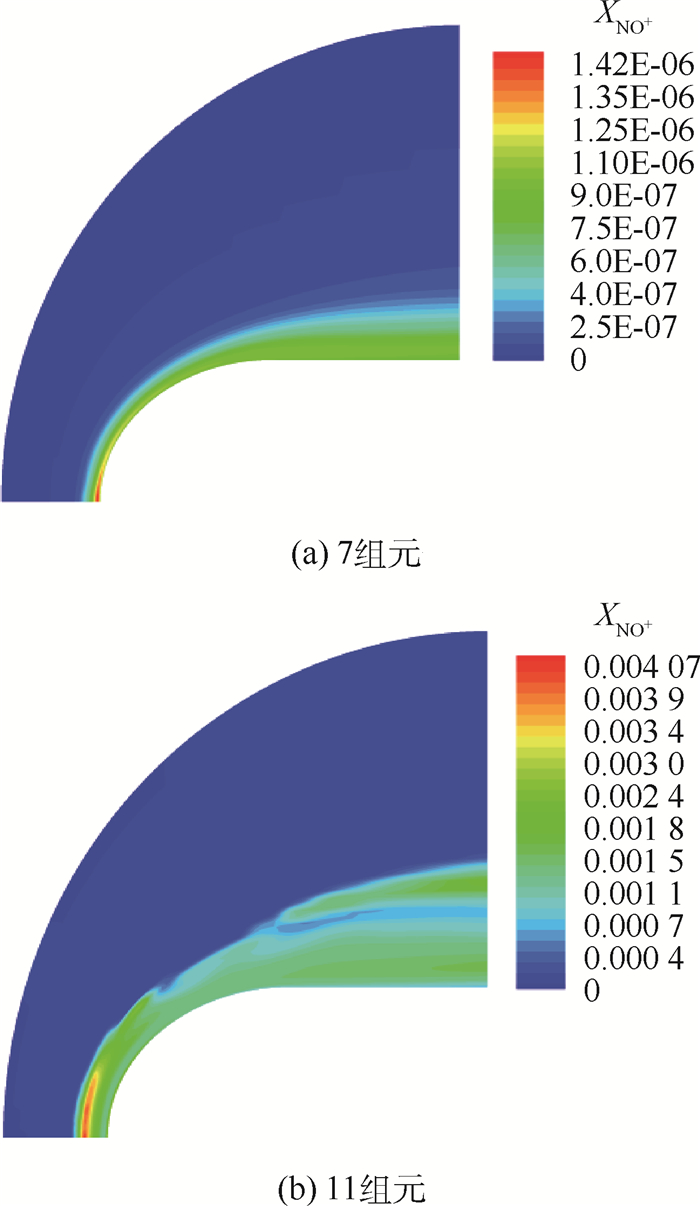 |
| 图 7 7组元和11组元热化学非平衡流场NO+摩尔分数 Fig. 7 NO+ mole fractions in 7 and 11 species thermo-chemical non-equilibrium flow fields |
| 图选项 |
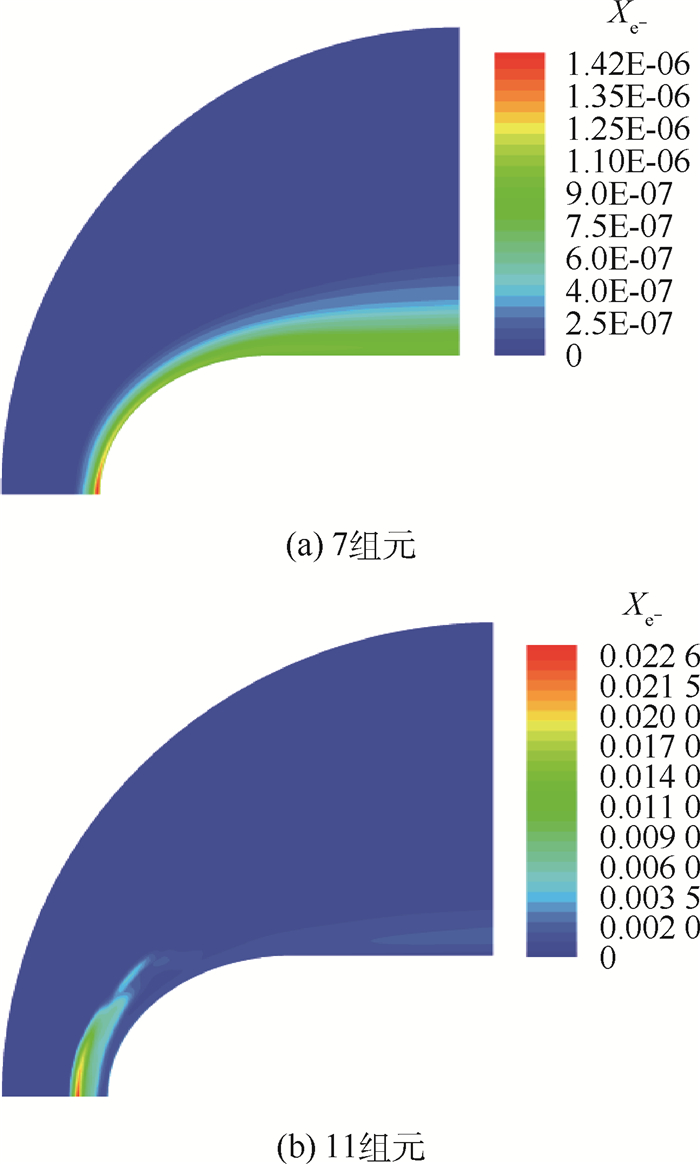 |
| 图 8 7组元和11组元热化学非平衡流场e-摩尔分数 Fig. 8 e- mole fractions in 7 and 11 species thermo-chemical non-equilibrium flow fields |
| 图选项 |
图 9(a)中,不同电离状态下的壁面压强分布几乎完全相同。由于中性粒子因电离生成离子体和电子引发的流场压强变化较微弱,混合气体中离子体和电子数量也相对较少,电离作用对气动力载荷影响很小。图 9(b)中,7组元、11组元热化学非平衡和11组元热化学平衡状态驻点热流密度与实验值相对误差分别为17.1%、1.6%和7.5%。7组元热化学非平衡流场温度最大,而11组元热化学平衡状态下逆向化学反应得以充分进行,会在壁面附近释放大量热能,其获得的壁面热流密度均比实验结果偏大。不同组元电离反应对气动热载荷比对气动力载荷的影响要大。
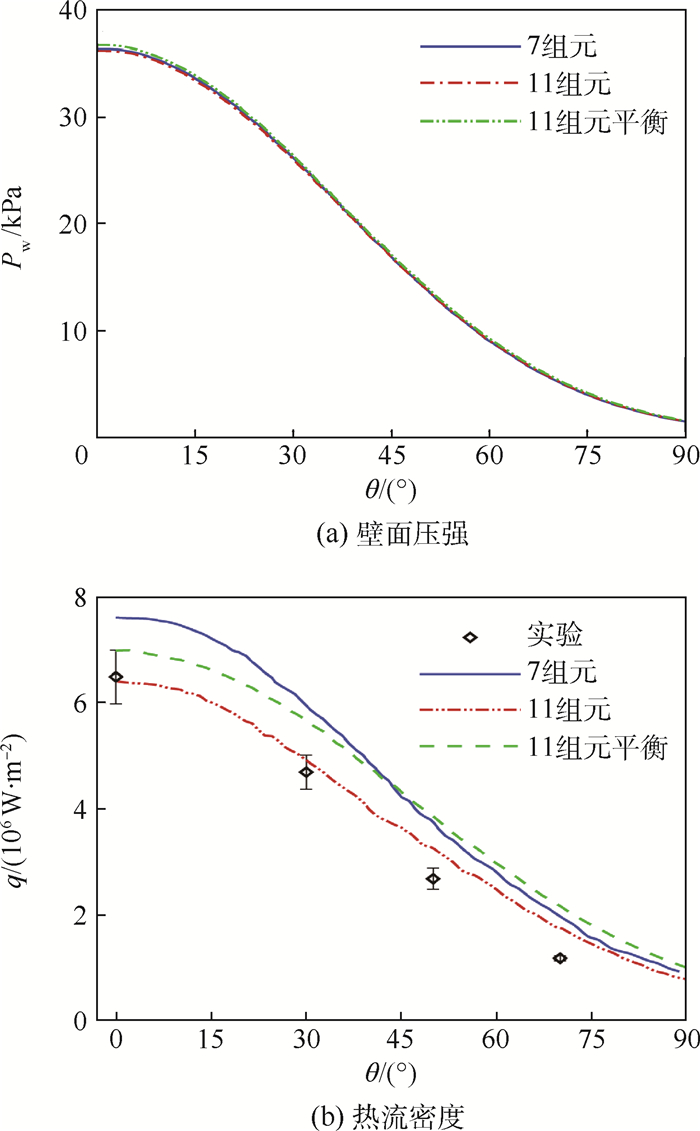 |
| 图 9 不同电离状态下壁面压强与热流密度对比 Fig. 9 Comparison of wall pressures and heat fluxes calculated in different ionization conditions |
| 图选项 |
3.3 壁面催化作用对热化学非平衡电离气动热环境影响 选用文献[24]中的高超声速再入体实验验证模型,采用11组元热化学非平衡反应,数值研究壁面不同催化条件对实验模型热化学非平衡电离气动热环境影响。实验模型前缘半径rn=175.26 mm,基圆半径rb=73.025 mm,肩部圆角半径rc= 7.3 mm,后半锥角β=-32.5°,模型全长L= 96.04 mm。自由来流参数:速度U∞= 4 167 m/s,静温T∞= 522 K,静压P∞= 245.36 Pa,迎角α=0°;等温壁面Tw= 300 K。自由来流中组元N2、O2、NO和O的质量分数分别为cN2= 0.735,cO2= 0.171,cNO= 0.065和cO= 0.029。二维再入体模型网格结点数分布为150×100(流向×法向)。
图 10为再入体实验模型在非催化壁面和完全催化壁面条件下的热化学非平衡电离流场平动-转动温度分布。2种壁面催化条件下的流场平动-转动温度分布特性几乎相同。完全催化壁面条件下的流场最大平动-转动温度为7 362 K,略大于非催化壁面条件下的流场最大平动-转动温度7 346 K。完全催化壁面条件下,由于部分原子,离子体和电子在壁面处发生复合反应而释放热能,但因其所释放的热能量有限,却不能导致流场温度大幅升高。因此,壁面催化作用对高超声速热化学非平衡电离流场温度影响很小。
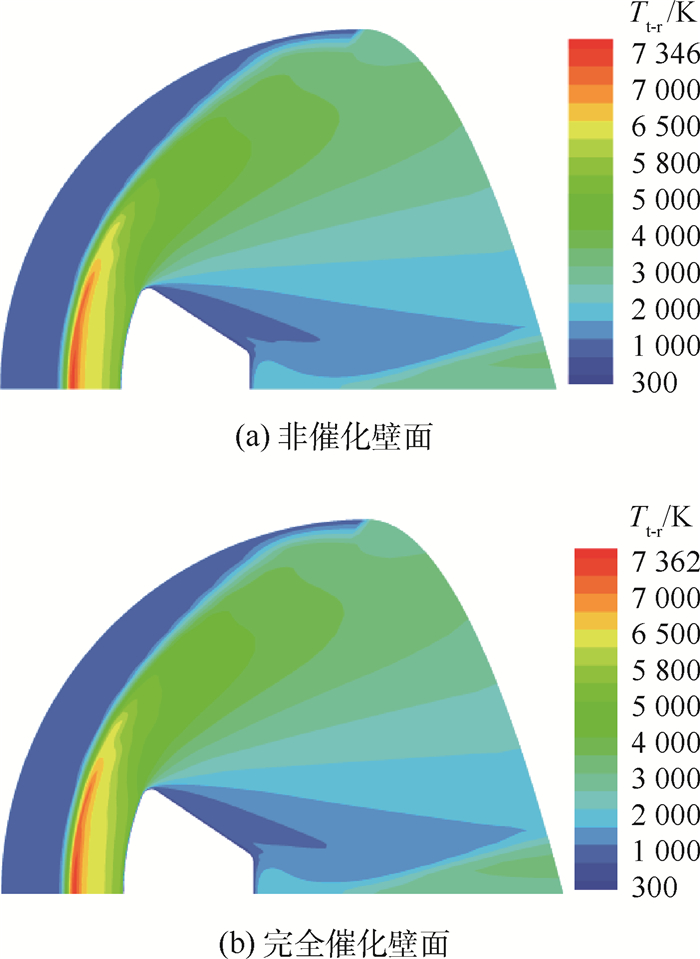 |
| 图 10 不同催化壁面热化学非平衡电离流场平动-转动温度 Fig. 10 Translational-rotational temperatures in thermo-chemical non-equilibrium ionization flow fields in different wall catalytic conditions |
| 图选项 |
图 11将再入体模型在不同催化壁面条件下数值计算壁面压强和壁面热流密度与实验值进行对比。图 11(a)所示,数值计算采用11组元热化学非平衡反应,所获得非催化和完全催化壁面条件下的壁面压强分布曲线几乎重合,而且都与实验结果符合的较好。虽然有部分电子和其他粒子会在壁面上发生复合反应并释放热能,但因壁面附近的粒子数量和气体温度变化并不大,因而热化学非平衡电离状态下,壁面压强受壁面催化作用的影响并不明显。
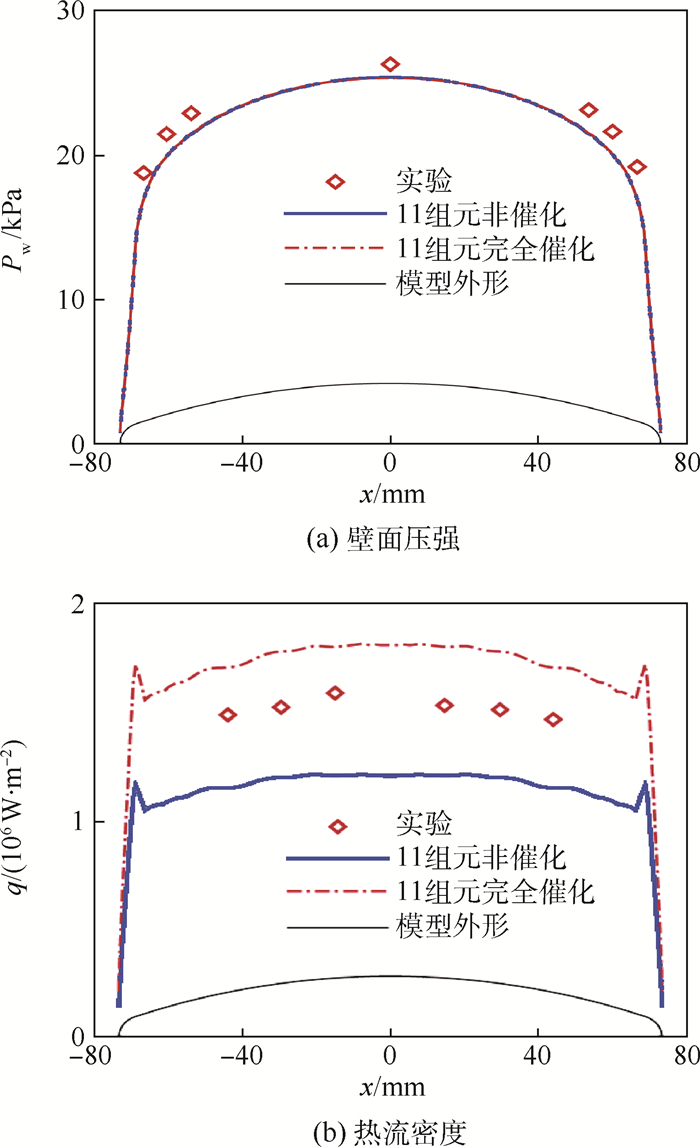 |
| 图 11 不同催化壁面压强与热流密度 Fig. 11 Wall heat fluxes and pressures calculated in different wall catalytic conditions |
| 图选项 |
图 11(b)中,因前缘半径较大,前缘壁面上的热流密度平缓地逐渐减小。由于激波强度在再入体模型肩部圆角减弱,但肩部圆角半径小,肩部出现了热流密度峰值。热化学非平衡电离流场环境,壁面热流密度实验值介于非催化和完全催化壁面条件数值计算值之间。原子、离子体和电子在壁面上发生复合反应会释放热能,壁面热流密度增大,因而未考虑壁面催化作用时的壁面热流密度过于偏小。完全催化壁面条件是壁面催化作用的一种极限假设情况,相关组元粒子在壁面上的复合反应得以充分进行,会释放大量热能,而实际壁面催化作用介于非催化和完全催化条件之间。因此,热化学非平衡电离状态下,壁面催化作用对壁面热流密度的影响较大。
4 结论 通过数值研究电离作用对高超声速热化学非平衡气动热环境的影响,得到:
1) 高超声速热化学非平衡气动热环境数值计算时,气动加热产生的热能主要被空气分子离解和化学置换反应所消耗,电离反应消耗的热能较少,因此,5组元热化学非平衡因不考虑电离作用,其流场温度和壁面热流密度均要比考虑了电离作用影响的11组元热化学非平衡的略大。电离反应产生的离子体和电子引发的激波后气体密度和压强变化较弱,电离作用对激波离体距离和高超声速热化学非平衡气动力载荷影响很小。
2) 随着电离作用加剧,能量消耗增大,流场温度不断降低,11组元热化学平衡强电离流场温度最低。7组元化学反应考虑生成NO+和e-的化学反应式数量少,7组元热化学非平衡弱电离流场NO+和e-组元数值计算生成量偏低。7组元热化学非平衡弱电离流场温度最大,而11组元热化学平衡逆向化学反应在壁面附近释放热能较多,因而7组元热化学非平衡和11组元热化学平衡状态分别获得的壁面热流密度均比实验结果偏大,而11组元热化学非平衡状态壁面热流密与实验符合较好。因此,11组元化学反应能更好地对高超声速飞行器热化学非平衡电离流场中的气动热和气动力载荷进行可靠预测。
3) 高超声速热化学非平衡电离状态,壁面催化条件会使得中性原子,离子体和电子在壁面上发生复合反应而释放能量,壁面热流密度增大较明显。壁面附近的粒子数量和气体温度变化受催化壁面条件下的复合反应影响并不是很大,因此,壁面气动力载荷变化很小。由于只有部分气体组元在壁面上发生复合反应,释放的热能有限,热化学非平衡电离流场最大温度受壁面催化作用的影响小。
参考文献
| [1] | PARK G, GAI S L, NEELY A J. Base flow of circular cylinder at hypersonic speeds[J]. AIAA Journal, 2016, 54(2): 458-468. DOI:10.2514/1.J054270 |
| [2] | SHAO C, NIE L, CHEN W F. Analysis of weakly ionized ablation plasma flows for a hypersonic vehicle[J]. Aerospace Science and Technology, 2016, 51: 151-161. DOI:10.1016/j.ast.2016.02.005 |
| [3] | BURT J M, JOSYULA E. Vibrational nonequilibrium quantification for state-resolved simulation of a hypersonic flow[J]. Journal of Thermophysics and Heat Transfer, 2017, 31(3): 660-673. DOI:10.2514/1.T5044 |
| [4] | ZENG M, XU D, LIU J, et al. Novel method to calculate vibrational thermal conduction in hypersonic nonequilibrium flow[J]. Journal of Thermophysics and Heat Transfer, 2016, 30(1): 12-24. DOI:10.2514/1.T4611 |
| [5] | IBRAHIM A, SUMAN S, GIRIMAJI S S. On air-chemistry reduction for hypersonic external flow applications[J]. International Journal of Heat and Fluid Flow, 2015, 51: 298-308. DOI:10.1016/j.ijheatfluidflow.2014.10.021 |
| [6] | KIM M, KEIDAR M, BOYD I D. Analysis of an electromagnetic mitigation scheme for reentry telemetry through plasma[J]. Journal of Spacecraft and Rockets, 2008, 45(6): 1223-1229. DOI:10.2514/1.37395 |
| [7] | KIM M, BOYD I D, KEIDAR M. Modeling of electromagnetic manipulation of plasmas for communication during reentry flight[J]. Journal of Spacecraft and Rockets, 2010, 47(1): 29-35. DOI:10.2514/1.45525 |
| [8] | FARBAR E, BOYD I D, MARTIN A. Numerical prediction of hypersonic flowfields including effects of electron translational nonequilibrium[J]. Journal of Thermophysics and Heat Transfer, 2013, 27(4): 593-606. DOI:10.2514/1.T3963 |
| [9] | SHANG J S, ANDRIENKO D A, HUANG P G, et al. A computational approach for hypersonic nonequilibrium radiation utilizing space partition algorithm and Gauss quadrature[J]. Journal of Computational Physics, 2014, 266: 1-21. DOI:10.1016/j.jcp.2014.02.007 |
| [10] | 屈程, 王江峰. 电离对高超声速稀薄流飞行器气动热影响[J]. 航空动力学报, 2016, 31(9): 2156-2163. QU C, WANG J F. Ionization effects on aerodynamic heat for vehicle in hypersonic rarefied flow[J]. Journal of Aerospace Power, 2016, 31(9): 2156-2163. (in Chinese) |
| [11] | HAO J A, WANG J Y, LEE C H. Numerical study of hypersonic flows over reentry configurations with different chemical nonequilibrium models[J]. Acta Astronautica, 2016, 126: 1-10. DOI:10.1016/j.actaastro.2016.04.014 |
| [12] | GUPTA R N, YOS J M, THOMPSON R A, et al.A review of reaction rates and thermodynamic and transport properties for an 11-species air model for chemical and thermal nonequilibrium calculations to 30000K: NASA RP-1232[R].Washington, D.C.: NASA, 1990. |
| [13] | PARK C.On convergence of computation of chemical reacting flows: AIAA-1985-0247[R].Reston: AIAA, 1985. |
| [14] | LORZEL H, MIKELLIDES P G.Validation of a nonequilibrium air chemistry model in MACH2 and applications to weakly-ionized hypersonic flow: AIAA-2009-0279[R].Reston: AIAA, 2009. |
| [15] | PARK C.Problems of rate chemistry in the flight regimes of aeroassisted orbital transfer vehicles: AIAA-1984-1730[R].Reston: AIAA, 1984. |
| [16] | MASSIMI H S, SHEN H, WEN C Y, et al. Numerical analysis of hypersonic flows around blunt-nosed models and a space vehicle[J]. Aerospace Science and Technology, 2015, 43: 360-371. DOI:10.1016/j.ast.2015.03.017 |
| [17] | ALLOUCHE R, HAOUI R.Ionising air in thermal and chemical nonequilibrium flow behind a plane shock wave: AIAA-2006-8154[R].Reston: AIAA, 2006. |
| [18] | KIM M, GVLHAN A, BOYD I D. Modeling of electron energy phenomena in hypersonic flows[J]. Journal of Thermophysics and Heat Transfer, 2012, 26(2): 244-257. DOI:10.2514/1.T3716 |
| [19] | GAO Z X, JIANG C W, LEE C H.Aeroheating study of hypersonic chemical nonequilibrium flows around a reentry blunt body: AIAA-2014-4415[R].Reston: AIAA, 2014. |
| [20] | CHI D, CHAKRAVARTHY S, GOLDBERG U.Flow prediction around the SACCON configuration using CFD++: AIAA-2010-4563[R].Reston: AIAA, 2010. |
| [21] | GVR H B, EYI S.Diffusion effect on hypersonic flow using Fick's law: AIAA-2015-3797[R].Reston: AIAA, 2015. |
| [22] | CHEN X H, CHEN F, ZHANG S T, et al.The effects of chemical nonequilibrium and surface catalytic on aerodynamic characteristics of hypersonic vehicles: AIAA-2016-1252[R].Reston: AIAA, 2016. |
| [23] | MACLEAN M, MARINEAU E, PARKER R, et al. Effect of surface catalysis on measured heat transfer in expansion tunnel facility[J]. Journal of Spacecraft and Rockets, 2013, 50(2): 470-474. DOI:10.2514/1.A32327 |
| [24] | MACLEAN M, MUNDY E, WADHAMS T, et al.Analysis and ground test of aerothermal effects on spherical capsule geometries: AIAA-2008-4273[R].Reston: AIAA, 2008. |
