航空发动机作为航空器的核心设备，其系统的结构复杂且长期工作于高温、高压的恶劣环境下，限制了一些传统设备对航空发动机尾气进行监测，基于电容层析成像技术(Electrical Capacitance Tomography，ECT)的航空发动机尾气检测系统为解决此问题提供了可能性。
ECT技术的优点在于非侵入性、安全性、响应速度快、安装便捷及成本低等，使得其在工业过程可视化检测中成为一项极具发展潜力的技术^[1]。
1984年，Brown对电学成像技术进行了综述，并且提出了反投影算法^[2]；1985年，Murai和Kagawa^[3]根据Geselowitz灵敏度原理将灵敏度系数法引入到电学成像中；1998年，Vauhkonen等^[4]提出了卡尔曼滤波法，并将其应用到电学层析成像中；1999年，杨五强等^[5]提出了改进的Landweber迭代算法，并成功应用到电学成像领域；2002年，Kim等^[6]研究出一种扩展的卡尔曼滤波算法；2003年，杨五强等^[7]对ECT技术中常用的算法进行了综述；2005年，王化祥等^[8]提出了基于灵敏度矩阵的奇异值分解理论及正则化共轭梯度(Conjugate Gradient, CG)法；2007年，王化祥等^[9]提出了基于自适应网格的改进总变差算法。
本文将双共轭梯度(Biconjugate Gradient, BICG)算法引入到ECT技术中。为了得到更好的效果，对该算法做了一些改进，将BICG算法与正则化算法相结合，并与传统的迭代类算法进行比较^[10-11]。
1 ECT系统 1.1 系统组成 传统的ECT系统主要由三大子系统组成：传感器系统、数据采集系统和上位机成像系统。3个系统具有各自的功能。传感器系统主要测量极板间的电容值，数据采集系统将测得的电容值传输到上位机，上位机通过软件及程序进行图像重建，这就是一个简单的ECT系统的成像过程。图 1为传统ECT系统模型。

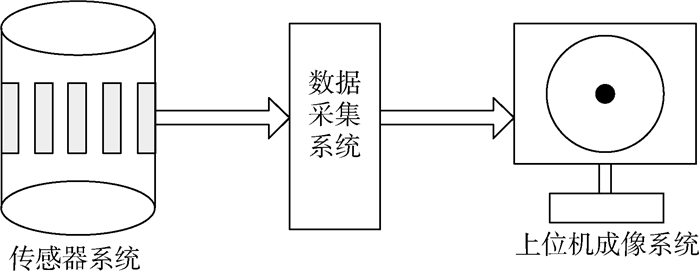图 1 传统ECT系统模型 Fig. 1 Traditional ECT system model

图选项

1.2 算法介绍 CG算法一般适用于求解大型线性方程，属于最速下降法的一种改进，误差不计的条件下，CG算法在N步内就可以达到收敛效果。虽然CG算法在有限的步骤内就可到达收敛，但对于求解出的矩阵G来说，N的取值是非常大的。因此，本文在经典CG算法的基础上引进了BICG算法来提高计算速度。BICG算法使用2组共扼向量作为搜索方向，而CG算法仅使用1组共轭向量作为搜索方向，因此BICG算法的速度得到大幅度提高。如果系数矩阵A为实对称阵，且求解节点数较多时，BICG算法收敛速度将会更快。通过实验仿真和数据对比，验证了BICG算法效果明显高于其他几种迭代类算法。图 2为BICG算法的计算流程。

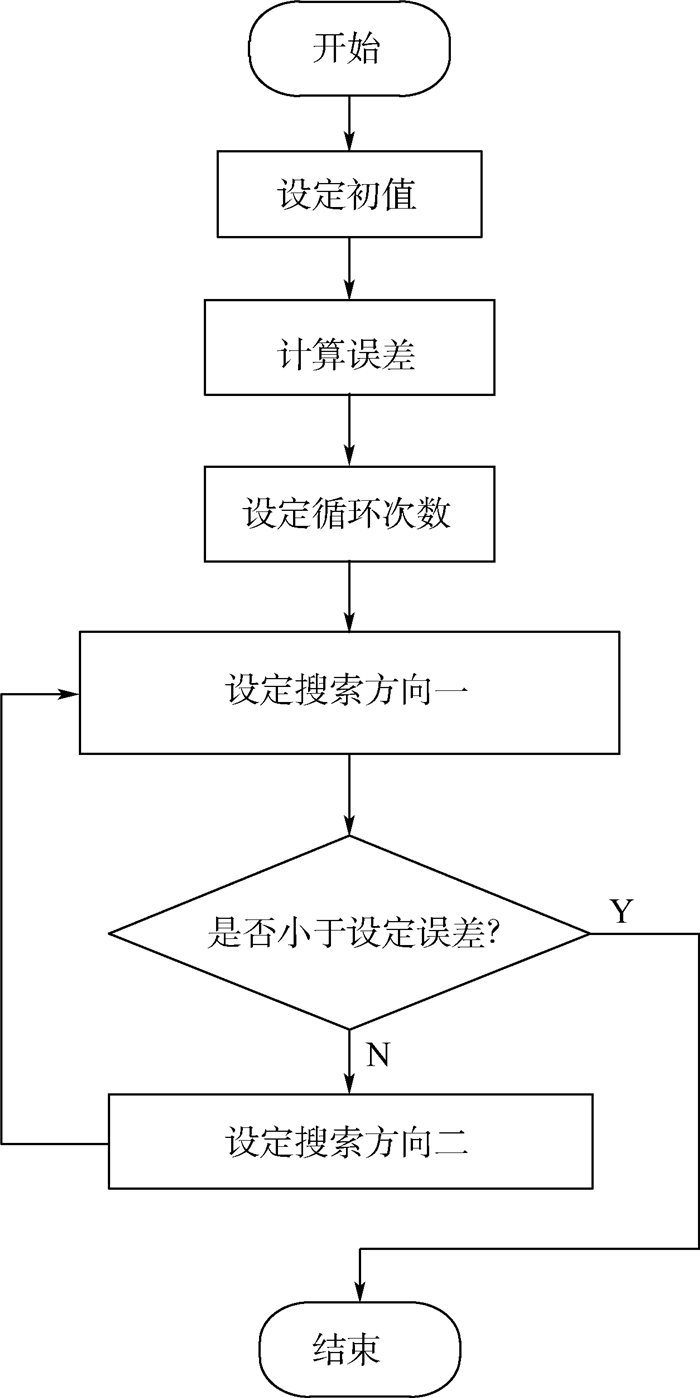图 2 BICG算法计算流程 Fig. 2 BICG algorithm calculation flowchart

图选项

2 仿真设计 仿真使用COMSOL5.3软件对12电极的ECT系统进行建模，对系统进行有限元分割，分割网络设置为64×64，共有3228个有效单元，通过有效网络来求解场内的电容值及灵敏度分布情况，即ECT技术的正问题。空场材料的介电常数设为1，屏蔽罩及电极的介电常数为2.2，管道内被测物体的介电常数设为4.2。图 3(a)为电极数目为12的传统ECT系统模型, 图 3(b)为通过有限元分割后得到的模型。

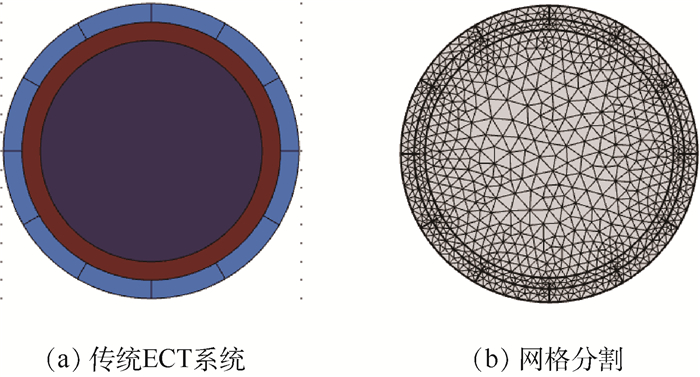图 3 ECT系统仿真 Fig. 3 ECT system simulation

图选项

通过有限元方法分割完网格后，对场内进行计算，计算结果可通过静电场电势(见图 4(a))及场内电场线分布情况(见图 4(b))呈现出来。

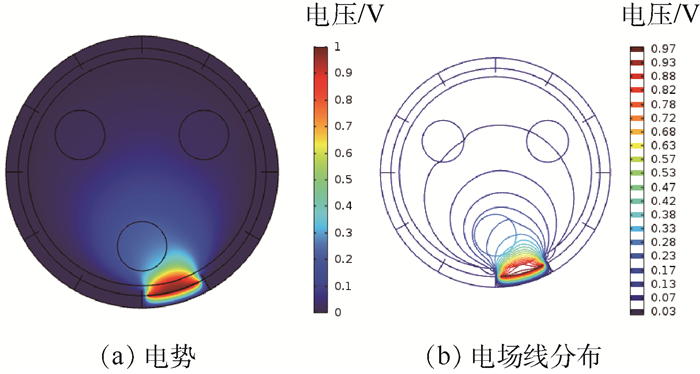图 4 传感器电势分布 Fig. 4 Sensor potential distribution

图选项

3 图像重建算法 实验通过5种图像重建算法，即Tikhonov算法、Landweber算法、CG算法、BICG算法及本文改进算法对各模型仿真进行图像重建^[12-13]。
3.1 LBP算法 LBP算法基于以下2个理想条件：①灵敏度系数均匀分布在场内；②电容值与灵敏度矩阵和介质分布有关。

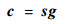(1)

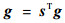(2)

式中：c为电容值矩阵；s为灵敏度矩阵；g为介质分布向量；s^T为s的转置矩阵，用来代替s的逆矩阵。
3.2 Landweber算法 Landweber算法计算过程如下：

(3)

把式(3)展开为

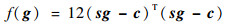(4)

函数f(g)的最速下降方向, 即梯度为

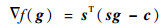(5)

以LBP算法作为图像初值, Landweber算法为

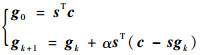(6)

设λ_max为s^Ts的最大特征值, α≤2λ_max保证Landweber算法收敛。
3.3 CG算法 CG算法计算过程为：在式(7)的两边乘以S的转置矩阵S^T, 得到式(8)。

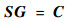(7)

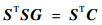(8)

式中：S为灵敏度矩阵；G为介电常数矩阵；C为电容值。
1) 记初始灰度值为向量G₀，设为零向量。
2)给定参数令S^TS=S′，S^TC=C′，得到新的未知方程S′G=C′。r₀=C′－S′G₀, p₀=r₀；进行循环迭代计算。
3) 当k=0, 1, 2, …, n时，进行循环计算。

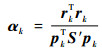(9)

式中：p_k为第k次的搜索方向；r_k为残差向量。
如果||r_k|| < e或k>n, 则停止，否则进行式(12)的计算。其中：e为迭代终止的误差。

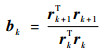(12)

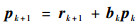(13)

转到式(11)。
3.4 BICG算法 BICG算法计算过程如下：
1) 记初始灰度值为向量G₀，设为零向量。
2) 给定参数r₀=C′－S′G₀, p₀=r₀, p_t0=r_t0, r_t0为r₀的共轭矩阵；进行循环迭代计算。
3)当k=0, 1, 2, …, n时，进行循环计算。

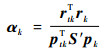(14)

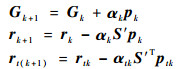(15)

如果||r_k|| < e或k>n, 则停止，否则进行式(16)的计算。

(16)

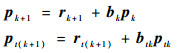(17)

转到式(16)。
3.5 Tikhonov算法 正则化算法是以最小二乘准则及平滑准则作为理论依据计算的，目标泛函为

(18)

式中：α为正则化参数；L为正则化算子。
对于给定的正则化算子L，选取合适的正则化参数α>0, 最小化方程，可以得到Tikhonov算法的解为

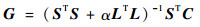(19)

其原理就是引入一个正则化参数，使原来不能求逆的矩阵可以求逆矩阵。设L为单位矩阵，可得标准Tikhonov算法的解为

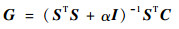(20)

正则化参数α的取值是至关重要的，直接影响到图像重建的质量，而且正则化参数α的选择是很难确定的。本文实验选取的正则化参数为0.003。
3.6 改进算法 本文改进算法是在BICG算法基础上加入了正则化的思想。传统的BICG算法应用时针对不同的流型所要的迭代次数会有很大的变化，为了改进这一不足，加入了正则化的思想。将BICG算法经过Tikhonov正则化后变为

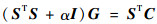(21)

(22)

式中：y₀=S^Tx₀，x₀为正则化向量。选取合适的x₀，令y₀=S^Tx₀，S′=S^TS+y₀y₀^T, 取初始灰度值G₀为零向量，r₀=C′－S′G₀, p₀=r₀，其循环迭代过程与BICG算法相同。
4 实验与分析 4.1 图像重建 运行MATLAB 2014a软件，首先，对建模完成的程序分别进行空场、物场、满场电容值和灵敏度的计算，并进行归一化处理；其次，分别通过Tikhonov算法、Landweber算法、CG算法、BICG算法及改进算法等5种算法对各模型进行图像重建。仿真模型选择核心流、双泡流、三泡流、层流和环流。图像重建结果如图 5所示。

图 5 各模型重建图像 Fig. 5 Reconstructed images of each model

图选项

4.2 图像重建分析 仿真实验中，通过计算重建图像的图像错误率(IME)和图像相关系数(CORR)来对重建图像进行评估，对重建图像的效果进行评价^[14-15]。将Tikhonov算法、Landweber算法、CG算法、BICG算法及改进算法的重建图像的图像错误率和图像相关系数进行对比，分析改进算法的成像优缺点。图像错误率IME和图像相关系数CORR的计算公式分别为

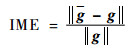(23)

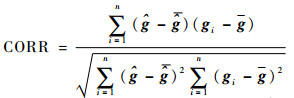(24)

式中：g为仿真中设定的介电常数；为图像重建的介电常数；g为g和的平均值。
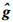
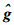
由式(23)和式(24)计算得IME和CORR，分别如表 1和表 2所示。
表 1 IME计算值 Table 1 Calculated values of IME

仿真模型	Tikhonov算法	Landweber算法	CG算法	BICG算法	改进算法
核心流	0.3880	0.2537	0.2420	0.2857	0.2524
双泡流	0.4201	0.3813	0.4227	0.3512	0.3503
三泡流	0.4802	0.4254	0.5012	0.4003	0.4010
层流	0.5046	0.4213	0.9344	0.3612	0.3410
环流	0.6548	0.5826	0.5802	0.2013	0.2106

表选项






表 2 CORR计算值 Table 2 Calculated values of CORR

仿真模型	Tikhonov算法	Landweber算法	CG算法	BICG算法	改进算法
核心流	0.7012	0.8063	0.7901	0.7886	0.8095
双泡流	0.6325	0.6418	0.6558	0.7802	0.7795
三泡流	0.5361	0.5904	0.5418	0.6217	0.6223
层流	0.5241	0.6908	0.0130	0.7146	0.7134
环流	0.4529	0.4608	0.4621	0.8592	0.8786

表选项






通过数据对比可以看出，使用CG算法得到核心流模型的成像效果最佳，改进算法效果也相差不大，但BICG算法迭代次数少，成像时间快，效率会更高一些。一般使用核心流模型验证传感器系统的基本性能。反观其他模型的图像重建数据对比，BICG算法和改进算法成像效果优于其他成像算法，尤其在环流模型中，其成像效果远远超出其他算法。
实验中，除了计算图像错误率和相关系数，还对各算法成像时间和迭代算法的迭代次数做了统计。表 3为各成像算法数据对比。通过多次调节对比，各迭代算法选取的迭代次数不同，选择各算法最优成像效果。通过选择的迭代次数进行成像时长对比。由数据可以直接看出，改进算法迭代次数相对其他迭代类算法大大减少，而且成像时间也大大缩短。
表 3 成像算法数据对比 Table 3 Comparison of imaging algorithm data

算法	迭代次数	成像时间/s
Tikhonov算法		3.06
Landweber算法	120	4.47
CG算法	200	10.32
BICG算法	50	3.12
改进算法	20	2.77

表选项






5 结论 1) 本文提出了将BICG算法应用到ECT技术，而且图像重建的分辨率更高，误差减小，通过仿真实验可以发现BICG算法的可行性，不同的流型都具有较好的成像效果，得到更高质量的重建图像，大幅度缩短重建图像的成像时间，可以更好地应用于在线监测。
2) 针对不同流型所对应的参数和迭代次数有所不同，而且变化幅度较大，在实际应用中可能会受到一些约束，为此将BICG算法与正则化算法相结合，通过调节一个正则化参数便可得到较好的成像效果。
3) 为使改进算法在ECT技术和其他领域可以得到更广泛、更有效的应用，还需要对其进行进一步的研究和发展。

参考文献

[1]	张立峰. 压缩感知在电容层析成像中的应用[J]. 北京航空航天大学学报, 2017, 43(11): 2316-2321. ZHANG L F. Application of compressed sensing in electrical capacitance tomography[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(11): 2316-2321. (in Chinese)
[2]	BROWN B E. International society for reef studies[J]. Coral Reefs, 1984, 3(1): 58. DOI:10.1007/BF00306141
[3]	KAGAWA Y, MURAI T.Numerical simulation of acoustic levitation[C]//IEEE 1985 Ultrasonics Symposium.Piscataway, NJ: IEEE Press, 1985: 198574.
[4]	VAUHKONEN M, KARJALAINEN P A, KAIPIO J P.A Kalman filter approach applied to the tracking of fast movements of organ boundaries[C]//Proceedings of the 20th Annual International Conference of the IEEE Engineering in Medicine and Biology Society.Piscataway, NJ: IEEE Press, 1998: 6345874.
[5]	YANG W Q, SPINK D M, YORK T A, et al. An image reconstruction algorithm based on Landweber's iteration method for electrical capacitance tomography[J]. Measurement Science and Technology, 1999, 10(11): 1065-1069. DOI:10.1088/0957-0233/10/11/315
[6]	KIM D K, KIM S B, KIM H K. Image processed tracking system of multiple moving objects based on Kalman filter[J]. KSME International Journal, 2002, 16(4): 427-435. DOI:10.1007/BF03185072
[7]	YANG W Q, STOTT A L, GAMIO J C. Analysis of the effect of stray capacitance on AC-based capacitance transducer for tomography[J]. IEEE Transactions on Instrumentation and Measurement, 2003, 52(5): 1674-1681. DOI:10.1109/TIM.2003.817925
[8]	王化祥, 朱学明, 张立峰. 用于电容层析成像技术的共轭梯度算法[J]. 天津大学学报, 2005, 38(1): 1-4. WANG H X, ZHU X M, ZHANG L F. Conjugate gradient algorithm for electrical capacitance tomography[J]. Journal of Tianjin University, 2005, 38(1): 1-4. (in Chinese)
[9]	王化祥, 胡理, 赵波.基于自适应网格剖分的EIT图像重建算法[C]//中国生物医学工程进展——2007中国生物医学工程联合学术年会, 2007: 5. WANG H X, HU L, ZHAO B.EIT image reconstruction algorithm based on adaptive meshing[C]//Progress in Biomedical Engineering in China—2007 China Biomedical Engineering Joint Academic Annual Meeting, 2007: 5(in Chinese).
[10]	田沛, 秦京建, 秦旭刚. 基于两相流电容层析成像系统的正则化Landweber算法[J]. 仪器仪表用户, 2018, 25(9): 90-92. TIAN P, QIN J J, QIN X G. Regularized Landweber algorithm based on two-phase electrical capacitance tomography system[J]. Instrumentation Users, 2018, 25(9): 90-92. DOI:10.3969/j.issn.1671-1041.2018.09.027 (in Chinese)
[11]	袁俊峰.基于并行稳定双共轭梯度算法的不可压缩管流数值模拟[D].杭州: 杭州电子科技大学, 2013. YUAN J F.Numerical simulation of incompressible tube flow based on parallel stable double conjugate gradient algorithm[D].Hangzhou: Hangzhou University of Electronic Science and Technology, 2013(in Chinese).
[12]	彭政, 陈东方, 王晓峰. 正则化超分辨率重建过程的自适应阈值去噪[J]. 计算机应用, 2017, 37(7): 2084-2088. PENG Z, CHEN D F, WANG X F. Adaptive threshold denoising of regularized super-resolution reconstruction process[J]. Journal of Computer Applications, 2017, 37(7): 2084-2088. DOI:10.3969/j.issn.1001-3695.2017.07.036 (in Chinese)
[13]	陈德运, 陈宇, 王莉莉, 等. 基于改进Gauss-Newton的电容层析成像图像重建算法[J]. 电子学报, 2009, 37(4): 739-743. CHEN D Y, CHEN Y, WANG L L, et al. Image reconstruction algorithm based on improved Gauss-Newton for electrical capacitance tomography[J]. Chinese Journal of Electronics, 2009, 37(4): 739-743. DOI:10.3321/j.issn:0372-2112.2009.04.012 (in Chinese)
[14]	CUI Z, WANG H, YIN W. Electrical capacitance tomography with differential sensor[J]. IEEE Sensors Journal, 2015, 15(9): 5087-5094. DOI:10.1109/JSEN.2015.2446982
[15]	马平, 司志宁. 基于小波变换的CT/ECT图像融合方法[J]. 计量学报, 2018, 39(4): 536-540. MA P, SI Z N. CT/ECT image fusion method based on wavelet transform[J]. Acta Metrologica Sinica, 2018, 39(4): 536-540. DOI:10.3969/j.issn.1000-1158.2018.04.18 (in Chinese)