滑环摩擦副是典型的载流摩擦副,摩擦副磨损受多因素影响,除触头和盘面的机械磨损外,由于电流介入,使得摩擦副的摩擦比同等条件下的干摩擦磨损更为严重[1], 电流流经触头和盘面产生焦耳热,伴随着电弧放电现象使得摩擦副磨损加剧,产生的大量磨屑将导致滑环出现短路、断路现象,进而导致滑环的失效[2]。针对载流摩擦,国内外****也取得了很多成果,Ding等[3]通过载流摩擦试验机测量不同载荷下磨屑量产生情况,发现磨损总量随载荷的增加呈“U”字形变化,且存在最优接触载荷使得磨屑量最低,阐述了磨屑量和接触载荷间的关系;Xie等[4]通过试验的方法在不同载荷和滑动速度下,观察滑环摩擦副的电接触性能,得出接触电压与接触载荷、速度的关系。热力电多场耦合建模方面,Monnier等[5]通过有限元分析方法建立了热力电多场耦合下的电接触静摩擦模型,分析电流流通区的接触形变,针对接触区域,将有限元法与赫兹理论比较,证明赫兹接触理论在热力电耦合场下预测接触面形变的适用性,但其只分析了静态环境下的电接触摩擦;于艳艳[6]研究了风电滑环导电环与刷丝的硬度匹配对寿命的影响,探寻了温度对材料硬度的影响,但其模型是纯机械磨损模型。目前的研究更多集中在接触载荷、材料特性、摩擦副匹配[7-8]等磨损机理的揭示,未针对载流摩擦副运行过程中的微观磨损进行建模,提出量化摩擦副磨损程度的可靠性评估方法。
采用摩擦磨损模型进行滑环可靠性评估时,主要的困难是模型指定环境参数下, 模型预测的寿命结果只有一组,由于数据量极少,无法进行可靠性分析。可靠性分析领域已经有很多涉及小子样的可靠性分析方法,其中Bootstrap方法作为可靠性分析中常用的样本增广方法,应用广泛[9-10]。但由于传统的Bootstrap方法在随机样本的生成方面存在不足,样本的取值局限于原始样本范围内,已有大量专家****对此进行了改进。黄玮等[11]采用Sigmoid形Boltzmann函数和三次多项式函数分别拟合全局样本以修正样本经验分布函数,拓宽了采样范围;刘建等[12]针对此问题每个样本点做邻域拓展,并给出拓展经验公式,但在邻域内部区间上采样概率是一致的,当邻域范围设置不合理、样本量较小时,均匀抽样可能将导致抽样结果偏离真实分布;邹艳和罗文强[13]对抽样方法最大统计量与最小统计量进行重新界定,将采样范围拓展至非观测点,从而降低了样本极值本身存在偏差时对抽样结果的影响,但针对连续型变量,此方法在样本点采集范围上有所欠缺。
本文提出的基于多场耦合建模与改进Bootstrap的空间用滑环可靠性评估方法,主要的贡献点如下:①对空间用滑环摩擦副进行微观机理研究,建立了基于热、力、电多物理场耦合的摩擦副磨损预测模型,可有效地进行滑环摩擦副的寿命预估;②结合虚拟样本增广技术以及改进Bootstrap方法,在保留邻域拓展方法的同时,用截断正态分布拟合样本点邻域内部的样本经验分布函数,拓宽样本抽样范围的同时,增加了样本点本身的抽样权重,仿真对比结果表明,改进后的方法具有更高的估计精度;③空间用滑环的全寿命预测与可靠性评估表明,模型的输出结果符合工程实际,对提高空间用滑环的可靠性与质量一致性具有重要意义。
1 摩擦磨损建模与可靠性评估流程 近年来,导电滑环在在役卫星投入使用过程中发生的各类严重故障,均是因为导电滑环失效而导致的整星报废,其中大部分是由于摩擦副磨损产生的磨屑过多,从而引起如短路、断路等致命性问题[14],针对这些问题,对滑环工艺优化和可靠性测试分析也在持续开展中,但由于滑环造价昂贵,可靠性试验成本高,如何充分运用已有的材料特征、工艺参数等信息构建可靠性评估模型,对降低可靠性评估成本,优化工艺参数具有重要意义。
本文所提的滑环可靠性评估方法流程见图 1,具体包括3个部分:
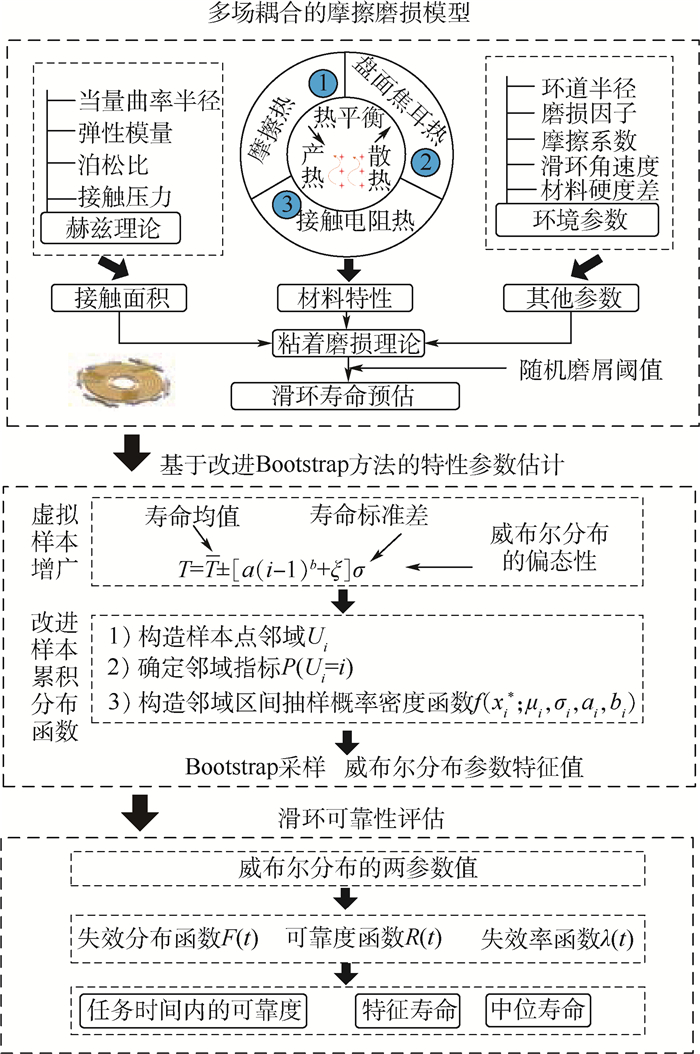 |
| 图 1 滑环可靠性评估流程图 Fig. 1 Reliability evaluation flowchart of slip ring |
| 图选项 |
1) 针对滑环摩擦副热力电多场耦合环境,提出基于赫兹理论的摩擦副接触模型,计算多耦合场下摩擦副接触面积的变化,运用热辐射理论与传热学相关知识,计算摩擦副的温升变化,结合粘着磨损理论,量化热力电多场耦合对摩擦副的影响,建立多场耦合磨损计算模型。
2) 根据模型所得的寿命均值与方差,运用虚拟样本增广法进行扩充,为Bootstrap方法提供原始样本数据点,针对方法的不足之处,在拓宽采样范围的基础上增加原样本点的权重,修改采样的经验分布函数,最后对威布尔两参数进行特征参数的估计,得到了寿命分布的参数值。
3) 由威布尔分布的可靠性相关公式,结合Bootstrap方法所得的寿命分布参数值,对滑环进行可靠性分析,得到滑环的失效分布函数和失效密度函数,进而可得到滑环的可靠度函数与失效率函数,得出包括中位寿命、特征寿命在内的可靠性指标。
2 基于热力电耦合的摩擦副磨损建模 滑环运行过程中,摩擦副触头和汇流盘之间通过一定的压力连接在一起,传递稳定的电信号与功率电流,触头和汇流盘两者间产生相对滑动,滑环处在热、力、电三个场组成的耦合场中,电流和摩擦的存在使得摩擦副温度升高,温度的升高影响摩擦材料的性能,进而影响磨损过程。
通过对磨损后滑环滑道微观形貌的分析得知滑环的电弧侵蚀作用并不显著,磨损形式主要为粘着磨损,本文运用赫兹理论和传热学相关知识,将热力电三场耦合对摩擦副的影响转化为温升对摩擦副硬度的影响,提出了热力电耦合场的粘着磨损计算模型,解决了热力电三场耦合问题。
1) 基于赫兹理论的摩擦副接触模型
导电滑环摩擦副电刷触头和汇流盘之间为点接触,由于材料的弹性形变,两者的接触面向邻近四周逐渐扩展变成半径为c的近似圆[15],根据赫兹理论可计算半径c的值,从而得到摩擦副的接触面积为
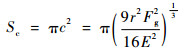 | (1) |
式中:E为当量弹性模量;Fg为两球体上的法向接触压紧力,在本文体现为簧片触头与汇流盘间的接触压力;r为当量曲率半径。E和r由式(2)和式(3)得
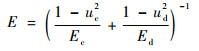 | (2) |
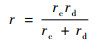 | (3) |
式中:Ec与Ed分别为触头与汇流盘材料的弹性模量;uc与ud分别触头与汇流盘材料的泊松比;rc与rd分别为触头与汇流盘初始接触点处的曲率半径,在此模型中汇流盘接触半径rd视为无穷大,即取极限后的当量曲率半径r值为rc。
2) 摩擦副温升计算
滑环摩擦副运行时,热量的产生通常由三部分组成:接触电阻热、盘面焦耳热与摩擦热,其产热功率分别记为P1、P2与P3。接触电阻热与盘面焦耳热都属于焦耳热,由电阻产热公式计算可得,后者摩擦产热可由摩擦产热公式计算。滑环在运行过程中不断地产生焦耳热和摩擦热,同时又处在不断散热的状态,两者最终会达到动态平衡,散热速率由热辐射公式[16]得出,从而得到产热与散热的动态平衡公式:
 | (4) |
式中:Tt为产热功率与散热功率达到动态平衡时的稳态温度;Sa为单个盘道的有效散热面积;C0为常数,值为5.76W(m2·K4)。代入相应计算式,可得稳态温度的为
 | (5) |
式中:P2计算代入的电阻值为旋转一周的电阻平均值,由积分式所得;R1为触头与汇流盘之间的接触电阻;I为滑环工作电流;Rd为汇流盘环道半径;ρ为盘面镀层材料电阻率;μ为汇流盘与触头间的摩擦系数;v为触头和汇流盘间的相对速度。
由式(5)可知摩擦副温度受到包括接触载荷、电流等多因素的影响,融合了热、力、电三因素的耦合关系,耦合场下滑环的温升变化将影响摩擦副材料的硬度特性,进而影响摩擦副的磨损速率,硬度随温度的变化关系尚无准确函数来表征,一般根据摩擦副的材料特征查表或试验得到。
3) 基于粘着磨损的多场耦合模型
导电滑环磨损阶段同一般磨损阶段一致,可分为三阶段:跑合预磨损阶段、稳定磨损阶段、剧烈磨损阶段,本文研究的内容都是基于稳定磨损阶段展开的。稳定阶段粘着磨损满足如下基本定律:①磨损的体积与滑动距离、载荷成正比;②磨损产生的磨屑量与较软材料的屈服极限(或硬度)成反比。在稳定磨损阶段下,粘着磨损产生的磨屑体积[17]为
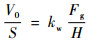 | (6) |
式中:S为摩擦副触头滑动距离;kw为粘着磨损常系数,需要在试验中测定;H为材料硬度,受温度影响。定义摩擦副粘着磨损强度σm,表示摩擦副在一定粘着磨损因子下的磨损程度:
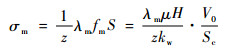 | (7) |
式中:z为安全系数,大于1;fm为粘着磨损因子;λm为材料的影响系数,与材料硬度有关,其计算公式为[18]
 | (8) |
按照上述定义,当触头和盘面结构实际磨损程度超过指定失效磨屑量阈值所对应的σm*时,滑环失效,此时对应的摩擦副滑动距离即为滑环寿命时间内跑合的距离。在磨损过程中,触头和盘面在某一时刻获得的能量密度分别为总能量的一半,设盘面结构镀层磨去的厚度为δd,触头结构磨去厚度为δc,总磨损厚度为δ,根据能量守恒定律结合式(7)可得摩擦副触头滑动距离S的表达式:
 | (9) |
式中:σc与σd分别为触头与汇流盘的粘着磨损程度,可由式(7)得出。由于摩擦副间是圆周滑动,根据圆周长公式, 联立式(6)~式(9)进一步可得摩擦副运转圈数N的表达式为
 | (10) |
式中:C为摩擦副旋转一周轨迹的周长;Hc、Hd分别代表触头、汇流盘硬度值。
由公式可知,滑环的运转寿命与摩擦副接触面积、材料的硬度等密切相关,而摩擦副接触面积又受到摩擦副电流、温度、载荷等影响,综合考虑了多耦合场对滑环寿命的影响,在此基础上,结合磨屑失效阈值可对滑环进行寿命预估。
3 基于Bootstrap方法的特征参数估计 3.1 Bootstrap方法 Bootstrap方法是一种常用的统计推断方法,目的是用现有的样本去模仿未知的分布,经典的Bootstrap方法是美国Stanford大学统计系教授Efron于1979年提出的,方法大致步骤如下:
1) 观测样本X={x1, x2, …, xn}的值为有限的总体样本,对其按自小到大的顺序排列,可得到样本的顺序统计量x(1), x(2), …, x(n),式中:x(1)=
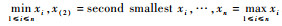
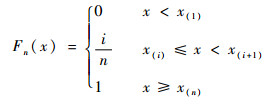 | (11) |
2) 据原始样本构造的经验分布函数,得到N组随机抽样集合X(k)={x1(k), x2(k), …,xn(k)},k=1, 2, …, N, X(k)称为Bootstrap子样。
3) 设参数θ是样本总体的一个未知参数,Fn(x)为小子样试验样本得到的经验累积分布函数(样本量为n),直接由Fn(x)运用参数估计方法得到的未知参数估计用

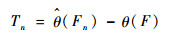 | (12) |
根据Bootstrap子样集合也可得到参数θ的估计
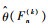
 | (13) |
式(13)中由于真实的θ(F)无从得知,可用
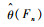
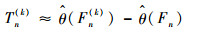 | (14) |
根据统计理论,用Tn(k)分布逼近Tn分布,当得到大量θ(F)样本后,运用这些样本即可统计求出参数θ估计值的分布及其特征值。
3.2 修正样本累积经验分布函数 由3.1节的步骤可知,Bootstrap方法可通过大量的再生子样进行参数的估计,但其中采样方式具有一定的局限性,样本的累积经验分布函数将样本的取值范围限制在了[x(1), x(n)]中,且样本的取值是离散的,对于连续取值的变量无法获取样本点之外的信息。针对这些问题,构造新的样本累积经验分布函数,采用对称分布(截断正态分布)修正样本点邻域的采样密度函数,具体做法如下:
1) 把观测样本x1, x2, …, xn, 按照从小到大的顺序进行排列,得到样本的顺序统计量x(1), x(2), …, x(n),对每个观测值x(i)做如下邻域[12]:
 | (15) |
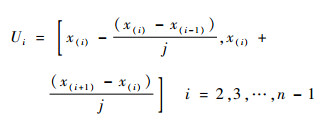 | (16) |
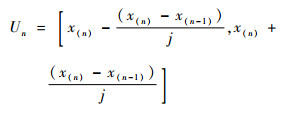 | (17) |
式中:j为控制系数(j≥2),系数值的大小控制着每个抽样子区间的长度,值越大,区间长度越窄,抽取的新样本越集中在原始样本点的附近,当样本量较小时,宜取较小的j值,增大邻域区间的宽度, 当样本量较大时,可适当增大j值。
2) 确定邻域指标P(Ui),其分布特性满足:
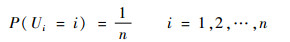 | (18) |
3) 确定邻域内抽样的概率密度函数,每个邻域区间内部取值的概率密度函数都服从截断正态分布,截断的上下界即为上述邻域区间的左右端点值, 从属于第i个邻域区间的随机变量xi*的概率密度函数为
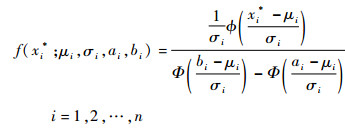 | (19) |
式中:μi为邻域区间的中心值,即自助样本的观测值;ai与bi分别对应各邻域区间的始末端点;σi为各邻域区间取值的标准差,依据原观测样本的样本容量大小和样本点数据经验给出,不同的标准差将反映自助样本对原样本的依赖程度高低;?(·)与Φ(·)分别为标准正态分布的概率密度函数和标准正态分布的累积分布函数。
仿真产生服从这种改进经验累积分布函数Fn*(x)的随机样本的方法如下:
1) 产生[0, n]区间的均匀分布的随机数β,令i=|β|,即本次抽样应在顺序统计量x(1), x(2), …, x(n)的第i个邻域区间内进行采样。
2) 产生[0, 1]区间的均匀随机数γ,记第i个邻域区间取值的概率密度函数f(xi*; μi, σi, ai, bi)的累积概率分布为F(xi*; μi, σi, ai, bi),则
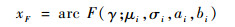 | (20) |
即为此次抽取的一个新数据样本。
3) 重复上述两步骤共n次,产生一组新样本记为X(1)={x1(1), x2(1), …,xn(1)},根据3.1节所述,共需抽取N组,从而得到N组随机抽样集合X(k)={x1(k), x2(k), …,xn(k)},k=1, 2, …, N。
4 多场耦合模型的验证与寿命预估 为验证多场耦合摩擦磨损模型的合理性,得到合理的滑环寿命数据,将同型号的滑环进行跑合试验,对比磨屑值。
用于试验验证的滑环需进行两次跑合试验和一系列环模试验,试验的顺序一般为:大气跑合试验→加速度试验→冲击试验→正弦振动试验→随机振动试验→热真空试验→真空跑合试验,两次跑合试验的参数见表 1。
表 1 滑环跑合试验参数 Table 1 Running-in test parameters of slip ring
| 参数 | 数值 | |
| 大气跑合 | 真空跑合 | |
| 温度 | 常温 | (20±5)℃ |
| 湿度 | 相对湿度不大于50% | 真空 |
| 压力 | 常压 | 真空度优于1×10-3Pa |
| 通电情况 | 功率环和信号环全部通0.25A | 功率环通7A,信号环通0.25A |
| 跑合速度 | 2r/min | 0.3r/min |
| 跑合时长 | 正反转各跑合24h | 累计运转5万转 |
表选项
将5组滑环进行大气条件下预跑合,跑合试验主要在常温、常压、空载条件下进行,跑合采用快速模式,正反转各跑合24h,每隔12h变换一次跑合方向,并保证跑合过程中正反转累计跑合时间一致。跑合过程中主要检查产品正、反向运转是否正常,并持续监测产品的单刷通断测试数据,根据单刷通断数据判断滑环内部环刷接触状态是否良好。跑合结束时,需保证滑环产品正反转连续12h均无断点,磨屑总量不大于10mg,且电压降和电噪声符合性能指标要求。
在产品完成力学试验和热真空试验后,在真空环节下进行产品的连续跑合,设置摩擦副接触载荷Fg的范围为0.2~0.36N,间距为0.04N,5组滑环均在真空环境下累计运转5万转,跑合期间滑环正常通电,跑合过程中,连续监测产品的电性能、绝缘性能,跑合结束后利用精度优于1mg的电子天平检测磨屑质量,磨屑实测质量分别为1112、1192、1230、1280mg与1290mg,利用电镜观察到触头磨损后表面形貌如图 2所示。
 |
| 图 2 触头表面电镜形貌图 Fig. 2 Contact surface morphology by electron microscopy |
| 图选项 |
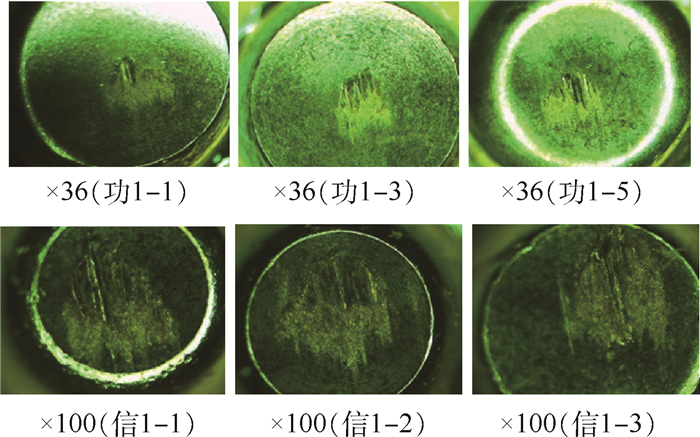
将真空跑合的环境参数输入到多场耦合摩擦磨损模型中,同样设置运转5万转进行仿真试验,所得磨屑结果与真实试验结果进行对比,对比结果如图 3所示。由图可知,多场耦合摩擦磨损模型的计算结果与试验结果吻合程度高,最大偏差出现在0.36N处,为52mg,偏差仅为4.03%,其余波动均在合理范围内,可见模型的预测结果具有较高的合理性与准确性。
 |
| 图 3 试验结果与模型结果对比图 Fig. 3 Comparison between test results and model results |
| 图选项 |
摩擦磨损模型建立了一定环境参数范围下滑环磨屑值和跑合圈数的数学模型,在实际运行过程中,滑环由于受到环境变量和滑环工艺参数波动的影响,磨屑阈值应在一定范围内小幅波动。某厂制造的某型号空间用盘式滑环,在指定工艺环境条件下,技术指标书中指定的失效阈值为1000mg,为得到更加合理滑环的伪寿命值,设定模型磨屑阈值输入在950~1050mg间随机波动。
其余参数的余量控制范围由该厂提供的技术指标书可得,为了简化参数波动对模型结果的影响,综合考虑参数本身加工精度、对寿命的影响程度,只设定接触载荷在一定范围内随机波动,环境参数设定如表 2所示。
表 2 模型部分输入参数 Table 2 Some of model input parameters
| 参数 | 设定值 |
| 接触载荷 | 0.17~0.20N |
| 功率电流 | 7A |
| 汇流盘电阻率 | 1.65×10-8Ω·m |
| 旋转半径 | 6.5cm |
| 信号电流 | 0.25A |
| 汇流盘角速度 | 0.6πrad/min |
表选项
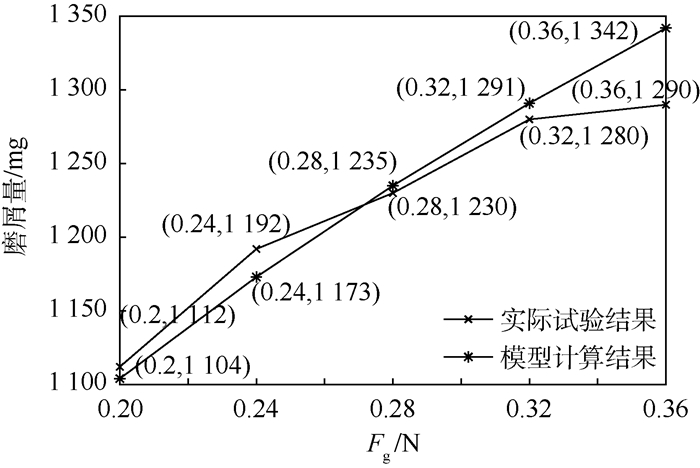
设定好环境和条件参数后,在磨屑阈值950~1050mg之间抽取10000组随机阈值输入到模型中,得到的滑环跑合寿命分布图如图 4所示,这里将转数寿命转化为在轨寿命,按低轨运行14.4r/d折算。寿命的均值和标准差为:4280.9d、123.2d。
 |
| 图 4 模型寿命分布图 Fig. 4 Life distribution of model |
| 图选项 |
5 特征参数估计与可靠性评估 卫星长寿命机电产品主要的寿命分布类型为威布尔分布和对数正态分布[19],威布尔分布是可靠性中最常用的分布之一,其最大的特点在于,分布形状参数的不同能够拟合多种不同失效机理的分布,大量的实际经验说明[20-21],凡是因某一局部失效而导致全局不能正常工作的原件、设备等,其寿命都可看成或近似看成威布尔分布,滑环本质上是机电部件,普遍认为其寿命服从威布尔分布。
5.1 威布尔分布参数特征值估计 运用修正后的累积经验分布函数进行Bootstrap采样,需要确定原始样本的数量,Bootstrap方法很好地解决了样本量n≥10的小子样试验评估问题[22],一般在10~15之间取值[23-25], 本文参照文献[25]的做法,取虚拟样本增广的样本数为13,即原始样本的数量为13。
与文献[23]经验公式不同,考虑到威布尔分布的偏态性,虚拟拓展的取值将不再是对称取值,考虑在寿命均值T0的左侧取8个虚拟值,右侧取4个虚拟拓展值,记增广后的样本取值为Ti, i=1, 2, …, 13,根据文献[25],不妨T1=0.42T0, T2=0.61T0, T3=0.63T0, T4=0.66T0, T5=0.7T0, T6=0.74T0, T7=0.92T0, T8=0.98T0, T9=T0, T10=1.08T0 T11=1.26T0, T12=1.39T0,
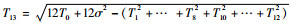
针对增广后的寿命样本,运用改进后的Bootstrap理论进行参数特征值的估计,具体实现如下:
1) 先对原始的13个样本分别用威布尔分布和正态分布进行Kolmogorov-Smirnov(K-S)检验, 观察原始样本的分布拟合情况,分布假设检验结果如表 3所示。
表 3 分布假设检验结果 Table 3 Test results of distribution hypothesis
| 分布类型 | h | p | k | c′ |
| 威布尔分布 | 0 | 0.8449 | 0.1596 | 0.3614 |
| 正态分布 | 0 | 0.8398 | 0.1606 | 0.3614 |
表选项
表 3中,h=0表示接受假设,h=1表示拒绝假设;p为服从假设的分布函数的概率;k为K-S检验的统计量;c′为是否显著的临界值,当统计量不超过c′时,接受假设,反之拒绝。由检验结果可知,原样本均接受威布尔分布和正态分布,但威布尔分布的概率最高,由此可确定虚拟增广的寿命样本服从威布尔分布,符合预期,进而得出样本的威布尔分布的形状参数为3.2619,尺度参为4374.1。得到服从威布尔分布的原始样本及参数估计后,进行累积分布函数的构建。
2) 原始样本数量为13,因此每个样本点区间的取值概率
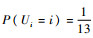
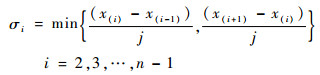 | (21) |
首末样本点的区间内部标准差取相应邻侧表达式值。
3) 构造样本累积经验分布函数后,抽样产生10000组Bootstrap子样,对得到的子样进行威布尔分布K-S检验,结果表明所有子样都接受威布尔分布假设,对每组子样进行威布尔分布参数估计,由此可得威布尔两参数估计误差Tn(k)的分布,用Tn(k)分布逼近Tn分布,可得威布尔分布尺度参数η和形状参数m的概率密度分布图如图 5和图 6所示。
 |
| 图 5 尺度参数η概率密度分布 Fig. 5 Probability density curves of scale parameter η |
| 图选项 |
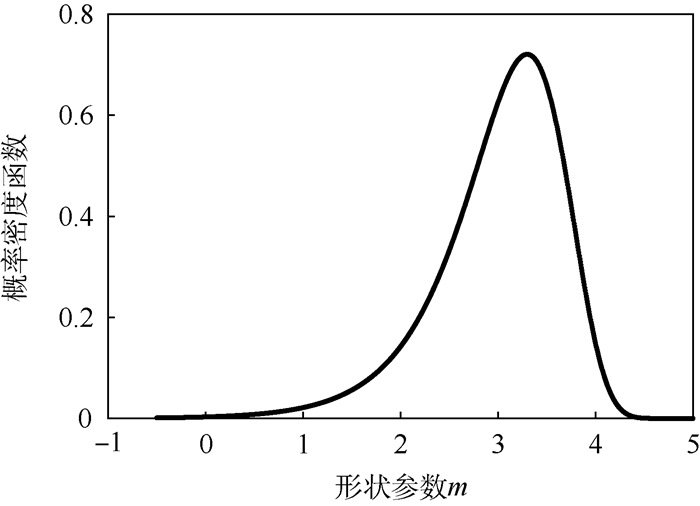 |
| 图 6 形状参数m概率密度分布 Fig. 6 Probability density curves of shape parameter m |
| 图选项 |
进而求得威布尔分布两参数的期望,形状参数
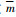

5.2 滑环可靠性评估 根据4.2节求得的威布尔分布两参数,代入威布尔分布的相关函数表达式,可得滑环相关的可靠性指标如下:
1) 失效分布函数F(t)和失效密度函数f(t)分别为
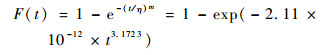 | (22) |
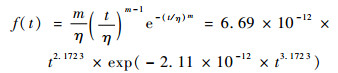 | (23) |
由式(23)可得滑环失效分布密度函数曲线,如图 7所示。
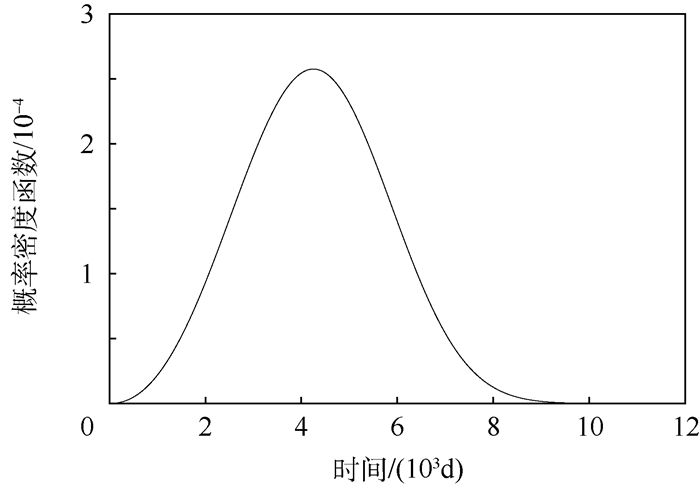 |
| 图 7 滑环概率密度函数曲线 Fig. 7 Probability density function curve of slip ring |
| 图选项 |
2) 由式(22)得滑环的可靠度函数式(24),可靠度函数的曲线如图 8所示。
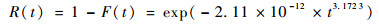 | (24) |
 |
| 图 8 滑环可靠度函数曲线 Fig. 8 Reliability function curve of slip ring |
| 图选项 |
由可靠性曲线可知,随着任务时间的增长,产品的可靠性呈现下降趋势,滑环寿命初期的可靠性较高,在该型号额定的任务时间5年(1825天)其可靠度为0.954,与设计要求0.998相差4.4%,评估效果较好;此外到2987天(8.18年)左右可靠度减至0.8,其后可靠度迅速递减,说明滑环是一个性能退化产品,在磨屑量增多情况下将加剧磨损,加速滑环的失效,和实际情况相符。
3) 滑环失效率函数为
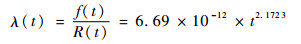 | (25) |
由此可得滑环失效率函数曲线如图 9所示。由图 9可知,滑环的失效率函数为递增型,在运行到6000天时,其失效率达到1.1×10-3个/天,即表示每1000组该型号的滑环在本文设定的环境条件下工作6000天后,单位时间内失效的滑环为1.1个。在此时间节点前,各时刻滑环的失效率均低于1.1×10-3个/天。由此可见,该型号滑环的可靠性较高。
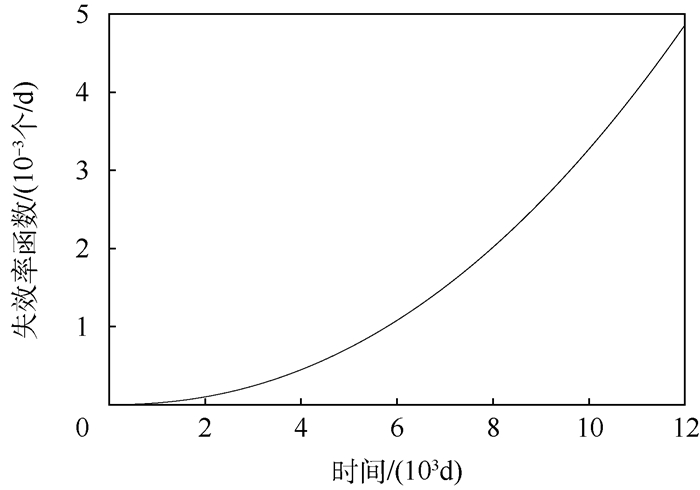 |
| 图 9 滑环失效率函数曲线 Fig. 9 Failure rate function curve of slip ring |
| 图选项 |
4) 滑环的可靠寿命表达式为
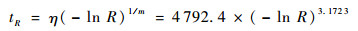 | (26) |
式中:R为可靠度。
在实际工程应用中,可通过式(26)计算可靠度要求为R时的可靠寿命tR,其代表着,要满足可靠度R,当该型号滑环在文中所设的运行参数中连续运转tR后,不论失效与否,都应进行更换。由式(26)可得该批次滑环的中位寿命t0.5和特征寿命t0.368分别为
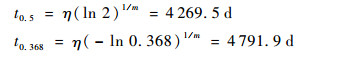 |
由中位寿命t0.5可知, 该滑环工作到4269.5天后,将约有一半的滑环失效。
6 对比分析 为了验证本文所提改进Bootstrap方法的优越性,与文献[23]所提的改进Bootstrap方法进行对比。根据文献[23]的改进思路,对累积分布函数的尾部运用指数分布进行拟合,拓宽右尾的采样范围,针对抽样样本的范围受限于原样本的最小次序统计量的问题,在次序统计量的最小值x(1)的左侧增设一个新样本, 修正后的累积经验分布函数为
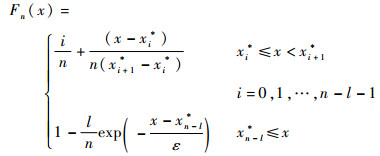 | (27) |
式中:l表示从顺序统计量的倒数第l个样本开始,用指数分布修正累积分布函数; 参数ε为
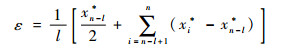 | (28) |
为了避免偶然性,采用威布尔分布随机数来验证两种改进方法的评估效果,仿真产生寿命分布服从m=3,η=4000威布尔分布的13个随机数为{1256.02, 2186.03, 2238.05, 2338.83, 2405.54, 2812.267994, 2894.59, 3195.05, 3310.01, 4461.38, 4966.09, 5108.06, 5113.49}, 代入两个模型当中计算相应的威布尔参数估计值,选取抽样次数为10000,根据两方法得到的威布尔参数值,绘制各自的概率密度函数曲线如图 10所示。
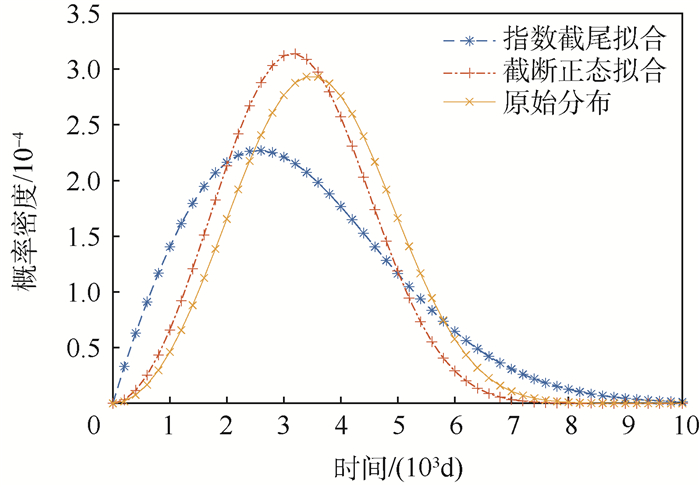 |
| 图 10 不同方法的估计结果 Fig. 10 Estimation result of different methods |
| 图选项 |
由图 10结果可知,本文提出的截断正态分布拟合法得出的概率密度函数曲线形状和趋势更加贴近真实分布,采用指数分布构造样本的累积分布函数,极大地增广了抽样的右尾范围,但方法赋予右尾区间的采样概率偏大,导致估计结果不理想,且方法在左尾新增样本的公式虽扩宽了样本的抽样下限,但主观性较大,不具有普适性,综上所示,本文所提的改进Bootstrap方法充分利用原始样本信息,有操作简单、估计精度高等优点。
7 结论 1) 针对某型号滑环多场耦合的环境特点,建立滑环摩擦副磨损物理模型,量化了多场环境对滑环磨损的影响,并针对模型进行了试验验证,结果表明,模型在一定环境参数范围内,跑合圈数最大偏差为4.03%,对该型号滑环的寿命预估结果精度较高。
2) 构造了新的样本累积经验分布函数,改进原Bootstrap方法,拓展抽样区间范围,包括样本点附近的数据以及样本极值点,对滑环寿命数据进行样本增广,对比分析表明,改进Bootstrap方法具有良好的评估效果,具有实用强、估计精度高等优点。
3) 由改进Bootstrap方法得到的寿命分布参数值,对滑环进行可靠性评估,得到的任务时间内可靠度估计偏差为4.4%,评估结果较为准确,方法得到的其他各项可靠性指标均符合工程实际,具有一定的工程应用价值。
参考文献
| [1] | HUANG S, FENG Y, LIU H, et al. Electrical sliding friction and wear properties of Cu-MoS2-graphite-WS2, nanotubes composites in air and vacuum conditions[J]. Materials Science and Engineering:A, 2013, 560(2): 685-692. |
| [2] | 刘军涛.导电滑环接触材料摩擦磨损特性研究[D].大连: 大连理工大学, 2013: 41-43. LIU J T.Research on the friction and wear characteristic of contact materials for the conductive slip ring[D]. Dalian: Dalian University of Technology, 2013: 41-43(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10141-1013199655.htm |
| [3] | DING T, CHEN G X, ZHU M H, et al. Influence of the spring stiffness on friction and wear behaviours of stainless steel/copper-impregnated metallized carbon couple with electrical current[J]. Wear, 2009, 267(5): 1080-1086. |
| [4] | XIE X L, ZHANG L, XIAO J K, et al. Sliding electrical contact behavior of AuAgCu brush on Au plating[J]. Transactions of Nonferrous Metals Society of China, 2015, 25(9): 3029-3036. DOI:10.1016/S1003-6326(15)63930-9 |
| [5] | MONNIER A, FROIDUROT B, JARRIGE C, et al. A mechanical, electrical, thermal coupled-field simulation of a sphere-plane electrical contact[J]. IEEE Transactions on Components & Packaging Technologies, 2007, 30(4): 787-795. |
| [6] | 于艳艳.风电滑环接触材料加速摩擦磨损试验研究[D].大连: 大连理工大学, 2016: 47-50. YU Y Y.Test on the accelerated friction and wear of contact materials for the wind energy slip ring[D]. Dalian: Dalian University of Technology, 2016: 47-50(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10141-1016216196.htm |
| [7] | GRANDIN M, WIKLUND U. Wear and electrical performance of a slip-ring system with silver-graphite in continuous sliding against PVD coated wires[J]. Wear, 2016. |
| [8] | KOBAYASHI T, SAWA K, ENDO K, et al.A study of sliding characteristics of small-size slip-ring system for electric power supply[C]//2007 IEEE Holm Conference on Electrical Contacts.Piscataway, NJ: IEEE Press, 2007: 194-199. |
| [9] | 杨兆军, 李洪洲, 陈传海, 等. 考虑定时截尾数据的数控机床可靠性Bootstrap区间估计方法[J]. 机械工程学报, 2017, 53(7): 129-137. YANG Z J, LI H Z, CHEN C H, et al. Bootstrap interval estimation of reliability for numerical controlled machine tools considering the time-censored data[J]. Journal of Mechanical Engineering, 2017, 53(7): 129-137. (in Chinese) |
| [10] | 吴云洁, 王建敏, 杨文光. 基于小样本的试验系统可信度评估方法[J]. 北京航空航天大学学报, 2016, 42(9): 1911-1917. WU Y J, WANG J M, YANG W G. Approach of credibility evaluation for testing system with small samples[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(9): 1911-1917. (in Chinese) |
| [11] | 黄玮, 冯蕴雯, 吕震宙. 基于Bootstrap方法的小子样试验评估方法研究[J]. 机械科学与技术, 2006(1): 31-35. HUANG W, FENG Y W, LU Z Z. Study on small scale sample test estimation method based on bootstrap method[J]. Mechanical Science and Technology for Aerospace Engineering, 2006(1): 31-35. DOI:10.3321/j.issn:1003-8728.2006.01.011 (in Chinese) |
| [12] | 刘建, 吴翊, 谭璐. 对Bootstrap方法的自助抽样的改进[J]. 数学理论与应用, 2006, 26(1): 69-72. LIU J, WU Y, TAN L. An Improvement to the resampling procedure of Bootstrap method[J]. Mathematical Theory and Applications, 2006, 26(1): 69-72. (in Chinese) |
| [13] | 邹艳, 罗文强. 改进的Bootstrap方法对比及应用研究[J]. 应用数学, 2008, 21(S1): 62-66. ZOU Y, LUO W Q. Comparative study anel application of improved Bootstrap method[J]. Mathematica Applicata, 2008, 21(S1): 62-66. (in Chinese) |
| [14] | 李超, 王学强, 戴飞, 等. 空间滑环磨屑特征与可靠性设计[J]. 电子产品可靠性与环境试验, 2018, 36(2): 1-5. LI C, WANG X Q, DAI F, et al. The debris characteristics and reliability design of aerospace slip ring[J]. Electronic Product Reliability and Environmental Testing, 2018, 36(2): 1-5. DOI:10.3969/j.issn.1672-5468.2018.02.001 (in Chinese) |
| [15] | HENNESSY R P, MCGRUER N E, ADAMS G G. Modeling of a thermal-electrical-mechanical coupled field contact[J]. Journal of Tribology, 2012, 134(4): 041402-041410. DOI:10.1115/1.4007270 |
| [16] | 王天壹, 宣益民. 热辐射对气膜冷却叶片冷却性能影响[J]. 航空动力学报, 2018, 33(8): 1801-1810. WANG T Y, XUAN Y M. Effect of thermal radiation on the heat transfer performance of a film cooling vane[J]. Journal of Aerospace Power, 2018, 33(8): 1801-1810. (in Chinese) |
| [17] | 李聪波, 何娇, 杜彦斌, 等. 基于Archard模型的机床导轨磨损模型及有限元分析[J]. 机械工程学报, 2016, 52(15): 106-113. LI C B, HE J, DU Y B, et al. Archard model based machine tool wear model and finite element analysis[J]. Journal of Mechanical Engineering, 2016, 52(15): 106-113. (in Chinese) |
| [18] | 周文韬.导电滑环的接触力学特征与磨损寿命分析[D].湘潭: 湘潭大学, 2014: 30-35. ZHOU W T.Analysis of the characteristics of contact mechanics and wear life of slip ring with electrical contact[D]. Xiangtan: Xiangtan University, 2014: 30-35(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10530-1014401427.htm |
| [19] | 刘强.基于失效物理的性能可靠性技术及应用研究[D].长沙: 国防科技大学, 2011: 6-8. LIU Q.Research on the performance reliability technology and the application based on physics of failure[D]. Changsha: National University of Defense Technology, 2011: 6-8(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-90002-1011303271.htm |
| [20] | 刘强, 黄秀平, 周经伦, 等. 基于失效物理的动量轮贝叶斯可靠性评估[J]. 航空学报, 2009, 30(8): 1392-1397. LIU Q, HUANG X P, ZHOU J L, et al. Failure-physics-analysis-based method of Bayesian reliability estimation for momentum wheel[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(8): 1392-1397. DOI:10.3321/j.issn:1000-6893.2009.08.006 (in Chinese) |
| [21] | 王大伟, 苗学问, 洪杰. 某发动机涡轮叶片使用寿命可靠性分析[J]. 北京航空航天大学学报, 2006, 32(8): 903-907. WANG D W, MIAO X W, HONG J. Reliability lifetime analysis of the turbine blade of turbofan engine[J]. Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(8): 903-907. DOI:10.3969/j.issn.1001-5965.2006.08.007 (in Chinese) |
| [22] | EFRON B, TIBSHIRANI R J. An Introduction to the Bootstrap[M]. London: Chapman and Hall, 1993. |
| [23] | 黄玮, 冯蕴雯, 吕震宙. 极小子样试验的虚拟增广样本评估方法[J]. 西北工业大学学报, 2005, 23(3): 384-387. HUANG W, FENG Y W, LU Z Z. Virtually expanded sample estimation method for extremely small-scale sample test[J]. Journal of Northwestern Polytechnical University, 2005, 23(3): 384-387. DOI:10.3969/j.issn.1000-2758.2005.03.024 (in Chinese) |
| [24] | 马宇鹏, 张建国, 邱继伟. 基于Bootstrap-SVR-SOC的小子样结构机构可靠性分析方法[J]. 北京邮电大学学报, 2018, 41(4): 81-85. MA P Y, ZHANG J G, QIU J W. Reliability analyzing method of small sample structures and mechanisms based on Bootstrap-SVR-SOC[J]. Journal of Beijing University of Posts and Telecommunications, 2018, 41(4): 81-85. (in Chinese) |
| [25] | 蒋喜, 刘宏昭, 刘丽兰, 等. 基于伪寿命分布的电主轴极小子样可靠性研究[J]. 振动与冲击, 2013, 32(19): 80-85. JIANG X, LIU H Z, LIU L L, et al. Extremely small-scale sample's reliability of an electric spindle based on distribution of false lifetime[J]. Journal of Vibration and Shock, 2013, 32(19): 80-85. DOI:10.3969/j.issn.1000-3835.2013.19.015 (in Chinese) |
