金属材料的长期服役过程中，在环境和载荷的作用下，微裂纹会逐渐萌生、扩展长大形成宏观裂纹，一旦裂纹扩展到临界尺寸，即会发生破坏，产生严重的后果^[1]。研究表明，金属材料早期微裂纹阶段占整个裂纹寿命的90%^[2], 因此，在金属材料微裂纹早期阶段开展相关的检测工作，对于避免重大安全生产事故、保障工程材料的安全服役，具有重要的意义。近年来的研究发现^[3]，材料力学性能的退化、微裂纹的产生等都会引起超声波传播的非线性畸变，显示出非线性超声技术在材料微裂纹检测中的巨大应用潜力，受到了非常广泛的关注^[4]。
微裂纹与超声波作用的非线性效应包括高次谐波、次谐波和谐振频率漂移^[4]等。在实际应用中，利用非线性超声的高次谐波进行材料的无损检测容易受到仪器非线性因素干扰，导致检测结果不准确。非线性超声混频检测^[5]是近年来出现的新型检测方法，其检测原理是：利用2列不同频率的超声波经过金属材料，如果材料中没有微裂纹，则2列波线性叠加不会产生新的频率成份；如果材料中有微裂纹，2列波在经过微裂纹相遇时，会产生非线性畸变，进而产生新的频率成份^[6]。该方法是利用2列波叠加产生的混合频率，不会受到仪器非线性效应的影响，将有效提高非线性超声检测的准确性。混合频率包含和频、差频、多倍和频和多倍差频等，本文对其中的和频信号进行了定量分析研究。
北京工业大学焦敬品教授等探索了混频非线性超声检测微裂纹的可行性^[7]，以及微裂纹的长宽因素对检测结果中和频分量振幅的影响^[8]；Croxford等^[9]利用混频非线性超声研究了材料的塑性和疲劳损伤在不同载荷下的变化；Sun等^[10]提出了利用混频非线性超声来检测和定位材料中的微损伤；Mcgovern和Reis^[11]利用混频非线性超声检测了不同温度下样品的弯曲强度。由此可见，目前混频非线性超声与微裂纹相互作用的研究主要集中在微裂纹的尺寸形貌、位置以及损伤畸变等方面，而且研究相对较少，尚未开展微裂纹取向与超声和频非线性效应的研究。
研究表明，不同的微裂纹取向会影响微裂纹生长速率的大小、传播数目的多少等，对材料微裂纹的产生、发展到形成断裂的过程研究非常重要^[12]。因此，本文开展了金属材料微裂纹取向与超声波的和频非线性效应研究。首先，利用2列不同频率的超声波，在经过不同取向的微裂纹时会引发微裂纹界面处不同大小的应变。然后，基于泰勒公式将应力应变的线性关系模型转化为非线性关系模型，获得2列超声波经过微裂纹时叠加产生的和频非线性频率分量，进而计算得到这些频率分量的位移场。最后，以位移场为桥梁，建立超声和频非线性特征系数与微裂纹取向角度的关系模型。有限元仿真计算和实验测试都验证了模型的有效性，为金属材料微裂纹早期的检测提供了一种新的有效手段。
1 理论模型 1.1 混频非线性超声检测中的频率分量 当金属材料存在微裂纹损伤时，其输入输出信号可用以下非线性方程表示^[13]：

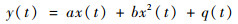(1)

式中：x(t)为输入信号；y(t)为系统响应；a、b为常数；q(t)为噪声，忽略不计。
输入信号中包含2种频率的简谐分量：

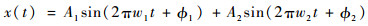(2)

式中：输入信号的基波频率为w₁和w₂; 2个简谐分量的幅值、相位分别为A₁和A₂、?₁和?₂。
将式(2)代入式(1)中可以得到对应输出为

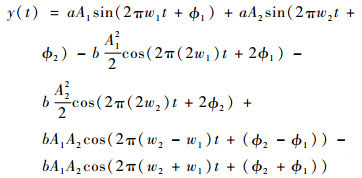(3)

由式(3)可知，输出信号y(t)中不仅出现了频率为2w₁和2w₂的二次谐波，还出现了频率为w₂－w₁的差频分量及频率为w₁+w₂的和频分量，因此在混频检测中可以通过输出信号的和频分量或者差频分量是否存在来说明被检测材料中是否存在微裂纹等非线性损伤。
1.2 非线性和频横波分量与微裂纹的相互作用 假设微裂纹的2个面是简单接触，2个界面之间施加的内应力为Δσ，即

(4)

式中：ξ为微裂纹受到入射波加载所产生的应变；K=K(ξ)表示界面的刚度为超声波经过微裂纹时引发的应变的函数。
利用泰勒公式，在K=K₀处展开并保留前两项，得

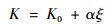(5)

式中：α为非线性系数，并且αξ?K₀。
将式(5)代入式(4)中得到

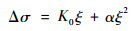(6)

假设混合信号分量频率w₃=w₁±w₂，其中w₁与w₂分别为2列入射超声波的频率，如图 1所示。

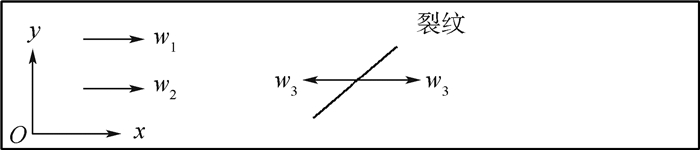图 1 混合频率信号示意图 Fig. 1 Schematic of mixed frequency signal

图选项

得到微裂纹分别在入射波1与入射波2作用下接触界面产生的形变分别为

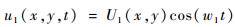(7a)

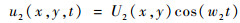(7b)

式中：U₁和U₂分别为入射波1和入射波2的位移场；x和y为微裂纹中心位置的坐标，坐标系原点位于中心位置。
假定微裂纹有效长度为h，宽度为D，通常认为微裂纹宽度远小于入射波的波长，所以在微裂纹宽度方向上，微裂纹受到入射波加载所产生的应变为

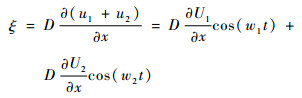(8)

将式(8)代入式(6)中，可以得到2列入射波驱动微裂纹产生的应力为

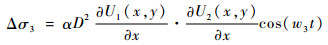(9)

应力Δσ₃作用于裂纹周围，使得经过微裂纹的超声波产生多个新的非线性频率分量。
超声波在各向同性弹性介质中传播的位移场可以用方程表示为^[14]

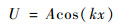(10)

式中：U为位移场；A为幅度；k为波数。
本文利用横波进行分析研究，在实际材料中，微裂纹的取向较散乱，超声波传播经过微裂纹时，只有垂直于微裂纹方向的振动分量会驱动微裂纹界面的两侧发生“张开”与“闭合”运动，对超声波起到非线性调制作用^[15]，产生和频横波。假设存在一个微裂纹与超声波振动方向的夹角θ(0°≤θ≤90°)，即微裂纹取向角度。
如图 2所示，垂直于微裂纹的振幅分量为Asin θ，则推导得到入射波1与入射波2垂直于微裂纹取向的位移场分别为

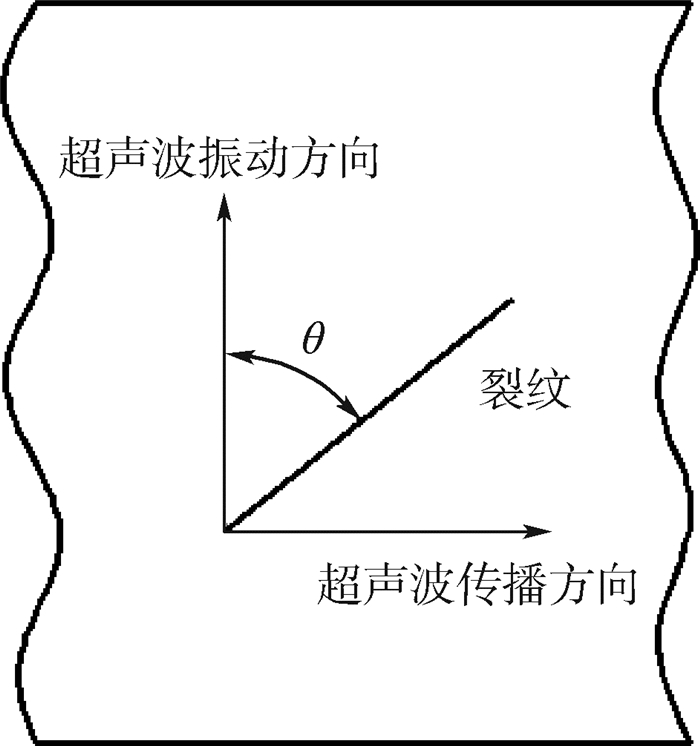图 2 微裂纹取向示意图 Fig. 2 Schematic of micro-crack orientation

图选项

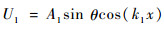(11a)

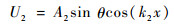(11b)

入射波1和入射波2驱动微裂纹运动所产生的应变可分别表示为

(12a)

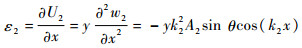(12b)

y=0表示试样的中心。
将式(12a)和式(12b)代入式(9)中可以得到应力为

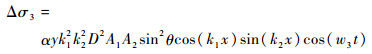(13)

整个裂纹内力为

(14)

式中：s为微裂纹的表面积。
假设该内力F均匀分布于(x₀, y₀)的微裂纹横截面上，产生混合信号分量，频率为w₃，该信号分量的位移场为U₃，推导得^[14]

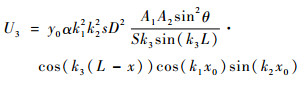(15)

式中：1/sin(k₃L)表示混合信号分量的谐振特性；S为试样的横截面积；L为试样的长度。
假设混合信号分量的位移场与2列入射波位移场具有相同的形式，即

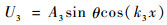(16)

定义超声和频非线性特征系数^[16]，可以用于定量评价金属材料早期损伤微裂纹特征参数的和频非线性效应^[17]。将式(16)代入式(15)中，可以得到超声和频非线性特征系数β为

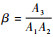
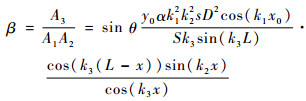(17)

因此，超声和频非线性特征系数β∝sin θ(0≤θ≤90°)。从式(17)中可以得到，超声和频非线性特征系数β与微裂纹取向角度θ成正相关趋势。
2 仿真分析 2.1 有限元模型建立 采用ABAQUS有限元仿真，在二维域建立金属试样截面模型，试样长×高为120 mm×8 mm，微裂纹尺寸长×宽为2 mm×0.04 mm，如图 3所示。材料密度ρ=7 800 kg/m³，泊松比ν=0.3，弹性模量E=200 GPa。微裂纹在试样中心位置，使用椭圆来模拟微裂纹的形状，其长轴和短轴尺寸分别是微裂纹的长和宽。在金属试样左端分别施加正弦横波激励信号1和激励信号2，在右端接收输出信号。

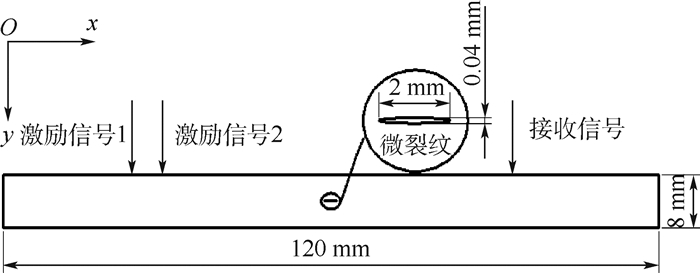图 3 有限元模拟板示意图 Fig. 3 Schematic of finite element simulation board

图选项

模型的网格划分采用了分区域划分的形式，整体尺寸划分的依据是在一个单位时间步内，各个频率的超声波均不能传播穿过一个网格。其中c为超声横波在低碳钢中的波速，约为3 230 m/s，为保证精度，取频率最高的和频分量(2.5 MHz)，计算得到最小波长约为1.3 mm，模型最大网格尺寸取为波长的十分之一，取为0.13 mm，时间步长设置为0.02 μs，并对微裂纹处的网格进行分区加密处理，设置为0.1 mm。
如图 4所示，仿真建模中激励信号采用连续正弦信号模式的压强来模拟横波信号，2列幅值均设置为10 GPa；计算完成后，对于不同角度的微裂纹，取相对于微裂纹中心同一位置处单元格，提取检测信号时域数据，再使用MATLAB进行傅里叶变换为频域数据进行分析对比。

图 4 激励及检测信号加载位置 Fig. 4 Excitation and detection signal loading position

图选项

如图 5所示，在保证微裂纹长宽均不变的情况下，设置有限元模型中微裂纹取向角度θ为0°、15°、30°、45°、60°、75°、90°，进行微裂纹取向特征参数的仿真计算。

图 5 不同微裂纹取向角度仿真模型图 Fig. 5 Simulation model illustration for different micro-crack orientation angles

图选项

2.2 仿真结果 激励信号采用包含2个中心频率分别为1 MHz和1.5 MHz的连续信号，其时域波形与经过傅里叶变换后的频域波形如图 6所示。当2列超声波经过取向角度为90°的微裂纹时，输出信号的时域波形和频域波形如图 7(a)和图 7(b)所示。可以看到，相比于原始激励信号的频域，不仅出现了1 MHz和1.5 MHz基波的二次谐波2 MHz和3 MHz的信号，而且出现了频率为2.5 MHz的和频信号。仿真结果表明，微裂纹的存在不仅产生了二次谐波非线性效应，而且出现了和频、差频等非线性效应。

图 6 激励信号的波形与频谱 Fig. 6 Excitation signal waveform and spectrogram

图选项

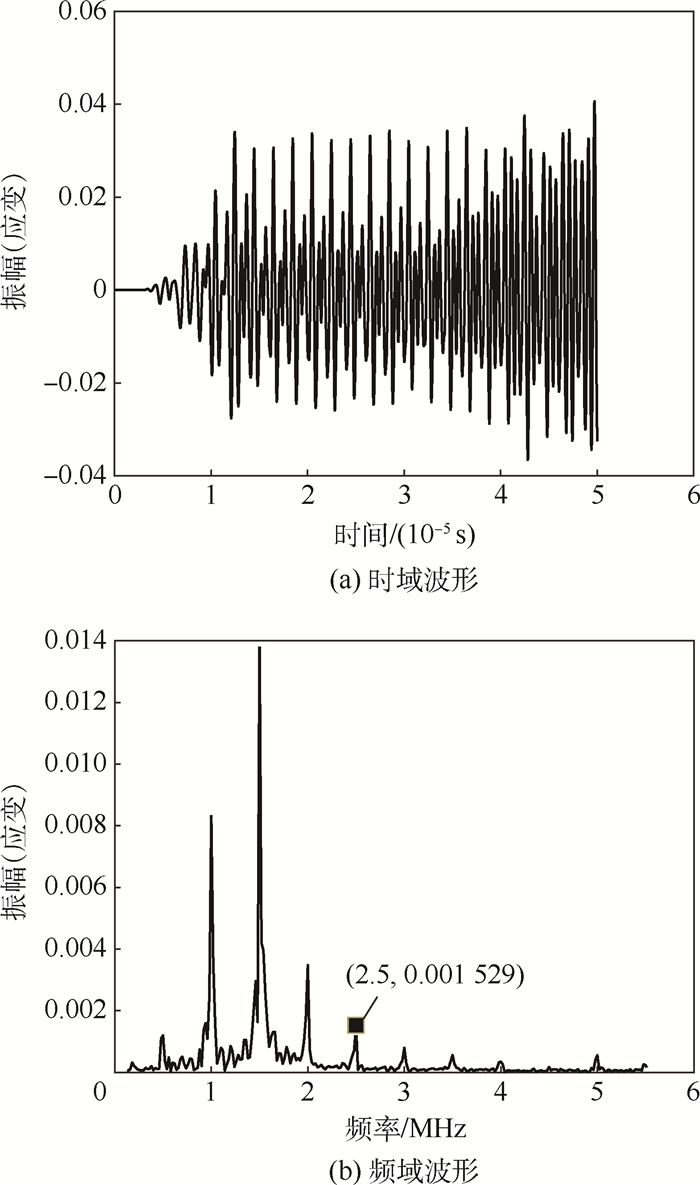图 7 微裂纹取向角度为90°时输出信号的波形与频谱 Fig. 7 Waveform and spectrogram of output signal when micro-crack orientation angle is 90°

图选项

采用同样的方法，依次对7组不同的微裂纹取向角度(0°、15°、30°、45°、60°、75°和90°)进行了仿真模拟，结果如图 8所示。

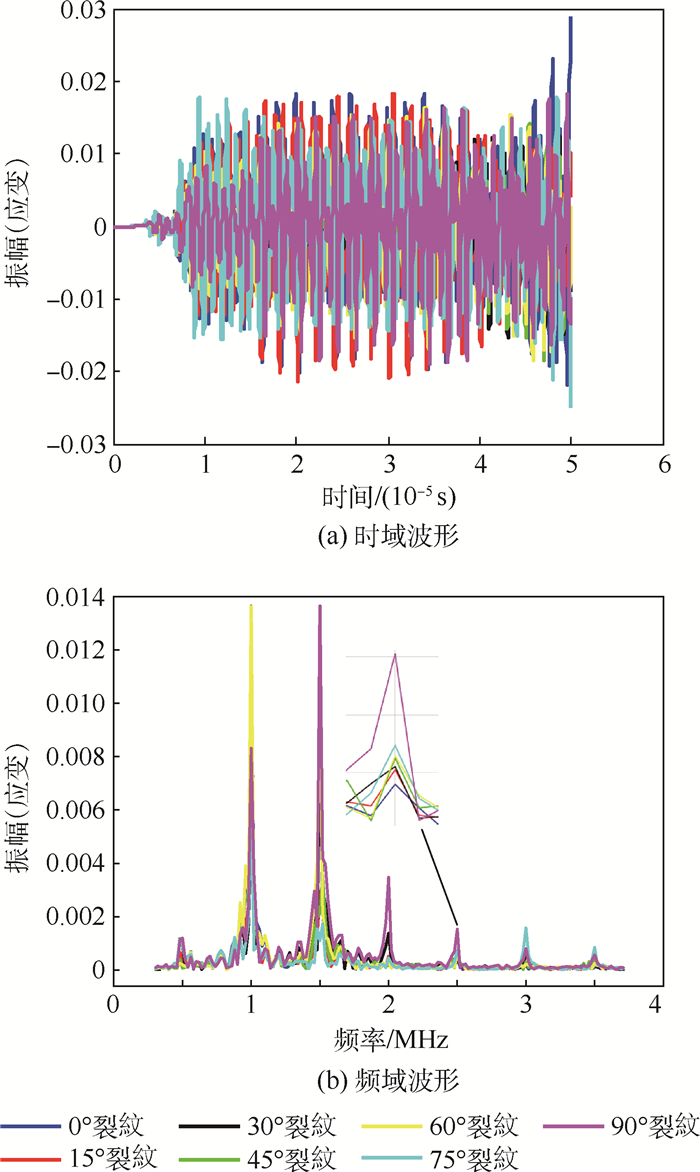图 8 混频检测仿真结果 Fig. 8 Mixed frequency detection simulation results

图选项

图 8给出了不同角度下仿真模拟得到的时域与频域波形。由图 8(b)可得，微裂纹取向角度0°变化到90°均观察到了2.5 MHz的和频波峰，产生了超声波的和频非线性效应；为方便对比分析，将图 8(b)中的信号数据提取出来绘制和频振幅，微裂纹取向变化趋势如图 9(a)所示，和频(w₃=2.5 MHz)振幅的总体趋势是随着微裂纹取向角度θ的增大而增大。利用式(17)计算超声和频非线性特征系数，如图 9(b)所示。计算结果表明，随着微裂纹取向与超声波振动方向的夹角不断增大，超声和频非线性特征系数也在不断增大，与理论结果相一致，验证了模型的正确性。

图 9 不同取向角度微裂纹的和频非线性效应 Fig. 9 Sum frequency nonlinear effect of microcracks at different orientation angles

图选项

为了说明超声波和频非线性特征效应对微裂纹取向的敏感性，将混频检测中的超声和频非线性特征系数β与单频检测中的二次非线性特征系数β′进行对比分析。其中，二次非线性特征系数β′为^[18]

(18)

式中：B₁为单频检测基波振幅；B₂为二次谐波振幅。
为便于对比分析，单频超声非线性检测仿真中设置信号的中心频率为1.25 MHz，其非线性二次谐波的中心频率与混频检测中和频信号频率相同，为2.5 MHz，由于单频检测只有一列激励信号，为了保持与混频检测相同激励水平，其幅值设置为混频检测激励信号的2倍，为20 GPa。其他各项参数设置均与混频计算保持一致，同样进行了7组计算模拟来研究微裂纹取向对二次谐波振幅及二次非线性特征系数的影响，仿真结果如图 10所示。

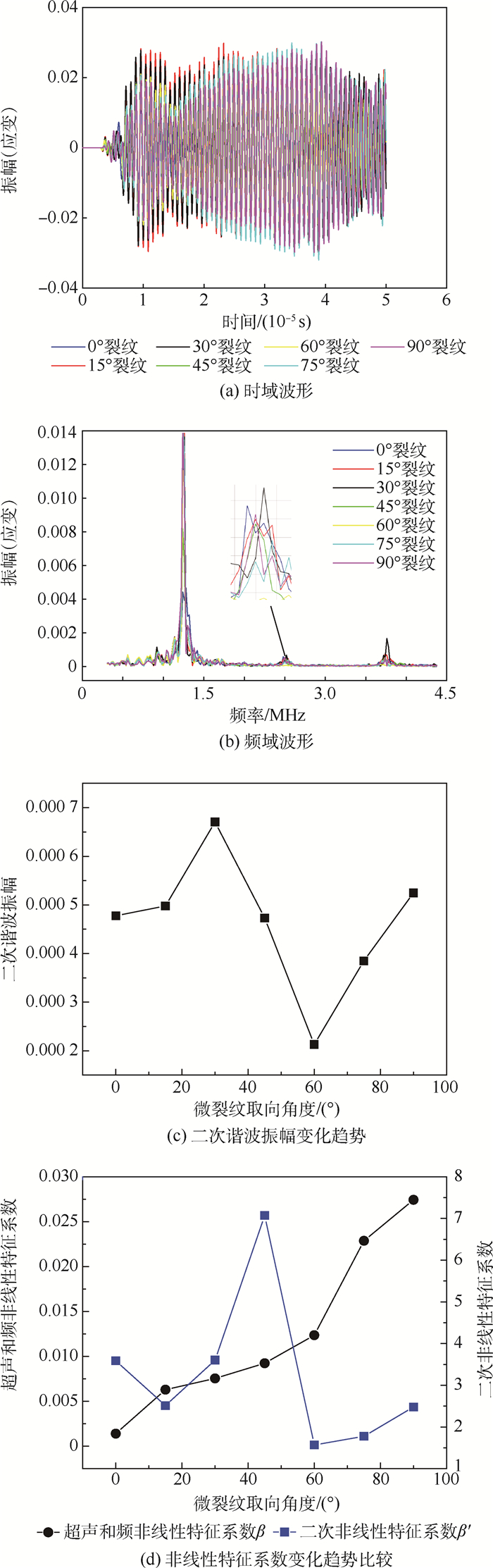图 10 单频检测仿真结果 Fig. 10 Single-frequency detection simulation results

图选项

图 10(a)、(b)分别给出了单频非线性超声与不同微裂纹取向角度相互作用的时域与频域波形。由图 10(b)可得，微裂纹取向角度从0°变化到90°时的输出信号频谱中均产生了频率为2.5 MHz的二次谐波信号。将振幅数据提取出来绘制成图 10(c)，可以得到，随着微裂纹取向角度θ的不断增大，二次谐波(w=2.5 MHz)振幅大小起伏不定，并未呈现明显的总体趋势。将基波振幅与二次谐波振幅提取出来，计算二次非线性特征系数β′，并将其与超声和频非线性特征系数β进行比较，结果如图 10(d)所示。由仿真结果可以看出，随着微裂纹取向角度θ的不断增大，超声和频非线性特征系数呈不断增大的趋势，而二次非线性特征系数变化起伏较大，没有一定规律。因此，相比于单频非线性超声检测，混频非线性超声检测中和频分量与微裂纹取向角度相互作用的非线性效应趋势更加明显。
2.3 讨论与分析 非线性特征系数不仅与特定角度下和频振幅或二次谐波的振幅有关，也与基波的振幅有关。因此，本节从超声波的平均能流密度(即声强)的角度对混频检测和单频检测的仿真模拟结果进行分析，综合考虑到基波振幅对非线性特征系数的影响；将混频非线性超声检测与单频非线性超声检测仿真模拟结果中的振幅数据分别提取出来，计算超声波声强的参考波的声强计算公式为

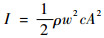(19)

分别计算混频检测与单频检测情况下系统的输入超声波的声强及各频率分量的声强，并计算和频分量声强占比η₁与二次谐波声强占比η₂，即

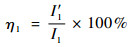(20)

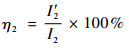(21)

式中：I₁为混频检测超声波输入信号声强；I′₁为混频检测和频分量信号声强；I₂为单频检测超声波输入信号声强；I′₂为单频检测二次谐波分量信号声强。
计算混频检测中和频分量声强与声强占比、单频检测中二次谐波声强与声强占比，结果如表 1所示。
表 1 各分量声强计算结果及占比 Table 1 Computation results and proportions of sound intensity of each component

微裂纹取向角度/(°)	I′1/(1013W·m－2)	I′2/(1013W·m-2)	η1/%	η2/%
0	1.247	1.797	0.289	0.681
15	2.163	1.951	1.290	0.498
30	1.608	3.541	1.455	0.958
45	3.074	1.762	1.428	1.321
60	3.262	0.3572	2.157	0.134
75	4.264	1.166	4.518	0.273
90	18.41	2.166	4.566	0.518

表选项






利用表 1中相关数据，绘制混频检测与单频检测中的声强对比，如图 11所示。如图 11(a)所示，随着微裂纹取向角度的增大，和频分量声强整体呈明显增大趋势，而二次谐波声强整体无明显波动。

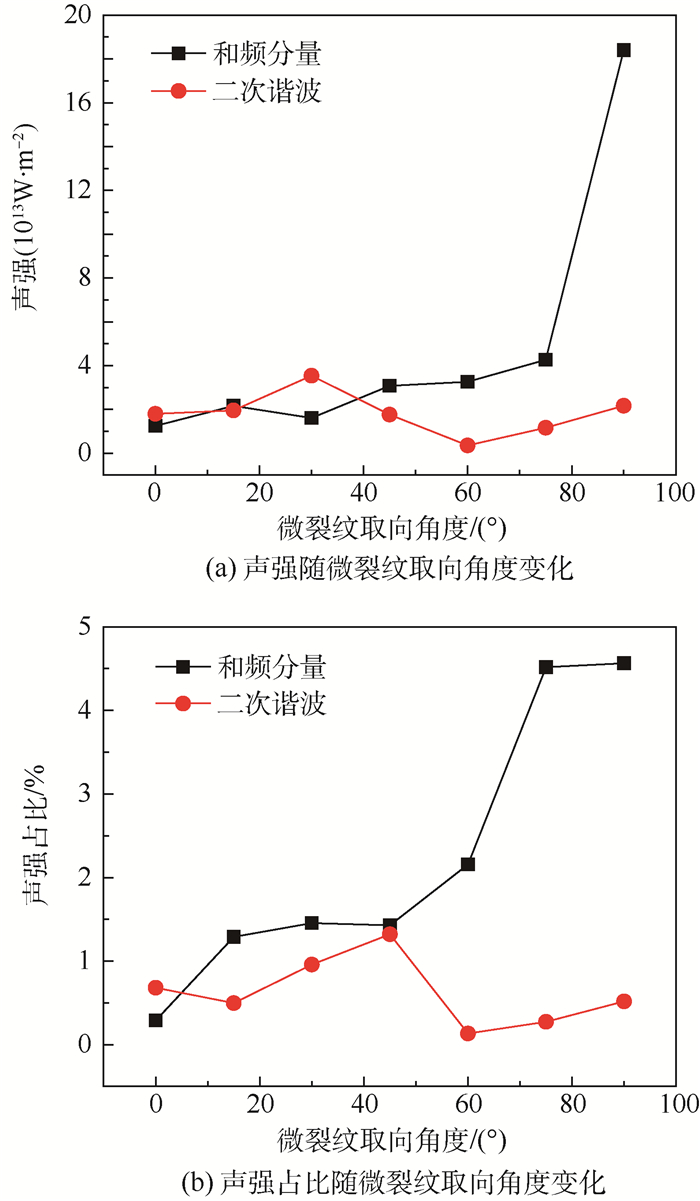图 11 和频分量与二次谐波声强对比 Fig. 11 Comparison of sound intensity of sum frequency component and second harmonic component

图选项

同时，如图 11(b)所示，随着微裂纹取向角度的不断增大，和频分量声强占比不断增大，而二次谐波声强占比有一定波动，但是并没有成一定趋势；同时对比和频分量的声强变化与声强占比变化发现，声强占比曲线的增大趋势更为均匀显著，说明基波振幅对于微裂纹取向的和频非线性效应也具有一定的影响。
分别计算各角度下和频分量声强相对二次谐波声强的增长程度，就各个微裂纹取向角度下平均而言，和频分量比二次谐波声强提高了5倍以上。这证实了相比于单频检测，混频检测微裂纹取向的和频非线性效应趋势更加明显、有效。
3 实验验证 3.1 实验系统设计 实验流程的示意图如图 12所示。首先由双通道信号发生器产生2个频率分别为1 MHz和1.5 MHz的正弦连续横波信号，经过放大和滤波后，使用超声波压电陶瓷横波探头施加在试样上。超声波信号沿着试样的长度方向传播，由于微裂纹的存在，2列波在微裂纹处会叠加产生和频分量信号，采用中心频率为2.5 MHz的超声波压电陶瓷横波探头接收和频信号，然后进行傅里叶变换，得到接收信号中的基波分量与和频分量。对不同微裂纹取向角度的试样重复上述步骤。对于微裂纹试样的制备，首先将试样按照一定角度切断，再将其按照原状使用夹持设备夹紧来模拟特定取向的微裂纹，为尽可能保证夹持时模拟微裂纹的宽度一致，实验中通过控制虎钳旋转的角度一致，3个试样的夹持位置一致，保证了3个不同角度模拟微裂纹的夹紧力度相一致；同时，激励探头、接收探头与试样的相对位置保持一致，如图 13所示。在实际测试过程中，选取试样微裂纹夹角为0°、45°、90°进行实验验证，如图 14所示。

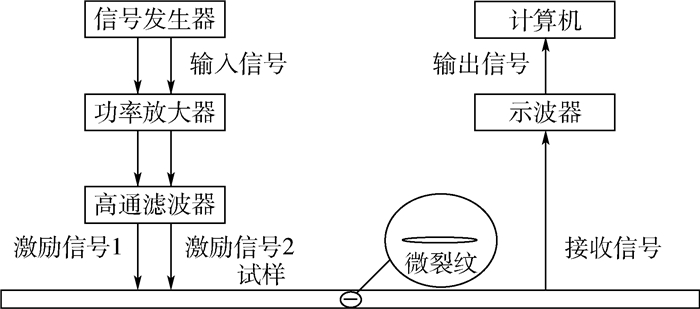图 12 实验流程示意图 Fig. 12 Schematic of experiment process

图选项

图 13 实验实物图 Fig. 13 Experiment equipment

图选项

图 14 试样制备图 Fig. 14 Sample preparation

图选项

3.2 实验结果 实验测试的输出信号如图 15所示。和频信号相较于基频信号较为微弱，但频谱中出现了较为明显和频分量，如图 15(a)、(b)、(c)所示。从图 15(d)中可以看出，和频振幅随着微裂纹取向角度θ的增大而增大，其结果与理论结果及仿真计算结果的趋势基本吻合。

图 15 不同微裂纹取向角度输出信号频域波形 Fig. 15 Frequency domain waveform of different orientation angle micro-crack output signal

图选项

利用和频信号振幅与基波信号振幅计算超声和频非线性特征系数，如图 16所示。可以看出，实验结果与模拟仿真及理论推导的结果相似，超声和频非线性特征系数随着微裂纹取向角度的增大而增大，成明显的正相关趋势，与计算模拟结果同样一致。

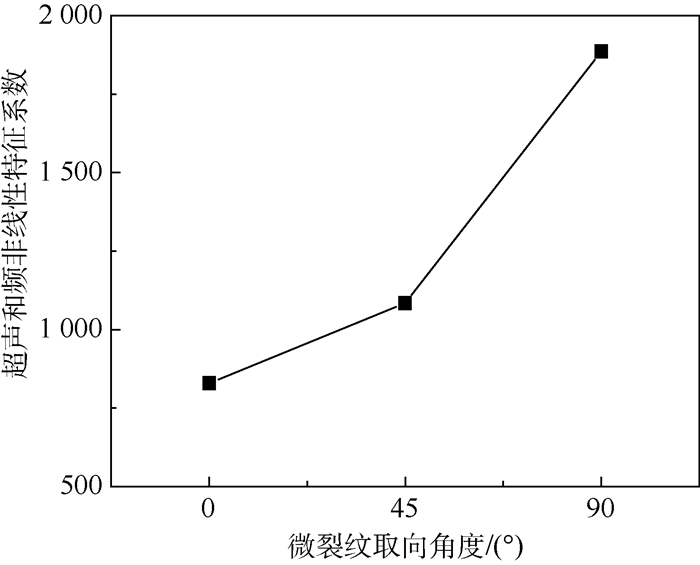图 16 超声和频非线性特征系数变化趋势 Fig. 16 Tendency of ultrasound nonlinear characteristic coefficient of sum frequency

图选项

4 结论 本文开展了金属材料微裂纹取向与超声波的和频非线性效应研究，以位移场为桥梁，建立了超声和频非线性特征系数与微裂纹取向角度的关系模型。实验结果表明:
1) 随着微裂纹取向角度的逐渐增大，混频检测中和频振幅呈增大趋势，超声和频非线性特征系数与微裂纹取向角度之间呈现明显的正相关趋势。
2) 相比二次非线性特征系数，超声和频非线性特征系数对微裂纹取向检测更为敏感有效。
3) 和频分量声强与声强占比会随着微裂纹取向角度的增大而增大。基波振幅对于微裂纹取向的和频非线性效应也具有一定的影响。
综上所述，利用超声波与金属材料微裂纹相互作用的和频非线性效应，可以有效检测微裂纹的取向角度趋势，为检测金属材料早期损伤提供了一种有效手段。

参考文献

[1]	MEYENDORF N G, R?SNER H, KRAMB V, et al. Thermo-acoustic fatigue characterization[J]. Ultrasonics, 2002, 40(1-8): 427-434. DOI:10.1016/S0041-624X(02)00155-5
[2]	税国双, 汪越胜, 曲建民. 材料力学性能退化的超声无损检测与评价[J]. 力学进展, 2005, 35(1): 52-68. SHUI G S, WANG Y S, QU J M. Advances in nondestructive test and evaluation of material degradation using nonlinear ultrasound[J]. Advances in Mechanics, 2005, 35(1): 52-68. DOI:10.3321/j.issn:1000-0992.2005.01.006 (in Chinese)
[3]	高桂丽, 李大勇, 董静薇, 等. 铝合金薄板疲劳裂纹的非线性声学特性[J]. 机械工程学报, 2010, 46(18): 71-76. GAO G L, LI D Y, DONG J W, et al. Nonlinear acoustic characteristics of fatigue cracks in aluminum alloy sheet[J]. Journal of Mechanical Engineering, 2010, 46(18): 71-76. (in Chinese)
[4]	JHANG K Y. Nonlinear ultrasonic techniques for non-destructive assessment of micro damage in material:A review[J]. International Journal of Precision Engineering and Manufacturing, 2009, 10(1): 123-135. DOI:10.1007/s12541-009-0019-y
[5]	周正干, 刘斯明. 非线性无损检测技术的研究、应用和发展[J]. 机械工程学报, 2011, 47(8): 2-11. ZHOU Z G, LIU S M. Nonlinear ultrasonic techniques used in nondestructive testing:A review[J]. Journal of Mechanical Engineering, 2011, 47(8): 2-11. (in Chinese)
[6]	焦敬品, 樊仲祥, 吴斌, 等. 闭合裂纹非共线混频超声检测试验研究[J]. 声学学报, 2017, 42(2): 205-213. JIAO J P, FAN Z X, WU B, et al. Experiments of non-collinear mixed frequency ultrasonic for closed crack detection[J]. Acta Acustica, 2017, 42(2): 205-213. (in Chinese)
[7]	焦敬品, 孙俊俊, 吴斌, 等. 结构微裂纹混频非线性超声检测方法研究[J]. 声学学报, 2013, 38(6): 648-656. JIAO J P, SUN J J, WU B, et al. A frequency-mixing nonlinear ultrasonic technique for micro-crack detection[J]. Acta Acustica, 2013, 38(6): 648-656. (in Chinese)
[8]	JIAO J, MENG X, HE C, et al. Nonlinear Lamb wave-mixing technique for micro-crack detection in plates[J]. NDT & E International, 2016, 85: 63-71.
[9]	CROXFORD A J, WILCOX P D, DRINKWATER B W, et al. The use of non-collinear mixing for nonlinear ultrasonic detection of plasticity and fatigue[J]. Journal of the Acoustical Society of America, 2009, 126(5): 117-122. DOI:10.1121/1.3231451
[10]	SUN M, XIANG Y, DENG M, et al. Scanning non-collinear wave mixing for nonlinear ultrasonic detection and localization of plasticity[J]. NDT & E International, 2018, 93: 1-6.
[11]	MCGOGERN M, REIS H. Damage characterization in dimension limestone cladding using noncollinear ultrasonic wave mixing[J]. Optical Engineering, 2015, 55(1): 011012.
[12]	冯侠, 邢修三. 微裂纹取向对金属断裂过程的影响[J]. 北京理工大学学报, 1994, 14(3): 234-239. FENG X, XING X S. On the effects of random orientation of microcracks upon the fracture process of metals[J]. Journal of Beijing Institute of Technology, 1994, 14(3): 234-239. (in Chinese)
[13]	COURTNEY C R P, NEILD S A, WILCOX P D, et al. Application of the bispectrum for detection of small nonlinearities excited sinusoidally[J]. Journal of Sound & Vibration, 2010, 329(20): 4279-4293.
[14]	DONSKOY D, SUTIN A, EKIMOV A. Nonlinear acoustic interaction on contact interfaces and its use for nondestructive testing[J]. NDT & E International, 2001, 34(4): 231-238.
[15]	SOLODOV I Y, KROHN N, BUSSE G. An example of nonclassical acoustic nonlinearity in solids[J]. Ultrasonics, 2002, 40(1-8): 621-625. DOI:10.1016/S0041-624X(02)00186-5
[16]	BREAZEALE M A, PHILIP J. Determination of third-order elastic constants from ultrasonic harmonic generation measurements[M]. Pittsburg: Academic Press, 1987.
[17]	CROXFORD A J, DRINKWATER B W, WILCOX P D.Nonlinear ultrasonic characterization using the noncollinear method[C]//37th Annual Review of Progress in Quantitative Nondestructive Evaluation.New York: AIP, 2011: 330-337. https://aip.scitation.org/doi/abs/10.1063/1.3591872
[18]	李海洋, 安志武, 廉国选, 等. 粗糙接触界面超声非线性效应的概率模型[J]. 声学学报, 2015, 40(2): 247-253. LI H Y, AN Z W, LIAN G X, et al. A probability model for ultrasonic nonlinear effects of rough contact interface[J]. Acta Acustica, 2015, 40(2): 247-253. (in Chinese)