许多****针对水平井裂纹之间的相互作用也展开了诸多研究。Gale等[4-5]在页岩地层中加入了大量的材料间断元素,例如岩层的交界面以及闭合的天然裂纹等,探讨了这些间断对水压裂纹扩展的影响。Lee等[6]通过研究水压裂纹在预制弱间断层的偏折现象,认为间断层会对地层中裂纹网的形成产生重要的作用。曾青冬和姚军[7]建立了多裂纹同步扩展的数学模型,利用扩展有限元方法研究了应力阴影对裂纹扩展形态的影响。郭印同[8]和衡帅[9]等利用自建的一套页岩水力压裂物理模拟与压裂缝表征方法分析了水压裂纹在含天然层理面的页岩中的开裂状况,揭示了层理在页岩网状压裂缝形成过程中的重要作用。陈勉[10]从断裂力学角度出发,通过三维空间中水力裂缝激活和转向控制方程,分析了控制裂缝转向扩展形态的关键因素和力学特征并进行实例计算。Chuprakov和Zhubayev[11]采用变分原理的方法,通过解析模型得到闭合裂纹的张开滑移区域的大小对水压裂纹在交汇及穿透期间重新起裂的影响。
上述研究都是针对于裂纹之间或者裂纹与间断面之间相互作用而展开的,即探究应力影对裂纹扩展的影响。然而,多数****的着重点都在试图建立一个与实际情况很接近的分析模型,然后通过最终的计算结果来描述各种因素对裂纹萌生情况的影响。他们很少提及裂纹在扩展过程中裂纹受应力影响所发生偏折的具体原因。经研究表明[12],在薄层和低渗地层中,纵向开裂水平井比竖直井的产量要高,因此本文只针对水平井钻孔技术部分进行分析,先根据裂尖附近应力场特征建立一个全新的裂尖权函数,在验证完裂尖权函数的正确性后,试图结合网格重划分方法与最大主应力方法分析影响水平井多裂纹扩展路径的多种因素,例如,应力差、裂纹数目和裂纹间距等,再探讨多裂纹在相互干扰情况下发生转向的原因。
1 裂尖权函数 1.1 权函数的建立 由于裂尖位置是一个奇异点,在有限元分析中,裂尖位置处的应力应变值是无法直接得到的,它需要通过裂尖邻近单元的高斯点插值得到。因此直接对这个点进行应力状态分析的误差是很大的。为了在有限元分析中能更加准确地捕捉裂尖处的应力状态,需要在裂尖附近的单元中收集更多的信息。因此,本文想通过建立一个权函数来连接裂尖与其附近单元高斯点处的信息,间接获得裂尖处的受力情况。
裂尖附近的单元以及高斯点的分布如图 1所示,高斯点距离裂尖的长度为D,高斯点和裂尖连线与x′轴所夹角为θ。裂尖处以r为半径所绘制的区域圆是收集附近单元信息的范围,r的取值可以参考扩展有限元对裂尖的处理[13]。这里的r取为3倍的裂尖附近单元平均边长。在裂尖处建立一个x′O′y′的局部坐标系,它是权函数建立的基础,沿着裂纹面的方向为x′方向,垂直于裂纹面的方向为y′方向。只要能找到一个充分描述裂尖附近应力特征的权函数w,则裂尖处的应力就可以等效为
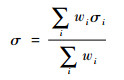 | (1) |
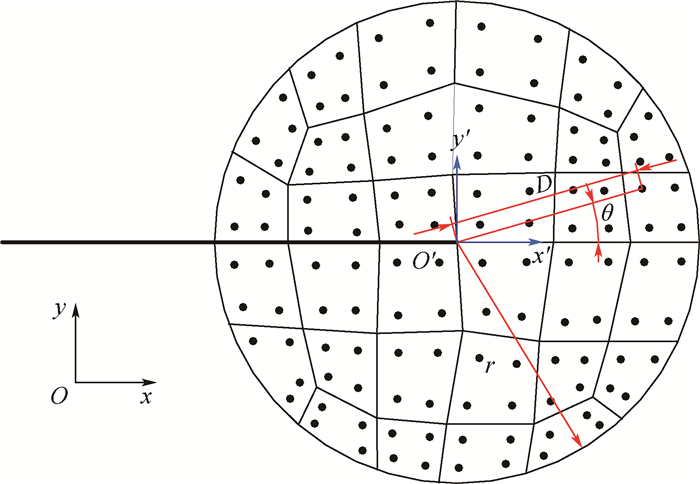 |
| 图 1 裂尖附近单元及高斯点分布图 Fig. 1 Distribution diagram of element and Gauss point near crack tip |
| 图选项 |
式中:σ为裂尖处的等效应力;wi与σi分别为第i个高斯点处的权函数值与应力值。
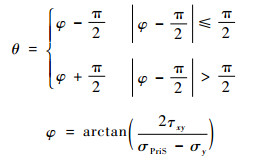
裂尖开裂的方向角θ为
 | (2) |
式中:σPriS、σy和τxy分别为裂尖处的等效主应力、等效y方向应力和等效xy方向应力。而裂尖的开裂条件可由最大主应力准则来确定,即σ>σ1时,裂纹起裂。其中σ1为等效主应力。
从图 1可知,构造得到的权函数w不仅与高斯点到裂尖的距离D有关,还与角度θ有关。为了能保证周围高斯点处应力值提取的正确性,需要首先用有限元高斯点处应力值与该点处的解析解[14]进行对比,舍弃两者之间差异比较大的部分。由于本文研究的是平面问题,因此只需要考虑Ⅰ型与Ⅱ型的应力状态即可。高斯点应力值与解析解的对比结果如图 2和图 3所示。
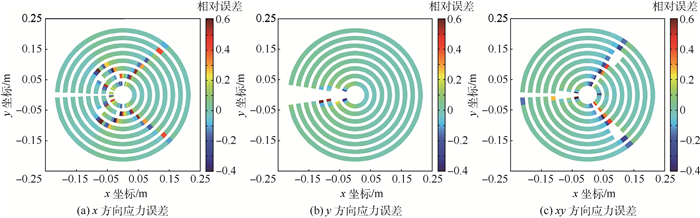 |
| 图 2 Ⅰ型裂尖附近的应力误差云图 Fig. 2 Error contour of stresses near model-Ⅰ crack tip |
| 图选项 |
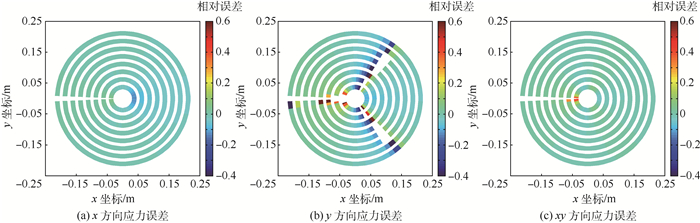 |
| 图 3 Ⅱ型裂尖附近的应力误差云图 Fig. 3 Error contour of stresses near model-Ⅱ crack tip |
| 图选项 |
为了便于分析,图 3中误差大于100%的部分均被删除。从图中可以发现,在裂尖大约±60°、±120°和180°方向上的应力误差偏大,而其他方向上的误差均不超过5%。因此应该将这些应力误差偏大方向上的权函数值设置为零,以保证最终计算结果的精度。至于与距离有关的项,由于裂尖的影响,离裂尖越近的应力值越大,并且由裂尖近场解析解可知,裂尖近场应力随着距离的增加而呈现
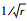
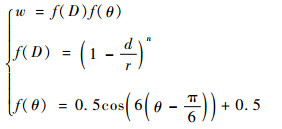 | (3) |
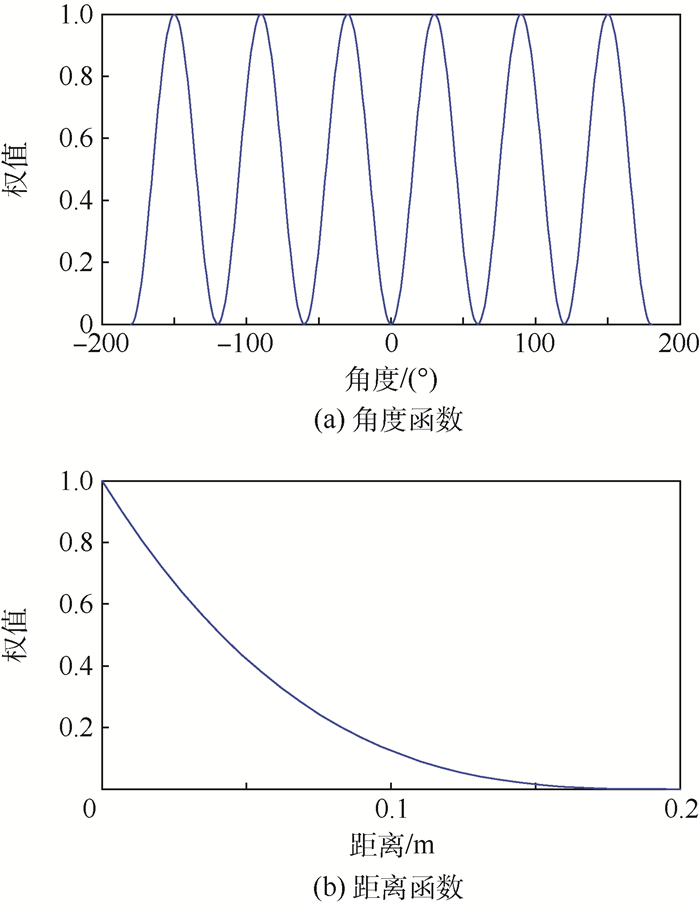 |
| 图 4 角度与距离函数曲线 Fig. 4 Curves of angle and distance function |
| 图选项 |
经验算后,本文中的n取值为3,具体的确定过程可见附录A。
1.2 权函数的验证 权函数建立之后,需要对它的正确性进行验证。本文选取了2个裂纹扩展的算例,通过裂纹扩展路径的偏差大小来验证该方法。参考路径采用最大周向拉应力方法(MCS)[16]和另一种权函数方法(文献[17]方法)的计算结果。为了量化偏差值,需要引入一个计算公式:
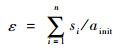 | (4) |
式中:ainit为裂纹的初始长度;si为从曲线l2上第i个点到曲线l1的距离,如图 5所示。
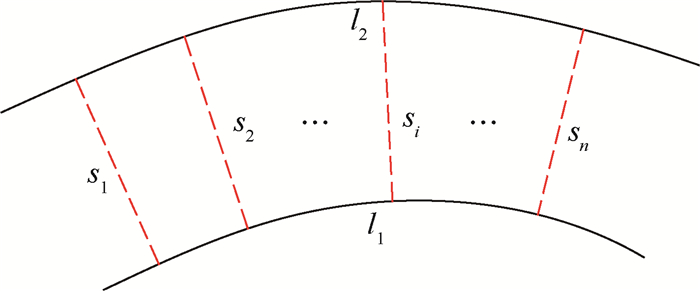 |
| 图 5 裂纹路径误差示意图 Fig. 5 Schematic of crack path error |
| 图选项 |
式(4)表示的是拟合曲线与目标曲线之间参考点的距离之和。这里需要注意的是在同一组曲线比较中,所选取的点数必须是一样的。最理想的拟合结果是计算公式的结果为0。
1.2.1 算例1 含有2个中心对称圆孔的矩形平板,底部固定,顶端承受拉伸位移,使平板只能在竖直方向上移动。2条长度均为1 mm的预制裂纹在孔洞离边界的较远一侧,并且呈中心对称分布,模型示意图如图 6所示。模型的材料参数如下:弹性模量E=200 GPa,泊松比ν=0.3,材料的临界应力强度因子KC =1 500 N/mm3/2。
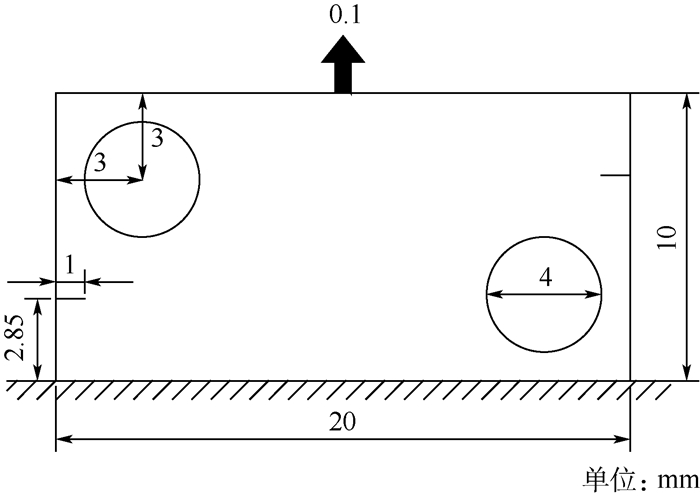 |
| 图 6 带孔板边缘多裂纹扩展的模型示意图 Fig. 6 Schematic of model of multiple edge cracks propagation of hole plate |
| 图选项 |
最终的对比结果如图 7所示,3条开裂路径都非常接近,利用本文权函数计算得到的开裂路径介于MCS方法与文献[17]方法的中间,且几乎与MCS方法的结果重合。路径之间的偏差通过式(4)可以得到,本文方法与MCS方法的偏差在1.75,而文献[17]方法与MCS方法的偏差达到了3.64。
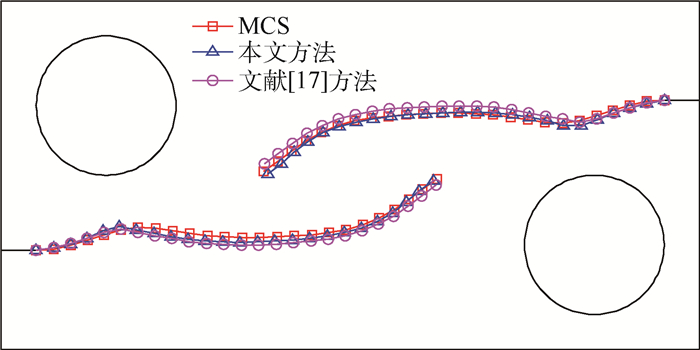 |
| 图 7 不同方法的开裂路径对比(算例1) Fig. 7 Comparison of crack path among different methods (Example 1) |
| 图选项 |
1.2.2 算例2 该算例采用的是四点弯曲梁试件开裂模型,具体参数如图 8所示, L和h分别为四点弯曲梁试件的长度和高度。简支梁在靠近左支座处有一条初始裂纹,梁顶端的三分点处均承受了集中力F的作用。
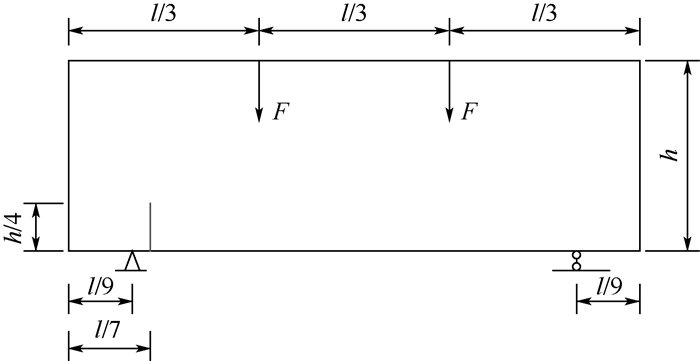 |
| 图 8 四点弯曲梁试件模型 Fig. 8 Model of 4-point bending beam specimen |
| 图选项 |
计算结果如图 9所示,图中箭头所指的是局部放大图。3条裂纹扩展路径很接近,其中下半部分的偏差略大于上半部分的偏差。本文方法和文献[17]方法与MCS的偏差分别为1.41和1.59。
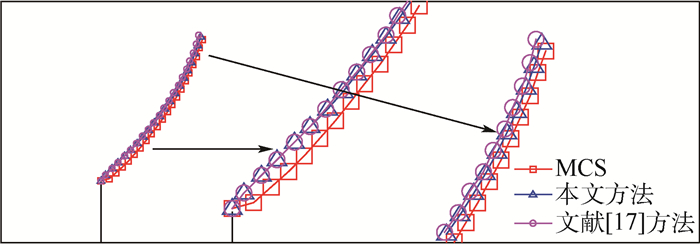 |
| 图 9 不同方法的开裂路径对比(算例2) Fig. 9 Comparison of crack path among different methods (Example 2) |
| 图选项 |
综上所述,通过2个算例的结果可以看出,本文所采用的权函数方法具有分析裂尖应力场的能力,是一种可靠的方法,能较准确地描述裂尖的应力状态。由于该方法是基于开口型裂纹开发的,因此对于闭口型裂纹或者压缩接触裂纹需要另外考虑。然而,在水力压裂分析中,主裂纹的开裂方式主要是张拉破裂,并且对于地应力差异较小的情况下,地层沿天然裂缝发生剪切的破裂的可能性也较小[9]。所以在随后的水平井钻井技术分析中,不考虑天然裂缝的起裂与大应力差情况时,可采用同样权函数来分析裂纹发生偏折的原因。
2 水平井多裂纹有限元模型的建立 2.1 模型描述 水平井多裂纹扩展的有限元模型如图 10所示,模型水平长度为100 m,竖直高度为50 m,最大水平主应力为σv,最小水平主应力为σh,射孔的长度为l,射孔间距为d,射孔内的水压为p,正三角形△表示只约束竖直方向位移,水平三角形?表示只约束水平方向位移,模型中(m)为射孔的编号,编号顺序从右向左逐渐增大。考虑到边界效应,取模型尺寸为射孔最大深度的20倍[18], 另外因为模型具有对称性,所以分析时可以考虑只取一半。由于模拟裂纹扩展形态的方法为网格重剖分方法,为了增加模型的计算效率,只需要将射孔附近的网格细化即可,具体网格划分见图 11。
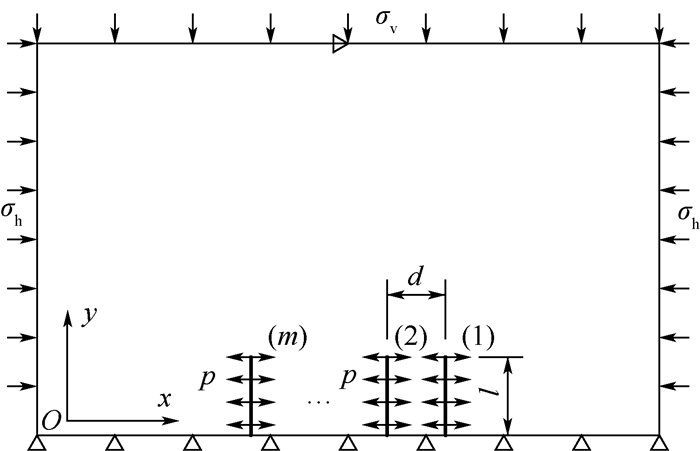 |
| 图 10 有限元模型示意图 Fig. 10 Schematic of finite element model |
| 图选项 |
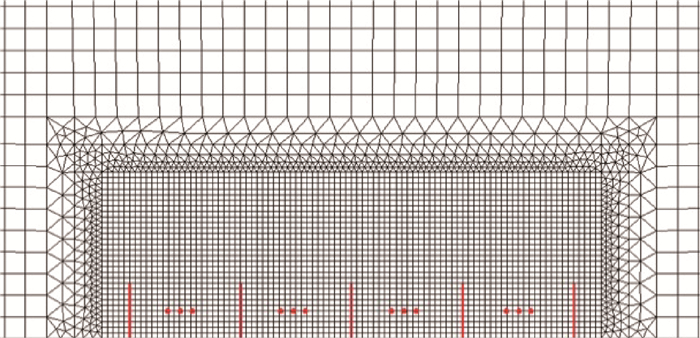 |
| 图 11 有限元网格模型 Fig. 11 Mesh of finite element model |
| 图选项 |
2.2 模型假设 为了问题研究的方便,本文忽略套管和水泥环的影响;视地层为线弹性均质各向同性、无限大平面;裂纹开裂是一个准静态的过程;重力作用在较短的计算段内产生的压力比起裂时的井筒压力小得多,可以忽略不计[19];不考虑流体渗入地层中所引起的附加应力,压裂液均匀分布在裂纹中;一般情况下,射孔都会被模拟成圆柱状,但是在实际中,射孔的形状与标准的圆柱是有差异的[20]。因此本文在计算时,忽略了射孔的形状。
裂纹内的液体压力被看作是常压力,但研究表明井口处的压力在裂纹开裂后会出现小幅度的下降[21]。这说明裂纹内的液体压力并不是恒定不变的。为了让模拟过程接近工程实际,本文在处理液体压力时,采用如下方法:在开裂前,裂纹内的液体压力是随着时间逐渐增加的;当液体压力提升到裂纹开裂后,液体的压力值会突然减小,再在随后的加压过程中逐步增大。每一条裂纹之间的液体压力是独立变化的,它们之间的压力加载不会相互影响。
3 水平井多裂纹扩展结果 水平井多裂纹扩展模型的具体计算参数为:最小水平主应力σh=15 MPa,最大水平主应力σv=15~25 MPa,岩层的弹性模量E=14 GPa,泊松比ν=0.37,裂纹内水压p的最大值为25 MPa,岩层的等效断裂韧度KC=3 N/mm3/2。为了便于问题的分析,本文把水压裂纹的间距d与初始长度l的比值d/l作为一个变量来讨论,称之为间长比(RSL)。接下来通过网格重剖分与权函数方法计算多裂纹扩展,研究裂纹数目、RSL以及应力差等参数对裂纹扩展过程中路径的影响,然后再由权函数方法分析扩展路径发生变化的原因。
3.1 间长比的变化 此节考虑在同样的裂纹射孔条件下,裂纹扩展过程中裂纹间长比对裂纹开裂的影响。这里将先从两条裂纹开始分析,只考虑σh=σv的情况,通过增加裂纹数目来分析多条裂纹扩展时的开裂规律。
设定裂纹间长比的变化范围为1.0~3.0,通过权函数方法计算得到的扩展路径如图 12所示。从图 12中可以看出,当裂纹的间长比变大时,裂纹开裂的偏转角反而越小,并且裂纹的扩展长度随着RSL的增加而逐渐增长。这是因为当裂纹之间的间距增大时,裂纹之间的相互作用会越来越小,从而减弱了裂纹的偏折角度和阻碍裂纹扩展的作用力。
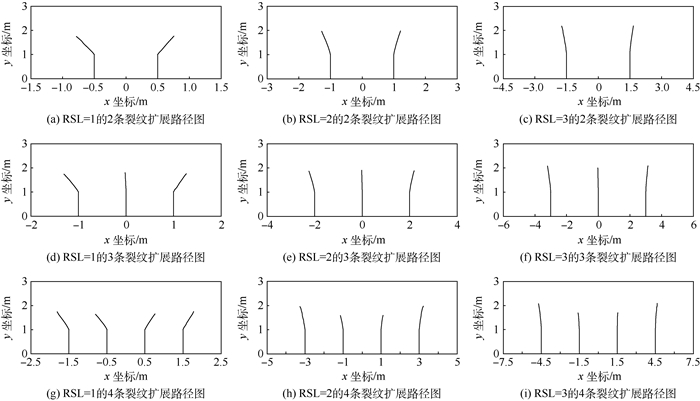 |
| 图 12 不同间长比条件下裂纹扩展路径 Fig. 12 Crack propagation path under different RSL |
| 图选项 |
从裂纹扩展路径图中可以看出,由于裂纹起裂后的方向大致确定了裂纹后续的扩展方向,因此在分析裂纹偏折原因时可以结合裂尖权函数,把整个过程简化成只研究裂纹起裂那一刻的偏折原因。
裂纹发生偏折的具体原因通过图 13曲线给出。图中的横坐标代表的是裂纹数目,纵坐标则代表无因次化应力的大小,它等于裂纹开裂时裂尖的等效应力值与单条裂纹开裂时裂尖等效应力的比值。这里只分析最外侧的1号裂纹,其他裂纹的分析类似。应力方向是基于裂尖局部坐标确定的,从图 13中可知,多条裂纹在开裂时,裂尖的xy方向等效应力是单裂纹情况下的十倍至几十倍,而其他方向的应力与单裂纹情况相比基本没发生变化,通过方向角公式式(2)可以分析出裂纹是向右侧偏折的。裂纹间长比越小,裂纹的偏折就越明显,这个原因可以由图 14中曲线进行解释。其中间长比为0的点表示是只有一条裂纹的情形。随着间长比变大,xy方向的应力会明显减小,只有原来的一半。但是主应力与y方向应力的差异并不明显,裂纹起裂偏折的角度也就越趋近于单裂纹的开裂状态,所以裂纹偏折角度是变小的。之所以1号裂纹裂尖处的xy方向等效应力会发生改变,是因为1号裂纹的左侧增加裂纹之后,水压力与最小水平主应力的大小不一样而造成裂尖位置受力会发生突变。由于增加裂纹数目对裂纹偏折角度的影响不如改变间长比的大,因此将不同间长比条件下角度和水压的变化情况如图 15所示。从图 15中可以很清楚地发现,裂纹间长比对偏折角度和水压有较大的影响,这是因为增加间长比会减弱裂纹之间的相互作用。
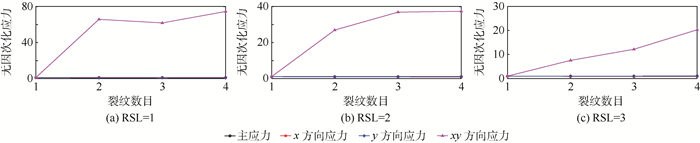 |
| 图 13 不同间长比条件下裂尖等效应力随裂纹数目的变化情况 Fig. 13 Variation of equivalent stress at crack tip with crack number under different RSL |
| 图选项 |
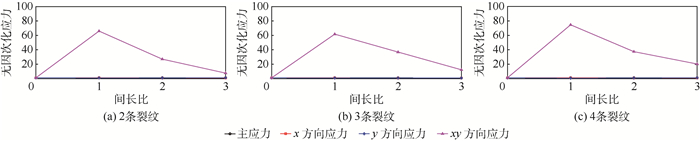 |
| 图 14 不同裂纹数目条件下裂尖等效应力随间长比的变化情况 Fig. 14 Variation of equivalent stress at crack tip with RSL under different crack numbers |
| 图选项 |
 |
| 图 15 不同裂纹数目条件下裂纹偏折角度与水压随间长比的变化情况 Fig. 15 Variation of deflection angle and hydraulic pressure with RSL under different crack numbers |
| 图选项 |
3.2 应力差的变化 本节固定RSL=1,改变应力差σv-σh的值,研究不同应力差条件下裂纹的开裂状态。由加权等效应力方法所计算出来的裂纹扩展路径如图 16所示,当应力差由0变化到20 MPa的过程中,裂纹扩展的扩展角度有明显减小,但是应力差的变化对裂纹扩展的长度影响并不大,而且相同应力差条件下,增加裂纹数目对裂纹扩展偏折角度的影响也不大。因此应力差值增加会减小裂纹开裂时的扩展角度。角度变小原因可以通过图 17中进行分析,图中没有考虑x方向的应力是因为x方向应力与式(2)并不直接相关。
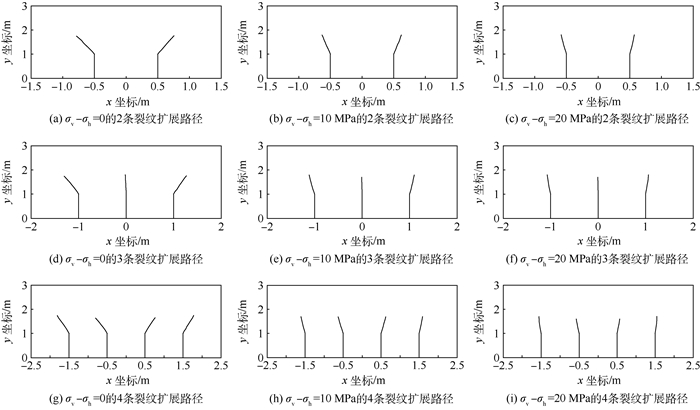 |
| 图 16 不同应力差条件下的裂纹扩展路径 Fig. 16 Crack propagation path under different stress contrast |
| 图选项 |
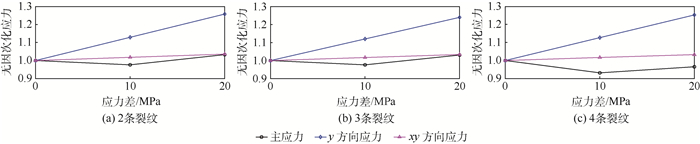 |
| 图 17 不同裂纹数目条件下裂尖等效应力随应力差的变化情况 Fig. 17 Variation of equivalent stress at crack tip with stress contrast under different crack numbers |
| 图选项 |
当应力差变大时,变化最明显的是y方向应力,而其他方向应力变化很小,因此根据角度公式可知方向角也是相应变小的。对应角度变化曲线如图 18所示,角度随着应力差增加而减小,水压略有增加但是幅度并不明显,其中角度数据是以应力差为0 MPa时2条裂纹的开裂数据为基准进行无因次化的。
 |
| 图 18 不同裂纹数目条件下裂尖偏折角度与水压随应力差的变化情况 Fig. 18 Variation of deflection angle and hydraulic pressure at crack tip with stress contrast under different crack numbers |
| 图选项 |
4 结论 本文根据裂尖应力场的特征建立了裂尖权函数,其可以准确地描述裂尖受力状态,并有效地对裂纹开裂原因进行分析。在以水平井压裂技术为背景的前提下,利用裂尖权函数分析了多裂纹同步扩展过程中裂纹发生偏折的原因,得到:
1) 相比一条裂纹而言,裂纹数目增加后,裂纹的开裂方向会向外产生偏折,这是因为裂纹尖端的xy方向的等效应力突然增大,而其他方向的等效应力基本不发生变化而导致的。
2) 当裂纹的间长比逐渐增加时,裂尖的xy方向等效应力会明显减小,而主应力与y方向的等效应力差值并没变化,因此裂纹的偏折角度会相应地变小。
3) 在应力差变大的过程中,相比同裂纹数目应力差为0的条件下,xy方向的等效应力与主应力并没有什么太大变化,但是y方向的等效应力明显地增加,因此偏折角度逐渐减小。
附录A 式(3)中系数n的确定 式(3)中n的确定是由本文的算例1和算例2总结得到的,通过改变系数n的取值来观察权函数所计算出来的扩展路径与利用MCS所得到的路径之间的差异,然后以MCS结果为基准,由式(4)计算出的ε进行定量比较,从而确定出最终的n值。
算例1中的模型和数据如图 6所示,最终的计算结果如图 A1所示。从图 A1中可以看出,当n=3时的扩展路径与MCS的差异最小。
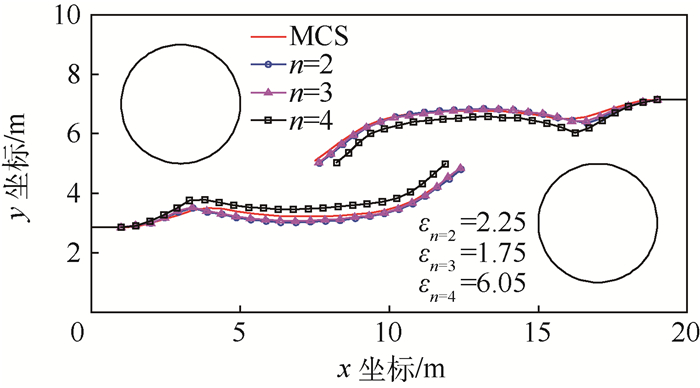 |
| 图 A1 不同系数n下带孔板边缘的裂纹扩展对比 Fig. A1 Comparison of edge crack propagation of hole plate under different coefficient n |
| 图选项 |
算例2中的模型和数据如图 8所示,最终计算结果和误差对比如图 A2所示。
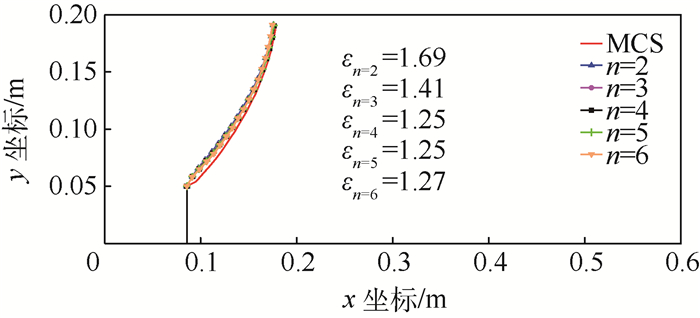 |
| 图 A2 不同系数n下四点弯曲梁试件模型的裂纹扩展对比 Fig. A2 Crack propagation comparison of 4-point bending beam specimen under different coefficient n |
| 图选项 |
从图 A2中可以看出虽然当n=4和n=5时的误差最小并且n=3与他们之间的差距达到了12%,但是结合算例一模型进行考虑时可知n=4在处理该问题时它与n=3之间的差距过大,效果并不好。综合以上因素,最优化系数应该取为n=3。
参考文献
| [1] | BA?ANT Z P, SALVIATO M, CHAU V T, et al. Why fracking works[J]. Journal of Applied Mechanics, 2014, 81(10): 101010. DOI:10.1115/1.4028192 |
| [2] | WANG X L, LIU C, WANG H, et al. Comparison of consecutive and alternate hydraulic fracturing in horizontal wells using XFEM-based cohesive zone method[J]. Journal of Petroleum Science & Engineering, 2016, 143: 14-25. |
| [3] | ZENG X, WEI Y. Crack deflection in brittle media with heterogeneous interfaces and its application in shale fracking[J]. Journal of the Mechanics and Physics of Solids, 2017, 101: 235-249. DOI:10.1016/j.jmps.2016.12.012 |
| [4] | GALE J F W, LAUBACH S E, OLSON J E, et al. Natural fractures in shale:A review and new observations[J]. AAPG Bulletin, 2014, 98(11): 2165-2216. DOI:10.1306/08121413151 |
| [5] | GALE J F W, REED R M, HOLDER J. Natural fractures in the Barnett shale and their importance for hydraulic fracture treatments[J]. AAPG Bulletin, 2007, 91(4): 603-622. DOI:10.1306/11010606061 |
| [6] | LEE H P, OLSON J E, HOLDER J, et al. The interaction of propagating opening mode fractures with preexisting discontinuities in shale[J]. Journal of Geophysical Research Solid Earth, 2015, 120(1): 169-181. DOI:10.1002/2014JB011358 |
| [7] | 曾青冬, 姚军. 水平井多裂缝同步扩展数值模拟[J]. 石油学报, 2015, 36(12): 1571-1579. ZENG Q D, YAO J. Numerical simulation of multiple fractures simultaneous propagation in horizontal well[J]. Acta Petrolei Sinica, 2015, 36(12): 1571-1579. DOI:10.7623/syxb201512012 (in Chinese) |
| [8] | 郭印同, 杨春和, 贾长贵, 等. 页岩水力压裂物理模拟与裂缝表征方法研究[J]. 岩石力学与工程学报, 2014, 33(1): 52-59. GUO Y T, YANG C H, JIA C G, et al. Research on hydraulic fracturing physical simulation of shale and fracture characterization methods[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(1): 52-59. (in Chinese) |
| [9] | 衡帅, 杨春和, 郭印同, 等. 层理对页岩水力裂缝扩展的影响研究[J]. 岩石力学与工程学报, 2015, 34(2): 228-237. HENG S, YANG C H, GUO Y T, et al. Influence of bedding planes on hydraulic fracture propagation in shale formations[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(2): 228-237. (in Chinese) |
| [10] | 陈勉. 页岩气储层水力裂缝转向扩展机制[J]. 中国石油大学学报(自然科学版), 2013, 37(5): 88-94. CHEN M. Re-orientation and propagation of hydraulic fractures in shale gas reservoir[J]. Journal of China University of Petroleum(Edition of Natural Sciences), 2013, 37(5): 88-94. DOI:10.3969/j.issn.1673-5005.2013.05.013 (in Chinese) |
| [11] | CHUPRAKOV D A, ZHUBAYEV A S. A variational approach to analyze a natural fault with hydraulic fracture based on the strain energy density criterion[J]. Theoretical & Applied Fracture Mechanics, 2010, 53(3): 221-232. |
| [12] | HUANG J, GRIFFITHS D V, WONG S W. Initiation pressure, location and orientation of hydraulic fracture[J]. International Journal of Rock Mechanics & Mining Sciences, 2012, 49(1): 59-67. |
| [13] | DOLBOW J, BELYTSCHKO T. A finite element method for crack growth without remeshing[J]. International Journal for Numerical Methods in Engineering, 1999, 46(1): 131-150. DOI:10.1002/(ISSN)1097-0207 |
| [14] | 范天佑. 断裂理论基础[M]. 北京: 科学出版社, 2003: 74-75. FAN T Y. Foundation of fracture theory[M]. Beijing: Science Press, 2003: 74-75. (in Chinese) |
| [15] | VENTURA G, GRACIE R, BELYTSCHKO T. Fast integration and weight function blending in the extended finite element method[J]. International Journal for Numerical Methods in Engineering, 2010, 77(1): 1-29. |
| [16] | CASTONGUAY S T, MEAR M E, DEAN R H, et al.Predictions of the growth of multiple interacting hydraulic fractures in three dimensions[C]//SPE Annual Technical Conference and Exhibition.Richardson: Society of Petroleum Engineers, 2013: 1-12. https://www.onepetro.org/conference-paper/SPE-166259-MS |
| [17] | 师访.岩石破裂过程的扩展有限元法研究[D].北京: 中国矿业大学, 2015. SHI F.Study on the cracking process of rock using the extended finite element method[D].Beijing: China University of Mining and Technology, 2015(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10290-1015972349.htm |
| [18] | 李根生, 刘丽, 黄中伟, 等. 水力射孔对地层破裂压力的影响研究[J]. 中国石油大学学报(自然科学版), 2006, 30(5): 42-45. LI G S, LIU L, HUANG Z W, et al. Study of effect of hydraulic perforating on formation fracturing pressure[J]. Journal of China University of Petroleum(Edition of Natural Sciences), 2006, 30(5): 42-45. DOI:10.3321/j.issn:1000-5870.2006.05.010 (in Chinese) |
| [19] | 彪仿俊, 刘合, 张劲, 等. 螺旋射孔条件下地层破裂压力的数值模拟研究[J]. 中国科学技术大学学报, 2011, 41(3): 219-226. BIAO F J, LIU H, ZHANG J, et al. A numerical study of fracture initiation pressure under helical perforation conditions[J]. Jouranl of University of Science and Technology of China, 2011, 41(3): 219-226. (in Chinese) |
| [20] | BRINER A, CHAVEZ J C, NADEZHDIN S, et al.Impact of perforation tunnel orientation and length in horizontal wellbores on fracture initiation pressure in maximum tensile stress criterion model for tight gas fields in the sultanate of oman[C]//SPE Middle East Oil & Gas Show and Conference.Richardson: Society of Petroleum Engineers, 2015: 63-75. https://www.onepetro.org/conference-paper/SPE-172663-MS |
| [21] | 彪仿俊, 刘合, 张士诚, 等. 水力压裂水平裂缝影响参数的数值模拟研究[J]. 工程力学, 2011, 28(10): 228-235. BIAO F J, LIU H, ZHANG S C, et al. A numerical study of parameter influences on horizontal hydraulic fracture[J]. Engineering Mechanics, 2011, 28(10): 228-235. (in Chinese) |
