目前建立短纤维增强复合材料RVE的方法有:随机顺序吸附(Random Sequential Adsorption, RSA)方法[10-12]、基于RSA的纤维生长法[13]、分子动力学方法[14]、粒子群优化算法[15]、蒙特卡罗方法[16]和图像重建技术[17]等。其中,RSA方法凭借其操作简单、计算量小的优点被广泛应用。该方法的核心是每次在RVE区域内生成位置随机、取向按给定函数随机分布的一根纤维后,判断新纤维与已存在纤维是否相交,仅当不相交时认为新纤维可以存在于RVE中,循环此过程直到纤维体积分数达到规定值为止[10]。纤维相交与否关系的判断通常通过几何方法实现[18]。考虑到几何方法计算复杂且计算量大,Liu等[19]采用布尔运算方法判断纤维是否相交,进而提出了基于布尔运算的随机顺序吸附(Boolean Operation based Random Sequential Adsorption, BORSA)方法。但是,布尔运算判断法耗时也较长,并且对一些非常容易判断位置关系的纤维进行布尔运算判断影响了RVE的建立效率。
本文对Liu等[19]的方法进行了改进,在对纤维进行布尔运算判断前,加入了新纤维与已存在纤维的形心距计算,当形心距小于规定距离时不进行布尔运算,直接重新随机生成纤维位置,这相当于过滤掉了部分随机生成的新纤维,进而提出了考虑过滤的随机顺序吸附(Filter based Random Sequential Adsorption, FRSA)方法。然后,采用RVE生成算例验证了方法的先进性。
1 BORSA方法 Liu等[19]提出的BORSA方法如下。给定建模所需的纤维体积分数VCmax,纤维长径比AR,纤维直径D,单根纤维体积Vf和RVE模型长、宽、高(L, W, H)等参数。定义描述纤维的5个参数:纤维形心的三维坐标(x, y, z),纤维轴线在XOY平面内的投影与X轴的夹角θ,纤维轴线与Z轴的夹角φ。给定纤维参数取值范围:x∈(0, L),y∈(0, W),z∈(0, H),θ∈(0°, 180°),φ∈(0°, 180°)。规定最大布尔运算次数为Tmax。生成RVE中所有纤维的步骤如下:
1) 生成第1根纤维fi(i=1)。随机生成符合均布函数的纤维形心位置参数(x1, y1, z1),随机生成符合相应函数的取向参数(θ, φ),并在模型中生成纤维。
2) 计算RVE当前纤维体积分数VC,当VC<VCmax时,i=i+1,执行步骤3);当VC≥VCmax时,输出纤维模型,RVE建模结束。
3) 随机生成纤维fi的参数(xi, yi, zi, θi, φi)。设定布尔运算次数T=0。
4) T=T+1,将纤维fi向(±L, 0, 0),(0, ±W, 0),(0, 0, ±H),(±L, ±W, 0),(0, ±W, ±H),(±L, 0, ±H),(±L, ±W, ±H)共26个方向复制。然后执行布尔运算:用27个新纤维fi减现有的i-1根纤维,当i-1根纤维的剩余体积小于(i-1)Vf时,表明纤维间有相交关系,进行步骤5);当i-1根纤维的剩余体积等于(i-1)Vf时,认为纤维fi与纤维fj(j=1, 2, …, i-1)均不相交,进行步骤6)。
5) 当T<Tmax时,将fi平移到RVE内随机位置,返回步骤4);当T=Tmax时,则认为已不能在当前模型中放入新纤维,RVE生成失败,建模结束。
6) 保存纤维fi的信息,返回步骤2)。
由上述过程可见,每生成一根纤维或对纤维进行一次平移,均需进行一次布尔运算。由于纤维位置是随机生成的,其中必然存在新生成的纤维形心位置与现有纤维形心非常接近的情况,比如小于纤维直径,此时的新纤维必然与现有纤维相交。如果通过设置过滤函数使得对这部分新纤维不需要进行布尔运算,则可以提高RVE生成速度。
2 FRSA方法 2.1 FRSA方法原理 为了实现纤维过滤,定义新生成纤维与现有纤维形心距最小值di为
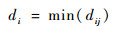 | (1) |
式中:dij为纤维fi和fj的形心距离, 定义为
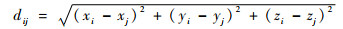 | (2) |
并在进行布尔运算前判断di是否小于一个常数dc(dc为临界距离)。当di<dc时,认为不必进行布尔运算。当di≥dc,时认为可以进行布尔运算。从而实现过滤掉一部分纤维。
2.2 临界距离dc对FRSA方法的影响 空间中2个纤维的距离dij存在2个特殊情况:
1) 当dij=D时,以fi形心为球心的纤维内切球体与以fj形心为球心的纤维内切球体相外切,如图 1所示。
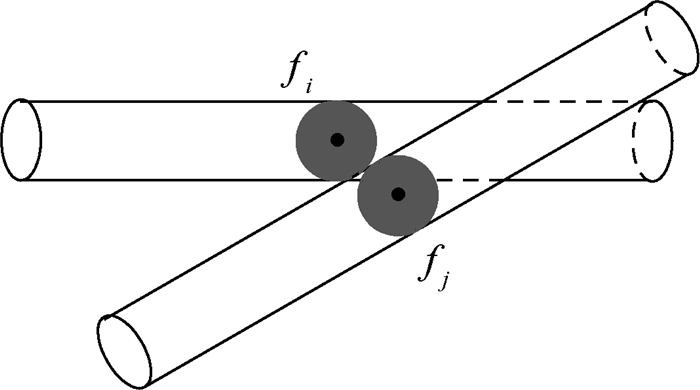 |
| 图 1 fi内切球体与fj内切球体相外切 Fig. 1 Circumscribed inner spheres of fi and fj |
| 图选项 |
2) 当dij=
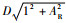
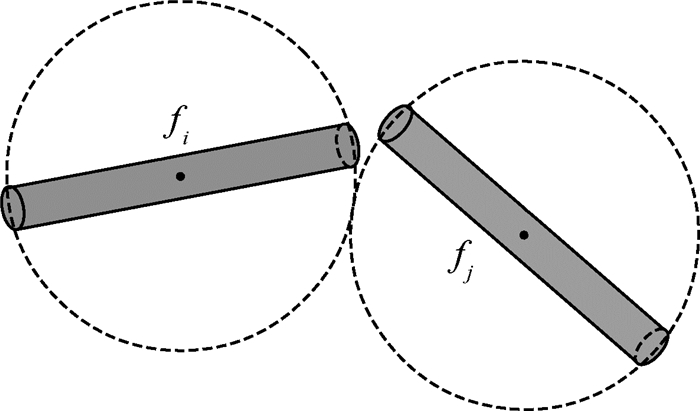 |
| 图 2 fi外切球体与fj外切球体相外切 Fig. 2 Circumscribed outer spheres of fi and fj |
| 图选项 |
根据上述2种情况可以将纤维之间的相交关系分为必然相交、必然不相交和可能相交3种情况:
1) 当0≤dij<D时,fi的内切球体与fj的内切球体相交,即fi与fj必然相交。
2) 当dij>
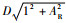
3) 当D<dij<
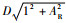
则dc的取值会导致4种过滤状态:
1) 当0<dc<D时,过滤掉的fi是一定与fj相交的,但会有一定与fj相交的fi未被过滤掉。
2) 当dc=D时,过滤掉的fi是一定与fj相交的,并且一定与fj相交的fi均被过滤掉。
3)当D<dc<
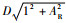
4) 当dc>
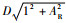
由上述分析可知,如果dc<D,则会有与fj必然相交的fi未被滤掉,所以dc的最小值应是D。状态2)和3)除了会过滤掉所有必然与fj相交的fi外,还会过滤掉不与fj相交的fi,此时过滤能起到提高建模效率的作用,但是会降低纤维位置的可行域,降低RVE的最大纤维体积分数,即提前出现RVE的纤维拥塞[20-21]。dc的取值对本方法影响很大,因此FRSA方法应用时需要选择合适的dc取值。
2.3 FRSA方法步骤 FRSA方法将生成RVE的步骤4)改为:计算fi与fj(j=1, 2, …, i-1)形心距的最小值di。当di<dc时进行步骤5)。当di≥dc时,T=T+1,将纤维fi向(±L, 0, 0),(0, ±W, 0),(0, 0, ±H),(±L, ±W, 0),(0, ±W, ±H),(±L, 0, ±H),(±L, ±W, ±H)共26个方向平移。然后执行布尔运算:用27个新纤维fi减现有的i-1根纤维,当i-1根纤维的剩余体积小于(i-1)Vf时,表明纤维之间有相交关系,进行步骤5);当i-1根纤维的剩余体积等于(i-1)Vf时,认为纤维fi与纤维fj(j=1, 2, …, i-1)均不相交,进行步骤6)。
需要指出的是,为了避免降低计算效率,上述方法中计算di时没有对跨边界纤维进行特别处理。
3 FRSA方法先进性验证 3.1 典型参数下的FRSA方法先进性验证 设置RVE参数,取纤维直径D=20 μm,RVE长、宽及高(L, W, H)均为10D,纤维长径比AR=2,纤维体积分数VCmax=8%。设置方法参数,令最大布尔运算次数Tmax=103,dc=
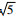
考虑到过滤法是通过减少布尔运算次数提高建模效率的,图 3给出采用BORSA方法和FRSA方法,各生成1个RVE模型时,生成每根纤维的布尔运算次数。
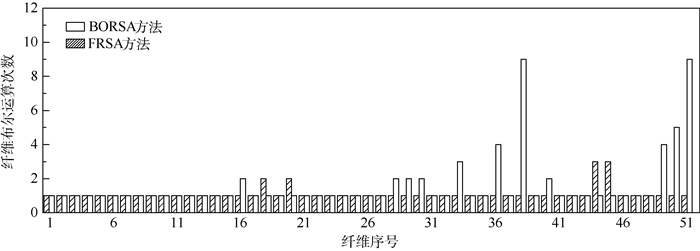 |
| 图 3 改进前后2种方法在一个RVE算例中每根纤维的布尔运算次数 Fig. 3 Number of Boolean operation times per fiber in one RVE example with two methods before and after improvement |
| 图选项 |
由图 3可见,当VCmax=8%时,一个RVE中需要生成51根纤维。BORSA方法中生成1根纤维的布尔运算次数最大为9次,而FRSA方法中最多为3次。总体来看,FRSA方法明显减少了纤维布尔运算的次数。
采用2种方法各生成10个RVE。计算生成一个RVE的总布尔运算次数,并对10个RVE取平均值,可知BORSA方法和FRSA方法生成一个RVE的平均布尔运算次数分别为87.5和61.8次,改进后FRSA方法布尔运算次数降为BORSA方法的70.6%。
建模效率的最好指标是建模时间。比较2种方法各生成10个算例的总时间,发现BORSA方法耗时1 079 s,改进后FRSA方法耗时921 s,可见建模时间降为原方法的85.4%,明显提高了RVE的建模效率。
采用FRSA方法生成的一个RVE如图 4所示,可以用来进行后续的材料性能分析。
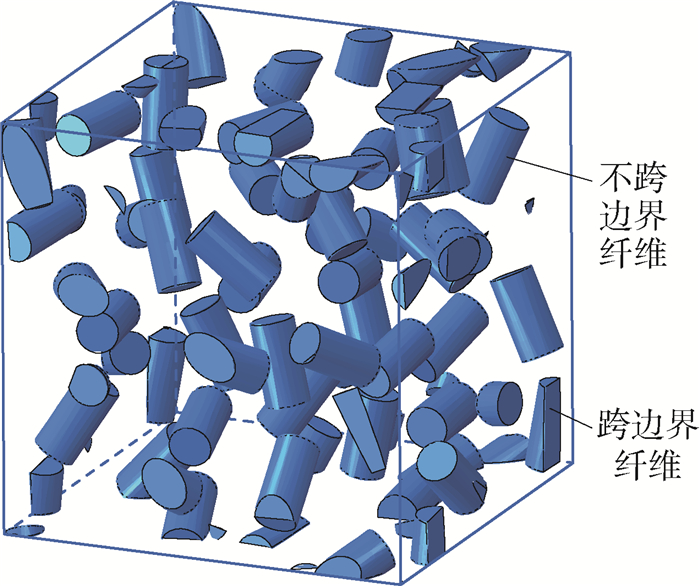 |
| 图 4 FRSA方法生成的RVE Fig. 4 RVE generated with FRSA method |
| 图选项 |
3.2 RVE参数和方法参数对FRSA方法先进性的影响 工程中通常需要生成不同纤维体积分数VCmax和不同长径比AR的RVE;另外由2.2节可知,临界距离dc对FRSA方法效率有影响,因此本节在不同的VCmax、dc和AR取值下对FRSA方法建模效率进行研究。
3.2.1 VCmax对建模效率的影响 选取VCmax的变化范围为5%~11%,每种条件均生成10个RVE。计算采用FRSA生成一个RVE进行的布尔运算次数T′和采用BORSA生成一个RVE进行的布尔运算次数T″的比值(T′/T″),采用FRSA生成一个RVE所用时间t′和采用BORSA生成一个RVE所用时间t″的比值(t′/t″),并对10次模拟数据取平均值,结果列于表 1。由表 1可知,在不同VCmax情况下FRSA方法可将生成RVE所需布尔运算次数降低18%~29%,所需的时间降低14%~15%,改进效果明显。
表 1 不同VCmax情况下的RVE建模效率对比 Table 1 Comparison of RVE modeling efficiency for various VCmax
| VCmax/% | T′/T″ | t′/t″ |
| 5 | 0.76 | 0.86 |
| 8 | 0.71 | 0.85 |
| 11 | 0.82 | 0.86 |
表选项
3.2.2 dc对建模效率的影响 在3.2.1节的算例中,设置了FRSA方法的临界距离dc=
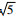
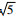
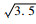
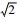
分别计算2种方法生成一个RVE所需时间的比值t′/t″,并对10次模拟数据取平均值,结果如表 2所示。
表 2 不同dc情况下的RVE建模时间比 Table 2 Ratios of RVE modeling time for various dc
| VCmax/% | t′/t″ | |
dc=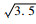 D D | dc=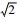 D D | |
| 5 | 0.84 | 0.86 |
| 8 | 0.81 | 0.82 |
| 11 | 0.66 | 0.72 |
| 14 | 0.56 | 0.74 |
| 17 | 0.48 | 0.52 |
| 20 | — | 0.63 |
| 23 | — | 0.37 |
表选项
由表 2可知,2种情况下FRSA方法生成RVE所需时间比原方法均有所减少,且同一个VCmax时,dc取值越大所需时间减少越明显,建模效率提高的程度越大。结合表 1结果可知,dc取值为
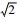
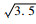
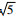
3.2.3 AR对建模效率的影响 取AR=4、6和8 3种情况分别进行RVE生成模拟,以验证FRSA方法在不同AR取值下的改进效果。RVE建模所需时间的比值的10次模拟平均值如表 3所示。
表 3 不同AR情况下的RVE建模时间比 Table 3 Ratios of RVE modeling time for various AR
| AR | t′/t″ | ||
dc=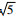 D D | dc=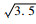 D D | dc=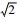 D D | |
| 4 | 0.74 | 0.87 | 0.85 |
| 6 | 0.82 | 0.92 | 0.94 |
| 8 | 0.88 | 0.93 | 0.94 |
表选项
结合表 1、表 2和表 3,AR=4、6和8 3种情况下结果可见,FRSA方法生成RVE的用时比BORSA方法均有所减少,验证了FRSA方法在不同AR取值下均具有先进性。并且,相同的dc取值条件下,AR取值越小, 建模时间减少越明显,建模效率提高的程度越大。AR取值越大, 建模效率改进效果降低,是因为在相同dc取值条件下,当AR取值增大时,临界距离dc与纤维外切球直径的比值减小,导致过滤程度降低,从而导致了方法改进效果的下降。
4 结论 本文通过在BORSA方法进行布尔运算前引入纤维形心距判断,过滤掉大量可能与已存在纤维相交的新纤维,提出了FRSA方法。在不同RVE参数和方法参数下对比了2种方法的纤维布尔运算次数和建模时间,证明了FRSA方法的先进性。主要结论如下:
1) 依据形心距可将纤维位置关系分为必然相交、必然不相交和可能相交3种情况。
2) 可通过纤维形心距判断,过滤掉所有必然相交和部分可能相交的纤维。
3) FRSA方法能够提高RVE的建模效率,且效率提高程度随纤维体积分数增大而增加,随纤维长径比增大而减少。
4) 增大临界形心距可以增加改进效果,但是更易出现纤维拥塞现象。
参考文献
| [1] | 郭云竹. 热塑性复合材料研究及其在航空领域中的应用[J]. 纤维复合材料, 2016, 33(3): 20-23. GUO Y Z. Research on thermoplastic composites and its application in aviation[J]. Fiber Composites, 2016, 33(3): 20-23. DOI:10.3969/j.issn.1003-6423.2016.03.005 (in Chinese) |
| [2] | 郭茹南.低密度纤维骨架增强泡沫碳的制备与结构性能演化[D].哈尔滨: 哈尔滨工业大学, 2016: 1-4. GUO R N.Preparation and structural properties evolution of low density fiber reinforced foamed carbon[D].Harbin: Harbin Institute of Technology, 2016: 1-4(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10213-1016913443.htm |
| [3] | 张兴福, 曹永敏, 崔洪涛, 等. 菱镁复合保温建筑墙板研究[J]. 21世纪建筑材料, 2010, 2(5): 20-24. ZHANG X F, CAO Y M, CUI H T, et al. Study on magnesium composite insulation wallboard[J]. 21st Century Building Materials, 2010, 2(5): 20-24. DOI:10.3969/j.issn.1003-1324.2010.05.007 (in Chinese) |
| [4] | 孔徐洁.不同长度玻璃纤维增强复合材料力学性能与界面性能的研究[D].上海: 东华大学, 2016: 1-3. KONG X J.Study on mechanical properties and interfacial properties of glass fiber reinforced composites with different lengths[D].Shanghai: Donghua University, 2016: 1-3(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10255-1016756346.htm |
| [5] | 孔莉莉, 成玲, 万培培, 等. 苎麻纤维复合材料医用夹板的开发及智能化[J]. 材料导报, 2018, 32(7): 1202-1208. KONG L L, CHENG L, WAN P P, et al. Development and intelligentization of ramie fiber composite material splints[J]. Materials Review, 2018, 32(7): 1202-1208. (in Chinese) |
| [6] | 姚树镇. 短切玻璃纤维毡在玻璃钢船艇上的应用[J]. 中外船舶科技, 2011(2): 37-38. YAO S Z. Application of chopped glass fiber mat on fiberglass boat[J]. Chinese and Foreign Shipbuilding Technology, 2011(2): 37-38. (in Chinese) |
| [7] | 郑晓霞, 郑锡涛, 缑林虎. 多尺度方法在复合材料力学分析中的研究进展[J]. 力学进展, 2010, 40(1): 41-56. ZHENG X X, ZHENG X T, GOU L H. Research progress of multi-scale methods in mechanical analysis of composite materials[J]. Advances in Mechanics, 2010, 40(1): 41-56. (in Chinese) |
| [8] | 刘振宇, 叶燎原, 潘文. 等效体积单元(RVE)在砌体有限元分析中的应用[J]. 工程力学, 2003, 20(2): 31-35. LIU Z Y, YE L Y, PAN W. Application of equivalent volume element (RVE) in masonry finite element analysis[J]. Engineering Mechanics, 2003, 20(2): 31-35. DOI:10.3969/j.issn.1000-4750.2003.02.007 (in Chinese) |
| [9] | 谢悦, 宿晓如, 冯春冬, 等. 颗粒增强橡胶复合材料有效力学性能预测分析[J]. 兵器装备工程学报, 2017, 38(7): 142-147. XIE Y, SU X R, FENG C D, et al. Predictive analysis of effective mechanical properties of particle reinforced rubber composites[J]. Journal of Ordnance Equipment Engineering, 2017, 38(7): 142-147. DOI:10.11809/scbgxb2017.07.030 (in Chinese) |
| [10] | 田文龙, 齐乐华, 周计明, 等. 基于随机顺序吸附法的Csf/Mg周期性体胞模型的建立及其应用[J]. 稀有金属材料与工程, 2013, 42(8): 1601-1605. TIAN W L, QI L H, ZHOU J M, et al. The establishment and application of Csf/Mg periodic cell model based on random sequential adsorption method[J]. Rare Metal Materials and Engineering, 2013, 42(8): 1601-1605. DOI:10.3969/j.issn.1002-185X.2013.08.013 (in Chinese) |
| [11] | 霍金星, 齐乐华, 周计明. ABAQUS二次开发在Csf/Mg复合材料微观几何建模中的应用[J]. 特种铸造及有色合金, 2011, 31(4): 322-324. HUO J X, QI L H, ZHOU J M. Application of secondary development of ABAQUS in micro geometry modeling of Csf/Mg composites[J]. Special Casting & Nonferrous Alloys, 2011, 31(4): 322-324. DOI:10.3870/tzzz.2011.04.009 (in Chinese) |
| [12] | KARI S, BERGER H, GABBERT U. Numerical evaluation of effective material properties of randomly distributed short cylindrical fibre composites[J]. Computational Materials Science, 2007, 39(1): 198-204. |
| [13] | TIAN W, QI L, ZHOU J, et al. Representative volume element for composites reinforced by spatially randomly distributed discontinuous fibers and its applications[J]. Composite Structures, 2015, 131(1): 366-373. |
| [14] | GHOSSEIN E, LéVESQUE M. Random generation of periodic hard ellipsoids based on molecular dynamics:A computationally-efficient algorithm[J]. Journal of Computational Physics, 2013, 253: 471-490. DOI:10.1016/j.jcp.2013.07.004 |
| [15] | SCHNEIDER M. The sequential addition and migration method to generate representative volume elements for the homogenization of short fiber reinforced plastics[J]. Computational Mechanics, 2017, 59(2): 247-263. |
| [16] | GUSEV A A. Representative volume element size for elastic composites:A numerical study[J]. Journal of the Mechanics & Physics of Solids, 1997, 45(9): 1449-1459. |
| [17] | FAESSEL M, DELISéE C, BOS F, et al. 3D modelling of random cellulosic fibrous networks based on X-ray tomography and image analysis[J]. Composites Science & Technology, 2005, 65(13): 1931-1940. |
| [18] | EBERLY D, TOOLS G. Intersection of cylinders[J]. Israel Journal of Mathematics, 2000, 113(1): 231-241. |
| [19] | LIU H, ZENG D, LI Y, et al. Development of RVE-embedded solid elements model for predicting effective elastic constants of discontinuous fiber reinforced composites[J]. Mechanics of Materials, 2016, 93: 109-123. DOI:10.1016/j.mechmat.2015.10.011 |
| [20] | WILLIAMS S R, PHILIPSE A P. Random packings of spheres and spherocylinders simulated by mechanical contraction[J]. Physical Review E, 2003, 67(5): 051301. DOI:10.1103/PhysRevE.67.051301 |
| [21] | 刘钊, 朱平, 朱超.长纤维复合材料随机结构生成及其弹性性能预测方法:CN 106815408 A[P].2016-12-23. LIU Z, ZHU P, ZHU C.Random structure generation and prediction of elastic properties of long fiber composites: CN 106815408 A[P].2016-12-23(in Chinese). |
