航空电子全双工交换式以太网(Avionics Full Duplex Switched Ethernet，AFDX)标准定义于ARINC664 Part7^[1]，是新一代民用航空总线标准。AFDX网络是基于商用以太网IEEE802.3标准进行改进使其成为适合航空电子系统数据传输的全双工确定性交换式以太网，已经成功应用于空客公司的A380飞机和波音公司波音787飞机^[2]。
近年来复杂网络(complex network)^[3]受到了来自科学与工程等各个领域的强烈关注，作为研究复杂性网络的全新视角和有力工具，由于其模型不仅兼顾样本个体属性，还更加注重从宏观结构上将样本局部与整体的关系紧密连接，这些优势促使复杂网络在网络生成研究问题中应用广泛。依据复杂网络视角对一般网络建模的研究，文献[4]从复杂网络的统计特性出发，提取真实的互联网所具备的统计特征，对互联网进行建模抽象。复杂网络的拓扑结构如何影响网络的动力学行为已有大量研究，例如，文献[5]对基于流量感知路由策略的复杂网络拓扑结构对流量传输的影响进行研究，考虑网络拓扑、信息生成速率和各个节点的信息处理能力，解决拓扑对复杂网络流量动态的影响问题。复杂网络视角与其他视角的不同之处在于它可以定量描述一个复杂网络的属性^[6]。然而定量描述网络的前提是必须要对其进行测量，其中度中心性^[7](degree centrality)作为复杂网络中研究的重要测度，是网络拓扑中与节点直接相连边的数目的累加和，体现了网络中个体与相邻个体的交互能力^[6]。度中心性的概念已广泛应用于社交网络关系的分析中，文献[8]利用测量度中心性的方法分析了社交网络中有影响力的人物关系以及交互次数的关系权重。文献[9]则从多层社交网络角度出发，提取多层社交网络的组成结构，针对不同程度的度中心性进行网络分析，得出节点在社交网络中的关键程度。在航电网络中，由于端系统之间信息交互差异巨大，采用度中心性理论可以有效分析信息交互频繁的端节点在网络中的关键地位，并以此为依据对航电网络进行拓扑设计。
现有航空电子网络拓扑的设计大多依靠人工，技术人员一般依据终端节点之间的通信关系以及交换机的特有连接构型对航电网络拓扑进行设计。然而，当面对航电网络节点规模日益庞大，信息交互量级不断增加，任务性能保障诉求逐渐严格的情况下，依赖于设计人员经验和技术的网络设计就显得捉襟见肘。因此，本文用节点度的大小表征节点间交互关系，将节点间数据交互规模加以考虑，提出基于度中心性理论依据节点间通信数据帧长的航空电子网络拓扑自动生成算法，构建2种不同的组网规模，利用确定性网络演算方法和仿真方法对生成网络的实时性能进行评估。
1 AFDX网络拓扑生成 1.1 AFDX网络模型 对AFDX网络研究一般采用离散事件的建模方法。离散事件建模的系统由模型实体以及实体之间的关系构成^[10]。AFDX网络拓扑由3部分组成：端系统、交换机和虚拟通信链路。AFDX网络消息的通信过程由驻留于端系统的分区产生，并交由端系统上的虚拟链路来承载，虚拟链路从源端系统发出，经过交换机网络的静态路由转发，最后到达目的端系统分区中。AFDX网络的拓扑结构具有一定灵活性，适应大中型飞机的航空电子综合化互联。
AFDX网络模型主要由端系统和交换机组成，采用双冗余拓展型星型拓扑结构，异步传输模式，终端节点之间通过虚拟链路进行数据帧的交换。
1) 端系统模型
AFDX网络的端系统中存在UDP/IP协议处理栈负责与应用分区的接口。端系统模型抽象如图 1^[10]所示。依据抽象出的结构模型，可将端系统细分为发送端系统和接收端系统。

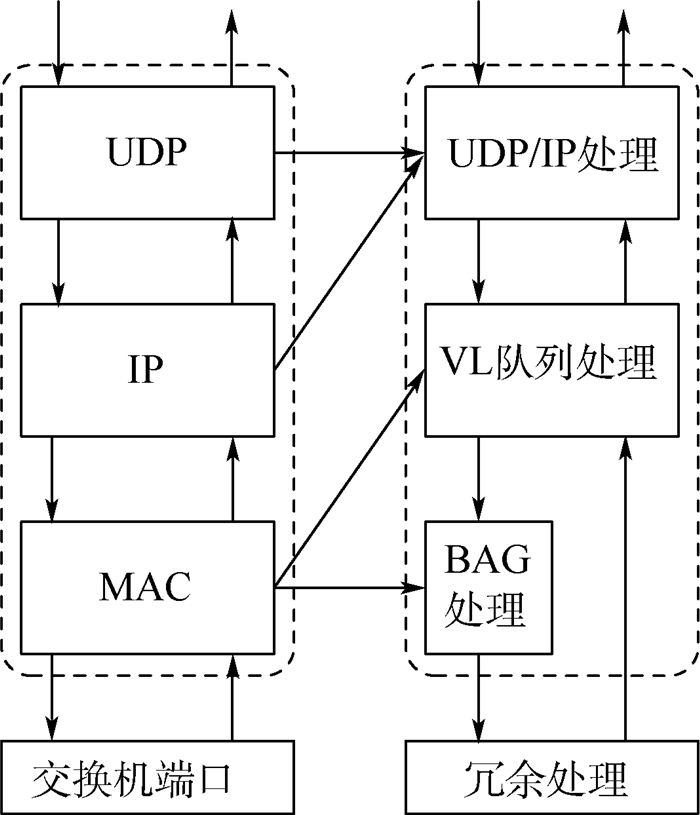图 1 端系统模型抽象图[10] Fig. 1 Schematic of end system model[10]

图选项

2) 交换机模型
交换机是具备网络收发功能的模型，内部通过总线和交换控制模块完成数据帧的交换转发功能，且交换机各端口相互独立。交换机端口具有接收和发送2种功能，在完成对数据的接收后查询配置表，即可将数据转发到目的端口。一组交换机端口从接收到发送的功能模型如图 2^[10]所示，交换机模型则由多个端口模型共同构成。

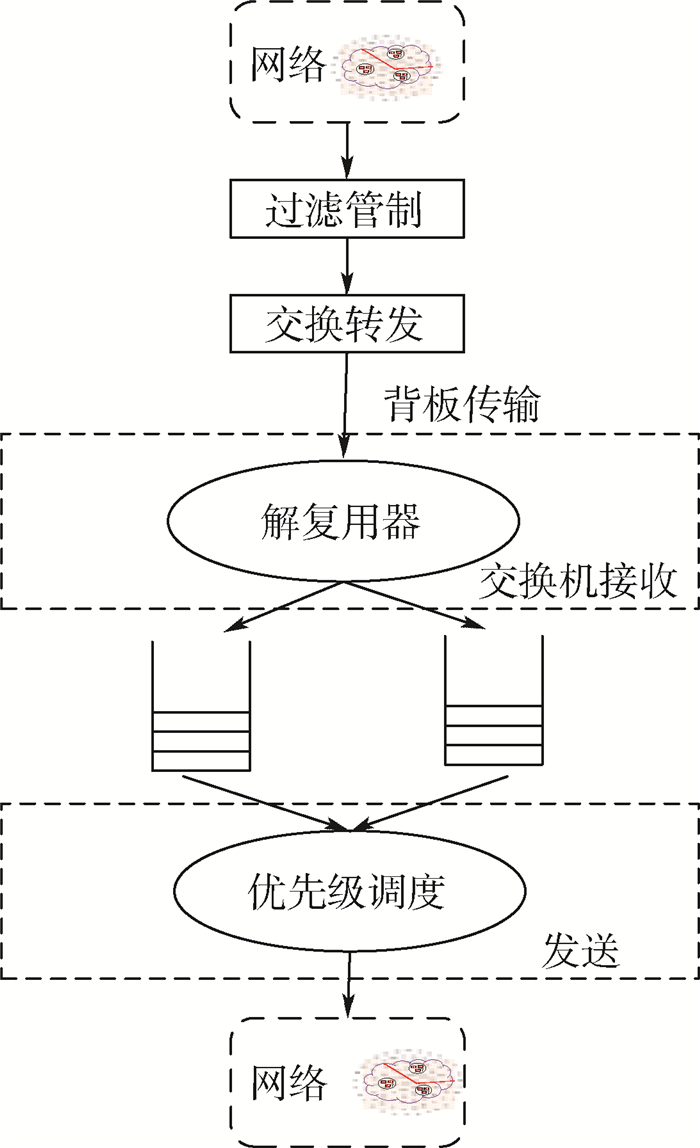图 2 一组交换机端口模型图[10] Fig. 2 One set of switch port models[10]

图选项

3) 通信链路
AFDX网络中的通信物理链路，指的是2个节点之间的连接。例如2个交换节点或1个交换节点和1个终端节点之间，它可以为消息传输提供给定的数率。此外，在一个物理连接中可能有多个逻辑链接。逻辑链接又叫虚拟链路(VirtualLink，VL)，是消息源和其目的端之间的逻辑链接，可以看作是用于消息交换的全局逻辑通道。通常，虚拟链路可以用带宽分配间隔和最大数据包长度来表示。
1.2 AFDX网络拓扑生成算法 AFDX网络中不同终端节点所承载的通信任务紧要程度不同，根据所承载任务的紧要程度，可以将终端节点分为2种类型，即核心处理节点与外围接入节点。核心处理节点承载了对实时性等性能要求较高的任务，同时也承载了部分对实时性要求较低的任务；外围接入节点所承载的任务对实时性等性能要求相对较低。因此，在AFDX网络拓扑生成算法中可将终端节点分成两类考虑。
网络拓扑生成算法将源终端节点与目的终端节点之间的数据交互规模加以考虑，AFDX网络节点之间信息交互规模较大，任务通信较频繁，则需要尽量满足通信链路所经过的交换机跳数较少，使数据在传输过程中的延迟较小，保证数据传输的实时性。在AFDX网络中，消息具体的传输过程包含固定时延和有界时延。有界时延包括多路复用排队时延和链路传输时延，二者都与数据帧长紧密相关。考虑到AFDX网络拓扑中端节点之间边的实际意义与数据帧长的关系，将两节点之间存在所有VL的数据帧长度求和作为节点的度中心性抽象指标。
对于AFDX网络，两节点间通信帧长总和越大，表征节点度越大，就意味着这个节点的度中心性越高，说明该节点在AFDX网络中的数据交互规模庞大，任务通信繁杂。由于度中心性高的核心处理端节点占网络所有信息交互规模比重较大，因此需要将两节点之间的通信帧长总和以及交换机对于信息的处理转发能力加以考虑，按照核心处理节点占总终端节点的比例将端节点进行集合划分，尽可能减少虚拟链路经过交换机的跳数，降低数据传输的排队转发延迟以及链路传输延迟。在进行交换机连接拓扑的生成过程中，由于交换机需要对其上连接的所有端节点的数据进行存储转发操作，因此将划分集合后的端节点作为整体考虑，进行交换机连接判断。算法具体流程如下：
1) AFDX网络配置设定
输入AFDX网络的交换机配置、各个终端节点的通信配置以及虚拟链路的配置。
在配置过程中，将AFDX网络中用到的交换机个数，交换机端口数以及交换机技术延迟等参数进行说明。将终端节点之间交互信息的属性进行说明，包括：源终端节点、目的终端节点、数据帧长，帧间间隔以及虚拟链路路由规则。
对于本算法虚拟链路的配置，其路径皆要遵循最短路径原则。
2) 核心处理节点集合划分
集合的数量等于交换机的数量，集合序号与交换机序号一一对应。选取某一核心处理节点作为种子节点，计算该节点与其他所有核心节点间所有VL的数据帧长和，并作为节点度，按照数据帧长和的大小对其他核心节点进行降序排列。在集合划分过程中，按照降序依次选择其他核心处理节点与种子节点划分到同一集合中，若某核心节点已经成为其他集合中的元素，则跳过该节点的划分。为了对交换机端口做出一定预留，根据核心节点占所有节点数量的比例，在每个交换机上挂载核心处理节点的端口数占该交换机所有端口数的比例不超过该比例值。考虑交换机负载均衡的原因，为了避免将通信数据量规模较大的端系统分配到同一集合，挂载到同一交换机上，“集合划分”会分两轮进行。当集合第一轮分配结束后，还有剩余核心处理节点未划分，针对剩余每个核心节点，分别比较该节点与各个集合中已有的所有核心节点的数据帧长之和，选择和最大的集合，将该核心节点加入其中，直至所有核心节点划分结束。核心处理节点集合划分流程图如图 3所示。

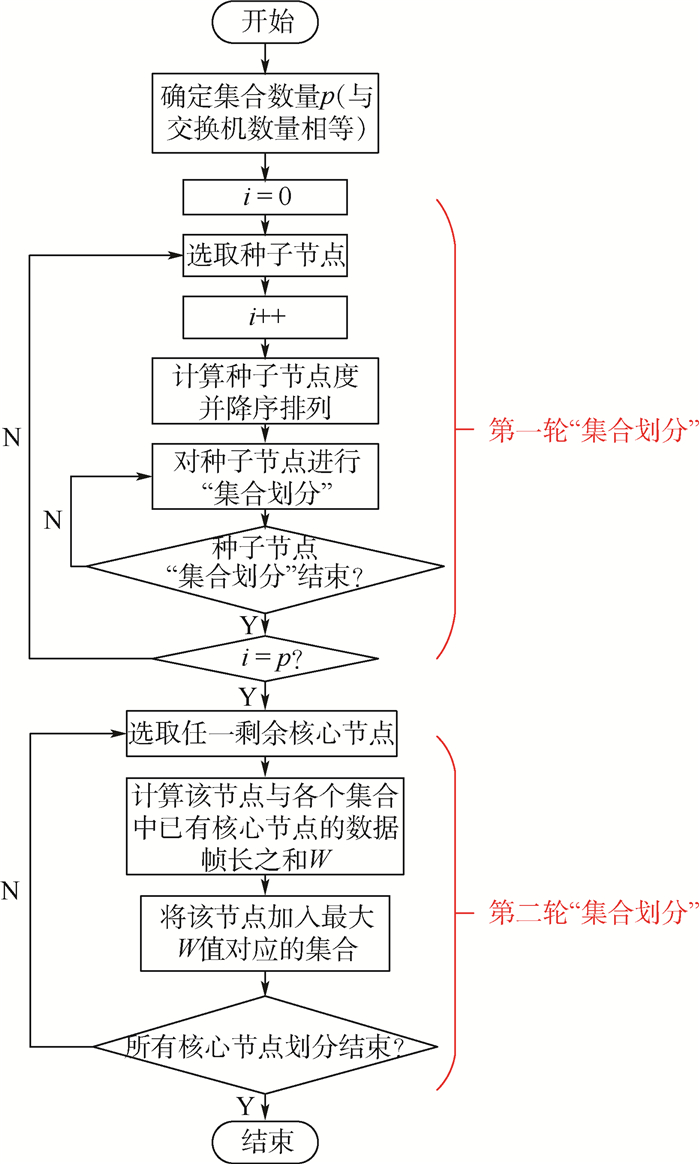图 3 核心处理节点集合划分流程图 Fig. 3 Core processing node set division flowchart

图选项

3) 外围接入节点集合划分
对任意一个外围节点计算与各个集合中已有的每一个核心节点的所有VL通信数据帧长的总和，选择和最大的集合，将外围节点加入到该集合中，直至所有外围节点集合划分完毕。
4) 终端节点与交换机连接
将每个集合中的节点分别挂载到交换机上。
5) 交换机拓扑构建
分别将两集合内不同节点间的所有VL通信数据帧长求和，根据上述各集合间通信总帧长求集合间通信总帧长的平均值，将两集合通信总帧长大于平均值所对应的交换机进行连接。
算法简化示意图如图 4所示。

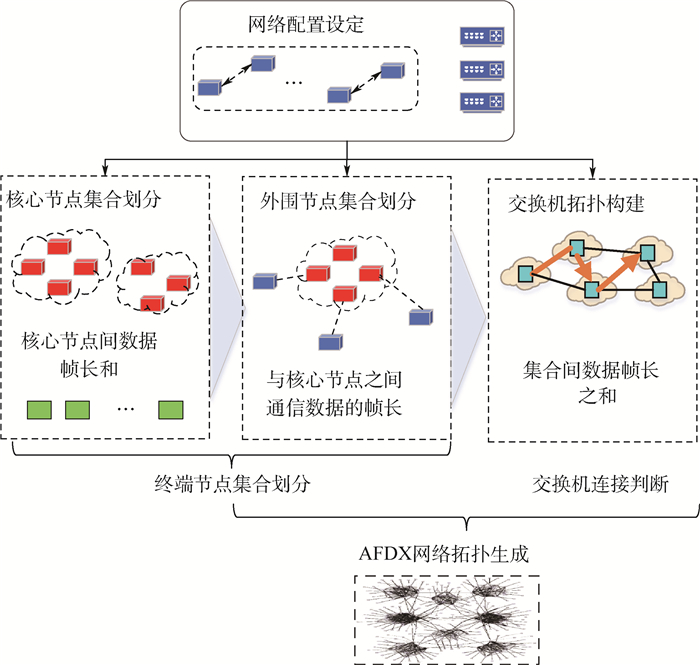图 4 基于度中心性的AFDX网络拓扑生成算法 Fig. 4 AFDX network topology generation algorithm based on degree centrality

图选项

2 算法效能评估 2.1 算法评价 对于一个规划完成的AFDX网络，所有的终端节点的数据业务都是提前规定好的，而且网络拓扑一旦设计完成，交换机的路由转发也就固定不变。因此网络拓扑生成算法的实时性能可以根据数据流的端到端延迟进行评价。
参照空客公司提出的典型AFDX网络拓扑中交换机连接结构^[11]，根据端系统之间通信联系紧密程度、信息交互数据量大小以及减少交换机发生拥堵可能性的均衡原则将端系统挂载到各个交换机上，由此构建由8个交换机(S1~S8)和24个终端节点(E1~E24)组成的互联网络如图 5所示。

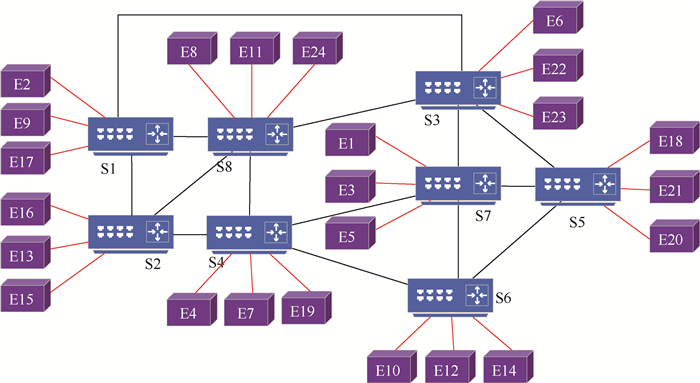图 5 人为规划网络拓扑 Fig. 5 Artificially designed network topology

图选项

假定节点1~16承载的大部分任务实时性能较强，为核心处理节点；节点17~24承载的任务关键性较弱，为外围接入节点。
终端节点之间通信配置信息如表 1所示。利用基于度中心性AFDX网络拓扑生成算法，生成的网络拓扑如图 6所示。
表 1 网络参数配置信息 Table 1 Network parameter configuration information

VL	源节点	目的节点	每条VL最大通信帧长/Byte	BAG/ms
1~50	1	3	540	128
51~100	1	5	334	32
101~110	1	23	200	32
111~160	2	9	1510	64
161~210	2	17	55	64
211~260	2	24	100	32
261~280	2	4	144	32
281~330	4	7	670	8
331~380	4	19	126	4
381~430	5	20	203	4
431~480	6	16	132	16
481~530	6	23	411	16
531~560	7	6	90	16
561~590	7	19	46	2
591~620	8	11	76	32
621~680	8	17	23	64
681~730	10	2	258	64
731~780	10	8	560	32
781~810	11	9	640	8
811~840	11	8	710	32
841~870	13	16	861	16
871~880	14	12	96	16
881~900	15	13	147	64
901~1000	18	21	100	128
1001~1100	22	6	460	128
1101~1200	24	11	200	32
1201~1300	16	21	340	32
1301~1400	17	14	260	32

表选项

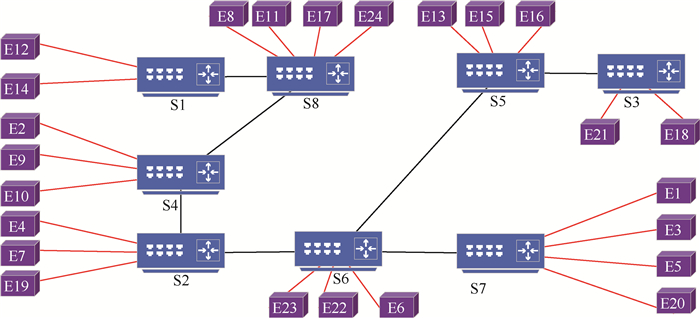图 6 算法生成网络拓扑 Fig. 6 Algorithm generated network topology

图选项

分别采用解析方法(网络演算)和仿真方法实现网络性能的分析与评价，依据于具体的网络和流量配置参数，探寻流量干扰影响，实现信息交互的端到端延迟评估。
2.2 解析方法 解析方法一般指利用数学建模方法计算消息端到端延迟上界，最常见的即为网络演算方法。确定性网络演算^[12-13]是一种基于最小加代数(min-plus)理论的网络性能分析方法，通过到达曲线和服务曲线的约束来计算消息最坏情况下的延迟上限。网络演算中常用的核心公式包括到达曲线^[14]α(t)、服务曲线^[15]β(t)以及延迟上界h(α, β)，延迟上界为到达曲线α(t)和服务曲线β(t)之间的最大水平距离，由图 7中标记有h(α, β)的水平箭头给出。图中：α_σ，ρ(t)为数据流的到达曲线，表示数据流允许最大发度为σ，且持续流量为ρ，β_{C, T}(t)为输出节点的服务曲线，表示具有固有技术时延为T, 输出速率为C。

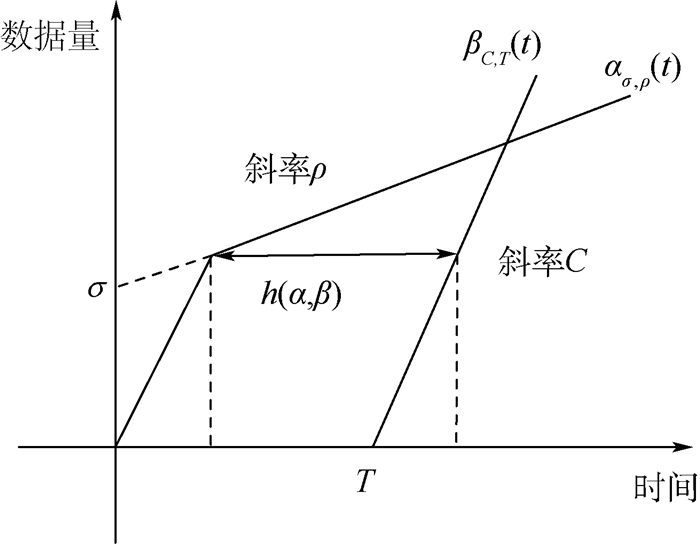图 7 确定性网络演算分析模型 Fig. 7 Deterministic network calculus analysis model

图选项

根据交叉通信且通信链路源和目的端涵盖大多数端节点的原则，由表 1提取核心节点之间、核心节点与外围接入节点之间以及外围接入节点之间部分VL配置，如表 2所示，利用确定性网络演算方法进行数据流的端到端延迟计算来验证网络拓扑生成算法的实时性能，路径规划遵循最短路径原则，网络链路传输为100Mbit/s，交换机技术延迟为16μs^[16]。
表 2 网络演算配置信息 Table 2 Network calculus configuration information

VL	源节点	目的节点	每条VL最大通信帧长/Byte	BAG/ms
1~5	1	3	540	128
111~116	2	9	1510	64
161~165	2	17	55	64
381~385	5	20	203	4
431~435	6	16	132	16
561~565	7	19	46	2
781~785	11	9	640	8
871~875	14	12	96	16
1101~1105	24	11	200	32
1301~1305	17	14	260	128

表选项






在相同配置下人为规划网络拓扑与基于度中心性的AFDX网络拓扑生成算法生成的网络拓扑的端到端延迟对比，如图 8所示。从图 8中可以看出在50条VL组网规模下基于度中心性的拓扑生成算法生成的网络拓扑中75%的VL实时性能优于人为规划网络拓扑，且端到端延迟平均减小9.37%。

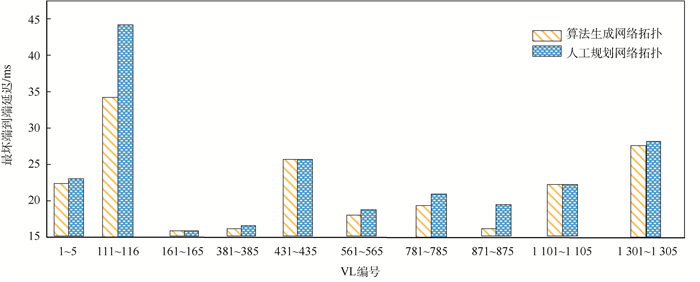图 8 网络演算对比人为规划网络拓扑和算法生成拓扑最坏端到端延迟 Fig. 8 Network calculus comparison of the worst end-to-end delay between artificially designed network topology and algorithm generated network topology

图选项

2.3 仿真方法 利用OMNet++平台构建网络仿真模型，模拟AFDX网络^[17]，配置参数如表 1所示，共1400条VL。网络链路传输为100Mbit/s，交换机技术延迟为16μs^[16]。
结果分析：利用仿真实验对比人为规划网络拓扑与基于度中心性的拓扑生成算法生成的网络拓扑的平均端到端延迟，如图 9所示。在图 9中，横坐标代表虚拟链路编号，纵坐标表示各条虚拟链路的平均端到端延迟，红色实线表示人为规划拓扑中不同虚拟链路的平均端到端延迟，蓝色虚线则表示算法生成拓扑的不同虚拟链路的平均端到端延迟。从图 9中可以看出算法生成的网络拓扑中94.3%的VL实时性能优于人为规划网络拓扑，且平均端到端延迟平均减小50.2%。然而虚拟链路编号681~730以及781~810处，算法生成拓扑的平均端到端延迟要略高于人为规划拓扑的端到端延迟。针对本案例，是由于承载上述虚拟链路必经的交换机上连接的皆为核心处理节点，且上述核心处理节点处理的数据规模相对于其他核心节点较大，造成当前时刻交换机瞬时拥塞，引起转发排队延迟时间较长，增加了排队延迟，因此导致这一小部分数据流端到端延迟没有明显改善。

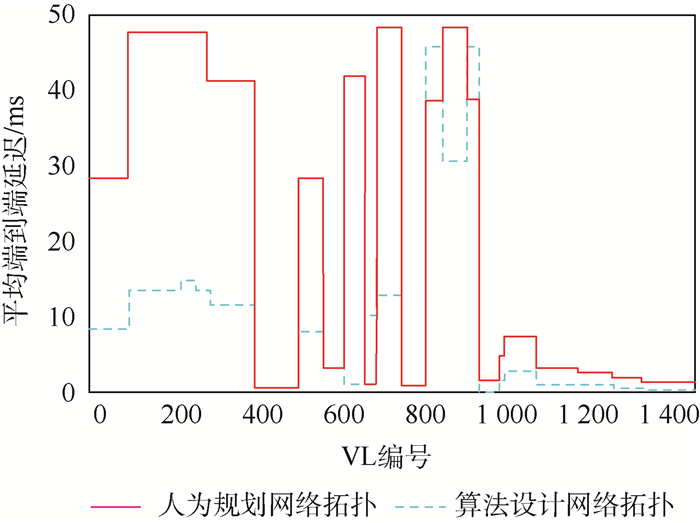图 9 人为规划拓扑和算法生成拓扑平均端到端延迟仿真对比 Fig. 9 Simulation comparison of average end-to-end delay between artificially designed network topology and algorithm generated topology

图选项

3 结论 1) 本文基于复杂网络中的度中心性理论，以AFDX网络节点之间所有VL通信数据帧长之和为度，根据两节点间通信帧长总和，提出了适应于AFDX网络的拓扑结构生成算法。
2) 应用网络演算方法对比分析了人为规划的网络拓扑与自动生成算法生成的网络拓扑的实时性能。从计算结果可以看出自动生成算法生成的拓扑中75%的虚拟链路的实时性优于人为规划的拓扑。
3) 基于OMNet++平台，设计人为规划拓扑与算法生成拓扑的行为仿真模型，对人为规划拓扑和算法生成拓扑实时性进行了仿真对比分析。在1400条数据流量的配置下，其中有1320条流量在算法生成拓扑中实时性能较好，较人为规划拓扑实时性提高了50.2%；算法改善了大部分虚拟链路的实时性能，然而由于数据流突发等原因，增加了小部分虚拟链路的排队延迟，导致80条流量端到端延迟没有很大改善。
本算法以流量均衡分布和就近接入为目标，可以在绝大多数情况下为流量的接入交换和骨干交换提供一个平稳的流量交互网络拓扑，保证了大多数流量传输的实时性。从数据分析中也可以看出算法在很大程度上提高了AFDX网络的实时性能。

参考文献

[1]	WANG H C, NIU W S. Design and analysis of AFDX network based high-speed avionics system of civil aircraft[J]. Advanced Materials Research, 2012, 462: 445-451. DOI:10.4028/www.scientific.net/AMR.462.445
[2]	SUTHAPUTCHAKUN C, SUN Z, KAVADIAS C, et al. Performance analysis of AFDX switch for space onboard data networks[J]. IEEE Transactions on Aerospace & Electronic Systems, 2016, 52(4): 1714-1727.
[3]	SHENG L, GUANG X, CHEN F, et al.A review on complex network dynamics in evolutionary algorithm[C]//IEEE Trustcom/BigDataSE/ISPA.Piscataway, NJ: IEEE Press, 2017: 2221-2226. http://www.researchgate.net/publication/313543668_A_Review_on_Complex_Network_Dynamics_in_Evolutionary_Algorithm
[4]	BATOOL K, NIAZI M A. Modeling the internet of things:A hybrid modeling approach using complex networks and agent-based models[J]. Complex Adaptive Systems Modeling, 2017, 5(1): 1-4. DOI:10.1186/s40294-016-0040-9
[5]	DOU B L, ZHANG S Y.Model for congestion dynamics on complex networks with traffic-awareness routing strategy[C]//20108th World Congress on Intelligent Control and Automation.Piscataway, NJ: IEEE Press, 2010: 5325-5330. http://www.researchgate.net/publication/238517086_model_for_congestion_dynamics_on_complex_networks_with_traffic-awareness_routing_strategy?ev=auth_pub
[6]	杨海涛. 复杂信息网络性能设计[M]. 北京: 中国宇航出版社, 2014: 39-50. YANG H T. Complex information network performance design[M]. Beijing: China Aerospace Publishing House, 2014: 39-50. (in Chinese)
[7]	ANDRES V, LLOPIS L J.Topology control for wireless mesh networks based on centrality metrics[C]//Proceedings of the 10th ACM Symposium on Performance Evaluation of Wireless Ad Hoc, Sensor, & Ubiquitous Networks, 2013: 25-32.
[8]	RACHMAN Z A, MAHARANI W.The analysis and implementation of degree centrality in weighted graph in social network analysis[C]//2013 International Conference of Information and Communication Technology (ICoICT), 2013: 72-76.
[9]	PIOTR B, SKIBICKI K, KAZIENKO P, et al.A degree centrality in multi-layered social network[C]//International Conference on Computational Aspects of Social Networks.Piscataway, NJ: IEEE Press, 2011: 19-21. http://www.oalib.com/paper/4035130
[10]	黄臻, 张勇涛, 熊华钢. 基于离散事件方法的AFDX建模与仿真[J]. 北京航空航天大学学报, 2011, 37(10): 1326-1333. HUANG Z, ZHANG Y T, XIONG H G. AFDX modeling and simulation based on discrete event method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(10): 1326-1333. (in Chinese)
[11]	赵琳, 何锋, 熊华钢. 航空电子AFDX与AVB传输实时性抗干扰对比[J]. 北京航空航天大学学报, 2017, 43(12): 2359-2369. ZHAO L, HE F, XIONG H G. Comparison of real-time anti-jamming transmission for avionics AFDX and AVB[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(12): 2359-2369. (in Chinese)
[12]	ZHANG X, WANG Y.Research of AFDX network delay based on modified network calculus[C]//IEEE International Conference on Network Infrastructure & Digital Content.Piscataway, NJ: IEEE Press, 2012: 178-181. http://www.researchgate.net/publication/261236734_Research_of_AFDX_network_delay_based_on_modified_network_calculus
[13]	SONI A, LI X, SCHARBARG J L, et al.Work in progress paper: Pessimism analysis of network calculus approach on AFDX networks[C]//International Symposium on Industrial Embedded Systems (SIES).Piscataway, NJ: IEEE Press, 2017: 1-4.
[14]	MOY M, ALTISEN K.Arrival curves for real-time calculus: The causality problem and its solutions[C]//International Conference on Tools & Algorithms for the Construction & Analysis of Systems, 2010: 358-372. http://www.springerlink.com/content/r3616574876751g1
[15]	CIUCU F, BURCHARD A. A network service curve approach for the stochastic analysis of networks[J]. ACM Sigmetrics Performance Evaluation Review, 2005, 33(1): 279-290. DOI:10.1145/1071690.1064251
[16]	BAUER H, SCHARBARG J L, FRABOUL C. Improving the worst-case delay analysis of an AFDX network using an optimized trajectory approach[J]. IEEE Transactions on Industrial Informatics, 2010, 6(4): 521-533. DOI:10.1109/TII.2010.2055877
[17]	REJEB N, SALEM A K, SAOUD S B.AFDX simulation based on TTEthernet model under OMNeT++[C]//2017 International Conference on Advanced Systems and Electric Technologies(IC_ASET).Piscataway, NJ: IEEE Press, 2017: 423-429.