近年来，中国航空运输业实现蓬勃发展。根据中国民用航空局的统计数据^[1]，“十二五”期间，中国航空运输总周转量增长58.2%，旅客运输量增长62.7%，货邮运输量增长11.8%。2017年，中国航空运输总周转量达到1 083.1亿吨公里，旅客运输量5.52亿人次，货邮运输量705.8万吨。《中国民用航空发展第十三个五年规划》^[2]提出，截止到2020年，中国航空运输总周转量将达到1 420亿吨公里，相较于“十二五”末的2015年，年均增长10.8%；旅客运输量将达到7.2亿人次，年均增长10.4%；货邮运输量将达到850万吨，年均增长6.2%。急剧增长的空中交通流量使得空中交通网络日趋拥挤，尤其是在恶劣天气等不确定条件下，航班延误现象十分严重。据统计，2017年，中国航空公司的平均航班正常率为71.67%，在全部航班不正常的原因中，天气原因所占比例高达51.28%^[3]。
时隙分配(Time Slot Allocation, TSA)是进行空中交通流量管理、实现空中交通容流匹配、解决航班延误的关键技术。时隙分配过程包括：航空公司提出时隙请求，流量管理部门按照一定的方式或依靠某种机制，将时隙分配给航班或航空公司，形成航班时隙计划，短期根据环境和条件变化进行时隙二次分配，调整航班计划，获得最终航班运行时刻。
时隙分配作为空中交通管理的重要手段，一直是国内外空管领域研究的热点。时隙分配方法方面，比较经典的有先到先服务(First Come First Serve, FCFS)^[4]、按时刻分配(Ration By Schedule, RBS)^[5]、压缩分配(compression)^[5]、时隙信用交换(Slot Credit Substitutions, SCS)^[6]、累积延误分配(Accrue Delay Based, ADB)^[7]等。Madas和Zografos^[8]对各时隙分配方法进行了对比分析，指出了各方法的适用性。时隙分配模型方面，1987年，Odoni^[9]首次提出通过航班时隙调整，将空中拥挤转化为地面等待问题(Groud Holding Problem, GHP)，开启了时隙分配问题研究的先河。Terrab等^[10]提出了网络流模型，并运用最小费用流理论来求解模型。Gilbo^[11]将研究对象从单航班扩展到全部进离场航班，建立了多元受限下的时隙分配模型。Oussedik、Delahaye^[12]和Pulugurtha、Nambisan^[13]将智能算法引入时隙分配模型求解，提升了模型的求解速度，促进了模型在实际中的推广和应用。Madas和Zografos^[14]对各时隙分配模型进行了对比分析。国内对时隙分配模型研究起步较晚，在时隙分配模型、时隙分配方法等方面比较有代表性的研究包括文献[15-20]。
容量等易受恶劣天气等不确定条件的影响，呈现不确定性特点。针对此现象，相关模型也得到了研究。1987年，Andreatta和Romanin-Jacur^[21]第一次提出了单时间区间静态随机型模型，并提出了动态规划方法进行模型求解。随后，随机型时隙分配模型及求解方法也得到了国内外****的广泛研究^{[4, 10, 21-25]}。随机型模型要求在大量历史数据基础上获得机场容量的概率分布，然而并非所有情况下均能够获取足量数据，此时需要有新的规划方法，解决不确定容量下的时隙分配问题。
从对时隙分配过程的描述可以看出，时隙分配要经历先后2次分配过程。第1次时隙分配输出的航班时隙计划是开展第2次时隙分配的输入。现有模型的问题在于：将2次时隙分配独立研究，第1次时隙分配采用名义容量约束，即给定时间段内能够服务的最大航空器数量；第2次时隙分配采用实际容量约束，在不确定条件影响下，容量名义值与实际值差距较大，造成2次分配结果差距过大，导致延误大面积产生，分配结果缺乏灵活性。为此，Corolli等^[26]首次将2次时隙分配纳入统一模型，针对不确定容量下的时隙分配问题，对“请求时隙-计划时隙差”和“计划时隙-运行时隙差”进行权衡，获得最优的时隙分配结果，但研究仅限于单机场模型，以航班数作为决策变量，限制了模型的实用性。岳仁田等^[27]提出了带补偿的两阶段随机规划航班时隙分配模型，但同样仅限于单机场模型。
本文以不确定容量下的时隙分配问题为研究对象，针对时隙分配问题的现实需求和已有模型的不足，基于不确定理论^[28-29]，以航班而非航班数为决策变量，提出了不确定容量下时隙分配两阶段规划模型，从单机场时隙分配模型扩展到多机场时隙分配模型。为了提升求解效率，本文基于人工蜂群(Artificial Bee Colony，ABC)算法设计了一种渐进二元启发式方法，并验证了模型和方法的有效性，分析了模型参数设置。
1 问题描述与建模 1.1 问题定义 时隙分配过程可以分为2个阶段，如图 1所示。第1个阶段，流量管理部门根据航空公司的时隙请求，进行初次分配，得到各航空公司的航班时隙计划；第2个阶段，在实际运行中，流量管理部门(或航空公司)根据短期(一般指24 h以内)的实际情况(如天气变化、突发事件等)对航班时隙计划进行实时调控，完成时隙的再次分配，获得最终的航班运行时隙表。

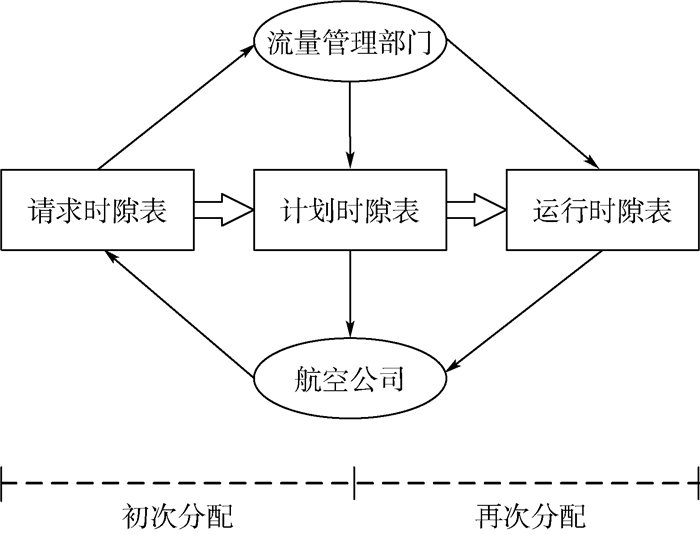图 1 时隙分配的2个阶段 Fig. 1 Two stages of time slot allocation

图选项

根据时隙分配的两阶段过程，将机场容量作为唯一受限元，不涉及扇区、航路点容量，构建不确定容量条件下单机场时隙分配两阶段规划模型和多机场时隙分配两阶段规划模型。建模的基本思路为：第1个阶段，在已知航班时隙请求的条件下，将第2个阶段才能获得的容量实现值设置为不确定变量，取代传统模型中的名义容量，以最小化“请求时隙-计划时隙差”与“计划时隙-运行时隙差(即延误)”的加权和为目标函数，以不确定容量等条件为约束，构建第1阶段模型，求解航班时隙计划；第2个阶段，以最小化“计划时隙-运行时隙差”为目标，以容量实现值条件为约束，求解航班运行时隙。
为构建模型做以下几点基本假设：①航班实际运行时隙不早于计划时隙；②航班的飞行时间是固定的；③初次时隙分配时，机场容量未知，且难以获取足够样本以获取其概率分布。
1.2 单机场模型 单机场时隙分配问题要求保证在该机场的每个时隙内，进场航班和离场航班在容量等约束范围内，否则要对一些航班的进离场时隙进行调整以适应容量约束要求。
定义模型符号如下：T为离散化时隙集，其中时隙t∈{0, 1，…, T－1}；F为航班集，航班f∈F；F_A为进场航班集，进场航班f_A∈F_A；F_D为离场航班集，离场航班f_D∈F_D；P为联程航班集，联程航班对(f, f′)∈P；l_ff′为联程航班最小周转时间；W为权重向量；t_f^a为航班f的进场请求时隙；t_f^d为航班f的离场请求时隙；分别为第1个阶段机场在时隙t的进场容量、离场容量、总容量，为不确定变量；α^t(ξ)、β^t(ξ)、γ^t(ξ)分别为第2个阶段机场在时隙t的进场容量、离场容量、总容量实现值。
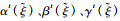
构建单机场时隙分配第1阶段模型如下：第1阶段决策变量定义为

第1阶段目标函数定义为

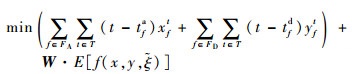(1)

第1阶段约束函数定义为

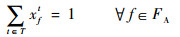(2)

(3)

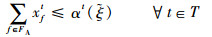(4)

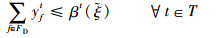(5)

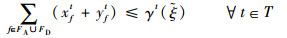(6)

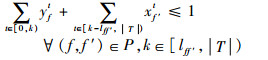(7)

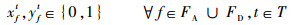(8)

式(1)定义了第1阶段的目标函数，即最小化“请求时隙-计划时隙差”与“计划时隙-运行时隙差(即延误)”的加权和，前半部表示航班请求时隙与航班计划时隙的差，后半部表示航班延误(航班计划时隙与航班运行时隙的差)的期望值，为定义在不确定空间上的不确定变量，为补偿函数。式(2)~式(8)定义了第1阶段模型的约束函数：式(2)和式(3)表示航班f的进场和离场能且仅能分配到1个时隙，式(4)~式(6)保证了在任意时隙中机场进场容量、离场容量和总容量限制总能满足，式(7)保证了联程航班周转时间的充足性，式(8)表示决策变量为0-1整数变量。
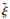
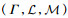
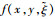
单机场时隙分配第2阶段模型如下：
第2阶段决策变量定义为

给定第1阶段决策变量(x_f^t, y_f^t)和不确定容量的实现值α^t(ξ)、β^t(ξ)、γ^t(ξ)，一定数量的航班不得不采取延误措施以平衡流量和容量。
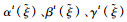
第2阶段目标函数定义为

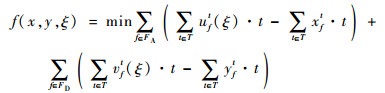(9)

第2阶段约束函数定义为

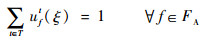(10)

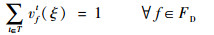(11)

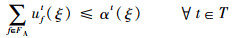(12)

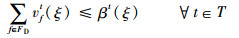(13)

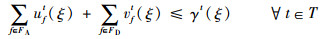(14)

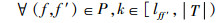(15)

(16)

式(9)定义了第2阶段的目标函数，即最小化“计划时隙-运行时隙差”，也就是最小化航班的总延误时间。式(10)~式(16)定义了第2阶段模型的约束函数：式(10)和式(11)表示航班f的进场和离场能且仅能分配到1个时隙，式(12)~式(14)保证了在任意时隙中机场进场容量、离场容量和总容量限制总能满足，式(15)保证了联程航班周转时间的充足性，式(16)表示决策变量为0-1整数变量。
从单机场两阶段规划模型可以看出，第1阶段模型和第2阶段模型的目标函数不同，第1阶段模型在不确定容量条件下，最小化“请求时隙-计划时隙差”与“计划时隙-运行时隙差(即延误成本)”加权和，而第2阶段模型是在容量确定条件下，最小化“计划时隙-运行时隙差(即延误成本)”。第1阶段容量约束与第2阶段容量约束不同，第1阶段模型中容量为不确定变量，第2阶段模型中容量为确定值，其他约束函数相同。
1.3 多机场模型 单机场模型实质上是假设各机场间的时隙分配相互独立、互不影响。但实际上，在不更改航路和飞行速度的情况下，航班在起飞机场离场时隙的调整，肯定会导致航班在降落机场进场时隙的变化，加之机场容量的限制，时隙调整可能产生连锁反应，导致整个机场网络时隙的变化。此外，由于联程航班的存在，前序航班的时隙调整就会影响后续航班，造成时隙调整在机场网络上的传播。因此，有必要研究不确定容量下多机场时隙分配两阶段规划模型。
考虑相互连通的机场网络，构建不确定容量下多机场时隙分配两阶段规划模型。
定义模型符号如下：I为机场集，机场i∈I；F_Aⁱ为机场i的进场航班集，进场航班f∈F_Aⁱ；F_Dⁱ为机场i的离场航班集，离场航班f∈F_Dⁱ；etf_f为航班f的飞行时间；分别为第1阶段机场i在时隙t的进场容量、离场容量、总容量，为不确定变量；α_i^t(ξ)、β_i^t(ξ)、γ_i^t(ξ)分别为第2阶段机场i在时隙t的进场容量、离场容量、总容量实现值。
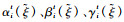
构建多机场时隙分配第1阶段模型如下：
第1阶段决策变量定义为

第1阶段目标函数定义为

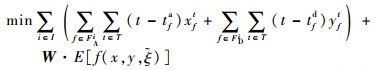(17)

第1阶段约束函数定义为

(18)

(19)

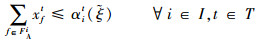(20)

(21)

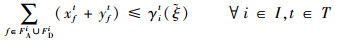(22)

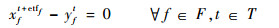(23)

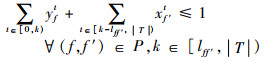(24)

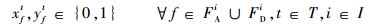(25)

式(17)定义了第1阶段的目标函数，即最小化“请求时隙-计划时隙差”与“计划时隙-运行时隙差(即延误)”的加权和，前半部表示航班请求时隙与航班计划时隙的差，后半部表示航班延误(航班计划时隙与航班运行时隙的差)的期望值。式(18)~式(25)定义了第1阶段模型的约束函数：式(18)~式(19)表示航班f的进场和离场能且仅能分配到一个时隙，式(20)~式(22)保证了在任意时隙中机场进场容量、离场容量和总容量限制总能满足，式(23)表示所有航班飞行时间都是固定的，式(24)保证了联程航班周转时间的充足性，式(25)表示决策变量为0-1整数变量。
多机场时隙分配第2阶段模型如下：
第2阶段决策变量定义为

给定第1阶段决策变量(x_f^t, y_f^t)和不确定容量的实现值α_i^t(ξ)、β_i^t(ξ)、γ_i^t(ξ)，一定数量的航班不得不采取延误措施以平衡流量和容量。
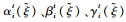
第2阶段目标函数定义为

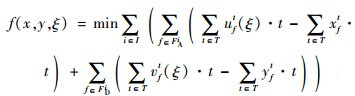(26)

第2阶段约束函数定义为

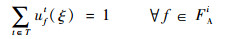(27)

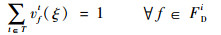(28)

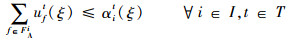(29)

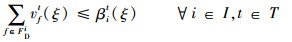(30)

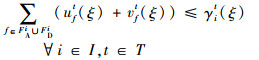(31)

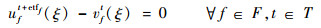(32)

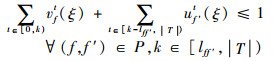(33)

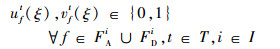(34)

式(26)定义了第2阶段的目标函数，即最小化“计划时隙-运行时隙差”，也就是最小化航班的总延误成本。式(27)~式(34)定义了第2阶段模型的约束函数：式(27)和式(28)表示航班f的进场和离场能且仅能分配到一个时隙，式(29)~式(31)保证了在任意时隙中机场进场容量、离场容量和总容量限制总能满足，式(32)表示所有航班飞行时间都是固定的，式(33)保证了联程航班周转时间的充足性，式(34)表示决策变量为0-1整数变量。
2 方法设计 针对模型规模大、二进制的特点，本文设计了基于ABC算法的渐进二元启发式方法对模型进行求解。
2.1 渐进二元启发式方法框架 渐进二元启发式方法主要针对模型二进制特点，其主要思想是：首先求解原问题的松弛问题，然后判断解的二元性，对不符合二进制约束的解渐进地增加二进制约束，最终求得符合模型约束的二进制最优解。渐进式二元启发式计算过程如下：
步骤1????读取原问题的松弛问题，并初始化迭代次数i=1。
步骤2????求解松弛问题，得到两阶段模型最优解(x¹, y¹)和(u¹, v¹)，同时得到对应的第1阶段目标值V′_RP和第2阶段目标值V″_RP。
步骤3????设置模型下界LB=V′_RP+V″_RP。
步骤4????检查所有子问题是否均有二进制解，若结果为是，则转入步骤8，否则转入步骤5。
步骤5????对存在分数解的子问题增加二进制约束。
步骤6????更新迭代次数i=i+1。
步骤7????求解新问题，并更新最优解(xⁱ, yⁱ)、(uⁱ, vⁱ)和目标函数值V′_RP、V″_RP，并转入步骤4。
步骤8????输出(xⁱ, yⁱ)和(uⁱ, vⁱ)，判断V′_RP+V″_RP=LB是否成立，若是，则(xⁱ, yⁱ)和(uⁱ, vⁱ)为模型最优解，否则，(xⁱ, yⁱ)和(uⁱ, vⁱ)为模型ε-最优解。
2.2 基于ABC算法的求解器设计 2.1节提出了求解两阶段0-1整数规划模型的渐进二元启发式方法，从方法框架中可以看出，步骤2和步骤7都要进行问题求解，考虑到时隙分配问题特别是多机场时隙分配问题规模大的特点，本文将ABC算法引入到渐进二元启发式方法框架，作为求解器用于步骤2和步骤7的求解。
ABC算法是2005年Karaboga^[30]通过模拟工蜂采蜜的整个过程提出的一种新型智能优化算法，与其他智能优化算法相比，其具有结构简单、易于实现、参数较少、鲁棒性强等优点^[31]。
基于ABC算法的渐进二元启发式方法流程框图如图 2所示。

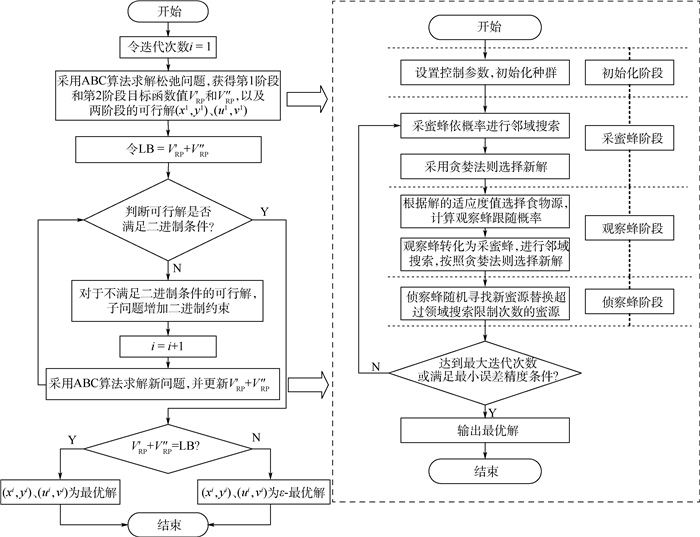图 2 基于ABC算法的渐进二元启发式方法计算框架 Fig. 2 Progressive binary heuristic method computation framework based on ABC algorithm

图选项

3 算例验证 本节分别对本文提出的模型和算法进行算例验证，采用MATLAB进行仿真实验，仿真环境为Intel Core i7 CPU@2.30 GHz，8 GB内存。
3.1 单机场模型算例验证 选取国内某机场终端区典型日运行数据为例，首先给出初始数据，然后采用本文提出的单机场时隙分配规划模型进行建模，并采用基于ABC算法的渐进二元启发式方法进行求解，最后进行分析说明。

3.1.1 初始数据 该机场10:00—12:00的航班时隙请求如表 1所示，其中时隙数量为8，时隙长度为15 min。联程航班需求如表 2所示。表 3给定了第1阶段不确定容量的分布及第2阶段容量实现值，其中第1阶段将容量设为不确定变量，并给出其不确定分布函数，如表示容量服从线性不确定分布，机场容量有0%的可能小于8，100%的可能小于等于10。
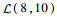
表 1 航班时隙请求 Table 1 Request of flight time slot

(a)进场航班
航班	时隙		航班	时隙
A1	10:00		A16	11:05
A2	10:05		A17	11:10
A3	10:10		A18	11:15
A4	10:15		A19	11:20
A5	10:20		A20	11:20
A6	10:25		A21	11:25
A7	10:35		A22	11:30
A8	10:35		A23	11:35
A9	10:40		A24	11:40
A10	10:50		A25	11:40
A11	10:50		A26	11:40
A12	10:55		A27	11:40
A13	11:00		A28	11:50
A14	11:00		A29	11:55
A15	11:00		A30	11:55
(b)离场航班
航班	时隙		航班	时隙
D1	10:00		D21	10:50
D2	10:00		D22	10:55
D3	10:05		D23	10:55
D4	10:05		D24	11:00
D5	10:10		D25	11:00
D6	10:10		D26	11:00
D7	10:15		D27	11:05
D8	10:15		D28	11:10
D9	10:15		D29	11:15
D10	10:20		D30	11:20
D11	10:20		D31	11:20
D12	10:20		D32	11:25
D13	10:25		D33	11:30
D14	10:25		D34	11:30
D15	10:30		D35	11:30
D16	10:30		D36	11:35
D17	10:30		D37	11:45
D18	10:35		D38	11:45
D19	10:40		D39	11:50
D20	10:45		D40	11:55

表选项






表 2 联程航班 Table 2 Connecting flights

联程航班对	最小周转时间/min
A1, D12	25
A4, D18	25
A7, D20	30
A10, D27	30
A15, D28	20
A16, D30	20
A20, D38	30
A22, D40	25

表选项






表 3 机场两阶段容量 Table 3 Airport capacity in two stages

时段	第1阶段不确定容量分布				第2阶段容量实现值
	进场	离场	机场		进场	离场	机场
10:00—10:30		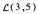		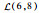	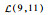4	7	10
10:30—11:00		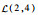		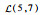	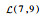3	6	8
11:00—11:30		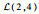		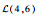	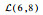2	5	6
11:30—12:00		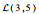		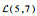	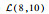4	6	9

表选项







3.1.2 仿真结果 分别采用本文两阶段模型和传统模型进行仿真计算，其中两阶段模型的权重系数设为1。算法参数设置如表 4所示。仿真结果列于表 5，其中“请求时隙-计划时隙差”表示第1阶段初次时隙分配请求时隙和计划时隙的差值，“计划时隙-运行时隙差”表示第2阶段再次时隙分配计划时隙与运行时隙的差值。
表 4 ABC算法控制参数设置 Table 4 Control parameter setting of ABC algorithm

控制参数	取值
种群规模	100
最大循环次数	1 000
最大限制搜索次数	50
观察蜂数量	种群规模的一半
采蜜蜂数量	种群规模的一半
侦察蜂数量	1

表选项






表 5 时隙分配结果 Table 5 Results of time slot allocation

时段	两阶段模型				传统模型
	请求时隙-计划时隙差	计划时隙-运行时隙差	合计		请求时隙-计划时隙差	计划时隙-运行时隙差	合计
10:00—10:15	0	0	0		0	0	0
10:15—10:30	1	0	1		0	1	1
10:30—10:45	0	0	0		0	1	1
10:45—11:00	0	0	0		0	0	0
11:00—11:15	3	1	4		0	4	4
11:15—11:30	3	2	5		0	6	6
11:30—11:45	4	2	6		0	7	7
11:45—12:00	2	2	4		0	5	5
总计	13	7	20		0	24	24

表选项







3.1.3 结果分析 由表 5可以看出，本文模型所得出的“请求时隙-计划时隙差”为13，即航班请求时隙和航班计划时隙有13个时隙的差异，“计划时隙-运行时隙差”为7，即第2阶段航班运行延误时隙为7，总体差异为20；传统模型所得出的“请求时隙-计划时隙差”为0，即满足所有航班时隙请求，“计划时隙-运行时隙差”为24，即航班运行延误为24。由此可以看出，本文模型虽然在初次时隙分配时增加了“请求时隙-计划时隙差”，但在第2阶段减少了运行延误，实现了总体目标的优化。从总体来看，时隙分配不确定两阶段模型较传统模型提升了16.7%。
分析其原因，本文模型以牺牲航班时隙请求为代价，换取了更少的运行延误，从而实现时隙分配结果总体的优化。本质上，本文模型是对时隙资源的优化利用，模型在进行初次时隙分配时即考虑第2阶段时隙再次分配时容量的不确定性，通过提前调整航班时隙请求，安排更合理的航班时隙计划，从而实现了时隙分配结果的整体优化。本节算例中，本文模型虽然仅比传统模型提升了16.7%，但在实际中，乘客所感受到的是第2阶段运行延误的减少，算例中，运行延误减少了70.8%，对乘客满意度的提升是巨大的。
3.2 多机场模型算例验证 京津冀、长三角、珠三角地区是中国在“十三五”期间着力打造的3个世界级机场群。本节选取3个区域的主要机场作为3个独立算例，对多机场时隙分配规划模型进行仿真验证，并对权重的影响进行分析。
首先列出3个算例中所含机场，以及国际民用航空组织(ICAO)给出的机场代码。
1) 京津冀。北京首都国际机场(ZBAA)、天津滨海国际机场(ZBTJ)、石家庄正定国际机场(ZBSJ)。
2) 长三角。上海浦东国际机场(ZSPD)、上海虹桥国际机场(ZSSS)、南京禄口国际机场(ZSNJ)、杭州萧山国际机场(ZSHC)、合肥新桥国际机场(ZSOF)。
3) 珠三角。广州白云国际机场(ZGGG)、深圳宝安国际机场(ZGSZ)、珠海金湾机场(ZGSD)。

3.2.1 初始数据及仿真结果 算例选取08:00—10:00三个机场群的典型运行数据，给定模型输入，包括各机场在第1个阶段的不确定容量分布、第2个阶段的容量实现值，各航班请求时隙、起飞机场、降落机场、飞行时间，联程航班及最小周转时间、权重系数等初始数据。算例规模如表 6所示。采用基于ABC算法的渐进二元启发式方法进行模型求解，计算过程与单机场模型相同，最终统计结果如表 7、图 3所示。
表 6 算例规模 Table 6 Scale of computation samples

机场群	航班数量	进场航班数量	离场航班数量
京津冀	248	82	166
长三角	372	137	235
珠三角	309	84	225

表选项






表 7 模型结果对比 Table 7 Model result comparison

机场群	权重系数	与传统模型对比
		请求时隙-计划时隙差增加值	运行延误减少值	时隙分配优化百分比
京津冀	1	36	51	15.3
	3	67	176	66.9
长三角	1	63	91	10.3
	3	102	516	62.5
珠三角	1	75	139	62.7
	3	81	445	71.3

表选项

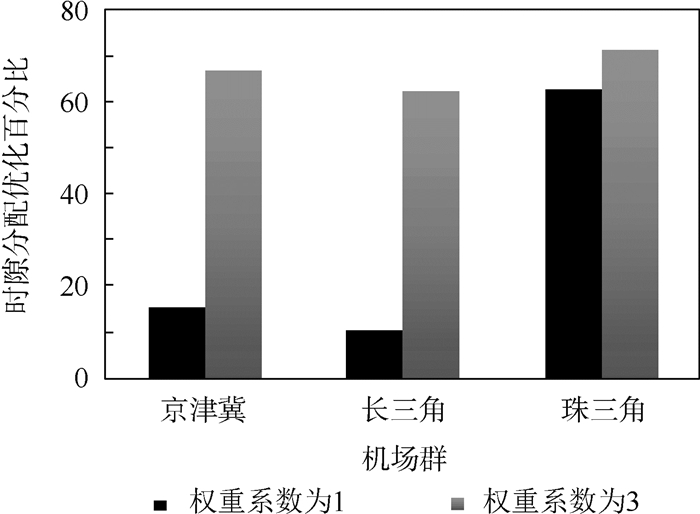图 3 时隙分配优化百分比示意图 Fig. 3 Schematic diagram of time slot allocation optimization percentage

图选项

3.2.2 结果分析 从表 7和图 3中可以看出，对比传统模型，本文模型在总体上体现了较大的优越性，提升比例均大于10%，最大的提升是珠三角、权重系数为3的算例，提升比例达到了71.3%，提升最小的是长三角、权重系数为1的算例，提升比例达到了10.3%。这种提升的原因在3.1.3节中已经进行了分析，本文模型实现了对“请求时隙-计划时隙差”和“计划时隙-运行时隙差”的权衡，以牺牲时隙请求为代价，通过合理安排时隙计划，充分利用时隙资源，达到了总体优化的目标。
下面分析权重系数对模型结果的影响。如表 7中所示，算例分别设定权重系数为1和3，可以看出，在其他输入数据相同的情况下，权重系数为3时本文模型比传统模型提升更大。具体来说，权重系数为3时，京津冀算例比权重系数为1时多提升了51.6%，长三角算例多提升了52.2%，珠三角算例多提升了8.6%。这是因为当设置权重系数为3时，就意味着把减少运行延误(“计划时隙-运行时隙差”)置于更加重要的位置，由于传统模型的特点，运行延误水平将被放大，而本文模型虽然可能牺牲更多的航班请求，但也会显著降低运行水平，因此显示出更大的优越性。
4 结论 1) 本文提出的不确定容量下时隙分配两阶段规划单机场模型和多机场模型符合时隙分配两阶段过程，以航班而不是航班数为变量，将两阶段规划模型从单机场推广到多机场，与传统时隙分配模型相比，能够有效地对时隙分配结果进行优化。
2) 本文设计的基于ABC算法的渐进二元启发式方法，充分考虑了模型的二进制特点，从原问题的松弛问题出发，渐进增加二进制约束，降低了模型求解复杂度；利用ABC算法结构简单、易于实现、参数较少、鲁棒性强的优点，将ABC算法设计为启发式计算求解器，算例证明，方法可以有效地对模型进行求解。
3) 算例对模型和方法进行了可行性和有效性验证。算例结果显示，在单机场和多机场情况下，本文模型均体现了较大优势；同时，模型权重系数越大，本文模型优势越大，对时隙分配结果提升效果越大。
未来应从模型完善及应用方面开展进一步研究。模型主要从考虑机型不同、优先级策略、航路变更等方面进行完善；应用方面主要考虑在更大规模的应用场景中对算法有效性进行验证。

参考文献

[1]	中国民用航空局.2015年民航行业发展统计公报[EB/OL].(2016-05-30)[2018-12-24].http://www.caac.gov.cn/XXGK/XXGK/TJSJ/201605/t20160530_37643.html. Civil Aviation Administration of China. 2015 civil aviation industry development statistics bulletin[EB/OL].(2016-05-30)[2018-12-24].http://www.caac.gov.cn/XXGK/XXGK/TJSJ/201605/t20160530_37643.html (in Chinese).
[2]	中国民用航空局, 国家发展和改革委, 交通运输部.中国民用航空发展第十三个五年规划[EB/OL].(2017-02-15)[2018-12-24].http://www.caac.gov.cn/XXGK/XXGK/FZGH/201704/t20170405_43502.html. Civil Aviation Administration of China, National Development and Reform Commission, Ministry of Transport. The Thirteenth Five-Year Plan for the development of civil aviation in China[EB/OL].(2017-02-15)[2018-12-24].http://www.caac.gov.cn/XXGK/XXGK/FZGH/201704/t20170405_43502.html(in Chinese).
[3]	中国民用航空局运行监控中心.2017年全国民航航班运行效率报告[EB/OL].(2018-03-01)[2018-12-24].http://www.caac.gov.cn/XWZX/MHYW/201803/t20180328_56080.html. Operation Monitoring Center of Civil Aviation Administration of China. 2017 national civil aviation flight operation efficiency report[EB/OL].(2018-03-01)[2018-12-24].http://www.caac.gov.cn/XWZX/MHYW/201803/t20180328_56080.html(in Chinese).
[4]	HOFFMAN R L.Integer programming models for ground-holding in air traffic flow management[D].City of College Park: University of Maryland, 1997.
[5]	HOFFMAN R L, HALL W, BALL M O, et al.Collaborative decision making in air traffic flow management[R].Berkeley: University of California, Berkeley, 1999.
[6]	VOSSEN T W.Fair allocation methods in air traffic management[D].City of College Park: University of Maryland, 2002.
[7]	BALL M O, HOFFMAN R L, VOSSEN T. An analysis of resource rationing methods for collaborative decision making[C]//Proceeding of ATM 2002-System Architectures and CNS Technologies Needed to Cope with the Air Traffic Capacity Problem and Related Evaluation Tools, 2002: 64-70.
[8]	MADAS M A, ZOGRAFOS K G. Airport slot allocation:From instruments to strategies[J]. Journal of Air Transport Management, 2006, 12(2): 53-62. DOI:10.1016/j.jairtraman.2005.08.001
[9]	ODONI A R.The flow management problem in air traffic control[M]//ODONI A R, BIANCO L, GIORGIO S.Flow control of congested networks.Berlin: Springer, 1987: 269-288.
[10]	TERRAB M, ODONI A, DEUTSCH O.Ground-holding strategies for ATC flow control[C]//AIAA Guidance, Navigation and Control Conference.Reston: AIAA, 1989: 1635-1646.
[11]	GILBO E P. Optimizing airport capacity utilization in air traffic flow management subject to constraints at arrival and departure fixes[J]. IEEE Transactions on Control Systems Technology, 1997, 5(5): 490-503. DOI:10.1109/87.623035
[12]	OUSSEDIK S, DELAHAYE D.Reduction of air traffic congestion by genetic algorithms[C]//International Conference on Parallel Problem Solving from Nature.Berlin: Springer, 1998: 855-864.
[13]	PULUGURTHA S S, NAMBISAN S S. Using genetic algorithms to evaluate aircraft ground holding policy in real time[J]. Journal of Transportation Engineering, 2001, 127(5): 442-448. DOI:10.1061/(ASCE)0733-947X(2001)127:5(442)
[14]	MADAS M A, ZOGRAFOS K G. Airport slot allocation:A time for change?[J]. Transport Policy, 2010, 17(4): 274-285. DOI:10.1016/j.tranpol.2010.02.002
[15]	胡明华, 徐肖豪. 空中交通流量控制的地面保持策略[J]. 南京航空航天大学学报, 1994, 26(增刊): 26-30. HU M H, XU X H. Ground-holding strategies for ATC flow control[J]. Journal of Nanjing University of Aeronautics and Astronautics, 1994, 26(S): 26-30. (in Chinese)
[16]	周茜, 张学军, 柳重堪. 时隙分配算法在CDM GDP程序中的应用[J]. 北京航空航天大学学报, 2006, 32(9): 1043-1045. ZHOU Q, ZHANG X J, LIU Z K. Slots allocation in CDM GDP[J]. Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(9): 1043-1045. DOI:10.3969/j.issn.1001-5965.2006.09.011 (in Chinese)
[17]	徐肖豪, 王飞. 地面等待策略中的时隙分配模型与算法研究[J]. 航空学报, 2010, 31(10): 1993-2003. XU X H, WANG F. Research on slot allocation models and algorithms in ground holding policy[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(10): 1993-2003. (in Chinese)
[18]	张洪海, 胡明华. CDM ADGDP机场容量与时隙协同配置[J]. 系统工程理论与实践, 2010, 30(10): 1901-1908. ZHANG H H, HU M H. Collaborative allocation of capacity and slot in CDM ADGDP airport[J]. Systems Engineering-Theory & Practice, 2010, 30(10): 1901-1908. (in Chinese)
[19]	田勇, 李永庆, 万莉莉, 等. 基于市场机制的地面等待时隙分配方法[J]. 系统工程理论与实践, 2014, 34(6): 1614-1619. TIAN Y, LI Y Q, WAN L L, et al. Slot allocation based on market mechanism in ground holding policy[J]. Systems Engineering-Theory & Practice, 2014, 34(6): 1614-1619. (in Chinese)
[20]	刘丽华.市场机制下飞机推出时隙分配模型与算法研究[D].哈尔滨: 哈尔滨工业大学, 2017. LIU L H.Research on model and algorithm for aircraft pushback slot allocation under market mechanism[D].Harbin: Harbin Institute of Technology, 2017(in Chinese).
[21]	ANDREATTA G, ROMANIN-JACUR G. Aircraft flow management under congestion[J]. Transportation Science, 1987, 21(4): 249-253. DOI:10.1287/trsc.21.4.249
[22]	RICHETTA O, ODONI A R. Solving optimally the static ground-holding policy problem in air traffic control[J]. Transportation Science, 1993, 27(3): 228-238. DOI:10.1287/trsc.27.3.228
[23]	MUKHERJEE A, HANSEN M M. A dynamic stochastic model for the single airport ground holding problem[J]. Transportation Science, 2007, 41(4): 444-456. DOI:10.1287/trsc.1070.0210
[24]	杨尚文, 胡明华, 张洪海. 随机型协同时隙分配模型[J]. 系统工程理论与实践, 2014, 34(1): 153-157. YANG S W, HU M H, ZHANG H H. Stochastic collaborative slot allocation models[J]. Systems Engineering-Theory & Practice, 2014, 34(1): 153-157. (in Chinese)
[25]	乐美龙, 李星灿, 高金敏. 机场到达时刻数量决策随机模型[J]. 系统工程理论与实践, 2017, 37(11): 2948-2954. LE M L, LI X C, GAO J M. Stochastic model of determining airport arrival slots number[J]. Systems Engineering-Theory & Practice, 2017, 37(11): 2948-2954. DOI:10.12011/1000-6788(2017)11-2948-07 (in Chinese)
[26]	COROLLI L, LULLI G, NTAIMO L. The time slot allocation problem under uncertain capacity[J]. Transportation Research Part C:Emerging Technologies, 2014, 46: 16-29. DOI:10.1016/j.trc.2014.05.004
[27]	岳仁田, 赵胖胖, 赵嶷飞. 带补偿的两阶段随机规划航班时隙分配研究[J]. 航空计算技术, 2018, 48(1): 4-8. YUE R T, ZHAO P P, ZHAO Y F. Study on slot allocation based on two-stage stochastic programming with recourse[J]. Aeronautical Computing Technique, 2018, 48(1): 4-8. DOI:10.3969/j.issn.1671-654X.2018.01.002 (in Chinese)
[28]	LIU B. Uncertainty theory[M]. 4th ed. Berlin: Springer, 2015: 111-130.
[29]	ZHENG M F, YUAN Y, WANG Z T, et al. Study on two-stage uncertain programming based on uncertainty theory[J]. Journal of Intelligent Manufacturing, 2017, 28(3): 633-642. DOI:10.1007/s10845-014-1012-6
[30]	KARABOGA D.An idea based on honey bee swarm for numerical optimization[R].Kayseri: Erciyes University, 2005.
[31]	江铭炎, 袁东风. 人工蜂群算法及其应用[M]. 北京: 科学出版社, 2014: 47-55. JIANG M Y, YUAN D F. Artificial bee colony algorithm and its application[M]. Beijing: Science Press, 2014: 47-55. (in Chinese)