桁架结构拓扑优化是结构优化领域的一个重要分支。结构拓扑优化的很多经典问题都是从桁架结构优化中出现并逐步得到解决的，一些新的结构拓扑优化方法往往也通过求解典型的桁架拓扑优化算例进行可行性和有效性的验证。优化过程中桁架拓扑会发生变更，这是拓扑优化不同于尺寸优化的一个显著特点。虽然也有****研究进化类的拓扑变更策略^[1-5]，但基于退化策略的基结构法(Ground Structure Method，GSM)^[6]一直是桁架拓扑优化领域应用最为广泛的方法。从拓扑变更角度讲，在基结构法框架下，初始桁架结构中的部分杆件将被删除，优化结果容易出现稳定性不足的情况；从力学性能角度讲，实际工程结构受载时，失稳破坏往往发生于强度破坏之前，满足强度条件的结构不一定满足稳定性要求。因此，优化过程中若不考虑稳定性约束，优化结果往往不能通过稳定性校验，这将严重影响其工程实用性。
桁架结构拓扑优化中常见的稳定性现象主要包括3类，即局部稳定性、几何稳定性和全局稳定性^[7-8]。局部稳定性与欧拉屈曲相关，当桁架中的杆件所受压载荷超过其临界欧拉屈曲载荷时，杆件发生欧拉屈曲，称桁架出现局部不稳定(失稳)。几何稳定性也称为运动稳定性，当结构由于存在不能承载的自由度而变为机构时，称其为几何不稳定。对受载的机构，即使很小的扰动也可能破坏其平衡状态，导致整体垮塌。节点不稳定是最常见的一种几何不稳定现象，通常出现于成串受压杆件的中间节点缺少横向支撑的情况。全局稳定性是基于线性稳定性理论定义的：当载荷达到临界屈曲载荷时，结构的平衡状态发生分支，称结构出现全局不稳定。在有限元方法中，线性稳定性问题是关于结构刚度矩阵和几何刚度矩阵的广义特征值问题。
桁架结构的局部和全局稳定性均可通过临界屈曲载荷进行定量评价。在优化模型中，要求临界屈曲载荷不小于实际载荷即可构成对应的约束条件。相比而言，桁架几何稳定性则较难描述和度量。文献中常用某些替代约束方案在一定程度上确保优化结果的几何稳定性。第1类方案是限制节点处的杆件连接情况。例如，Ohsaki和Katoh^[9]、Cerveira等^[10]的策略是对拓扑中的所有自由节点，强制要求连接到该节点的杆件总数大于某给定值，并且对存在杆件的横截面积给定合适的下限，以保证拓扑中的节点都有足够的横向支撑。但满足这种要求的拓扑并不一定几何稳定。第2类方案是考虑附加载荷。在桁架节点处作用非轴向载荷能够迫使最优结构中保留对该节点的横向支撑，从而使结构在这些载荷下保持稳定。该思想最简单的实现方法是对桁架施加附加载荷，可参考Tyas等^[7]、Descamps和Coelho^[8]以及Mela^[11]的相关工作。此类方案往往需要引入一些复杂的主观策略以确定附加载荷施加的位置和幅值。第3类方案是考虑基频约束或全局稳定约束。冷国俊等^[12]在桁架结构拓扑优化中加入基频约束以避免出现机构；Guo等^[13]将全局稳定约束引入优化问题数学模型，要求结构的临界屈曲载荷大于实际载荷。Ko?vara^[14]用算例说明，使用基频约束代替全局稳定约束得到的最优结构并不相同，但未作深入讨论。
可见，桁架结构拓扑优化中对几何稳定性的约束方案多种多样，各方案的约束原理和使用效果也不尽相同，实际应用时存在方案选择和优化结果不统一等困难。实际上，由于对此类问题处理方式的主观性，目前尚无被广泛采用的几何稳定性的严格定义，这对桁架结构几何稳定性的判定带来了困难。
针对上述问题，本文对比了桁架拓扑几何稳定性的几种判定方法，给出了一套简单有效的判定流程；基于半定规划(Semidefinite Programming, SDP)模型，结合具体算例对桁架拓扑优化中处理几何稳定性的3种常见约束方案进行了对比分析，通过对优化结果几何稳定性的讨论，说明了各类方案的有效性。
1 桁架结构几何稳定性的判定 1.1 桁架结构几何稳定性的判定方法 几何不稳定的拓扑形式已成为机构，但为叙述方便，本文仍将由轴向受力杆件通过铰接节点连成的结构形式统称为桁架。可靠的判定准则是是对桁架几何稳定性进行讨论的前提。相关文献中桁架几何稳定性的判定方法主要有以下4类。
1) 检查节点处连接杆件的情况
一般要求与某个节点相连的杆件数量不小于给定数值。例如，平面桁架中的自由节点(即可动节点)至少应连接2根不共线的杆件；而空间桁架则要求自由节点至少应连接3根不共面的杆件。实施过程中，还要分别考虑载荷作用节点、固定节点和一般自由节点的连杆数要求。
2) 检查是否满足Maxwell准则
记桁架的空间维度为d(二维桁架d=2，三维桁架d=3)，包含的杆件总数为m，节点总数为n，被边界条件限制的自由度数为c，则可定义桁架结构的某种自由度度量n_DOF=d×n－m－c。按照Maxwell准则，若n_DOF≤0则可认为桁架拓扑几何稳定。Maxwell准则也称为Grubler准则^[15-16]或Chebyshev-Grübler-Kutzbach准则^[17]。
3) 检查刚度矩阵K的正定性
根据有限元理论，结构刚度矩阵K总是半正定的。该方法认为，若结构刚度矩阵正定(表示为，O为全零矩阵)则桁架是几何稳定的。否则K是奇异矩阵，此时结构具有不能承载的自由度。这种判定方法需组装结构刚度矩阵K，且一般需要利用某种数值过程来确定矩阵是否正定，如计算K的特征值^[16]或条件数^[18]。
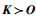
4) 检查结构平衡矩阵A是否行满秩
Pellegrino和Calladine^[19-20]指出，与结构平衡矩阵A(即几何矩阵B的转置，杆件内力向量q与外载荷向量f满足q=Af)相关的向量子空间能够提供结构动静态稳定性方面的详细信息。记平衡矩阵A的行数为n_r、列数为n_c、矩阵的秩为r，则结构的静不定度为s_DOF=n_c－r，动不定度为k_DOF=n_r－r。平衡矩阵A行满秩，即动不定度k_DOF=0时，认为桁架几何稳定。这种方法需要构造平衡矩阵A并求其秩。需说明，这里的动不定度是指桁架结构中不能承载的自由度(沿该自由度的微小位移导致的结构形变不能使结构产生对应的内力来抵抗这种位移趋势)的数量，与其他文献(如文献[21])中“动不定”的含义不尽相同。
1.2 对几何稳定性判定方法的讨论 本节使用1.1节方法对若干简单二维拓扑进行几何稳定性判定，以说明各种判定方法的合理性。
表 1第2列给出4个桁架拓扑。在每个拓扑中，实心圆圈“·”表示固定节点，其位置不变；空心圆圈表示自由节点，其位置可变；连接2个节点的粗直线表示一根杆件；箭头表示一些可能的载荷。第3~6列分别是使用不同方法对这些拓扑的几何稳定性进行判定的结果，“√”表示判定为几何稳定，“×”表示判定为几何不稳定。最后2列给出对应拓扑在Maxwell准则下的自由度度量n_DOF以及通过平衡矩阵特性计算的动不定度k_DOF的具体数值。
表 1 不同方法对几何稳定性的判定结果 Table 1 Geometric stability determined by different methods

编号	拓扑	方法1)	方法2)	方法3)	方法4)	nDOF	kDOF
1		×	×	×	×	2	2
2		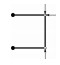√	×	×	×	1	1
3		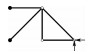√	×	×	×	1	1
4		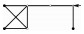×	√	×	×	0	1

表选项






表 1的4个拓扑均包含机构，显然是几何不稳定的。对拓扑1，所有判定方法均判定其为几何不稳定。方法1)对拓扑2和拓扑3判定错误：2个拓扑中的自由节点各连接了2根或以上不共线杆件，各节点均满足连杆数量要求，但这2个拓扑都是几何不稳定的。方法2)对拓扑4判定错误：该拓扑n_DOF=0，满足Maxwell准则要求，但其中存在无横向支撑的共线杆件，显然也是几何不稳定的，且此时n_DOF≠k_DOF。相关文献[16-17]已指出，方法1)和方法2)使用的判定准则仅是桁架几何稳定的必要非充分条件。方法3)和方法4)则能正确识别全部4个几何不稳定拓扑。本文认为，方法4)具有严密的理论基础，结构动不定度为零(k_DOF=0)可作为桁架结构几何稳定的定义。实际上，从数学上可以证明，桁架刚度矩阵K正定等价于平衡矩阵A行满秩(见附录A)，也即方法3)和方法4)的判定准则是等价的。
观察发现，不论是各节点连接杆件的计数，或是Maxwell准则中自由度度量n_DOF的计算，还是结构相关矩阵K和A的构造与分析，4类方法的判定过程均不涉及载荷条件。可见，桁架结构的几何稳定性是一种仅与拓扑构型(包含空间维度、杆件连接关系和边界条件等)相关的结构属性，与结构材料、杆件粗细及所受载荷均无关。桁架的几何稳定性即指其拓扑的几何稳定性。
1.3 评估桁架结构几何稳定性的一种简单流程 对比可见：方法1)和方法2)相对简单易行，其判定准则虽然是桁架几何稳定的必要非充分条件，但这2种方法对几何不稳定拓扑的识别却有很好的效果；方法3)和方法4)则能准确反映结构的几何稳定性，但需要构造相关矩阵，并使用特定的数值过程得出矩阵特性。为减少计算量，本文给出如图 1所示的几何稳定性判定流程。

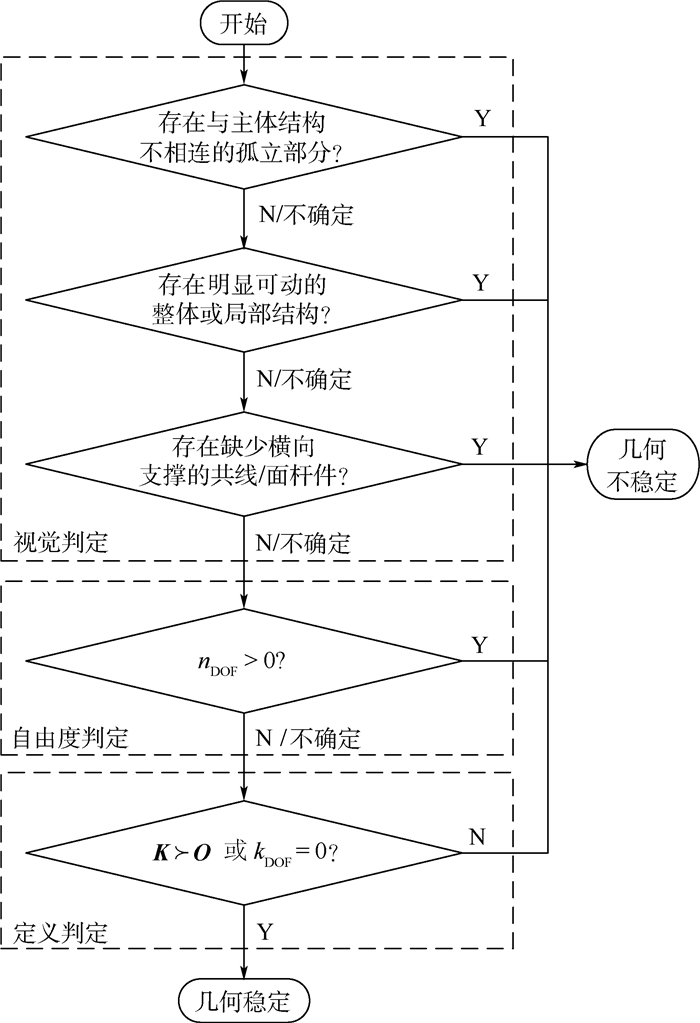图 1 桁架结构几何稳定性的判定流程 Fig. 1 Flowchart for determining truss geometric stability

图选项

第1步为视觉判定。对一些明显的几何不稳定拓扑，视觉上的直观判断比考察准则是否满足更加直接高效。本文在该阶段提出识别几何不稳定模式的方法。定义如下3种几何不稳定模式：①存在与主体结构不相连的孤立部分；②存在明显可动的整体或局部结构；③存在缺少横向支撑的共线或共面杆件。拓扑中存在任何一种几何不稳定模式时，即可将其判定为几何不稳定。几何不稳定模式可能并不止这3种，但是，除非新的模式能够被很直接地识别出来，否则本文不建议在该阶段列出更多模式或对其进行明确地分类。第2步为自由度判定，即检查Maxwell准则的满足情况。统计给定拓扑中的杆件总数、节点总数和被约束的自由度数，根据问题维度计算n_DOF。若n_DOF>0，直接将拓扑判定为几何不稳定，否则进入下一步。第3步为定义判定。考虑边界条件，构造桁架结构的刚度矩阵K或平衡矩阵A，根据K是否正定或A是否行满秩准确判定拓扑是否几何稳定。需要时可由A的秩计算拓扑的动不定度和静不定度。
该流程能够快速给出桁架结构是否几何稳定的定性结论。视觉和自由度判定阶段的任何判断环节均可跳过(相当于认为该环节的判断结果为“不确定”)。使用计算机进行判定时，可跳过视觉判定阶段。
2 桁架结构几何稳定约束方案对比 结构优化的数学模型中通常只对结构的典型响应量(如柔度、应力、节点位移、振动基频、临界屈曲载荷等)进行约束。由1.1节讨论，桁架几何稳定的定义涉及刚度矩阵K和平衡矩阵A，它们并不是常见的结构响应量，因此目前的桁架结构拓扑优化模型中还没有对几何稳定性的直接约束。本文在引言中介绍了一些替代性的方案，选取其中3种进行研究。结构优化问题存在可行域为空集的可能性，但对体积最小化问题，通常总能通过增加结构尺寸使约束条件满足，因此一般不会出现这种情况。本文在体积最小化模型的基础上对以下3种约束方案进行详细讨论：A.考虑附加载荷；B.考虑基频约束；C.考虑全局稳定约束。
2.1 基于半定规划的优化问题建模 为对比不同的几何稳定约束方案，给出统一的优化模型。其中包含多工况下的柔度约束、结构基频约束和全局稳定约束，数学表达式为

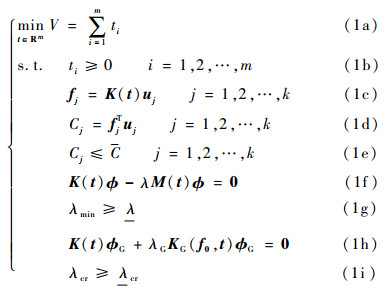式(1a)为目标函数，其中V为桁架结构的总体积；各杆件体积t_i(i=1, 2，…, m)构成杆件体积向量t∈R^m；m为杆件总数。
式(1b)~式(1i)均为约束。式(1b)为杆件体积非负约束。式(1c)为工况j下的平衡方程，K(t)为结构刚度矩阵；f_j为第j个工况下的载荷向量；u_j为该工况下的节点位移，k为工况总数。式(1d)为结构柔度定义式，C_j为工况j下的柔度值。式(1e)为柔度约束，C为各个载荷工况下的统一柔度上限。式(1f)为无阻尼自由振动的动力学方程，λ为结构自由振动的特征值，其最小值记作λ_min; ?为特征向量; M(t)为结构质量矩阵。式(1g)为基频约束，λ为与基频下限f对应的特征值下限。式(1h)为线性稳定性方程，?_G为结构屈曲模态向量; K_G为结构的几何刚度矩阵；结构所受实际载荷为f_G=λ_Gf₀；λ_G为载荷因子；f₀为载荷模式，本文取为实际载荷。式(1h)的最小正特征值即为结构的临界屈曲载荷因子，记作λ_cr，临界屈曲载荷则为f_cr=λ_crf₀。式(1i)为全局稳定约束，表示临界屈曲载荷应不小于实际载荷的λ_cr倍；λ_cr为给定的临界屈曲载荷因子下限，应取为不小于1的值。
将优化模型(1)转换为SDP形式，以便采用适当的SDP求解器进行优化求解。SDP是传统的数学规划在矩阵空间中的推广^[22]，20世纪90年代末开始应用于结构优化领域。SDP模型有利于问题的凸化和对多重特征值问题的处理。研究人员将传统优化模型中的典型约束表示为等价的半定约束形式，建立了桁架拓扑优化的SDP模型，为优化问题的求解奠定了基础。优化模型(1)对应的SDP模型为

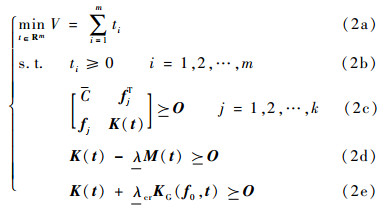式中:符号表示矩阵X半正定。式(2c)是与式(1c)~式(1e)对应的柔度约束，式(2d)是与式(1f)和式(1g)对应的基频约束，式(2e)是与式(1h)和式(1i)对应的全局稳定约束。约束的等价转化过程可参考Ben-Tal、Nemirovski、Ohsaki、Achtziger和Ko?vara等****的研究工作^{[14, 23-26]}。
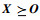
本文考虑的3种几何稳定约束方案分别对应3个桁架拓扑优化问题。问题A的优化模型由式(2a)~式(2c)组成。柔度是结构在静态载荷下形变量的一种度量，加入柔度约束可使优化问题存在体积下限，从而使问题适定。问题B的优化模型由式(2a)~式(2d)组成。由于同一拓扑构型下各杆横截面积等比例缩放时结构基频不变，仅在基频约束下最小化结构体积时，各杆横截面积将趋于无穷小(详见文献[26])，加入柔度约束可使优化问题适定。问题C的优化模型由式(2a)~式(2c)和式(2e)组成，为使问题适定，该模型中也考虑了柔度约束，其作用可见后文算例中的讨论。
在实际求解时，一般还需通过特定的数学处理方法将上述模型转化为标准SDP形式。问题A和问题B可转化为标准的线性SDP问题，可使用SeDuMi^[27]、SDPT3^[28]等求解器进行求解；问题C是一个非线性SDP问题，可用PENLAB求解器^[29]或序列SDP方法^[30]进行求解。
2.2 桁架结构拓扑优化算例 本节首先对3个不同的简单桁架分别求解优化问题A、B和C，通过分析结果的几何稳定性，详细说明了不同约束方案的特点；然后使用3种约束方案对同一空间桁架进行优化，进一步对比了3种约束方案的有效性。
本节的所有图示中，杆件均具有实心圆截面并用直线表示，直线粗细表示杆件的相对直径大小；静态载荷用箭头表示，同一图示中的不同箭头长度表示该图内载荷幅值的相对大小(若幅值过小，箭头尾部可能不显示)。节点沿水平和竖直方向均匀分布，若无特别说明，算例中各方向相邻节点间距均为1个单位长度；材料的弹性模量和密度均取单位1；初始杆件直径均取为单位1。物理量经适当缩放，无需给出具体单位。图示注释文字最后的“(Y)”表示拓扑几何稳定，“(N)”表示几何不稳定，“N”后的数字表示动不定度k_DOF的具体数值(几何稳定特性由图 1流程给出)。

2.2.1 算例1——考虑附加载荷 对图 2(a)所示的10杆桁架基结构考虑如下3个集中载荷：主要载荷①作用于顶部右侧节点，水平向左，幅值为1；附加载荷②和③分别作用于顶部右侧和中间节点，竖直向下，幅值为0.1。柔度上限取C=1。

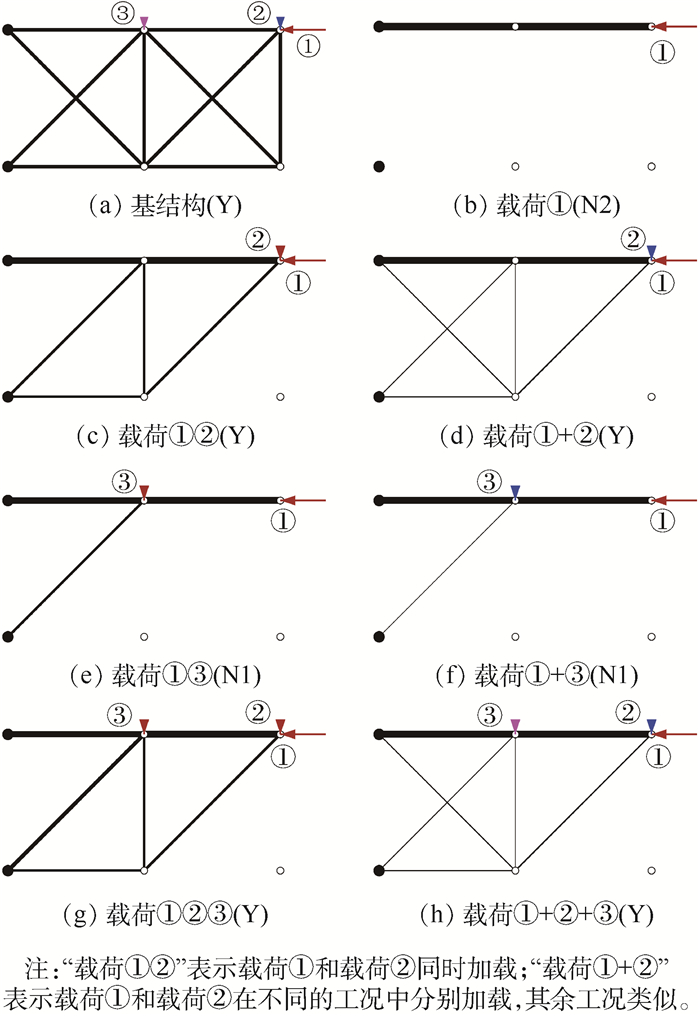图 2 10杆桁架基结构及不同工况下优化后的拓扑 Fig. 2 10-bar truss ground structure and optimized topologies under different load combinations

图选项

使用SeDuMi求解半定优化问题A，不同载荷组合情况下优化后的拓扑如图 2(b)~图 2(h)所示。优化后拓扑去掉了横截面积小于优化结果中最大横截面积特定百分比的过细杆件(根据经验，本文将过滤阈值取为0.1%)。
图 2(a)所示基结构是几何稳定的。仅考虑载荷①时，优化后拓扑(图 2(b))几何不稳定。在载荷①基础上考虑附加载荷②，优化后拓扑(图 2(c)、图 2(d))均几何稳定；在载荷①基础上考虑附加载荷③，不论是同时加载还是分工况加载，优化后拓扑(图 2(e)、图 2(f))相同，且均几何不稳定；在载荷①基础上考虑附加载荷②和③，优化后拓扑均几何稳定，且与同时考虑载荷①②时得到的拓扑(图 2(c)、图 2(d))相同。可见，附加载荷作用节点的选择对优化后拓扑几何稳定性的影响很大。另外，多载荷分工况加载比同时加载时得到的优化后拓扑往往更倾向于几何稳定，前者中包含后者的所有杆件，且通常还有更多的横向支撑。
对删除细杆前后桁架的力学特性进行对比可发现，优化结果中的细杆对结构体积和柔度几乎没有影响。需注意，几何不稳定桁架的刚度矩阵K奇异，求解平衡方程时可采用其Moore-Penrose逆矩阵^[31]。

2.2.2 算例2——考虑基频约束 如图 3(a)所示的33杆桁架基结构，各方向相邻节点间距均为0.5个单位长度，最左侧3个节点为固定节点，最右侧中间节点处作用水平向左、幅值为1的静态载荷。33根杆件考虑了除固支点之间连接之外的所有可能连接情况，包含跨节点的长杆。

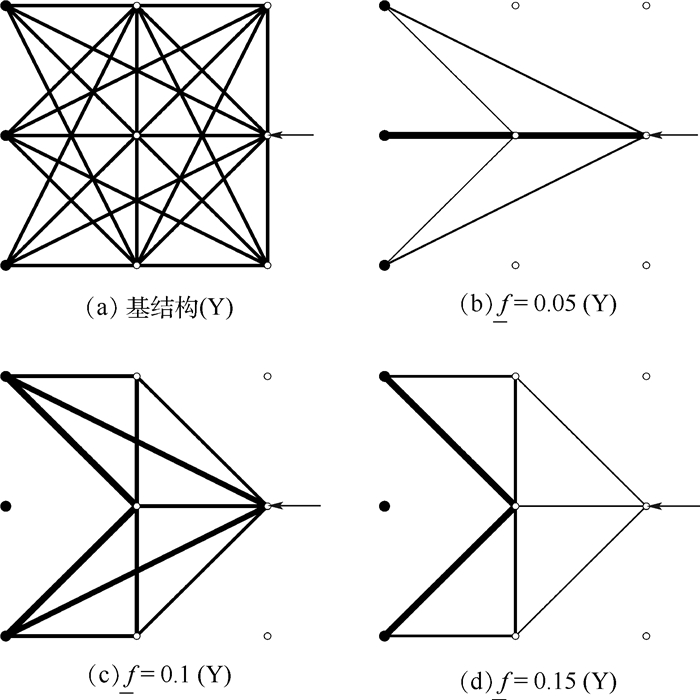图 3 33杆桁架基结构及不同基频约束下优化后的拓扑 Fig. 3 33-bar truss ground structure and optimized topologies under different fundamental frequency constraints

图选项

基结构体积为21.543 1，柔度为0.265 2，基频为0.059 2。使用SeDuMi求解半定优化问题B。柔度上限设置为C=1，基频下限f分别取0.05、0.1和0.15时，优化后拓扑(消去过细杆件)分别如图 3(b)~图 3(d)所示，其最优体积分别为1.103 0、2.488 6和10.703 7。各结果的柔度值均为1.000 0，基频均达到给定下限(数值分别为5.000 0×10^-2、1.000 0×10^-1和1.500 0×10^-1)，柔度和基频约束均为临界约束。观察可见：对不同的基频下限值f，优化结果中杆件的横截面积和结构拓扑均发生了显著变化；随着f的不断增大，越来越多的材料被用于满足基频约束。通过判别，本例在基频约束下得到的优化后拓扑均是几何稳定的。
对本例，仅考虑单一约束(柔度或基频约束)的体积最小解将趋于不同的构型。柔度上限固定，取不同的基频下限f进行试算时，出现2种极端情况。若柔度约束相比基频约束(取f=0.001)过于严格，则基频约束为宽松约束，所得优化结果(图 4(a))体积为1.000 0，柔度为1.000 0，基频为9.999 9×10^-4(振型见图 4(b))，在一定误差范围内可认为满足柔度和基频约束。去掉过细杆件后的2杆拓扑(图 4(c))柔度值为1.000 1，可认为仍满足柔度约束；但该拓扑动不定度为2，其前2阶振动频率均为0，不再满足基频约束(细杆的存在对一阶振型的维持不可或缺，去除细杆后的桁架拓扑动不定)。若基频约束(取f=0.2)相比柔度约束过于严格，则柔度约束为宽松约束，数值计算停止时得到的结果(图 4(d))体积为238.850 5，柔度为1.000 0，基频为0.159 4(对应过细杆件的振动模态，见图 4(e))，不满足基频约束，结果不可行，求解失败。去掉过细杆件后的8杆拓扑(图 4(f))基频为0.200 4，满足基频约束；但其柔度值为1.041 7，不再满足柔度约束(细杆对满足柔度约束不可或缺)。对上述2种情况，优化问题中约束上下限取值不合理，不同约束的相对严格程度差距较大，得到的计算结果不合理甚至不可行。

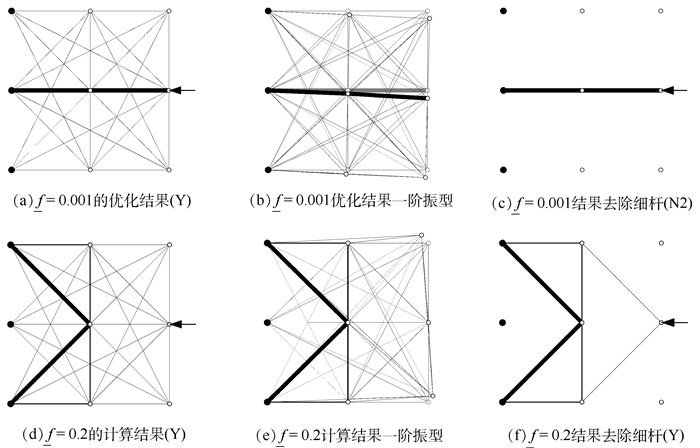图 4 33杆桁架不合理基频约束下的拓扑优化结果 Fig. 4 Topology optimization results of 33-bar truss under unreasonable fundamental frequency constraints

图选项

2.2.3 算例3——考虑全局稳定约束 如图 5(a)所示的4杆桁架基结构，顶部右侧节点作用竖直向下的集中载荷。使用文献[30]中的序列SDP方法，调用SeDuMi求解器求解非线性SDP问题C。柔度上限取C=1，临界屈曲载荷因子下限取λ_cr=1。

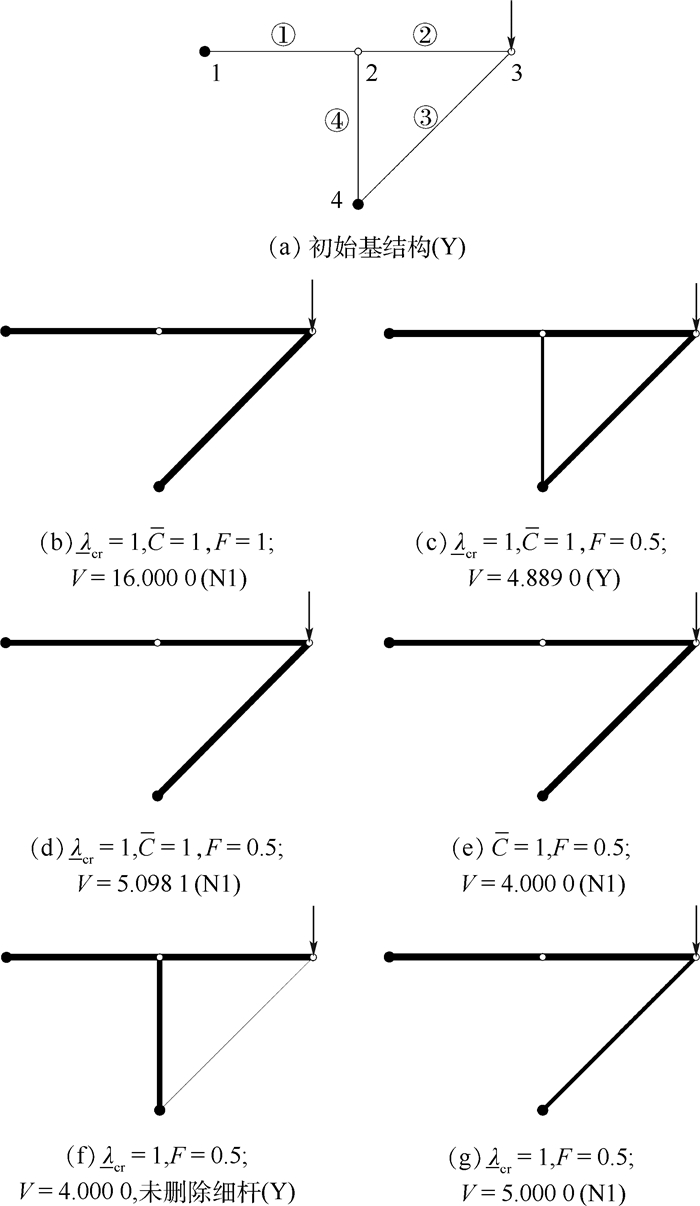图 5 4杆桁架基结构及不同约束和载荷值下的拓扑优化结果 Fig. 5 4-bar truss ground structure and topology optimization results under different constraints and loads

图选项

为说明载荷对优化结果的影响，将载荷幅值F分别取为1和0.5，优化后拓扑(消去过细杆件)分别如图 5(b)和图 5(c)所示。图 5(b)所示拓扑的临界屈曲载荷因子为1.211 1，满足全局稳定约束且非临界；结构柔度为1.0000，柔度约束临界。该解与仅考虑柔度约束(C=1)的解完全相同，为几何不稳定拓扑。图 5(c)所示拓扑的临界屈曲载荷因子为1.000 0，全局稳定约束临界；结构柔度为1.000 0，柔度约束也临界，该解几何稳定。实际上，若基结构几何不稳定(仅含杆①②③)，优化结果也可满足全局稳定约束。取F=0.5时，问题C的解如图 5(d)所示，虽然几何不稳定，但该解的临界屈曲载荷因子为1.000 0，载荷下的柔度为1，严格满足全局稳定约束和柔度约束。相比灵活性更大的4杆基结构下的最优解(图 5(c)，体积为4.889 0)，3杆基结构下的优化空间变小，最优解满足约束所需的材料体积(5.098 1)略有增加。可见满足全局稳定约束时，桁架拓扑可能几何稳定，也可能几何不稳定，载荷的影响很大。
下面考虑F=0.5时约束单独作用的情况。若不考虑全局稳定约束而仅考虑柔度约束，所得解(图 5(e))的柔度为临界值1.000 0，但其临界屈曲载荷因子为0.605 6，不满足全局稳定约束。若不考虑柔度约束而仅考虑全局稳定约束，所得解(图 5(f))的临界屈曲载荷因子为临界值1.000 0，但该解柔度值为4.209 2×10⁴，远超过柔度上限C=1。可见，不同约束下的优化结果存在极大差异，优化结果并不一定能满足未考虑的约束条件。
全局稳定解(图 5(f))存在更加严重的问题：为满足全局稳定约束，内力为零的杆④具有相当大的横截面积；作为主要承力杆件的杆③横截面积却很小，其应力绝对值远远高出杆①②(相差约5个数量级)；若杆③因过细而在后处理过程中被删除，剩余的①②④杆拓扑将不能承担给定载荷。若对仅含杆①②③的几何不稳定基结构求解仅考虑全局稳定约束的体积最小化问题，所得解如图 5(g)所示。对比可见，增大杆④的横截面积同时减小杆③的横截面积，能够以更小的结构总体积满足全局稳定约束。
应当说明，K奇异时，线性稳定的广义特征值方程(1h)必然存在零特征值。几何不稳定拓扑必然存在与结构动不定度k_DOF对应个数的零值(数值求解时一般是绝对值近似为0的值)载荷因子。若桁架(近似)几何不稳定，在计算临界屈曲载荷因子时，应将这些近似为0的值排除。

2.2.4 算例4——不同约束方案对比 如图 6(a)所示的88杆空间桁架基结构，其空间尺寸为8×1×2，左侧4个节点固定，右侧顶部的2个节点处作用竖直向下、幅值分别为0.666 7的集中载荷。该算例取自文献[14]。

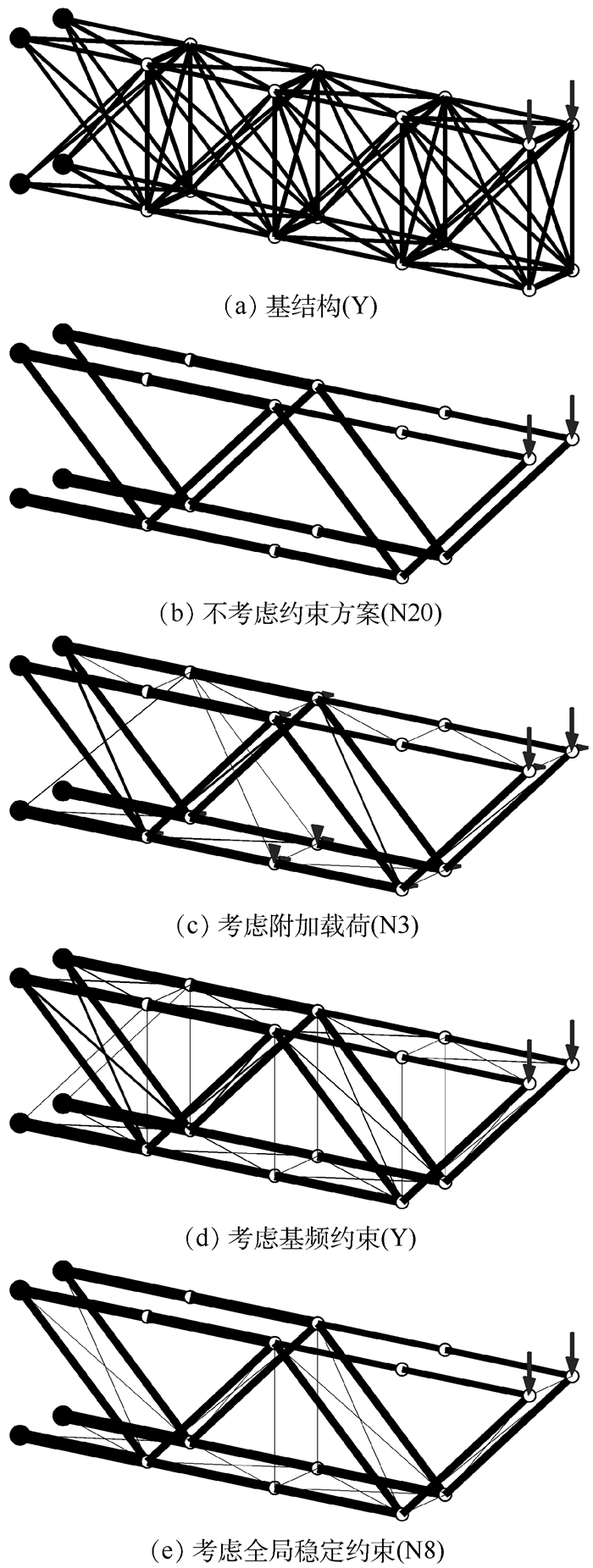图 6 88杆桁架基结构及不同设定下优化后的拓扑 Fig. 6 88-bar truss ground structure and optimized topologies under different settings

图选项

取C=0.03，在不考虑任何约束方案的情况下求解问题A，优化后拓扑见图 6(b)；根据图 6(b)结果，在受压杆件连接的节点上施加附加载荷，幅值取为主载荷的1%，取C=0.03求解问题A，优化后拓扑见图 6(c)；考虑基频约束，取C=0.03、f=0.080 9求解问题B，优化后拓扑见图 6(d)；考虑全局稳定约束，取C=0.03、λ_cr=1求解问题C，优化后拓扑见图 6(e)。结构特性对比见表 2。
表 2 88杆桁架基结构及优化结果特性 Table 2 Properties of ground structure and optimized topologies for 88-bar truss

结构	杆数	体积	几何稳定	柔度	基频	临界屈曲载荷因子
基结构	88	157	是	0.03	0.080 9	64.244*
图 6(b)	22	66.879	否(N20)	0.03		307.39
图 6(c)	42	67.704	否(N3)	0.03		1.133 8
图 6(d)	55	67.392	是	0.03	0.079 5	0.548 9
图 6(e)	41	66.927	否(N8)	0.03		0.869 1
注：*表示本文分析所得基结构的临界屈曲载荷因子为64.244，与Nastran分析结果一致；文献[14]中该数据值为1.074，疑有误。

表选项






对本例，仅方案B(考虑基频约束)所得优化后拓扑是几何稳定的，其余方案所得拓扑均存在不同程度的几何不稳定。该例有以下问题需要说明：①图 6(c)和图 6(e)所示结果中的不稳定节点在主载荷下均为受拉节点，在其周围不形成横向支撑可能更加符合工程要求，本文仅研究优化结果的几何稳定性，对此不作讨论；②优化完成后滤除细杆对结构柔度几乎没有影响，但对基频、临界屈曲载荷因子等特征值类的特性影响较大，图 6(d)所示拓扑的基频和图 6(e)所示拓扑的临界屈曲载荷因子相比约束值均有一定程度的降低，但结果的几何稳定性未发生质变；③所有优化结果中22根主要杆件的构型基本类似，图 6(c)~图 6(e)所示拓扑相比图 6(b)多了细杆支撑，临界屈曲载荷因子却小了很多，这是因为细杆的加入使原先被忽略的近似为0的特征值变为很小的有限值，从而被提取为临界屈曲载荷因子。
2.3 对几何稳定约束方案的讨论 根据算例1，考虑附加载荷并不能确保优化后拓扑几何稳定。附加载荷作用节点的选择对优化结果的几何稳定性有很大影响。几何不稳定桁架存在不能承载的自由度。当载荷不作用于这些自由度时，平衡方程相容，位移有解；否则结构将垮塌，节点位移和结构柔度将趋于无穷大，此时平衡方程不相容，位移无解。柔度约束的存在能够避免优化结果出现第2种情况，但几何不稳定拓扑处于不稳定平衡状态(第1种情况)时并不影响柔度约束的满足。可见，考虑附加载荷的实质是使优化结果保留对附加载荷的承载能力，该方案只是在一定程度上增加了优化结果几何稳定的概率，并不一定能保证优化后拓扑几何稳定。
算例2中，在约束上下限合理取值的前提下，优化模型中考虑基频约束可保证优化后的拓扑几何稳定。实际上可以证明，满足基频约束的结构必然几何稳定(详见附录B)。一个关键问题在于，约束的满足是否需要过细杆件。若不同约束的相对严格程度差距较大，优化结果中保留的粗杆主要用于满足严格约束，当粗杆不能同时满足宽松约束时，结果中的细杆对满足宽松约束具有不可或缺的作用，一旦过细杆件在后处理过程中被删除，这些宽松约束往往就不再满足。算例2的两种极端情况说明，即使对适定的优化问题，约束上下限取值不合理也会导致计算结果不合理甚至引起数值求解方面的困难。
根据算例3，不论初始结构是否几何稳定，满足全局稳定约束均不能保证优化后拓扑的几何稳定性。本文强调，全局稳定性是与载荷作用下的内力分布密切相关的结构属性，几何稳定性则是桁架拓扑的固有属性，前者与载荷相关，后者与载荷无关，二者之间没有必然联系。仅考虑全局稳定约束的桁架结构体积最小化问题，虽然通过计算得到了最优解，但该问题目标与约束函数的设定可能并不合理。至少从本文给出的算例来看，优化结果中部分杆件的横截面积大小与其内力水平并不是正相关的，由此造成了各杆应力水平的巨大差距。分析发现，这种不合理的应力分布的确能以更小的结构体积满足全局稳定约束，但并不符合实际工程的要求。
3 结论 1) 通过对4种判定方法的对比，确定了桁架结构几何稳定的准确定义，可避免无效判定方法的盲目使用；结合不同判定方法的特点给出一种简单流程，可用于桁架结构几何稳定性的快速准确判定。
2) 使用统一的SDP模型对3种几何稳定约束方案的对比表明，在优化模型中考虑附加载荷或全局稳定约束均不能确保优化后拓扑的几何稳定性，但在约束合理设置的情况下，考虑基频约束则可以保证。
3) 传统的基结构法框架存在删除过细杆件的后处理方式。由于删除细杆对结构特性的影响，约束上下限设置的合理性会影响计算结果的合理性甚至优化问题数值求解的正确性。为避免对细杆的处理，下一步可考虑在基于独立拓扑变量的基结构法框架下进行对比研究。
4) 指出桁架结构的几何稳定性是一种仅与拓扑构型相关的属性，与载荷无关，这是桁架几何稳定性与局部稳定性、全局稳定性的本质区别。桁架结构全局稳定并不能保证其几何稳定。
5) 仅在全局稳定约束下进行桁架结构体积最小化设计，所得结果的应力分布水平可能极不合理，不满足实际工程要求。可见，随着结构优化问题建模和求解能力的不断提高，对不同约束组合下优化问题的适定性、约束之间的相互作用以及约束本身特性的研究也应引起足够注意。
附录A 刚度矩阵K正定与平衡矩阵A行满秩的等价性证明 记矩阵A的秩为rank(A)，首先给出矩阵秩的一些性质：
① 对任意矩阵A∈C_r^m×n，有

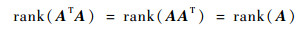(A1)

② 若矩阵P∈C^m×m和Q∈C^n×n均可逆，则对任意矩阵A∈C_r^m×n，有

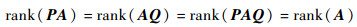(A2)

根据有限元理论，桁架结构的刚度矩阵K∈R^{(d×n－c)×(d×n－c)}，平衡矩阵A=B^T∈R^{(d×n－c)×m}。其中:d为问题的空间维度；n为节点数量；c为被约束的自由度数量；m为杆件数量；B为结构的几何矩阵。
由于桁架结构的弹性矩阵D∈R^m×m是对角线元素均为正值的对角满秩方阵，因此存在对角满秩方阵P∈R^m×m使得D=PP^T。故刚度矩阵:

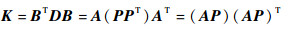由于AP∈R^{(d×n－c)×m}，根据性质①有

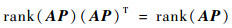又由于矩阵P可逆，由性质②可知：

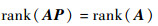因此可得

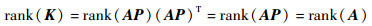(A3)

刚度矩阵K正定即满秩，rank(K)=d×n－c，由式(A3)知rank(A)=d×n－c，也即平衡矩阵A行满秩，等价关系得证。
附录B 满足基频约束的桁架必然几何稳定证明 很多文献提到基频约束能够确保桁架结构的几何稳定性，但没有给出相关说明。本文给出一种简单解释。
基频约束的半定形式为，其中的特征值下限λ>0；结构几何稳定的等价条件为刚度矩阵正定，即。仅需证明

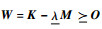
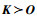
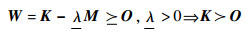记结构相关矩阵K、M和W的维度均为l×l。满足基频约束时，矩阵W半正定，其特征值均非负，即有λ_i(W)≥0, i=1, 2, …, l。根据有限元理论，桁架结构的质量矩阵M总是对称正定的，其特征值均为正，记其最小特征值为ε>0，则有λ_i(M)≥ε，i=1, 2, …, l。则对i=1, 2，…, l，总有


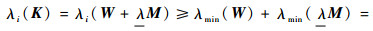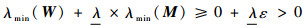其中：第1个不等式使用了矩阵理论中的Weyl定理(可参见文献[31])。矩阵K的特征值均为正，故，命题得证。直观上，W半正定，正定项λM的存在使K=W+λM的正定性得到了强化。

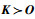
参考文献

[1]	RULE W K. Automatic truss design by optimized growth[J]. Journal of Structural Engineering, 1994, 120(10): 3063-3070. DOI:10.1061/(ASCE)0733-9445(1994)120:10(3063)
[2]	MCKEOWN J J. Growing optimal pin-jointed frames[J]. Structural Optimization, 1998, 15(2): 92-100.
[3]	MARTíNEZ P, MARTí P, QUERIN O M. Growth method for size, topology, and geometry optimization of trusss structures[J]. Structural and Multidisciplinary Optimization, 2007, 33(1): 13-26.
[4]	HAGISHITA H, OHSAKI M. Topology optimization of trusses by growing ground structure method[J]. Structural and Multidisciplinary Optimization, 2009, 37(4): 377-393. DOI:10.1007/s00158-008-0237-4
[5]	HOOSHMAND A, CAMPBELL M I. Truss layout design and optimization using a generative synthesis[J]. Computers and Structures, 2016, 163: 1-28. DOI:10.1016/j.compstruc.2015.09.010
[6]	DORN W, GOMORY R, GREENBERG M. Automatic design of optimal structures[J]. Journal de Mechanique, 1964, 3: 25-52.
[7]	TYAS A, GILBERT M, PRITCHARD T. Practical plastic layout optimization of trusses incorporating stability considerations[J]. Computers and Structures, 2006, 84: 115-126. DOI:10.1016/j.compstruc.2005.09.032
[8]	DESCAMPS B, COELHO R F. The nominal force method for truss geometry and topology optimization incorporating stability considerations[J]. International Journal of Solids and Structures, 2014, 51: 2390-2399. DOI:10.1016/j.ijsolstr.2014.03.003
[9]	OHSAKI M, KATOH N. Topology optimization of trusses with stress and local constraints on nodal stability and member intersection[J]. Structural and Multidisciplinary Optimization, 2005, 29(3): 190-197.
[10]	CERVEIRA A, AGRA A, BASTOS F, et al. A new branch and bound method for a discrete truss topology design problem[J]. Computational Optimization and Applications, 2013, 54(1): 163-187. DOI:10.1007/s10589-012-9487-6
[11]	MELA K. Resolving issues with member buckling in truss topology optimization using a mixed variable approach[J]. Structural and Multidisciplinary Optimization, 2014, 50(6): 1037-1049. DOI:10.1007/s00158-014-1095-x
[12]	冷国俊, 张卓, 保宏, 等. 考虑重叠过滤及稳定性约束的桁架拓扑优化方法[J]. 工程力学, 2013, 30(2): 8-12. LENG G J, ZHANG Z, BAO H, et al. Topology optimization of truss structure based on overlapping-filter and stability constraints[J]. Engineering Mechanics, 2013, 30(2): 8-12. (in Chinese)
[13]	GUO X, CHENG G D, OLHOFF N. Optimum design of truss topology under buckling constraints[J]. Structural and Multidisciplinary Optimization, 2005, 30(3): 169-180. DOI:10.1007/s00158-004-0511-z
[14]	KO?VARA M. On the modelling and solving of the truss design problem with global stability constraints[J]. Structural and Multidisciplinary Optimization, 2002, 23(3): 189-203.
[15]	DEB K, GULATI S. Design of truss-structures for minimum weight using genetic algorithms[J]. Finite Elements in Analysis and Design, 2001, 37(5): 447-465. DOI:10.1016/S0168-874X(00)00057-3
[16]	SAVSANI V J, TEJANI G G, PATEL V K, et al. Modified meta-heuristics using random mutation for truss topology optimization with static and dynamic constraints[J]. Journal of Computational Design and Engineering, 2017, 4(2): 106-130. DOI:10.1016/j.jcde.2016.10.002
[17]	RICHARDSON J N, ADRIAENSSENS S, BOUILLARD P, et al. Multiobjective topology optimization of truss structures with kinematic stability repair[J]. Structural and Multidisciplinary Optimization, 2012, 46(4): 513-532. DOI:10.1007/s00158-012-0777-5
[18]	AHRARI A, DEB K. An improved fully stressed design evolution strategy for layout optimization of truss structures[J]. Computers and Structures, 2016, 164: 127-144. DOI:10.1016/j.compstruc.2015.11.009
[19]	PELLEGRINO S, CALLADINE C R. Matrix analysis of statically and kinematically indeterminate frameworks[J]. International Journal of Solids and Structures, 1986, 22(4): 409-428. DOI:10.1016/0020-7683(86)90014-4
[20]	PELLEGRINO S. Structural computations with the singular value decomposition of the equilibrium matrix[J]. International Journal of Solids and Structures, 1993, 30(21): 3025-3035. DOI:10.1016/0020-7683(93)90210-X
[21]	阎军, 杨春秋. 计算结构力学[M]. 北京: 科学出版社, 2014: 1-3. YAN J, YANG C Q. Computational structural mechanics[M]. Beijing: Science Press, 2014: 1-3. (in Chinese)
[22]	修乃华, 罗自炎. 半定规划[M]. 北京: 北京交通大学出版社, 2014: 1-79. XIU N H, LUO Z Y. Semidefinite programming[M]. Beijing: Beijing Jiaotong University Press, 2014: 1-79. (in Chinese)
[23]	BEN-TAL A, NEMIROVSKI A. Robust truss topology design via semidefinite programming[J]. SIAM Journal on Optimization, 1997, 7(4): 991-1016. DOI:10.1137/S1052623495291951
[24]	OHSAKI M, FUJISAWA K, KATOH N, et al. Semi-definite programming for topology optimization of trusses under multiple eigenvalue constraints[J]. Computer Methods in Applied Mechanics and Engineering, 1999, 180(1-2): 203-217. DOI:10.1016/S0045-7825(99)00056-0
[25]	BEN-TAL A, JARRE F, KO?VARA M, et al. Optimal design of trusses under a nonconvex global buckling constraint[J]. Optimization and Engineering, 2000, 1(2): 189-213. DOI:10.1023/A:1010091831812
[26]	ACHTZIGER W, KO?VARA M. On the maximization of the fundamental eigenvalue in topology optimization[J]. Structural and Multidisciplinary Optimization, 2007, 34(3): 181-195. DOI:10.1007/s00158-007-0117-3
[27]	STURM J F. Using SeDuMi 1.02, a MATLAB toolbox for optimization over symmetric cones[J]. Optimization Methods and Software, 1999, 11(1-4): 625-653. DOI:10.1080/10556789908805766
[28]	TüTüNCü R H, TOH K C, TODD M J. Solving semidefinite-quadratic-linear programs using SDPT3[J]. Mathematical Programming, 2003, 95(2): 189-217. DOI:10.1007/s10107-002-0347-5
[29]	FIALA J, KOČVARA M, STINGL M.PENLAB: A MATLAB solver for nonlinear semidefinite optimization[J/OL].(2013-11-20)[2018-08-20].http://arxiv.org/abs/1311.5240.
[30]	KANNO Y, OHSAKI M, KATOH N. Sequential semidefinite programming for optimization of framed structures under multimodal buckling constraints[J]. International Journal of Structural Stability and Dynamics, 2001, 1(4): 585-602. DOI:10.1142/S0219455401000305
[31]	张贤达. 矩阵分析与应用[M]. 2版. 北京: 清华大学出版社, 2013: 61-67. ZHANG X D. Matrix analysis and applications[M]. 2nd ed. Beijing: Tsinghua University Press, 2013: 61-67. (in Chinese)