时间触发网络中TT流量的调度问题常用可满足模理论(Satisfiability Modulo Theories,SMT)进行求解,通过设置网络拓扑和流量关系等约束,生成满足约束的TT时间触发调度表[3]。此方法的缺点是不能直接对得出的调度表进行优化,且计算速度过于缓慢,对于实际的大型拓扑很难在短时间内得到封闭解,并且很难在短时间内适应设计的变化。文献[4]采用了增量化调度方法,但在增量化过程中却并没有给出有效的指导信息或启发式函数,致使最终调度表性能无法优化。还存在部分方法采用遗传算法等进行优化,但是此类方法常常相当耗费时间,且完全无法泛化,对于稍有改变的消息分布即需要完全重新计算,缺乏计算效率[4-5]。
近年来,基于神经网络强化学习在搜索、规划等领域取得了非常大的成功,对于旅行商人等NP问题均有较好的表现[6-7]。在围棋领域,强化学习与树搜索结合的AlphaGo超越了人类水平[8]。强化学习的方法也将会被用到更多的场景。
本文贡献在于将基于增量化调度方法的调度任务用马尔可夫过程来完全描述,将每次增量化调度用状态、动作、奖励表示,以此在搜索过程中提供尽量多的辅助搜索信息。同时,利用深度强化学习的方法,结合树搜索,以尽量减小延迟时间为目标,寻找近似最优的时间触发调度表。并且,模型具备一定的泛化能力,可在较短时间内响应消息分布近似的时间触发调度求解问题;在消息分布与之前完全不同时,可以退化为随机搜索方法,也能较快地得出一个可行解。
1 流量调度方法 1.1 马尔可夫模型与强化学习 由于消息的帧长、周期、偏置时间各不相同而导致搜索特别复杂。但是从调度的角度看,每一次调度一条消息均可以看作一个状态,当前状态可以反映所有信息,不需要考虑历史状态、动作等。以上调度过程非常符合马尔可夫过程的特点,在这个基础上,可以将此转换为一个马尔可夫模型,用树搜索的方法处理,每一个状态即为一个节点。此时这个问题也能看作一个条件优化问题[9],在特定的约束条件下满足目标或最大化收益。
由于使用到强化学习,定义状态、动作、奖励如下。
状态?状态定义为链路目前的排布方式。状态尽量表示当前调度表的所有特征。但是状态的表示不能太过复杂以致于计算过于缓慢。
动作?动作定义为当前消息在当前链路中的偏置。这里将每条消息的每一项偏置分离,分为第一项偏置和其余偏置。第一项可决定消息的传输位置信息,后面的偏置均为在可得出调度表的情况下越小越好。
奖励?奖励定义为这次调度的成功与否和端到端延迟的数值。在调度过程中,很难知道当前的调度方式是否为全局最优,采用如下方法:在一次调度结束后,从总体情况判断应该给出的奖励。奖励值的大小可以根据全局延迟时间的大小进行确定。
图 1所示为强化学习的基本原理。将调度过程转换为一个具有马尔可夫特性的过程,将整个调度的信道作为强化学习的环境。首先根据状态使用动作与周围环境进行交互,在动作和环境的作用下,可以得到新的环境,同时环境会给出奖励信号,以反馈在这个环境下使用这个动作的价值。如此循环下去,策略与环境进行不断地交互从而产生新的数据。强化学习算法利用产生的数据不断优化自身使用动作的选择,并再与环境交互,产生新的数据,并利用新的数据进一步改善自身动作的策略。经过数次迭代学习后,最终可以学习到完成相应任务的最优策略。
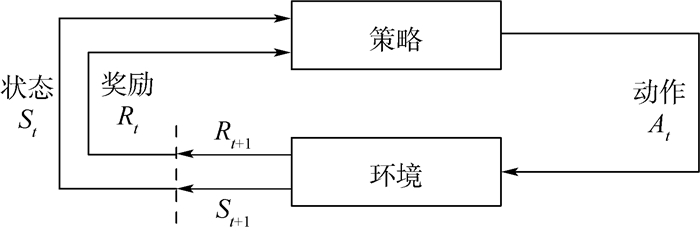 |
| 图 1 强化学习的基本原理 Fig. 1 Fundamental principle of reinforcement learning |
| 图选项 |
但是在很多情况下,仅仅依靠随机探索很难得到有用的样本,需要使用树搜索的方法加强探索,使在训练初期尽快得到较好的样本训练[10]。
1.2 搜索策略 在本文提出的调度方法的搜索框架中采用深度优先与最优优先结合的搜索,并剪掉明显不能找到结果的分支,以尽快找到可行解,如算法1所示, 此搜索框架仅考虑每条消息在第一条链路中的偏置时间,消息在后续转发节点中的偏置采用算法2的策略来选择,以完成消息在整个传输路径上的偏置区间搜索。
算法1?消息调度方法(SCHEDULE)。
1 初始化最大探索次数tmax,消息数目x。
2 i =0, t=0
3 while i < x
4 ??while t < tmax
5 ????search()
6 ????if t==tmax
7 ??????backtracking()
8 ??????t=0
9 ????else
10 ??????t+=1
11 ????i+=1
注:search()为搜索偏置可用时间片;backtracking()为回溯。
算法2 ?各级单跳延迟时间的选择。
1 初始化探索次数t,最大探索次数tmax,
2 技术延迟lower,最坏延迟上限upper,参数alpha。
3 search()
4 while t < tmax
5 ????diff=alpha*(upper-lower)*t/tmax
6 ????higher=lower+diff
7 ????delay=random_choice(lower, higher)
8 ????t+=1
9 ??backtracking()
注:random_choice为在这个范围内随机选择。
对于后续转发节点的偏置时间,有3种选择方法:①完全随机搜索;②完全贪婪搜索;③两者结合,进行限制选择区间的随机搜索。方法①不对端到端延迟作额外限制,这样容易也能够较快地得出结果,但是相应的所得到的调度表可能存在较大端到端延迟。方法②严格限制端到端延迟,如果能搜索出结果,那么此结果即为最优结果,但是很多情况下根本不存在这样的调度表,或者需要近乎遍历所有状态,造成开销过于庞大。方法③为两者结合,将搜索的端到端延迟限制在一定的置信区间,在这个区间内进行随机搜索。如果能得到一个调度表,那么将这一个调度表作为一个样本。这种方法的优势在于,搜索轨迹不会快速收敛到局部最优;得到的调度表不会存在特别大的端到端延迟,对于进一步探索和训练有很大的促进作用;同时此方法存在置信区间,可以非常方便地调整,既不会难以得出调度表结果,也不会耗费大量时间,并可以在区间中继续增加条件,使搜索成功率更高,以得到更优的调度表。
1.3 强化学习训练 在搜索阶段,可以迅速得到端到端延迟较小的调度表,但是由于搜索策略的限制,这样的调度表仍然有很大的优化空间。希望根据输入消息的分布的不同,能得出相应分布更好的消息调度表,在本文中使用强化学习的方法进行训练。由于消息调度问题为NP问题[11],难以求得全局最优解,可以认为不存在样本的标签,只能采用强化学习的方法进行训练和测试。
在训练阶段,由于消息的偏置可选择的范围太大,计算梯度时会造成梯度太大而无法优化,在具体计算时对其采用对数化的处理方法。同时考虑到同样的方差对较大偏置和较小偏置的贡献并不一样,本文对不同偏置处的方差影响通过权重进行度量。用初始搜索所得样本对神经网络进行预训练,将已得到的轨迹赋予标签。在这个阶段,目标函数采用改进的均方差计算:
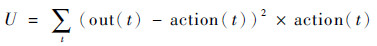 | (1) |
此时已经得到一整条训练轨迹,即可在每个状态state(t),使神经网络输出out(t)逼近action(t),不能只逼近所提供的样本,相应地需要对输出提供一定的噪声,以此作进一步的探索和适应。取神经网络的输出作为中心,取一个宽度有限的区间,在这个区间中均匀采样作为消息偏置,将此操作记作linear函数。详细算法如算法3所示。
算法3?模仿学习方法(IMITATION)。
1 初始化神经网络参数,总训练次数Kmax,
2 端到端延迟阈值end2end。
3 k=0
4 while k < Kmax
5 ??delay=SCHEDULE(linear())
6 ??if delay < end2end
7 ????end2end=delay
8 ??train(L) use(1)
9 ??k+=1
对于TT消息而言,当消息数量增加、帧长增长时,初始偏置对于调度表设计将产生直接的影响。虽然消息的偏置为一个个确定的、离散的值,但是由于可以选择的值太多,动作空间太大,所以将它化为连续值来处理,处理完毕后将其离散化得到调度表。
可以采用策略梯度的方法[12-13]。在最初收集轨迹阶段采用改进的贪婪策略,在每一个状态处都采取尽量最小化端到端延迟的动作,并用神经网络将策略参数化,寻找最优的参数使强化学习的目标最大,即最小化所有消息的端到端延迟,直到算法收敛或迭代次数到达上限的时候即算法收敛。此时搜索空间相比于初始阶段较小,在这个阶段应使用较小学习率。
首先设置目标函数为
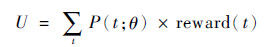 | (2) |
式中:P(t; θ)为t时刻,策略选择到已执行动作action的概率;reward(t)为在时刻t执行了action后所得到的奖励值。那么U的含义即为:这一条轨迹所得到的总的奖励值。损失函数即为对参数化后的目标函数求梯度,以使目标函数以最快的速度向最大化目标函数的方向收敛:
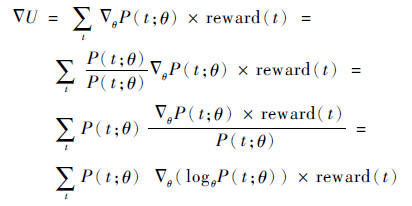 | (3) |
在强化学习训练过程中,由于需要不断探索,于是将输出值采用正态分布描述,使神经网络的输出为此正态分布的均值和方差。这样既能使效果较好的能被更多选择到,也能同时探索更丰富的偏置值,在较优值附近常能得到更优选择,同时亦有小概率探索距离较远的样本,不会过早收敛。将这种输出分布的选择记作normal,如算法4所示。
算法4 ?强化学习方法(REINFORCEMENT)。
1 初始化神经网络参数,总训练次数Kmax。
2 k=0
3 while k < Kmax
4 ??reward=SCHEDULE(normal)
5 ??train(U) use (3)
6 ??k+=1
这个阶段的探索,需要限制探索方向,首先这是一个条件优化问题,不能进行完全随机探索。文献[12, 14]采用的均为带惩罚项的优化策略,但是实际操作中不能出现不符合要求的解。其次探索相对的随机性不一定能得到更优的轨迹,样本利用率十分低。于是选择向下模拟数步搜索,即n步展开的方法。较多算法常采用1步展开,即每一步均判断是否符合需求,但是由于探索的深度浅,模型会较为短视,且一定程度上会由于阈值选择不够合理而造成搜索成功率降低;后者深度较深,模型较为有远见,阈值可随深度的变化而加以处理,但是计算量较大。同时,两者均能试探是否可以在探索过程中找到可行解。
这里拓展n步展开的方法,每到一个状态时,模拟之后n步搜索。如果在n步以后可以满足预先设定的端到端延迟最低要求,那么采用这一条轨迹继续进行;如果没有满足或消息无法调度,那么选择其他轨迹。此时预先设定的阈值可以使用动态方法确定,根据搜索的深度进行自适应[15]。同时需要选择模拟的最大深度n,如果n小,容易过早收敛到由初始值所限制的轨迹中,进而陷入局部最优解;如果n过大,计算开销则会非常大。可根据消息的总数等特征来确定。
由于是基于梯度的方法,在这个阶段的搜索具有较强的方向性;同时具备较强鲁棒性,在下一次遇到类似状态时,将会自适应地选择动作,并且策略能够不断进行学习和优化。
强化学习的训练方法分为时间差分方法和蒙特卡罗方法,由于本任务目标为得到全局最优调度表,在搜索过程中很难判断是否是一个阶段性的优秀的选择,所以采用蒙特卡罗方法进行训练。完整得出一条轨迹以后,再对整个搜索过程进行评估和训练。这种方法训练可能会使梯度有较大的方差,但是梯度是无偏的。
此时的训练可以继续采用模仿学习的方法,但搜索区域需要更为严格地限制,采用分段函数描述算法3中的linear函数。在策略梯度方法中常常会限制策略更新的速度,防止更新过快造成无法收敛的情况[12, 14],这里采用限制搜索区间宽度的方法。随着探索和训练的进行,由于算法逐渐收敛,大多数的探索所得结果均对训练没有帮助,可以适当改变区间宽度以探索更多区域。此时linear函数表示为
 | (4) |
式中:upper为随机探索区间的上界;lower为此区间的下界;backk(0 < k≤n, k∈N)为回溯次数; wku、bku(0 < k≤n, k∈N)为每个区间所对应的参数,可事先人为确定。
由于将偏置值进行了对数化,不同的偏置量需要采用不同的探索区间。具体算法同样如算法3所示。
2 实验 2.1 实验条件 设链路速率为100 Mbit/s,以太网帧的帧长范围为64~1 518 Byte,则每一帧传输的执行时间范围为6.72~123.04 μs,TT流量的周期通常为1~128 ms。为使环境既考虑逼真度,又考虑到复杂度,将消息执行周期与时间均取整数,参照ARINC 664 P7协议中对虚拟链路最小帧间间隔的约定,取流量周期仅为2的幂次[16]。采用空客A380客机的核心交换结构如图 2所示,其中SW为交换机,ES为端系统。与A380的消息规模类似,采用1 050条消息进行实验验证,规定好传输路线,仅进行调度不进行路径规划。即默认调度前已用算法优化选择传输链路,典型地,可以采用最短路径方法进行路径生成。
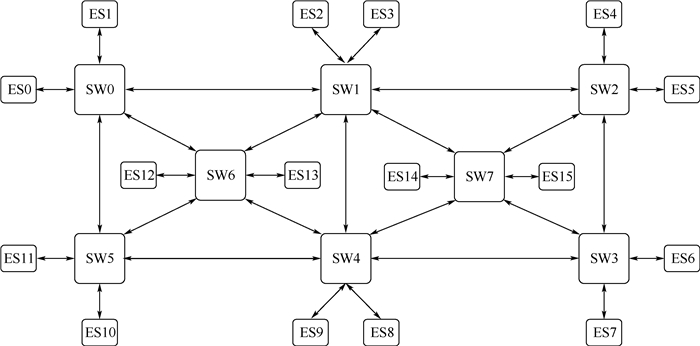 |
| 图 2 A380拓扑结构 Fig. 2 Topology of A380 |
| 图选项 |
为计算方便,将所有帧长归一化,且均取整数,将最短帧长取6 μs,化为3 000,其他均按此比例计算。单跳技术延时为最短帧执行时间,即3 000,最坏延时上限为最短帧执行时间的4倍。所有消息共2 656个调度实例,全网的技术延时归一化后为7 968 000,此时总延迟与平均延迟均为0。
神经网络参数:深度为4层,每层256个节点,激活函数采用elu函数。优化器采用adam优化器,模仿学习时学习率采用0.0005,强化学习时学习率采用0.000 1。n步模拟中n值取10。
2.2 实验结果 通过实验,可以得到如下结果,其中表 1为各方法的计算时间与平均延迟,图 3和图 4分别为预训练的损失函数与无预训练的强化学习延迟优化情况。可以看出,由于强化学习和经过由模仿学习预训练的强化学习有训练的过程,收敛后效果优于直接使用树搜索所得的结果。
表 1 各方法调度结果 Table 1 Each method scheduling results
| 方法 | 单次计算时间/s | 平均延迟(归一化) |
| SMT | 265.00 | 1355.30 |
| 树搜索 | 2.17 | 4.10 |
| 强化学习 | 5.03 | 1.70 |
| 强化学习* | 4.29 | 0.75 |
| 注:*表示使用模仿学习进行预训练。 | ||
表选项
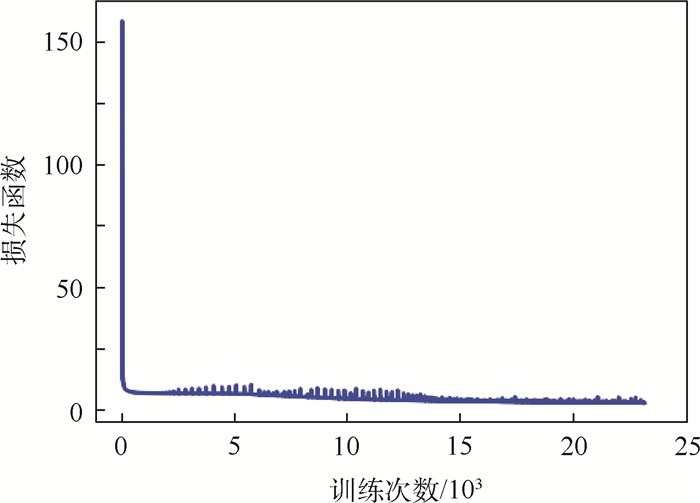 |
| 图 3 预训练损失函数变化 Fig. 3 Loss function change in pre-training |
| 图选项 |
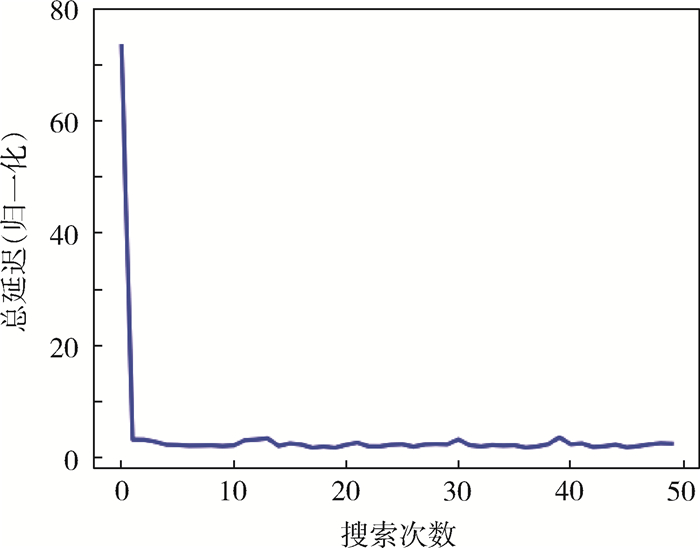 |
| 图 4 强化学习端到端延迟结果 Fig. 4 Reinforcement learning end-to-end delay results |
| 图选项 |
2.3 模型鲁棒性测试
2.3.1 帧长变化 将消息帧长按倍数变化,以此使消息分布与之前实验不同,将消息编号1~1 050。其中对2,3,5,7,11倍数编号的消息,其帧长乘以不同系数,详细操作如表 1所示。使消息的分布发生改变。端到端延迟及算法速度如表 2~表 5所示。图 5反映了算法收敛情况,其中实线为均值,着色区域为变化范围。
表 2 4种变化详细操作 Table 2 Detailed operation of four change methods
| 编号倍数 | 变化1 | 变化2 | 变化3 | 变化4 |
| 2 | 1.1 | 1.1 | 0.8 | 0.8 |
| 3 | 1.1 | 1.2 | 1.2 | 1.2 |
| 5 | 0.9 | 1.1 | 1.1 | 1.3 |
| 7 | 1.1 | 1.1 | 0.9 | 0.9 |
| 11 | 0.9 | 1.2 | 1.2 | 1.2 |
表选项
表 3 4种变化后端到端延迟结果 Table 3 End-to-end delay results of four variations
| 方法 | 变化1 | 变化2 | 变化3 | 变化4 |
| SMT | 1360.2 | 1365.6 | 1284.2 | 1324.1 |
| 树搜索 | 4.4 | 5.5 | 4.5 | 4.4 |
| 强化学习 | 2.3 | 2.1 | 2.1 | 2.1 |
| 强化学习* | 0.74 | 0.65 | 0.61 | 0.71 |
表选项
表 4 4种变化后收敛速度 Table 4 Convergence speed of four variations
| 方法 | 收敛速度/s | ||||
| 变化1 | 变化2 | 变化3 | 变化4 | ||
| SMT | |||||
| 树搜索 | |||||
| 强化学习 | 36 | 58 | 33 | 44 | |
| 强化学习* | 43 | 63 | 40 | 56 | |
表选项
表 5 4种变化后单次运行速度 Table 5 One-time running speed of four variations
| 方法 | 运行速度/s | |||
| 变化1 | 变化2 | 变化3 | 变化4 | |
| SMT | 281 | 287 | 267 | 274 |
| 树搜索 | 2.85 | 3.21 | 2.45 | 2.87 |
| 强化学习 | 5.12 | 6.45 | 5.58 | 6.25 |
| 强化学习* | 4.32 | 5.26 | 4.97 | 5.07 |
表选项
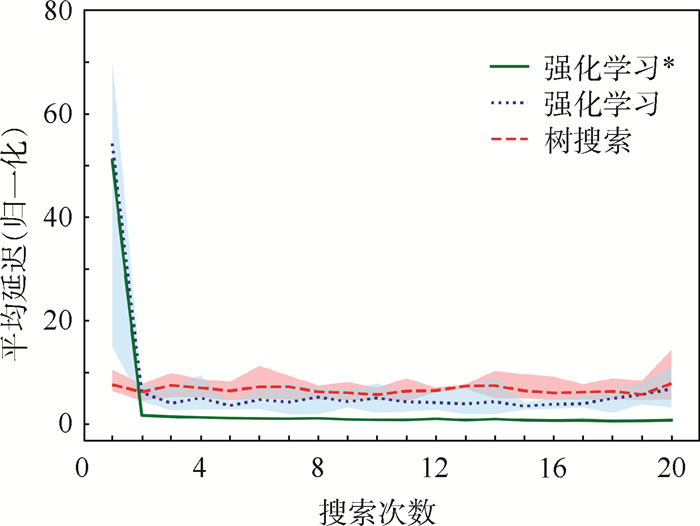 |
| 图 5 各项变化的平均端到端延迟收敛情况 Fig. 5 Average end-to-end delay until convergence for each change |
| 图选项 |
2.3.2 增加消息数量 在之前的1 050条消息中随机抽取一些消息并添加到最后,使需要调度的消息总数目增加。表 6为详细操作,表 7~表 9为端到端延迟和算法速度,图 6显示了算法收敛情况。
表 6 3种增加消息详细操作 Table 6 Detailed operation of three adding methods
| 操作 | 增加1 | 增加2 | 增加3 |
| 增加信息条数 | 6 | 60 | 120 |
| 总技术延时 | 8019000 | 8478000 | 8988000 |
表选项
表 7 增加消息后端到端延迟结果 Table 7 End-to-end delay results after adding frames
| 方法 | 增加1 | 增加2 | 增加3 |
| SMT | 1352.3 | 1586.7 | 1324.6 |
| 树搜索 | 2.5 | 2.9 | 4.5 |
| 强化学习 | 1.7 | 1.6 | 1.4 |
| 强化学习* | 0.68 | 0.86 | 0.85 |
表选项
表 8 增加消息后收敛速度 Table 8 Convergence speed after adding frames
| 方法 | 收敛速度/s | ||
| 增加1 | 增加2 | 增加3 | |
| SMT | |||
| 树搜索 | |||
| 强化学习 | 35 | 50 | 58 |
| 强化学习* | 32 | 41 | 48 |
表选项
表 9 增加消息后单次运行速度 Table 9 One-time running speed after adding frames
| 方法 | 运行速度/s | ||
| 增加1 | 增加2 | 增加3 | |
| SMT | 268 | 358 | 731 |
| 树搜索 | 2.24 | 2.34 | 2.52 |
| 强化学习 | 5.05 | 5.87 | 6.43 |
| 强化学习* | 4.56 | 5.15 | 6.37 |
表选项
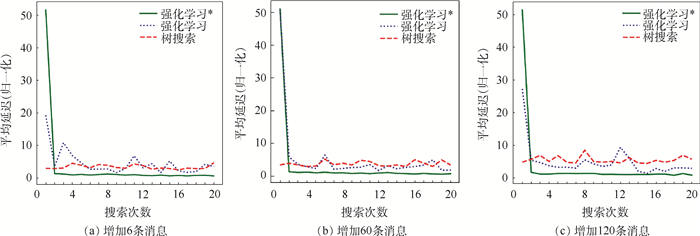 |
| 图 6 增加6,60,120条消息的平均端到端延迟收敛情况 Fig. 6 Average end-to-end delay until convergence of adding 6, 60, 120 frames |
| 图选项 |
可以看到,神经网络在最初的搜索中均会由于消息分布的变化而不适应,得出端到端迟极大的调度表,但是很快可以调整过来,尤其是经过预训练之后的神经网络能够稳定地拥有很小的端到端延迟。经过了强化学习和用模仿学习预训练过后的神经网络能够单次很快地搜索出表现优秀的调度表。在速度上和端到端延迟上均优于SMT求解器。两者相比,由于模仿学习与随机探索的组合添加了更多人为限制,在短时间内表现较之直接强化学习更加优秀。但是模仿学习需要预训练的过程,若当前消息与之前已训练的消息分布差异过大时,需要重新进行预训练;而直接强化学习方法则会退化为随机搜索,能够直接得出结果,并在这基础上进一步探索,整个训练过程时间大大快于模仿学习。此2种方法速度均快于SMT求解。
3 结论 本文建立了以马尔可夫描述的调度任务模型,并基于此提出了采用强化学习的TT通信调度方法,以可尽量获得调度表和缩短延迟时间作为优化目标,选择并调整流量发送时间的偏移量,得到具有全局优化意义的时间触发调度表,通过与A380组网规模类似的案例进行了模型验证。
基于所验证案例,本文方法计算速度为SMT方法的数十倍,且可以及时观察到有哪些难以调度的流量,以方便快速进行调整。
此外,实验证明了本文方法的有效性,基于强化学习的调度算法传输延迟大幅低于基于Yices的SMT方法,可以更快得到更好的调度表。
参考文献
| [1] | 王国庆, 谷青范, 王淼, 等. 新一代综合化航空电子系统构架技术研究[J]. 航空学报, 2014, 35(6): 1473-1486. WANG G Q, GU Q F, WANG M, et al. Research on architecture technology for new generation integrated avionics system[J]. Acta Aeronautica et Aastronautica Sinica, 2014, 35(6): 1473-1486. (in Chinese) |
| [2] | 熊华钢, 王中华. 先进航空电子综合技术[M]. 北京: 国防工业出版社, 2009: 2-13. XIONG H G, WANG Z H. Advanced avionics integration techniques[M]. Beijing: National Defense Industry Press, 2009: 2-13. (in Chinese) |
| [3] | STEINER W.An evaluation of SMT-based schedule synthesis for time-triggered multi-hop networks[C]//Real-Time Systems Symposium.Piscataway, NJ: IEEE Press, 2011: 375-384. |
| [4] | 孔韵雯, 李峭, 熊华钢, 等. 片间综合化互连时间触发通信调度方法[J]. 航空学报, 2018, 39(2): 321590. KONG Y W, LI Q, XIONG H G, et al. Time-triggered communication scheduling method for off-chip integrated interconnection[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(2): 321590. (in Chinese) |
| [5] | 李炳乾, 王勇, 谭小虎, 等. 基于混合遗传算法的TTE静态调度表生成设计[J]. 电子技术应用, 2016, 42(10): 96-99. LI B Q, WANG Y, TAN X H, et al. Hybrid-GA based static schedule generation for time-triggered Ethernet[J]. Application of Electronic Technique, 2016, 42(10): 96-99. (in Chinese) |
| [6] | RUMELHART D E, HINTON G E, WILLIAMS R J. Learning representations by back-propagating errors[J]. Nature, 1986, 323: 533-536. DOI:10.1038/323533a0 |
| [7] | KHALIL E B, DAI H, ZHANG Y, et al.Learning combinatorial optimization algorithms over graphs[C]//Neural Information Processing Systems, 2017: 6348-6358. |
| [8] | SILVER D, SCHRITTWIESER J, SIMONYAN K, et al. Mastering the game of Go without human knowledge[J]. Nature, 2017, 550(7676): 354-359. DOI:10.1038/nature24270 |
| [9] | GAL D, KRISHNAMURTHY D, MATEJ V, et al.Safe exploration in continuous action spaces[EB/OL].(2018-01-26)[2019-01-01].https://arxiv.org/abs/1801.08757. |
| [10] | KOCSIS L, SZEPESVARI C.Bandit based monte-carlo planning[C]//European Conference on Machine Learning, 2006: 282-293. |
| [11] | CRACIUNAS S S, OLIVER R S.SMT-based task-and network-level static schedule generation for time-triggered networked systems[C]//International Conference on Real-Time Networks and Systems, 2014: 45-54. |
| [12] | SCHULMAN J, LEVINE S, ABBEEL P, et al.Trust region policy optimization[EB/OL].(2015-02-19)[2019-01-01].https://arxiv.org/ahs/1502.05477. |
| [13] | SILVER D, LEVER G, HEESS N, et al.Deterministic policy gradient algorithms[C]//International Conference on Machine Learning, 2014: 387-395. |
| [14] | SCHULMAN J, WOLSKI F, DHARIWAL P, et al.Proximal policy optimization algorithms[EB/OL].(2017-07-20)[2019-01-01].https://arxiv.org/abs/1707.06347. |
| [15] | KORF R E. Depth-first iterative-deepening:An optimal admissible tree search[J]. Artificial Intelligence, 1985, 27(1): 97-109. |
| [16] | ARINC.Aircraft data network, Part 7.Avionics full-duplex switched ethernet network: ARINC 664P7[R].Washington, D.C.: ARINC, 2005. |
