随着军用无人机大量装备部队以及民用无人机的广泛应用，专业无人机操控手的需求缺口较大，加强对无人机操控手的基础训练，客观合理的评价操控手的飞行技能水平成为无人机发展应用亟待解决的关键问题^[1]。对飞机驾驶人员飞行技能的评价主要有主观法和客观法两种：主观法一般由专家观察飞行过程后对驾驶人员进行打分，如Kolb-Harper评价^[2]；客观法是选取飞行数据中的参数对驾驶员的飞行技能进行评价的方法。主观评价法具有实际操作简便等优势，应用较为广泛，但评价结果受评价人员情绪、动机、偏好、认知等因素影响较大，有时不能反映飞行操纵人员的实际操作情况。客观评价法克服了主观法的上述缺点，并随着快速数据存取记录器(QAR)等监控技术的进步^[3]越来越受到国内外专家的重视。
根据飞行数据快速、准确地识别飞行动作是利用客观法评估飞行质量的基础。在飞行动作识别方面，张玉叶等^[4]提出了一种基于主成分分析和距离判别分类的飞行动作识别方法，沈一超等^[5]利用贝叶斯网络实现了飞行动作的识别，但两种方法均需要典型飞行动作数据作为样本数据，在一定程度上限制了其应用。
目前评估无人机自身飞行品质和有人驾驶飞机操纵质量的研究较多，但研究无人机地面操纵人员的操纵质量评估的文献较少。如Holmberg^[6]、Cotting^[7]等提出了类似有人驾驶飞机的无人机飞行品质评估标准，但无人机本身和无人机地面操控人员属于不同的评价对象，不可混淆；刘莉雯^[8]、张龙^[9]、柳忠起^[10]等采用不同方法对有人驾驶飞机飞行员的操纵质量进行了评价，但有人驾驶飞机和无人机操纵方式和操纵环境差别较大，相关评价体系不能完全适用于无人机。在无人机操纵质量评估方面，夏长俊等^[11]对无人机平飞质量分析的主要内容及计算分析方法做了阐述，给出了相关参数的误差分析，但没有给出具体的平飞动作质量评价模型。彭阳和彭晓明^[12]提出了一种基于关键参数偏差的飞行动作质量分析方法，并以某型无人机“坡度45°~60°盘旋”飞行动作为例进行了分析。Zhou等^[13]利用VIKOR方法对某型无人机的着陆质量进行了评价。但无人机起飞、着陆、平飞、机动等不同飞行阶段，不同飞行动作的特点差异较大，评价指标和参数也应不同。单一的评价体系难以有效评定无人机操控手不同飞行技能的好坏，所以针对不同的飞行动作建立不同的评价体系成为需要解决的重要问题。平飞动作是无人机地面操纵人员首先需要掌握的基础技能，是考验无人机操控手的判断能力、心理素质以及操控能力的最基本的飞行动作，本文针对无人机操控手的平飞技能评估问题，建立了无人机平飞动作质量评价模型。
1 无人机平飞动作质量评价模型的建立 无人机平飞动作质量评价模型主要包含平飞动作识别和平飞动作打分两个环节，具体实现流程如图 1所示。

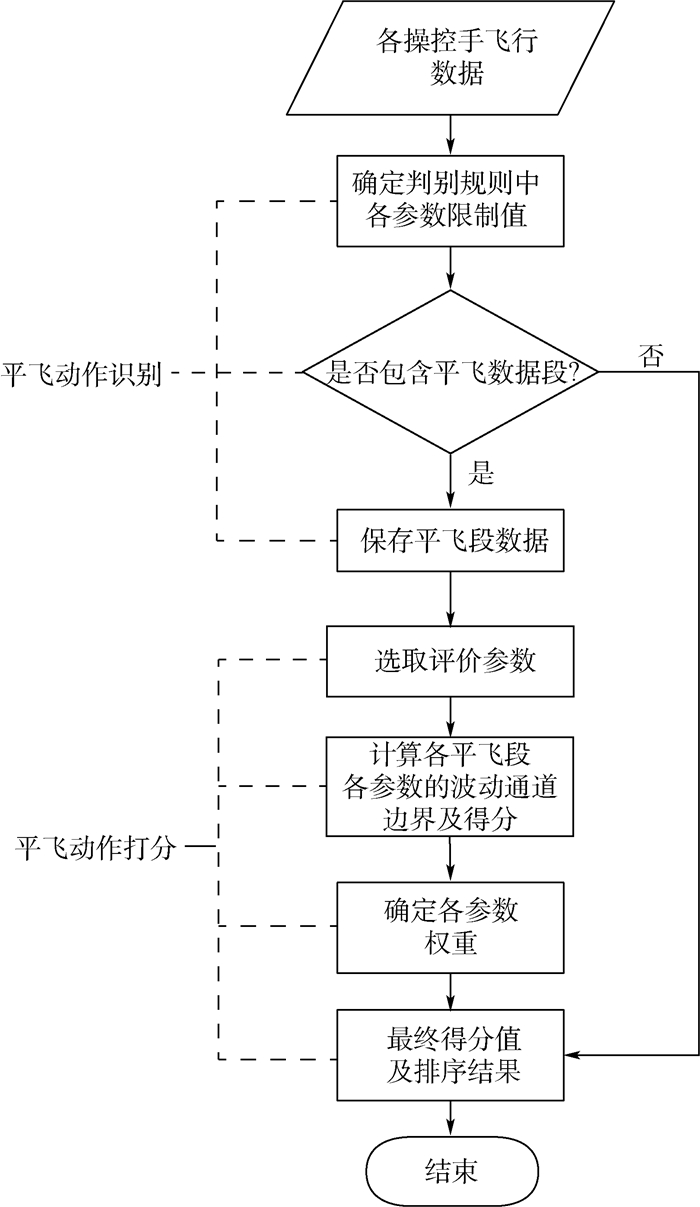图 1 评价模型实现流程图 Fig. 1 Flowchart for realizing evaluation model

图选项

1.1 平飞动作识别 飞行数据记录了无人机在空中的飞行状态及操控手对无人机的操作信息。根据无人机飞行数据可以进行基本飞行动作识别^[14]，从无人机飞行历程中提取有代表性的基本飞行动作的时间序列数据。
飞行动作最终体现在飞行参数的响应上，比如平飞就是无人机高度维持在某一稳定范围，爬升即为高度连续正变化，下滑即为高度连续负变化，所以可以根据飞行数据中的高度参数h及其变化率v_h来判别飞机的平飞动作，根据无人机平飞、爬升和下滑的不同特点，可以构建出下面的判别规则：

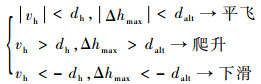其中:d_h为高度变化率的限制值; Δh_max为平飞段的最大高度差; d_alt为平飞动作的高度判别精度。加州伯克利大学^[15]的无人机自主着陆系统在各坐标轴上距离误差小于5 cm、角度误差小于5°；李樾等^[16]研究的无人机航迹跟踪方法的精度能达到2 m以内，本文选取d_alt=2 m作为平飞动作的高度判别精度，而高度变化率限制值应满足d_h＜d_alt，本文取d_h=0.8 m/s。即飞行高度变化率稳定在0.8 m/s以内且高度稳定在2 m以内的连续数据作为平飞动作数据。
平飞精度及高度变化率限制值的大小可以根据操控手的不同训练阶段进行设置，同一次评价中采用相同的平飞精度和高度变化率限制值。首先通过高度变化率限制值d_h确定可能的平飞范围，即判断无人机飞行是否趋于稳定状态，然后通过平飞动作的高度判别精度d_alt进一步判断无人机是否处于平飞状态。识别出的平飞数据段为时间段和对应的飞行参数，为直观表示平飞数据段，采用平飞时间段及其对应的高度数据表示，如图 2所示。

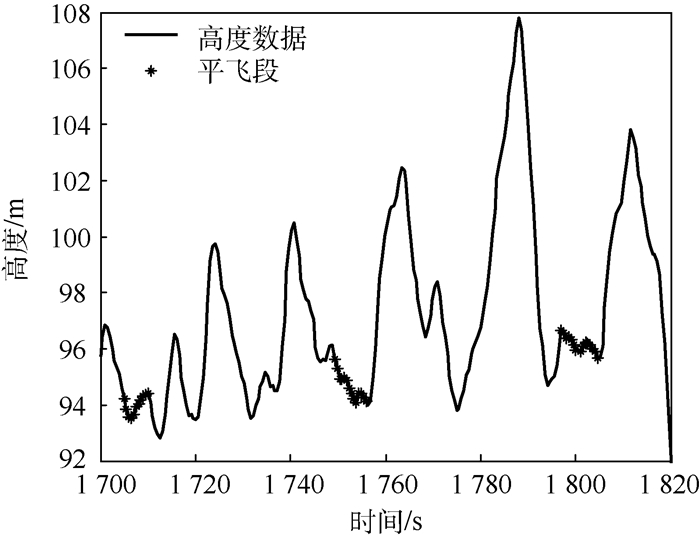图 2 典型平飞数据段 Fig. 2 Typical horizontal flight data segment

图选项

1.2 评价参数选取与波动通道的构建 飞行数据记录了无人机的多种飞行信息，这为评估操控手操作无人机的水平提供了重要依据。目前评估飞行员对各种飞行动作的完成情况，主要通过对某一个或两个飞行参数值的变化范围进行检测，如果变化范围没有超出指定飞行动作规定的参数值要求，那么操作合格。然而实际操作中，因为飞机的飞行动作取决于若干参数，所以要对飞行员操作的飞行动作进行正确评估，需要综合考虑多个参数的信息。本文选取对平飞动作较敏感的高度、速度、偏航角、滚转角和俯仰角作为平飞动作的评价参数，这5个参数的稳定性能够反映操控手控制无人机的平稳程度，确定评价参数后，即可构建各参数的波动通道。
数据通道的宽窄与数据本身波动幅度大小的变化直接相关，通道大小随着数据的形态和趋势自动调整，因而也可以反映无人机平飞趋势的变化。参考布林带(Bollinger Band)理论^[17]，布林带一共由3条线组成：通道上限制边界线U(t)、中轨线M(t)和下限制边界线D(t)，其表达式分别为

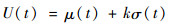(1)

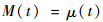(2)

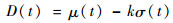(3)

式中：μ(t)为均值函数；σ(t)为标准差函数；k为通道宽度限制值，可以根据实际情况选取，本文取k=2。依据统计学的相关公式，可以通过样本函数x(t)(t=1, 2, …, N)计算得到时间序列的均值函数μ(t)和标准差函数σ(t)，继而确定飞行数据的波动范围。时间序列均值函数的估计值可由下式计算得到：

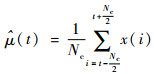(4)

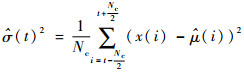(5)

均值估计函数和标准差估计函数在求解时要注意所选数据的窗长度，可选为连续数据点个数N_c，本文取N_c=20。高度数据的部分布林通道如图 3所示。

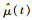
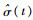
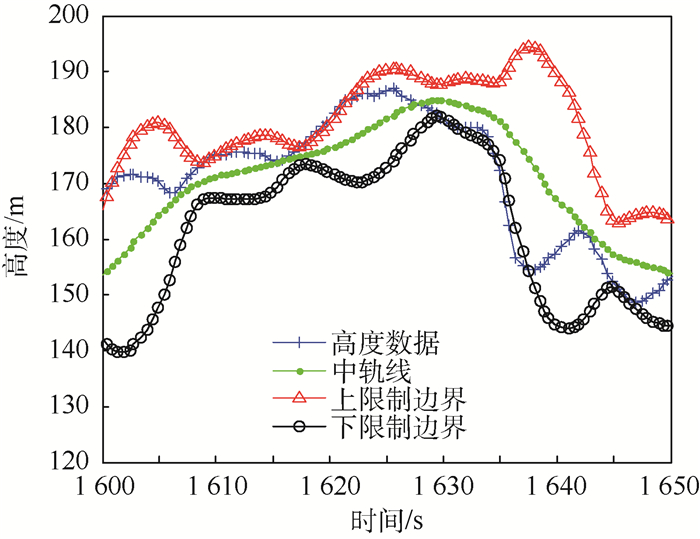图 3 布林线构成的数据带 Fig. 3 Data band constituted by Bollinger lines

图选项

以高度参数为例，将高度数据h(t)分别与下限制边界D(t)和中轨线M(t)作差，求两个差值的均值，即可得到高度参数的打分值s^h为

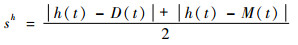(6)

将某操控手的第i个平飞段对应的高度数据输入波动通道模型，即可计算得到该操控手第i个平飞段的高度参数得分s_i^h。因为得分值大小从本质上是反映了飞行数据与均值的偏离程度和方差大小，所以平飞数据段得分值越低，表示操控手的平飞质量越好。
1.3 权重系数的确定 因为不同飞行参数对于评估操控手的权重是不同的，所以选择客观准确的评价指标权重系数对于准确评估飞行成绩起着非常重要的作用。本文采用“熵权法”计算指标权重，熵权法是一种客观的指标权重选取方法。
设某无人机操控手一次飞行任务数据中有m个平飞段，选取飞行数据中的n个监控参数，以X_ij表示第i个平飞段的第j个参数的得分值，则各个平飞段的评价矩阵如表 1所示。
表 1 无人机操控手飞行参数评分 Table 1 Scoring for flight parameters of UAV manipulators

平飞段	参数1	参数2	…	参数n
1	X11	X12	…	X1n
2	X21	X22	…	X2n
?	?	?	?	?
m	Xm1	Xm2	…	Xmn

表选项






由表 1中的评分数据组成多属性决策矩阵：

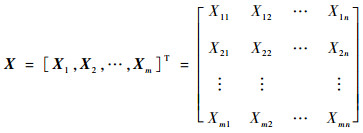为消除指标间数量级不同造成的影响，对决策矩阵进行规范化处理，即每个参数向量的单位化：

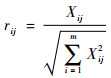(7)

式中：r_ij为单位化后的得分值。由各参数单位向量组成新的决策矩阵R=(r_ij)_m×n。

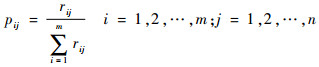(8)

式中：p_ij为第j个参数下第i个平飞段的贡献度。形成贡献度矩阵P=(p_ij)_m×n。

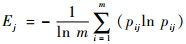(9)

式中：E_j为所有平飞段对参数j的贡献总量。当p_ij=0，定义p_ijln p_ij=0，即可求得各参数所占的权重：

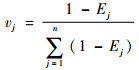(10)

从而组成权重向量v=[v₁, v₂, …, v_n]，v_j>0，。R_i为归一化决策矩阵的第i行向量，于是该次飞行任务第i个平飞段所有参数的加权得分值为

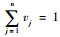
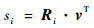(11)

该次飞行任务平飞动作得分为

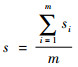(12)

至此，无人机平飞动作质量评价模型就构建完成了。
2 平飞动作质量评价的实现 2.1 数据预处理 数据预处理包含伪读数、无效幅值去除和数据长度一致性处理。伪读数是指数据变化超过了该参数变化的合理范围或短时间突变，属于噪声、振动或传感器故障等原因引起的误差，数据中的伪读数可以采用稳健回归算法^[18]进行处理。提取无人机的飞行高度、经纬度数据描述无人机整个飞行历程在空间的航迹示意图，如图 4所示，操控手操纵无人机升空后在100 m高度上下做四边飞行训练。

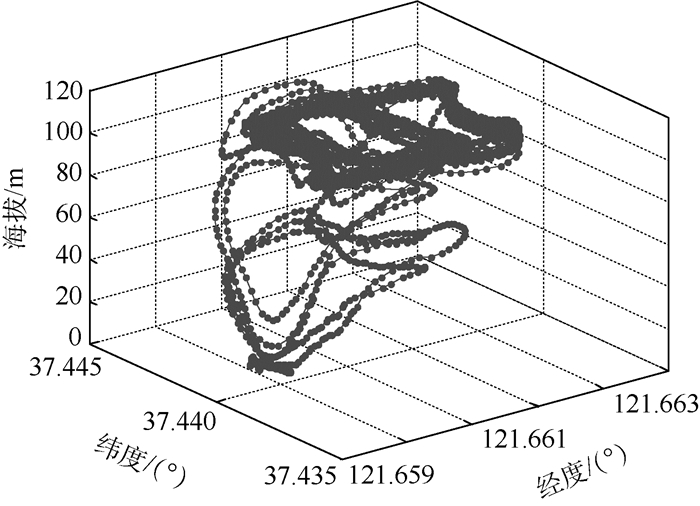图 4 无人机航迹图 Fig. 4 UAV path map

图选项

飞行数据记录的时间单位为天，为便于分析处理，将其换算为秒。图 5为某无人机四边飞行训练过程中飞行高度随时间的变化情况，显然无人机升空执行任务是1 000~2 400 s左右，前后两段属于起飞和降落阶段，对平飞动作来说属于无效数据段，应予以去除。对于平飞动作的识别来说，无人机地面停留数据属于干扰识别准确度的无效值，可以通过定义最小高度h_min，删除小于h_min的数据的方式进行处理。

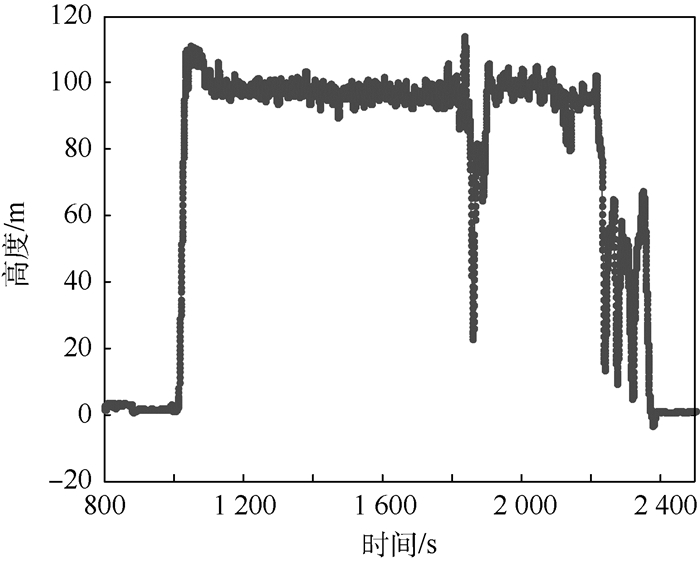图 5 高度随时间的变化 Fig. 5 Variation of height with time

图选项

无人机飞行数据记录系统采集的参数只有高度和对应的时间信息，无人机高度变化率的近似计算表达式为

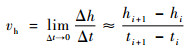(13)

因各参数传感器采集频率不一致，在数据处理过程中需要进行不同参数的向量长度一致性处理，长度不一致的参数可以通过插值或拟合等方式进行数据的补充或者删除。本文采用了拉格朗日插值的方式进行数据长度一致性处理。拉格朗日插值函数为

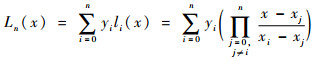(14)

式中：x_i和y_i分别为第i个数据点的横、纵坐标。
插值前后数据对比如图 6所示，米字符代表插值点数据，空心圆代表原始数据。

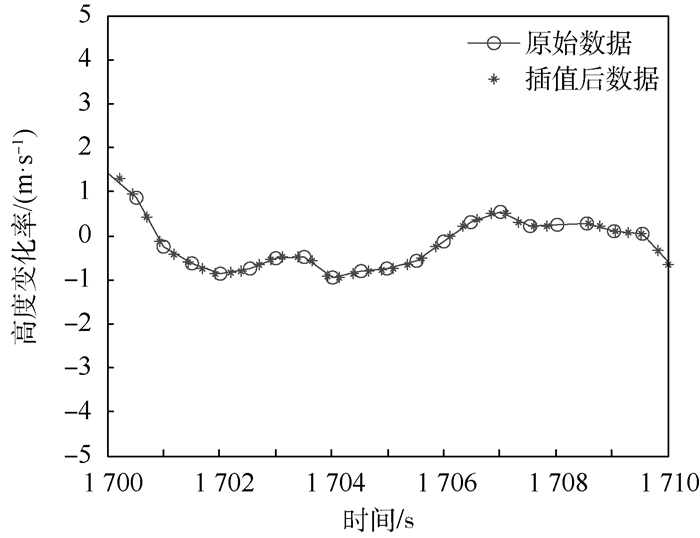图 6 高度变化率插值结果 Fig. 6 Interpolation results of height change rate

图选项

2.2 识别平飞动作 根据构建的平飞判别规则可以识别出符合该规则的平飞时间段。识别出的平飞时间段存在持续时间过短或中间存在间断点的情况，选定连续飞行5 s以上的数据段作为具有代表性的平飞数据段，如表 2所示。
表 2 平飞数据段 Table 2 Horizontal flight data segments

序号	起始时间/s	结束时间/s
1	4 666	4 688
2	4 698	4 721
3	4 757	4 783
4	4 849	4 872
5	5 428	5 457
6	5 787	5 808
7	6 172	6 206
8	6 366	6 393
9	6 674	6 699
10	6 787	6 808
11	6 871	6 892
12	7 045	7 074
13	7 237	7 269
14	8 089	8 114
15	8 186	8 210
16	8 266	8 300
17	8 428	8 458
18	8 662	8 698
19	8 852	8 888

表选项






2.3 各参数评分值及权重计算 得到平飞段后，计算各平飞时间段对应的各参数的布林带及得分值，分别得到高度、空速、俯仰角、偏航角和滚转角等参数的得分值向量。经过对操控手1的19个平飞数据段的5个飞行参数的打分，最终得到如表 3所示的评分表。
表 3 评分表 Table 3 Score sheet

序号	高度得分	速度得分	俯仰得分	偏航得分	滚转得分
1	1.400 4	0.627 5	0.202 2	0.220 6	0.901 7
2	4.208 2	0.672 7	0.339 7	0.275 3	1.118 8
3	1.737 1	0.819 9	0.332 7	0.226 7	0.859
4	1.185 9	0.684 1	0.066 5	0.147 9	0.515 1
5	1.307 8	0.557 7	0.281 8	0.213 3	0.747 4
6	1.006 2	0.450 3	0.120 5	0.183	0.698 8
7	1.735 8	0.784 9	0.132 9	0.197 4	0.746 8
8	4.139 5	0.564	0.152 1	0.165 5	0.674 2
9	1.528 7	0.422 2	0.086 1	0.152 7	0.527
10	1.49 2	0.462 8	0.174	0.232 8	0.773 3
11	1.009 7	0.445 4	0.059 3	0.163 6	0.540 6
12	0.999 9	0.371 8	0.130 1	0.197 4	0.704 5
13	1.951 1	0.465 5	0.148 8	0.201 5	0.680 9
14	2.379 8	0.641 2	0.065 9	0.152 3	0.483
15	1.930 5	1.171 6	0.301 9	0.367 6	1.366 6
16	1.957 7	0.594 1	0.157 8	0.191 6	0.808 9
17	3.418 5	0.724 9	0.123 6	0.209 6	1.010 2
18	0.876 7	0.595 5	0.213	0.252 8	0.955 1
19	0.653 1	0.556 6	0.118 5	0.165 8	0.646 3

表选项






在参数评分表的基础上，通过熵权法确定各参数权重，通过式(11)得到操控手1的19个平飞数据段得分情况如图 7所示。

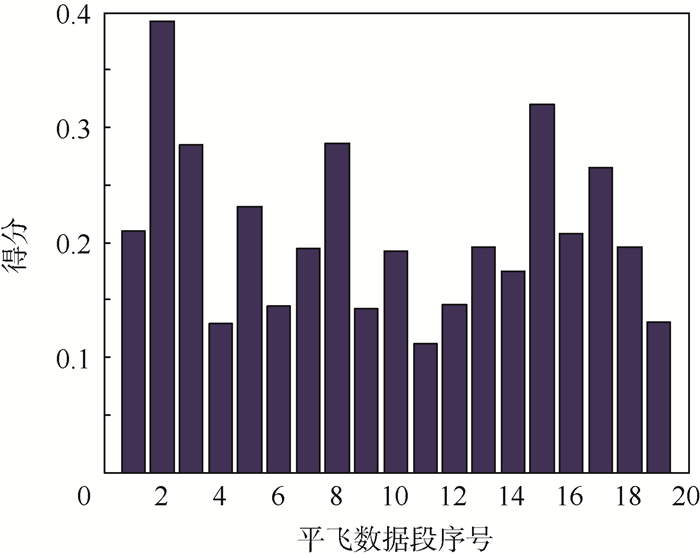图 7 操控手1得分 Fig. 7 Scores of Manipulator 1

图选项

通过式(12)即可得到操控手1的最终评分值为0.208 07。
3 模型验证与分析 4名操控手和无人机全自主控制模式执行四边飞行任务均在同一场地环境下进行，风速等天气情况相同，突风一定程度上会影响模型的评价结果，因为无法确定突风发生的时间点，进而修正模型，所以模型暂时无法排除风扰动的影响，利用平飞动作质量评价模型计算得到各操控手的得分及排名情况如表 4所示。
表 4 最终得分排名 Table 4 Final score ranking

操控主体	得分	平飞段数	排名
操控手1	0.208 07	19	第4名
操控手2	0.170 01	28	第3名
操控手3	0.145 02	39	第2名
操控手4	0.351 29	5	第5名
自主操纵	0.100 78	49	第1名

表选项






从各操控手得分情况可以看出，该模型可以较好地区分4位操控手平飞动作的好坏。考虑到操控无人机平飞时，主要强调操控的平衡性和稳定性，所以可以采用无人机自主控制执行四边飞行任务的数据来验证算法的准确性。验证采用低空无人机航测系统控制的无人机飞行数据，该系统的航迹跟踪精度可达厘米级，相对4名处于训练状态的无人机操控手具有更好的平飞稳定性，通过本文的算法筛选出的平飞数据段得分如图 8所示。

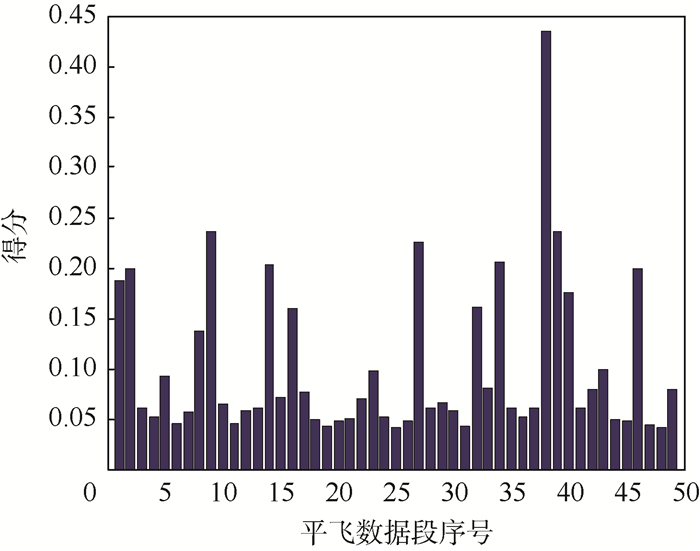图 8 自主控制模式下的平飞数据段 Fig. 8 Horizontal flight data segments in autonomous control mode

图选项

从图 8可以看出，无人机自主飞行时满足平飞动作判别规则的数据段有49段，明显比4位操控手的19、28、39、5段更多。而经模型计算，无人机自主控制飞行的平均得分为0.100 78，明显优于4位操控手的得分0.208 07，0.170 01，0.145 02，0.351 29，从侧面验证了算法的准确性。
4 结论 本文通过建立平飞动作判别规则识别无人机平飞动作，通过建立无人机平飞动作质量评价模型评价了无人机操控手平飞动作质量，利用4名无人机操控手和自主控制模式飞行的无人机四边飞行数据验证了模型的合理性，结果表明：
1) 平飞动作判别规则能够有效识别平飞动作，为平飞动作质量评价提供数据基础。
2) 平飞动作质量评价模型能够较好地区分不同水平操控手平飞操纵质量的高低，可以为无人机操控手的训练提供参考。
后期可以针对不同的飞行动作，建立不同的飞行动作识别和操纵质量评价模型，实现对无人机操控手的综合飞行技能评估。

参考文献

[1]	DAS S, MATTHEWS B L, LAWRENCE R. Fleet level anomaly detection of aviation safety data[C]//IEEE Conference on Prognostics and Health Management.Piscataway, NJ: IEEE Press, 2011: 1-10.
[2]	ZHOU K, WANG L X, TAN X S. Flying qualities reduction of fly-by-wire commercial aircraft with reconfiguration flight control laws[J]. Procedia Engineering, 2011, 17: 179-196. DOI:10.1016/j.proeng.2011.10.021
[3]	WANG L, WU C X, SUN R S. An analysis of flight quick access recorder(QAR) data and its applications in preventing landing incidents[J]. Reliability Engineering and System Safety, 2014, 127: 86-96. DOI:10.1016/j.ress.2014.03.013
[4]	张玉叶, 王颖颖, 王春歆, 等. 分析参数相关和时序特征的飞行动作识别方法[J]. 计算机工程与应用, 2016, 52(5): 246-249. ZHANG Y Y, WANG Y Y, WANG C X, et al. Acrobatic maneuver reorganization method compared with parameters relevance and feature of sequence change[J]. Computer Engineering and Applications, 2016, 52(5): 246-249. DOI:10.3778/j.issn.1002-8331.1403-0283 (in Chinese)
[5]	沈一超, 倪世宏, 张鹏. 基于贝叶斯网络的飞行动作识别方法[J]. 计算机工程与应用, 2017, 53(24): 161-167. SHEN Y C, NI S H, ZHANG P. Flight action recognition method based on Bayesian network[J]. Computer Engineering and Applications, 2017, 53(24): 161-167. DOI:10.3778/j.issn.1002-8331.1707-0156 (in Chinese)
[6]	HOLMBERG J, LEONARD J, KING D, et al.Flying qualities specifications and design standards for unmanned air vehicles[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit.Reston, VA: AIAA, 2008: 1-14.
[7]	COTTING C M.An initial study to categorize unmanned aerial vehicles for flying qualities evaluation[C]//AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition.Reston, VA: AIAA, 2009: 1-12.
[8]	刘莉雯, 张天伟, 茹斌. 多参数融合的飞行品质评估模型的建立[J]. 计算机工程与科学, 2016, 38(6): 1262-1268. LIU L W, ZHANG T W, RU B. A flying qualities assessment model based on multi-parameter integration[J]. Computer Engineering and Science, 2016, 38(6): 1262-1268. DOI:10.3969/j.issn.1007-130X.2016.06.030 (in Chinese)
[9]	张龙, 徐开俊. 采用模糊逻辑理论的飞行操纵品质评估模型[J]. 中国民航飞行学院学报, 2016, 27(5): 9-13. ZHANG L, XU K J. Flight operation quality assessment model using fuzzy logic theory[J]. Journal of Civil Aviation Flight University of China, 2016, 27(5): 9-13. DOI:10.3969/j.issn.1009-4288.2016.05.002 (in Chinese)
[10]	柳忠起, 袁修干, 樊瑜波. 基于BP神经网络的飞行绩效评价模型[J]. 北京航空航天大学学报, 2010, 36(4): 403-406. LIU Z Q, YUAN X G, FAN Y B. Pilot performance evaluation model based on BP neural networks[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(4): 403-406. (in Chinese)
[11]	夏长俊, 孙校书, 李冰. 基于飞行数据的无人机平飞质量分析方法[J]. 海军航空工程学院学报, 2017, 32(5): 478-482. XIA C J, SUN X S, LI B. Analysis method of UAV level flight quality based on flight data[J]. Journal of Naval Aeronautical and Astronautical University, 2017, 32(5): 478-482. (in Chinese)
[12]	彭阳, 彭晓明. 一种无人机飞行动作质量分析方法[J]. 飞行力学, 2017, 35(6): 65-69. PENG Y, PENG X M. A flight maneuver quality evaluation method for UAVs[J]. Flight Dynamics, 2017, 35(6): 65-69. DOI:10.3969/j.issn.1002-0853.2017.06.015 (in Chinese)
[13]	ZHOU S H, QIAN S L, QIAO X D, et al. The UAV landing quality evaluation research based on combined weight and VIKOR algorithm[J]. Wireless Personal Communications, 2018, 102(2): 2047-2062. DOI:10.1007/s11277-018-5254-z
[14]	杨俊, 谢寿生. 基于模糊支持向量机的飞机飞行动作识别[J]. 航空学报, 2005, 26(6): 738-742. YANG J, XIE S S. Fuzzy support vector machines based recognition for aero-plane flight action[J]. Acta Aeronautica et Astronautica Sinica, 2005, 26(6): 738-742. DOI:10.3321/j.issn:1000-6893.2005.06.016 (in Chinese)
[15]	SHARP C S, SHAKERNIA O, SASTRY S S.A vision system for landing an unmanned aerial vehicle[C]//Proceedings of the 2001 IEEE International Conference on Robotics & Automation.Piscataway, NJ: IEEE Press, 2001: 1720-1727.
[16]	李樾, 陈清阳, 侯中喜. 自适应引导长度的无人机航迹跟踪方法[J]. 北京航空航天大学学报, 2017, 43(7): 1481-1490. LI Y, CHEN Q Y, HOU Z X. Path following method with adaptive guidance length for unmanned aerial vehicles[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(7): 1481-1490. (in Chinese)
[17]	LIU W, ZHENG W A. Stochastic volatility model and technical analysis of stock price[J]. Acta Mathematica Sinica, English Series, 2011, 27(7): 1283-1296. DOI:10.1007/s10114-011-9468-1
[18]	王玉伟, 高永. 基于稳健回归算法的无人机数据预处理技术研究[J]. 舰船电子工程, 2018, 38(11): 38-41. WANG Y W, GAO Y. Research on UAV data preprocessing technology based on robust regression algorithm[J]. Ship Electronic Engineering, 2018, 38(11): 38-41. DOI:10.3969/j.issn.1672-9730.2018.11.011 (in Chinese)