垂直/短距起降(Vertical and/or Short Take-Off and Landing，V/STOL)飞机是对垂直起降(Vertical Take-Off and Landing，VTOL)和短距起飞/垂直降落(Short Take-Off and Vertical Landing，STOVL)固定翼飞机的统称，它兼具旋翼和固定翼飞机的优势，既可以减少甚至摆脱对飞行跑道的依赖，又具备较大的飞行速度、航程、载荷和优异的机动性能。自20世纪40年代至今，诞生的各类V/STOL飞机型号达30余种^[1-2]。特别是近年来，随着美国第5代战斗机F-35B的研发和服役，关于V/STOL飞机的研究越来越受到重视。但是相比常规起降飞机，V/STOL飞机具有更为复杂的动力学特性^[3]和操控性^[4]，这主要是由于其采用了诸多的推力矢量装置，如单发四转向喷管、引射增升器、升力风扇和矢量尾喷管等，从而使其诸如垂直/短距起飞、过渡、悬停/平移、垂直着陆等非常规飞行模式的控制律设计难度大为增加。其中，悬停模式是实现其他模式的基础，平移模式是小范围地改变悬停的位置以实现定点着陆的前提，两者的动力学关系是一致的，因而实现悬停/平移模式的有效控制尤为关键。
对此，国内外****从不同的角度进行了研究。较常见的一种是将VTOL飞机简化为平面VTOL(Planar VTOL，PVTOL)飞机模型，使其成为2输入3输出的欠驱动系统，然后分别采用近似反馈线性化^[5]、最优控制^[6]、基于观测器的输出反馈控制^[7]和滑模控制^[8]等方法设计控制器。然而，由于简化后的系统并不能有效地反映VTOL飞机的实际运动状态，选择推力和滚转力矩作为设计控制量，也难以将其转换为实际的多操纵面控制信号，因此这些研究更侧重于理论方法的探索而非工程问题的解决。另一种是直接针对V/STOL模型机/验证机建立相应的动力学模型，然后结合多操纵面分配方法设计相应的解耦控制器^[9-10]。此外，文献[11]提出了一种基于新姿态解算方法的滞后切换策略，解决了尾座式推力矢量飞机的悬停控制问题。总的来说，现有研究大多是基于精确的飞机模型设计控制律，没有充分考虑系统的鲁棒性问题，且通过控制分配算法得到实际控制量，往往会破坏系统的稳定性。
由于V/STOL飞机在悬停/平移模式下飞行速度很小，使其极易受到局部扰动风的影响。特别是短时的突风，它会使飞机的空速、迎角和侧滑角等发生改变，进而影响飞行轨迹和姿态。因此，必须设计具有强抗风能力的鲁棒飞行控制律。对此，自抗扰控制(Active Disturbance Rejection Control，ADRC)应是一种行之有效的应对方案。大量理论^[12-14]和应用^[15-16]方面的研究表明，ADRC不依赖被控对象的精确数学模型，对具有未建模动态、参数摄动和外界干扰的系统均能有效控制，具有“天生”的鲁棒性和抗干扰性。但受限于原始ADRC中非线性、非光滑的反馈结构，其理论分析十分困难，在应用中需要调节的控制器参数也较多。为简化ADRC的分析和实现，文献[17]利用带宽概念，提出了单参数调节的线性ADRC(Linear ADRC，LADRC)方法，并在文献[18]中直接假设系统不确定性的导数有界，证明了LADRC的收敛性，但由于该假设本质上是一个先验条件，因而很难得到验证。在此基础上，笔者基于单参数高增益观测器的思想，提出了一种高阶LADRC方法，并进一步放宽假设条件给出了收敛性证明，但缺少对该方法的实际应用^[19]。
本文在上述研究的基础上，以先进的“矢量发动机+升力风扇”型V/STOL飞机为研究对象，首先构建推力矢量模型和基于扰动风影响的悬停/平移运动模型，然后在高阶LADRC的控制框架内对模型进行变换并选取适当控制量，来分别设计姿态和位置的自抗扰控制律。本文的意义在于展现如何应用LACRC实现V/STOL飞机在悬停/平移模式下的动力学解耦和多操纵量协调控制，同时验证LADRC对该模式控制的有效性和鲁棒性。
1 悬停/平移模式非线性模型 1.1 V/STOL飞机概念模型 本文研究的V/STOL飞机为美国国家航空航天局(NASA)的某型STOVL验证机^[20]，采用单发动机、三角翼、鸭翼、双垂尾的布局形式，如图 1(a)所示。推进系统采用类似F-35B的设计方案，由一个矢量发动机和一个轴驱动升力风扇组成，具体形式和参数如图 1(b)和表 1所示(y_LRN、y_RRN分别为左、右滚转控制喷管推力的侧向力臂)。矢量尾喷管在飞机对称平面内可向下偏转90°，同时可侧向偏转±12°，能够产生80 000 N的悬停升力；升力风扇竖直安装于驾驶舱后方，可向前偏转20°、向后偏转60°，也可侧向偏转±12°，能够产生高达89 000 N的悬停升力；由发动机外涵道引出的2个滚转控制喷管位于两翼根处，由压气机供气，共可产生占全机总推力9.3%的推力，用于滚转控制。

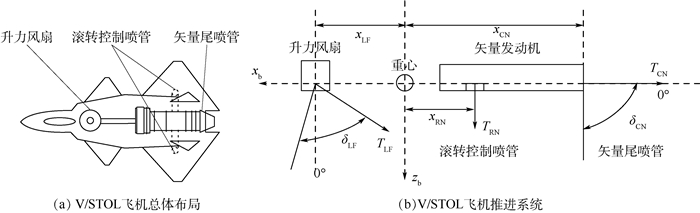图 1 V/STOL飞机概念方案 Fig. 1 Conceptual scheme of V/STOL aircraft

图选项

表 1 V/STOL飞机推进系统的参数配置 Table 1 Configured parameters of V/STOL aircraft propulsion system

部件	推力/N (规定为正)	纵向偏转角/(°) (下偏或后偏为正)	侧向偏转角/(°) (左偏为正)	力臂/m (遵循机体坐标系)
矢量尾喷管	TCNmax=80000	δCN∈[0, 90]	δCNy∈[－12, 12]	xCN=－6.01
升力风扇	TLFmax=89000	δLF∈[－20, 60]	δLFy∈[－12, 12]	xLF=3.57
滚转控制喷管	TRNmax=17330			xRN=－1.91 yRRN=－yLRN=2

表选项






1.2 推力矢量模型 V/STOL飞机的推进系统可为其悬停/平移模式提供直接控制力和力矩。将各矢量推力在机体坐标系下分解后叠加，可得到由推进系统产生的纵向力T_xb、侧向力T_yb和法向力T_zb表达式为

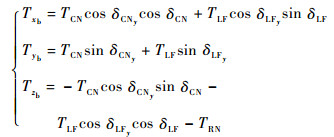(1)

式中：滚转控制喷管的总推力占全机总推力的9.3%，有

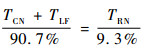(2)

式中：T_RN=－T_RRN－T_LRN，T_LRN和T_RRN分别为左、右滚转控制喷管的推力(遵循机体坐标系)。
假设矢量尾喷口、升力风扇喷口和滚转控制喷口与飞机重心处于同一平面上，则由各轴向力产生的滚转力矩l_prop、俯仰力矩m_prop和偏航力矩n_prop的表达式为

(3)

此外，V/STOL飞机特有的大推力大范围偏转还会产生喷气诱导效应(Jet-Induced Effect，JIE)，导致升力损失和抬头力矩。根据文献[21]的描述，可得JIE模型：

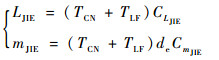(4)

式中：L_JIE和m_JIE分别为喷气诱导升力和喷气诱导俯仰力矩；C_LJIE和C_mJIE分别为对应的增量系数；d_e为总的等效环流喷气直径。
当飞机处于悬停状态时，所有矢量喷管都竖直向下，由力和力矩平衡可得

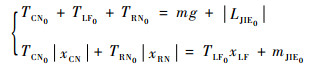(5)

式中：m为飞机质量；g为重力加速度；次下标0代表悬停平衡状态。
这样，由式(2)、式(5)即可得到飞机悬停状态下的平衡推力T_CN0、T_LF0和T_RN0。
1.3 考虑扰动风影响的飞机运动模型 下面首先给出无风状态下的飞机运动模型。当V/STOL飞机处于悬停/平移模式时，飞行速度很小，气动力和力矩几乎为零，同时姿态角变化幅度也不大，可以将与姿态角相关的小值作为扰动项，从而得到仅由推进系统作用的简化六自由度非线性运动模型：

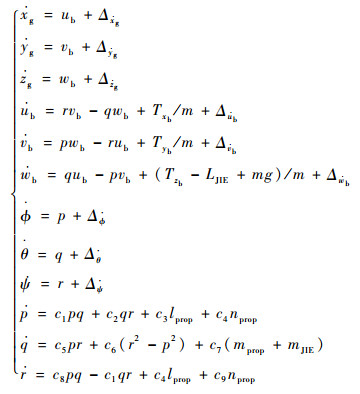(6)

式中：(x_g, y_g, z_g)为飞机在地面坐标系下的位置，且有h=－z_g为飞行高度；(u_b, v_b, w_b)为飞机在机体坐标系下的纵向、侧向和法向速度；(?, θ, ψ)为飞机的姿态角；(p, q, r)为绕机体轴转动的对应角速度；c₁~c₉为与转动惯量相关的常系数；Δ为与姿态角相关的小扰动项。
对式(6)中的位置、姿态方程求导并代入式(1)、式(3)，可得纵向运动方程：

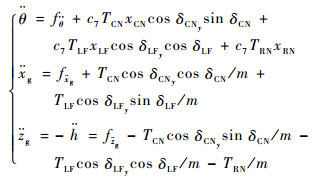(7)

式中：

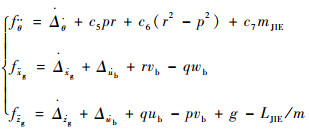横侧向运动方程：

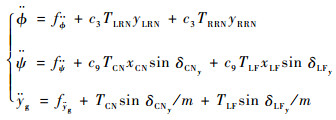(8)

式中：

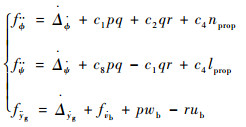当飞机受到扰动风影响时，就需要对上述运动模型进行修正。在有风影响的情况下，飞机的飞行速度矢量V、航迹速度矢量V_k和风速矢量V_w之间，具有如下的速度三角形关系：

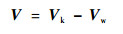(9)

将式(9)分别在机体坐标系和地面坐标系下投影，可以得到如下的修正关系：

(10)

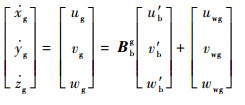(11)

式中：(u′_b, v′_b, w′_b)为飞机受扰动风影响并投影在机体坐标系下的修正速度；(u_wg, v_wg, w_wg)为基于地面坐标系给出的轴向风速；(u_wb, v_wb, w_wb)为转换到机体坐标系下的轴向风速；B_g^b=(B_b^g)^T为地面坐标系到机体坐标系的转换矩阵，因而有

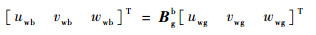由于机体尺度相比风场尺度很小，因而可忽略由扰动风速矢量沿翼展和机身方向的微小差异所造成的气动力矩变化。这样，将式(10)、式(11)代入式(6)，可得到扰动风影响下的飞机质心运动模型：

(12)

式中：小扰动项、和作相应改变即可。
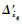
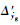
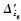
在式(12)的基础上仍然可以得到如式(7)、式(8)的飞机纵向和横侧向运动方程，只是其中的扰动项、和变为

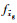
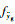
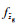
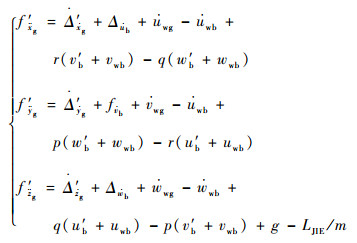2 高阶LADRC方法 考虑如下单输入单输出不确定非线性系统：

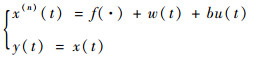(13)

式中：u为控制输入；y为系统输出；f(·)为不确定的内部动态；w为未知的外部干扰；b为不确定的控制量系数，满足b₁ < b < b₂，b₁和b₂为常数。
取状态变量x₁=x, x₂=, …, x_n=x^(n－1)，将系统的所有不确定性当作总扰动并将其扩充为新的状态变量x_n+1=f(·)+w+(b－b₀)u，其中b₀∈(b₁, b₂)，可得系统(13)的扩张状态方程：

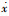
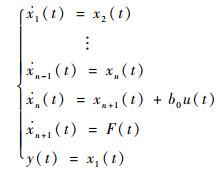(14)

为方便表示，在不引起歧义的前提下，后文将省略时间变量t。针对系统(14)，可设计如下具有“扰动估计补偿”功能的LADRC控制器，它由线性跟踪微分器(Linear Tracking Differentiator，LTD)、线性扩张状态观测器(Linear Extended State Observer，LESO)和线性状态误差反馈(Linear State Error Feedback，LSEF)3部分组成。
2.1 线性跟踪微分器 LTD在LADRC中相对独立，其作用在于跟踪给定的输入信号v₀并得到输入的各阶微分信号v₀⁽ⁱ⁾，即v₁→v₀，v_i+1→v₀⁽ⁱ⁾(i=1, 2, …, n)。高阶LTD的具体形式为

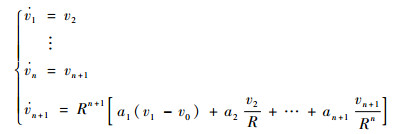(15)

式中：R为决定跟踪快慢的调节增益；系数a_j(j=1, 2, …, n+1)需满足矩阵A是Hurwitz的。

关于高阶LTD式(15)的收敛性有如下结论^[22]。
引理1??若光滑函数v₀(t):[0, ∞)→R满足, i=1, 2, …, n，其中常数T₁>0, B> 0，则对任意给定的LTD式(15)的初始值以及任意的ρ>0, τ₁>0，存在常数R₀>0，使得对任意的R>R₀，|v_j－v₀^(j－1)|<ρ(j=1, 2, …, n+1)在t∈[τ₁, T₁]上都成立。
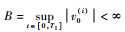
2.2 线性扩张状态观测器 LESO是LADRC的核心技术。可利用实时的输入u、输出y信息构造如下的高阶LESO：

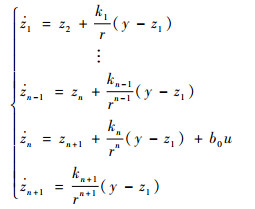(16)

式中：z₁, z₂, …, z_n+1分别为系统(14)状态x₁, x₂, …, x_n+1的估计；r为LESO调节增益的倒数；系数k_j(j=1, 2, …, n+1)需满足矩阵K是Hurwitz的。

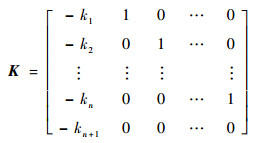2.3 线性状态误差反馈 定义系统的状态误差e₁=z₁－v₁, …, e_n=z_n－v_n，并考虑对总扰动x_n+1的实时补偿，可设计如下的LSEF：

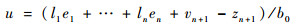(17)

式中：系数l_i(i=1, 2, …, n)需满足矩阵L是Hurwitz的。

关于LADRC式(15)~式(17)的收敛性，笔者在文献[19]中给出如下结论。
引理2??对于不确定非线性系统(13)，若其内部动态f(·)和外部干扰w有界且关于自变量的所有偏导数连续且有界，设计如式(15)~式(17)的LADRC控制器，则对任意给定的闭环系统初始值，存在常数r₀>0, T₂>0，使得对任意的r∈(0, r₀)，满足。
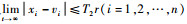
注1??对于实际飞机系统，由于飞行状态和控制输入总是有界的，外界干扰亦是有限的，因此总能满足引理2中关于不确定性及其偏导数有界的假设。
根据引理1和引理2，当R→∞, r→0时，可得系统的跟踪误差满足：

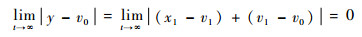(18)

3 悬停/平移模式控制器设计 3.1 控制策略 在稳定悬停状态下，飞机的姿态和位置保持不变，总推力与重力相平衡，各推力矢量(大小和方向)亦保持不变。当飞机受扰使平衡状态被破坏，或飞机需要改变悬停位置时，根据各推力矢量的功能特点，飞机姿态和位置的控制可由如下几种策略来实现，具体如表 2所示。
表 2 V/STOL飞机悬停/平移模式的控制策略 Table 2 Control strategy for V/STOL aircraft in hover/translation mode

控制通道		控制策略
姿态控制	滚转	①左、右滚转控制喷管之间不同推力的转换
	俯仰	②升力风扇与矢量尾喷管之间不同推力的转换
		③升力风扇与矢量尾喷管在对称平面内的偏转
		④升力风扇与矢量尾喷管之间不同推力的转换与各自的偏转同时作用
	偏航	⑤升力风扇与矢量尾喷管的侧向偏转
位置控制	纵向	③升力风扇与矢量尾喷管在对称平面内的偏转
	侧向	⑤升力风扇与矢量尾喷管的侧向偏转
	法向	⑥保持飞机俯仰力矩平衡的条件下，改变飞机的总推力
注：对于纵向通道，若仅改变推力的大小，无法实施控制；对于法向通道，若仅改变推力的方向，飞机会掉高度，无法进行有效控制。

表选项






对应1.3节的运动模型，将悬停/平移模式的控制分成纵向控制和横侧向控制。根据表 2给出的控制策略，在纵向控制中，为了避免控制冗余，选择策略③来实现俯仰和纵向通道的耦合控制，利用策略⑥实现法向通道的控制；在横侧向控制中，利用策略①实现滚转通道的控制，利用策略⑤来实现偏航和侧向通道的耦合控制。
实际上，任意控制量的改变都会引起相应状态量的变化，进而通过动力学耦合影响其他状态量，但是这种影响反映在式(7)、式(8)中，是被当作系统的未知内部动态来处理的。接下来，将通过适当变换，利用LESO式(16)和LSEF式(17)对这种耦合不确定性连同其他扰动项进行实时的估计和补偿，进而实现各通道的动力学解耦以及多推力矢量的协调控制。
3.2 纵向运动控制器
3.2.1 俯仰和纵向通道控制器 对于俯仰和纵向通道运动方程：

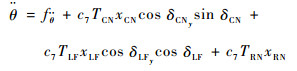(19)

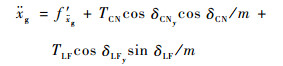(20)

其包含关于控制量δ_CN和δ_LF的三角函数形式。
通常，当角度δ在小范围内(±15°)变化时，有如下近似表达式成立：cos δ≈1，sin δ≈δ(δ以弧度计量)。但δ_CN和δ_LF的变化范围较大，使系统(19)、(20)难以转化为系统(14)的形式。对此，直接取u₁=sin δ_CN、u₂=sin δ_LF分别作为系统(19)、(20)的虚拟控制量。
由于δ_CNy和δ_LFy在其变化范围内有cos δ_CNy≈1、cos δ_LFy≈1，因而可估计到虚拟控制量系数b₁=c₇x_CNT_CN0、b₂=T_LF0/m，而将其余部分作为系统的总扰动，即

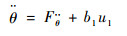(21)

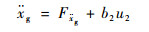(22)

其中总扰动为

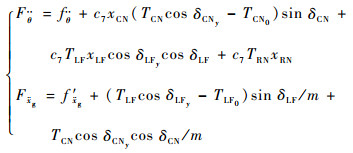这样，通过将系统的内部耦合动态、推力矢量冗余控制和外部干扰一起作为系统的总扰动，利用LADRC式(15)~式(17)对其进行实时估计和补偿，可分别对系统(21)、(22)设计如下的鲁棒协调解耦控制器：

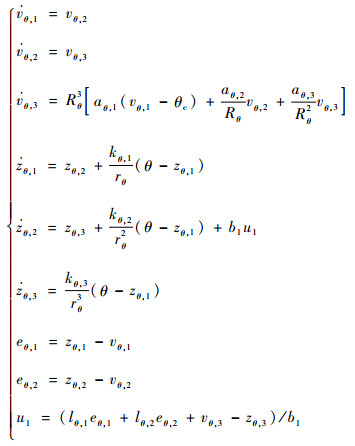(23)

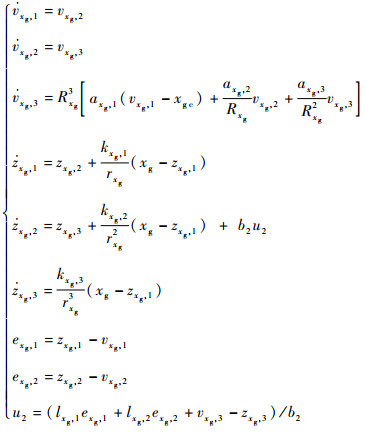(24)

式中：θ_c、x_gc分别为俯仰和纵向通道的参考输入指令。进而可得δ_CN=arcsin u₁，δ_LF=arcsin u₂。

3.2.2 法向通道控制器 法向通道控制器设计的关键在于如何选择控制量，实现推力T_CN、T_LF和T_RN控制的同时保持三者的协调。
对于法向通道运动方程：

(25)

可将其转化为

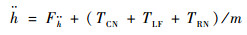(26)

其中总扰动为

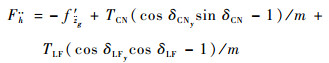根据式(5)的力矩平衡和式(2)、式(4)可得

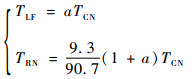(27)

式中：

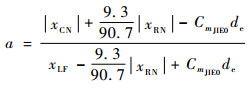将式(27)代入式(26)，可得

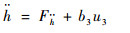(28)

式中：u₃=T_CN；b₃=100(1+a)/(90.7m)。
对式(28)，同样可设计如式(24)的法向通道控制器，只是为区别起见，需将x_g、b₂、u₂替换为h、b₃、u₃。
3.3 横侧向运动控制器
3.3.1 滚转通道控制器 滚转控制喷管的总推力T_RN可通过u₃由式(27)得到，在此基础上，滚转通道控制器设计的目的在于，如何将T_RN合理分配给T_LRN和T_RRN以保持滚转姿态稳定。
对于滚转通道运动方程：

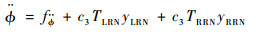(29)

将T_RN=－T_RRN－T_LRN和y_LRN=－y_RRN代入可得

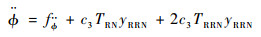从而有

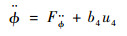(30)

式中：；u₄=T_RRN；b₄=2c₃y_RRN。
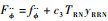
这样，即可对式(30)设计如式(23)的滚转通道控制器，为区别起见，需将θ、b₁、u₁替换为?、b₄、u₄。

3.3.2 偏航和侧向通道控制器 对于偏航和侧向通道运动方程：

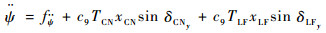(31)

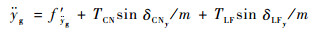(32)

由于δ_CNy和δ_LFy的变化范围小，有sin δ_CNy≈δ_CNy、sin δ_LFy≈δ_LFy，因而可将式(31)、式(32)分别变换为

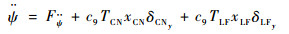(33)

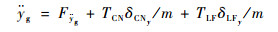(34)

其中总扰动为

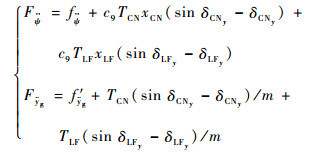对于如式(33)、式(34)的双输入单输出系统，可直接取虚拟控制量：

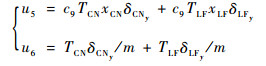从而得到

(35)

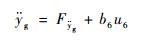(36)

式中：b₅=1，b₆=1。
对式(35)、式(36)，可分别设计如式(23)、式(24)的偏航和侧向通道控制器，其中需将θ、b₁、u₁和x_g、b₂、u₂分别替换为ψ、b₅、u₅和y_g、b₆、u₆。在此基础上，可得实际控制量：

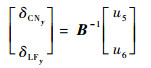式中：矩阵是非奇异的。
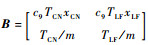
4 悬停/平移模式控制仿真 4.1 系统仿真参数 根据文献[20]提供的STOVL验证机数据，有m=13 608 kg，c₁=0，c₂=－0.685 3，c₃=5.157 8×10^-5，c₄=0，c₅=0.950 7，c₆=0，c₇=8.087 4×10^-6，c₈=－0.761 4，c₉=7.302 7×10^-6。当V/STOL飞机处于稳定悬停的状态时，有C_LJIE0=－0.016 5，C_mJIE0=0.083 3，另有d_e=2.523。
假设V/STOL飞机在某位置稳定悬停时受到外界扰动，飞行姿态发生改变，为此设定仿真初始状态：?₀=10°，θ₀=15°，ψ₀=5°，u_b0=v_b0=w_b0=p₀=q₀=r₀=0，x_g0=50 m，y_g0=－20 m，h₀=100 m。控制目标是使飞行姿态恢复到平衡状态，同时进行平移运动以实现定点悬停，即?_c=θ_c=ψ_c=0，x_gc=y_gc=0 m，h_c=100 m。
仿真过程中，考虑到JIE会随着喷管偏转角度、射流速度等因素的改变而改变，根据文献[22]的试验数据，设定C_LJIE在0.7C_LJIE0~1.1C_LJIE0、C_mJIE在0.4C_mJIE0~1.1C_mJIE0范围内变化是合理的。
另外，考虑突风对飞机的干扰，采用典型的半波长(1-consine)离散突风模型描述风场：

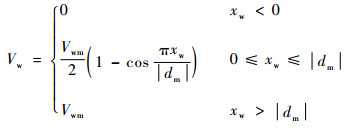式中：d_m为突风尺度，V_wm为突风强度，分别代表突风最大时的位置和速度；x_w为进入风场后的飞行距离。仿真中，设定x_g、y_g、h方向的d_m分别为80、－30、150 m，对应的V_wm分别为－8、10、5 m/s。
4.2 控制器参数整定 基于控制器带宽的概念，LADRC的参数选取具有很强的规律性，其具体表现如下：
1) 选择a_j、k_j(j=1, 2, …, n+1)在满足矩阵A、K是Hurwitz的前提下，使h(λ_A)=(λ_A+w_A)ⁿ⁺¹, h(λ_K)=(λ_K+w_K)ⁿ⁺¹往往比其他选择要好，其中h(λ_A), h(λ_K)分别代表矩阵A, K的特征多项式，通常使w_A=w_K=1即可，这是因为还可通过R和r来任意调节LTD和LESO。
2) l_i(i=1, 2, …, n)决定LADRC反馈控制量的大小，一般可先使h(λ_L)=(λ_L+w_L)ⁿ且w_L=1，其中h(λ_L)代表矩阵L的特征多项式，然后调节R和r。
3) 对于R，由于LTD在LADRC中的相对独立性，R的取值变化对系统的性能影响不大，无需进行精确调节，通常取R∈{10, 20, 30, 40, 50}可满足需要。
4) 需要重点调节LESO参数r，对此，可兼顾控制精度与控制量的要求，在[0.001, 1)之间进行调节。通常，系统的不确定性越大，r取值越小；若要减少控制量，可适当增大r。当调节r仍无法获得满意的控制性能(如超调量或稳态误差较大)时，可对l_i进行调整。
据此整定控制器参数如下：首先取a_{i, 1}=－1，a_{i, 2}=－3，a_{i, 3}=－3，k_{i, 1}=3，k_{i, 2}=3，k_{i, 3}=1，R_i=10，i=?, θ, ψ, x_g, y_g, h；然后通过调试，取l_{?, 1}=－0.05，l_{θ, 1}=－1，l_{ψ, 1}=－0.01，l_{xg, 1}=－1，l_{yg, 1}=－0.001，l_{h, 1}=－1，l_{i, 2}=－2以及r_?=0.002，r_θ=0.005，r_ψ=0.002，r_xg=0.001，r_yg=0.6，r_h=0.1。
4.3 仿真结果分析 为验证LADRC对V/STOL飞机悬停/平移模式控制的有效性，设定3种不同的情况进行仿真比较：情况1为不考虑JIE系数变化和突风影响，情况2为仅考虑JIE系数变化，情况3为既考虑JIE系数变化又考虑突风影响。
仿真时，考虑施加较为严重的干扰：即在0~20 s附加C_LJIE和C_mJIE的随机变化，变化规律服从均匀分布；在1~6 s加入水平的纵向和侧向突风干扰，10~15 s加入垂直突风干扰。此外，还需具体考虑T_CN的约束范围：根据式(27)的限定可知，悬停/平移模式下矢量尾喷管的最大推力T_CNmax^HT=53 200 N；同时要求矢量发动机的推力不能为零，将其最小推力限制在总推力的5%，即T_CNmin^HT=9 320 N。取仿真步长d=0.001，仿真结果如图 2、图 3所示。从图中可以看出：

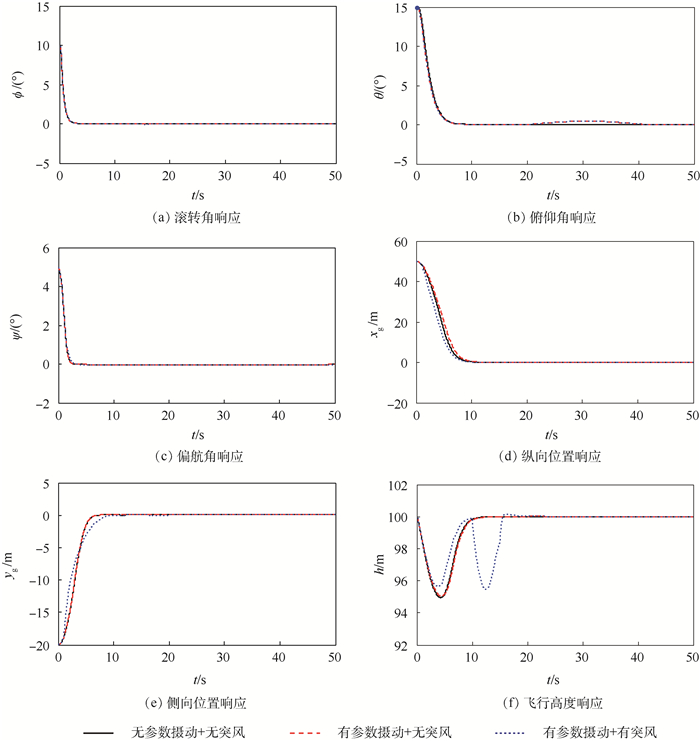图 2 悬停/平移模式的飞行状态响应 Fig. 2 Flight state responses in hover/translation mode

图选项

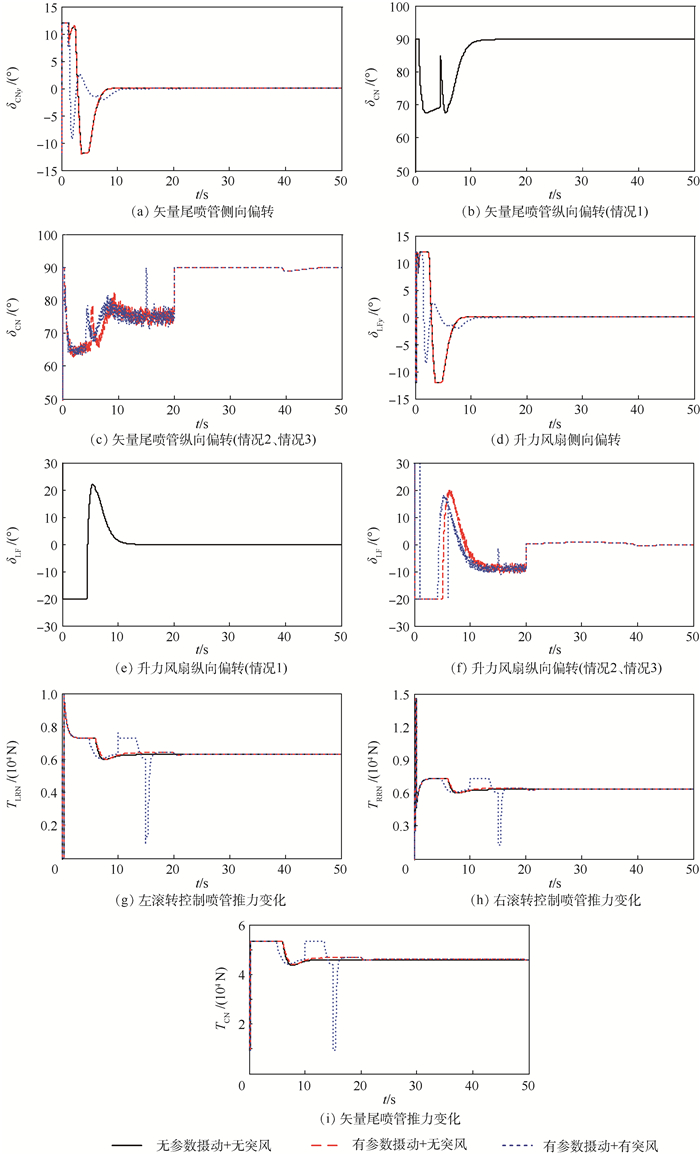图 3 悬停/平移模式的推力矢量控制输入 Fig. 3 Thrust vector control inputs in hover/translation mode

图选项

1) 在情况1下(无参数摄动+无突风)，V/STOL飞机的姿态角以及纵向、侧向位置均能平稳响应指令信号，无振荡和超调；但由于升力风扇和矢量尾喷管的偏转，导致力平衡被打破，飞机法向净推力小于重力，使飞机出现小幅掉高度的现象，但在推力的补偿下，飞行高度很快恢复并保持在设定值；表明LADRC实现协调解耦控制的有效性。此外，各推力矢量亦能在约束范围内较为平滑的变化并最终稳定在初始值，其中，δ_CNy^st=δ_LFy^st=0°，δ_CN^st=90°，δ_LF^st=0°，T_CN^st=45 943 N，T_LF^st=76 851 N，T_LRN^st=T_RRN^st =6 295 N，上标st代表稳定状态。
2) 在情况2下(有参数摄动+无突风)，各飞行状态依然能够保持原有的响应性能，这是源于LESO和LSEF对参数随机摄动的实时估计和补偿，表明LADRC对V/ STOL飞机的内部参数变化具有很好的鲁棒性。但由于设定的C_LJIE和C_mJIE是随d随机变化的，在补偿作用下不免地造成δ_CN和δ_LF也随d作相应变化而产生高频震颤；而实际情况下，C_LJIE和C_mJIE并不会在如此短的时间内作这样随机的大幅度变化，因而不必担心作动器的工作负担；其他控制量几乎不受参数变化的影响。
3) 在情况3下(有参数摄动+有突风)，飞机遭遇强风干扰时依然能够保持姿态响应不变，水平轨迹受到的影响也很小，虽然飞行高度受向下突风的影响而出现小幅下降，但在可接受的范围内并很快恢复，这都得益于各控制量的即时调整。表明LADRC具有较强的抗干扰性，对存在参数摄动和突风干扰的悬停/平移模式具有良好的解耦控制性能。
5 结论 针对固定翼V/STOL飞机在低速模式下受多推力矢量操纵而存在的动力学耦合、控制冗余和不确定干扰等问题，提出了一种直接式的鲁棒协调解耦飞行控制方法，有效避免了以往用多种控制方法糅合的方式来分别解决系统鲁棒性、冗余性和耦合性所产生的算法复杂、参数不易整定的控制难题。
1) 推导了一类“矢量发动机+升力风扇”型V/STOL飞机在低速悬停/平移模式下，受扰动风影响的全状态动力学模型，体现了多推力矢量控制下的运动特性。
2) 提出了一种基于高阶LADRC的鲁棒协调解耦控制策略，并在此框架内通过模型变换以提取适当控制量，而将其他控制项、动力学耦合项以及各类不确定干扰项当做总扰动，设计了V/STOL飞机的六通道解耦控制器。
3) 给出了控制器参数整定的一般准则，并在此基础上通过仿真比较，验证了所提出的飞行控制策略在实现动力学解耦和多操纵量分配方面的有效性，以及对参数摄动和外界干扰的鲁棒性。

参考文献

[1]	索德军, 梁春华, 张世福, 等. S/VTOL战斗机及其推进系统的技术研究[J]. 航空发动机, 2014, 40(4): 7-13. SUO D J, LIANG C H, ZHANG S F, et al. Technology of short/vertical takeoff and landing fighter and propulsion system[J]. Aeroengine, 2014, 40(4): 7-13. (in Chinese)
[2]	MADDOCK I A, HIRSCHBERG M J.The quest for stable jet borne vertical lift: ASTOVL to F-35 STOVL: AIAA-2011-6999[R].Reston: AIAA, 2011.
[3]	WANG X Y, ZHU J H, ZHANG Y J.Dynamics modeling and analysis of thrust-vectored V/STOL aircraft[C]//Proceedings of the 32nd Chinese Control Conference.Piscataway, NJ: IEEE Press, 2013: 1825-1830.
[4]	TIAN Y, HE Y, LI X Y, et al.Simulation testing method of V/STOL flight control strategy[C]//Proceedings of the 10th World Congress on Intelligent Control and Automation.Piscataway, NJ: IEEE Press, 2012: 1969-1975.
[5]	HAUSER J, SASTRY S, MEYER G. Nonlinear control design for slightly non-minimum phase systems:Application to V/STOL aircraft[J]. Automatica, 1992, 28(4): 665-679. DOI:10.1016/0005-1098(92)90029-F
[6]	LIN F, ZHANG W, BRANDT R D. Robust hovering control of a PVTOL aircraft[J]. IEEE Transactions on Control Systems Technology, 1999, 7(3): 343-351. DOI:10.1109/87.761054
[7]	CHWA D. Fuzzy adaptive output feedback tracking control of VTOL aircraft with uncertain input coupling and input-dependent disturbances[J]. IEEE Transactions on Fuzzy Systems, 2015, 23(5): 1505-1518. DOI:10.1109/TFUZZ.2014.2362554
[8]	CARLOS A I, MIGUEL S S C, JULIO M M, et al. Output feedback stabilization for the PVTOL aircraft system based on an exact differentiator[J]. Journal of Intelligent and Robotic Systems, 2018, 90(3-4): 443-454. DOI:10.1007/s10846-017-0660-0
[9]	FAN Y, ZHU J H, MENG X Y, et al.Intelligent method based coordinated integrated flight control of a tailless STOVL[C]//Proceedings of the 8th World Congress on Intelligent Control and Automation.Piscataway, NJ: IEEE Press, 2010: 85-90.
[10]	ZHANG Y, ZUO J, ZHANG B.Modularized modeling and inversed dynamics control design for a lift-fan UAV in hover[C]//Proceedings of the IEEE International Conference on Information and Automation.Piscataway, NJ: IEEE Press, 2013: 570-575.
[11]	KUANG M C, ZHU J H. Hover control of a thrust-vectoring aircraft[J]. Science China Information Sciences, 2015, 58(7): 1-5.
[12]	GUO B Z, ZHAO Z L.On convergence of nonlinear active disturbance rejection for SISO systems[C]//Proceedings of the 24th Chinese Control and Decision Conference.Piscataway, NJ: IEEE Press, 2012: 3507-3512.
[13]	QI X H, LI J, XIA Y Q, et al. On the robust stability of active disturbance rejection control for SISO systems[J]. Circuits, Systems, and Signal Processing, 2017, 36(1): 65-81.
[14]	XUE W, HUANG Y. Performance analysis of 2-DOF tracking control for a class of nonlinear uncertain systems with discontinuous disturbances[J]. International Journal of Robust Nonlinear Control, 2018, 28(4): 1456-1473. DOI:10.1002/rnc.v28.4
[15]	LI Z Y, LI X M, ZHOU Z Y.Active disturbance rejection controller for loitering unit with parameter uncertainty[C]//Proceedings of the 16th International Conference on Control, Automation and Systems.Piscataway, NJ: IEEE Press, 2016: 140-144.
[16]	LONG Y, DU Z J, CONG L, et al. Active disturbance rejection control based human gait tracking for lower extremity rehabilitation exoskeleton[J]. ISA Transactions, 2017, 67: 389-397. DOI:10.1016/j.isatra.2017.01.006
[17]	GAO Z Q.Scaling and bandwidth-parameterization based controller tuning[C]//Proceedings of the American Control Conference.Piscataway, NJ: IEEE Press, 2003: 4989-4996.
[18]	ZHENG Q, GAO Z Q, GAO L Q.On stability analysis of active disturbance rejection control for nonlinear time-varying plants with unknown dynamics[C]//Proceedings of the 46th IEEE Conference on Decision and Control.Piscataway, NJ: IEEE Press, 2007: 3501-3506.
[19]	高阳, 吴文海, 高丽.高阶不确定非线性系统的线性自抗扰控制[J/OL].控制与决策, (2018-10-12)[2018-11-02].http://kns.cnki.net/KCMS/detail/21.1124.TP.20181012.1727.010.html. GAO Y, WU W H, GAO L.Linear active disturbance rejection control for high-order nonlinear systems with uncertainty[J/OL].Control and Decision, (2018-10-12)[2018-11-02].http://kns.cnki.net/KCMS/detail/21.1124.TP.20181012.1727.010.html(in Chinese).
[20]	FRANKLIN J A.Revised simulation model of the control system, displays, and propulsion system for a ASTOVL lift fan aircraft: NASA-TM-112208[R].Washington, D.C.: NASA, 1997.
[21]	BIRCKELBAW L G, MCNEILL W E, WARDWELL D A.Aerodynamics model for a generic ASTOVL lift-fan aircraft: NASA-TM-110347[R].Washington, D.C.: NASA, 1995.
[22]	GUO B Z, ZHAO Z L.On convergence of tracking differentiator and application to frequency estimation of sinusoidal signals[C]//Proceedings of the 8th Asian Control Conference.Piscataway, NJ: IEEE Press, 2011: 1470-1475.