通用图形处理器(Graphic Processing Unit, GPU)能够提供高速的并行计算能力,而计算设备统一构架(Compute Unified Device Architecture, CUDA)使基于NVIDIA公司GPU产品的并行计算能够方便地推广到一般工程应用。NVIDIA公司GPU和CUDA相结合,为数值计算效率的提升提供了新的实现手段,在成像算法、物理场模拟等方面得到了广泛的应用[3-6]。
本文基于CUDA将并行计算技术应用于超声声场的EFIT,对钢材料中的声场分布进行仿真计算,测试基于GPU并行计算和传统CPU计算的效率差异。
1 弹性动力学有限积分算法 1.1 算法的积分形式 EFIT由Fellinger和Langenberg[7]在1989年提出。该算法基于牛顿动量定理和广义胡克定律给出了弹性动力学运动方程的积分形式,并对方程组进行离散化,基于数值计算的方式在时间和空间上进行迭代求解。通过研究表明,EFIT不但能够模拟计算各向同性固体介质中弹性波的传播和散射情况,而且对于各向异性固体材料也具有较好的算法收敛性[8-10]。
假设一个封闭的固体单元,体积以V表示,封闭表面的面积以S表示, 则根据牛顿动量定理可得
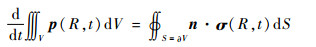 | (1) |
根据动量密度矢量定义:
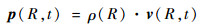 | (2) |
将式(2)代入式(1)可得
 | (3) |
根据变形定律可得[2, 9]
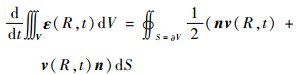 | (4) |
式中:R为质点的空间位置;t为时间;n为曲面外法向向量;p(R, t)为质点的动量密度矢量;σ(R, t)为应力张量;ε(R, t)为应变张量;v(R, t)为质点速度矢量;ρ(R)为密度。
根据广义胡克定律可知,在弹性假设前提下,应力与应变之间为单值线性关系,从而建立了式(3)与式(4)中应力与应变之间的联系。
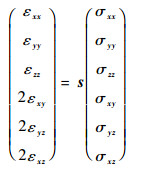 | (5) |
式中:s为顺度系数矩阵。
1.2 积分形式的离散化 在获得弹性动力学运动方程积分表达式的基础上,为进行数值计算需要对相关物理量进行离散化。
假设整个仿真计算区域由紧密排布的相邻物质单元构成,每个物质单元均为直角坐标系下边长相等的立方体单元网格,同一个物质单元网格内各相关物理量是恒定的。按照EFIT,在整个计算区域内需要将离散应力点和离散速度点交叉配置。在一个网格单元中,3个正应力分量处于网格单元的中心,3个切应力分量分别处于3个边的中点,3个速度分量则分别处于物质单元的3个面的中心位置,从而构成速度分量与应力分量相互交错的网格放置方式(见图 1)。
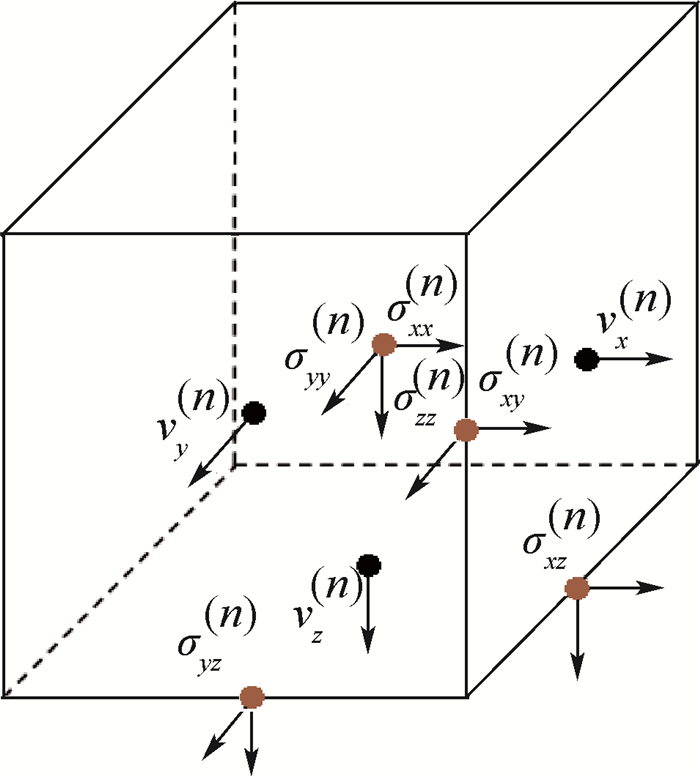 |
| 图 1 单个计算单元内速度与应力的分布 Fig. 1 Velocity and stress distribution in single calculation unit |
| 图选项 |
对于各向同性材料,弹性常数矩阵中独立常数个数减少为2个,各向同性材料弹性常数矩阵形式如下:
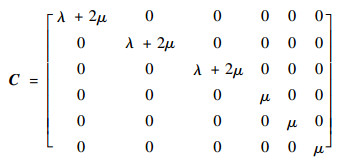 |
式中:λ和μ为拉梅常数的2个参数。
因此,当在二维条件下计算各向同性材料中超声波的传播和散射时,弹性动力学运动方程离散后可以简化为
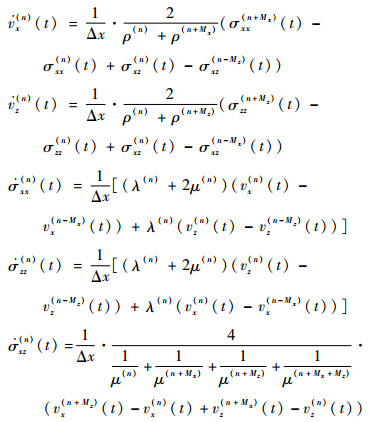 |
式中:n为迭代步数;Mx、Mz分别表示x、y方向计算单元的步进量。
在此基础上,在时间序列k上进行迭代计算,从而计算得到各时刻超声在固体介质中的传播和散射情况。
 |
1.3 吸收边界 在实际工程应用中,有时检测对象体积较大,如果对完整对象建模计算,将需要巨大的网格单元数量,由于硬件资源的限制,实际很难实现,因此,在实际工程中经常只对有限区域的声场进行计算。
但当以有限区域模拟较大区域时,由于存在计算区域边界,将引入额外的计算边界反射。为了避免模型中由于计算区域的限制形成边界反射回波,本文采用完全匹配层(Perfect Matched Layer,PML)吸收边界条件[11-14],在计算区域边界处设置了一定数量的吸收层,达到较好的边界吸收效果。图 2为未添加吸收边界时的声场分布情况,图 3为添加吸收边界后的声场分布情况。
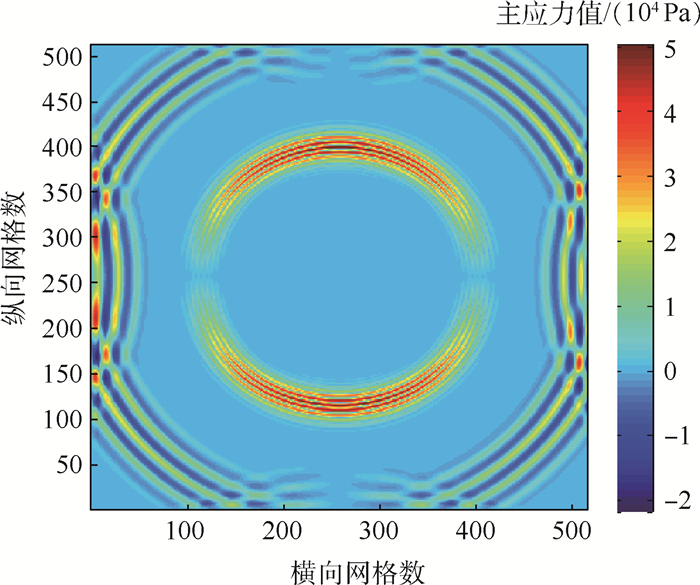 |
| 图 2 未设置吸收边界的声场分布 Fig. 2 Sound field distribution without absorption boundary |
| 图选项 |
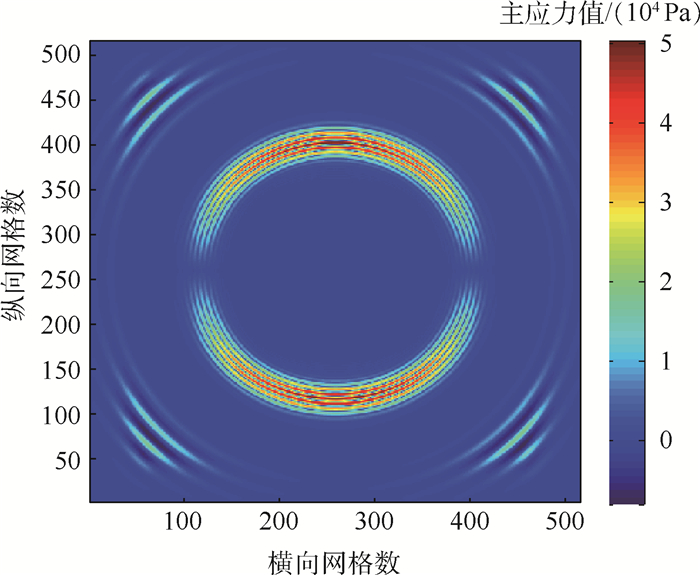 |
| 图 3 设置吸收边界的声场分布 Fig. 3 Sound field distribution with absorption boundary |
| 图选项 |
2 基于CUDA的EFIT模型优化 2.1 GPU与CUDA 与传统CPU流水线型的数据处理方式不同,为了适应大规模并行计算的需要,GPU采用并行多线程的内部构架,有效提升并行计算任务的执行效率。
2016年,NVIDIA公司发布了第一款基于CUDA的通用图形处理器(GPGPU),为GPU广泛应用于通用计算领域奠定了基础。
在提供高速并行计算能力的同时,GPU也存在自身的技术限制。为了达到高速的并行计算能力,GPU减少了逻辑计算单元的数量,因此逻辑判断能力相对于CPU存在差距;同时,只有相同的计算操作才能并行化,不同外部条件导致的算法变更可能会由GPU自行转为串行处理,过多的逻辑判断将极大地降低计算效率。在极端情况下,不合理的程序设计会导致GPU计算速度远低于CPU。
因此,在使用GPU进行并行计算时,首先需要对计算模型进行分析,判断是否具备并行计算的条件; 然后对程序逻辑进行优化,合理分配GPU与CPU之间的工作内容,从而基于CUDA实现高质量的并行计算[15]。
2.2 EFIT模型的并行实现 根据EFIT,当前速度场每个单元的变化量由前一时间节点应力场相关单元的数值计算得出,而当前应力场变化量则由计算后的速度场相关单元的数值计算得出。可见,在EFIT的计算模型中,待计算场量仅与已获得的计算结果相关,而待计算场量各个单元之间在当前计算步骤中没有关联。因此,并行计算方式可以简单、高效地实现EFIT,而无需考虑计算过程中不同计算结果间的同步问题。
基于以上分析,建立EFIT并行计算模型,算法实现流程如图 4所示。由于GPU主要进行并行计算,GPU中存储单元的分配仍通过CPU进行控制。在EFIT计算模型初始化时,分别为vx、vz、σxx、σzz和σxz在GPU内存中分配二维的存储空间。在计算过程中,为实现仿真计算中间变量的灵活保存,通过CPU控制GPU分别完成速度场和应力场的分步计算。
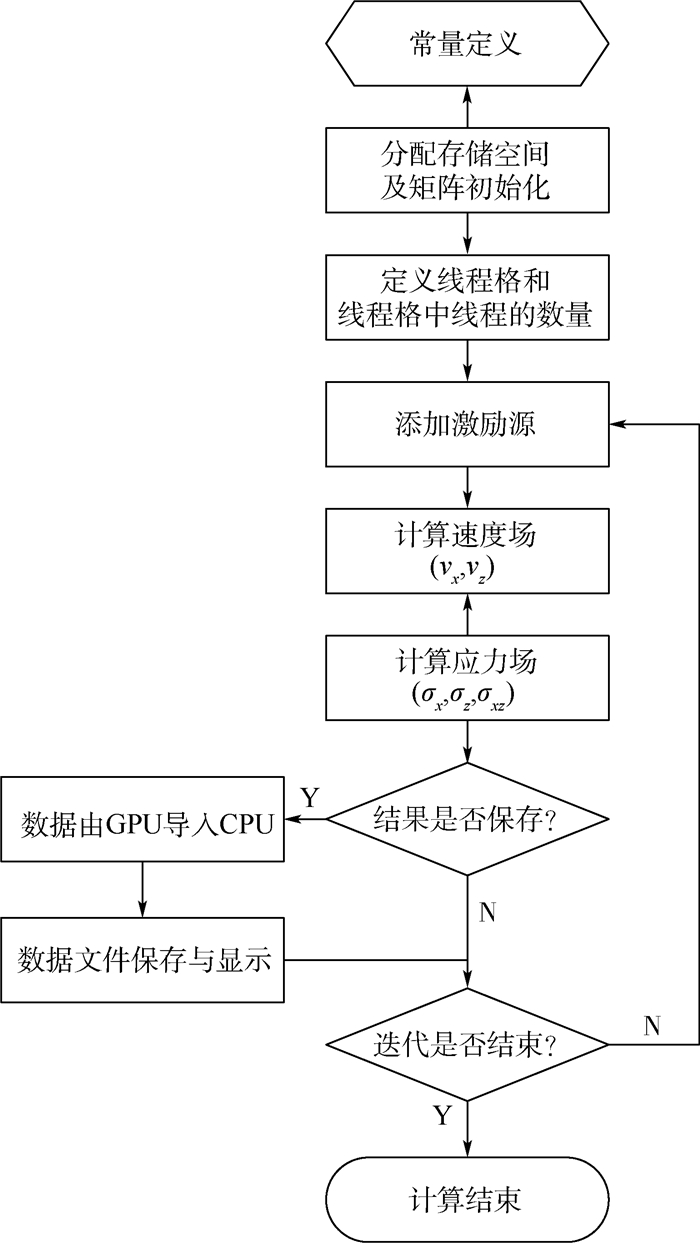 |
| 图 4 并行计算流程 Fig. 4 Flowchart of parallel calculation |
| 图选项 |
在程序的具体实现中,分别针对vx、vz、σxx、σzz和σxz设计各自的核函数。对于空间各单元,首先将二维矩阵转换为一维向量,然后通过idx=blockIdx.x*blockDim.x+threadIdx.x方式对所有空间计算单元进行遍历;对于时间迭代则通过CPU控制程序循环实现。
2.3 纹理内存 在传统图像处理GPU中,纹理内存是专门针对内存访问模式中存在大量空间局部性的图形应用程序所设计的,对线程读取相邻近的内存位置进行了优化。实现方式是通过将全局内存绑定为纹理内存,对其读写操作通过专门的纹理缓存(texture cache)进行。而将纹理内存应用于通用计算,则可以利用纹理缓存针对二维空间的局部性访问优化,实现二维矩阵邻域访问速度的有效提升。
在EFIT计算模型中,每个单元的值都是通过另一个二维矩阵中相邻单元的值计算获得,如图 5所示。由于地址非连续,在采用一般内存进行计算时,这些地址没有被缓存,因此每次访问时需要重新进行寻址,导致内存访问速度较低。而采用纹理内存时,相邻单元的地址将被整体缓存,极大降低访存时间,从而使程序性能得到有效提升[16]。
 |
| 图 5 纹理内存线程寻址示意图 Fig. 5 Schematic diagram of texture memory thread addressing |
| 图选项 |
本文计算模型中,将速度场与应力场相关矩阵均与纹理内存进行绑定,从而实现模型计算速度的优化。由于GPU中纹理内存容量有限,在设计实际算法时需要考虑纹理内存容量限制,当计算区域超出纹理内存容量时,需要进行分块计算。
2.4 吸收边界优化 为对有限区域进行模拟计算,在EFIT模型边界设置一定数量的吸收层,形成吸收区域。与模型中一般的计算单元不同,每个吸收层需要采用包含衰减因子的波动方程,通过多个吸收层的衰减近似达到边界声场吸收的效果。
引入衰减系数,导致吸收区域波动方程形式变化。模型中可以按照单元位置判断是否处于吸收区域,从而决定是否增加衰减系数。但这种实现方式可能导致GPU在同一线程束(wrap)内的分支语句执行不同的指令路径,此时条件判断的不同指令路径线程只能被顺序执行,程序的并行性被破坏,导致计算速度降低[17]。
因此,在基于CPU的模型初始化过程中,增加了吸收系数矩阵的定义,对于一般计算区域,吸收系数预置为1.0,而对于吸收区域单元则设置为小于1.0的衰减系数。在基于GPU进行计算时,只需调用相应的衰减系数矩阵元素即可,从而保证模型计算的并行性。
2.5 数据传输优化 GPU具有高速的并行计算能力,但CPU与GPU之间的数据传输却受限于传输的带宽,成为GPU并行计算的瓶颈。因此在进行模型并行计算过程中,需要合理设计CPU和GPU之间的数据传输,使数据传输量与传输带宽相匹配。
对于EFIT计算模型,由于计算过程为迭代计算,当前计算参数为前一时间节点的计算结果,因此在算法实现时,只需在程序初始化时完成相关参数和参数矩阵的初始化,在并行计算过程中,无需外部数据传入GPU,避免数据传输带来的速度降低。
如果每次都将计算得到声场分布结果输出显示,数据由GPU输出到CPU的时间将成为主要的时间消耗,同时在实际应用中过于密集的声场成像也没有意义。因此,在算法实现中,应根据实际需要合理设置计算结果的输出频率,从而平衡实际应用需求和数据传输效率。
3 仿真结果与效率分析 为了定量测量并行计算对于EFIT的加速效果,本文建立二维点源激励声场模型。模型中,检测对象为钢材料,弹性模量为207 GPa,泊松比为0.289,材料密度为7.9×103 kg/m3,纵波声速设置为5 900 m/s。计算区域选取单元数为512×512,单个单元边长设置为纵波波长的1/10,时间步长为换能器周期的1/20。激励源选用中心频率为100 kHz的点源,振动5个周期,振动方向为x方向,激励源施加于计算区域的中心点。选取计算区域边缘64层单元作为吸收边界。各单元系数采用单精度浮点数进行存储。
在并行计算时,选取GPU型号为NIVIDIA NVS 5400M,CUDA核心数为96。CUDA运算在Visual Studio 2010环境下基于C语言编程,计算结果通过MATLAB界面进行显示。
进行CPU和GPU计算结果对比之前,首先确定GPU计算时选用的核函数参数。分别设置GPU线程块内线程数为16×16和32×32时进行对比,选取最优的GPU计算参数。在进行200次迭代计算时,线程格内线程数为16×16的条件下,并行计算时间为1 060.826 ms,而采用线程格内线程数为32×32的条件下,并行计算时间为1 088.902 ms。可见,两者耗时基本相同,线程格内线程数为16×16时计算耗时略短,因此,后续计算中均采用线程格内线程数16×16的参数设置。
分别通过CPU和GPU运行程序进行计算,选取第450次迭代和第650次迭代时主应力的计算结果进行观察,显示图像如图 6所示。
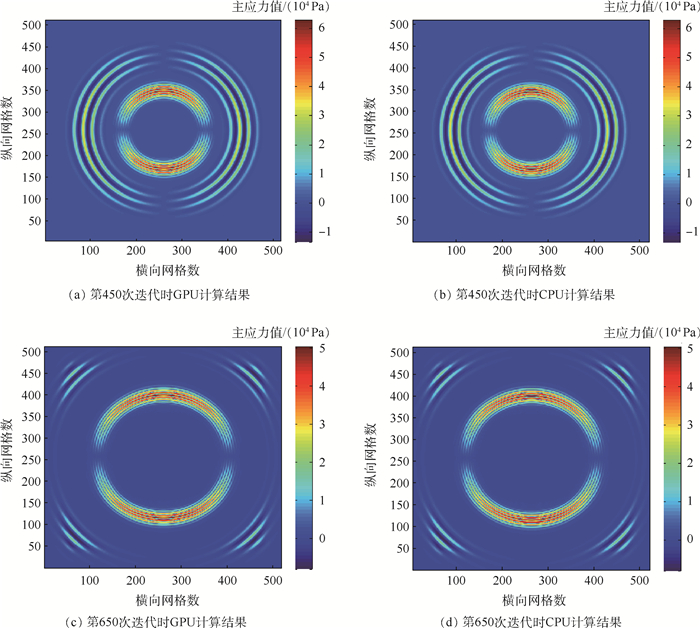 |
| 图 6 GPU与CPU计算结果对比 Fig. 6 Comparison of GPU and CPU computing results |
| 图选项 |
通过对比可以看出,基于CPU和GPU计算结果完全一致。在此基础上,分别统计不同迭代次数时计算耗时。
在统计计算时间时,无论是CPU程序或GPU程序,仅统计计算本身耗时,程序开始运行时的初始化和计算结果导出、显示时间等部分不计入统计时间。统计结果如图 7和图 8所示。
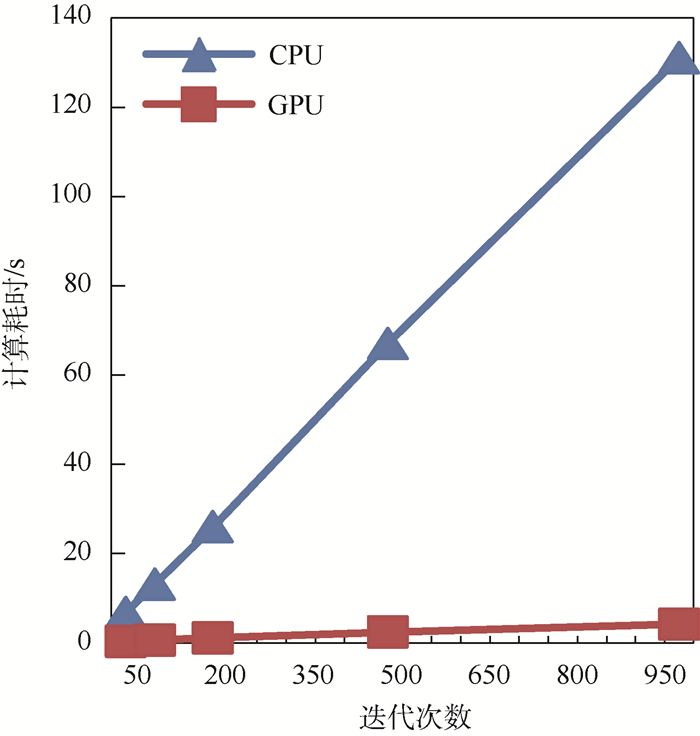 |
| 图 7 GPU与CPU计算耗时对比 Fig. 7 Comparison of computing time consumption of GPU and CPU |
| 图选项 |
 |
| 图 8 GPU与CPU平均每秒迭代次数对比 Fig. 8 Comparison of average iteration times in one second of GPU and CPU |
| 图选项 |
通过图 7和图 8统计结果可以看出,采用GPU并行计算对EFIT模型进行迭代计算时,相对于CPU计算速度有明显的提升。本文模型中,对于不同的迭代次数,计算速度提升在23~31倍之间。
4 结论 本文基于CUDA编程,实现了EFIT模型的并行计算,并在此基础上对于EFIT模型的GPU和CPU计算速度进行了对比,可以得到如下结论:
1) EFIT模型中,当前单元的计算只与对应位置的已知计算结果有关,具有良好的并行计算条件。
2) 基于CUDA框架能够完成EFIT模型的并行计算程序开发,计算结果与CPU程序计算结果一致。
3) EFIT模型采用并行计算方法进行计算,能够有效提升计算速度,而随着GPU性能的快速提升,并行计算方法对于复杂声场仿真应用具有广阔的应用前景。
由于本文中模型主要用于测试,需要获取部分中间变量,如在实际应用中主要关注最终计算结果,EFIT模型的并行计算仍可进行进一步优化。
参考文献
| [1] | 徐娜, 李洋, 周正干, 等. FDTD方法的改进及在超声波声场计算中的应用[J]. 北京航空航天大学学报, 2013, 39(1): 78-82. XU N, LI Y, ZHOU Z G, et al. Improvement of finite difference time domain method and its application to calculation of ultrasonic sound fields[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(1): 78-82. (in Chinese) |
| [2] | FELLINGER P, MARKLEIN R, LANGENBERG K J, et al. Numerical modeling of elastic wave propagation and scattering with EFIT-Elastodynamic finite integration technique[J]. Wave Motion, 1995, 21: 47-66. DOI:10.1016/0165-2125(94)00040-C |
| [3] | 张霞, 何兴无. CUDA平台下的超声弹性成像并行处理算法[J]. 计算机与数字工程, 2012, 40(9): 113-116. ZHANG X, HE X W. A Parallel algorithm of ultrasound strainimaging based on CUDA[J]. Computer & Digital Engineering, 2012, 40(9): 113-116. DOI:10.3969/j.issn.1672-9722.2012.09.038 (in Chinese) |
| [4] | 贾春刚, 郭立新, 刘伟. 基于GPU的并行FDTD方法在二维粗糙面散射中的应用[J]. 电波科学学报, 2016, 31(4): 683-687. JIA C G, GUO L X, LIU W. GPU-based FDTD method for analysis of electromagnetic scattering from a 2D rough surface[J]. Chinese Journal of Radio Science, 2016, 31(4): 683-687. (in Chinese) |
| [5] | 付小波, 马中高, 余嘉顺, 等. 基于多图形处理单元加速的各向异性弹性波正演模拟[J]. 科学技术与工程, 2018, 18(11): 16-22. FU X B, MA Z G, YU J S, et al. Anisotropic elastic wave forward modeling based on multiple graphics processing unit[J]. Science Technology and Engineering, 2018, 18(11): 16-22. DOI:10.3969/j.issn.1671-1815.2018.11.002 (in Chinese) |
| [6] | 杨尚琴. 地震正演数值模拟仿真计算的并行优化设计方法[J]. 地球物理学进展, 2017, 32(3): 1290-1296. YANG S Q. Parallel optimization design method for seismic forward modeling numerical simulation calculation[J]. Progress in Geophysics, 2017, 32(3): 1290-1296. (in Chinese) |
| [7] | FELLINGER F, LANGENBERG K J.Numerical techniques for elastic wave propagation and scattering[C]//Proceedings of the IUTAM Symposium on Elastic Wave Propagation and Ultrasonic Evaluation, 1990: 81-86. |
| [8] | SCHUBERT F. Numerical time-domain modeling of linear and nonlinear ultrasonic wave propagation using finite integration techniques-Theory and applications[J]. Ultrasonics, 2004, 42(1-9): 221-229. DOI:10.1016/j.ultras.2004.01.013 |
| [9] | 丁辉. 计算超声学——声场分析及应用[M]. 北京: 科学出版社, 2010: 33-36. DING H. Computational ultrasonics-Analysis and application of ultrasonic fiels[M]. Beijing: Science Press, 2010: 33-36. (in Chinese) |
| [10] | 余涛.超声波在混凝土中传播的数值模拟[D].长沙: 中南大学, 2013: 4-9. YU T.Numerical simulation of ultrasonic wave propagation in concrete[D].Changsha: Central South University, 2013: 4-9(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2426440 |
| [11] | BERENGER J. A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics, 1994, 114(2): 185-200. DOI:10.1006/jcph.1994.1159 |
| [12] | 廉西猛, 单联瑜, 隋志强, 等. 地震正演数值模拟完全匹配层吸收边界条件研究综述[J]. 地球物理学进展, 2015, 30(4): 1725-1733. LIAN X M, SHAN L Y, SUI Z Q, et al. An overview of research on perfectly matched layers absorbing boundary condition of seismic forward numerical simulation[J]. Progress in Geophysics, 2015, 30(4): 1725-1733. (in Chinese) |
| [13] | 刘洋. 波动方程时空域有限差分数值解及吸收边界条件研究进展[J]. 石油地球物理勘探, 2014, 49(1): 35-46. LIU Y. The review of finite difference numerical solution for wave equation in time domain and obsorption boundary conditions[J]. Oil Geophysical Prospecting, 2014, 49(1): 35-46. (in Chinese) |
| [14] | 秦臻, 任培罡, 姚姚, 等. 弹性波正演模拟中PML吸收边界条件的改进[J]. 地球科学——中国地质大学学报, 2009, 34(4): 658-664. QIN Z, REN P G, YAO Y, et al. Improvement of PML absorbing boundary conditions in elastic wave forward modeling[J]. Earth Science-Journal of China University of Geosciences, 2009, 34(4): 658-664. (in Chinese) |
| [15] | 卢风顺, 宋君强, 银福康, 等. CPU/GPU协同并行计算研究综述[J]. 计算机科学, 2011, 38(3): 5-9. LU F S, SONG J Q, YIN F K, et al. Survey of CPU/GPU synergetic parallel computing[J]. Computer Science, 2011, 38(3): 5-9. DOI:10.3969/j.issn.1002-137X.2011.03.002 (in Chinese) |
| [16] | SANDERS J, KANDROT E.GPU高性能编程CUDA实战[M].聂雪军, 等, 译.北京: 机械工业出版社, 2011: 84-100. SANDERS J, KANDROT E.CUDA by example——An introduction to general-purpose GPU programming[M].NIE X J, et al., translated.Beijing: China Machine Press, 2011: 84-100(in Chinese). |
| [17] | 方民权, 张卫民, 方建滨, 等. GPU编程与优化:大众高性能计算[M]. 北京: 清华大学出版社, 2016: 273-276. FANG M Q, ZHANG W M, FANG J B, et al. GPU programming and code optimization:High performance computing for the masses[M]. Beijing: Tsinghua University Press, 2016: 273-276. (in Chinese) |
