在利用机器人进行表面加工作业，如抛光^[1]、打磨^[2]、去毛刺^[3]等时，往往需要机器人对未知工件的轮廓进行跟踪，并且机器人末端工具和工件之间应该保持恒定的期望接触力^[4]。如果接触力变化过大，会对加工产品质量产生影响^[5]，甚至损坏工件或机器人。为了实现恒力跟踪，Qiao和Lu^[6]利用在线力反馈数据对未知约束环境的形状进行估计以获得目标阻抗模型的虚拟参考运动轨迹，在力误差信号的驱动下由目标阻抗模型产生机器人的指令运动轨迹，通过跟踪该指令运动轨迹使机器人臂与环境的接触力误差限制在可接受的范围内，但是生成的参考运动轨迹需要获得终端与环境之间的摩擦系数，使系统分析变得复杂，而且难以建模，适应环境的不确定性能力会降低。李正义等^[7]设计了沿任意倾斜面的机器人自适应阻抗控制方法，实现机器人末端在任意参数未知斜面的接触力控制。Duan等^[8]设计了不确定环境下动态接触力跟踪的自适应变阻抗控制方法。Pliego-Jiménez和Arteaga-Pérez^[4]通过设计一种自适应控制方案，实现机器人跟踪未知刚性表面时的接触力控制。李二超等^[9]通过视觉传感器建立跟踪曲线图像特征与机器人关节角度映射关系，再通过模糊调节机器人阻抗模型参数进行跟踪，但是由于图像处理时间比伺服控制时间长，导致了延迟。Baeten和de Schutter^[10]设计了一种混合视觉/力的控制方法，通过接触力引起的相机工具变形来检测路径中的突变点实现边缘定位，并激活有限状态控制器以在最佳条件下绕过拐角实现恒力跟踪，但是对于连续光滑的曲线无法很好的识别。Jeon等^[11]通过使用视觉传感器检测图像中心到轮廓的距离和角度获得轮廓的边缘点和曲率，然后通过应变计力传感器获得的力信息控制工具与任务对象之间的接触力，并通过移动机器人实现恒力轮廓跟踪，但是由于移动机器人刚度不足，只能满足曲面轮廓跟踪的工况，不利于后续的加工过程。Lange和Hirzinger^[12]通过力反馈控制的迭代自我控制实现轮廓跟踪，但是没有将传感器反馈的力转化为垂直于曲面的法向力进行控制器参数迭代，难以补偿曲面曲率变化的不确定性，而且没有进行收敛性分析，难以保证算法的收敛。Visioli等^[13]设计了迭代学习混合力/速度控制方法用于曲面的轮廓跟踪。Roveda等^[14]通过迭代学习和强化学习算法进行自动化控制器参数调整实现机器人对未知环境顺应性控制，但是设计的算法过于复杂。Winkler和Suchy^[15]通过在力/位置传感器中加入双积分器，降低了力控制的稳态误差，但是双积分器的力控制方向固定，不能跟随轮廓的改变而调整力控制方向。Kumar^[16]和Jung^[17]等提出通过神经网络来学习机器人机械手的未知动力学，补偿机器人运动学中的参数不确定性造成的干扰，从而实现机器人的恒力控制。Karayiannidis等^[18]通过设计一种神经网络自适应控制器，利用权值神经网络中的线性逼近功能，保证对于任意小集合的力和位置误差的一致最终有界性。He等^[19]设计了一种自适应神经网络阻抗器，用于处理跟踪控制过程中的不确定性和输入饱和度，实现力的控制。但是以上研究都只停留在仿真阶段。
这些控制方法中，传统控制方法难以补偿机器人实际跟踪过程中的不确定性，如机器人运动学的不确定性^[20]；而智能算法设计复杂，且大多停留在仿真阶段。本文提出了一种基于自适应迭代学习算法的机器人力/位混合曲面恒力跟踪控制方法，从而解决在机器人内部传递函数未知和环境刚度未知的情况下，通过多次迭代补偿跟踪过程中的不确定性问题，使机器人末端与工件的接触力收敛到期望值。
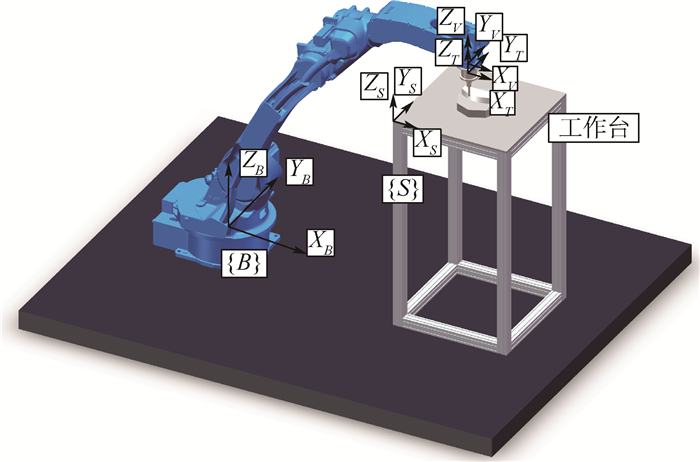
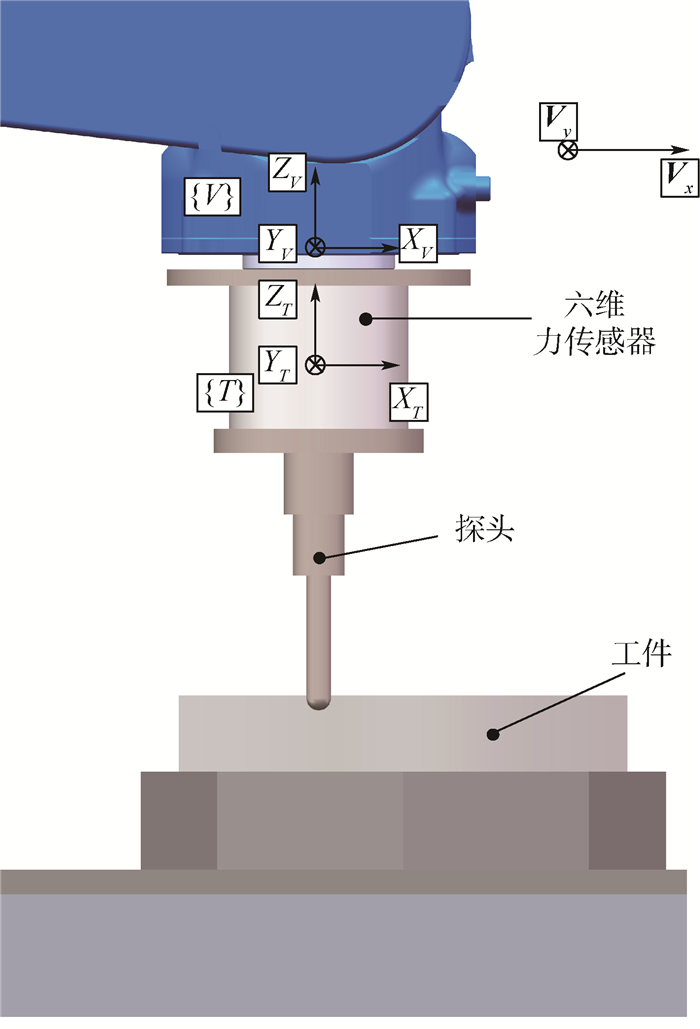
1 曲面跟踪受力分析 机器人曲面恒力跟踪实验平台如图 1和图 2所示。工作台坐标系{S}、传感器坐标系{T}、机器人运动坐标系{V}的姿态相对于机器人基坐标系{B}始终保持不变。机器人始终保持速度v_s沿着V_x方向移动。当探头和曲面接触时，探头受到曲面的法向力F_n和切向力F_τ。保持恒定的法向力F_n可以得出曲面的轮廓，为了得到法向力F_n的大小，需要将曲面坐标系{C}中的力映射到已知传感器坐标系{T}中，曲面坐标系{C}中心与传感器坐标系{T}中心重合，X轴方向与曲面切向方向相同，Y轴方向始终垂直于曲面轮廓^[21]。由图 3受力分析可知：

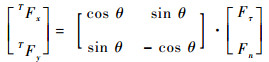(1)

图 1 机器人曲面恒力跟踪实验平台模型 Fig. 1 Experimental platform model of robot constant-force curved-surface-tracking

图选项

图 2 机器人模型末端局部图 Fig. 2 Partial view of end-effector of robot model

图选项

图 3 机器人末端受力分析 Fig. 3 Analysis of force on robot end-effector

图选项

式中：^TF_x和^TF_y分别为传感器坐标系{T}下F_x和F_y的力；θ为传感器坐标系{T}的X轴方向X_T和曲面坐标系{C}的X轴方向X_C的夹角。
将式(1)解耦可得

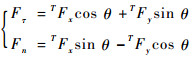(2)

式中：^TF_x和^TF_y的大小可通过六维力传感器测得。
由于夹角θ未知，需要对其进行估计，根据V_x和V_y方向的位移差分可得到每一步长的切线倾斜角，即

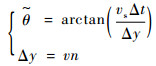(3)

式中：为差分后的曲线倾斜角；v_s为机器人沿着V_x方向的速度；Δt为机器人沿着V_x方向每个周期的时间；Δy为机器人沿着V_y方向的偏移量，其大小与上位机在每个周期内给机器人的偏置电压成正比；v为偏置电压；n为常数。当得到曲线倾斜角后，需对其进行平均值滤波，最终得到稳定的曲线倾斜角θ。实验中，角度平均误差小于5°，满足实际应用的需要。
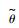
2 自适应迭代学习算法 当使用机器人进行曲面恒力跟踪时，为了得到精确的轨迹，需要对曲面进行重复多次的跟踪，在这种情况下，可以使用迭代学习技术来逐渐提高跟踪性能^[22]。
2.1 迭代学习控制律设计 当机器人末端与曲面相接触时，实际接触力与期望接触力满足如下阻抗模型：

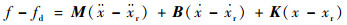(4)

式中：f为实际的接触力；f_d为期望的接触力；x为机器人末端的位置；x_r为参考运动位置；M、B、K分别为质量矩阵、阻尼矩阵和刚度矩阵。
当机器人与环境接触时，常将环境当作线性弹簧^[23]，接触力可表示为

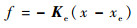(5)

式中：K_e为环境的刚度矩阵；x_e为环境的位置。
所以当机器人末端位置为参考位置x_r时，对应接触力为

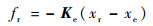(6)

由式(4)~式(6)得

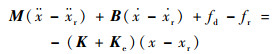(7)

参考文献[7]设计迭代学习控制律，将式(7)化为

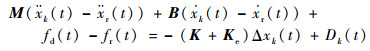(8)

式中：t为时间；非负整数k(k∈Z₊)为迭代次数；Δx_k(t)为控制的末端轨迹偏移调整量；D_k(t)为机器人系统参数不确定项和干扰。
为了方便起见，将式(8)化为

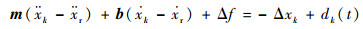(9)

式中：m=M/(K_e+K)；b=B/(K_e+K)；Δf=f_d-f_r；d_k(t)=D_k(t)/(K+K_e)。
假设系统参数未知，且系统满足如下假设：
假设1??系统的初始状态一致且可重复，即x₁(0)=x₂(0)=…=x_k(0)。
假设2??微扰量的一阶及二阶导数和有界。
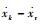
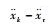
假设3??
假设4??
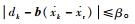
由式(9)所示系统以及假设1~假设4，设计迭代学习控制律为

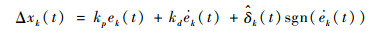(10)

式中：

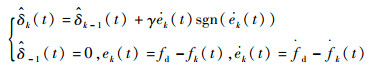(11)

式中：f_k(t)为第k次迭代时传感器测得的接触力。如果k_p、k_d、γ均大于0，则e_k(t)、及Δx_k(t)对于任何k∈Z₊都有界，且
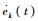
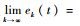
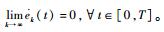
2.2 收敛性分析 1) 第1步：证明W_k的递增性。
取如下Lyapunov函数：

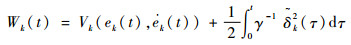(12)

式中：δ为不确定项，且定义为δ=β－ζ，；V_k(e_k(t), )项选取如下：

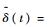
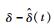
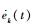
(13)

则

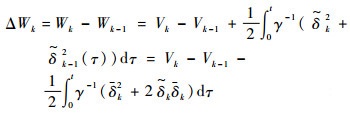(14)

式中：
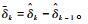
对V_k(e_k(t), )求一阶导数，两边积分可得

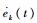
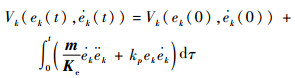(15)

由，且f_d为常数，所以，又由式(6)可得，，再利用式(9)可得

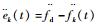
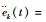
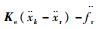
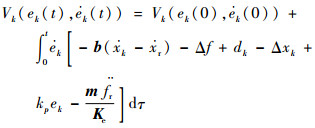(16)

由假设3和假设4可得

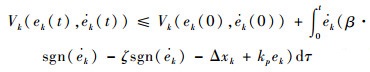(17)

将式(10)、式(11)和式(17)代入式(14)得

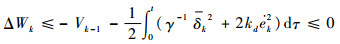(18)

式(18)说明W_k是非增序列，现只要证明W₀有界就说明了W_k是有界的。
2) 第2步：证明W₀的有界性。
对W₀求导可得

(19)

又因，且，因此可得

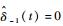
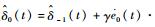
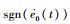
(20)

由，代入式(20)可得

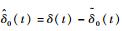
(21)

对于λ>0，如下不等式

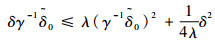(22)

恒成立，则可得

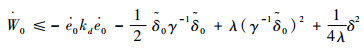(23)

因初始给定的值都有界，故有界，存在

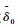
(24)

式中：
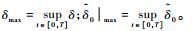
故W₀在[0, T]上是一致连续有界，因而W_k有界，进而可知e_k(t)、及Δx_k(t)对于任意k∈Z₊都有界。
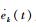
3) 第3步:证明e_k(t)和的收敛性。
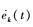
W_k可改写为

(25)

由式(18)可得

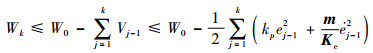(26)

由式(26)可推得

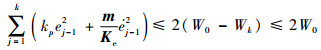(27)

因此，
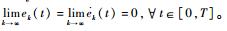
3 力/位混合曲面恒力跟踪控制方法 第2节中已经设计了针对机器人末端位置控制量和位置参考量之间修正量的迭代学习控制律，因此当获得机器人末端位置参考控制量时，便可对机器人进行恒力跟踪控制。当机器人末端与环境接触时，如果环境的刚度K_e和位置x_e已知，则可根据设定的恒力f_d获得机器人的末端参考位置^[24]为

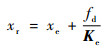(28)

实际接触过程中，环境的刚度K_e和位置x_e是很难测得的，所以就必须通过在线估计的方法求得参考位置x_r。参考文献[24]的方法^[25]，使用PID控制律进行在线估计：

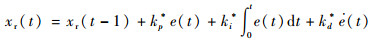(29)

为了避免误差积累^[26]，用前一采样时刻的接触位置x(t－1)代替上一控制周期的参考位置x_r(t－1)，可得

(30)

由式(10)、式(11)和式(30)得机器人末端位置控制律为

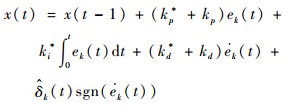(31)

式中：
根据式(31)设计的机器人末端位置控制律，设计机器人的控制框图如图 4所示。

图 4 基于自适应迭代学习算法的力/位混合控制 Fig. 4 Hybrid force/position control based on adaptive iterative learning algorithm

图选项

4 曲面恒力跟踪实验 曲面恒力跟踪实验装置如图 5所示。采用安川机器人MA24，机器人在运动过程中通过内置软件MotoPlus接受外部-10~10 V的模拟信号产生偏移，偏移位移方向与模拟信号符号一致，偏移位移与电压绝对值成正比；六维力传感器选用ME-FKD40，实验中采集的力信号通过上位机处理发送到倍福模块，倍福模块产生电压模拟信号传送给机器人控制器；用于曲面恒力跟踪实验的探头和工件尺寸如图 6和图 7所示，末端执行件为圆柱阶梯状探头，做成阶梯状的原因是为了在保证末端执行件刚度情况下使末端探头尺寸尽可能小，以减少摩擦力的影响。曲面工件形状为y=－0.006x²+0.9x－6的抛物线，机器人运动起始点为A，终止点为B，设置期望接触力为30N，设置初始实验的参数：k_p^*+k_p=0.08，k_i^*=0.005，k_d^*+k_d=0.5，得到没有迭代时的PID控制的接触力如图 8所示。可知，接触力波动范围在(30±6)N的范围之内。采用式(31)的控制律取学习因子γ=0.2进行迭代，每次实验后将传感器采回的力信号通过MATLAB编写的迭代程序离线迭代得到更新序列，再在下一次迭代时，在控制器中在线调用通过式(31)的控制律进行控制，得到迭代1次、7次和15次的跟踪接触力，如图 9所示。可知，经过15次迭代，接触力波动范围在(30±3)N之内，经过15次迭代的误差绝对值平均值、方差和标准差如表 1所示。说明与PID控制相比，经过迭代之后，接触力波动范围更小，控制效果更好。实验中所用的曲面工件的曲线轨迹表达式为y=－0.006x²+0.9x－6，利用MATLAB拟合得出的15次迭代之后机器人末端实际跟踪曲线表达式为y=－0.005 73x²+0.858 4x－5.892，二次方程的系数差异是由于机器人末端和环境产生了相对位移，所以实际跟踪轨迹相比于工件曲线轨迹有所不同，如图 10和图 11所示，可以看出通过15次迭代之后轨迹跟踪效果良好。

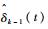
图 5 机器人曲面恒力跟踪实验平台 Fig. 5 Experimental platform of robot constant-force curved-surface-tracking

图选项

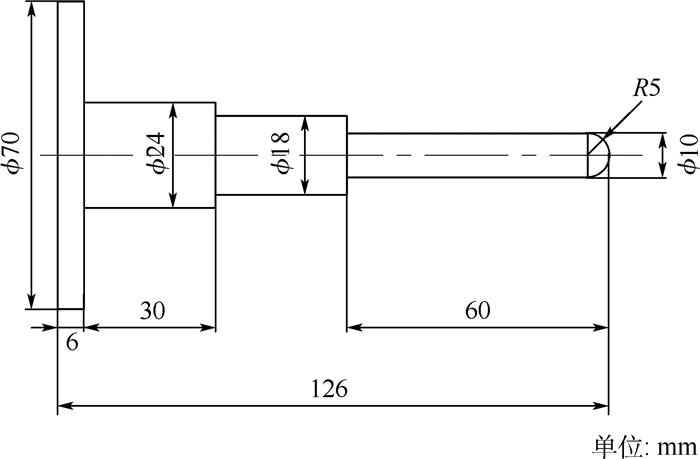图 6 探头尺寸 Fig. 6 Size of probe detector

图选项

图 7 曲面工件尺寸 Fig. 7 Size of curved-surface workpiece

图选项

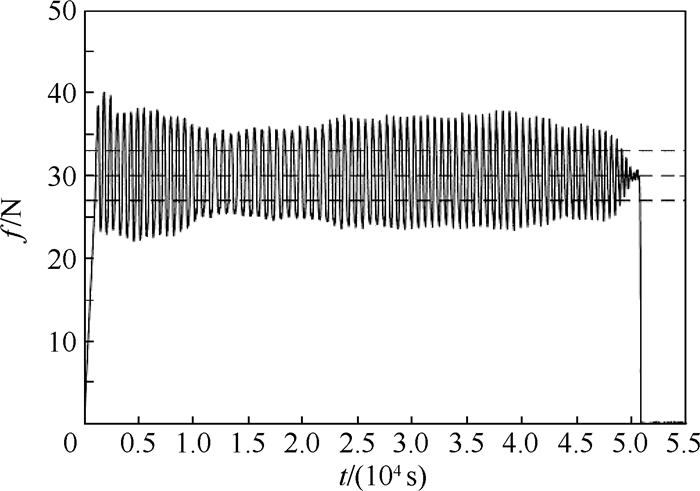图 8 没有迭代的跟踪过程 Fig. 8 Tracking process before iteration

图选项

图 9 迭代1次、7次和15次的跟踪过程 Fig. 9 Tracking process after 1 iteration, 7 iterations and 15 iterations

图选项

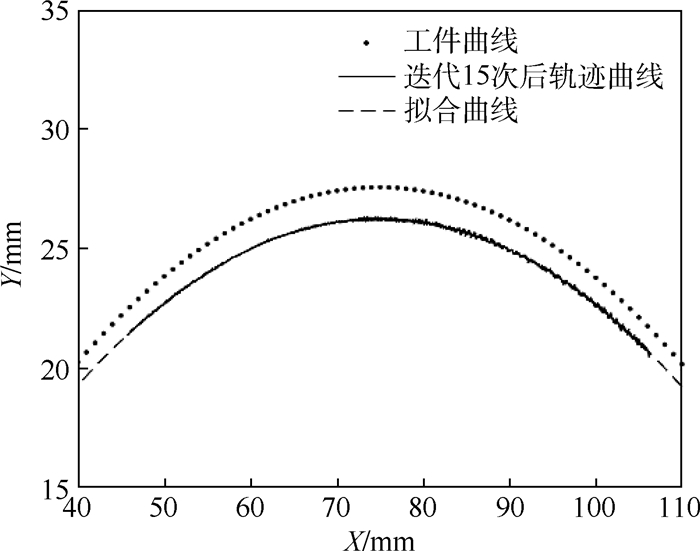图 10 工件曲线与实际跟踪曲线轨迹对比 Fig. 10 Comparison between curve of workpiece and curve of tracking trajectory

图选项

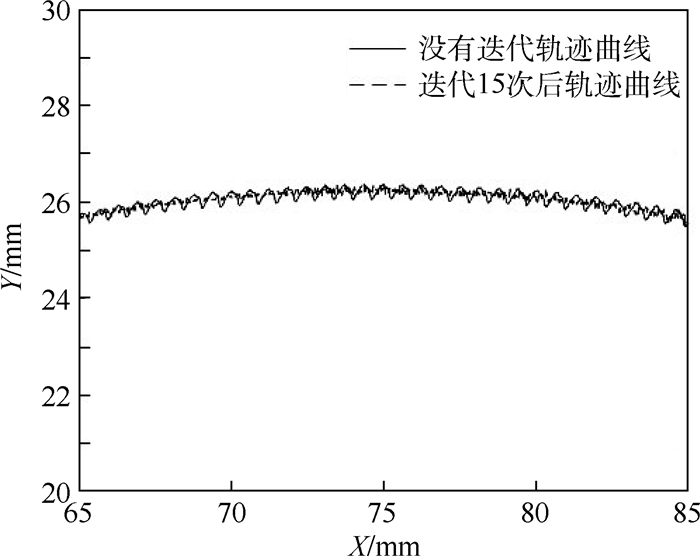图 11 没有迭代与迭代15次之后的跟踪曲线轨迹对比 Fig. 11 Comparison between curve of tracking trajectory without iteration and curve of tracking trajectory after 15 iterations

图选项

表 1 误差分析 Table 1 Error analysis

迭代次数	接触力/N
	误差绝对值平均值	误差标准差	误差方差
0	4.179 8	2.423 4	5.872 6
1	3.609 1	1.983 2	3.932 9
2	3.063 5	2.218 6	4.922 1
3	2.860 2	2.440 7	5.957 0
4	2.522 3	2.079 6	4.324 8
5	2.260 9	1.661 3	2.759 8
6	1.997 8	2.002 7	2.010 8
7	1.700 3	1.368 5	1.872 7
8	1.613 2	1.283 5	1.647 4
9	1.686 4	1.344 6	1.808 0
10	1.475 7	1.224 4	1.499 1
11	1.352 7	1.147 7	1.317 1
12	1.326 1	1.144 1	1.384 4
13	1.260 4	0.996 0	1.006 3
14	1.021 7	0.976 3	0.953 1
15	0.886 1	0.870 5	0.757 7

表选项






5 结论 1) 针对使用机器人进行打磨、抛光、去毛刺过程中难以得到稳定接触力的问题，对曲面工件轮廓恒力跟踪控制进行研究。对机器人末端执行器与曲面接触进行了受力分析，得到各个坐标系间的映射关系，构建了法向接触力和传感器采集的力信号之间的映射关系。
2) 利用机器人和环境接触时的阻抗模型设计了一种针对机器人末端位置控制量和位置参考量之间修正量的自适应迭代学习控制律，并通过构建Lyapunov能量函数对迭代学习控制律进行了收敛性分析和证明。
3) 将迭代学习控制律与力/位混合控制方法结合起来，用于机器人的曲面恒力跟踪中。实验表明，使用基于自适应迭代学习算法的机器人力/位混合曲面恒力跟踪控制方法可以实现恒力跟踪控制，并且经过15次迭代后得到的接触力误差绝对值平均值相比于没有迭代时减少了79%，误差标准差减少了64%，误差方差减少了87%，同时曲面跟踪精度提高。
本文提出的控制方法得到的轨迹可以用于机器人打磨、抛光、去毛刺时对工件轮廓进行跟踪，具有一定的法向接触力控制精度。

参考文献

[1]	TIAN F, LI Z, LV C, et al. Polishing pressure investigations of robot automatic polishing on curved surfaces[J]. The International Journal of Advanced Manufacturing Technology, 2016, 87(1-4): 639-646. DOI:10.1007/s00170-016-8527-2
[2]	NAGATA F, KUSUMOTO Y, FUJIMOTO Y, et al. Robotic sanding system for new designed furniture with free-formed surface[J]. Robotics and Computer-Integrated Manufacturing, 2007, 23(4): 371-379. DOI:10.1016/j.rcim.2006.04.004
[3]	ZILIANI G, VISIOLI A, LEGNANI G. A mechatronic approach for robotic deburring[J]. Mechatronics, 2007, 17(8): 431-441. DOI:10.1016/j.mechatronics.2007.04.012
[4]	PLIEGO-JIMéNEZ J, ARTEAGA-PéREZ M A. Adaptive position/force control for robot manipulators in contact with a rigid surface with uncertain parameters[J]. European Journal of Control, 2015, 22: 1-12. DOI:10.1016/j.ejcon.2015.01.003
[5]	ROSWELL A, XI F J, LIU G. Modelling and analysis of contact stress for automated polishing[J]. International Journal of Machine Tools and Manufacture, 2006, 46(3-4): 424-435. DOI:10.1016/j.ijmachtools.2005.05.006
[6]	QIAO B, LU R J. Impedance force control for position controlled robotic manipulators under the constraint of unknown environments[J]. Journal of Southeast University(English Edition), 2003, 19(4): 359-363.
[7]	李正义, 唐小琦, 熊烁, 等. 沿任意倾斜面的机器人力/位置控制方法研究[J]. 中国机械工程, 2012, 23(3): 304-309. LI Z Y, TANG X Q, XIONG S, et al. Study on robot force position control method for arbitrarily inclined plane tracking[J]. China Mechanical Engineering, 2012, 23(3): 304-309. DOI:10.3969/j.issn.1004-132X.2012.03.012 (in Chinese)
[8]	DUAN J, GAN Y, CHEN M, et al. Adaptive variable impedance control for dynamic contact force tracking in uncertain environment[J]. Robotics and Autonomous Systems, 2018, 102: 54-65. DOI:10.1016/j.robot.2018.01.009
[9]	李二超, 李战明, 李炜. 基于视觉的机器人模糊自适应阻抗控制[J]. 中南大学学报(自然科学版), 2011, 42(2): 409-413. LI E C, LI Z M, LI W. Fuzzy adaptive impedance control of robot based on vision[J]. Journal of Central South University(Science and Technology), 2011, 42(2): 409-413. (in Chinese)
[10]	BAETEN J, DE SCHUTTER J. Hybrid vision/force control at corners in planar robotic-contour following[J]. ASME Transactions on Mechatronics, 2002, 7(2): 143-151.
[11]	JEON S W, AHN D S, BAE H J, et al.Object contour following task based on integrated information of vision and force sensor[C]//International Conference on Control, Automation and Systems.Piscataway, NJ: IEEE Press, 2007: 1040-1045.
[12]	LANGE F, HIRZINGER G.Iterative self-improvement of force feedback control in contour tracking[C]//IEEE International Conference on Robotics and Automation.Piscataway, NJ: IEEE Press, 1992: 1399-1404.
[13]	VISIOLI A, ZILIANI G, LEGNANI G. Iterative-learning hybrid force/velocity control for contour tracking[J]. IEEE Transactions on Robotics, 2010, 26(2): 388-393. DOI:10.1109/TRO.2010.2041265
[14]	ROVEDA L, PALLUCCA G, PEDROCCHI N, et al. Iterative learning procedure with reinforcement for high-accuracy force tracking in robotized tasks[J]. IEEE Transactions on Industrial Informatics, 2018, 14(4): 1753-1763. DOI:10.1109/TII.2017.2748236
[15]	WINKLER A, SUCHY J.Force controlled contour following on unknown objects with an industrial robot[C]//IEEE International Symposium on Robotic and Sensors Environments.Piscataway, NJ: IEEE Press, 2013: 208-213.
[16]	KUMAR N, PANWAR V, SUKAVANAM N, et al. Neural network based hybrid force/position control for robot manipulators[J]. International Journal of Precision Engineering and Manufacturing, 2011, 12(3): 419-426. DOI:10.1007/s12541-011-0054-3
[17]	JUNG S, HSIA T C. Robust neural force control scheme under uncertainties in robot dynamics and unknown environment[J]. IEEE Transactions on Industrial Electronics, 2002, 47(2): 403-412.
[18]	KARAYIANNIDIS Y, ROVITHAKIS G, DOULGERI Z. Force/position tracking for a robotic manipulator in compliant contact with a surface using neuro-adaptive control[J]. Automatica, 2007, 43(7): 1281-1288. DOI:10.1016/j.automatica.2006.12.019
[19]	HE W, DONG Y, SUN C. Adaptive neural impedance control of a robotic manipulator with input saturation[J]. IEEE Transactions on Systems, Man, and Cybernetics:Systems, 2016, 46(3): 334-344. DOI:10.1109/TSMC.2015.2429555
[20]	丁希仑, 周乐来, 周军. 机器人的空间位姿误差分析方法[J]. 北京航空航天大学学报, 2009, 35(2): 241-245. DING X L, ZHOU L L, ZHOU J. Pose error analysis of robot in three dimension[J]. Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(2): 241-245. (in Chinese)
[21]	张铁, 胡广. 曲面轮廓恒力跟踪的非线性双闭环控制[J]. 电机与控制学报, 2017, 21(7): 99-106. ZHANG T, HU G. Nonlinear dual-loop force controller of contour following[J]. Electric Machines and Control, 2017, 21(7): 99-106. (in Chinese)
[22]	TAYEBI A. Adaptive iterative learning control for robot manipulators[J]. Automatica, 2004, 40(7): 1195-1203. DOI:10.1016/j.automatica.2004.01.026
[23]	GRAIG J J. Introduction to robotics mechanics and control[M]. London: Pearson, 2004.
[24]	乔兵, 吴洪涛, 朱剑英, 等. 面向位控机器人的力/位混合控制[J]. 机器人, 1999, 21(3): 217-222. QIAO B, WU H T, ZHU J Y, et al. Hybrid force position control for position-controlled robotic manipulators[J]. Robot, 1999, 21(3): 217-222. DOI:10.3321/j.issn:1002-0446.1999.03.010 (in Chinese)
[25]	SERAJI H, COLBAUGH R.Force tracking in impedance control[C]//IEEE International Conference on Robotics and Automation.Piscataway, NJ: IEEE Press, 1993: 409-506.
[26]	李二超, 李战明. 基于力/力矩信息的面向位控机器人的阻抗控制[J]. 控制与决策, 2016, 31(5): 957-960. LI E C, LI Z M. Impedance control for positional-controlled robotic manipulators based on force/torque information[J]. Control and Decision, 2016, 31(5): 957-960. (in Chinese)