近些年来，无人机得到了长足发展。为了延长航行时间并降低能源消耗，无人机一般采用大展弦比高柔性机翼设计以追求较高的气动效率^[1]。同时为了减轻飞机重量，机翼设计大都选择轻质材料，所以大展弦比无人机机翼一般都是柔性机翼。然而，机翼的展弦比增大以及重量减小会带来新的挑战，这就要求对机翼在正常飞行载荷下的大变形问题做进一步研究，因为大变形问题会带来几何非线性行为及相关的气动弹性问题^[2-3]。这些大变形会改变机翼的固有频率，从而使其气动弹性行为发生显著变化^[4]。
在进行气动弹性特性理论计算的同时，通过风洞试验来确定飞机的气动弹性特性是必不可少的^[5]。缩比模型的气动弹性试验是飞机研制过程中最基本的保证，缩比模型应尽可能地反映出全尺寸飞机的气动弹性响应^[6]。使用缩比模型来进行试验可以更好地理解机翼的物理行为，同时降低制造全尺寸飞机的风险与成本^[7]。
气动弹性模型缩比设计要求同时考虑气动力和结构的物理特性。气动力的模拟可以通过气动外形几何缩比再进行分析计算得到。而通常情况下，通过结构的几何尺寸缩比对结构进行模拟是不现实的。根据缩比设计的要求，指定几何缩比的结构，其制造所用的材料通常是不存在的，而且很大程度上用于制造全尺寸飞机的加工技术在缩比模型上是不可能实现的。唯一可行的方法是对内部结构进行重新设计并优化，比如对结构的质量、刚度、阻尼特性进行缩比，并且与全尺寸飞机保持协调^[8]。
目前研究考虑非线性的气动弹性模型缩比的相关文献较少，只是最近几年该课题才热门起来，这些研究主要针对的是具有大展弦比高柔性机翼的高空长航时无人机^[9]和联翼布局飞机^[10-11]。
Wan和Cesnik^[9]推导得到包含大变形引起的非线性刚度和预应力影响的气动弹性运动方程的缩比参数，研究表明线性和几何非线性的气动弹性运动方程的缩比因子在形式上是相同的。同时Wan和Cesnik^[9]对大柔性飞机2种形式的缩比设计进行了分析，其中一种设计有意忽略了Froude数，他们对包括结构模态、非线性气动弹性配平、不同载荷下的线性长周期稳定性以及非线性瞬态阵风响应等特性进行了计算。结果表明:包含Froude数的缩比模型响应与全尺寸模型吻合得很好，所以Froude数的相似在验证的问题上不能被忽略。
Bond等^[10]提出了一个非线性气动弹性模型缩比方法，用来设计具有几何非线性特征的联翼飞机缩比模型。其设计的结构可以匹配前3阶频率、前3阶模态振型以及第1阶线性屈曲特征解，且缩比模型的气动弹性频率和阻尼在整个速度包线上都匹配得很好。同时，结果表明，缩比模型的非线性静响应，在60%屈曲载荷下都匹配得很好。
Ricciardi等^[11]发展的几何非线性气动弹性模型缩比设计方法可以直接匹配缩比的线性和非线性静响应，同时可以满足模态频率的约束。他们用该方法设计的模型同利用传统方法并经过优化的模型进行比较，发现用前面提到的方法设计并优化的缩比模型其非线性气动弹性响应同目标响应吻合较好，而利用传统方法设计的缩比模型其非线性气动弹性响应同目标响应相比误差较大。
基于上述观点，本文提出一个新的非线性气动弹性模型缩比方法，称为动力学有限元模型的非线性静响应-模态协同优化方法，其中非线性静响应的匹配是基于等效静态载荷法来实现的。这是首次将处理非线性静力学的等效静态载荷法与大展弦比机翼结构动力学相结合的优化方法。
另外该方法与Ricciardi等^[11]提出的方法主要区别是缩比方法的实现过程不同。本文方法中刚度和质量分布设计是在2个优化循环过程中进行的，而Ricciardi等的方法只是在一个优化循环中进行的。而且本文验证的实例是一架具有超大展弦比高柔性机翼的某型无人机，它的几何非线性效应比上述文献中验证的飞机要强得多。
1 理论方法 1.1 相似准则 缩比因子的选择是气动弹性缩比模型设计过程中关键的第1步。通常选定气动弹性缩比模型设计的3个基本缩比因子：k_b、k_v和k_ρ。这里，k_b为缩比模型与全尺寸模型的长度比，k_v为缩比模型与全尺寸模型的速度比，k_ρ为缩比模型与全尺寸模型所处环境的空气密度比。
为了满足缩比模型和全尺寸模型之间的气动弹性相似性，在前3个基本缩比因子^[12-13]的基础上，必须满足下面描述的4个相似准则。当要求在重力作用下气动弹性响应满足相似要求时，必须满足重力相似准则作为附加条件。
1) 几何相似
几何相似的缩比因子即前述的k_b。几何相似意味着缩比模型与全尺寸模型之间的所有尺寸比(包括翼展比，弦长比等)都与k_b相同。同时还假定缩比模型和全尺寸模型具有相同的翼型。
2) 质量相似
满足质量相似可以写为

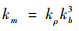(1)

这意味着缩比模型的分布质量应该通过质量缩比因子k_m与全尺寸模型的分布质量成比例。
3) 刚度相似
满足刚度相似可以描述为

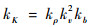(2)

这意味着缩比模型的分布刚度应该通过刚度缩比因子k_K与全尺寸模型的分布刚度成比例。
基于固有频率与质量和刚度的关系，频率的缩比因子即为

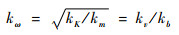(3)

4) 气动相似
当缩比模型和全尺寸模型之间的马赫数与雷诺数分别满足一致性要求时，几何相似便会带来气动相似。但是，马赫数相似和雷诺数相似都是不容易满足的。对于大展弦比高柔性无人机的典型低速飞行，马赫数效应可以忽略。但是，缩比模型与全尺寸模型之间的雷诺数应该相同或至少在相同的数量级上。
雷诺数的缩比因子可以定义为

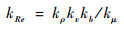(4)

式中：k_μ为空气动黏度的缩比因子。
基于升力方程，升力的缩比因子为

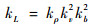(5)

5) 重力相似
Froude数决定了重力载荷下挠度与空气动力和惯性载荷下挠度的比值。当颤振试验中考虑重力效应，缩比模型和全尺寸模型之间的Froude数应相同，可以通过式(6)来满足^[10]：

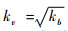(6)

与线性结构相比，考虑几何非线性的结构具有其特殊的刚度特性，其特殊性取决于当前的结构变形。显然，当缩比模型和全尺寸模型在未变形状态和任一给定的变形状态下均满足几何相似，质量相似和Froude数相似要求，则缩比模型和全尺寸模型在任何变形状态下上述相似关系也是成立的。因此，这取决于考虑几何非线性的结构随结构变形而变化的刚度是否可以在缩比模型和全尺寸模型之间保持相似。这将直接影响线性气动弹性相似准则对考虑几何非线性的结构的适用性。
Wan和Cesnik^[9]的研究表明线性和几何非线性气动弹性运动方程的缩比因子形式上是相同的。因此，若缩比模型是基于上述缩比因子设计的，则缩比模型与全尺寸模型之间的气动弹性行为在小变形状态和大变形状态下都是相似的。由式(1)~式(6)可知，对于考虑几何非线性的气动弹性缩比模型而言，当重力相似准则作为附加条件时，在长度比k_b、空气密度比k_ρ确定的情况下，作为模型设计目标的模型质量、模型固有频率、模型颤振速度和颤振频率便可随之确定。
1.2 缩比方法
1.2.1 传统线性缩比方法 从线弹性的控制方程可以看出，经过对全尺寸飞机适当的缩比，对于不同结构形式的缩比模型，只要具有相同的几何缩比，以及相同的分布刚度和质量缩比，将带来相同的模态特性(固有频率和模态振型)^[14]。因此可以利用这一理论从全尺寸飞机那里获得缩比模型的目标值(质量、惯性矩、固有频率、模态振型和气动外形)。通过设计一个与全尺寸模型相似的模态特性的缩比模型，得到与内部结构无关的分布刚度和质量相似性，即可采用简化的内部结构。一般情况下，为了匹配目标缩比值，有2种不同的传统线性缩比方法：刚度质量耦合匹配模态响应法(方法A)；刚度质量解耦匹配模态响应法(方法B)。图 1和图 2分别是方法A和B的优化设计流程图。

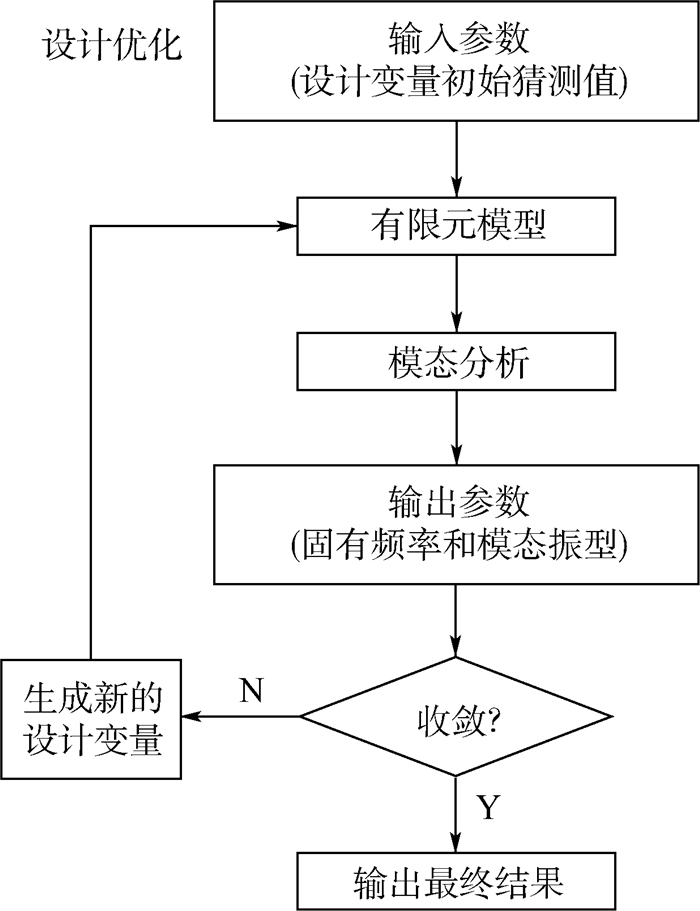图 1 传统线性缩比方法(方法A) Fig. 1 Traditional linear scaling method (Method A)

图选项

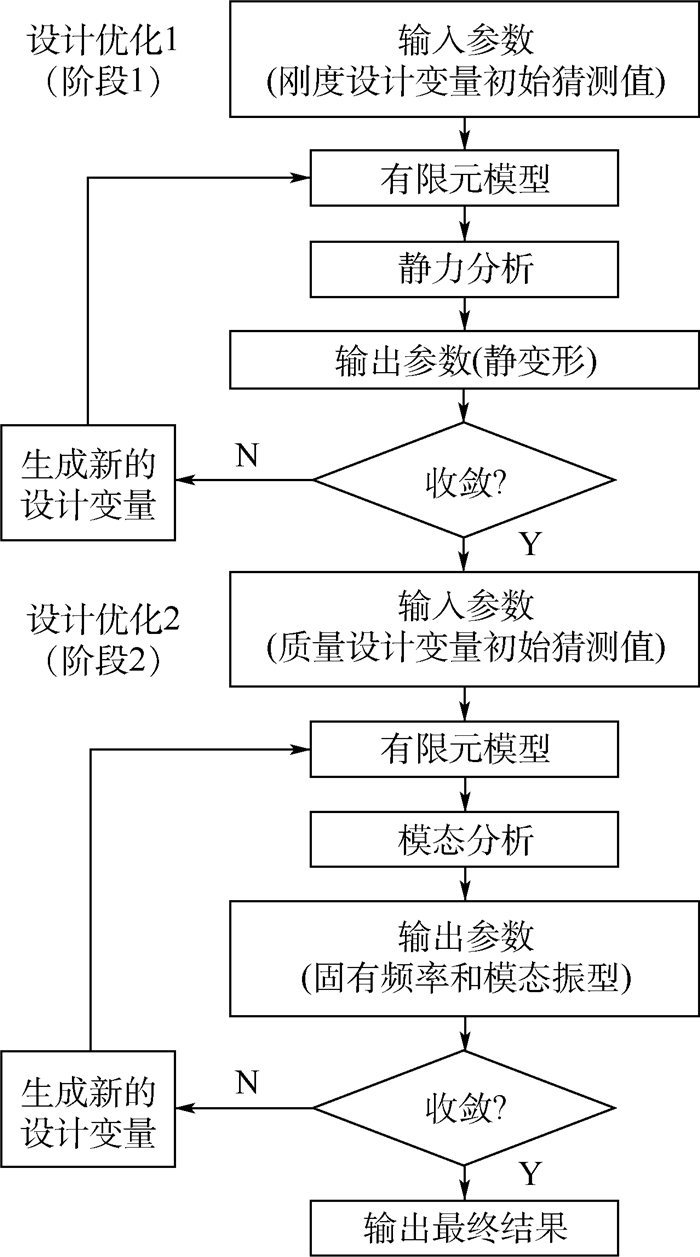图 2 传统线性缩比方法(方法B) Fig. 2 Traditional linear scaling method (Method B)

图选项

方法A类似于Bisplinghoff等^[12]提出的方法，方法B则是French和Eastep^[6]提出的。不过上述2种方法都是针对大部分的线性问题，对于非线性问题，这2个方法的适用性还需要进行进一步的验证。

1.2.2 考虑几何非线性的缩比方法 与方法B类似，通过分别匹配解耦的刚度和质量分布来匹配模态特性。该方法(方法C)的流程如图 3所示。方法B与方法C的区别体现在第1阶段的刚度优化过程中。在方法C中，缩比模型的刚度优化引入了等效静态载荷法，而且通过非线性静力分析来获得非线性广义位移场。这个优化过程可以在MATLAB中实现，静力分析与模态分析使用MSC.Nastran软件，优化准则使用粒子群寻优算法。当第1阶段的刚度优化完成后，就可以进行第2阶段的质量优化，质量优化的目的是在匹配了非线性静响应后匹配模态特性(固有频率和模态振型)。

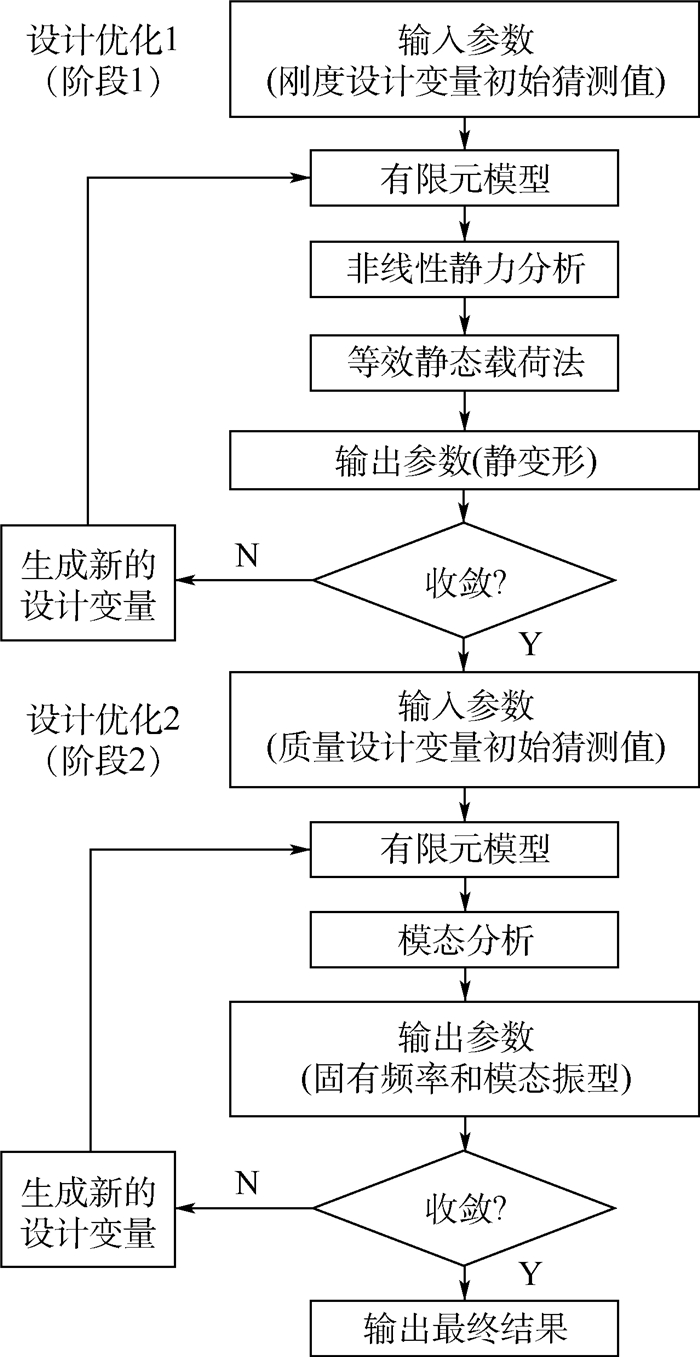图 3 考虑几何非线性的缩比方法(方法C) Fig. 3 Scaling method considering geometric nonlinearity (Method C)

图选项

研究发现，对非线性静力响应的直接优化很困难。对于这项任务，基于等效静态载荷法来应用等效线性系统的效率会更高^[15]。等效静态载荷法就是通过不断迭代更新线性系统中的设计变量来获得与非线性静力分析结果相同的广义位移场。
首先给定当前或初始设计变量{d}和载荷条件{F}，然后非线性静力分析通过求解非线性平衡方程(式(7))得到非线性变形{x_NL}。

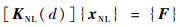(7)

由线性刚度矩阵[K_Lin(d)]乘以非线性变形{x_NL}得到等效载荷{F_eq}：

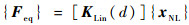(8)

由等效载荷{F_eq}和线性刚度矩阵[K_Lin(d)]将可得到等效线性静态广义位移{x_Lin}：

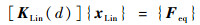(9)

接下来在等效线性系统中便可以执行高效的优化，等效静态载荷法需要一个迭代过程来更新线性化系统的设计变量，优化收敛时的线性化的最佳响应与非线性系统的响应相匹配。

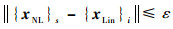(10)

式中：i为迭代次数；ε为误差参数(满足设计要求的小值)。应用等效静态载荷法的过程如图 4所示。

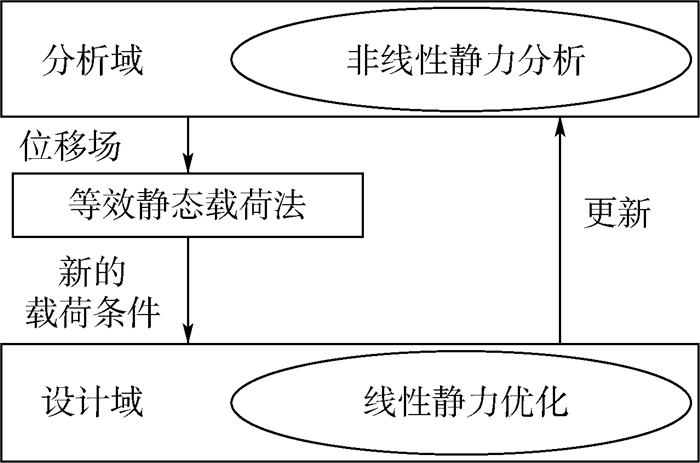图 4 分析域和设计域优化流程图 Fig. 4 Flowchart of analysis and design domain optimization

图选项

该优化过程是在2个域(分析域和设计域)里实施的。首先，在分析域中进行非线性静力分析，获得非线性广义位移场；然后，利用位移场通过等效静态载荷法获得新的载荷条件，把新的载荷条件应用到设计域的线性静力优化中；最后，通过不断迭代更新设计域中的设计变量来使非线性系统和线性系统的广义位移场误差满足要求。该过程的具体实现如图 5所示。

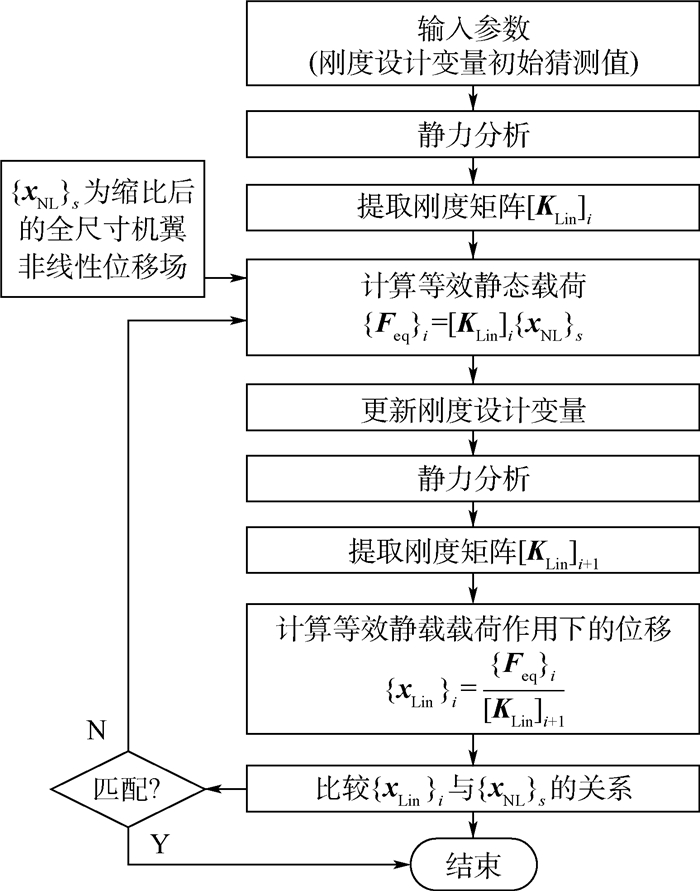图 5 等效静态载荷法的实现过程图 Fig. 5 Implementation procedure of equivalent static loads method

图选项

本文目的是对具有几何非线性特征的结构进行气动弹性缩比，设计出的缩比模型要与全尺寸飞机的模态特性吻合，所以笔者根据传统线性缩比方法结合等效静态载荷法来实现这一缩比过程。
2 模型 2.1 全尺寸模型 本文缩比的全尺寸模型是一架具有大展弦比柔性机翼的某型机。该机机翼的展弦比为31.25，属于超大展弦比机翼。该机的巡航马赫数Ma=0.1，巡航高度为20 km。机翼的主要参数在表 1中列出。
表 1 全尺寸机翼的主要参数 Table 1 Main parameters of full-scale wing

参数	数值
机翼面积/m2	80
内翼展长/m	36
外翼展长/m	14
翼根弦长/m	2
翼尖弦长/m	1
结构总质量/kg	202.5

表选项






整个机翼包括1段10 m长的中央翼，2段10 m长的中外翼，2段10 m长的外翼。整个机翼包括梁、肋和前后缘，翼梁为盒形梁，梁截面宽度为240 mm，高度为170 mm。翼肋采用夹芯肋，前后缘为壳形蜂窝夹芯结构。全尺寸机翼的平面布局如图 6所示，该机结构布局如图 7所示。本文使用MSC.Nastran软件对全尺寸模型进行求解计算。

图 6 机翼平面布局 Fig. 6 External configuration of wing

图选项

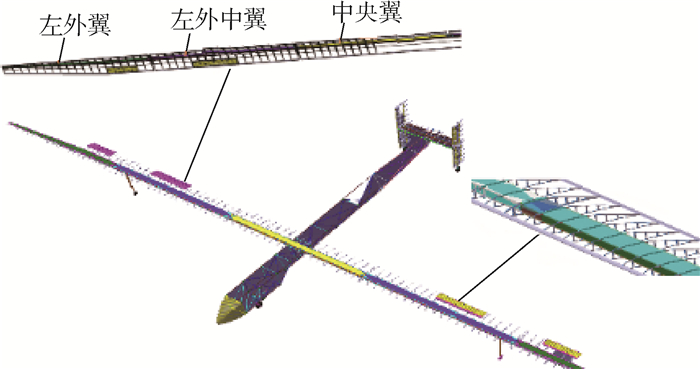图 7 全机结构及内部结构 Fig. 7 Whole aircraft structure and internal structure

图选项

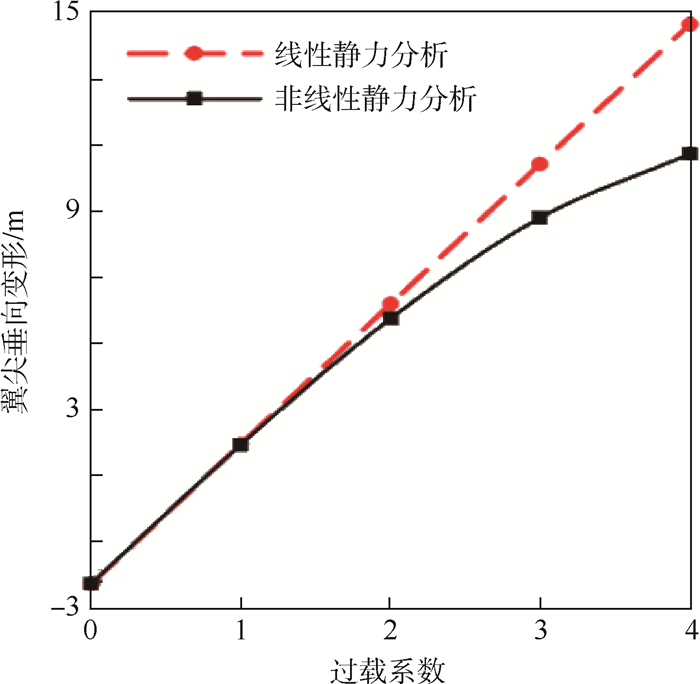
本文首先对全尺寸模型进行线性和非线性静力分析，以评估2种分析之间的差异。图 8显示了随着过载系数的增加，翼尖线性与非线性垂向变形量变化趋势的差异。根据定义，通过增加升力来实现不同的过载系数：

图 8 翼尖变形趋势 Fig. 8 Variation of wing tip deflection

图选项

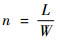(11)

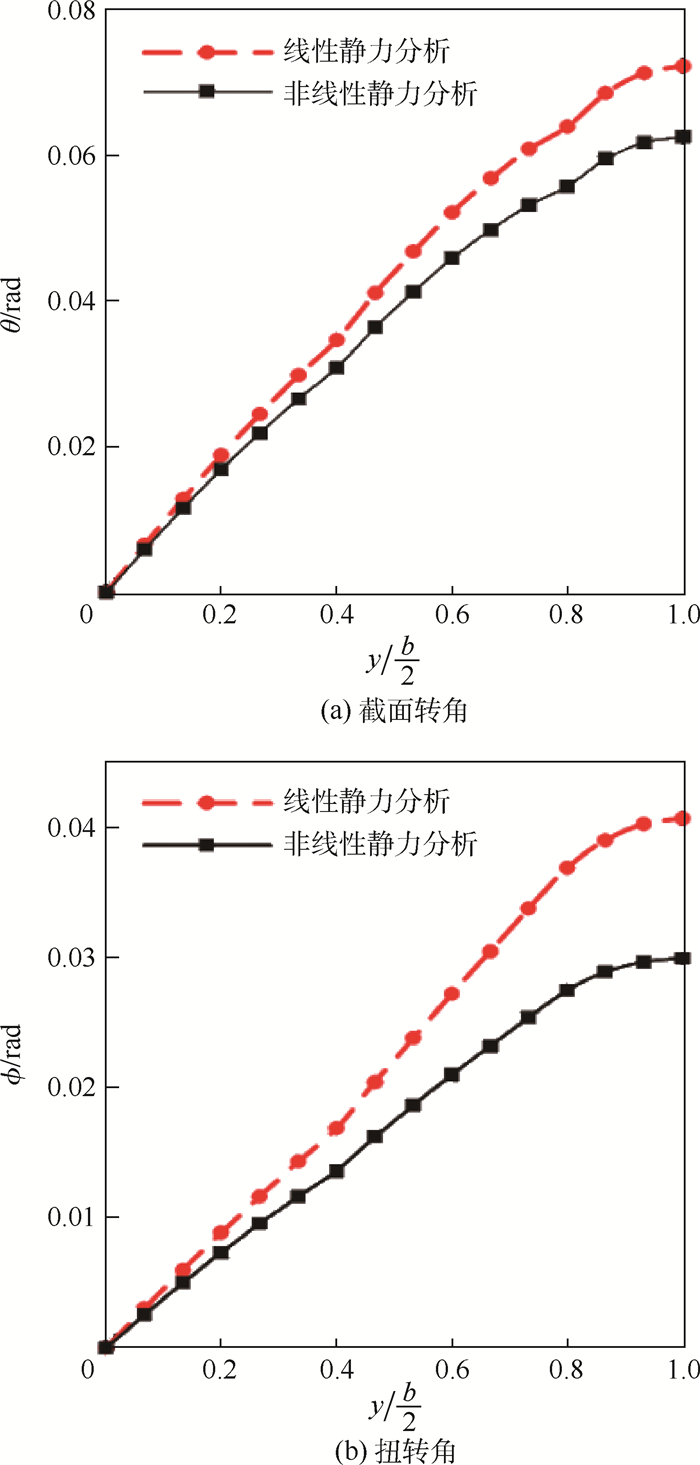
式中：n为过载系数; L和W分别为飞机的总升力和总重力。分析发现，随着过载系数的增加，线性和非线性变形量变化曲线逐渐分离。当过载系数是4时，翼尖非线性变形量与线性变形量相差4.07 m。这是因为线性静力分析时不考虑升力跟随后的轴向分力，所以翼尖不会向翼根方向移动。从图 8还可以看出，过载系数为1.5时，非线性效应还不明显，这是因为机翼刚度稍大，载荷较小时，结构还没有到达非线性状态造成的。当过载系数为3时，截面转角θ和扭转角?沿展向的非线性和线性变化趋势如图 9所示，其中b为翼展长度。由图 9可知，当进行非线性静力分析时，结构会经历一个刚度硬化效应。在图 9中线性和非线性变化趋势分离的地方出现在翼展20%站位的位置，这是由刚度变化引起的。

图 9 截面转角和扭转角的变化趋势 Fig. 9 Variation of cross-section bend angle and twist angle

图选项

针对本文的研究，结构几何非线性主要归因于大位移状态，处理大位移问题时，利用跟随力的非线性求解器可以大幅改变系统的载荷和刚度矩阵，从而改变变形状态。图 8和图 9说明了线性和非线性静力分析之间的区别以及随着结构的变形增大，不断地引入附加刚度造成的这些差异。
2.2 缩比模型 本文缩比模型选取基本缩比因子k_b=0.1，k_ρ=13.764，k_v=0.316，进而目标缩比参数可以通过这些缩比因子确定。为了增大优化过程中可行解区域，设计变量选取截面的“刚度底层控制信息”，即截面积A、截面惯性矩I_a和I_b以及截面扭转常数J。因此在缩比优化之前不需要对缩比模型结构形式进行设计，可在优化结束后对截面“刚度底层控制信息”进行逆运算来获取截面几何信息。为了使缩比模型正确描述全尺寸模型的气动弹性特性，确定匹配两者前10阶固有频率和相应的模态振型，其相似度不低于90%。全尺寸模型颤振主要由第4阶模态(水平二弯)和第5阶模态(一扭)参与，所以主要看第4阶与第5阶模态匹配相似度。同时，缩比模型和全尺寸模型的总质量匹配相似度不低于90%。
就外部几何布局而言，缩比模型是全尺寸模型的精确几何缩比。在缩比的过程中，还要寻找最佳材料来模拟缩比模型的结构部件。全尺寸模型所采用的材料为7075铝合金，然而精确缩比后的材料是不存在的。所以在缩比之前要对缩比模型的材料进行研究并选择。最终决定使用较靠近材料缩比目标值的铸铝青铜作为缩比模型的材料。
最优设计变量的目标是使缩比模型和全尺寸模型的一些特性(质量、固有频率、模态振型以及在考虑几何非线性的方法中的非线性静响应)匹配。残差平方和(SSR)是量化响应差异的一个基本参考值。
3 计算结果 本文采用粒子群寻优算法对缩比模型的设计变量进行优化，来使得缩比模型的各阶固有频率和模态振型与全尺寸模型对应阶的固有频率和模态振型相似度达到90%以上。1.2节提到了2种传统线性缩比方法(方法A与方法B)以及考虑几何非线性的缩比方法(方法C)。
表 2为传统线性缩比方法与考虑集合非线性缩比方法结果参数比较，其中方法B和方法C分别给出了阶段1和阶段2的参数值。从表 2可以看出，方法A和方法B相比于方法C耗时较少，所以当结构非线性效应不明显时，推荐使用传统线性缩比方法。然而，当考虑了结构的非线性效应，用传统线性缩比方法设计的模型计算结果误差较大，无法处理考虑几何非线性的模型设计。
表 2 传统线性缩比方法与考虑几何非线性的缩比方法结果参数比较 Table 2 Comparison of result parameters between traditional linear scaling method and scaling method considering geometric nonlinearity

方法	设计变量数	求解时间/h	误差/%
方法A	27	1.5	8.11
方法B	30(24+6)	0.9(0.5+0.4)	9.95
方法C	30(24+6)	2.9(2.4+0.5)	2.80

表选项






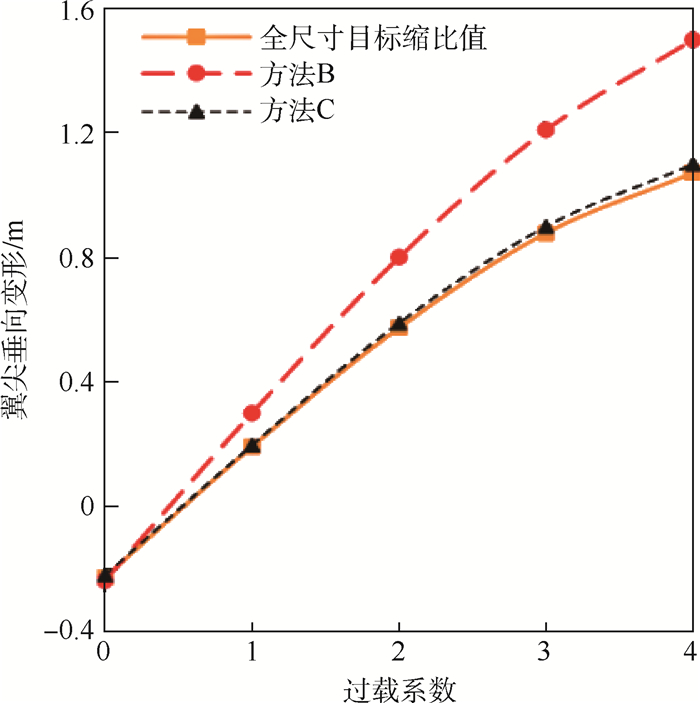
为了高效地捕捉结构的非线性行为，本文提出使用等效静态载荷法进行非线性静响应匹配，来对动力学有限元模型的非线性静响应-模态进行协同优化。对使用考虑几何非线性的方法获得的非线性翼尖变形量和传统线性缩比方法设计的模型翼尖变形量以及变形量目标缩比值进行了比较。分析发现，方法C设计的模型非线性静变形量相比于方法B，更为靠近目标值(图 10)。

图 10 非线性翼尖垂向变形 Fig. 10 Nonlinear wing tip vertical deformation

图选项

图 11显示了传统线性缩比方法(方法A、方法B)和考虑几何非线性的缩比方法(方法C)在前10阶的固有频率、模态振型上匹配相似度的差异。目标缩比值是从全尺寸模型的相关计算中获得到。

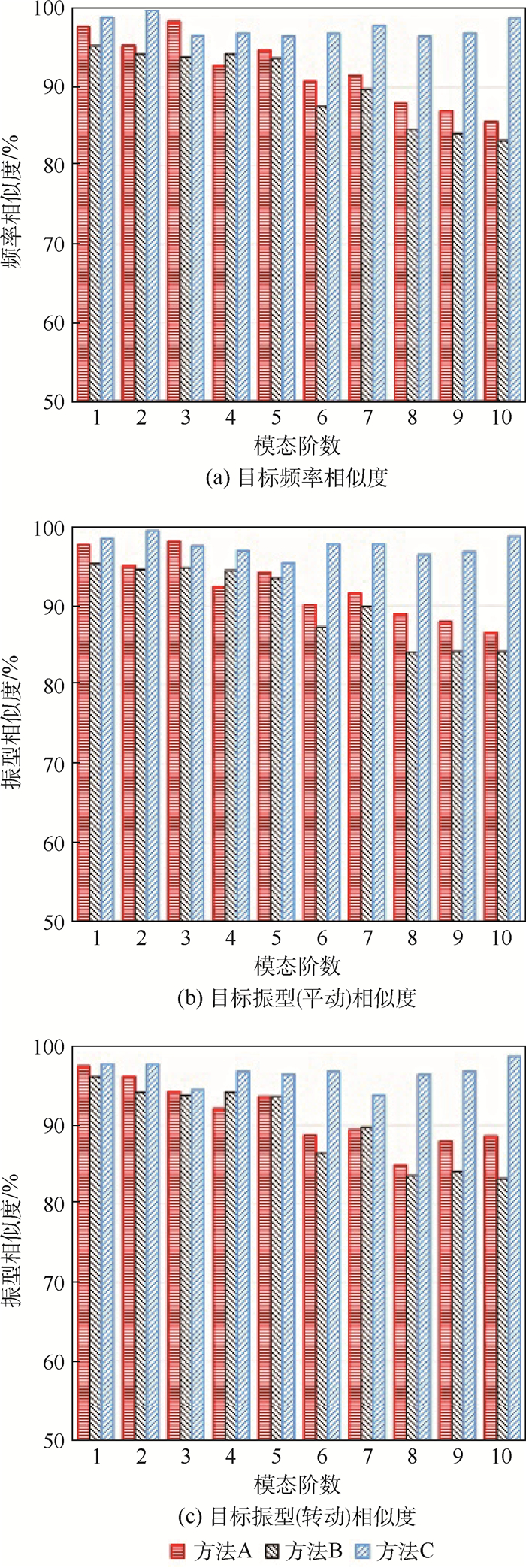图 11 3种方法结果与目标频率相似度、目标振型(平动)相似度和目标振型(转动)相似度差异 Fig. 11 Difference in similarity between results of three methods and target frequency, target translational mode shapes and target rotational mode shapes

图选项

本文的颤振计算使用偶极子格网法求解非定常气动力模型。为了匹配全尺寸模型的气动弹性响应，分别采用方法B和方法C对模型进行设计，表 3是2种模型颤振求解结果与目标缩比值的比较，通过考虑几何非线性的气动弹性模型缩比方法设计的模型，其颤振结果误差得到了显著降低。图 12(a)为第4阶和第5阶模态的V-g(速度-阻尼系数)图，图 12(b)为第4阶和第5阶模态的V-f(速度-频率)图。为了便于观察，图中是把缩比模型的颤振计算结果进行逆缩比，其逆缩比的值可直接与全尺寸机翼的颤振计算结果进行对比。因为颤振主要是第4阶模态(面内二弯)和第5阶模态(一扭)引起，所以在图 12中，只显示了这2阶模态。当采用几何非线性缩比方法时，气动弹性响应匹配相似度有所改进，其精度明显优于传统线性缩比模型得到的结果。
表 3 两种方法结果与目标颤振速度及频率误差 Table 3 Flutter speed and frequency differences between Method B and C in relation to associated target scaled values

%
方法	颤振速度误差	颤振频率误差
方法B	8.25	16.84
方法C	1.18	5.67

表选项

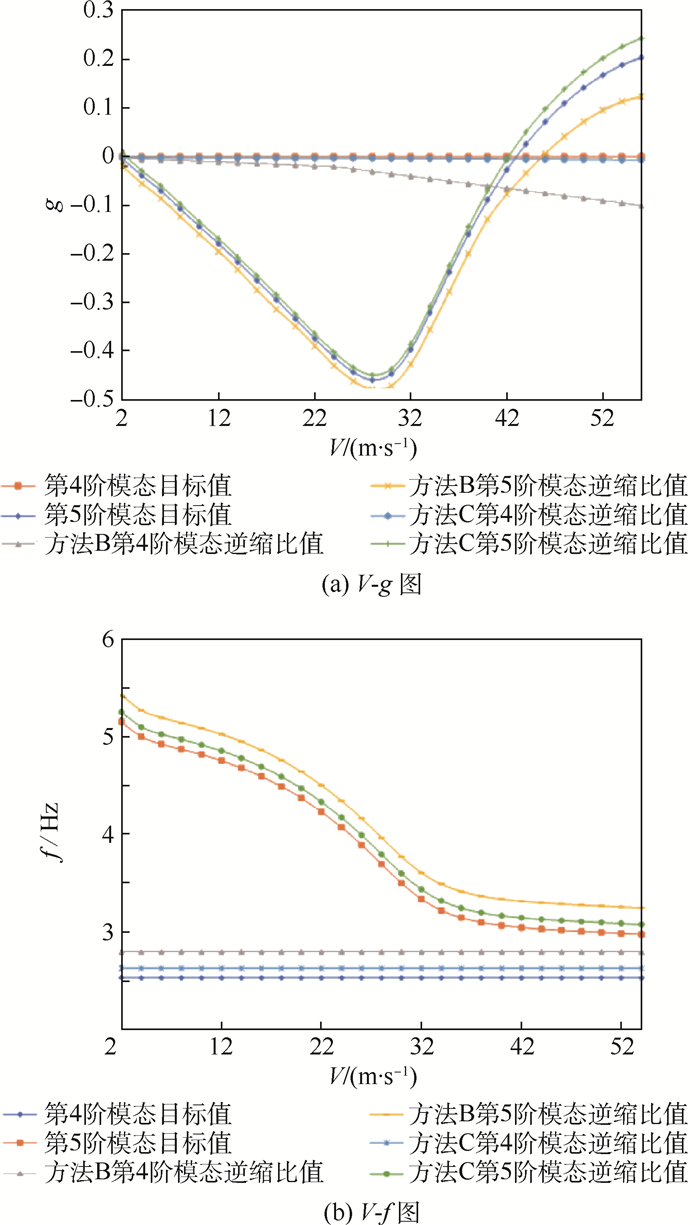图 12 V-g和V-f 图 Fig. 12 V-g and V-f diagram

图选项

4 结论 本文研究了气动弹性模型的传统线性缩比方法和考虑几何非线性的缩比方法，得到以下结论：
1) 本文提出的考虑几何非线性的气动弹性模型缩比方法能够针对几何非线性效应明显的气动弹性模型进行缩比，缩比模型与全尺寸模型的高阶模态匹配度较高，说明该方法可以捕捉到传统线性缩比方法无法捕捉到的高阶信息，进而缩比模型能够更好地再现全尺寸飞机的非线性气动弹性行为。
2) 传统线性缩比方法求解平均时间为1.2 h，平均误差为9.03%；几何非线性气动弹性模型缩比方法求解时间为2.9 h，误差为2.80%。可以看出，虽然传统线性缩比方法求解时间少于几何非线性气动弹性模型缩比方法求解时间，但是前者误差已经无法满足模型设计要求。所以对于考虑几何非线性的结构，从缩比设计相似精度要求来看，传统线性缩比方法是不适用的，推荐使用本文的新方法。
3) 方法A(耦合)求解时间高于方法B(解耦)求解时间，但方法A误差略低于方法B误差，虽然两者对于考虑几何非线性的结构缩比问题都无法满足设计要求，但对于几何非线性效应不明显的结构，这2种方法都是可以处理相关缩比问题的。
4) 等效静态载荷法的优化逻辑是把原先非线性求解过程中的刚度无规律低效更新转变为刚度有方向高效更新，使用等效静态载荷法来进行非线性静响应的匹配在保证匹配精度的同时能大大降低时间成本。
本文的后续工作是要对具有大展弦比机翼的飞机按照文中提出的考虑几何非线性的缩比方法缩比后进行风洞试验。从长远来看，本文所得结论也能应用到设计飞行试验的模型上，验证飞行过程中的几何非线性气动弹性响应。同时，还需要将本文所提的考虑几何非线性的缩比方法应用于更复杂的结构以及更高精度的气动模型，并进一步验证其有效性。

参考文献

[1]	徐江锋.大展弦比无人机机翼预变形研究[D].南昌: 南昌航空大学, 2013: 1-2. XU J F.Research on pre-deformation for high-aspect-ratio wing of UAV[D].Nanchang: Nanchang Hangkong University, 2013: 1-2(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10406-1014006538.htm
[2]	HARMIN M Y, COOPER J E. Aeroelastic behaviour of a wing including geometric nonlinearities[J]. Aeronautical Journal, 2016, 115(1174): 767-777.
[3]	PALACIOS R, MURUA J, COOK R. Structural and aerodynamic models in nonlinear flight dynamics of very flexible aircraft[J]. AIAA Journal, 2010, 48(11): 2648-2659. DOI:10.2514/1.J050513
[4]	PATILM J, HODGES D H, CESNIK C E S. Nonlinear aeroelasticity and flight dynamics of high-altitude long-endurance aircraft[J]. Journal of Aircraft, 2001, 38(1): 88-94. DOI:10.2514/2.2738
[5]	吕斌, 刘德广, 谢长川, 等. 机翼低速风洞试验颤振模型优化设计方法[J]. 北京航空航天大学学报, 2006, 32(2): 163-166. LV B, LIU D G, XIE C C, et al. Optimization designing method of wing flutter model for low-speed wind tunnel test[J]. Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(2): 163-166. DOI:10.3969/j.issn.1001-5965.2006.02.009 (in Chinese)
[6]	FRENCH M, EASTEP F E. Aeroelastic model design using parameter identification[J]. Journal of Aircraft, 1996, 33(1): 198-202. DOI:10.2514/3.46922
[7]	赵延新.机翼气动弹性模型RTM工艺研究及模具设计[D].大连: 大连理工大学, 2014: 1-2. ZHAO Y X.Research on the RTM process of aeroelastic model of wing and mold design[D].Dalian: Dalian University of Technology, 2014: 1-2(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10141-1015571724.htm
[8]	RICCIARDI A P.Geometrically nonlinear aeroelastic scaling[D].Blacksburg: Virginia Tech, 2014: 2-5.
[9]	WAN Z Q, CESNIK C E S. Geometrically nonlinear aeroelastic scaling for very flexible aircraft[J]. AIAA Journal, 2014, 52(10): 2251-2260. DOI:10.2514/1.J052855
[10]	BOND V L, CANFIELD R A, SULEMAN A, et al. Aeroelastic scaling of a joined wing for nonlinear geometric stiffness[J]. AIAA Journal, 2012, 50(3): 513-522. DOI:10.2514/1.41139
[11]	RICCIARDI A P, EGER C A G, CANFIELD R A, et al. Nonlinear aeroelastic-scaled-model optimization using equivalent static loads[J]. Journal of Aircraft, 2014, 51(6): 1-10.
[12]	BISPLINGHOFF R L, ASHLEY H, HALFMAN R L. Aeroelasticity[M]. Cambridge: Addison-Wesley Publishing, 1955: 695-716.
[13]	WU Q, WAN Z Q, YANG C. Design optimization of scaled FLUTTER model considering structural dynamics and flutter constraints[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(7): 1210-1216.
[14]	PEREIRA P, ALMEIDA L, SULEMAN A, et al.Aeroelastic scaling and optimization of a joined-wing aircraft concept[C]//AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference.Reston: AIAA, 2013: 2145-2148. https://www.researchgate.net/publication/268477619_Aeroelastic_Scaling_and_Optimization_of_a_Joined-Wing_Aircraft_Concept
[15]	PARK G J. Technical overview of the equivalent static loads method for non-linear static response structural optimization[J]. Structural & Multidisciplinary Optimization, 2011, 43(3): 319-337.