FDA一经提出就引起广泛的关注,大量文献对其结构特性进行了分析研究。文献[4]对FDA方向图的时间与角度的周期性进行研究; 文献[5-6]指出FDA与正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)[7-8]和多输入多输出(Multiple-Input Multiple-Output,MIMO)[9-10]不同,是一种体制的创新,由于阵元间频偏这一自由度的扩展,从而使阵列的方向图随距离、角度、时间变化,从而具有了距离依赖干扰抑制能力,新的雷达可控自由度催生更先进的信号处理技术。
干扰是现代雷达完成探测任务面临的严峻挑战,FDA的诞生为抑制干扰提供了新的思路,文献[11]将FDA与MIMO结合,并提出一种基于直接数据域的稳健波束形成方法,从而区分出目标和干扰信号。文献[12]提出一种基于样本选择的欺骗干扰抑制方法,在一定条件下能够对抗主瓣干扰。
自适应波束形成是阵列信号处理的一个主要方面[13],常规Capon波束形成器能够有效接收目标信号并抑制干扰,但前提是目标方向准确已知,而实际应用中,导向矢量误差的存在及有限的样本导致波束形成器性能严重下降。为了解决上述问题,国内外****提出了许多改进的自适应波束形成算法。对角加载算法能够提高常规Capon波束形成器的稳健性,但加载系数难以确定[14]。基于特征空间的波束形成算法能够减缓常规波束形成器对指向误差的敏感性,但在低信噪比条件下,信号-干扰子空间难以正确估计导致算法性能下降[15]。文献[16]提出一种基于不确定集约束的波束形成方法,该方法将导向矢量限定在一个椭圆形的不确定集内,可以证明这种方法属于对角加载范畴,区别在于加载系数与导向矢量误差产生联系,通过求解不确定集选择合适的加载系数,对于导向矢量失配具有稳健性。
目前对于自适应波束形成的研究主要是基于相控阵进行,对于FDA自适应波束形成很少涉及。因此,本文基于FDA这一新的雷达体制,采用文献[17]中所给出的3种FDA接收信号处理机制,考虑到距离不确定性带来的导向矢量失配问题,比如目标运动造成距离测不准等,运用稳健Capon波束形成(RCB)算法,分析在指向误差存在情况下算法的稳健性。
1 FDA信号模型 1.1 FDA发射信号 假设一均匀线阵频控阵列(ULA-FDA),每个阵元的物理性质完全相同,但阵元的频率依次递增,其结构如图 1所示。
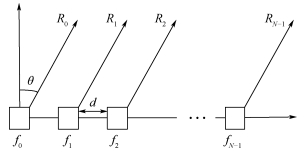 |
| 图 1 均匀线阵FDA Fig. 1 Uniform linear array frequency diverse array |
| 图选项 |
窄带条件下,各阵元发射信号可表示为
 | (1) |
式中:发射频率fn=f0+nΔf, n=0, 1, …, N-1,f0、Δf和N分别为载频、频偏和阵元总数。
设空间中一个目标到阵元0的斜距为R0,角度为θ,阵元n发射的信号到达目标的信号可表示为
 | (2) |
式中:Rn=R0-ndsin θ,d为阵元间距;c为光速。
为使阵列的波束指向目标位置
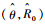
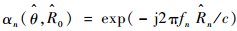 | (3) |
则到达目标的信号可表示为
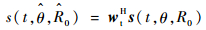 | (4) |
式中:wt为发射阵列通道权矢量,即
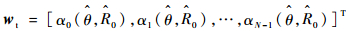 | (5) |
s(t, θ, R0)为信号构成的矢量,即
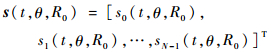 | (6) |
可以得到
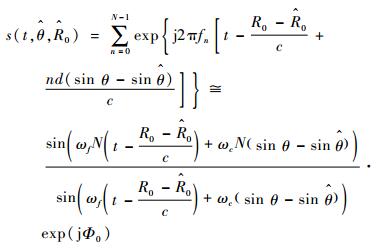 | (7) |
式中:
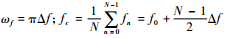
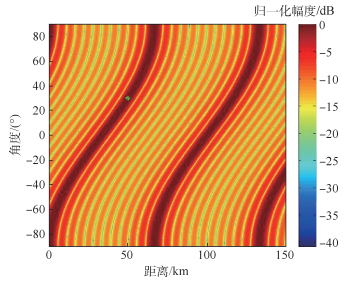 |
| 图 2 ULA-FDA发射方向图 Fig. 2 Transmitting beampattern of ULA-FDA |
| 图选项 |
表 1 仿真参数 Table 1 Simulation parameters
| 参数 | 数值 |
| ULA-FDA阵元总数N | 12 |
| 载频f0/GHz | 10 |
| 频偏Δf/kHz | 4.5 |
| 阵元间距d | c/(2f0) |
目标位置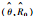 | (30°, 50 km) |
表选项
1.2 FDA接收信号 根据1.1节分析,通道n发射的信号经过加权到达远场目标后,反射回到接收阵列,则FDA第m通道接收的回波信号可表示为
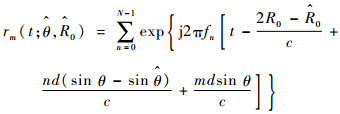 | (8) |
式中:阵列的发射阵元与接收阵元数相同。
2 三种接收信号处理机制 2.1 第1种接收信号处理机制 这种接收信号处理机制的接收通道中,每个阵元接收所有发射阵元的信号信息,通过接收通道中加入的滤波器hm(1)(fm),使第m接收通道只允许载频为fm的发射信号通过,再经过波束形成器调整各通道的权矢量,最终得到期望的信号,回波信号经过滤波器后为
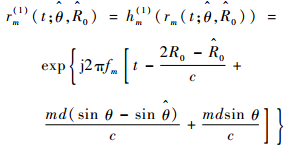 | (9) |
然后,对各个通道进行加权,其中接收通道权矢量为
 | (10) |
则可以得到输出信号为
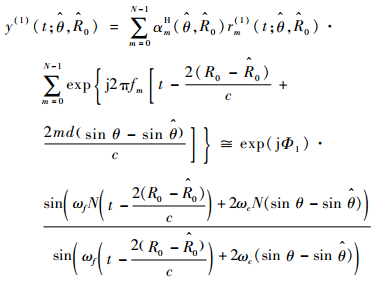 | (11) |
2.2 第2种接收信号处理机制 这种接收信号处理机制通过在接收通道中加入滤波器h(2)(f0~fN-1),从而接收每一个接收通道中的所有信号,此时接收信号权矢量wr(2)与第1种接收信号权矢量相同,在滤波器后同样接入波束形成器,调整各通道的权矢量,则经过滤波器后的信号为
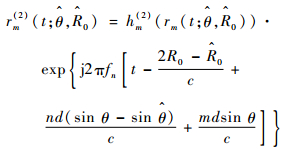 | (12) |
再对接收信号通过权矢量w(2)r加权,得到输出信号为
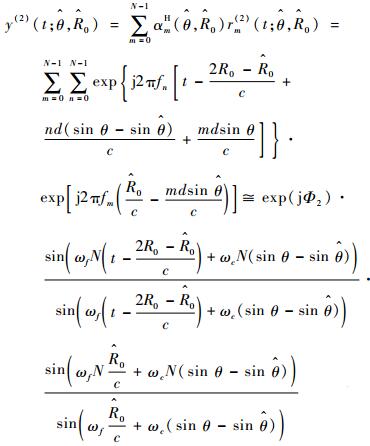 | (13) |
2.3 第3种接收信号处理机制 这种接收信号处理机制是3种机制中最有效率的一种,通过在接收通道中加入滤波器组Hm,每一个滤波器组中包含N个窄带滤波器hn,每一个窄带滤波器hn后接入波束形成器并做矢量合成。这种处理机制可以看作在每个接收通道中接入了滤波器hnm(3)(fnm),接收每一个接收通道中的所有信号,对接收到的信号按照通道编号进行重排,可得到一组N×N的数据,由此可得到经过滤波器的回波信号为
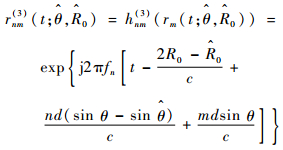 | (14) |
对于重排后的接收信号权矢量为
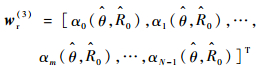 | (15) |
式中:
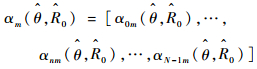 | (16) |
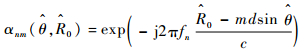 | (17) |
再对信号通过权矢量wr(3)加权,得到输出信号为
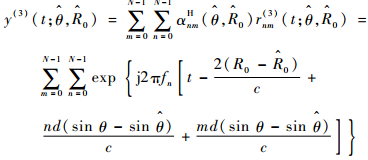 | (18) |
经过变形,可得第3种处理机制的闭式解为
 | (19) |
3 稳健Capon波束形成算法 波束形成功能的实现有一个重要前提,就是目标位置与干扰位置必须精确已知。但在实际应用中,由于估计的期望信号位置存在偏差,即存在指向误差,会使目标的导向矢量存在失配,进而引起波束形成器性能的下降,甚至失效[18]。为了解决导向矢量失配的问题,本文采用Li等[16]提出的稳健的Capon波束形成模型,并对其给出闭式解,得到修正后的目标导向矢量。模型可表示为
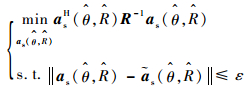 | (20) |
式中:‖·‖表示二范数;ε为限定导向矢量最大失配量;as

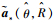
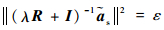 | (21) |
其中:λ为拉格朗日乘子,将式(21)变形为
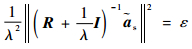 | (22) |
接收信号的样本协方差矩阵可分解为
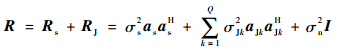 | (23) |
式中:Q为干扰个数;σs2为期望信号功率;σJk2和aJk(k=1, 2, …, Q)分别为第k个干扰信号的功率和导向矢量;σn2为噪声功率。结合式(22)、式(23),采用矩阵求逆定理,可以得到
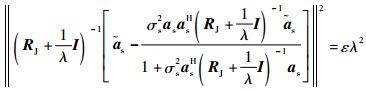 | (24) |
对干扰加噪声数据协方差矩阵特征分解得
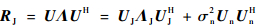 | (25) |
式中:ΛJ=diag{β1, β2,…,βQ}为干扰子空间特征值矩阵; UJ=[μ1, μ2, …, μQ]为干扰子空间特征向量; Un=[μQ+1, μQ+2, …, μN]为噪声子空间特征向量。一般情况下,干扰的强度远大于噪声,目标信号导向矢量在干扰子空间的投影很小,可得到
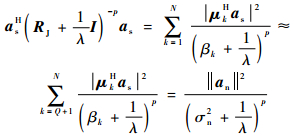 | (26) |
其中:p为正整数;an=UnHas为真实目标信号导向矢量在噪声子空间的投影。同理
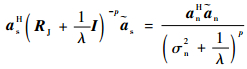 | (27) |
式中:
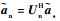
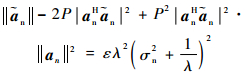 | (28) |
式中:
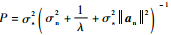
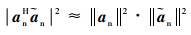 | (29) |
代入式(28)可得
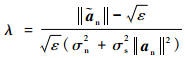 | (30) |
因此,可以得到修正后的目标导向矢量估计值
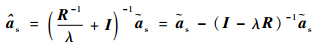 | (31) |
利用求出的修正后的导向矢量解析解,替换常规Capon波束形成器中的目标信号导向矢量,可得到对应权矢量为
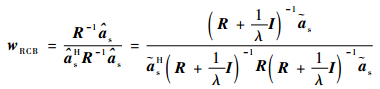 | (32) |
4 仿真分析 仿真1??3种接收信号处理机制的接收方向图
实验的基本参数与1.1节发射方向图相同,如图 3所示,图中绿点代表目标位置。从仿真结果可以看出,第1种和第3种接收信号处理机制都在目标位置形成了高增益,处理机制有效,而第2种处理机制未能在目标位置形成高增益,即主瓣位置发生偏移,不能有效接收目标信号,处理机制不具有实际意义。第3种处理机制相对于第1种处理机制而言,波束的高增益更集中,更有利于目标信号的接收,避免引入其他干扰及噪声。
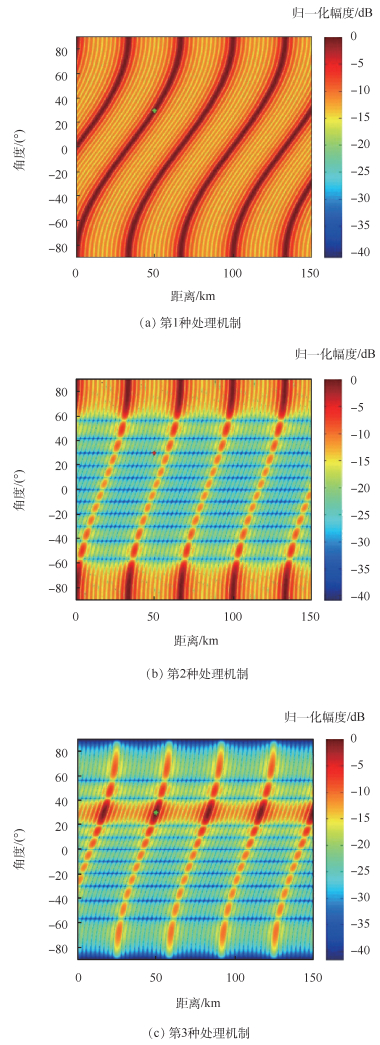 |
| 图 3 不同处理机制接收方向图(仿真1) Fig. 3 Receiving beampattern of different processing mechanism (Simulation 1) |
| 图选项 |
仿真2??第1种、第3种处理机制存在误差时的性能
由于第2种处理机制不具有实际意义,不作讨论。图 4仿真的是存在指向误差,未使用波束形成算法,第1种、第3种处理机制下的接收方向图。从图中可以看出,当存在指向误差时,目标的导向矢量失配,2种机制都未能在目标位置形成高增益,波束主瓣发生偏移,在这种情况下,信号处理机制性能下降。
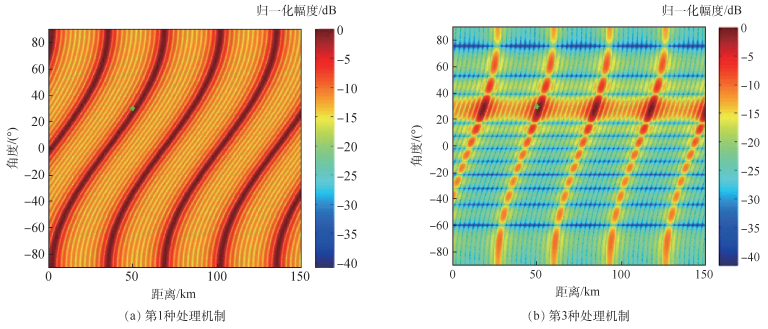 |
| 图 4 不同处理机制接收方向图(仿真2) Fig. 4 Receiving beampattern of different processing mechanism (Simulation 2) |
| 图选项 |
仿真3??RCB算法在第1种、第3种处理机制中的应用考虑空间中一个干扰信号位于(-65°,90 km),在强干扰环境下,令信噪比SNR=0,干噪比JNR=10 dB,快拍数为500,最大失配参数ε=2.5,目标的距离、角度估计误差分别为ΔR=1 km,Δθ=2°。图 5仿真的是误差存在时,利用RCB算法,在第1种处理机制下的发射、接收、发射-接收方向图,图 6为在目标位置处,距离维和角度维的发射-接收方向图。
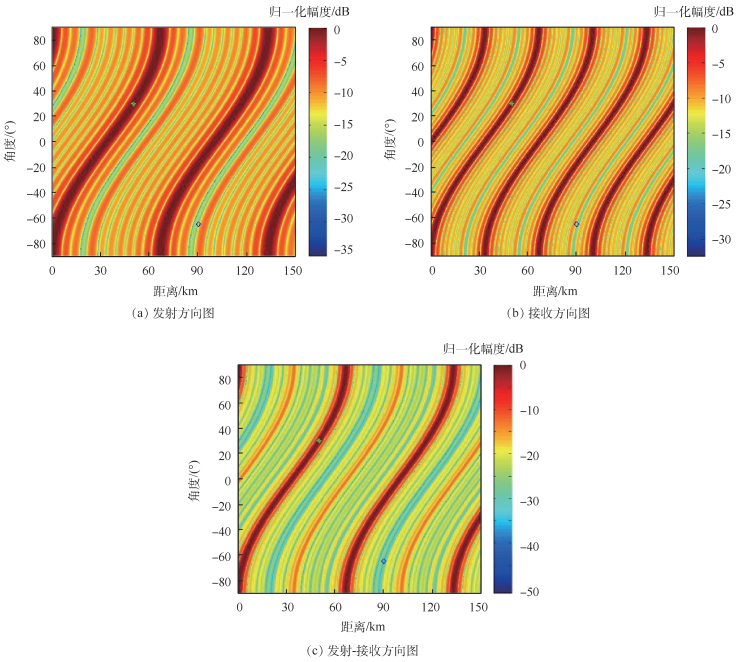 |
| 图 5 基于RCB的发射、接收和发射-接收方向图(机制1) Fig. 5 Transmitting, receiving and transmitting-receiving beampattern based on RCB (Mechanism 1) |
| 图选项 |
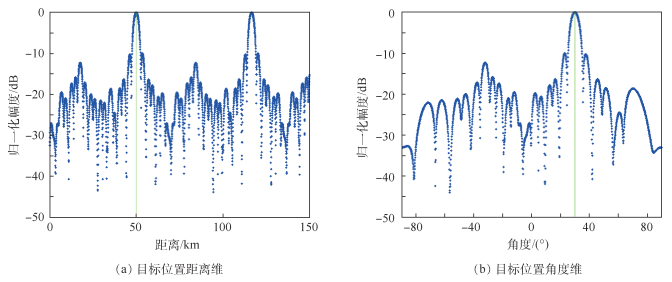 |
| 图 6 目标位置距离维和角度维发射-接收方向图(机制1) Fig. 6 Transmitting-receiving beampattern of range dimension and angle dimension at target position (Mechanism 1) |
| 图选项 |
从图 5、图 6可以看出,利用第1种处理机制,在误差存在情况下,应用RCB算法能够在目标位置形成高增益,在干扰位置形成零陷,验证了算法在第1种处理机制的有效性。
同理,可以得到第3种处理机制下的发射、接收、发射-接收方向图,目标位置距离维和角度维的发射-接收方向图,如图 7、图 8所示。
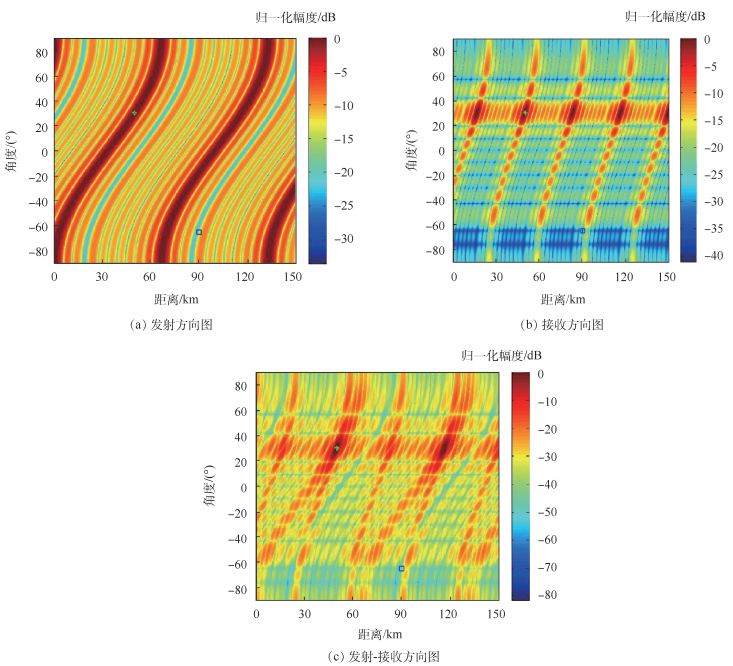 |
| 图 7 基于RCB的发射、接收和发射-接收方向图(机制3) Fig. 7 Transmitting, receiving and transmitting-receiving beampattern based on RCB (Mechanism 3) |
| 图选项 |
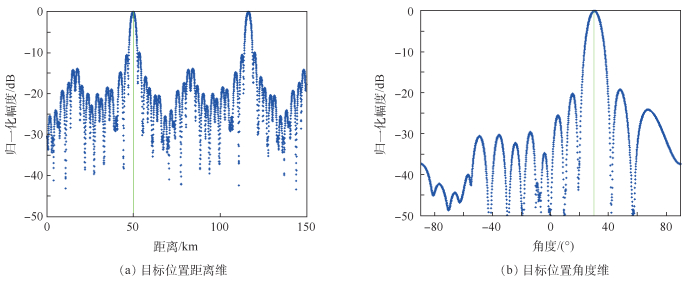 |
| 图 8 目标位置距离维和角度维发射-接收方向图(机制3) Fig. 8 Transmitting-receiving beampattern of range dimension and angle dimension at target position (Mechanism 3) |
| 图选项 |
从图 7、图 8可以看出,RCB算法在第3种处理机制下的有效性。实际上,第3种机制属于FDA-MIMO范畴,而FDA-MIMO雷达在实际中的合理性和可行性,已经被大多数****所接受,而第1种处理机制在实际应用中功率损失严重,可行性受限。
5 结论 本文介绍了ULA-FDA的结构,仿真说明了其发射方向图的距离-角度二维相关特性。
1) 引入了3种接收信号处理机制,对其结构进行理论推导及分析,仿真结果验证了第1种、第3种处理机制的有效性,并在此基础上,引申到在指向误差存在的情况下,即估计的目标导向矢量与真实的目标导向矢量存在偏差。
2) 应用稳健的Capon波束形成算法,对估计的目标导向矢量进行“纠偏”,使波束在目标位置形成高增益,仿真结果验证了算法的有效性。
参考文献
| [1] | WANG W Q. Subarray-based frequency diverse array radar for target range-angle estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(4): 3057-3067. DOI:10.1109/TAES.2014.120804 |
| [2] | GAO K D, WANG W Q, CAI J Y, et al. Decoupled frequency diverse array range-angle-dependent beampattern synthesis using non-linearly increasing frequency offsets[J]. IET Microwaves, Antennas & Propagation, 2016, 10(8): 880-884. |
| [3] | ANTONIK P, WICKS M C, GRIFFITHS H D, et al.Frequency diverse array radars[C]//Proceedings of the IEEE Radar Conference.Piscataway, NJ: IEEE Press, 2006: 215-217. |
| [4] | SECMEN M, DEMIR S, HIZAL A, et al.Frequency diverse array antenna with periodic time modulated pattern in range and angle[C]//Proceedings of the IEEE Radar Conference.Piscataway, NJ: IEEE Press, 2007: 427-430. |
| [5] | WANG W Q. Overview of frequency diverse array in radar and navigation applications[J]. IET Radar, Sonar & Navigation, 2015, 10(6): 1001-1012. |
| [6] | WANG W Q. Frequency diverse array antenna:New opportunities[J]. IEEE Antennas and Propagation Magazine, 2015, 57(2): 145-152. DOI:10.1109/MAP.2015.2414692 |
| [7] | WANG Z B, TIGREK F, KRASNOV O, et al. Interleaved OFDM radar signals for simultaneous polarimetric measurements[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(3): 2085-2099. DOI:10.1109/TAES.2012.6237580 |
| [8] | ZHANG T X, XIA X G, KONG L J. IRCI free range reconstruction for SAR imaging with arbitrary length OFDM pulse[J]. IEEE Transactions on Signal Process, 2014, 62(18): 4748-4759. DOI:10.1109/TSP.2014.2339796 |
| [9] | AHMED S, ALOUINI M S. MIMO-radar waveform covariance matrix for high SINR and low side-lobe levels[J]. IEEE Transactions on Signal Process, 2014, 62(8): 2056-2065. DOI:10.1109/TSP.2014.2307282 |
| [10] | CUI G L, LI H B, RANGASWAMY M. MIMO radar waveform design with constant modulus and similarity constraints[J]. IEEE Transactions on Signal Processing, 2014, 62(2): 343-353. DOI:10.1109/TSP.2013.2288086 |
| [11] | XU J W, XU Y H, LIAO G S.Direct data domain based adaptive beamforming for FDA-MIMO radar[C]//Proceedings of IEEE Statistical Signal Processing Workshop.Piscataway, NJ: IEEE Press, 2016: 1-5. |
| [12] | XU J W, KANG J L, LIAO G S, et al.Mainlobe deceptive jammer suppression with FDA-MIMO radar[C]//Proceedings of IEEE 10th Sensor Array and Multichannel Signal Processing Workshop.Piscataway, NJ: IEEE Press, 2018: 504-508. |
| [13] | 张小飞, 陈华伟, 仇小锋, 等. 阵列信号处理及MATLAB实现[M]. 北京: 电子工业出版社, 2015: 50-55. ZHANG X F, CHEN H W, QIU X F, et al. Array signal processing and MATLAB implementation[M]. Beijing: Publishing House of Electronics Industry, 2015: 50-55. (in Chinese) |
| [14] | XU J W, LIAO G S, ZHU S Q.Robust adaptive beamforming based on response vector optimization[C]//Proceedings of IEEE International Conference on Acoustic, Speech and Signal Processing.Piscataway, NJ: IEEE Press, 2014: 6043-6046. |
| [15] | FENG Y, LIAO G S, XU J W, et al. Robust adaptive beamforming against large steering vector mismatch using multiple uncertainty sets[J]. Signal Processing, 2018, 152: 320-330. DOI:10.1016/j.sigpro.2018.06.017 |
| [16] | LI J, STOICA P, WANG Z S. On robust Capon beamforming and diagonal loading[J]. IEEE Transactions on Signal Processing, 2003, 51(7): 1702-1715. DOI:10.1109/TSP.2003.812831 |
| [17] | JONES A M, RIGLING B D.Frequency diverse array radar receiver architectures[C]//2012 International Waveform Diversity & Design Conference.Piscataway, NJ: IEEE Press, 2012: 211-217. |
| [18] | 陈明建, 罗景青, 唐希雯, 等. 最差性能最优的稳健宽带Capon波束形成算法[J]. 宇航学报, 2013, 34(3): 434-441. CHEN M J, LUO J Q, TANG X W, et al. Robust broadband Capon beamforming algorithm based on worst case performance optimization[J]. Journal of Astronautics, 2013, 34(3): 434-441. DOI:10.3873/j.issn.1000-1328.2013.03.020 (in Chinese) |
