文献[1-3]提出了地球重力下的着陆冲击实验方法,研究了腿式着陆器在典型工况下的软着陆性能。文献[4-7]建立了着陆器的动力学仿真模型,研究了典型工况下的着陆器软着陆性能,其中文献[6]通过对比仿真与实验结果,证明了建模的准确性。文献[8-9]基于理论分析给出着陆参数稳定性边界,其中文献[9]通过实验对边界进行验证。文献[10-11]基于腿式着陆器非0高度关机软着陆模式下的动力学仿真模型,结合离散化搜寻的仿真策略,给出了主要工况参数的二维稳定性边界,其中文献[11]在给出稳定性边界的过程中引入了响应面方法,提高了计算效率。文献[12-14]在腿式着陆器的动力学仿真模型中添加了主发动机与姿态控制发动机的推力等效模型,研究了着陆器的触地关机软着陆稳定性,但未给出直观的稳定性边界。
有鉴于此,本文以某型着陆器为研究对象,利用ADAMS软件建立其触地关机软着陆模式下的动力学仿真模型,结合仿真模型与优化方法确定了多组极恶劣地形工况,并结合径向基函数(RBF)神经网络代理模型,给出了速度的三维稳定性边界。
1 着陆器动力学建模 1.1 着陆器整机模型 本文研究的某型着陆器装有4套中心对称分布于主体的缓冲机构,如图 1所示,着陆器是由多个构件通过运动副连接且受到复杂的外力作用的多体系统,分析着陆器软着陆性能,需基于多体动力学理论,建立着陆器的多体动力学模型。其基本动力学方程如下[15]:
 | (1) |
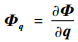 | (2) |
 | (3) |
 |
| 图 1 着陆缓冲机构 Fig. 1 Landing buffer mechanism |
| 图选项 |
式中:M为广义质量矩阵,由着陆器各构件质量和转动惯量构成;Ф为运动副约束方程矢量;q为广义坐标矢量;Фq为约束方程的雅克比矩阵;Q为广义力,主要考虑发动机推力和接触力;λ为拉格朗日乘子矢量;t为时间。结合所建立的着陆器的动力学模型,利用ADAMS软件进行仿真分析。
缓冲机构主要由主支柱、缓冲杆、左右辅助支柱和足垫组成[12-14]。缓冲杆在受到冲击时会发生塑性变形,其建模方法参考文献[12]的刚体等效法。如图 2所示,αe、Me和Se分别为缓冲杆的等效转角、等效弯矩和等效轴向位移,先在有限元软件中建立缓冲杆的模型,进行仿真分析,可以得到图 3所示的αe-Me和αe-Se曲线,然后将曲线导入刚体模型之中即可完成缓冲杆的等效建模。
 |
| 图 2 缓冲杆等效模型 Fig. 2 Equivalent model of buffer rod |
| 图选项 |
 |
| 图 3 缓冲杆力学特性 Fig. 3 Mechanical behavior of buffer rod |
| 图选项 |
辅助支柱内外筒之间的缓冲元件力学特性通过有限元分析获得,进而确定辅助支柱的压缩位移DS和缓冲力FS之间关系如图 4所示。将DS-FS曲线导入刚体模型之中完成其等效建模。
 |
| 图 4 缓冲元件力学特性 Fig. 4 Mechanical behavior of cushion element |
| 图选项 |
足垫和着陆面的接触采用库伦摩擦模型模拟切向力,采用非线性弹簧阻尼模型模拟法向碰撞力[12]。
1.2 发动机动力系统等效建模 着陆器主体上装有一个用于制动的主发动机和多台用于姿态调节的姿控发动机。触地关机软着陆模式下,发动机作用对着陆器的软着陆稳定性不能忽视,因此需要建立考虑发动机作用效果的着陆器动力学仿真模型。
1.2.1 姿控发动机控制策略 除主发动机外,触地关机软着陆模式下还有10台姿控发动机处于开启状态,各发动机的位置如图 5所示。其中,2台位于主体上方,编号A1、A2,8台位于着陆器主体下方,编号B1~B8。
 |
| 图 5 坐标系定义及发动机位置 Fig. 5 Coordinate system definition and engine position |
| 图选项 |
此外,图 5还包括了与姿态控制相关的坐标系。其中,O-XYZ为地面固定坐标系(右手系),X轴沿重力方向指向天空,Z轴水平指向下坡方向。Oc-XcYcZc为随体控制坐标系(右手系),原点在着陆平台中心,Xc轴垂直着陆平台表面且指向天空,Zc轴在着陆平台内且在俯视图中指向相邻两足垫的中点。定义O-XYZ按照Z-Y-X的顺序旋转到与Oc-XcYcZc平行位置时绕三轴转动的角度分别为θx、θy、θz;同时定义Oc-XcYcZc相对O-XYZ的角速度矢量在Oc-XcYcZc三轴上的投影分别为ωx、ωy、ωz。将上述6个参数作为控制输入。
为提升着陆器姿态的稳定性,A1、A2发动机的推力如式(4)和式(5)所示;B系列发动机的推力公式形式相同,均参考文献[12]建立,以B1、B2为例,其推力如式(6)所示:
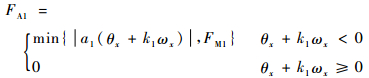 | (4) |
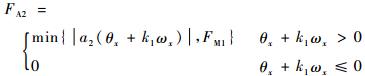 | (5) |
 | (6) |
式中:ai、bi、ki为控制策略中的相关参数;FM1与FM2分别为2个系列发动机推力最大值。
1.2.2 主发动机控制策略 主发动机位于主体下表面中心且喷口方向垂直主体下表面。正常工作时,其推力方程为[12]
 | (7) |
式中:m为着陆器整机质量;vx为竖直速度值。
触地关机软着陆模式下,若足垫与星球表面接触,则其内部的传感器将发出主发动机关机信号,但主发动机由于关机后效其推力不能马上减小到零,该情况会对着陆稳定性产生影响[16],因此,为了提高着陆稳定性,姿控发动机会在主发动机收到关机指令之后延迟关机。关机信号发出后,由于信号传输的延迟,主发动机推力下降开始时间会滞后。其推力变化过程如图 6所示。图中:t0为触地时刻,t1时刻发出关机信号,t2时刻推力开始下降,t3时刻姿控发动机关闭。
 |
| 图 6 主发动机推力变化过程 Fig. 6 Thrust changing process of main engine |
| 图选项 |
1.2.3 发动机推力等效建模 本文通过在发动机安装位置添加与发动机喷口方向相反的力来模拟发动机的推力作用效果,并利用测量函数实时反馈θx、θy、θz、ωx、ωy、ωz与vx的值。在真实情况下,由于传感器按给定周期采集和处理信号,故推力值不随位姿和速度参数连续变化[17],因此,本文在根据式(7)计算推力值的同时,也按照给定周期给模型中的推力赋值,以模拟发动机的真实工作情况。
2 着陆工况参数与软着陆稳定性判据 2.1 着陆工况参数 本文考虑的着陆工况参数有2类:
1) 地形参数。包括着陆面坡度(α)、足垫滑移状态(K)和着陆偏航角(ψ)。由于着陆器安装有地貌识别系统,正常情况下会降落在平原地区,坡度一般不超过12°,本文考虑着陆面坡度为0°~12°。正常情况下足垫可以在着陆面上滑移,但如果足垫遇到石块或者小坑,其将处于卡死状态,本文用K=0表示足垫可滑移,K=1表示足垫卡死。考虑着陆器的几何对称性,ψ取0°~45°即可以表征所有用于评判着陆器软着陆稳定性的姿态。
2) 着陆速度。指着陆器相对地面固定坐标系的速度,为空间矢量。为方便后文的研究,着陆速度采用柱坐标系(vh,β,vx)描述,vh(0~2.5 m/s)为速度在ZOY平面投影的模长,即水平速度大小;β(0°~360°)为从+X方向看,Z轴绕到水平速度方向转过的角度;vx为竖直速度大小(0~5 m/s),其方向沿-X方向。
部分着陆工况参数如图 7所示。
 |
| 图 7 部分着陆工况参数示意图 Fig. 7 Schematic diagram of partial landing conditions parameters |
| 图选项 |
2.2 软着陆稳定性判据 本文重点研究着陆器的软着陆稳定性,根据着陆器构型,确定其稳定性评判参数如下:
1) 缓冲杆最大等效转角αem(单位为(°))。缓冲杆通过塑性变形吸收冲击能量,若等效转角过大其极易发生损坏,故αem应小于许用值α*。
2) 辅助支柱最大压缩行程DSM(单位为mm)。一方面应避免DSM超过设计压缩范围,另一方面,DSM过大易导致着陆平台和坡面夹角过大,不利于探测车的转移,故DSM应小于许用值D*。
3) 着陆器质心到4个翻倒平面距离的最小值LD(单位为mm)。定义通过相邻两个足垫中心的竖直平面为翻倒平面[11],为保证着陆器在软着陆过程中不发生翻倒,LD应大于许用值L*。
4) 主发动机尾喷管底面中心到着陆面的最小距离HM(单位为mm)。触地关机软着陆过程中,主发动机大部分时间处于开启状态,考虑HM过小容易导致粉尘堵塞尾喷管或凸起撞击尾喷管等情况,故HM应大于许用值H*。
3 极恶劣地形的确定 着陆工况参数中,α、K、ψ依赖于星球的地形,难以主动预测或者控制,而vx、vh、β作为着陆器自身的参数,具有一定的可控性,为了研究可控参数对着陆器软着陆稳定性的具体影响方式,有必要事先确定α、K、ψ的最坏取值。基于动力学模型,本文采用优化方法寻找考虑着陆器水平速度、使稳定性指标αem、DSM、LD、HM最差的α、K、ψ取值。为了降低优化维度、提高计算效率,设定vx=2.5 m/s、vh=1.0 m/s,考虑水平速度大小固定的情况下,β取值的不同可能带来α、K、ψ最差取值的不同,故将β作为寻找最差工况的变量之一。综上,以寻找LD最差的工况为例,建立优化模型如下:
 | (8) |
式中:Ω为参数的取值范围。
本文使用多岛遗传算法(MIGA)、结合动力学模型实现优化计算,算法参数配置如表 1所示。
表 1 优化参数设置 Table 1 Setting of optimal parameters
| 参数 | 数值 |
| 岛屿种群规模 | 10 |
| 岛数 | 10 |
| 进化代数 | 25 |
| 交叉概率 | 0.9 |
| 迁移概率 | 0.01 |
| 迁移间隔 | 4 |
表选项
经优化计算,得到4组极恶劣工况如表 2所示。
表 2 极恶劣工况 Table 2 Worst landing conditions
| 指标 | 最优解X*=[α, K, ψ, β]T |
| max αem | [3.713, 1, 0.624, 174.35]T |
| max DSM | [1.995, 0, 17.32, 138.89]T |
| min LD | [12.00, 1, 35.51, 290.63]T |
| min HM | [0.405, 0, 13.98, 226.51]T |
| 注:α、ψ、β单位为(°);K无量纲。 | |
表选项
4 可控工况参数分析 4.1 单稳定性指标的速度稳定性边界 研究vx、vh、β对着陆器软着陆稳定性的具体影响方式的过程中,需进行大规模仿真计算,为了提高效率,本文引入RBF神经网络代理模型建立极恶劣工况下的vx、vh、β与4项软着陆稳定性指标值之间的映射关系[18]。通过随机抽点仿真,将仿真结果导入神经网络模型进行训练,用400个独立的样本测试模型,训练终止准则为均方根相对误差值RMSE(见式(9))小于0.05。
 | (9) |
式中:n为测试样本点数;yi为实际仿真结果;
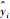
得到神经网络模型后,本文采用控制变量法,令vx、vh、β在取值范围内等间距抽取100个点,共得到106组样本点,将其代入神经网络模型中,计算得到106组软着陆稳定性指标值。综合考虑着陆器的软着陆可靠性与模型误差等因素,设定本文的各项软着陆稳定性指标许用值分别为α*=30°、D*=70 m、L*=50 m、H*=250 m,进而给出了不同vx取值下反映vh、β与αem、DSM、LD、HM关系的云图如图 8所示,vh单位为m/s。
 |
| 图 8 不同vx下的αem、DSM、LD及HM云图 Fig. 8 Contour of αem, DSM, LD and HM under different vx |
| 图选项 |
此外,本文还在柱坐标系下给出了vx、vh、β三维稳定性边界(许用值等值面),如图 9所示。
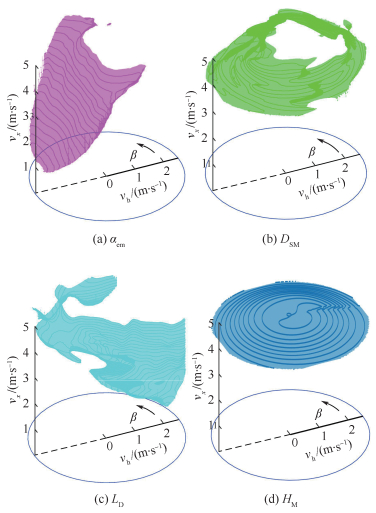 |
| 图 9 各指标下着陆速度三维稳定性边界 Fig. 9 3D stability boundary determined by landing velocity concerning different indicators |
| 图选项 |
1) 缓冲杆最大等效转角分析
由图 8(a)可知,在相同vx与vh下,β对αem影响非常显著,β越接近180°、αem越大。因此,图 8(a)所示的αem许用值等值线接近直线,并且集中在120° < β < 240°范围内,即偏坡上方向;另外随着vx增大,不稳定区域面积增大。以αem为稳定性指标的速度三维稳定性边界如图 9(a)所示,图中曲面为αem=30°的等值面。
2) 辅助支柱最大压缩行程分析
由图 8(b)可知,在相同vx下,DSM的许用值等值线接近环形,可知β对DSM影响比较小,DSM的主要影响因素为vh。此外,随着vx增大,不稳定区域面积增大。以DSM为稳定性指标的速度三维稳定性边界如图 9(b)所示,图中曲面为DSM=70 m的等值面。
3) 质心距翻倒平面最小距离分析
由图 8(c)可知,LD的许用值等值线集中在270° < β < 360°方向,即偏坡下方向,表明水平速度方向接近坡下方向时着陆器更容易翻倒。以LD为稳定性指标的速度三维稳定性边界如图 9(c)所示,图中曲面为LD=50 m的等值面。
4) 尾喷管底面中心到着陆面最小距离分析
由图 8(d)可知,在相同vx下,HM的许用值等值线非常光滑且接近圆,说明β对HM基本没有影响;以HM为稳定性指标的速度三维稳定性边界如图 9(d)所示,图中曲面为HM=250 m的等值面,图 9(d)直观显示边界集中在vx=4~5 m/s区间,一方面表明该指标主要受vx影响,同时vx小于4 m/s时,HM不会超过安全阈值。
4.2 综合多项稳定性指标的速度稳定性边界 将图 9所示的全部三维稳定性边界向同一柱坐标系内整合,得到图 10所示的综合三维稳定性边界,同时得到不同竖直速度下的切面图如图 11所示,图中稳定区域为各稳定区域的交集, vh单位为m/s。
 |
| 图 10 综合指标下着陆速度三维稳定性边界 Fig. 10 3D stability boundary determined by landing velocity considering comprehensive indicators |
| 图选项 |
 |
| 图 11 不同vx下综合稳定性边界 Fig. 11 Comprehensive stability boundary under different vx |
| 图选项 |
将图 10所示的三维稳定性边界向同一竖直面内做旋转投影,得到消除β影响的4项软着陆稳定性指标的保守速度稳定性边界,综合4条保守边界,可最终确定综合多项稳定性指标的速度稳定性边界,如图 12所示。由图 12可以直观地确定保证着陆器绝对稳定着陆的速度取值范围。
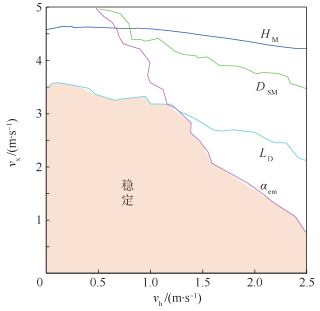 |
| 图 12 vx-vh综合稳定性边界 Fig. 12 vx-vh comprehensive stability boundary |
| 图选项 |
5 结论 本文建立某型着陆器触地关机模式下的动力学仿真模型,着重分析着陆速度对稳定性的影响,得到:
1) 结合动力学仿真模型及多岛遗传优化算法,确定了考虑着陆器水平速度下的极恶劣地形参数。
2) 基于仿真模型计算结果,利用RBF神经网络建立了反映极恶劣地形下着陆器速度参数与稳定性指标值之间映射关系的代理模型,进而计算得到了软着陆稳定性指标的速度稳定性边界,确定了保证着陆器安全软着陆的速度取值范围。
3) 本文研究方法具有低成本、高效率等特点,且适用于其他型号着陆器的研制过程。
参考文献
| [1] | 杨建中, 曾福明, 满剑锋, 等. 嫦娥三号着陆器着陆缓冲系统设计与验证[J]. 中国科学:技术科学, 2014, 44(5): 440-449. YANG J Z, ZENG F M, MAN J F, et al. Design and verification of the landing impact attenuation system for Chang'E-3 lander[J]. Scientia Sinica Techologica, 2014, 44(5): 440-449. (in Chinese) |
| [2] | CHEN J B, NIE H, WAN J L, et al. Investigation on landing impact dynamic and low-gravity experiments for deep space lander[J]. Science China (Physics, Mechanics & Astronomy), 2014, 57(10): 1987-1997. |
| [3] | 孙泽洲, 张熇, 贾阳, 等. 嫦娥三号探测器地面验证技术[J]. 中国科学:技术科学, 2014, 44(4): 369-376. SUN Z Z, ZHANG H, JIA Y, et al. Ground validation technologies for Chang'E-3 lunar spacecraft[J]. Scientia Sinica Techologica, 2014, 44(4): 369-376. (in Chinese) |
| [4] | 逯运通, 宋顺广, 王春洁, 等. 基于刚柔耦合模型的月球着陆器动力学分析[J]. 北京航空航天大学学报, 2010, 36(11): 1348-1352. LU Y T, SONG S G, WANG C J, et al. Dynamic analysis for lunar lander based on rigid-flexible coupled model[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(11): 1348-1352. (in Chinese) |
| [5] | MAEDA T, OTSUKI M, HASHIMOYO T, et al. Attitude stabilization for lunar and planetary lander with variable damper[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(8): 1790-1804. DOI:10.2514/1.G000325 |
| [6] | 曾福明, 杨建中, 朱汪, 等. 月球着陆器着陆缓冲性能研究[J]. 航天器工程, 2010, 19(5): 43-49. ZENG F M, YANG J Z, ZHU W, et al. Research on landing impact attenuation performance of lunar lander[J]. Spacecraft Engineering, 2010, 19(5): 43-49. DOI:10.3969/j.issn.1673-8748.2010.05.008 (in Chinese) |
| [7] | 岳帅, 聂宏, 张明, 等. 临近空间载人舱着陆动力学及影响因素分析[J]. 宇航学报, 2018, 39(3): 264-274. YUE S, NIE H, ZHANG M, et al. Analysis on landing dynamics and influence factors of near space manned capsule[J]. Journal of Astronautics, 2018, 39(3): 264-274. (in Chinese) |
| [8] | LAVENDER R E.Monte Carlo approach to touchdown dynamics for soft lunar landing: NASA TN D-3117[R].Washington, D.C.: NASA, 1965. |
| [9] | ROGERS W F.Apollo experience report: Lunar module landing gear subsystem: NASA TN D-6850[R].Washington, D.C.: NASA, 1972. |
| [10] | 朱汪, 杨建中. 月球着陆器软着陆机构着陆稳定性仿真分析[J]. 宇航学报, 2009, 30(5): 1792-1796. ZHU W, YANG J Z. Touch down stability simulation of landing gear system for lunar lander[J]. Journal of Astronautics, 2009, 30(5): 1792-1796. DOI:10.3873/j.issn.1000-1328.2009.05.008 (in Chinese) |
| [11] | LIU Y, SONG S, LI M, et al. Landing stability analysis for lunar landers using computer simulation experiments[J]. International Journal of Advanced Robotic Systems, 2017, 14(6): 1-15. |
| [12] | 吴宏宇, 王春洁, 丁宗茂, 等. 两种着陆模式下的着陆器缓冲机构构型优化[J]. 宇航学报, 2017, 38(10): 1032-1040. WU H Y, WANG C J, DING Z M, et al. Configuration optimization of landing gear under two kinds of landing modes[J]. Journal of Astronautics, 2017, 38(10): 1032-1040. (in Chinese) |
| [13] | WU H, WANG C, DING J, et al.Dynamics simulation analysis for novel lander based on two kinds of landing mode[C]//International Conference on Measuring Technology and Mechatronics Automation.Piscataway, NJ: IEEE Press, 2017: 8-12. |
| [14] | 丁宗茂, 王春洁, 吴宏宇, 等. 探测器触地关机软着陆稳定性分析[J]. 北京航空航天大学学报, 2018, 44(3): 614-620. DING Z M, WANG C J, WU H Y, et al. Stability analysis of explorer in soft landing mode of engine shutdown at touchdown[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(3): 614-620. (in Chinese) |
| [15] | 陈立平. 机械系统动力学分析及ADAMS应用教程[M]. 北京: 清华大学出版社, 2005: 25-30. CHEN L P. Mechanical system dynamics analysis and ADAMS application tutorial[M]. Beijing: Tsinghua University Press, 2005: 25-30. (in Chinese) |
| [16] | 张熇, 蔡国飙, 许映乔, 等. 嫦娥三号着陆器软着陆过程中羽流仿真分析及试验研究[J]. 中国科学:技术科学, 2014, 44(4): 344-352. ZHANG H, CAI G B, XU Y Q, et al. Simulation and experimental study of the plume during the Chang'E-3 lunar landing[J]. Scientia Sinica Techologica, 2014, 44(4): 344-352. (in Chinese) |
| [17] | 张洪华, 关轶峰, 黄翔宇, 等. 嫦娥三号着陆器动力下降的制导导航与控制[J]. 中国科学:技术科学, 2014, 44(4): 377-384. ZHANG H H, GUAN Y F, HUANG X Y, et al. Guidance navigation and control for Chang'E-3 powered descent[J]. Scientia Sinica Techologica, 2014, 44(4): 377-384. (in Chinese) |
| [18] | CAROZZA M, RAMPONE S. Function approximation from noisy data by an incremental RBF network[J]. Pattern Recognition, 1999, 32(12): 2081-2083. DOI:10.1016/S0031-3203(99)00101-6 |
