近年来中国民航业高速发展，民航旅客运输量逐年递增，2016年全国旅客吞吐量首次突破10亿人次，比2015年增长11.1%。航站楼传统的资源配置方式已不能满足机场客流量增长的需求。全国各大机场不同程度地出现了旅客排队时间长、旅客服务质量下降等现象。国内外****力图通过研究航站楼旅客服务流程优化与航站楼资源配置优化问题来提高旅客服务效率与质量。其中，航站楼客流量预测是航站楼旅客服务流程优化的关键核心问题，其预测精度的高低直接影响了上述难题的破解效果。
Grosche等^[1]采用重力学模型方法，将经济增长趋势与机场吞吐量相结合，建立了相关联的机场吞吐量重力学模型，该模型能对新建机场及已建机场的吞吐量做出较为准确的预测。Letavkova等^[2]结合小波变换和时间序列模型提出了一个机场吞吐量预测新方法，很好地预测了奥斯特拉瓦和蒙特利尔机场的旅客流量。黄飞虎等^[3]利用民航旅客订座数据分析了航空旅客群体移动的特性，发现吞吐量具有一定的周期性，易受节假日的影响，且与其相互通航的城市数量有很大关系。上述研究都属于机场宏观客流量的预测范畴，其颗粒度较大，无法指导机场每天甚至每小时资源精细化的配置。在微观客流量预测方面，Ashford和Ndoh^[4]提出了一种基于概率密度函数的航站楼短时客流量预测方法，证明离港旅客从出发到抵达航站楼的行程时间是随机变量，该方法需建立概率密度函数，花费大量时间确定与调节参数。Kim等^[5]将离港旅客到达航站楼的行程时间按长短分为12个组，12个概率密度函数分别属于正态或Pearson Type Ⅲ分布，从而计算出不同目标时刻航站楼离港旅客数量，该方法在旅客到达人数少的情况下预测精度不高。邢志伟等^[6-7]从人类行为动力学出发，以单航班离港旅客为研究对象，证明了单航班离港旅客抵达航站楼受航班离港时刻驱动对泊松特性的偏离且服从重尾分布，但仅以单航班作为研究对象，若将单航班客流量叠加预测多航班客流量，则会造成较大误差，对误差修正需花费大量时间。针对非线性时间序列的预测，田中大、李树江等^[8-12]采用组合预测法，成功对混沌时间序列^[8]、风速^[9]、网络流量^[10-12]进行预测，并取得了良好的预测效果。受此启发，本文拟借鉴组合预测思想研究航站楼短时客流量预测问题。由于航站楼短时客流量受如航班计划、天气等多种因素的影响呈现出复杂的非线性特点，基于确定数学模型的预测方法在模型构建和求解上都存在困难，同时，这类方法参数调整上需花费大量时间，难以满足航站楼资源配置优化实时性的需要。K近邻算法（K-Nearest Neighbor，KNN)^[13-14]是另一类无数学模型的预测算法，不需要任何的先验知识，其具备良好的移植与数据挖掘性能，新的数据可以方便地加入到模型中，符合航站楼短时客流量复杂的非线性特点。
但传统K近邻算法在预测场景中的精度并不高，多数****针对不同预测场景做了相应的算法改进^[15-20]，并取得了良好的预测效果。受文献[3, 7, 21]研究启发，具有相似航班计划的运营日，同一个目标时刻上的客流量变化波动具有相似的特征，以相似特征日作为基准向量用K近邻算法进行预测，模型精度将会提高。
综上，为了有效应对航站楼短时客流量准确预测，本文在传统K近邻算法基础上增加了航班计划状态模式匹配步骤，选取具有航班计划特征的相似历史运营日作为预测基准向量，建立基于航站楼短时客流量预测的双层K近邻模型。通过实例分析，与ARIMA算法^[12]和传统K近邻算法等进行比较，证明双层K近邻模型预测误差更小，精度更高，模型拟合度相对传统K近邻模型提高了8%~10%，平均拟合度高达90%，为机场资源的动态分配提供了指导性的意见。
1 K近邻模型 1.1 数据来源与算法构造 本文选取某航空公司离港旅客自助值机数据作为历史数据库。旅客进入航站楼后在完成值机、安检业务之前往往带有一定的焦虑心理，因此极少旅客会在值机之前在机场逗留。而自助值机时间通常在1 min之内完成，且排队时间较短，因此可将自助值机时间近似看作旅客到达时间。
航站楼客流量预测分为短期、中期、长期，认为预测单位小于1天为短期预测，以天和周为预测单位为中期预测，以季度和年为预测单位为长期预测。根据实际业务情况，飞机起飞前1 h对航站楼值机柜台、安检口、登机口等资源的需求几乎已经确定，不能再更改，因此以1 h为预测时间间隔更具有实际意义，但为了进一步验证算法的鲁棒性，综合考虑，选择更小的30 min为时间间隔。
选取2016-03-26—2016-10-26期间旅客自助值机数据，将测试数据与预测数据之前的数据作为历史数据库，以30 min为间隔，一天分为48个时段。建立异常数据识别标准，对必要冗余数据剔除，这样便完成了历史数据库的建立。
构建大容量且包含了客流量变化趋势和典型规律历史数据库后，再设定K近邻非参数回归模型中状态向量、距离度量准则、近邻K值的取值及预测算法等相关要素，从历史数据库中找到与预测日相匹配的近邻。
通过上述相关要素近邻匹配，假设在历史数据库中找到K个近邻，实际数据和这K个近邻的距离为d_i(i=1, 2, …, K), 设p为客流量，则p(t)为第t时刻客流量，p(t+1)为第t+1时刻客流量，这些近邻所对应的历史时刻航站楼旅客到达客流量为p_hi(t)(i=1, 2, …, K)。再利用预测算法，便可得到预测日各个时段的客流量。
等权重的预测算法采用如下形式：

(1)

带权重的预测算法采用如下形式：

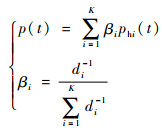(2)

采用带权重的预测算法认为距离小的近邻在预测值中占有更大的权重，该算法符合人们的一般认知，更能体现出航站楼旅客到达状况变化趋势，因此本文采取带权重的预测算法。该算法流程可以简要表述为图 1。

图 1 K近邻算法流程 Fig. 1 Flowchart of KNN algorithm

图选项

1.2 结果分析 在对K近邻模型的相关要素定义完成后，通过K近邻算法对预测日各个时段的客流量进行预测。随机抽取连续5天(2016-09-09—2016-09-13)作为预测日，选择预测日的前一天作为预测基准向量，并选择相应基准向量前半部分运营日作为历史数据库，其中K=7；选择3个评价指标：平均绝对误差MAE、均方误差MSE、拟合优度R²来评价本文所有实验的预测精度，MAE、MSE与R²的定义式分别为

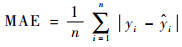(3)

(4)

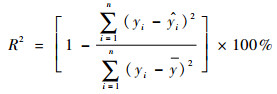(5)

式中：y_i为真实值；为预测值；y为平均值。
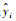
预测精度评价指标如表 1所示，其预测结果如图 2所示。

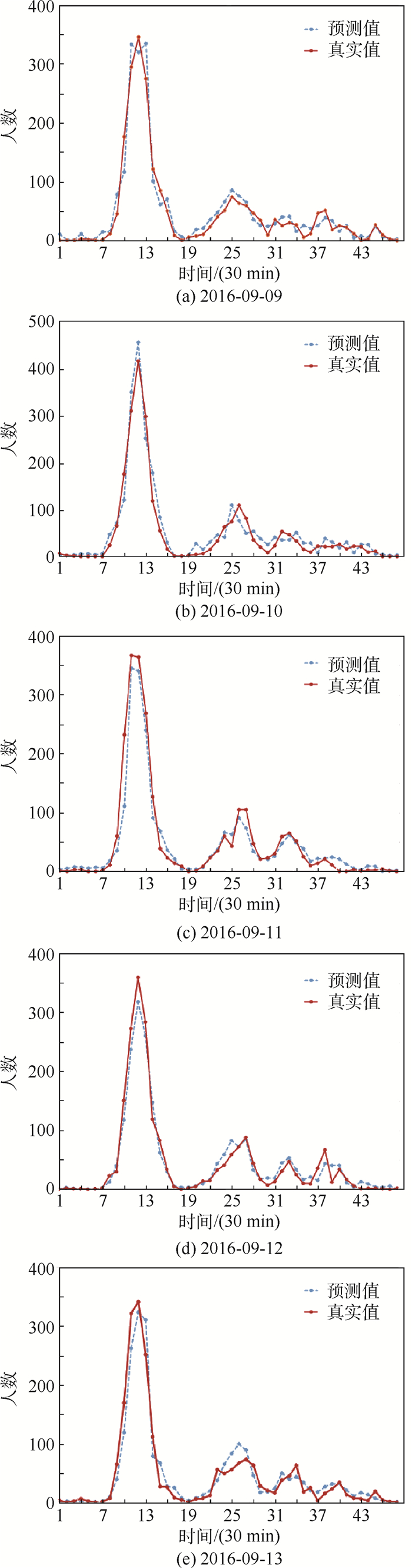图 2 K近邻模型预测值与真实值对比 Fig. 2 Comparison of predictive value of KNN model with true value

图选项

表 1 K近邻模型预测精度分析 Table 1 KNN model prediction accuracy analysis

日期	MSE	MAE	R2/%
2016-09-09	351.893 0	11.451 1	83.65
2016-09-10	386.675 2	12.254 9	82.33
2016-09-11	345.365 1	10.931 5	89.31
2016-09-12	342.478 3	10.547 2	89.54
2016-09-13	411.579 2	13.367 3	79.14

表选项






从表 1与图 2可以看出，传统K近邻模型在机场场景中直接使用的缺点明显，预测精度变化波动较大，其中2016-09-11—2016-09-13这3日的预测精度相差了近10%，说明其不具备良好的鲁棒性。这是因为传统K近邻模型单纯选择预测日的前一天作为预测基准向量，并没有考虑到影响旅客到达航站楼规律的因素。在机场项目中，影响旅客流量的主要因素有天气、航班计划、节假日、突发事件和机场周围交通状况。对于不同的两日，若其特征因子差异过大，则两日中目标时刻上航站楼客流量大小也会有较大差异，从历史数据库中选取K个近邻日, 利用加权平均得出短时客流量的预测值则会与预测日有较大的误差。综上，传统K近邻模型不适合在机场短时客流量预测场景中直接使用。
基于相似日的预测算法^[21]起源于电力系统短期负荷预测，是电力负荷预测的基本方法之一。在电力系统短期负荷预测中，通常认为在气象状况、日类型等影响因素相似的2天，负荷也比较接近。若以历史上相似日为预测基准向量进行预测，再根据相似日的负荷加以修正，则可以很好地预测结果。
借鉴电力系统的预测方法，考虑各个运营日的特征属性，将历史运营日的特征与预测日的特征进行匹配，选取相似历史运营日内各个时刻客流量的测定序列作为训练序列来对预测日目标时刻的客流量进行预测有望解决此难题。然而，如何确定一个运营日的特征属性及如何选取与预测日相似的历史运营日是一个关键的问题。
根据文献[7]可知，旅客出行受到航班离港时刻的强制约束，会在航班起飞前一段时间密集到达航站楼，旅客到达航站楼的绝大多数情况为早于航班起飞1~2.5 h，离港航班量直接决定了航站楼旅客的聚集量。整个航站楼旅客的聚集可以看做是多个航班离港时刻约束条件下的结果，旅客聚集趋势与航班离港时刻直接相关。
综上分析，旅客行为从本质上讲是由截止时间约束的群体行为，因此每个时段的航班计划是影响旅客航站楼聚集的重要因素。如图 3所示，t时段的旅客聚集人数是由后期时段的航班计划m4、m5、m6影响。所以确定航班计划为一个运营日的特征属性，并通过航班计划特征属性来选取与预测日相似的历史运营日。

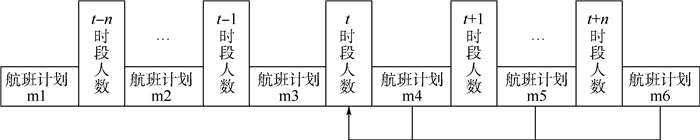图 3 航班计划对旅客聚集量的影响 Fig. 3 Influence of flight schedule on arrived passenger number

图选项

2 改进K近邻模型 2.1 双层K近邻算法 通过第1节的分析，离港旅客的聚集行为由航班离港时刻即航班计划驱动。本节将选取航班计划为一个运营日的特征属性，在传统K近邻算法基础上增加航班计划状态模式匹配步骤，采取K最近邻法(K=1)选取与预测日相似的历史运营日，并将选取相似历史运营日内各个时刻客流量的测定序列作为训练序列对预测日目标时刻的客流量进行预测。
定义1??设在机场场景中，不同运营日一天中各个时段在相似的航班计划条件下为相似特征运营日。
定义2??设X(t)表示当前时段的状态向量，同时有相邻航班计划v(t)和相邻时段旅客流量p(t)两个指标，以此来表示数据特征。X_h(t)表示历史同一时段的状态向量，且近邻产生于历史同一时段。则状态向量可表示为

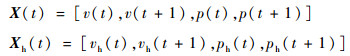定义3??设K为近邻个数；R为历史数据状态向量的维数；P(t)为第t时段的客流量状态向量；V(t)为第t时段的航班计划状态向量；d为两向量之间的欧氏距离。
历史客流量状态向量为

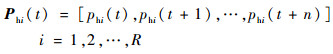历史航班计划状态向量为

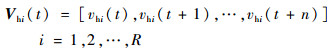为了更方便、直观地分析各时段客流量与航班计划，分别给出客流量状态矩阵及航班计划状态矩阵。
客流量状态矩阵为

历史数据库中一共有R天的客流量数据，p₁(t)表示第一天t时刻的客流量，则p_R(t)代表第R天t时刻的客流量。
航班计划状态矩阵为

历史数据库中一共有R天的航班计划数据，v₁(t)表示第一天t时刻的航班计划，则v_R(t)代表第R天t时刻的航班计划。
在双层K近邻(T-KNN)客流量预测模型中，先计算当前航班计划状态向量V(t)与历史状态向量V_hi(t)之间的度量距离，即欧氏距离d₁为

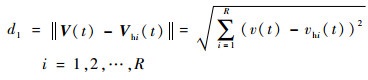(6)

选择与预测日航班计划状态向量距离最小的一天，设其航班计划状态向量为V_m(t)=[v_m(t), v_m(t+1), …, v_m(t+n)], 则其对应的客流量状态向量为P_m(t)=[p_m(t), p_m(t+1), …, p_m(t+n)], 并在历史航班计划状态矩阵及客流量状态矩阵中除去对应向量。再计算P_m(t)与历史客流量状态向量P_hi(t)之间的度量距离，即欧氏距离d_i为

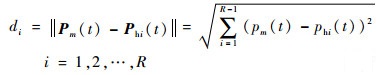(7)

按照距离从小到大排序，并选择出K个最近历史客流量状态向量P_hi(t)=[p_hi(t), p_hi(t+1), …，p_hi(t+n)](i=1, 2，…，K)。再计算当前t时刻的客流量p_i(t), 并作为预测值，表达式为

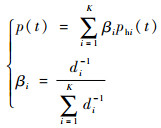建立针对航站楼短时客流量预测的双层K近邻模型, 该模型具体步骤如下：
步骤1?将旅客自助值机数据进行预处理，通过建立异常数据识别标准，对必要冗余数据剔除，完成历史数据库的建立，并将测试数据做同样的处理。
步骤2?根据已有数据的实际情况、算法效率、工程限制及数据获取的限制，提取数据中航班计划与相邻时段旅客流量2个特征作为状态向量。设X(t)=[v(t), v(t+1), p(t), p(t+1)]表示当前时段的状态向量，v(t)表示当前时段航班计划，p(t)表示当前时段旅客流量。
步骤3?根据测试数据第N天的航班计划及K最近邻法(K=1)，利用式(6)，计算当前航班计划状态向量V(t)=[v(t), v(t+1), …, v(t+n)]与历史航班计划状态向量V_hi(t)=[v_hi(t), v_hi(t+1), …, v_hi(t+n)]之间的欧氏距离，根据距离从小到大进行排序，再根据距离从历史数据库中找寻与其最接近的基准向量第M天(M < N)。
步骤4?以第M天基准向量的一天中间隔30 min的旅客到达人数作为基础，在历史数据库中除去第M天，利用式(7)，计算第M天的客流量P_m(t)=[p_m(t), p_m(t+1), …, p_m(t+n)]与历史客流量P_hi(t)=[p_hi(t), p_hi(t+1), …, p_hi(t+n)]之间的欧氏距离，根据距离从小到大排序，找到K个与M天最相近的天数，并利用加权平均预测算法(即式(2))得到预测值。
步骤5??计算3个评价指标：平均绝对误差MAE、均方误差MSE、拟合优度R²值，并进行误差分析。
双层K近邻算法流程如图 4所示。

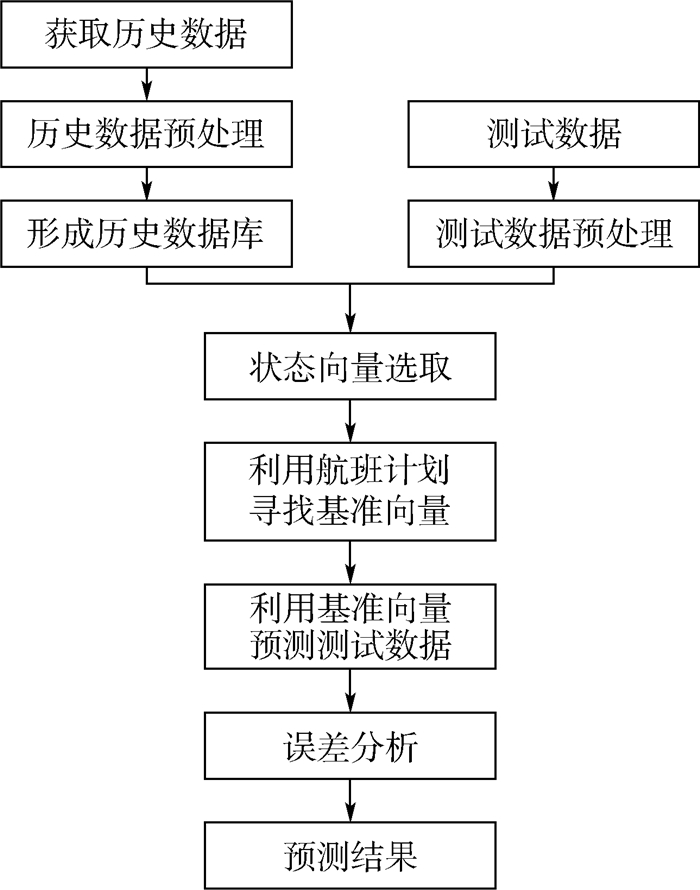图 4 双层K近邻算法流程 Fig. 4 Flowchart of T-KNN algorithm

图选项

2.2 结果分析 为了深入探究2.1节建立的双层K近邻模型在航站楼短时客流量预测的适用性，本文从方法与时间2个维度验证分析。选择2016-09-09—2016-09-13这5日作为预测日，预测日之前的航班数据作为测试日，并与传统K近邻模型、文献[7]的航班离港时刻主导的单航班离港旅客聚集(Arrived Passenger Model in Single Flight based on the Time of Departure, TD-SFAPM)模型、文献[12]的自回归求和滑动平均(Autoregressive Integrated Moving Average, ARIMA)模型、文献[22]的支持向量机(Support Vector Machine, SVM)模型作预测精度对比。
在对双层K近邻模型的相关要素定义完成后，先进行航班计划状态模式匹配步骤，根据2.1节中步骤3、式(6), 利用K最近邻法(K=1)在2016-03-26—2016-09-08数据中找出与2016-09-09—2016-09-13航班计划最接近的一天，即相似历史运营日。根据实验，最近的一天依次为2016-06-10、2016-04-11、2016-04-18、2016-05-09和2016-08-10。
根据2.1节中步骤4，以相似历史运营日作为对应预测日的基准向量，选取K=7，利用式(7)对2016-09-09—2016-09-13每天中48个时段客流量进行预测。同时，预测结果与传统K近邻模型、TD-SFAPM模型^[7]、ARIMA模型^[12]、SVM模型^[22]对比。
由于文章篇幅限制，预测仿真对比图只展示2016-09-09这一天，如图 5所示。各预测日精度评价指标平均绝对误差MAE、均方误差MSE、拟合优度R²结果如表 2所示。

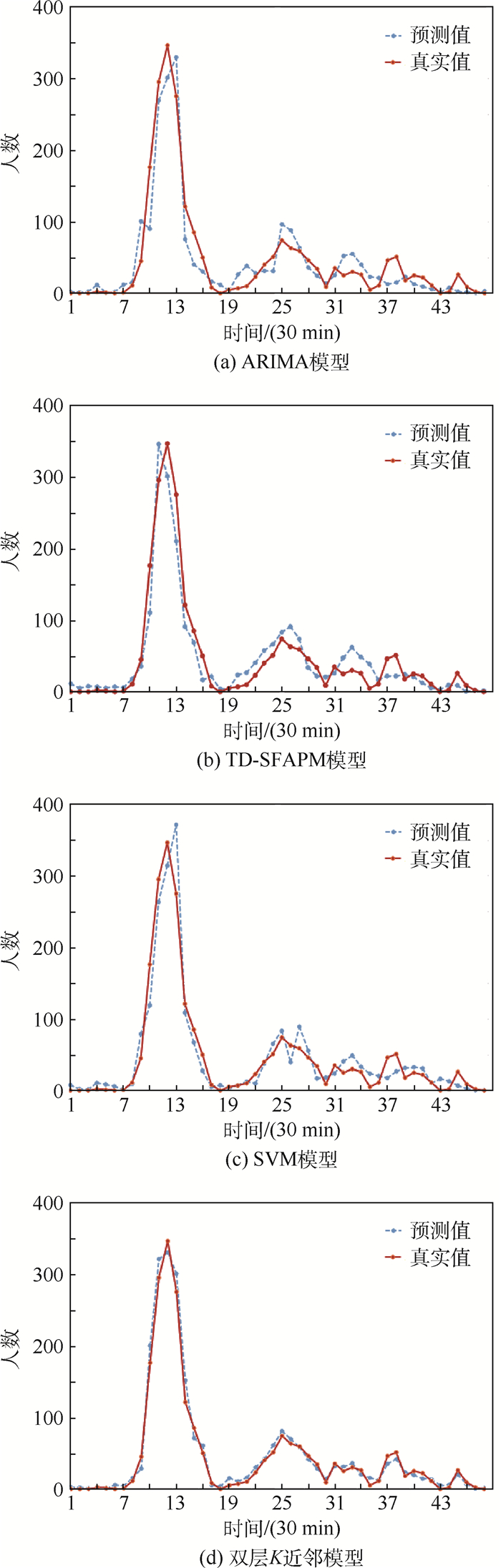图 5 不同模型预测值与真实值对比 Fig. 5 Comparison of predictive value of different models with true value

图选项

表 2 不同模型预测精度分析 Table 2 Different models prediction accuracy analysis

日期	模型	MSE	MAE	R2/%
2016-09-09	ARIMA	393.735 7	13.195 3	80.27
	KNN	351.893 0	11.451 1	83.65
	TD-SFAPM	411.358 6	13.258 9	79.11
	SVM	343.256 8	12.158 9	83.35
	T-KNN	273.253 5	10.332 5	90.31
2016-09-10	ARIMA	423.658 1	14.652 8	78.13
	KNN	386.675 2	12.254 9	82.33
	TD-SFAPM	422.598 7	14.857 0	77.28
	SVM	379.876 3	12.268 9	83.22
	T-KNN	289.326 5	10.659 9	90.21
2016-09-11	ARIMA	387.365 7	13.986 3	81.55
	KNN	345.365 1	10.931 5	89.31
	TD-SFAPM	404.586	13.896 7	79.58
	SVM	385.897	11.857 0	81.80
	T-KNN	271.325 9	9.587 9	91.13
2016-09-12	ARIMA	435.578 9	14.587 3	77.97
	KNN	342.478 3	10.547 2	89.54
	TD-SFAPM	412.583 0	14.058 0	78.20
	SVM	378.368 7	11.235 8	82.58
	T-KNN	286.687 2	10.253 1	90.63
2016-09-13	ARIMA	426.875 3	13.087 5	78.96
	KNN	411.579 2	13.367 3	79.14
	TD-SFAPM	385.350	13.589 7	80.25
	SVM	365.257	11.587 0	82.58
	T-KNN	268.657 8	9.324 6	91.35

表选项






从预测方法维度对比分析，根据2016-09-09—2016-09-13实验结果表明，传统K近邻模型的评价指标MSE与MAE均小于其相对应的ARIMA模型，拟合优度R²均大于ARIMA模型，表明传统K近邻模型预测效果优于ARIMA模型。这是由于ARIMA模型仅对平稳的时间序列有较好的预测效果，对具有复杂性、不确定性和非线性特点的航站楼短时客流量来讲，数据并不是十分平稳。TD-SFAPM模型仅针对单航班预测，若将其直接叠加预测多航班客流量则会造成更大的误差，且误差修正需花费大量时间，不满足短时预测的实时性要求。SVM模型虽然针对非线性时间序列有较好的效果，但其参数难以确定，预测精度受核函数影响很大，参数调整费时，也很难满足机场资源配置实时性的需求。
传统K近邻模型单纯选择预测日的前一日作为预测基准向量，忽略了航站楼客流量在短时期内体现准周期的规律性变化，且受航班计划、天气等多种因素的影响。若预测日与其前一日在目标时刻客流量波动较大，则选择预测日的前一日作为基准向量会带来较大的误差。
相对传统K近邻模型，双层K近邻模型借鉴电力系统的预测方法，选取航班计划为一个运营日的特征属性，将历史运营日的航班计划特征与预测日的航班计划特征进行匹配，选取相似历史运营日内各个时刻客流量的测定序列作为训练序列来对预测日目标时刻的客流量进行预测。该方法合理避免了因天气、节假日等随机因素对航站楼客流量造成的影响，选择的相似历史运营日与预测日客流量波动不大，使得双层K近邻模型拥有更高的精度。
从双层K近邻模型评价指标来看, 其拟合优度R²稳定在90%左右，相对传统K近邻模型平均提高了8%~10%。双层K近邻模型良好的预测效果也证明了具有相似航班计划的不同两日为相似特征运营日，其客流量大小及波动具有一定相似性，且以相似特征运营日作为基准向量预测预测日短时客流量的精度更高，具体表现为：双层K近邻模型相对传统K近邻模型平均绝对误差MSE与均方误差MAE减小，拟合优度R²增大。
为了排除随机性对双层K近邻模型的影响，本文再从时间维度出发，随机抽取5日验证分析，并且每个预测日都分布在不同的月份。实验结果如表 3所示。
表 3 不同模型时间维度预测精度分析 Table 3 Time dimension prediction accuracy analysis of different models

日期	模型	MSE	MAE	R2/%
2016-04-05	ARIMA	372.354 6	13.257 9	79.32
	KNN	331.389 6	12.132 4	82.65
	TD-SFAPM	393.251	14.258 9	77.52
	SVM	345.367 4	13.235 7	81.25
	T-KNN	252.178 6	10.258 9	90.71
2016-05-20	ARIMA	365.578 9	13.189 6	80.56
	KNN	342.236 5	11.438 1	81.36
	TD-SFAPM	362.576 8	13.025 7	81.03
	SVM	332.216 0	11.268 7	82.03
	T-KNN	265.796 3	10.568 6	89.62
2016-07-15	ARIMA	363.589 7	12.328 6	81.36
	KNN	342.358 6	11.327 3	83.22
	TD-SFAPM	421.354 0	14.258 9	78.70
	SVM	378.235 5	12.963 0	80.25
	T-KNN	275.265 8	10.981 1	90.26
2016-08-08	ARIMA	378.998 5	14.265 7	78.25
	KNN	353.865 7	11.188 2	83.55
	TD-SFAPM	423.587 9	15.025 7	77.25
	SVM	373.568 0	12.524 0	82.56
	T-KNN	266.788 4	9.712 3	91.68
2016-10-01	ARIMA	355.562 3	11.589 6	80.33
	KNN	324.337 8	11.045 1	82.44
	TD-SFAPM	380.257 9	13.257 0	79.33
	SVM	352.248 7	11.568 7	81.57
	T-KNN	258.365 7	9.865 2	91.70

表选项






实验结果表明，双层K近邻模型在时间维度上有很好的契合效果，并无较大波动，与真实数据的平均拟合度达到90%以上，相对于传统K近邻模型提高了8%~10%，显示了双层K近邻模型良好的鲁棒性。
3 结论 本文通过分析某航空公司旅客自助值机数据，展开对航站楼短时客流量变化规律的探究，研究表明：
1) 传统K近邻算法适用于短时交通流的预测，但针对航站楼短时客流量预测场景时需要对算法进行改进。
2) 旅客到达航站楼受到航班离港时刻的强制约束，具有相似航班计划特征的运营日同一个目标时刻上的客流量变化波动具有相似特征。
3) 增加航班计划状态模式匹配步骤选取相似历史运营日的各个时刻客流量的测定序列作为训练序列来对预测日目标时刻的客流量进行预测时，即利用双层K近邻模型时预测误差更小，精度更高，模型拟合度相对传统K近邻模型提高了8%~10%。
人类行为是高度复杂的，影响旅客到达航站楼的规律因素也错综复杂。本文模型在构建时只将航班计划作为旅客到达航站楼驱动力来寻找相似特征运营日，因此尚存在一定不足。未来将借助机场运行控制中心大数据平台，进一步挖掘运营日的特征属性(如天气状况，淡、旺季类型)来确定与预测日相似的历史运营日，完善理论模型，提高模型的普适性。

参考文献

[1]	GROSCHE T, ROTHLAUF F, HEINZL A. Gravity models for airline passenger volume estimation[J]. Journal of Air Transport Management, 2007, 13(4): 175-183. DOI:10.1016/j.jairtraman.2007.02.001
[2]	LETAVKOVA D, MATUSKOVA S, KEBO V, et al.Simulation model for regional airport passenger throughputs[C]//International Carpathian Control Conference.Piscataway, NJ: IEEE Press, 2015: 295-299.
[3]	黄飞虎, 彭舰, 由明阳. 航空旅客群体移动行为特性分析[J]. 物理学报, 2016, 65(22): 2289011. HUANG F H, PENG J, YOU M Y. Analyses of characetristics of air passenger group mobility behaviors[J]. Acta Physica Sinica, 2016, 65(22): 2289011. (in Chinese)
[4]	NDOH N N, ASHFORD N. Evaluation of airport access level of service[J]. Transportation Research Record, 1993, 1423: 34-39.
[5]	KIM W, PARK Y, KIM B J. Estimating hourly variations in pa-ssenger volume at airports using dwelling time distributions[J]. Journal of Air Transport Management, 2004, 10(6): 395-400. DOI:10.1016/j.jairtraman.2004.06.009
[6]	邢志伟, 文涛, 罗谦, 等. 基于效用价值驱动的旅客出行动力学研究与建模[J]. 北京航空航天大学学报, 2018, 44(2): 250-256. XING Z W, WEN T, LUO Q, et al. Utility value driven passenger travel dynamic study and modeling[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(2): 250-256. (in Chinese)
[7]	邢志伟, 冯文星, 罗谦, 等. 基于航班离港时刻主导的单航班离港旅客聚集模型[J]. 电子科技大学学报, 2015, 44(5): 719-724. XING Z W, FENG W X, LUO Q, et al. Arrived passenger model in single flight based on the time of departure[J]. Journal of University of Electronic Science and Technology of China, 2015, 44(5): 719-724. DOI:10.3969/j.issn.1001-0548.2015.05.014 (in Chinese)
[8]	TIAN Z D, LI S J, WANG Y H, et al. A prediction method based on wavelet transform and multiple models fusion for chaotic time series[J]. Chaos, Solitons & Fractals, 2017, 98: 158-172.
[9]	田中大, 李树江, 王艳红, 等. 基于ARIMA与ESN的短期风速混合预测模型[J]. 太阳能学报, 2016, 37(6): 1603-1610. TIAN Z D, LI S J, WANG Y H, et al. Short-term wind speed hybrid prediction model based on ARIMA and ESN[J]. Acta Energiae Solaris Sinica, 2016, 37(6): 1603-1610. DOI:10.3969/j.issn.0254-0096.2016.06.037 (in Chinese)
[10]	TIAN Z D, LI S J. A network traffic prediction method based on IFS algorithm optimised LSSVM[J]. International Journal of Engineering Systems Modelling and Simulation, 2017, 19(4): 200-213.
[11]	田中大, 李树江, 王艳红, 等. 基于混沌理论与改进回声状态网络的网络流量多步预测[J]. 通信学报, 2016, 37(3): 55-70. TIAN Z D, LI S J, WANG Y H, et al. Network traffic multi-step prediction based on chaos theory and improved echo state network[J]. Journal on Communications, 2016, 37(3): 55-70. DOI:10.3969/j.issn.1001-2400.2016.03.010 (in Chinese)
[12]	田中大, 李树江, 王艳红, 等. 高斯过程回归补偿ARIMA的网络流量预测[J]. 北京邮电大学学报, 2017, 40(6): 65-73. TIAN D Z, LI S J, WANG Y H, et al. Network traffic prediction based on ARIMA with Gaussian process regression compensation[J]. Journal of Beijing University of Posts and Telecommunications, 2017, 40(6): 65-73. (in Chinese)
[13]	DAVIS G, NIHAN N. Nonparametric regression and short-term freeway traffic forecasting[J]. Journal of Transportation Engineering, 1991, 117(2): 178-188. DOI:10.1061/(ASCE)0733-947X(1991)117:2(178)
[14]	林川.基于K近邻非参数回归的短时交通流预测算法研究[D].成都: 电子科技大学, 2015: 30-40. LIN C.Short-term traffic flow prediction algorithm based on K-nearest neighbor[D].Chengdu: University of Electronic Science and Technology of China, 2015: 30-40(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10614-1015711959.htm
[15]	张涛, 陈先, 谢美萍, 等. 基于K近邻非参数回归的短时交通流预测方法[J]. 系统工程理论与实践, 2010, 30(2): 376-384. ZHANG T, CHEN X, XIE M P, et al. K-NN based nonparametric regression method for short-term traffic flow forecasting[J]. Systems Engineering-Theory and Practice, 2010, 30(2): 376-384. (in Chinese)
[16]	于滨, 邬珊华, 王明华, 等. K近邻短时交通流预测模型[J]. 交通运输工程学报, 2012, 12(2): 105-111. YU B, WU S H, WANG M H, et al. K-nearest neighbor model of short-term traffic flow forecast[J]. Journal of Traffic and Transportation Engineering, 2012, 12(2): 105-111. DOI:10.3969/j.issn.1671-1637.2012.02.017 (in Chinese)
[17]	谢海红, 戴许昊, 齐远, 等. 短时交通流预测的改进K近邻算法[J]. 交通运输工程学报, 2014, 14(3): 87-94. XIE H H, DAI X H, QI Y, et al. Improved K-nearest neighbor algorithm for short-term traffic forecasting[J]. Journal of Traffic and Transportation Engineering, 2014, 14(3): 87-94. DOI:10.3969/j.issn.1671-1637.2014.03.017 (in Chinese)
[18]	豆飞, 贾利民, 秦勇, 等. 铁路客运专线模糊k近邻客流预测模型[J]. 中南大学学报(自然科学版), 2014, 45(12): 4422-4430. DOU F, JIA L M, QIN Y, et al. Fuzzy k-nearest neighbor passenger flow forecasting model of passenger dedicated line[J]. Journal of Central South University(Science and Technology), 2014, 45(12): 4422-4430. (in Chinese)
[19]	张晓利, 贺国光, 陆化普. 基于k-邻域非参数回归短时交通流预测方法[J]. 系统工程学报, 2009, 24(2): 178-183. ZHANG X L, HE G G, LU H P. Short-term traffic flow forecasting based on k-nearest neighbors nonparametric regression[J]. Journal of Systems Engineering, 2009, 24(2): 178-183. (in Chinese)
[20]	CAI P L, WANG Y P, LU G Q, et al. A spatiotemporal correlative k-nearest neighbor model for short-term traffic multistep forecasting[J]. Transportation Research Part C:Emerging Technologies, 2016, 62: 21-34. DOI:10.1016/j.trc.2015.11.002
[21]	陈通, 孙国强, 卫志农, 等. 基于相似日和CAPSO-SNN的光伏发电功率预测[J]. 电力自动化设备, 2017, 37(3): 66-71. CHEN T, SUN G Q, WEI Z N, et al. Photovoltaic power generation forecasting based on similar day and CAPSO-SNN[J]. Electric Power Automation Equipment, 2017, 37(3): 66-71. (in Chinese)
[22]	WANG Y S, WU D L, GUO C X, et al.Short-term wind speed prediction using support vector regression[C]//IEEE Power and Energy Society General Meeting.Piscataway, NJ: IEEE Press, 2010: 1-6.