为了解决这一问题,北京市计算中心赵楠研究员成功地在弱磁场强度下将CPMG (Carr-Purcell-Meiboom-Gill)[9]序列用于纯净化同位素的金刚石化学蒸汽沉积样品[10](12C丰度>99.99%),探测距离NV-色心大约为3.5 nm的单个13C核自旋[11]。由于实验所用样品纯度太高,这一探测方法不具有普适性。于是该组在CPMG的基础上,利用变化的自由演化时间代替原有不变的自由演化时间,构成新的脉冲序列来进行弱耦合作用的探测,提高了对自旋耦合噪声的分辨能力[12]。与此同时,代尔夫特理工大学的van der Sar基于量子门思想,将微波π-脉冲与量子门结合起来对单个核自旋进行探测[13-14]。上述序列都在单个周期内使用了大量脉冲,影响了金刚石核自旋操控的实时性。哈佛大学的Kolkowitz等使用XY4序列避免了这一问题,成功探测了距离NV-色心2个晶格以内的单个13C核子自旋[15],但其定位精度仍有待提高。
前期工作中,笔者团队对于金刚石色心的操控手段与原理做了深入研究[1, 16],在此基础上,本文设计出一种新型非均匀分布周期内对称的动态解耦序列--可调动态解耦(Adjustable-Parameter Dynamical Decoupling,APDD)序列来达到减少单周期内脉冲个数并同时尽可能保证13C核自旋定位精度的目的。本研究包括根据新型脉冲的分布设计,计算APDD序列的调制函数,推算NV-色心的模型,利用模型进行仿真并分析。
1 理论推导与计算 1.1 系统哈密顿量 NV-色心的电子基态为三重态,由|0〉和|±1〉构成。NV-色心自旋会与环境中的13C核自旋Ii进行耦合,其中13C核自旋的量子数为s=1/2,自然丰度为1.1%[17],并具有形如式(1)的哈密顿量[18]:
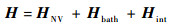 | (1) |
式中:HNV和Hbath分别为NV-色心和周围的环境哈密顿量; Hint为电子与环境之间的相互作用。当外加磁场B时,满足:
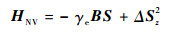 | (2) |
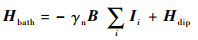 | (3) |
式中:γe和γn分别为电子自旋和13C核自旋的磁旋比;Δ为电子自旋的零场分裂;B为磁场强度;S为电子的自旋角动量;Sz为自旋角动量在z轴的分量;核自旋之间的偶极相互作用为
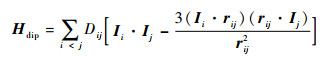 | (4) |
其中:rij为第i个核自旋到第j个核自旋的位移;Ii和Ij分别为第i和j个核子自旋;相互作用强度为
 | (5) |
其中:μ0为真空磁导率;电子和环境之间的相互作用为
 | (6) |
其中:Ai为第i个核自旋的超精细作用矢量,表达式为
 | (7) |
其中:z为z轴单位向量;riv为第i个核自旋到空位的位移。
1.2 动态解耦序列调制函数 CPMG作为等间隔均匀分布周期序列,周期为τ,其调制函数为F(t)=F(t+τ),进行傅里叶展开得
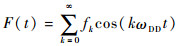 | (8) |
式中:ωDD=2π/τ,并且傅里叶系数fk为
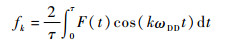 | (9) |
调制函数和傅里叶系数都是由脉冲数量以及脉冲间隔决定的,由于CPMG序列一个周期τ内有2个脉冲且脉冲间隔为τ/2,根据式(9)可以计算得
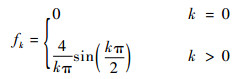 | (10) |
由式(10)可知,CPMG的傅里叶系数是不可变的。而对于同样是等间隔均匀分布周期序列的XY4,式(10)代表了CPMG与XY4的傅里叶系数。
本文APDD序列如图 1所示,一个周期内有4个π脉冲,脉冲间隔满足关系τ1+τ2=τ。
 |
| 图 1 APDD脉冲序列单周期内脉冲分布示意图 Fig. 1 Schematic of pulse distribution of APDD pulse protocol in single cycle |
| 图选项 |
根据APDD序列的脉冲分布情况,可以得到如式(11)所示的调制函数:
 | (11) |
根据式(9)的计算方法对式(11)所示调制函数进行计算得到傅里叶系数为
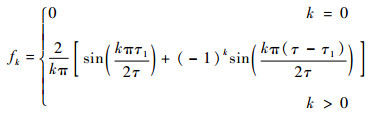 | (12) |
根据式(12),在k>0时,fk可以通过改变比值τ来进行调整,从而达到在同等脉冲数量的情况下对单个13C核自旋定位更加精确的效果。
2 仿真计算 2.1 金刚石模型的构建 根据金刚石晶胞结构来构造模型,金刚石晶胞结构中每个原子与相邻的4个原子形成正四面体,NV-色心结构为一个N原子与空位相邻,目前主要考虑的其他杂质粒子为13C核子,根据其1.1%的自然丰度进行随机分布在模型中。图 2中心最大粒子表示N核子,紧邻的粒子表示空位,它们构成了NV-色心,三角形粒子表示13C核子,最小的粒子表示没有参与耦合的12C核子和其他未参与到耦合中的其他原子。
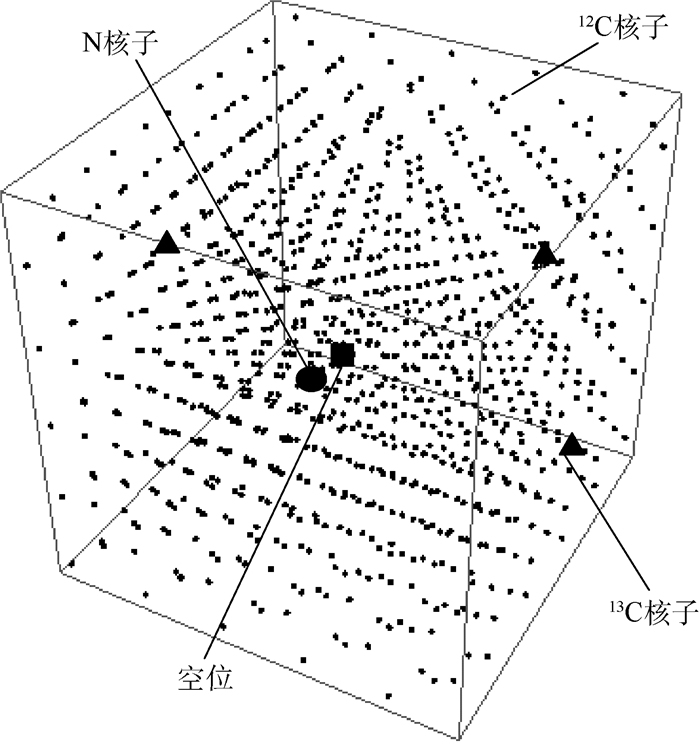 |
| 图 2 NV-色心金刚石模型 Fig. 2 NV- color center diamond model |
| 图选项 |
2.2 核子定位仿真计算 在旋转坐标系下,一个沿着x轴的微波π脉冲记为[19]
 | (13) |
式中:Sx为泡利算符。对于不同脉冲序列都可以用脉冲操作和自由演化算符来得到相应的表示。比如由4个沿x轴方向的π脉冲和2个沿着y轴的π/2脉冲构成的CPMG-4脉冲序列的表达式为[20]
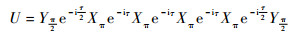 | (14) |
而对于一个周期XY4,其表达式为
 | (15) |
对于只含有一个周期的APDD脉冲序列的表达式为
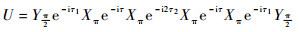 | (16) |
式(14)~式(16)中:
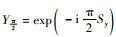
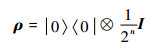 | (17) |
式中:

 | (18) |
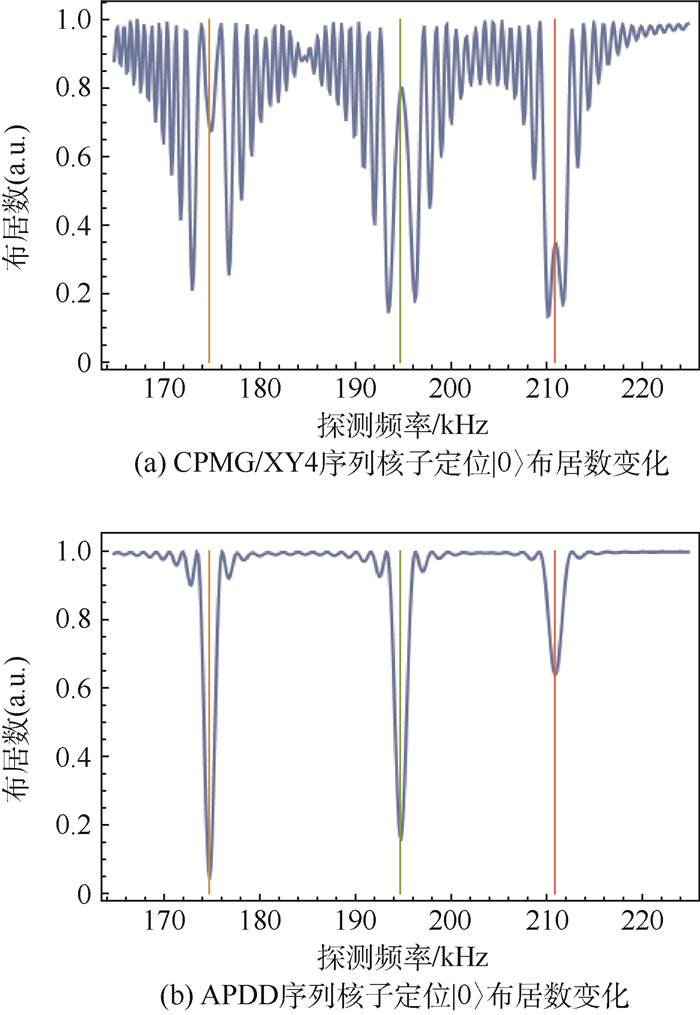
根据1.2节关于脉冲等间距均匀分布的CPMG和XY4序列以及脉冲非等间距均匀分布的APDD序列的调制函数计算,CPMG和XY4有着相同的调制函数。利用设计的NV-色心金刚石模型分别针对2种序列进行了仿真实验。给出的3个核子与NV-色心的距离分别为1.0、1.3和0.8 nm。沿着NV-色心的NV轴向添加180 G磁场,引起的拉莫尔进动频率要大于超精细场Ai,CPMG/XY4序列与APDD序列仿真所用脉冲数量均为480,仿真结果如图 3所示。其中,x轴表示探测频率,y轴表示|0〉布居数。3条直线表示3个核自旋的拉莫进动频率,分别为174.692、194.693和210.839 kHz,与3个核子一一对应,其计算式为
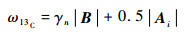 | (19) |
 |
| 图 3 CPMG/XY4序列与APDD序列核子定位比较 Fig. 3 Comparison of nuclear addressing between CPMG/XY4 and APDD protocols |
| 图选项 |
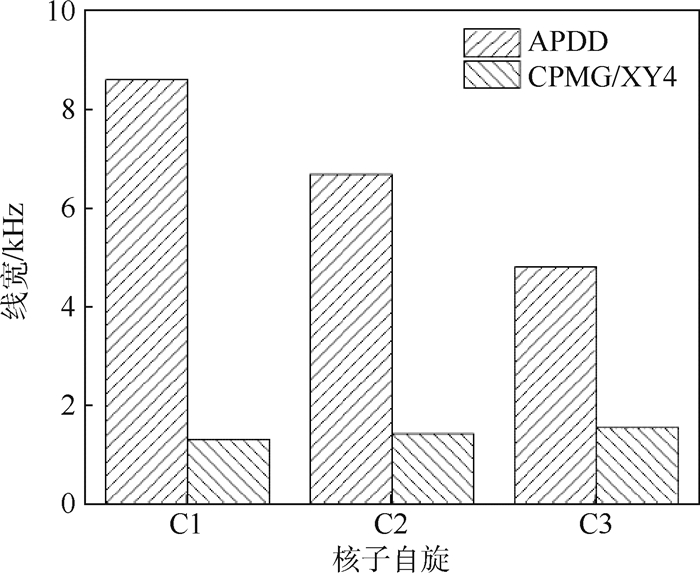
3 讨论 根据图 3,在CPMG、XY4序列用于探测13C核子自旋时,|0〉布居数在核子拉莫进动频率周围会出现较为激烈的振荡,而APDD序列只在3个核子处有共振峰。这是由于13C核子自旋周围存在超精细场,会对电子产生耦合作用,距离核子越近,影响越强烈,也就会出现更剧烈的振荡。正如式(10)给出的计算结果,CPMG/XY4序列调制函数的傅里叶系数是不可调的,因此在应对单个13C核自旋时,CPMG只能大致给出13C核子自旋拉莫进动频率的范围,偏差分别为8.62、6.70和4.83 kHz。使用APDD序列应对单个13C核自旋时,可以通过调整比值即周期内脉冲间距比例来降低线宽,从而提高定位的精度。如图 3(b)中|0〉布居数变化曲线求得的线宽分别为1.32、1.44和1.56 kHz,如图 4所示,图中C1、C2和C3分别对应3个核自旋。
 |
| 图 4 CPMG/XY4序列和APDD序列线宽条形图 Fig. 4 Bar chart of linewidth of CPMG/XY4 and APDD protocols |
| 图选项 |
通过设定APDD序列单个周期内比值为τ1/τ=0.58,相比于CPMG/XY4序列,APDD序列已经使得3个核子的线宽分别降低7.30、5.26和3.27 kHz。可以看出,对于这3个核子来说,单个周期内比值为τ1/τ=0.58的APDD相比于CPMG/XY4序列提高的精度可达6.27倍。由于比值可调,可以通过改变比值来研究核自旋定位的精度的稳定程度。比值τ1/τ从0.51变到1,步长为0.01,研究不同比值APDD核子定位|0〉布居数变化曲线的线宽变化情况如图 5所示。
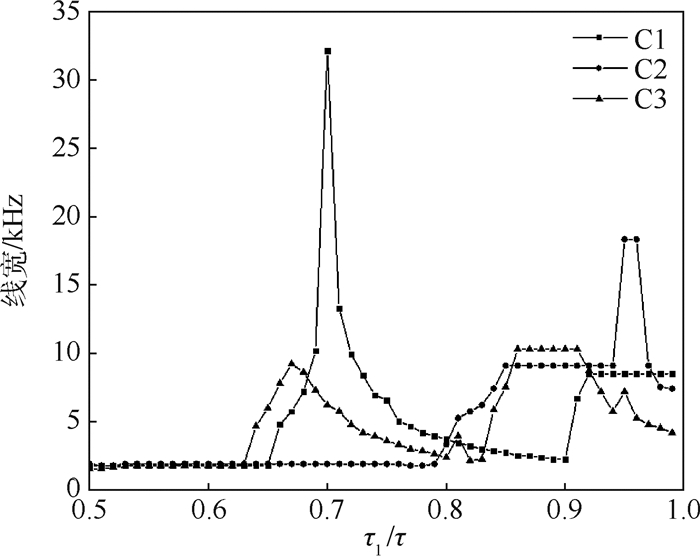 |
| 图 5 APDD序列线宽变化 Fig. 5 APDD protocols linewidth variation |
| 图选项 |
图 5中3个核子C1、C2和C3的拉莫进动频率为174.692、194.693和210.839 kHz。由于随着比值不断增大,即APDD序列内脉冲间隔τ1与τ2的差距越来越大,以4个脉冲为一周期,脉冲周期的间隔时间(2τ1)越来越长,周期内脉冲间隔时间(2τ+2τ2)越来越短。量子态中的|0〉态自由演化越来越不充分,布居数变化越来越小,同时|0〉布居数翻转加快,对13C核子自旋的定位受到影响从而线宽增大,所以相应的线宽从C1到C3呈递增的趋势,并且线宽呈现杂乱无章的状态,难以定位出目标核子的频率,进而越来越无法精确定位13C核子。因此,本文关注点是提出比值τ1/τ在位于0.51~0.58之间时3个核子的线宽都相对稳定且线宽值都小于1.8。并且,结合核子定位的结果可看出,本文APDD序列在该范围内有着比CPMG/XY4更优的能力。
4 结论 1) 本文提出APDD序列用于金刚石色心13C核自旋定位,针对其理论模型进行了推导计算与仿真分析。
2) APDD序列对于金刚石色心13C核自旋定位精度比常规的CPMG序列与XY4序列明显提高,以单个周期内比值τ1/τ=0.58为例,定位精度提高可达6.27倍。
3) 单个周期内比值τ1/τ介于0.51~0.58范围内APDD在用于核子定位时可以保持较高的精度。
4) 通过理论推导与仿真计算,CPMG序列与XY4序列在核自旋定位方面效果相同。
参考文献
| [1] | ZHANG C, YUAN H, TANG Z, et al. Inertial rotation measurement with atomic spins:From angular momentum conservation to quantum phase theory[J].Applied Physics Reviews, 2016, 3(4): 041305.DOI:10.1063/1.4972187 |
| [2] | BIGNEY E. Flawed to perfection:Ultra-pure synthetic diamonds offer advances in fields from quantum computing to cancer diagnostics[J].Nature News, 2014, 505: 472–474.DOI:10.1038/505472a |
| [3] | ALEGRE T P M, SANTORI C, MEDEIROS-RIBEIRO G, et al. Polarization-selective excitation of nitrogen vacancy centers in diamond[J].Physical Review B, 2007, 76(16): 165205.DOI:10.1103/PhysRevB.76.165205 |
| [4] | NEUMANN P, BECK J, STEINER M, et al. Single-shot readout of a single nuclear spin[J].Science, 2010, 329(5991): 542–544.DOI:10.1126/science.1189075 |
| [5] | ALBRECHT A, PLENIO M B. Filter design for hybrid spin gates[J].Physical Review A, 2015, 92(2): 02340. |
| [6] | LONDON P, SCHEUER J, CAI J M, et al. Detecting and polarizing nuclear spins with double resonance on a single electron spin[J].Physical Review Letters, 2013, 111(6): 467–473. |
| [7] | CYWINSKI L, LUTCHYN R M, NAVE C P, et al. How to enhance dephasing time in superconducting qubits[J].Physical Review B, 2008, 77(17): 998–1002. |
| [8] | YUGE T, SASAKI S, HIRAYAMA Y. Measurement of the noise spectrum using a multiple-pulse sequence[J].Physical Review Letters, 2011, 107(17): 170504.DOI:10.1103/PhysRevLett.107.170504 |
| [9] | MEIBOOM S, GILL D. Modified spin-echo method for measuring nuclear relaxation times[J].The Review of Scientific Instruments, 1958, 29(8): 688–691.DOI:10.1063/1.1716296 |
| [10] | MIZUOCHI N, ISOYA J, NⅡTSUMA J, et al. Isotope effects between hydrogen and deuterium microwave plasmas on chemical vapor deposition homoepitaxial diamond growth[J].Journal of Applied Physics, 2007, 101(10): 103501.DOI:10.1063/1.2727380 |
| [11] | ZHAO N, HONERT J, SCHMID B, et al. Sensing single remote nuclear spins[J].Nature Nanotechnology, 2012, 7: 657–662.DOI:10.1038/nnano.2012.152 |
| [12] | ZHAO N, WRACHTRUP J, LIU R B. Dynamical decoupling design for identifying weakly coupled nuclear spins in a bath[J].Physical Review A, 2014, 90(3): 032319.DOI:10.1103/PhysRevA.90.032319 |
| [13] | VAN DER SAR T, WANG Z H, BLOK M S, et al. Decoherence-protected quantum gates for a hybrid solid-state spin register[J].Nature, 2012, 484(7392): 82–86.DOI:10.1038/nature10900 |
| [14] | TAMINIAU T H, WAGENAAR J J, VAN DER SAR T, et al. Detection and control of individual nuclear spins using a weakly coupled electron spin[J].Physical Review Letters, 2012, 109(13): 137602.DOI:10.1103/PhysRevLett.109.137602 |
| [15] | KOLKOWITZ S, UNTERREITHMEIER Q P, BENNETT S D, et al. Sensing distant nuclear spins with a single electron spin[J].Physical Review Letters, 2012, 109(13): 137601.DOI:10.1103/PhysRevLett.109.137601 |
| [16] | ZHANG N, ZHANG C, XU L X, et al. Microwave magnetic field coupling with nitrogen-vacancy center ensembles in diamond with high homogeneity[J].Applied Magnetic Resonance, 2016, 47(6): 589–599.DOI:10.1007/s00723-016-0777-5 |
| [17] | WANG Z Y, HAASE J F, CASANOVA J, et al. Positioning nuclear spins in interacting clusters for quantum technologies and bio-imaging[J].Physical Review B, 2016, 93(17): 174104.DOI:10.1103/PhysRevB.93.174104 |
| [18] | ZHAO N, HO S W, LIU R B. Decoherence and dynamical decoupling control of nitrogen vacancy center electron spins in nuclear spin baths[J].Physical Review B, 2012, 85(11): 115303.DOI:10.1103/PhysRevB.85.115303 |
| [19] | áLVAREZ G A, AJOY A, PENG X, et al. Performance comparison of dynamical decoupling sequences for a qubit in a rapidly fluctuating spin-bath[J].Physical Review A, 2010, 82(4): 042306.DOI:10.1103/PhysRevA.82.042306 |
| [20] | WANG Z H, LANGE G, RISTèD, et al. Comparison of dynamical decoupling protocols for a nitrogen-vacancy center in diamond[J].Physical Review B, 2012, 85(15): 155204.DOI:10.1103/PhysRevB.85.155204 |
