目前,常用于校准相控阵天线的方法有近场扫描法[1-3]、旋转矢量法(REV)[4-5]、换相法[6-8]和互耦校准法[9]等。互耦校准法需要被测相控阵具备单通道收发功能,不适用于只有接收功能的相控阵接收机;近场扫描法[10-11]忽略了通道间的互耦效应,因此难以精确修正通道间的相位误差,且文献[11]测试中,需要确保探头的测试与天线口面要保持平行,这在外场实际操作过程中较难实现;旋转矢量法可以实现精确的相位校准[12],但需要对所有通道进行很多次的测试,测试时间长且计算量大;文献[13]中换相法以循环移位控制、Walsh函数、Hadamard矩阵等生成特殊的实验步骤控制矩阵,然后解得各通道的激励以确定其阵中方向图,但该方法需要精确知道测试探头的方向特性和位置,同样这在外场实际操作过程中难以实现。鉴于这些校准方法都有着特有的局限性,就产生了对这些校准方法组合修正的新方法,以适应特定校准环境。譬如文献[14]就结合互耦校准法、近场扫描法和旋转矢量法,对有源相控阵天线进行近场校准。
本文要求在只有相控阵接收机的系统中[15], 忽略幅度误差,但要求精确的相位误差校准,且要具有快速性、实时性。因此在换相法的基础上提出了一种相干换相校准的新方法,可以快速完成接收机各通道初始相位的初次校准,并应用旋转矢量法进行初始相位的精确校准。本文首先对校准原理进行了简单的理论推导,通过仿真验证了在特定场景中不需要精确知道测试探头的位置,然后在阵列微波辐射计平台上搭建相干换相校准系统进行验证,最后对测试数据进行分析。
1 相干换相校准原理及算法 1.1 相干换相校准原理 假设相控阵接收机有N个通道,每个通道由天线、低噪声放大器、混频器、移相器、功率分配网络和连接电缆等组成。如图 1所示,移相网络连接在混频器的本振支路上,通过改变混频器本振相位来改变接收机接收信号的相位。
 |
| 图 1 相干换相校准原理 Fig. 1 Schematic diagram of coherent phase-shift calibration |
| 图选项 |
假设通道1和通道2接收到放置在P点位置辐射源的信号S1和S2可以表示为
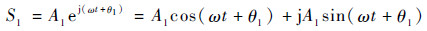 | (1) |
 | (2) |
式中:A1和A2分别为信号S1和S2的幅值;θ1和θ2分别为S1和S2的初始相位;ω为信号S1和S2的角频率。两路信号经过实部合路、功率分配网络后得到
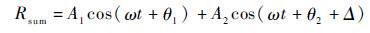 | (3) |
式中:Δ为附加在通道2上的增量相位。
则经过平方率检波和低通滤波器后得到
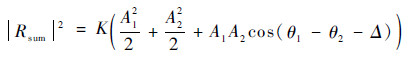 | (4) |
式中:K为平方率检波灵敏度,其值为常数。由式(4)可知,当Δ=θ1-θ2时,|Rsum|2取得最大值。通过控制Δ从0°,1°,…,360°的遍历,即可得到一组|Rsum|2的值,然后对其进行曲线拟合,即可得到最大值点对应的Δi,从而得到通道2相对通道1的相位差。同理可以得到相控阵其他通道相对通道1的相位差。
1.2 曲线拟合 式(4)表达式是余弦曲线形式,故采用余弦曲线拟合。余弦曲线参数方程可以用数学表达式表示为:f(Δi)=Acos(Δi+θ)+C,Δi为第i次相位调制值,A为信号振幅,θ为信号初始相位,C为信号幅度偏置。
以通道数为16的相控阵为例,相控阵各通道逐次进行Δi的360°相位遍历配置,计算机采集到如图 2所示的16通道的功率检波后数据,共16个余弦周期数。
 |
| 图 2 16通道的功率检波后相位数据 Fig. 2 16-channel phase data after power detection |
| 图选项 |
对图 2得到的数据进行周期截取,分别得到相控阵对应通道的数据。图 3(a)为相控阵通道1截取后的原始数据,图 3(b)是先对图 3(a)的同一相位遍历点的多个数据进行均值处理后再拟合得到的。索引图 3(b)中最大值点对应的横坐标,即为所要求的相位差δn。
 |
| 图 3 通道1截取后拟合曲线 Fig. 3 Truncated fitting curve of Channel 1 |
| 图选项 |
1.3 测试源位置误差分析 由1.2节计算出的相位差δn包括2个部分:测试源到各通道天线口面的空间距离产生的相位差和通道自身产生的相位差。前一部分是不需要的,需要在得到的δn中减去这一部分。以天线阵面中心建立坐标系,如图 1所示,O点为坐标原点。接收天线单元的坐标分别为(x1, y1, z1), (x2, y2, z2), …, (xn, yn, zn),测试源P点位置坐标为P(xp, yp, zp),测试源的波长设为λp。则测试源到各通道天线口面的相位可以写为
 | (5) |
则δn-Φn即最终所需的相位差。
在实际外场很难精确测得测试源相位中心的位置坐标P(xp, yp, zp),P点的误差会造成δn-Φn也带入相同的误差,这个误差对实际应用到底产生多大的影响,要根据具体的使用场景进行分析。接下来就相控阵接收机天线合成波束方向图进行仿真,分析测试源P点位置误差对其造成的影响。仿真流程如图 4所示。
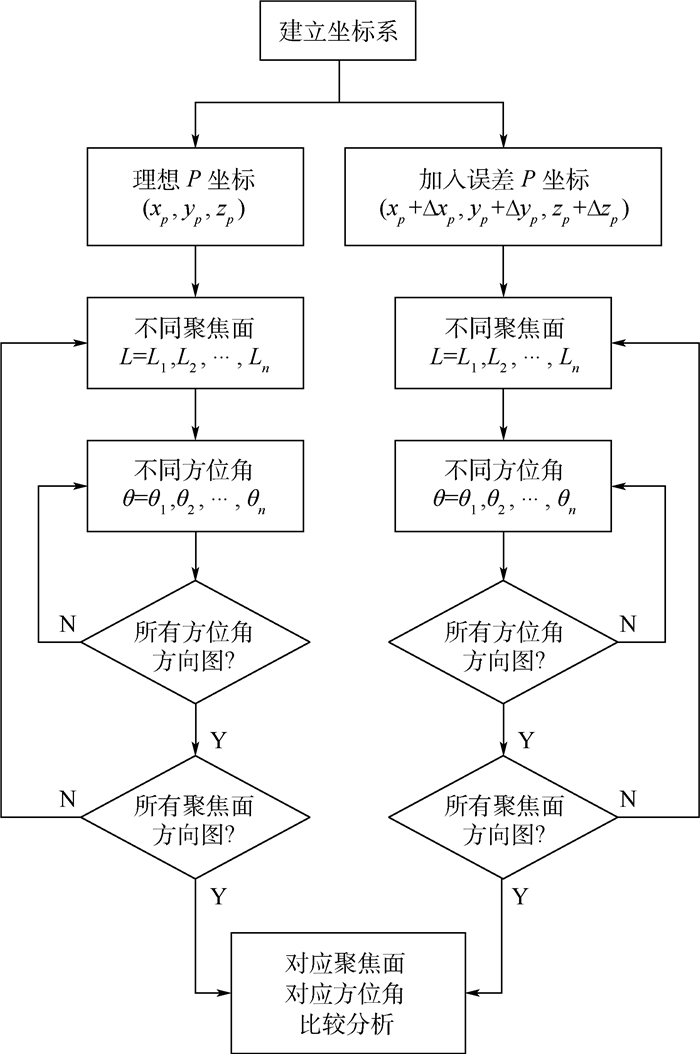 |
| 图 4 测试源位置误差仿真流程 Fig. 4 Test source position error simulation flowchart |
| 图选项 |
以接收机天线阵面几何中心为坐标原点建立坐标系,单位为m,定标源理想位置为(0, 0, 0.65) m,定标源实际位置在x、y、z方向分别偏离5 mm,即(0.005, 0, 0.65) m、(0, 0.005, 0.65) m、(0, 0, 0.65+0.005) m时,在不同的偏移情况下,在0.65~5 m纵向聚焦面,相控阵聚焦到0相位,进行相控阵方向图扫描,仿真观察波束偏离中心的距离或相位。
图 5为x、y、z方向偏离5 mm时,不同距离仿真结果。可以得出:在相控阵方向,x方向的偏移会造成波束指向的统一偏移,波束的偏移量和偏移误差相同;y方向的偏移不会对波束指向造成显著影响;z方向的偏移不会对波束指向造成显著影响。故相控阵方向的偏移不会对成像造成显著影响,只会造成图像的整体位移。
 |
| 图 5 x、y、z方向偏离5 mm时仿真结果 Fig. 5 Simulation results of 5 mm deviation in x、y、z direction |
| 图选项 |
2 测试验证及数据分析 现场实验测试在新研发出的被动式毫米波成像系统上进行,实物如图 6所示。
 |
| 图 6 被动式毫米波成像系统整机实物图 Fig. 6 Complete machine picture of passive millimeter wave imaging system |
| 图选项 |
校准控制的原理框图如图 7所示,矢量调制器可以实现0°~360°调相,调相精度在0.1°。同时可以实现-40 dB的幅度调制,以保证最大衰减时,对应接收机通道处于非工作状态。
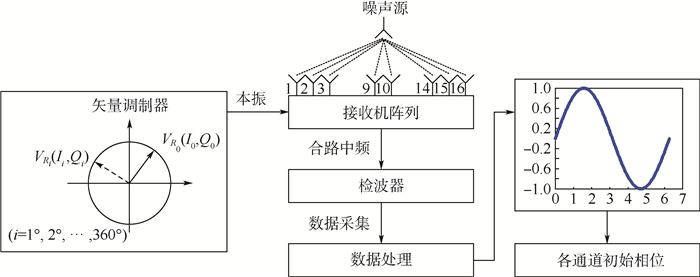 |
| 图 7 快速相位校准原理框图 Fig. 7 Functional block diagram of high-speed phase calibration |
| 图选项 |
通道1校准:矢量调制器控制相控阵通道1,依次增加1°,2°,…,360°的相位。在通道1进行360°范围相位旋转时,其他通道幅相控制器把其本振幅度衰减到工作点以下,使其通道处于关闭状态。在每个旋转相位上,计算16个通道的合路功率值,然后旋转完成后通过曲线拟合得到初始相位,即残余误差。
通道2校准:矢量调制器控制相控阵通道2,依次增加1°, 2°, …, 360°的相位。在通道2进行360°范围相位旋转时,其他通道幅相控制器把其本振幅度衰减到工作点以下,使其通道处于关闭状态。在每个旋转相位上,计算16个通道的合路功率值,然后旋转完成后通过曲线拟合得到初始相位,即残余误差。
同理完成16个通道的校准。这样就完成一个阵列的1次校准。依次可以进行第2次、第3次、…、第n次校准,直至满足系统要求的相位残余误差。
表 1为在图 6的实物系统中进行4次循环校准,校准后各阵列的通道残余误差的标准差大部分在5°左右。
表 1 实测16×16相控阵通道残差 Table 1 Channel residual measurement of 16×16 phased array
| (°) | |||||
| 阵列数 | 对齐次数 | ||||
| 0次 | 1次 | 2次 | 3次 | 4次 | |
| A1 | 37.8 | 12.8 | 17 | 14 | 5 |
| A2 | 114 | 82.6 | 96.4 | 18.3 | 3.6 |
| A3 | 28.7 | 17.2 | 7.5 | 2.5 | 3.4 |
| A4 | 26.4 | 11.2 | 4 | 2.7 | 2.7 |
| A5 | 73.3 | 30.4 | 13.9 | 8.3 | 6.1 |
| A6 | 86.2 | 25.2 | 8.2 | 15.9 | 10 |
| A7 | 102 | 32.2 | 11.5 | 11.6 | 6.3 |
| A8 | 53.7 | 18.3 | 20.3 | 7.1 | 3.8 |
| A9 | 113 | 115 | 23.8 | 5.1 | 4.4 |
| A10 | 108 | 43.2 | 4.7 | 4.6 | 2.5 |
| A11 | 44.1 | 12.4 | 7.1 | 4.5 | 11 |
| A12 | 21.4 | 26.2 | 32.9 | 8.4 | 3.4 |
| A13 | 17.6 | 16.7 | 2.9 | 3.1 | 3.2 |
| A14 | 38.3 | 13.6 | 3.6 | 9.7 | 7.7 |
| A15 | 48.3 | 33 | 20.6 | 6.4 | 3.5 |
| A16 | 109 | 36 | 14.5 | 15.8 | 13 |
表选项
图 7中,把毫米波辐射计天线的水平方向称为相控阵方向,把毫米波辐射计天线的垂直方向称为综合孔径方向。由于相控阵各阵列之间(A1,A2,…,A16)是相互独立的,故在相控阵方向进行校准时,可以同时完成综合孔径方向所有阵列通道的对齐。检波器的积分时间按10 ms计算,相位对齐时,每个相位点停留时间为10 ms,完成所有阵列16通道的360个相位点所需时间为60 s,同时进行采集功率补偿数据存储到计算机,然后由计算机拟合计算出相位差,再把计算出的相位差通过矢量调制器补偿到系统中需要大概1.5 min左右。这样2 min即可完成一次相位补偿过程。
3 结论 本文通过对不同相控阵相位校准方法局限性的分析,给出了一种相控阵接收机近场初始相位快速实时校准方法。该方法需要借助于矢量调制器,且满足相位调制精度和最大幅度衰减要求。得到以下结论:
1) 仿真论证了测试探头的位置偏差对相控阵天线方向图的定量分析,得出在毫米波成像系统中直接表现为图像的整体偏移,不影响成像效果。
2) 在实际系统进行了验证,经过4次循环校准后,通道相位残差的标准差大部分在5°左右,且每次相位补偿过程用时在2 min左右,可以应用到需要对相位实时快速进行相位校准的系统中。
参考文献
| [1] | KELLY D F, STUTZMAN W L. Array antenna pattern modeling methods that include mutual coupling effects[J]. IEEE Transactions on Antennas and Propagation, 1993, 41(12): 1625-1632. DOI:10.1109/8.273305 |
| [2] | SAYERS A E, DORSEY W M, O'HAVER K W, et al. Planar nearfield measurement of digital phased arrays using near-field scan plane reconstruction[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(6): 2711-2718. DOI:10.1109/TAP.2012.2194666 |
| [3] | MEDINA R H, SALAZAR J L, KNAPP E J, et al.Calibration and validation of the CASA phased array antenna[C]//Proceeding of the 42nd European Microwave Conference.Piscataway, NJ: IEEE Press, 2012: 940-943. |
| [4] | TAKAHASHI T, KONISHI Y, MAKINO S, et al. Fast measurement technique for phased array calibration[J]. IEEE Transactions on Antennas and Propagation, 2008, 56(7): 1888-1899. DOI:10.1109/TAP.2008.924682 |
| [5] | LIU M G, FENG Z H.Combined rotating-element electric-field vector (CREV) method for nearfield calibration of phased array antenna[C]//5th International Conference on Microwave and Millimeter Wave Technology.Piscataway, NJ: IEEE Press, 2007: 1-4. |
| [6] | SILVERSTEIN S D. Application of orthogonal codes to the calibration of active phased array antennas for communication sate-llites[J]. IEEE Transactions on Signal Processing, 1997, 45(1): 206-218. DOI:10.1109/78.552217 |
| [7] | SHANG J P, LI X R, SUN L C, et al.A novel fast measurement method and diagnostic of phased array antennas[C]//201210th International Symposium on Antennas, Propagation & EM Theory (ISAPE).Piscataway, NJ: IEEE Press, 2012: 219-222. |
| [8] | HAO S J, LI Q L, DING J, et al.Digital active phased array antenna measurement method based on correlation technique[C]//201210th International Symposium on Antennas, Propagation & EM Theory (ISAPE).Piscataway, NJ: IEEE Press, 2012: 11-14. |
| [9] | AUMAN H M, FENN A J, WILLWERTH F G. Phased array antenna calibration and pattern prediction using mutual coupling measurements[J]. IEEE Transactions on Antennas and Propagation, 1989, 37(7): 844-850. DOI:10.1109/8.29378 |
| [10] | 韦哲, 黄世钊. 相控阵天线测量校准方法分析与比较[J]. 四川兵工学报, 2014, 35(1): 119-122. WEI Z, HUANG S Z. Analysis and comparison of measurement and calibration methods for phased array antennas[J]. Journal of Sichuan Ordnance, 2014, 35(1): 119-122. DOI:10.11809/scbgxb2014.01.032 (in Chinese) |
| [11] | 王晓鹏, 赵海明, 张远航, 等. 基于近场测试的相控阵天线自动化校准与阵面监测方法[J]. 微波学报, 2012, 28(S3): 229-232. WANG X P, ZHAO H M, ZHANG Y H, et al. Auto-calibration and array monitoring of phased array antenna based on near field measurement[J]. Journal of Microwaves, 2012, 28(S3): 229-232. (in Chinese) |
| [12] | 刘明罡, 冯正和. 分组旋转矢量法校正大规模相控阵天线[J]. 电波科学学报, 2007, 21(3): 380-384. LIU M G, FENG Z H. Combined rotating-element electric-field vector method for calibration of large-scale phased array antenna[J]. Chinese Journal of Radio Science, 2007, 21(3): 380-384. DOI:10.3969/j.issn.1005-0388.2007.03.005 (in Chinese) |
| [13] | 尚军平, 傅德民, 焦永昌, 等. 基于最佳配相控制的相控阵天线快速测量方法研究[J]. 电波科学学报, 2008, 23(2): 331-334. SHANG J P, FU D M, JIAO Y C, et al. A novel method for fast measuring phased array antennas based on optimal phase control[J]. Chinese Journal of Radio Science, 2008, 23(2): 331-334. DOI:10.3969/j.issn.1005-0388.2008.02.028 (in Chinese) |
| [14] | 焦禹, 陈文俊. 有源相控阵天线的近场校准[J]. 电讯技术, 2016, 56(4): 453-457. JIAO Y, CHEN W J. Near-field calibration of active phased array antenna[J]. Telecommunication Engineering, 2016, 56(4): 453-457. DOI:10.3969/j.issn.1001-893x.2016.04.018 (in Chinese) |
| [15] | 尚军平.相控阵天线快速测量与校准技术研究[D].西安: 西安电子科技大学, 2010. SHANG J P. Study of fast measurement and calibration techniques for phased array antennas[D].Xi'an: Xidian University, 2010(in Chinese). http://cdmd.cnki.com.cn/article/cdmd-10701-2010128511.htm |
