当前众多稳频技术都是将激光频率稳定在原子共振线附近,例如,饱和吸收稳频技术[1]、塞曼效应稳频技术(DAVLL)[2-3]、萨格纳克(Sagnac)干涉稳频技术[4]和偏振光谱稳频技术[5-6]等。然而原子磁强计及激光冷却技术需要将激光频率稳定在远离原子跃迁频率几兆赫兹的大失谐处[7-9],上述几种稳频技术难以满足如此大的失谐要求。
通常采用的方法是通过波长计反馈以及温度闭环控制将激光频率稳定在远离原子共振线的大失谐处,这类方法简便易行。但是使用这类方法得到的激光频率的稳定性较低,频率漂移达到几十兆赫兹每小时,而且对波长计的性能要求高,所用的波长计昂贵。文献[10]提出了使用碱金属气室的法拉第旋光光谱作为频率参考的稳频方法,这种稳频技术利用碱金属气室的法拉第效应产生的法拉第光谱,能够将激光频率稳定在远离原子共振线几兆赫兹甚至十几兆赫兹处,并具有较高的频率稳定性,可以满足原子磁强计对激光频率的要求[10]。文献[11]对上述法拉第旋光光谱稳频方法进行改进,将碱金属气室温度稳定在±0.1 K范围内,并对比了反射光路与透射光路的法拉第旋光光谱,初步验证了使用多光程碱金属气室有助于提高稳频点的失谐[11]。然而法拉第旋光光谱稳频也有其不足,这种稳频方法需调节碱金属气室的温度来改变稳频点,所需稳频点对应的温度需要经过复杂的计算求得,温度需要几十分钟才能逐渐达到稳定,并且存在迟滞较大,重复性较差的问题,实现稳频点的快速精确调节较为困难。
本文在法拉第旋光光谱稳频基础上进行改进,提出了一种可快速精确调节稳频点的远共振线激光稳频方法,不仅弥补了利用温度调节控制稳频频率的速度慢的问题,还可以实现稳频点频率的精确调节。建立了法拉第旋光光谱的理论模型并给出光谱稳频点的计算公式,结合声光调制器(AOM)设计改进了法拉第旋光光谱稳频实验方案,并详细分析了温度对稳频方法的影响。分析改进后的稳频方法具有可以在大失谐处稳频、稳频点可快速精确调节等特点。
1 理论模型 法拉第效应属于一种色散现象。当施加轴向磁场时,碱金属原子蒸气中线偏振检测光的偏振面旋转角是随着光频率变化的。在磁场作用下塞曼效应使原子能级结构分裂,导致原子对于线偏振光不同旋向的圆偏振分量的折射率不同,产生圆双折射现象。圆双折射现象是产生法拉第效应的主要因素。在远离原子共振线的大失谐的条件下,色散现象占据着主导,而吸收现象并不明显,通过差分平衡探测的方式,可以检测到大失谐处的法拉第旋光光谱[12-13]。
介质的吸收和色散性质可以用电极化率来描述,χ=χr+iχi,χr+和χi分别为电极化率的实部和虚部。在多普勒展宽的碱金属原子蒸汽中,跃迁j对应的χ为[14]
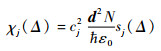 | (1) |
式中:cj2为跃迁强度;d为约化偶极矩阵元;?为普朗克常量h除以2π;ε0为真空介电系数;N为原子数密度;Δ为频率失谐;sj(Δ)为共振线型,是洛伦兹线型和高斯线型的卷积。
介质的吸收系数用来描述吸收的性质:α(Δ)=kχi(Δ),k为波数。折射率系数η(Δ)=
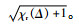
当沿着传播方向施加磁场B时,产生法拉第效应,使得σ+和σ-跃迁的谐振频率因塞曼效应产生相反的频移。因此,与左右旋光相关联的折射率η+和η-也产生相反的偏移。由此,通过碱金属原子蒸汽后的偏振方向旋转角为
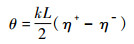 | (2) |
式中:L为光学路径长度。
当激光频率失谐很大时,原子共振线型的实部可以近似为
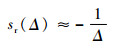 | (3) |
结合式(1)得到在大失谐处碱金属原子蒸汽的电极化率实部可以近似为
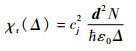 | (4) |
由于实际中碱金属原子密度很低,χr远小于1,假定塞曼频移导致左右旋光向相反方向失谐b,单位为Hz,结合式(2)、式(4)得到远共振线大失谐处的法拉第效应旋角为
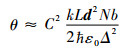 | (5) |
在法拉第旋光光谱稳频实验中,需要得到差分后光谱强度为零点处(稳频点)的失谐,此时对应θ=nπ/2,n为正整数。由此计算出稳频点的失谐为
 | (6) |
式中:A为稳频失谐方程中的常数,可以通过拟合得到。对于铯(Cs)原子,N计算式为[15]
 | (7) |
式中:T为开尔文温度。
2 实验设计 图 1为基于Cs原子D2线的远共振线激光稳频实验结构,图中,λ/2为二分之一波片;λ/4为四分之一波片;PBS为偏振分光棱镜。实验中使用外腔半导体激光器产生波长在852 nm附近的线偏振光,使产生的线偏振光通过二分之一波片经过反射镜射入PBS。PBS透射的p光可以通过光纤导入高精密波长计(测量精度为0.001 pm)中来监视激光波长/频率。本文结合AOM对激光频率进行控制和移动,但是当入射激光频率发生变化时,布拉格衍射的一级衍射光的衍射方向也发生变化,因为衍射角是调制频率的函数,在本实验中,如果一级衍射光衍射角变化将带来后续光路难以调控,实验精度受到影响等问题。本文使用双通(double-pass)声光调制系统来有效补偿一级衍射光的传播方向的偏移[16]。经过PBS反射的s光射入双通声光调制系统,双通声光调制系统由AOM、四分之一波片、平凸镜以及反射镜构成。线偏振光通过AOM后经过四分之一波片变为圆偏振光,后面的平凸镜和反射镜组成猫眼系统,未产生频移的零级光被吸收池吸收,一级光经过猫眼系统沿入射方向返回,经过四分之一波片后变为线偏振光,偏振方向与原偏振方向的夹角为90°,因此从AOM返回的一级衍射光可以完全透过PBS,传播方向不受激光频率变化影响,这样光的衍射效应产生的方向偏移被有效消除。从PBS出射的一级光继续穿过充有一滴碱金属Cs的圆柱形气室(长50 mm,直径25 mm),Cs气室被放置于一个与之等长的0.1 T的自制圆筒形钐钴磁铁中。磁铁和Cs气室被共同放置到恒温箱中以产生较高的碱金属原子密度,实验温度不宜过高,因为钐钴磁铁在超过200℃的情况下会失去磁性。由于一级光是激光器出射光经过双通声光调制系统得到,与原出射光具有恒定的频率差(等于2倍的AOM驱动频率f),因此,使用平衡光电探测器得到的法拉第旋光光谱将会产生2f的频移。将频移后的法拉第旋光光谱信号输入伺服控制器作为误差信号,伺服控制器的控制输出端与外腔半导体激光器控制器的频率调制端相连接,实现激光频率的闭环控制。如果使用频移后的法拉第旋光光谱的稳频点进行稳频,稳频点对应一级光的频率为f1,则实际稳频后激光器出射光频率为f0=f1-2f。实验中通过改变AOM的驱动射频频率既可以改变频移量2f,改变AOM的驱动射频频率后需要微调AOM改变声波波面与入射光的夹角以重新满足新的布拉格角θB。因此,通过调节AOM的驱动射频频率和AOM的声波波面与入射光的夹角即可实现对稳频点的频率调节,并且双通声光调制系统的使用使频率调节范围加倍,提高了系统对激光频率的调节和控制能力,这种调节稳频点的方法相对于调节温度具有快速精确可靠的特点。
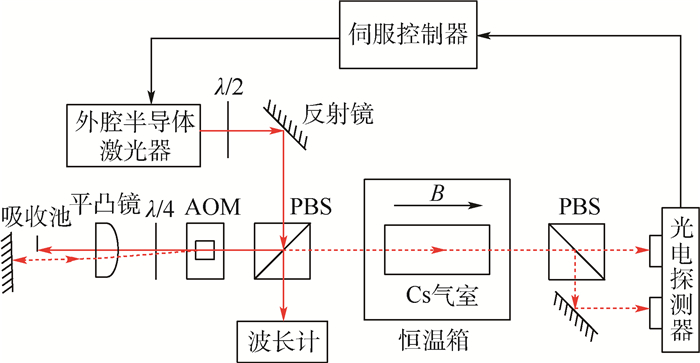 |
| 图 1 实验结构 Fig. 1 Experimental setup |
| 图选项 |
3 实验结果及分析 图 2为Cs碱金属气室温度130℃,AOM驱动射频频率为65 MHz,大失谐条件下的法拉第旋光光谱。其中蓝色光谱和红色光谱分别对应未产生频移的零级光法拉第旋光光谱及检测一级光得到的法拉第旋光光谱。为了科学有效地比较2个光谱,本文对得到的2个光谱信号进行了归一化同幅度处理。从图 2中可以观察到一级光对应的法拉第旋光光谱相对原光谱产生了红移。通过高精度波长计测量得到失谐为-6.2 GHz附近2个方形红蓝光谱稳频点(谱线过零点)的频率差近似为130 MHz(为AOM驱动射频频率的2倍),在失谐为-6.8 GHz附近的2个圆形红蓝光谱稳频点的频率差也近似为130 MHz。本实验使用的AOM的中心频率为80 MHz,使用双通声光调制结构可以将频率调节范围增大至120 MHz。目前部分AOM产品已经能够实现几百兆赫兹到1 GHz的频移,如加以使用,可实现范围足够大的频率调节、得到更为理想的实验结果。
 |
| 图 2 大失谐下的法拉第旋光光谱 Fig. 2 Faraday rotation spectra under large detuning |
| 图选项 |
如图 3所示,实验中分别将激光稳频在图 2中失谐为-6.2 GHz附近的2个方形稳频点处。使用零级光光谱和一极光光谱稳频获得的频率漂移均为3.3 MHz/h左右,波动均方根值分别为0.56 MHz/h和0.6 MHz/h,也是非常相近,可以满足原子磁强计对激光频率稳定性的要求。图 3中,红色曲线为使用未产生频移的零级光法拉第光谱稳频后得到的,蓝色曲线为使用一级光法拉第光谱稳频后得到的,从图中可以观察出红蓝曲线两者之间的频率差约为130 MHz,为AOM驱动频率的2倍。图 4为使用一级光光谱稳频点进行稳频的频率漂移图,对应图 3中的红色曲线。
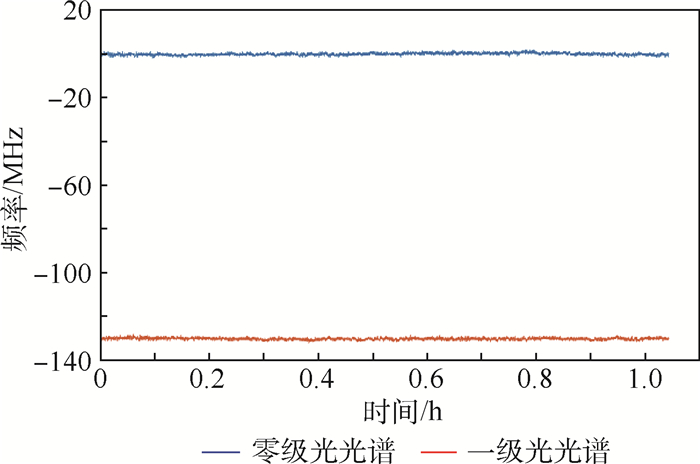 |
| 图 3 使用零级光光谱和一级光光谱分别进行稳频得到的频率漂移 Fig. 3 Frequency drift of laser stabilized by zero-order spectrum and first-order light spectrum |
| 图选项 |
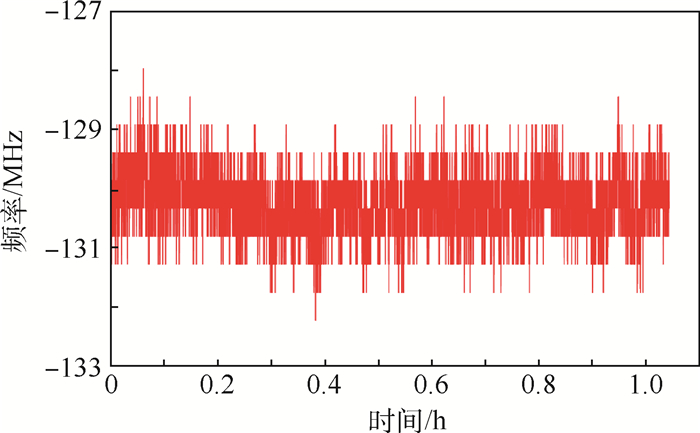 |
| 图 4 使用一级光光谱稳频点进行稳频的频率漂移 Fig. 4 Frequency drift of laser stabilized by first-order light spectrum frequency lock points |
| 图选项 |
本文还比较分析了在不同温度下Cs的法拉第旋光光谱。根据式(7)可知,随着温度升高,气室内部原子蒸汽密度增大,介质的折射率增大,导致在远离共振线的大失谐处法拉第旋光效应增强,使稳频点数目增加,失谐增大。图 5为不同温度下使用示波器记录的大失谐下的法拉第旋光光谱,可见温度对光谱稳频点的影响非常显著,随着气室温度升高,稳频点的数量逐渐增多、变得更加密集。温度对法拉第的光谱稳频点具有较大的影响,因此提高碱金属气室稳定的稳定性对保证较高的激光频率稳定性至关重要,实验中通过提高恒温箱气密性、优化温度控制器的PID参数、使用更高灵敏度的Pt1000温度传感器,有效地将碱金属气室的温度波动从±0.2 K改善到±0.02 K,激光稳频的精度也随之得到提高。
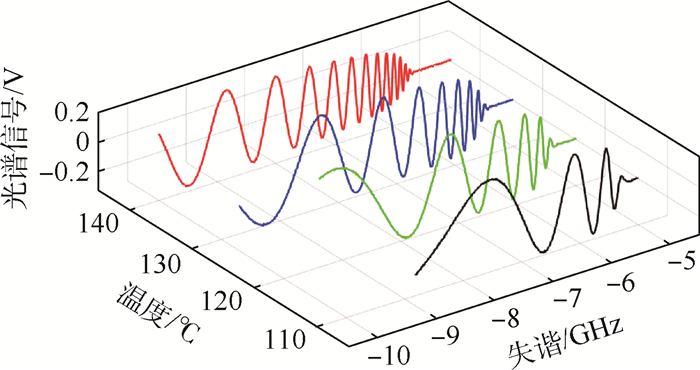 |
| 图 5 不同温度下Cs的法拉第旋光光谱 Fig. 5 Faraday rotation spectra of Cs at different temperatures |
| 图选项 |
通过分析处理不同温度下稳频点频率变化规律可以对实现某频率稳频点需要的实验温度进行预估。图 6为式(6)中n=1的第一级稳频点失谐大小随温度的变化,红色圆圈标记为实验测得的第一级稳频点失谐大小,蓝色曲线由式(6)对实验数据拟合得到,拟合得到的参数A=-1.565×10-6,拟合曲线与实验数据基本吻合,因此可以使用拟合的参数A估算稳频点的失谐。但使用式(6)估算的失谐与实验测得失谐的误差在100 MHz左右甚至更大,因而通过预估并调节温度很难将稳频点精确调节到实验所需的稳频点。
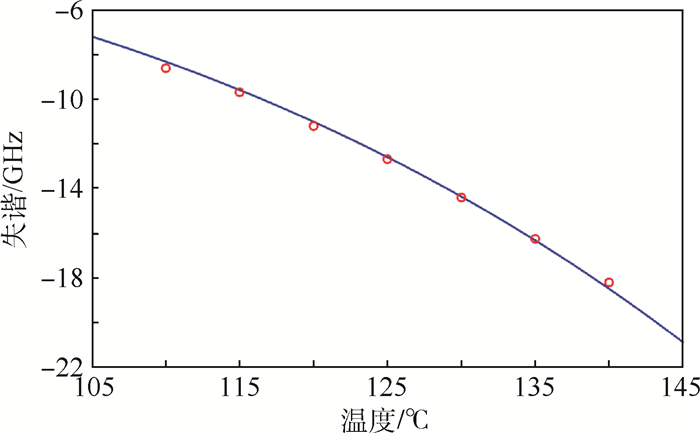 |
| 图 6 第一级稳频点失谐大小随温度的变化(n=1) Fig. 6 Inflence of temperature on frequency drift of the first-order lock point of Faraday signal (n=1) |
| 图选项 |
由以上实验结果可知,温度调节稳频点方法具有稳频点失谐调节范围大,可有效增加稳频点数目的特点。然而温度稳定需要的时间较长并难以实现精确调节,只能用来预估粗调。AOM调节稳频点虽然调节范围小,但可以快速精确调节。本文采用二者相结合的方案,用温度调节法预先估计所需要的大致温度,将碱金属气室温度调节到目标范围,再使用AOM将光谱上某一稳频点精确频移到所需要的激光频率上。
4 结论 本文介绍了一种快速精确调节稳频点的远共振线激光稳频方法。
1) 本文方法在法拉第旋光光谱稳频的方法上引入AOM,通过控制AOM的驱动射频频率来调节法拉第光谱稳频点对应的频率,相对于改变温度调节稳频点频率的方法具有快速且精确的特点。
2) 使用本文方法进行Cs的远共振线大失谐稳频,在气室温度130℃条件下,频率失谐-6.2 GHz附近使稳频点精确频移130 MHz,并实现频率漂移3.3 MHz/h、波动均方根值0.6 MHz/h的激光频率稳定度,很好地满足了原子磁强计对稳频精度的要求。
3) 观察分析了温度对本文方法稳频点个数及失谐大小的影响,优化了碱金属气室的温度控制精度,计算了式(6)中的物理参数A,这有助于在今后的实验中估算稳频点的失谐大小。
4) 将温度粗调和AOM精确调节相结合的方法进行应用,以更好地实现在远共振线大失谐处对激光频率的稳定和控制。
参考文献
| [1] | DEMTR?DER W. Laser spectroscopy:Basic concepts and instrumentation[M].1st edBerlin: Springer, 1996: 453-462. |
| [2] | SU D Q, MENG T F, JI Z H, et al. Application of sub-Doppler DAVLL to laser frequency stabilization in atomic cesium[J].Applied Optics, 2014, 53(30): 7011–7016.DOI:10.1364/AO.53.007011 |
| [3] | 江开军, 王谨, 李可, 等. 利用原子的塞曼光谱对半导体激光器进行稳频[J].光谱学与光谱分析, 2004, 24(6): 659–662. JIANG K J, WANG J, LI K, et al. Frequency stabilization of diode laser using Zeeman spectra[J].Spectroscopy and Spectral Analysis, 2004, 24(6): 659–662.DOI:10.3321/j.issn:1000-0593.2004.06.006(in Chinese) |
| [4] | GIMA T, KATO H, HONDA T, et al. Modulation-free frequency stabilization based on polarization-split Sagnac loop[J].IEEE Photonics Technology Letters, 2013, 25(11): 1031–1034.DOI:10.1109/LPT.2013.2259475 |
| [5] | SUN J F, YIN S Q, XU Z, et al. Optimization of polarization spectroscopy for rubidium D lines[J].Chinese Physics B, 2013, 22(2): 271–275. |
| [6] | TIWARI V B, SINGH S, MISHRA S R, et al. Laser frequency stabilization using Doppler-free bi-polarization spectroscopy[J].Optics Communications, 2006, 263(2): 249–255.DOI:10.1016/j.optcom.2006.01.028 |
| [7] | DANG H B, MALOOF A C, ROMALIS M V. Ultrahigh sensitivity magnetic field and magnetization measurements with an atomic magnetometer[J].Applied Physics Letters, 2010, 97(15): 151110.DOI:10.1063/1.3491215 |
| [8] | FANG J, WANG T, ZHANG H, et al. Optimizations of spin-exchange relaxation-free magnetometer based on potassium and rubidium hybrid optical pumping[J].Review of Scientific Instruments, 2014, 85(12): 123104.DOI:10.1063/1.4902567 |
| [9] | BARBOZA P M T, NASCIMENTO G G, ARAU'JO M O, et al. Stabilization of a laser on a large-detuned atomic-reference frequency by resonant interferometry[J].Journal of Physics B:Atomic, Molecular and Optical Physics, 2016, 49(8): 085401.DOI:10.1088/0953-4075/49/8/085401 |
| [10] | MARCHANT A L, H?NDEL S, WILES T P, et al. Off-resonance laser frequency stabilization using the Faraday effect[J].Optics Letters, 2011, 36(1): 64–66.DOI:10.1364/OL.36.000064 |
| [11] | QUAN W, LI Y, LI R, et al. Far off-resonance laser frequency stabilization using multipass cells in Faraday rotation spectroscopy[J].Applied Optics, 2016, 55(10): 2503–2507.DOI:10.1364/AO.55.002503 |
| [12] | KEMP S L, HUGHES I G, CORNISH S L. An analytical model of off-resonant Faraday rotation in hot alkali metal vapours[J].Journal of Physics B:Atomic, Molecular and Optical Physics, 2011, 44(23): 235004.DOI:10.1088/0953-4075/44/23/235004 |
| [13] | SIDDONS P, ADAMS C S, HUGHES I G. Off-resonance absorption and dispersion in vapours of hot alkali-metal atoms[J].Journal of Physics B:Atomic, Molecular and Optical Physics, 2009, 42(17): 175004.DOI:10.1088/0953-4075/42/17/175004 |
| [14] | SIDDONS P, ADAMS C S, GE C, et al. Absolute absorption on rubidium D lines:Comparison between theory and experiment[J].Journal of Physics B:Atomic, Molecular and Optical Physics, 2008, 41(15): 155004.DOI:10.1088/0953-4075/41/15/155004 |
| [15] | ALCOCK C B, ITKIN V P, HORRIGAN M K. Vapour pressure equations for the metallic elements:298-2500 K[J].Canadian Metallurgical Quarterly, 1984, 23(3): 309–313.DOI:10.1179/cmq.1984.23.3.309 |
| [16] | DONLEY E A, HEAVNER T P, LEVI F, et al. Double-pass acousto-optic modulator system[J].Review of Scientific Instruments, 2005, 76(6): 063112.DOI:10.1063/1.1930095 |
