针对IMU的随机噪声抑制,主要有3类方法:①基于数据时域建模的随机噪声抑制[7-8],该方法具有精度高的优势,但只能应用于平稳随机过程,并不适用于存在弱非平稳特性的激光陀螺IMU数据。②基于数据频域特征的随机噪声抑制[9-10],该方法主要依据噪声分布所在的频段,采用低通、带通滤波器对数据进行处理,但对于频带分布宽且交叠严重的激光陀螺IMU的随机噪声抑制效果有限。③基于前向线性预测(Forward Linear Prediction,FLP)、小波降噪等技术的随机噪声抑制[11-14],其中小波降噪效果严重依赖于小波基、分解层数和阈值估算方法的选择,缺乏自适应能力,而FLP滤波比小波变换滤波更有效地降低高频噪声,且在短时间陀螺数据的实时滤波中,比IIR数字滤波器表现得更为优越。
基于以上方法的优缺点,本文将激光陀螺IMU输出数据的滤波降噪与系统标定相结合,利用自适应FLP滤波对激光陀螺IMU的标定数据进行降噪处理,从而得到信噪比更高的标定数据,进一步利用降噪后的标定数据得到更高精度的标定参数。首先,通过开展激光陀螺IMU四方位正反速率标定试验,获得标定试验原始输出数据;其次,利用自适应FLP滤波器,对IMU的输出数据进行噪声抑制;最后,利用滤波后的数据计算得到激光陀螺IMU的标定参数。本文方法能够对激光陀螺IMU的随机噪声进行有效抑制,提高数据的信噪比,从而在标定数据量较小的情况下得到更高精度的标定参数。通过2套不同的激光陀螺IMU的标定与跑车试验对本文方法的有效性进行了验证。
1 激光陀螺IMU的随机噪声分析 激光陀螺IMU主要由3个高精度机抖激光陀螺仪、3个石英加速度计、机械结构、隔振系统和配套电路系统等部分组成。其中,3支陀螺仪和3个加速度计分别相互正交安装在惯性传感器集合的机械结构上,组成了x、y、z 3个轴向的测量通道。
为了消除闭锁效应,激光陀螺必须始终工作在高频抖动状态,这使得陀螺本身成为振动干扰源,IMU的测量输出数据中也叠加了振动噪声。除此之外,系统还存在着量化噪声和随机游走噪声等[15-16]。这些噪声一般由传感器敏感机理、自身构造特点以及生产工艺等因素引起,变化频率高,频带较宽,难以依据误差机理进行建模与补偿,共同组成系统的随机噪声,大大降低了输出信号的信噪比,影响了系统的标定与测量。
基于以上分析,结合激光陀螺IMU的工作原理和特点,可以得到激光陀螺IMU测量的数学模型。3个角速率测量通道可以表示为
 | (1) |
式中:Gi为激光陀螺i敏感轴的输出;Gbi和Si分别为激光陀螺i敏感轴的零偏值和标度因数;ωi为激光陀螺i敏感轴的输入角速率;Eij为激光陀螺j敏感轴的输入角速率对激光陀螺i敏感轴的输出的影响,是由激光陀螺3个敏感轴的非正交安装误差决定的;δGi为叠加在激光陀螺i敏感轴输出数据的各种随机噪声;i=x, y, z,j=x, y, z。
3个加速度测量通道可以表示为
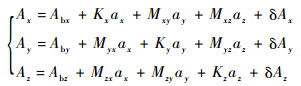 | (2) |
式中:Ai为加速度计i敏感轴的输出;Abi和Ki分别为加速度计i敏感轴的零偏值和标度因数;ai为加速度计i敏感轴的输入比力;Mij为加速度计j敏感轴的输入比力对加速度计i敏感轴的输出的影响,是由加速度计3个敏感轴的非正交安装误差决定的;δAi为叠加在加速度计i敏感轴输出数据的各种随机噪声;i=x, y, z,j=x, y, z。
现有的标定方法通过延长测量时间、增加测量数据量来消除随机误差的影响,这样无疑增加了工作量,降低了标定效率。因此,通过滤波的方法有效抑制随机噪声,不仅能够提高标定效率,而且能够充分有效利用标定数据从而提高标定精度。
2 自适应前向线性预测滤波 FLP滤波是一种有效抑制随机噪声的数据处理方法[13-14],其利用之前多个时刻的原始数据乘以对应的权重值来预测当前时刻的数据,作为滤波器的输出。考虑随机噪声信号数据前后具有弱相关性的特点,当其叠加在有用信号中通过滤波器后,噪声将被有效抑制,从而实现降噪。
N阶FLP滤波器的输出为
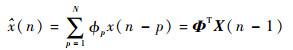 | (3) |
式中:
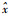
设计权重系数的过程为最优化的过程,本文采用均方误差(Mean Square Error,MSE)意义下的损失函数:
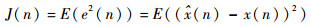 | (4) |
即最优权重值满足滤波输出数据与原始采样数据的均方误差为最小。可以证明,式(4)表示了一个超平面,在全局意义下存在最小值min J(n),对应的Φ=Φ0为最优权重值。通常采用最小均值方差(Least Mean Square, LMS)技术通过逐步迭代的方式确定Φ0。依据LMS准则,权重向量的递推估计公式为
 | (5) |
式中:ε(n)为迭代补偿控制函数。
基于LMS的FLP结构如图 1所示。
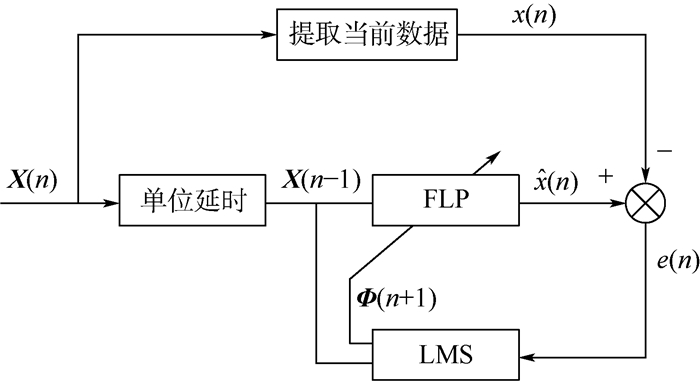 |
| 图 1 基于LMS的FLP结构 Fig. 1 FLP structure based on LMS |
| 图选项 |
控制函数ε(n)的选取直接影响了自适应LMS算法的跟踪能力和稳定精度,通常采用的固定步长的LMS算法无法实现跟踪能力和稳态精度同时达到最优。因此,本文采用一种基于误差信号e(n)与输入信号X(n)之间互相关系数估计值的变步长自适应滤波方法,依据估计值的大小实时调整函数ε(n),公式如下:
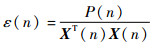 | (6) |
式中:P(n)为互相关系数的估计值。
由此,可将补偿递推公式重写为
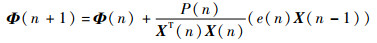 | (7) |
3 基于四方位正反速率的IMU标定 IMU的标定就是通过试验的方法确定式(1)和式(2)所示数学模型的标定参数,即12个角速率输出模型的参数和12个加速度输出模型的参数。要得到所有的标定参数,角速度和加速度通道都至少需要12个独立的误差方程。四方位正反速率标定法是一种实用的标定方法,需要单轴转台以及正六面体的工装来完成所有的标定操作,标定过程不需要转台指北,这一方法在实际的惯导系统标定中应用广泛。其标定的过程如图 2所示。
 |
| 图 2 四方位正反速率标定过程示意图 Fig. 2 Schematic diagram of four-position rotation calibration procedure |
| 图选项 |
坐标系OT-xTyTzT为转台坐标系,OT为坐标原点,平面OTxTyT保持水平,zT轴与当地地理坐标系的zn轴方向一致。在标定过程中,激光陀螺IMU通过4次翻转分别使得IMU的x、-x、y、z轴的指向与zT轴指向一致。对应每个位置处,转台以固定旋转角速率Ω顺时针和逆时针转动,转过的角度为2πn rad,n为旋转的周数,且n≥2。当IMU的z轴指向上时(见图 2(d)),则3个陀螺仪敏感到的角速率输入为
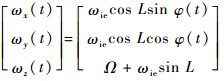 | (8) |
式中:ωie为地球自转角速率;L为当地纬度;Ω为转台的输入角速率;φ(t)为激光陀螺IMU的航向。
3个加速度计敏感到的加速度输入为
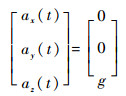 | (9) |
式中:g为重力加速度值。
在转台转过n周的过程中,IMU中3个陀螺仪敏感到的平均角速度可以表示为
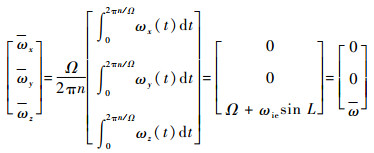 | (10) |
3个加速度计敏感到的平均加速度可以表示为
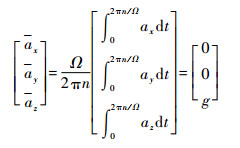 | (11) |
由此,标定过程结合激光陀螺IMU的标定数学模型,可以得到角速度和加速度的方程如下所示:
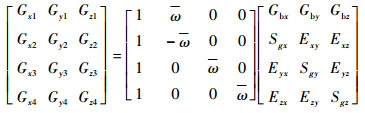 | (12) |
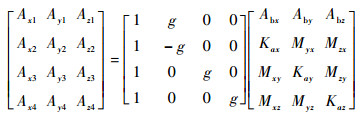 | (13) |
式中:Gim为激光陀螺i敏感轴在第m个方位的输出值; Sgi为激光陀螺i敏感轴标度因数;Aim为加速度计i敏感轴在第m个方位的输出值;Kai为加速度计i敏感轴标度因数;i=x, y, z,m=1, 2, 3, 4。
由式(12)和式(13)可以求解得到激光陀螺IMU的所有标定参数:
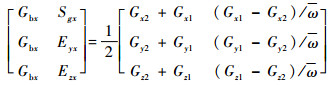 | (14) |
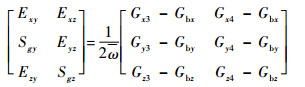 | (15) |
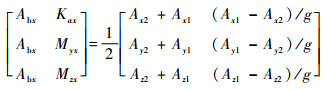 | (16) |
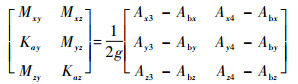 | (17) |
本文先通过3.2节中所述的标定过程获取IMU输出的原始数据,再通过自适应FLP滤波器对原始数据中的随机噪声进行抑制,从而获取随机噪声小、信噪比高的试验数据,在此基础上通过式(14)~式(17)计算得到较高精度标定参数。
4 试验验证 4.1 标定系统及试验过程 为了验证本文所提方法的有效性,针对实验室现有的2套激光陀螺IMU开展常温标定试验,试验设备包含2套高精度激光陀螺IMU、1套POS处理计算机系统(POS Computer System, PCS)、1套工装、1台带温箱的单轴转台以及数据处理计算机。其中,2套激光陀螺IMU的编号分别为TX-R610-01和TX-R610-02。按照3.2节中的四方位动静结合标定方法开展标定试验,激光陀螺IMU的测量频率为200 Hz,试验过程中,转台转速为Ω=±10 (°)/s,旋转周数为n=2。激光陀螺IMU试验系统如图 3所示。
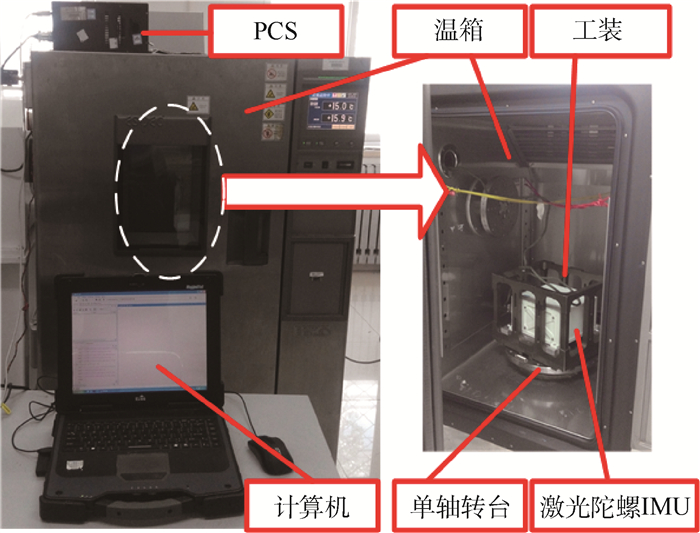 |
| 图 3 激光陀螺IMU标定试验系统 Fig. 3 Experiment system of ring laser gyro IMU calibration |
| 图选项 |
4.2 噪声抑制及标定参数求解 采集试验过程中激光陀螺和加速度计的原始数据,采用自适应FLP滤波器对数据进行降噪,FLP滤波器的阶数设为100,以x轴向上时x轴激光陀螺和加速度计的输出为例,给出降噪前后的标定数据对比情况,如图 4所示。
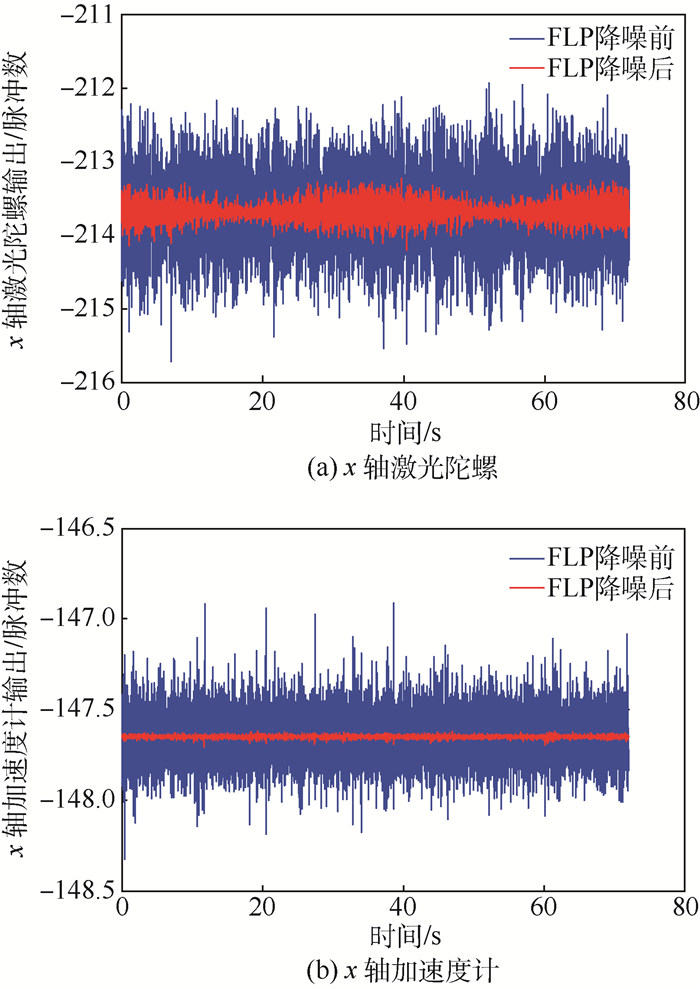 |
| 图 4 降噪前后激光陀螺和加速度计输出数据对比 Fig. 4 Comparison of ring laser gyro and accelerator output data before and after de-noising |
| 图选项 |
分析图 4中所示滤波结果可知,自适应FLP算法能够明显降低随机噪声的幅值,减小随机噪声对信号的影响,从而提高数据的信噪比。为了进一步定量分析自适应FLP算法的降噪效果,分别对原始数据和降噪后的数据进行功率谱分析,结果如图 5所示。可以看出,100阶的自适应FLP滤波能够有效抑制约20 Hz以上的激光陀螺随机噪声以及30 Hz以上的加速度计随机噪声。
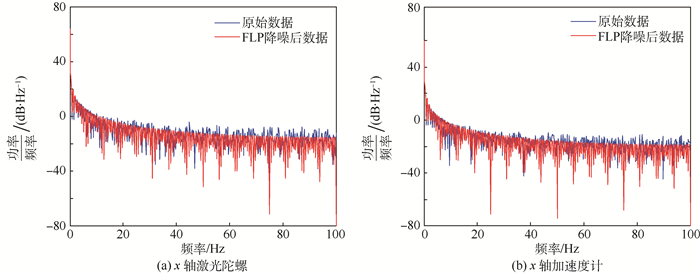 |
| 图 5 降噪前后激光陀螺和加速度计输出数据功率谱分析 Fig. 5 Power spectrum analysis of ring laser gyro and accelerator output data before and after de-noising |
| 图选项 |
利用降噪后的数据,按照式(14)~式(17)计算得到系统的标定参数,以TX-R610-01为例,给出系统降噪前后标定参数对比情况,如表 1和表 2所示。
表 1 激光陀螺IMU降噪前标定结果 Table 1 Calibration results of ring laser gyro IMU with original calibration data
| 参数类型 | FLP降噪前结果 |
| Gbx, Gby, Gbz/((°)·h-1) | -0.024 2, -0.234 0, 0.059 0 |
| Sgx, Sgy, Sgz/(″/^) | -0.842 6, 0.842 7, -0.842 8 |
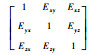 | 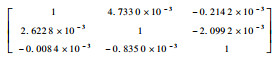 |
| Abx, Aby, Abz/(10-4g) | 1.399 7, 9.909 8, 22.828 9 |
| Kax, Kay, Kaz/(10-5g·s/^) | -3.386 7, 3.234 7, -3.389 6 |
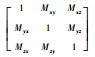 | 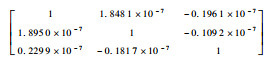 |
| 注:(″/^)为角秒每脉冲; (s/^)为秒每脉冲。 | |
表选项
表 2 激光陀螺IMU降噪后标定结果 Table 2 Calibration results of ring laser gyro IMU with de-noised calibration data
| 参数类型 | FLP降噪后结果 |
| Gbx, Gby, Gbz/(°)·h-1) | -0.021 1, -0.234 5, 0.077 8 |
| Sgx, Sgy, Sgz/(″/^) | -0.842 6, 0.842 7, -0.842 8 |
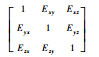 | 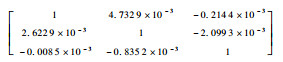 |
| Abx, Aby, Abz/(10-4g) | 1.387 2, 9.909 0, 22.849 1 |
| Kax, Kay, Kaz/(10-5g·s/^) | -3.386 7, 3.234 7, 3.389 7 |
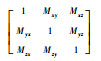 |  |
表选项
4.3 车载试验验证 为了充分验证本文方法得到的标定系数的准确性,对标定的2套激光陀螺IMU TX-R610-01和TX-R610-02进行跑车试验,分别考察两套系统的纯惯性精度,并与未降噪处理得到的标定参数的导航结果进行对比。跑车路线选为北京五环路,TX-R610-01和TX-R610-02安装在同一平台,在同一路线先后进行2次试验,试验的方法一致,跑车过程中以差分GPS的定位结果为位置基准,检验惯导系统的导航误差,车载试验系统如图 6所示。
 |
| 图 6 车载试验验证系统 Fig. 6 Vehicle experiment system for verification |
| 图选项 |
试验过程中,首先对系统通电30 min进行预热,然后行驶至起始点,重启开机后,保持5 min静止进行惯导系统的初始对准,然后保持平稳行驶1 h后停止,计算行驶过程中惯导系统的位置误差。2套系统的跑车结果如图 7和图 8所示。惯导系统1 h的导航定位误差如表 3所示。
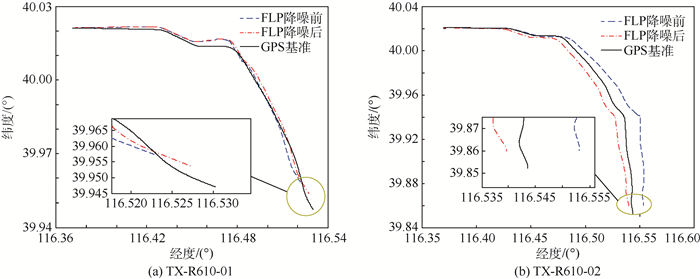 |
| 图 7 2套系统的跑车纯惯性导航定位曲线 Fig. 7 Inertial navigation positioning curves of two systems |
| 图选项 |
 |
| 图 8 2套系统的跑车纯惯性导航定位误差曲线 Fig. 8 Inertial positioning error curves of two systems |
| 图选项 |
表 3 1 h车载试验导航定位误差 Table 3 1 h positioning error of vehicle experiment
| nmile | ||
| 系统编号 | 导航定位误差 | |
| FLP降噪前 | FLP降噪后 | |
| TX-R610-01 | 0.871 256 | 0.595 590 |
| TX-R610-02 | 0.652 650 | 0.500 372 |
表选项
分析结果可知,与未经降噪处理得到的标定参数相比,利用自适应FLP降噪后得到的标定参数能够减小导航误差,从而提升导航精度,以此证明了本文方法的有效性。
5 结论 1) 机抖噪声、量化噪声以及随机游走噪声等降低了激光陀螺IMU数据信噪比,影响系统标定精度。
2) 利用自适应FLP滤波器能够有效对激光陀螺IMU测量数据进行抑制,获取随机噪声小、信噪比高的试验数据,进而减小标定工作量。
3) 利用自适应FLP对标定数据进行噪声抑制,能够在有限标定数据量情况下获得更高精度的标定参数。
参考文献
| [1] | 王琛琛, 王新龙. 机抖激光陀螺误差输出特性的分析[J].北京航空航天大学学报, 2013, 39(4): 521–524. WANG C C, WANG X L. Analysis of error output characteristics of DRLG[J].Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(4): 521–524.(in Chinese) |
| [2] | LI J, FANG J, GE S S. Kinetics and design of a mechanically dithered ring laser gyroscope position and orientation system[J].IEEE Transactions on Instrumentation & Measurement, 2013, 62(1): 210–220. |
| [3] | FANG J, CHEN L, YAO J. An accurate gravity compensation method for high-precision airborne POS[J].IEEE Transactions on Geoscience & Remote Sensing, 2014, 52(8): 4564–4573. |
| [4] | 程骏超, 房建成, 吴伟仁, 等. 一种激光陀螺惯性测量单元混合标定方法[J].中国惯性技术学报, 2014, 22(4): 445–452. CHENG J C, FANG J C, WU W R, et al. Integrated calibration method for RLG IMU[J].Journal of Chinese Inertial Technology, 2014, 22(4): 445–452.(in Chinese) |
| [5] | LI J, JIAO F, FANG J, et al. Integrated calibration method for dithered RLG POS using a hybrid analytic/Kalman filter approach[J].IEEE Transactions on Instrumentation & Measurement, 2013, 62(12): 3333–3342. |
| [6] | 李建利, 房建成, 马艳海, 等. INS全温六方位速率标定及分段线性插值补偿[J].北京航空航天大学学报, 2012, 38(10): 1331–1335. LI J L, FANG J C, MA Y H, et al. Six-position rotation rate calibration and piecewise linear interpolation compensation for INS in full temperatures[J].Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(10): 1331–1335.(in Chinese) |
| [7] | SANG M S, LEE J G, CHAN G P. Equivalent ARMA model representation for RLG random errors[J].IEEE Transactions on Aerospace & Electronic Systems, 2000, 36(1): 286–290. |
| [8] | HAN S, WANG J. Quantization and colored noises error modeling for inertial sensors for GPS/INS integration[J].IEEE Sensors Journal, 2011, 11(6): 1493–1503.DOI:10.1109/JSEN.2010.2093878 |
| [9] | 钟麦英, 闫东坤. 激光陀螺POS惯性数据滤波及时延补偿[J].中国惯性技术学报, 2011, 19(6): 670–675. ZHONG M Y, YAN D K. Predictive filtering and delay compensation of RLG position and orientation system[J].Journal of Chinese Inertial Technology, 2011, 19(6): 670–675.(in Chinese) |
| [10] | 李建利, 陈安升, 钟麦英, 等. 基于线性相位无限长单位冲击响应滤波器的机抖激光陀螺POS低时延降噪方法[J].中国惯性技术学报, 2012, 20(6): 644–649. LI J L, CHEN A S, ZHONG M Y, et al. Low time delay de-noising method for mechanically dithered RLG POS based on linear phase infinite impulse response filter[J].Journal of Chinese Inertial Technology, 2012, 20(6): 644–649.(in Chinese) |
| [11] | 高伟, 祖悦, 王伟, 等. 基于二代小波的光纤陀螺实时降噪方法研究[J].仪器仪表学报, 2012, 33(4): 774–780. GAO W, ZU Y, WANG W, et al. Research on real-time de-noising of FOG based on second generation wavelet transform[J].Chinese Journal of Scientific Instrument, 2012, 33(4): 774–780.(in Chinese) |
| [12] | 张通, 张骏, 张怡. 基于改进小波阈值的激光陀螺漂移信号降噪[J].仪器仪表学报, 2011, 32(2): 258–263. ZHANG T, ZHANG J, ZHANG Y. Ring laser gyro drift signal denoising based on improved wavelet threshold[J].Chinese Journal of Scientific Instrument, 2011, 32(2): 258–263.(in Chinese) |
| [13] | 陈熙源, 许常燕. 基于前向线性预测算法的光纤陀螺零漂的神经网络建模[J].中国惯性技术学报, 2007, 15(3): 334–337. CHEN X Y, XU C Y. Neural network modeling for FOG zero point drift based on forward linear prediction algorithm[J].Journal of Chinese Inertial Technology, 2007, 15(3): 334–337.(in Chinese) |
| [14] | 易康, 李廷志, 吴文启. FLP滤波算法在光纤陀螺信号预处理中的应用[J].中国惯性技术学报, 2005, 13(5): 58–62. YI K, LI T Z, WU W Q. Application of forward linear prediction filter in signal process of FOG[J].Journal of Chinese Inertial Technology, 2005, 13(5): 58–62.(in Chinese) |
| [15] | NG L C, PINES D J. Characterization of ring laser gyro perfor-mance using the Allan variance method[J].Journal of Guidance Control & Dynamics, 2012, 20(1): 211–214. |
| [16] | SAVAGE P G. Analytical modeling of sensor quantization in strapdown inertial navigation error equations[J].Journal of Guidance Control & Dynamics, 2012, 25(5): 833–842. |
