为解决转子转动与平动耦合,实现同时具备控制与敏感功能的陀螺仪,笔者课题组[12]设计研发了一种磁悬浮控制敏感陀螺(Magnetically Suspended Control Sensitive Gyroscope,MSCSG),这是一种新型陀螺,不仅继承了磁悬浮陀螺无接触、无摩擦、寿命长的优点,而且还通过双球形包络面转子结构的设计,从结构上消除了转子偏转与平动的耦合[13-14],为高精度二自由度姿态角速度敏感提供了结构基础。
然而,MSCSG的姿态角速度敏感依然存在着较多的误差源,转子磁极包络面非球形误差、转子质量不平衡、转子的偏中位移、定子磁极的加工装配误差都会引起陀螺定转子磁极间的变化,影响电磁合力产生的合力矩,进而产生漂移角速度误差[15]。通过对MSCSG机械结构与姿态角速度敏感原理的深入了解,发现除了文献[15]中提到的误差源外,力矩器非圆性同样会引起陀螺定转子磁极间的变化,造成干扰力矩,对姿态角速度敏感产生影响。本文力矩器即MSCSG中的洛伦兹力磁轴承(Lorentz Force Magnetic Bearing,LFMB)[16],为转子提供径向偏转力矩,可实现转子径向二自由度偏转。
为解决力矩器非圆性会造成姿态角速度敏感误差这一问题,进一步提高航天器姿态角速度敏感与控制精度,更好地完成各项航天任务,本文采用一种基于勒让德多项式级数的非圆性误差补偿方法,对力矩器非圆性误差进行补偿,进而补偿了MSCSG对陀螺载体姿态角速度的敏感误差。
1 磁悬浮控制敏感陀螺结构 图 1为MSCSG结构示意图,主要结构包括陀螺转子、转子内置磁极、转子轴向磁轴承、径向磁轴承、力矩器、高速电机和陀螺房。陀螺转子径向与轴向表面均设计成球形包络面,且两包络面球心重合,使作用于其表面的力均指向转子包络面球心,避免了磁干扰力矩的产生。径向磁轴承为纯电磁结构,由4对磁极组成,每2对控制一条径向通道,径向x通道与y通道用隔磁环隔开,避免两通道磁路耦合。轴向磁轴承由一对磁极构成,通过改变线圈电流控制转子受磁力的大小,实现z方向平动。LFMB由4个线圈固定于定子骨架上,成对串联使用,形成由2对磁极构成的力矩器。当对称的洛伦兹线圈中通入方向相反的激励电流时,便会产生方向相反大小相等的力作用于转子两侧,控制转子径向偏转。以上设计实现了径向x方向平动与y方向平动、x方向偏转与y方向偏转的解耦。高速电机用以实现转子绕自转轴高速旋转的功能,保证陀螺具有足够大的角动量。陀螺房为以上主要部件及其他部件提供支撑,并具有安全防护和密封等功能。
 |
| 图 1 MSCSG结构 Fig. 1 Structure of MSCSG |
| 图选项 |
为便于分析,定义如下坐标系:
r:转子坐标系Or-XrYrZr,与转子固连,但不与转子沿轴向高速旋转,原点Or为转子几何中心,Zr轴为转子自转轴。
b:定子坐标系Ob-XbYbZb,与陀螺房固连,原点Ob为轴向、径向磁轴承定子包络面几何中心,Zb轴为径向磁轴承中轴线,当转子位于平衡位置时,Ob-XbYbZb与Or-XrYrZr重合。
s:偏转轴承坐标系Os-XsYsZs,与LFMB定子固连,在初始零位置时,Os-XsYsZs与Ob-XbYbZb重合。
2 姿态角速度敏感原理 2.1 基本原理 根据欧拉动力学原理,陀螺载体姿态角速度矢量敏感方程可表示为
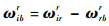 | (1) |
式中:ωrbr为陀螺转子相对于陀螺载体的姿态角速度;ωirr为陀螺转子相对惯性空间的姿态角速度;ωibr为陀螺载体相对于惯性空间非轴向的姿态角速度。
根据定点转动的欧拉动力学方程,磁悬浮转子动力学方程可表示为
 | (2) |
式中:Me为转子所受合外力矩;Hr为转子系下转子的角动量,可以表示为
 | (3) |
其中:Jr为转子径向转动惯量;Jz为转子极转动惯量;Ωi为转子的绝对角速度,由转子自转角速度Ω=[0?0?Ω′]T和牵连角速度ωirr组成,Ω′为转子绕z轴旋转的角速度,即
 | (4) |
设α、β分别为转子相对于x、y轴的角位移,
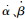
 | (5) |
式中:ωrbb为定子坐标系下陀螺载体相对于转子的姿态角速度;ωibb为定子坐标系下陀螺载体相对于惯性空间的姿态角速度;Cbr为定子坐标系向转子坐标系转换的转换矩阵。由于磁轴承间隙非常小,转子角位移α、β相对于载体转动可忽略不计,故
 | (6) |
代入式(5)可得
 | (7) |
根据式(4)可得
 | (8) |
将式(8)代入式(3)可得
 | (9) |
 | (10) |
根据式(5)、式(9)可得式(11),进而将式(10)、式(11)代入式(2)可得式(12):
 | (11) |
 | (12) |
由式(12)可见,转子所受的合外力矩中,既包含了由于陀螺载体转动所产生的陀螺耦合力矩,也包含了由于转子相对于定子坐标系偏转产生的陀螺耦合力矩,以及转子转动惯量不完全对称产生的陀螺耦合力矩,此外,合力矩中还包含了载体转动、转子偏转产生的惯性耦合力矩。
根据式(12),可得陀螺载体静止且转子转速恒定时磁悬浮转子所受合外力矩为
 | (13) |
从式(12)中减去Me (0),并假定陀螺载体沿z方向无转动,即可得载体转动时等效加在陀螺转子x、y方向上的力矩为
 | (14) |
当陀螺载体的姿态角加速度很小时,由于JzΩ′

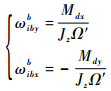 | (15) |
由上述分析可知,通过对Me和Me(0)的测量,即可得到陀螺载体转动时等效加载于陀螺转子上的力矩Md,进而可以根据式(15)间接得到陀螺载体在非转子轴向的姿态角速度。
由式(13)可知,Me(0)的值可以通过检测转子角位移获得,即
 | (16) |
式中:dx+、dx-分别为x轴方向正、负位置处位移传感器测得的转子在z方向的线性位移;dy+、dy-分别为y轴方向正、负位置处位移传感器测量值;ls为位移传感器安装位置至转子中心线距离。
理想情况下,MSCSG的结构决定了磁悬浮转子所受外力矩只可能来自力矩器,因此,Me即力矩器产生的偏转控制力矩。
2.2 姿态角速度模型 当位于磁场内长度为L的导线中通入与磁场方向垂直的电流i时,线圈将会受到洛伦兹力的作用,其方向由左手定则确定。洛伦兹力f可以表示为
 | (17) |
式中:B为导线所处磁场磁感应强度大小。
基于上述原理的MSCSG力矩器结构原理如图 2所示。力矩器的转子部分由周向永磁体组成,安装于陀螺转子边缘槽内随并随陀螺转子高速转动,LFMB定子与陀螺房固连。洛伦兹线圈安装于LFMB定子支撑盘上,来自控制系统的激励电流通过导电滑环进入洛伦兹线圈,4个线圈在定子坐标系中的圆周角分别表示为
 | (18) |
 |
| 图 2 MSCSG力矩器结构原理 Fig. 2 Structure principle of MSCSG torquer |
| 图选项 |
式中:?0为单个洛伦兹线圈所对应的半张角。
忽略转子的微小角位移,在洛伦兹线圈坐标系中,洛伦兹线圈微元Lrd?产生的力矩微元可表示为
 | (19) |
式中:r为洛仑兹力矩的力臂; Lr为力矩器半径; ?为洛伦兹线圈所对应的圆周角; n为洛伦兹线圈匝数; i(t)为洛伦兹线圈中实时测量的激励电流。按式(18)的圆周角范围对洛伦兹线圈上下两部分产生的力矩进行积分,可得悬浮转子在控制电流i=[ix+(t)??iy+(t)??ix-(t)??iy-(t)]作用下所受的偏转控制力矩大小为
 | (20) |
式中:ix+(t)和ix-(t)分别为x轴方向正负位置处洛伦兹线圈中的激励电流;iy+(t)和iy-(t)分别为y轴方向正负位置处洛伦兹线圈中的激励电流。如果相同方向上正负位置处洛伦兹线圈中通入的激励电流大小相等、方向相反,即ix+(t)=-ix-(t),iy+(t)=-iy-(t), 则式(20)可转化为
 | (21) |
将式(15)、式(16)、式(21)代入式(1)可得
 | (22) |
由式(22)可知,通过测量洛伦兹线圈中的激励电流和转子在z方向的线性位移,即可得到陀螺载体的姿态角速度,实现单个MSCSG对二自由度姿态角速度的敏感。
3 敏感误差模型 3.1 力矩器非圆性描述 在理想情况下,力矩器为理想圆柱环体,圆心到力矩器外表面半径恒定,LFMB安装支架的线圈匝数为常值,转子上线圈两侧永磁体产生的磁场强度分布均匀,单个洛伦兹线圈所对应的半张角不变,陀螺转子所受偏转力矩只与线圈激励电流有关。然而实际上,LFMB安装支架的机械加工精度、线圈缠绕方式以及陀螺房内温度变化都会影响力矩器的圆度,使得力矩器外半径随圆周角的不同发生不规则变化,这就带来了新的力矩器干扰力矩。由式(15)可知,力矩器干扰力矩将带来姿态角速度敏感误差。
如图 3所示,力矩器半径Lr由勒让德多项式级数描述如下:
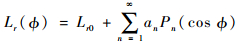 | (23) |
 |
| 图 3 MSCSG径向偏转力矩器实物图 Fig. 3 Photo of MSCSG radial deflection torquer |
| 图选项 |
式中:Lr0为理想圆柱外表面半径;an为描述包络面形状的谐波系数;Pn(cos ?)为勒让德多项式级数,可表示为
 | (24) |
力矩器的圆度参数可以用力矩器半径Lr的谐波系数an来表示,由式(23),利用MATLAB仿真得到由力矩器半径表示的力矩器外圆圆周表示如图 4所示,实线为理想圆形,虚线为受谐波影响的变形圆形。由图 4可知,一次谐波表示外圆径向平移变形;二次谐波表示外圆类椭圆变形;三次谐波表示类粽形变形;四次谐波表示类纺锤变形。力矩器半径Lr随圆周角变化,使力矩器对陀螺转子作用力产生干扰,形成方向、大小不一的干扰力矩,从而引起陀螺对陀螺载体姿态角敏感的漂移误差。
 |
| 图 4 勒让德多项式级数非圆性仿真 Fig. 4 Legendre polynomial series non-circular simulation |
| 图选项 |
3.2 姿态角速度敏感误差模型 陀螺力矩器半径误差模型为
 | (25) |
由于力矩器半径Lr随圆周角?变化,可看作关于?的函数,如式(23)所示。将式(23)代入式(19)可得非圆干扰力矩微元为
 | (26) |
式中:
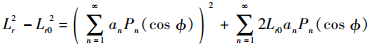 | (27) |
对式(26)按式(18)的圆周角范围对洛伦兹线圈上下两部分产生的力矩进行积分,可得偏转控制力矩误差模型为
 | (28) |
由式(15)、式(26)可得,陀螺载体姿态角速度敏感误差模型为
 | (29) |
式中:

4 力矩器非圆性误差补偿与仿真校验 4.1 实验测量与误差补偿 三坐标测量机由主体平台系统、测头、数据处理软件系统等组成,能够在6自由度空间范围内表现出被测物体的几何形状,是测量力矩器非圆性的理想仪器。
测量过程如下:首先,将力矩器固定于测量平台,在力矩器外圆圆周上任选3个点,通过测头测得3点坐标,进而确定力矩器外圆圆心坐标,重复以上操作,求取平均值得到较为精确的圆心坐标。在该圆心坐标基础上,测量力矩器外圆360°每一度的坐标,用以表示力矩器非圆性。实物测量实物图如图 5所示,通过三坐标测量机对力矩器实物进行圆度测量,并根据测量所得数据用MATLAB绘图如图 6所示。
 |
| 图 5 实验测量实物图 Fig. 5 Photo of experimental measurement |
| 图选项 |
 |
| 图 6 力矩器半径测量值随圆周角变化情况 Fig. 6 Change of measured value of torquer radius with inscribed angle |
| 图选项 |
由图 6可以看出,力矩器外圆半径随圆周角不规则变化,说明力矩器外圆并非理想圆,由姿态角速度敏感原理可知,不规则变化的力矩器外圆半径将产生偏转控制干扰力矩,从而影响姿态角速度敏感精度,干扰力矩如图 7所示。因此,为实现高精度的姿态控制,满足相关航天航空任务需求,有效补偿这类误差,本文提出了采用勒让德多项式级数方法描述力矩器非圆特性,从而得到更加符合敏感实际的姿态角速度。半径误差测量值由实验测量得到的半径与三坐标测量机确定的力矩器外圆半径之差表示。根据式(23)、式(25)可得半径误差拟合值可以表示为
 | (30) |
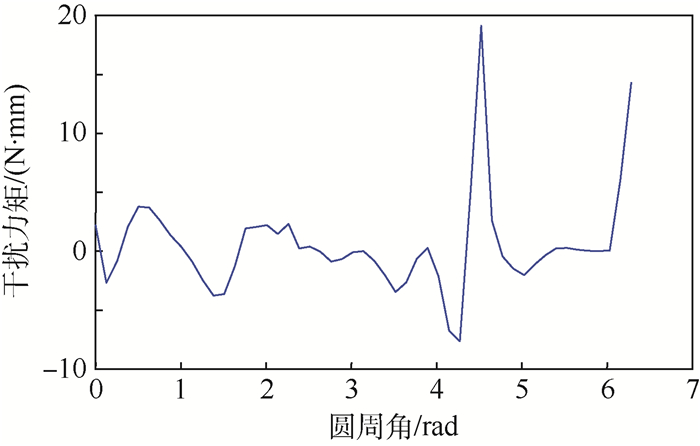 |
| 图 7 干扰力矩测量值随圆周角变化 Fig. 7 Change of measured value of disturbance torque with inscribed angle |
| 图选项 |
对比实验测量真值,进行力矩器非圆性误差拟合的情况如图 8所示。本次拟合采用6次谐波,从图 8可以看出,6次谐波可以较好拟合出力矩器半径随圆周角度的变化趋势,且避免了复杂的拟合运算。
 |
| 图 8 力矩器半径误差勒让德级数拟合 Fig. 8 Legendre series fitting of torquer radius error |
| 图选项 |
4.2 仿真校验 MSCSG载体姿态角速度敏感系统结构如图 9所示,ωi为载体姿态角速度给定值,ωo为载体姿态角速度系统敏感值,Δω为载体姿态角速度敏感误差。回路中,位移传感器检测到转子偏转信息与给定姿态角速度共同作为输入信号,通过抗混叠滤波器进行降噪处理,控制器根据偏转信号确定控制指令,经功率放大器转化为控制电流作用于LFMB, 产生偏转控制力矩,实现转子的偏转控制。
 |
| 图 9 MSCSG载体姿态角速度敏感系统框图 Fig. 9 Block diagram of MSCSG carrier attitude angular velocity measurement system |
| 图选项 |
位移传感器检测到转子在z方向的线性位移信号α, β与电流传感器检测到的LFMB的绕组线圈电流,经过功率放大器2可得敏感姿态角速度ωo。
干扰力矩为力矩器非圆性造成的偏转控制力矩,经补偿器作用于转子, 仿真系统参数如表 1所示。
表 1 仿真系统参数 Table 1 Parameters of simulation system
| 参数 | 取值 |
| LFMB支架半径/mm | 55.695 5 |
| LFMB线圈匝数 | 200 |
| LFMB线圈电流/A | 1 |
| LFMB磁场磁密/T | 0.4 |
| 转子径向转动惯量/(kg·m2) | 0.003 4 |
| 转子轴向转动惯量/(kg·m2) | 0.005 2 |
| LFMB线圈半张角/(°) | 37 |
表选项
仿真系统中,x通道与y通道在结构上是对称解耦的,其仿真结果一致,因此只给出x通道仿真结果。陀螺载体姿态角变化作为系统输入,当其按照正弦规律在x轴上沿z轴规律运动时,系统输出的补偿前与补偿后的误差如图 10所示。
 |
| 图 10 姿态角速度和角度仿真 Fig. 10 Simulation of attitude angle velocity and attitude angle |
| 图选项 |
由仿真结果可知:
补偿前,陀螺载体姿态角速度误差峰值为2.668×10-5 rad/s,随着时间的增长,陀螺载体姿态角角度趋于线性增长。当时间累积到一定程度时,姿态角角度误差就会超出控制电流的控制范围,为解决这一问题,不得不定期对陀螺载体姿态角角度进行复位控制,且复位频率必须足够高,以确保陀螺载体姿态角控制的精度,这就大大增加了陀螺的控制功耗。
补偿后,陀螺载体姿态角速度误差峰值为4.403×10-6 rad/s,较原来降低83.5%。且随时间的增长,陀螺载体姿态角角度误差一直稳定在0附近。避免了高频率施加偏转控制电流的弊端,减少了功耗。
5 结论 1) 通过利用三坐标测量机较为精确的测量了力矩器的圆周半径,测量精度达到10-6 m。为实现力矩器非圆性误差补偿,提高陀螺载体姿态角速度敏感精度提供了有效的数据支撑。
2) 利用勒让德多项式级数很好地描述力矩器的非圆特性,对实际测量半径误差曲线进行了拟合,为提高陀螺载体姿态角速度敏感精度提供了有效的补偿手段。
3) 提出了陀螺载体姿态角速度敏感误差模型,通过勒让德多项式级数拟合补偿了陀螺载体姿态角速度的敏感误差,使该误差降低了83.5%,提高飞行器姿态控制精度。
4) 通过MATLAB进行了陀螺载体姿态敏感系统的仿真校验,证实勒让德多项式级数拟合补偿方法能够有效补偿非圆性误差,且有效消除了陀螺载体姿态角速度累积误差,大大减少了陀螺载体姿态控制功耗。
参考文献
| [1] | FANG J, WANG C, TANG J. Modeling and analysis of a novel conical magnetic bearing for vernier-gimballing magnetically suspended flywheel[J].ARCHIVE Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 2013, 228(13): 2416–2425. |
| [2] | HAN B, ZHENG S, WANG Z, et al. Design, modeling, fabrication, and test of a large-scale single-gimbal magnetically suspended control moment gyro[J].IEEE Transactions on Industrial Electronics, 2015, 62(12): 7424–7435.DOI:10.1109/TIE.2015.2459052 |
| [3] | CUI P, CUI J, YANG Q, et al. The coupling characteristic investigation of double-gimbal magnetically suspended control moment gyro used on agile maneuver spacecraft[J].Mathematical Problems in Engineering, 2015, 2015: 278145. |
| [4] | REN Y, FANG J. Modified cross feedback control for a magnetically suspended flywheel rotor with significant gyroscopic effects[J].Mathematical Problems in Engineering, 2014, 2014: 325913. |
| [5] | BOLETIS A, BARROT F, MOSER R. Three axis active magnetic levitation for inertial sensing systems: US7252001[P]. 2007-08-07. |
| [6] | BOSGIRAUD T. Two degrees of freedom miniaturized gyroscope based on active magnetic bearings[D]. Lausanne: Ecole Polytechnique Federale de Lausanne, 2008: 1-15. |
| [7] | ZHANG H H. Measuring attitude rates through angular momentum gyros[J].Journal of Spacecraft & Rockets, 2012, 36(36): 919–921. |
| [8] | TYC G, STALEY D A, WHITEHEAD W R, et al. GyroWheel TM-An innovative new actuator/sensor for 3-axis spacecraft attitude control[C]//Proceedings of 13th Annual AIAA/USU Conference on Small Satellites. Reston: AIAA, 1999: 23-26. |
| [9] | WALKTY I, PETERSEN J, DOHERTY T, et al. SCISAT-1 ACE mission C&DH unit development[C]//Proceedings of 14th Annual AIAA/USU Conference on Small Satellites. Reston: AIAA, 2000: 1-13. |
| [10] | MARUYAMA Y, MIZUNO T, TAKASAKI M, et al. An application of active magnetic bearing to gyroscopic and inertial sensors[J].Journal of System Design & Dynamics, 2008, 2(1): 155–164. |
| [11] | 刘彬, 房建成, 刘刚. 一种磁悬浮陀螺飞轮方案设计与关键技术分析[J].航空学报, 2011, 32(8): 1478–1487. LIU B, FANG J C, LIU G. Design of a magnetically suspended growheel and analysis of key technologies[J].Acta Aeronautica et Astronautica Sinica, 2011, 32(8): 1478–1487.(in Chinese) |
| [12] | 任元, 王卫杰, 刘强, 等. 一种磁悬浮控制敏感陀螺: ZL201510006597. 5[P]. 2017-04-28. REN Y, WANG W J, LIU Q, et al. A kind of magnetically suspended control sensitive gyroscope: ZL201510006597. 5[P]. 2017-04-28(in Chinese). |
| [13] | 刘强, 武登云, 樊亚洪, 等. 双定子三自由度解耦洛伦兹力磁轴承: CN204572783U[P]. 2015-06-24. LIU Q, WU D Y, FAN Y H, et al. Double stator three degrees of freedom decoupling Lorentz force magnetic bearing: CN204572783U[P]. 2015-06-24(in Chinese). |
| [14] | 刘强, 任元, 王卫杰, 等. 一种双永磁体内转子永磁偏置球面径向磁轴承:, CN204267528U[P]. 2015-02-25. LIU Q, REN Y, WANG W J, et al. A permanent magnet bias spherical radial magnetic bearing with double permanent magnets: CN204267528U[P]. 2015-02-25(in Chinese). |
| [15] | 辛朝军. 磁悬浮控制敏感陀螺误差分析与补偿方法研究[D]. 北京: 航天工程大学, 2017: 15. XIN C J. Error analysis and compensation method study of a magnetically suspended sensitive gyroscope[D]. Beijing: Space Engineering University, 2017: 15(in Chinese). |
| [16] | 许国锋, 蔡远文, 任元, 等. 洛伦兹力磁轴承磁密均匀度设计与分析[J].北京航空航天大学学报, 2017, 43(3): 559–566. XU G F, CAI Y W, REN Y, et al. Design and analysis on uniformity of magnetic flux density in Lorentz force-type magnetic bearing[J].Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(3): 559–566.(in Chinese) |
