从空气动力学角度而言, 高超声速进气道的工作环境具有以下特征:第一, 飞行高度一般位于平流层, 来流密度低且湍流度小, 飞行器前体及进气道部分压缩面边界层通常为层流; 第二, 强增压效果使压缩面后部逆压梯度较大, 容易导致层流边界层失稳及转捩; 第三, 高超声速进气道压缩面通常具有复杂波系结构, 激波/边界层干涉现象也极易导致边界层发生转捩。
在高超声速飞行器进气道的设计和研究中, 充分考虑壁面边界层的流动状态, 准确模拟流动转捩的影响十分重要。边界层转捩具有分类复杂、影响因素多和预测难度大等特点[3], 对于高超声速流动, 还需要考虑激波/边界层干涉效应、强逆压梯度等的影响, 给数值模拟方法带来了很大挑战。
在目前阶段, 基于RANS(雷诺平均Navier-Stokes方程)的工程转捩模型方法仍然是工程上广泛采用的转捩预测方法[4-6], 而其中Langtry和Menter等[5-6]所发展的基于间歇因子输运方程的γ-Reθ转捩模型得到了非常广泛的应用。许多****对γ-Reθ转捩模型在低速流动中的转捩预测能力进行了校验及分析[7-9]。尽管该模型的经验关联公式是基于低速平板风洞试验数据的, 但也有****对该模型在高超声速流动中的适用性进行了研究[10-12], 其结果表明, 该模型对于部分工况, 尤其是隶属于分离诱导转捩的算例, 仍具有较为理想的预测精度, 但对于其他一些算例的计算结果则不够理想。
基于上述问题, 许多国内外****先后提出了γ-Reθ转捩模型在高超声速流动下的改进方法, Cheng等[13]在该模型中引入考虑马赫数的压力梯度修正, 并对马赫数为8的尖锥进行数值模拟; 张毅锋等[14-15]利用平板绕流、裙锥绕流算例对上述修正方法进行进一步校验; 张晓东和高正红[16]对模型中的转捩动量厚度雷诺数进行修正, 并利用双楔绕流算例进行验证; You等[17]认为对于简单几何模型的高超声速绕流, γ-Reθ转捩模型的经验关联公式可以改写为仅与来流参数相关的简单形式; 夏陈超等[18]利用多个算例对3种现有的修正方法进行了对比分析; 郑赟和李虹杨[19]参考部分高超声速实验数据, 对该模型的转捩动量厚度雷诺数经验关联公式进行改进, 改善了模型对于高湍流度旁路转捩的预测精度。
首先, 本文在笔者课题组HGFS(Hybid Grid Flow Solver)程序平台中所发展的γ-Reθ转捩模型的基础上, 对文献[19]中的高超声速改进方法进行进一步研究, 分析该方法对分离诱导转捩的预测精度的影响; 其次, 对来流马赫数为6.0的高超声速进气道进行数值模拟, 研究进气道的性能参数随飞行高度、来流湍流度和来流马赫数的变化规律。
1 数值方法 Langtry等提出的γ-Reθ转捩模型[5-6]有2个输运方程, 分别为间歇因子γ的输运方程以及转捩起始动量厚度雷诺数Reθt的输运方程, 表达式分别为
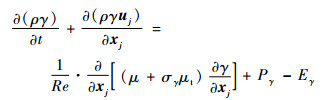 | (1) |
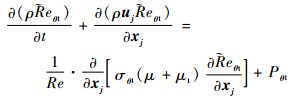 | (2) |
式中:ρ为密度; t为时间; uj为速度张量; xj为坐标张量; Re为来流雷诺数; σγ和σθt为湍流模型常数。
式(1)中等号右端第1项为间隙因子的交叉扩散项, μ为层流黏性系数, μt为湍流涡黏性系数; Pγ为间歇因子生成项; Eγ为间歇因子耗散项。式(2)中等号右端第1项为转捩起始动量厚度雷诺数Reθt的交叉扩散项; Pθt为转捩起始动量厚度雷诺数的源项。输运方程各项的完整表达式参见文献[5]。式(1)和式(2) 2个输运方程的目的是计算得到流场中间歇因子的分布, 还需要与k-ω SST模型的2个输运方程相结合才能实现边界层转捩的模拟。
郑赟和李虹杨[19]改进了γ-Reθ转捩模型经验关联公式, 引入一个以马赫数为变量的修正函数G(Ma), 重新定义转捩起始动量厚度雷诺数Reθt与当地湍流度Tu的经验关联, 如式(3)所示, λθ为当地加速因子, Ma为当地马赫数。其设计目标是在较低马赫数(Ma<2)时, Reθt与Tu的关系曲线近似与原始公式[5]一致; 而在较高马赫数(2≤Ma<12)时, Reθt与Tu的关系应尽量满足Denissen等[20]所建议的马赫数分别为2.5、3.5和4.5的风洞试验数据; 同时, 还需要保证在2≤Ma<12范围内, 修正函数G(Ma)要近似满足文献[21]中图 3的数据关系。经过多次的拟合与优化, 得到如式(4)所示的改进后的G(Ma)。
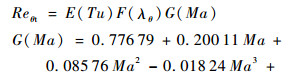 | (3) |
 | (4) |
 |
| 图 3 前缘带倒圆的压缩面的计算网格 Fig. 3 Computational mesh for blunt leading edge compression surface |
| 图选项 |
式(3)中等号右端的E(Tu)以及F(λθ)的表达式不做修改, 与文献[5]保持一致。新的经验关联公式的曲线如图 1所示, 可以看出当马赫数分别等于2.5、3.5和4.5时, 采用新的经验关联公式计算得到的Reθt值与目标值(参见文献[20])非常接近, 当马赫数为2.5和3.5时, 目标值几乎恰好位于曲线上, 只有当马赫数为4.5时目标值与曲线偏离稍大。总体来看新经验关联公式的改进效果还是非常理想的。
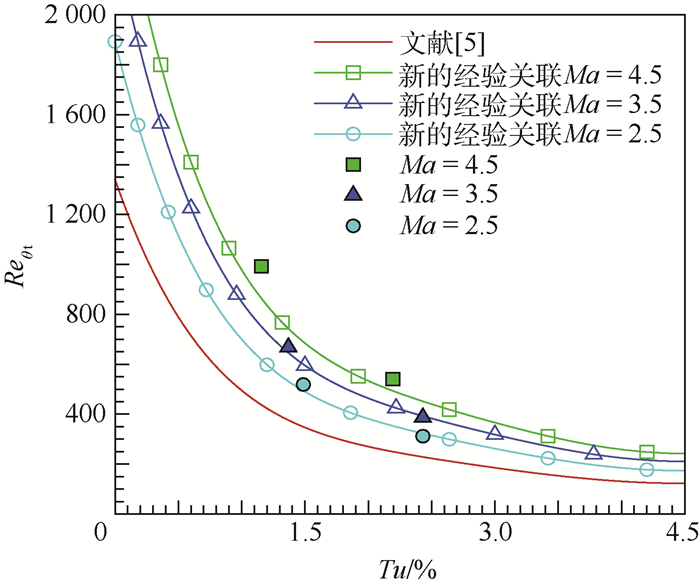 |
| 图 1 Reθt与Tu的新的经验关联曲线 Fig. 1 New empirical correlation curves of Reθt vs Tu |
| 图选项 |
2 模型验证 Langtry和Menter已经于2009年公开完整的γ-Reθ转捩模型的相关公式[22], 但研究结果表明该模型对CFD程序平台中的离散格式、数值方法等非常敏感, 添加该模型之后通常需要进行严格验证。本文所采用的HGFS平台中γ-Reθ转捩模型的验证参考了低压涡轮叶栅算例[23]、流/热耦合涡轮算例[24]、平板绕流算例及部分高超声速绕流算例[10]。文献[19]对改进的新经验关联公式进行了初步验证, 但其中仅涉及了平板绕流、圆锥绕流等简单算例, 而本文则重点对高超声速进气道压缩面的转捩问题进行研究。
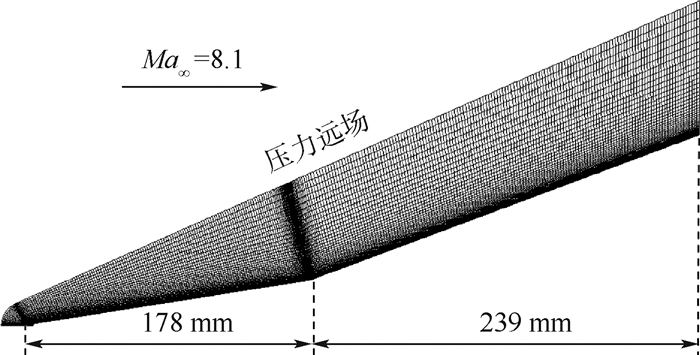
图 2为高超声速飞行器进气道示意图。压缩面由2部分组成:第1段压缩面角度δ1=9°, 第2段压缩面角度δ2=20.5°。来流马赫数Ma∞=8.1。Neuenhahn和Olivier[25]、Reinartz和Ballmann[26]分别对该进气道压缩面进行了风洞试验研究及数值模拟研究, 对进气道几何模型进行了一定的简化, 即在保持角度不变的情况下, 将第2段压缩面靠近喉部的3次样条曲面以平面代替, 并加以延长, 形成了近似“双楔”的结构, 本文研究中也采用了相同的几何模型。
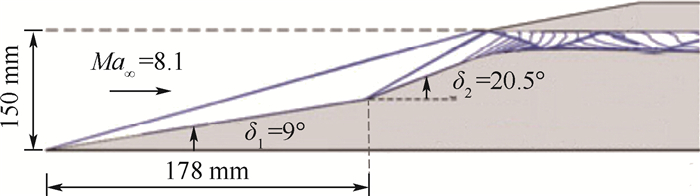 |
| 图 2 高超声速飞行器进气道示意图 Fig. 2 Schematic of air inlet of hypersonic aircraft |
| 图选项 |
图 3展示了前缘带倒圆的压缩面的计算网格, 为二维结构化网格, 其单元数量为351×91, 壁面处进行了加密, 第1层网格高度为1×10-6 m, 膨胀比为1.15。在本文所有的计算工况中, 第1层网格对应的y+均小于0.4。
分别利用k-ω SST模型、原始γ-Reθ转捩模型及改进的转捩模型对该压缩面绕流进行数值模拟。边界条件如下:来流进口、上边界以及出口均为压力远场, 前缘之前的引导区为无黏壁面, 双楔的两段为恒温黏性壁面; 来流马赫数Ma∞=8.1, 来流静压p∞=520 Pa, 来流静温T∞=106 K, 来流雷诺数Re∞=3.8×106, 来流湍流度Tu∞=0.9%。
图 4展示了不同模型计算得到的转角位置静压和流线的分布。x为实际位置的横坐标, 坐标原点在进气道转角处。y为纵坐标, 为方便对比将改进的转捩模型的结果进行了对称处理, 其y值为实际位置纵坐标的负数。由图 4可知改进的转捩模型的计算结果中转角位置出现了较大范围的高压区, 且存在分离泡, 而k-ω SST模型的计算结果中均没有出现。较强的分离泡一般会对壁面附近压力分布产生一定影响, 但从目前的结果尚不能推断出哪个结果更符合实际, 仍需要结合实验数据进一步分析。
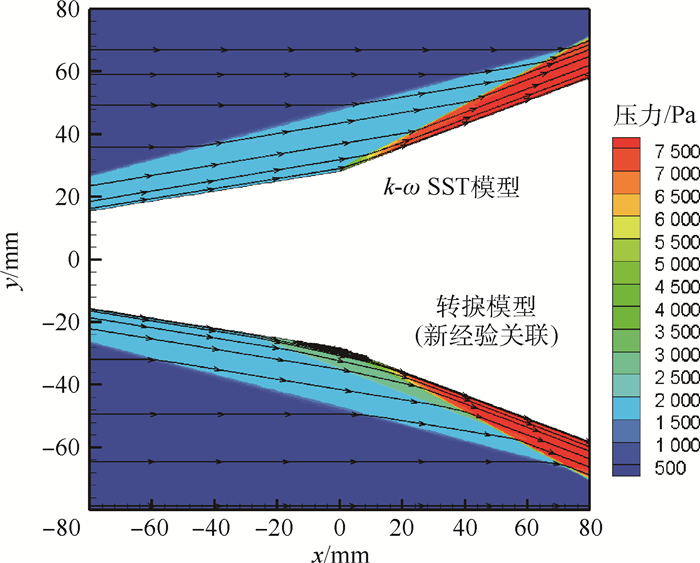 |
| 图 4 不同模型计算的静压和流线分布 Fig. 4 Distribution of static pressure and streamline calculated by different models |
| 图选项 |
图 5(a)~(c)分别展示了不同的前缘倒圆半径R(R=0 mm代表无倒圆)情况下, k-ω SST模型、原始γ-Reθ转捩模型及改进的转捩模型的计算结果, 横坐标进行了归一化处理, 即分别除以两段压缩面的x方向长度L。其中实心符号为相应工况的风洞试验数据[25]。Cp为压力系数, St为斯坦顿数, 其定义分别为
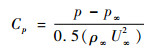 | (5) |
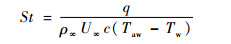 | (6) |
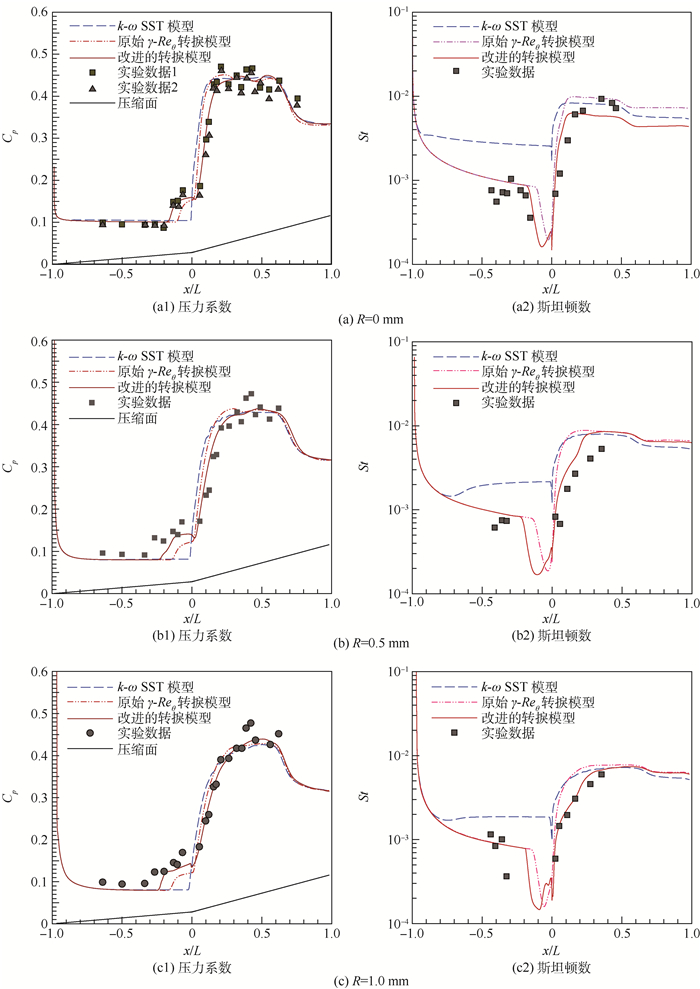 |
| 图 5 计算得到的压力系数和斯坦顿数与实验值的对比 Fig. 5 Comparison of calculated pressure coefficient and Stanton number with expemental values |
| 图选项 |
式中:p为当地静压; p∞为来流静压; ρ∞为来流密度; U∞为来流速度; c为气体的定压比热容; q为热流量; Tw为壁面温度; Taw为绝热壁面温度, 文献[25]中的方法是使用来流总温代替绝热壁面温度。
对图 5(a)、(b)、(c)中的计算结果进行分析, 可以得到以下结论:
1) 从图 5(a1)、(b1)、(c1)压力系数分布来看, 一方面, k-ω SST模型的计算结果没有捕捉到转角(即x/L=0)位置的压力曲线平台区; 原始γ-Reθ转捩模型捕捉到了转角位置的平台区, 但对于不同R的情况, 该平台区均比较小, 与实验值仍有一定差别; 而改进的转捩模型的计算结果则与实验结果非常接近。另一方面, k-ω SST模型与原始γ-Reθ模型计算得到的压力曲线上升段均过于陡峭, 而改进的转捩模型的结果与实验结果符合得更好。
2) 从图 5(a2)、(b2)、(c2)斯坦顿数分布来看, k-ω SST模型的计算结果在第1段压缩面以及转角位置均呈现非常高的数值, 与实验结果相差很大。而原始γ-Reθ转捩模型与改进的转捩模型的计算结果则与实验值符合得比较好, 但改进的转捩模型计算得到的斯坦顿数曲线低谷区更宽, 上升区更为平缓, 比原始γ-Reθ转捩模型的计算结果更准确。
上述高超声速进气道压缩面边界层转捩机制为分离诱导转捩。分离泡位置固定决定了转捩位置是基本固定的, 但改进的转捩模型在一定程度上解决了原始γ-Reθ转捩模型中转捩发生得过于“容易”的问题, 使边界层的层流区域保持得更长, 导致更大范围内的层流分离, 计算结果更符合实际。新经验关联公式利用修正函数增加了相同条件下转捩起始动量厚度雷诺数在流场中的分布, 进而使得输运到边界层内部的转捩起始动量厚度雷诺数增加, 相当于提高了转捩模型中转捩判据的“阈值”, 在一定程度上抑制了高超声速条件下转捩发生过早的问题, 从而提高了对转捩的预测精度。
3 计算结果及分析 选取中国科学院设计的高超声速进气道进行数值模拟研究, 计算采用的是按照某方法进行折算后的参数。进气道尺寸为2.2 m×0.4 m(长度×高度), 设计来流马赫数Ma∞=6.0, 设计飞行高度H=26 km。计算域及网格如图 6所示, 图中展示的是1/5密度的网格, 实际网格的单元总数为15 000, 第1层网格高度在10-7 m量级。在地表极限条件下, 相应的y+约为1.0, 而设计飞行高度下, 相应的y+约为0.3。计算采用了k-ω SST模型以及改进后的转捩模型。
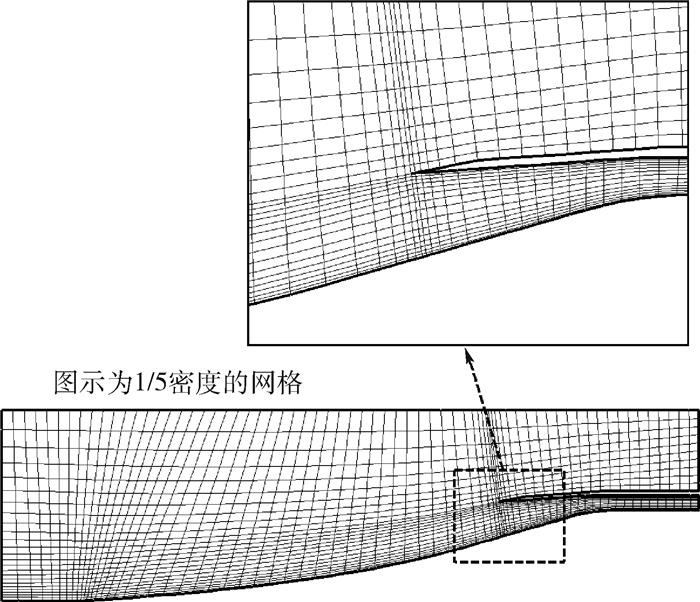 |
| 图 6 高超声速进气道的计算域和网格 Fig. 6 Computational domain and mesh of hypersonic air inlet |
| 图选项 |
图 7为计算得到的设计工况下, 即飞行高度H=26 km, 来流马赫数Ma∞=6.0时的压力分布。x为实际位置的横坐标, 坐标原点是进气道进口。从压力云图可以看出, 等熵压缩面上分布有一系列的强压缩波, 最外面的一道压缩波正好打在上唇口前缘。唇口位置出现了一道较强的OSW, 激波后的气流压力迅速升高, 由10 kPa升高到了约40 kPa, 增压效果明显。在之后的隔离段内激波出现了多次的壁面反射与交叉干涉现象。
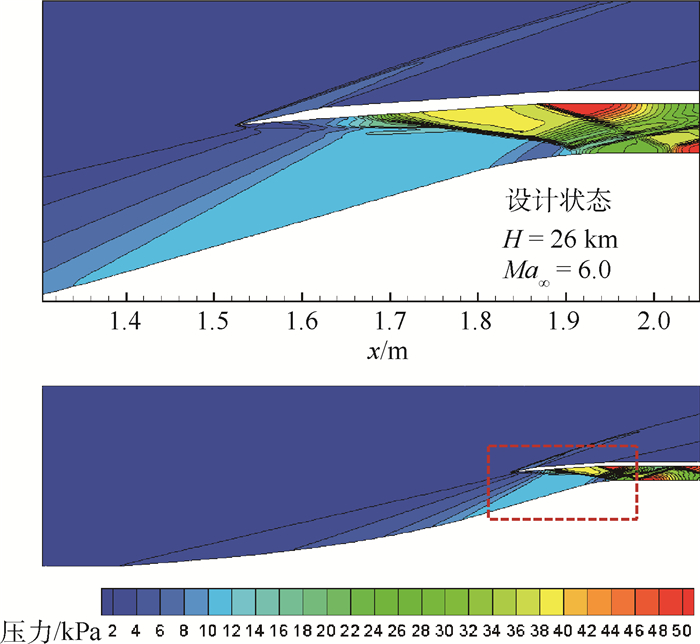 |
| 图 7 计算得到的设计状态静压分布 Fig. 7 Distribution of computed static pressure under design condition |
| 图选项 |
3.1 性能参数随飞行高度的变化 图 8(a)~(c)展示了进气道压缩面上压力系数Cp以及壁面摩阻系数Cf随飞行高度的变化规律, 来流湍流度Tu∞=1.0%, 来流马赫数Ma∞=6.0。分析图 8(a)~(c)可以得到如下结论:
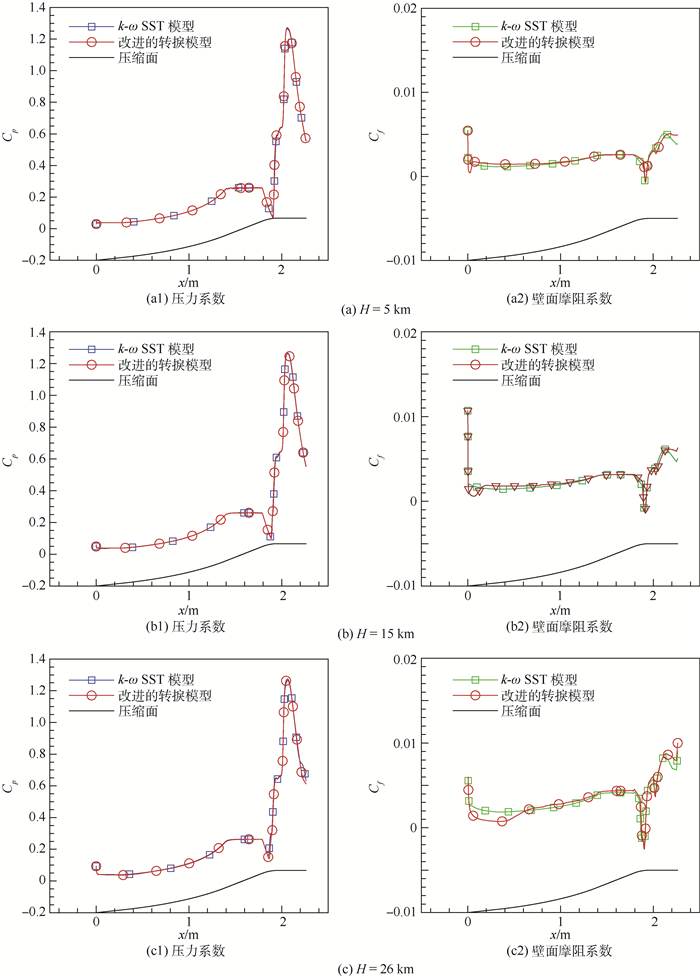 |
| 图 8 压力系数和壁面摩阻系数随飞行高度的变化 Fig. 8 Variation of pressure coefficient and skin friction resistance coefficient with flight height |
| 图选项 |
1) 从图 8(a1)、(b1)、(c1)可以看出, k-ω SST模型和改进的转捩模型计算得到的压力系数曲线非常接近, 说明边界层转捩对进气道压缩面压力分布影响不大, 进而也不会对其增压能力产生影响。
2) 将图 8(c1)和图 7结合起来分析, 可以看出在x=0~1.4 m的区间内, 压缩面上的压力是逐渐升高的, 对应于图 7中一系列的压缩波; 而在x=1.4~1.8 m区间内, 出现了很长的一段压力平台区, 对应于喉道前的一段平直压缩面, 该部分没有压缩波出现; 在x=1.9 m之后的区域, 即唇口OSW之后, 下表面压力迅速升高。
3) 从图 8(a2)、(b2)、(c2)可以看出, 壁面摩阻系数受边界层流动状态的影响很大, k-ω SST模型的计算结果近似代表了全湍流边界层, 压缩面上壁面摩阻系数几乎始终维持在较高的数值, 而改进的转捩模型的计算结果中可以看出壁面摩阻系数由较低水平突然增加的过程。层流边界层的壁面摩阻系数通常远低于湍流边界层, 使气动损失减小, 效率增加, 斯坦顿系数降低。
4) 对比图 8(a2)、(b2)、(c2)中改进的转捩模型的计算结果, 可以看出转捩位置随飞行高度的增加而延后。喉道位置的壁面摩阻系数曲线都存在一个低谷区, 且随着飞行高度的增加, 该低谷区范围更大, 最小值更小。这是因为随着飞行高度增加, 来流雷诺数降低, 压缩面上的边界层厚度增加, 激波/边界层干涉效果更强烈, 分离泡范围更大, 进而导致壁面摩阻系数低谷区范围更大, 数值更小。
图 9(a)~(c)分别展示了在设计飞行速度, 即来流马赫数Ma∞=6.0情况下, 唇口OSW与边界层干涉产生的分离泡随飞行高度的变化规律, 其中的彩色云图为密度分布。图中y为实际位置的纵坐标。由图 9可知:
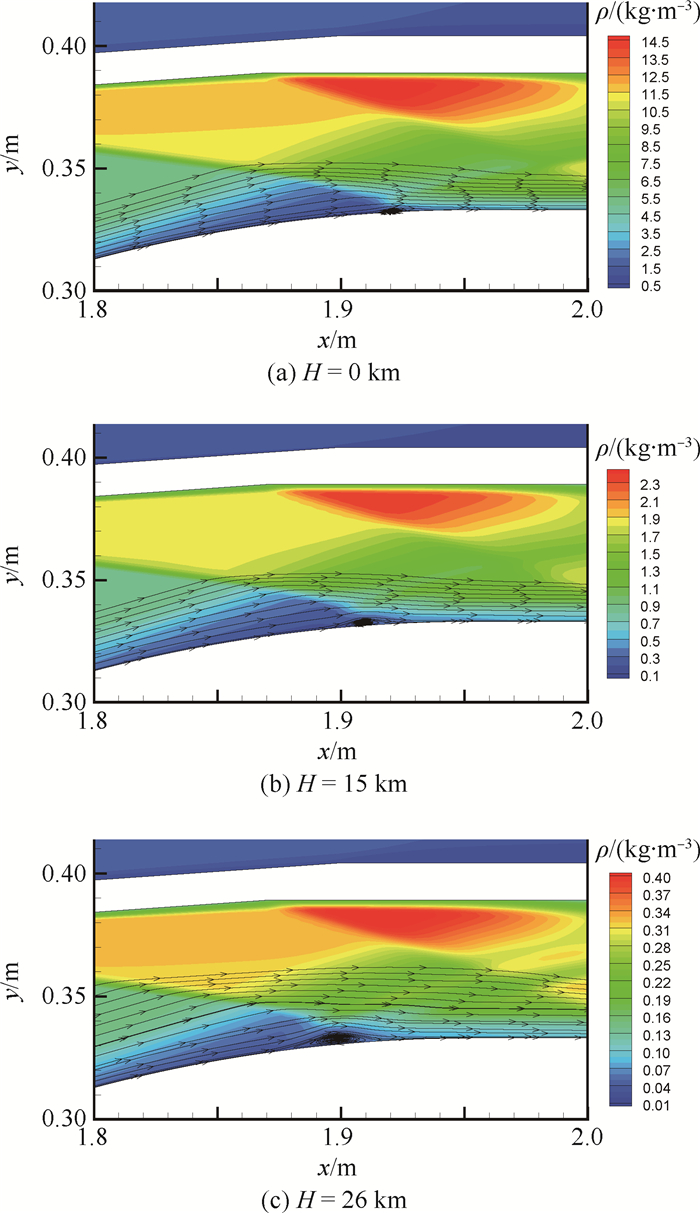 |
| 图 9 分离泡强度随飞行高度的变化(Ma∞=6.0) Fig. 9 Variation of separation bubble strength with flight height (Ma∞=6.0) |
| 图选项 |
1) 随着飞行高度的增加, 分离泡强度逐渐增强, 边界层内回流区的范围更广, 且逆流速度更大, 对壁面摩阻系数的的影响程度也更剧烈, 这与图 8(a2), (b2), (c2)中的变化规律相一致。
2) 随飞行高度的增加, 分离泡的位置略有提前, 由图 9(a)中的x=1.92 m提前到图 9(c)中的x=1.90 m。通过仔细对比密度云图可以发现, 对于不同的飞行高度, 唇口OSW的角度实际上几乎没有改变, 但边界层厚度的增加导致了激波/边界层干涉位置有所提前。
图 10为喉道位置边界层内速度型曲线随飞行高度的变化规律。为避开分离泡, 实际选择的是x=1.85 m位置的速度型曲线, 并补充了多个飞行高度的计算结果。纵坐标中的u为当地气流速度, Uref为边界层外自由流速度。从速度型的变化规律可以看出, 唇口附近位置的边界层厚度随飞行高度是逐渐增加的, 与图 8和图 9中的分析相符。
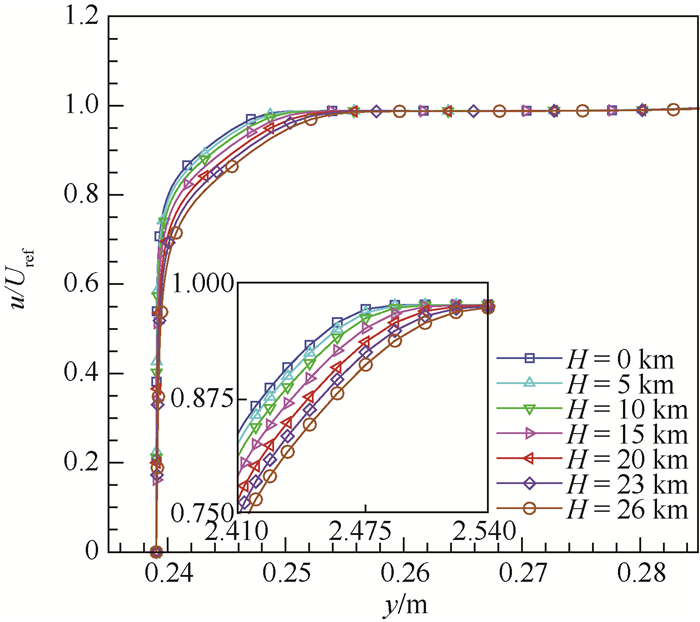 |
| 图 10 速度型曲线随飞行高度的变化(x=1.85 m) Fig. 10 Variation of velocity profile with flight height (x=1.85 m) |
| 图选项 |
表 1列出了一些关键性能参数在不同飞行高度下的数值模拟结果, 其中边界层厚度是相对于进气道出口高度的百分比, 第4列为压缩面上边界层转捩位置的横坐标。其中的转捩位置为近似数值, 这是因为高超声速流动边界层通常很薄, 即使通过间歇因子云图也难以分辨准确的转捩位置, 而壁面摩阻系数曲线则显得更为直观, 因此本文没有列出间歇因子云图。从表 1中的数据可以得到如下结论:
表 1 部分性能参数随飞行高度的变化 Table 1 Variation of some performance parameters with flight height
| 飞行高度/km | 总压恢复系数 | 边界层厚度(相对值)/% | 转捩位置/m |
| 0 | 0.750 | 8.8 | 0.025 |
| 5 | 0.750 | 9.6 | 0.04 |
| 10 | 0.749 | 10.4 | 0.065 |
| 15 | 0.743 | 11.2 | 0.12 |
| 20 | 0.733 | 12.0 | 0.24 |
| 23 | 0.725 | 13.6 | 0.35 |
| 26 | 0.718 | 15.2 | 0.55 |
表选项
1) 总压恢复系数随着飞行高度的增加逐渐下降, 而且飞行高度越高总压恢复系数下降得越快, 与地表状态相比, 在设计飞行高度总压恢复系数下降了约3.2%。同时, 边界层厚度增加了约73%。参考图 8~图 10的分析可知, 边界层厚度增加, 分离泡强度增大导致气动损失增加, 是总压恢复系数下降的主要原因。
2) 转捩位置随飞行高度的增加逐渐延后, 飞行高度在0~10 km的范围内转捩位置向后移动得较为缓慢, 但随着飞行高度继续增加, 转捩位置延后得十分明显。在地表状态, 即H=0 km, 转捩位置为x=0.025 m, 几乎在前缘位置立即转捩; 而在设计高度, 即H=26 km, 转捩位置为x=0.55 m, 约在压缩面长度的1/3位置处。
3.2 性能参数随来流湍流度的变化 来流湍流度对边界层的转捩位置有非常重要的影响, 来流湍流度的定义[5]为
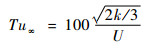 | (7) |
式中:k为湍动能, m2/s2; U为当地速度。
在高超声速流动的数值模拟中, 来流的速度通常是作为边界条件直接指定的, 因此高超声速流动中的来流湍流度实际上相当于在边界处设定了湍动能, 这与低速流动情况有所不同。
图 11(a)和(b)分别展示了在飞行高度为26 km和来流马赫数为6.0条件下, 压缩面上的压力系数和壁面摩阻系数随来流湍流度的变化规律。可以看出, 压力系数几乎没有受到来流湍流度的影响, 而壁面摩阻系数则有明显变化, 压缩面上的转捩位置随着来流湍流度增加逐渐提前。
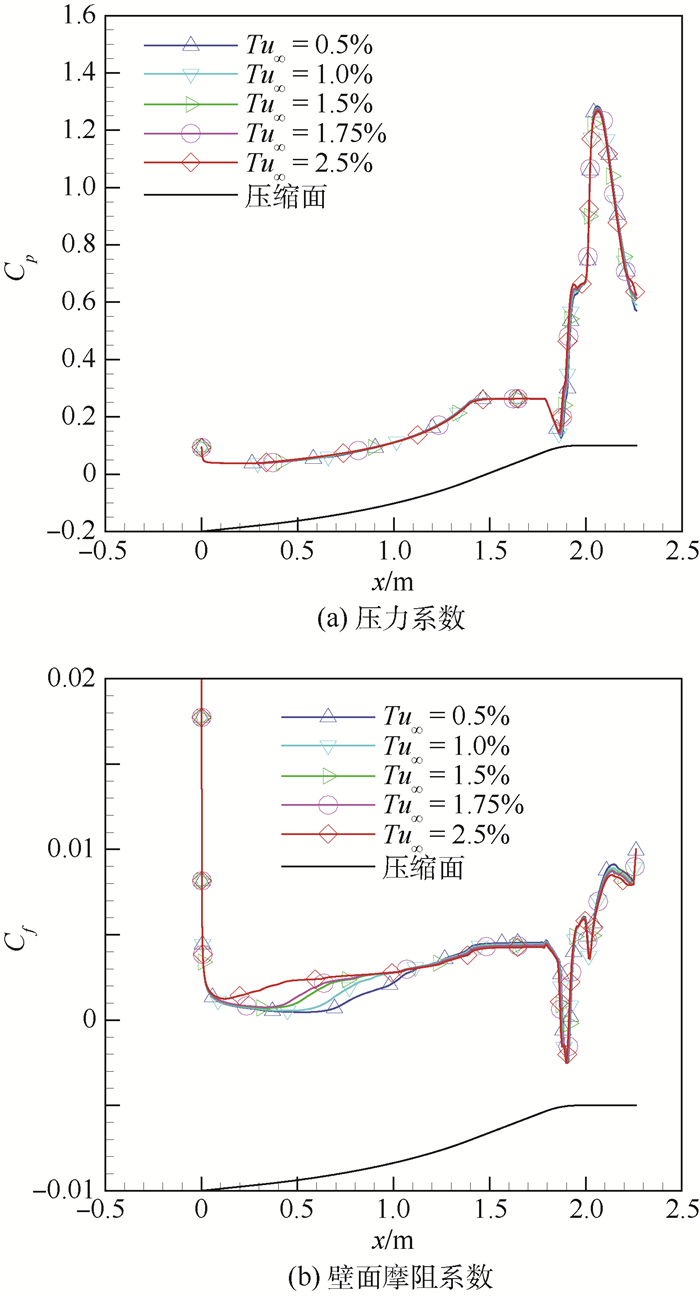 |
| 图 11 压力系数和壁面摩阻系数随来流湍流度的变化 Fig. 11 Variation of pressure coefficient and skin friction resistance coefficient with free stream turbulence intensity |
| 图选项 |
对比图 11(b)和图 8(a2)、(b2)可以看出, 尽管在较低飞行高度以及较高的来流湍流度条件下, 压缩面边界层转捩位置都非常靠前, 但转捩区长度却有很大差异, 较低飞行高度下转捩区长度很短, 而高来流湍流度条件下转捩区长度则较长。
表 2列出了进气道总压恢复系数和压缩面边界层转捩位置随来流湍流度的变化规律, 可以得出如下结论:转捩位置对来流湍流度的大小是非常敏感的, 来流湍流度变化0.5%可能引起转捩位置移动0.2 m左右; 进气道总压恢复系数随着来流湍流度的增加逐渐降低, 但变化幅度较小, 来流湍流度从0.5%增加到2.5%时, 总压恢复系数下降约0.8%。
表 2 部分性能参数随来流湍流度的变化 Table 2 Variation of some performance parameters with free stream turbulence intensity
| 来流湍流度/% | 总压恢复系数 | 转捩位置/m |
| 0.5 | 0.705 | 0.7 |
| 1.0 | 0.703 | 0.55 |
| 1.5 | 0.700 | 0.35 |
| 1.75 | 0.699 | 0.25 |
| 2.5 | 0.697 | 0.1 |
表选项
其原因可解释如下:来流湍流度增加使转捩位置提前, 压缩面上湍流边界层所占的范围更大, 使得整体的流动动能损失增加, 进而导致总压恢复系数在一定程度上有所下降, 但从数值模拟结果来看, 其影响效果比较小。
3.3 性能参数随来流马赫数的变化 高超声速进气道及压缩面的工作状态同样受到来流马赫数的影响。在马赫数过低时, 增压能力不足, 背压过高, 导致进气道“不启动”, 其特征是唇口前出现大范围分离区, 且发生严重溢流, 如图 12虚线框所示。本文进气道在Ma∞=4.0时为不启动状态, 而Ma∞=4.2时为启动状态。当来流马赫数继续增加时, 压缩波和唇口OSW的角度会发生改变, 进而影响隔离段内激波系的形态。
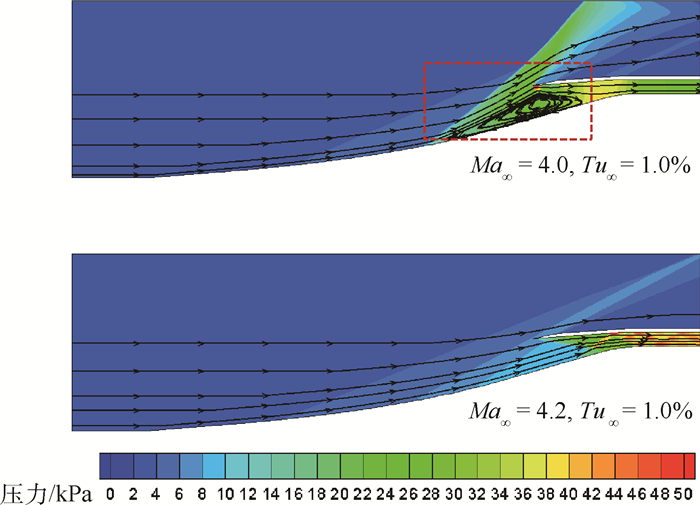 |
| 图 12 静压和流线随来流马赫数的变化 Fig. 12 Variation of static pressure and streamline with free stream Mach number |
| 图选项 |
本文研究了进气道启动状态, 即Ma∞>4.2情况下, 来流马赫数对总压恢复系数和边界层转捩位置等的影响规律。
图 13展示了来流马赫数在4.2~7.0范围内壁面摩阻系数的变化规律, 计算工况飞行高度为26 km, 来流湍流度为1.0%。其中虚线框内的关键位置进行了放大展示。可以看出来流马赫数在4.2~5.0时, 随着来流马赫数增加, 转捩位置逐渐延后且近似线性变化; 来流马赫数为5.5时转捩位置突然大幅延后, 但在5.5~7.0范围内, 转捩位置几乎不再发生改变, 压缩面上的壁面摩阻系数曲线也接近重合。
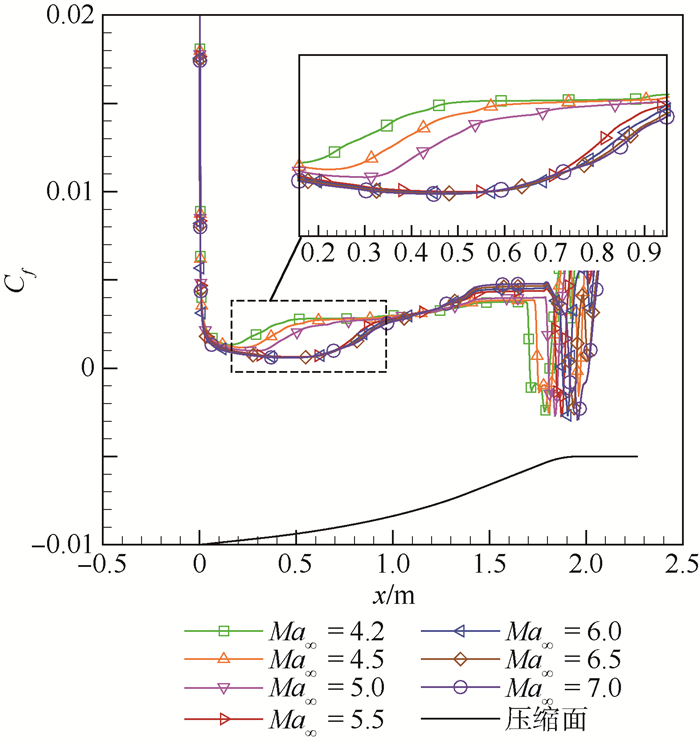 |
| 图 13 壁面摩阻系数随来流马赫数的变化 Fig. 13 Variation of skin friction resistance coefficient with free stream Mach number |
| 图选项 |
参考式(7), 在保证Tu∞不变的情况下, 可以看出随着来流马赫数增加, 湍动能k是逐渐减小的, 进而导致流场中Reθt的分布增加, 转捩位置会逐渐延后。图 13中的计算结果与之相符, 但转捩位置的详细变化规律仍需要通过计算才能得到。本文研究表明, 在接近设计马赫数时, 压缩面上的转捩位置是近似稳定的, 几乎不随来流马赫数的变化而改变。
表 3展示了总压恢复系数和转捩位置随来流马赫数的变化规律。可以看出在保证进气道启动状态下, 即使很低的来流马赫数也能保持相对较高的总压恢复系数; 来流马赫数略低于设计值时, 进气道达到最理想的总压恢复系数; 而来流马赫数高于设计值时, 总压恢复系数则下降得较为严重, 这主要是唇口OSW角度大幅改变, 引起隔离段内激波系偏离设计状态所导致的。表 3中的转捩位置为近似数值, 与图 13中所分析的规律相符。
表 3 部分性能参数随来流马赫数的变化 Table 3 Variation of some performance parameters with free stream Mach number
| 来流马赫数 | 总压恢复系数 | 转捩位置/m |
| 4.2 | 0.721 | 0.18 |
| 4.5 | 0.729 | 0.26 |
| 5.0 | 0.741 | 0.34 |
| 5.5 | 0.746 | 0.64 |
| 6.0 | 0.704 | 0.64 |
| 6.5 | 0.617 | 0.64 |
| 7.0 | 0.523 | 0.64 |
表选项
4 结论 本文首先采用某高超声速进气道压缩面的简化模型对γ-Reθ转捩模型的高超声速改进方法进行验证, 并分析了相关机理; 其次, 对中国科学院高超声速进气道进行数值模拟, 研究其性能参数随飞行高度、来流湍流度以及来流马赫数的变化规律。主要结论可归纳如下:
1) 改进的转捩模型利用特定的修正函数增加了相同条件下转捩起始动量厚度雷诺数在流场中的分布, 进而提高转捩判据的阈值, 在一定程度上抑制了转捩发生过早, 或者过于“容易”的问题。本文研究表明, 该改进方法对高超声速流动的分离诱导转捩同样有效。
2) 由计算结果可知, 等熵压缩面的高超声速进气道增压能力几乎不受边界层流动状态的影响。在地表极限状态以及高空设计状态, 边界层流动状态不同, 但均能保证近似一致的理想增压效果。
3) 随着飞行高度的增加, 压缩面边界层转捩位置延后, 边界层厚度增加, 唇口OSW与边界层干涉产生的分离泡强度增加。总体效果是使进气道总压恢复系数下降。与地表情况相比, 设计飞行高度的转捩位置延后了约0.525 m, 边界层厚度增加了约73%, 总压恢复系数下降了约3.2%。
4) 随着来流湍流度的增加, 压缩面上的压力系数曲线几乎保持不变, 而壁面摩阻系数曲线则变化较大, 主要是因为转捩位置对来流湍流度比较敏感。来流湍流度变化0.5%可引起转捩位置移动0.2 m左右。进气道总压恢复系数随着来流湍流度的增加略有降低, 当湍流度从0.5%增加到2.5%时, 总压恢复系数下降约0.8%。
5) 当来流马赫数在4.2~5.0范围内, 压缩面边界层转捩位置随马赫数的增加而延后, 且近似线性变化; 而当来流马赫数增大, 即在5.5~7.0范围内, 转捩位置则近似保持不变
本文对高超声速进气道的研究工作仅针对于二维模型, 实际上三维流动效应对边界层转捩以及进气道性能参数也有非常重要的影响, 将在后续的工作中加以研究。
参考文献
| [1] | 黄伟, 罗世彬, 王振国. 临近空间高超声速飞行器关键技术及展望[J].宇航学报, 2010, 31(5): 1259–1265. HUANG W, LUO S B, WANG Z G. Key techniques and prospect of near-space hypersonic vehicle[J].Journal of Astronautics, 2010, 31(5): 1259–1265.(in Chinese) |
| [2] | 李祝飞. 高超声速进气道起动特性机理研究[D]. 合肥: 中国科学技术大学, 2013: 1. LI Z F. An investigation on starting characteristics of hypersonic inlets[D]. Hefei: University of Science and Technology of China, 2013: 1(in Chinese). |
| [3] | 张玉伦, 王光学, 孟德虹, 等. γ-Reθ转捩模型的标定研究[J].空气动力学学报, 2011, 29(3): 295–301. ZHANG Y L, WANG G X, MENG D H, et al. Calibration of γ-Reθ transition model[J].Acta Aerodynamica Sinica, 2011, 29(3): 295–301.(in Chinese) |
| [4] | 许丁, 马晖扬. 高超声速边界层工程转捩模式研究[J].中国科学院研究生院学报, 2009, 26(1): 43–49. XU D, MA H Y. Engineering transition models for hypersonic boundary layer[J].Journal of the Graduate School of the Chinese Academy of Sciences, 2009, 26(1): 43–49.(in Chinese) |
| [5] | MENTER F R, LANGTRY R B, LIKKI S R, et al. A correlation-based transition model using local variables:Part Ⅰ:Model formulation[J].Journal of Turbomachinery, 2006, 128(3): 57–67. |
| [6] | LANGTRY R B, MENTER F R, LIKKI S R, et al. A correlation-based transition model using local variables: Part Ⅱ: Test cases and industrial applications: GT-2004-53454[C]//ASME Turbo Expo 2004: Power for Land, Sea, and Air. New York: ASME, 2004, 4: 69-79. |
| [7] | MALAN P, SULUKSNA K, JUNTASARO E. Calibrating the γ-Reθ transition model for commercial CFD[C]//47th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Aerospace Sciences Meetings. Reston: AIAA, 2009. |
| [8] | 陈奕, 高正红. γ-Reθ转捩模型在绕翼型流动问题中的应用[J].空气动力学学报, 2009, 27(4): 411–418. CHEN Y, GAO Z H. Application of γ-Reθ transition model to flows around airfoils[J].Acta Aerodynamica Sinica, 2009, 27(4): 411–418.(in Chinese) |
| [9] | 钟伟, 王同光. 转捩对风力机翼型和叶片失速特性影响的数值模拟[J].空气动力学学报, 2011, 29(3): 385–390. ZHONG W, WANG T G. Numerical analysis of transition effect on stall performance of wind turbine airfoils and blades[J].Acta Aerodynamica Sinica, 2011, 29(3): 385–390.(in Chinese) |
| [10] | 郑赟, 李虹杨, 刘大响. γ-Reθ转捩模型在高超声速下的应用及分析[J].推进技术, 2014, 35(3): 296–304. ZHENG Y, LI H Y, LIU D X. Application and analysis of γ-Reθ transition model in hypersonic flow[J].Journal of Propulsion Technology, 2014, 35(3): 296–304.(in Chinese) |
| [11] | 孔维萱, 阎超, 赵瑞. γ-Reθ模式应用于高速边界层转捩的研究[J].空气动力学学报, 2013, 31(1): 120–126. KONG W X, YAN C, ZHAO R. γ-Reθ model research for high-speed boundary layer transition[J].Acta Aerodynamica Sinica, 2013, 31(1): 120–126.(in Chinese) |
| [12] | BENSASSI K, LANI A, RAMBAUD P. Numerical investigations of local correlation-based transition model in hypersonic flows: AIAA-2012-3151[R]. Reston: AIAA, 2012. |
| [13] | CHENG G, NICHOLS R, NEROORKAR K, et al. Validation and assessment of turbulence transition models: AIAA-2009-1141[R]. Reston: AIAA, 2009. |
| [14] | 张毅锋, 雷净, 张益荣, 等. 高超声速数值模拟平台转捩模型的标定[J].空气动力学学报, 2015, 33(1): 42–47. ZHANG Y F, LEI J, ZHANG Y R, et al. Calibration of transition model for hypersonic numerical simulation platform[J].Acta Aerodynamica Sinica, 2015, 33(1): 42–47.(in Chinese) |
| [15] | 张毅锋, 何琨, 张益荣, 等. Menter转捩模型在高超声速流动模拟中的改进及验证[J].宇航学报, 2016, 37(4): 397–402. ZHANG Y F, HE K, ZHANG Y R, et al. Improvement and validation of menter's transition model for hypersonic flow simulation[J].Journal of Astronautics, 2016, 37(4): 397–402.(in Chinese) |
| [16] | ZHANG X D, GAO Z H. A numerical research on a compressibility-correlated langtry's transition model for double wedge boundary layer flows[J].Chinese Journal of Aeronautics, 2011, 24(3): 249–257.DOI:10.1016/S1000-9361(11)60030-7 |
| [17] | YOU Y C, LUEDEKE H, EGGERS T, et al. Application of the γ-Reθ transition model in high speed flows[C]//18th AIAA/3AF International Space Planes and Hypersonic Systems and Technologies Conference. Reston: AIAA, 2012. |
| [18] | 夏陈超, 姜婷婷, 郭中州, 等. 压缩性修正对γ-Reθ转捩模型的影响研究[J].空气动力学学报, 2015, 33(5): 603–609. XIA C C, JIANG T T, GUO Z Z, et al. Effects of compressibility correction on γ-Reθ transition model[J].Acta Aerodynamica Sinica, 2015, 33(5): 603–609.(in Chinese) |
| [19] | 郑赟, 李虹杨. 基于新的经验关联公式的γ-Reθ转捩模型在高超声速流动中的应用[J].推进技术, 2015, 36(6): 839–845. ZHENG Y, LI H Y. Application of γ-Reθ transition model in hypersonic flow based on new correlation equation[J].Journal of Propulsion Technology, 2015, 36(6): 839–845.(in Chinese) |
| [20] | DENISSEN N A, YODER D A, GEORGIADIS N J. Implementation and validation of a laminar-to-turbulent transition model in the wind-us code: NASA/TM-2008-215451[R]. Washington, D. C. : NASA, 2008: 27. |
| [21] | RESHOTKO E. Is retheta/me a meaningful transition criterion?[J].AIAA Journal, 2007, 45(7): 1441–1443.DOI:10.2514/1.29952 |
| [22] | LANGTRY R B, MENTER F R. Correlation-based transition modeling for unstructured parallelized computational fluid dynamics codes[J].AIAA Journal, 2009, 47(12): 2894–2906.DOI:10.2514/1.42362 |
| [23] | 李虹杨, 郑赟. 尾迹对涡轮叶栅边界层转捩的影响[J].推进技术, 2017, 38(3): 532–538. LI H Y, ZHENG Y. Effect of wake on boundary layer transition of turbine cascade[J].Journal of Propulsion Technology, 2017, 38(3): 532–538.(in Chinese) |
| [24] | LI H Y, ZHENG Y. Effect of surface roughness on conjugate heat transfer of a turbine vane: GT-2016-56744[C]//ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition. New York: ASME, 2016: V05AT13A012. |
| [25] | NEUENHAHN T, OLIVIER H. Influence of the wall temperature and the entropy layer effects on double wedge shock boundary layer interactions[C]//14th AIAA/AHI Space Planes and Hypersonic Systems and Technologies Conference. Reston: AIAA, 2006. |
| [26] | REINARTZ B, BALLMANN J. Computation of hypersonic double wedge shock/boundary layer interaction[C]//26th International Symposium on Shock Waves. Berlin: Springer, 2008: 1099-1104. |
