本文研究的协同导航方法在本质上属于多源信息融合滤波问题,主要有集中式和分布式2种。集中式滤波要求融合中心汇集所有节点的测量信息,进行集中式数据处理,一般会对融合中心造成较高的通信和计算压力,而且一旦该中心出现故障,则容易导致系统崩溃。为了分散通信和计算压力,降低节点故障对系统的影响,分布式滤波逐渐成为研究的热点问题[3]。Olfati-Saber[4]建立了一种分布式卡尔曼滤波(Distributed Kalman Filter,DKF)计算框架,但该方法在实际工程应用中容易受到系统非线性因素的限制。进而,Battistelli和Chisci[5]提出了适用于非线性系统的分布式扩展卡尔曼滤波(Distributed Extended Kalman Filter,DEKF)。然而,DEKF对非线性系统的一阶线性化近似精度较低,并且需要计算系统的雅可比矩阵。为了提高非线性系统滤波精度,****们相继提出了无迹卡尔曼滤波(Unscented Kalman Filter,UKF)[6]和容积卡尔曼滤波(Cubature Kalman Filter,CKF)[7]。其中,CKF将非线性高斯加权积分分解为球面积分和径向积分,并采用一组等权值的容积点计算非线性高斯加权积分,具有比EKF和UKF更高的滤波精度和数值计算稳定性[8],已在工程中取得广泛的应用[9-10]。Wang等[11]采用正则单形变换群计算球面积分,提出了球面单形-径向容积卡尔曼滤波(Spherical Simplex-Radial Cubature Kalman Filter,SSRCKF),并且指出球面单形准则具有比CKF中的球面准则更高的精度。然而,CKF和SSRCKF 2种方法均采用矩匹配法计算径向积分,而该方法无法保证径向积分计算的最优性。为了提高径向积分精度,Shovan和Swati[12]提出一种容积求积分卡尔曼滤波(Cubature Quadrature Kalman Filter,CQKF),其采用高阶高斯-拉盖尔求积分准则计算径向积分,具有比矩匹配法更高的精度。然而,上述非线性滤波需要向分布式滤波中推广。
本文将球面单形准则与高斯-拉盖尔求积分准则相结合,提出了一种新的球面单形-径向容积求积分准则,将该准则嵌入DKF框架,得到了一种适用于非线性系统的分布式球面单形-径向容积求积分卡尔曼滤波(Distributed Spherical Simplex-Radial Cubature Quadrature Kalman Filter,DSSRCQKF)算法,并将该算法应用于解决多颗卫星对空间合作目标的协同导航问题,仿真实验结果验证了本文算法的有效性。
1 分布式协同导航数学模型 用导航星表示自身具备自主导航能力的卫星,用目标星表示空间合作目标,协同导航示意图如图 1所示。s个导航星处在一个分布式通信网络中,使用无向图G=(V, E)对该通信网络进行建模[13]。其中,V={1, 2, …, s}为导航星集合,E={(d, q)|d, q∈V}为通信链路集合。当导航星d和q之间可以通信时,(d, q)∈E,此时称导航星d和q互为邻居星。导航星d的邻居星集合用Nd表示,同时记Jd=Nd∪(d)为邻居星集与自身的并集。假设每个导航星均具备对目标星的测距能力,通过与其邻居星的分布式数据融合实现对目标星的协同一致定轨。
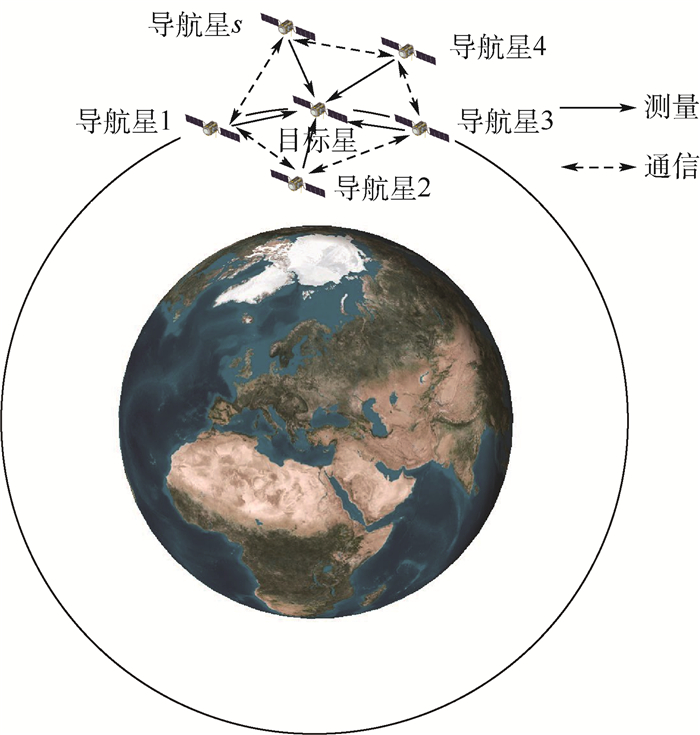 |
| 图 1 分布式协同导航示意图 Fig. 1 Schematic of distributed coordinated navigation |
| 图选项 |
1.1 协同导航状态方程 地球J2项非球形摄动是卫星所受到的最主要的摄动力。在J2000地心惯性坐标系中,考虑J2项摄动影响,卫星的轨道动力学模型为[14]
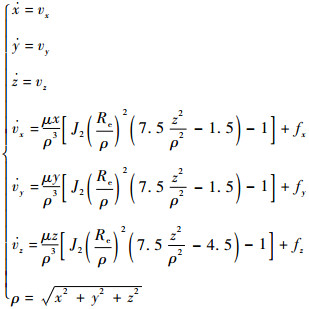 | (1) |
式中:X=(x y z vx vy vz)T为卫星的轨道状态;J2为带谐项系数;μ为地球引力常数;Re为地球半径;(fx fy fz)T为地球高阶非球形摄动、三体引力摄动和太阳光压摄动等摄动之和在3个坐标轴上的分量,在研究中可以等效成零均值的高斯白噪声。
用四阶龙格库塔法可以将式(1)写成如下离散状态方程的形式:
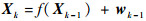 | (2) |
式中:Xk=(xk yk zk vx,k vy,k vz,k)T为k时刻的轨道状态;wk为系统噪声。
1.2 协同导航量测方程 使用微波测距技术可以直接测量目标星与导航星d之间的径向距离Rd,设导航星d的轨道位置为(xd yd zd)T,则测量值与轨道状态X有如下几何关系:
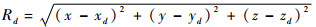 | (3) |
将式(3)的几何关系写成如下离散量测方程的形式:
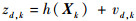 | (4) |
式中:zd,k为k时刻的量测值;vd,k为量测噪声。
2 分布式协同导航滤波算法 2.1 球面单形-径向容积求积分准则 考虑积分

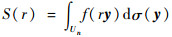 | (5) |
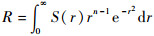 | (6) |
式中:Un为单位球体表面;σ(y)为面积分元素。
一般难以得到积分S(r)和R的解析解,因此考虑采用数值积分的方法对其进行近似。由文献[11, 15]可知,可以采用如下由2n+2个积分点构成的三阶球面单形准则对球面积分进行近似:
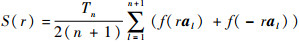 | (7) |
式中:
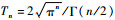
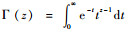
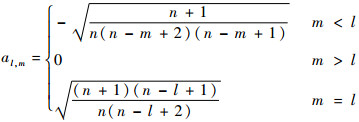 | (8) |
对径向积分
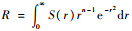
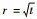
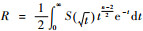
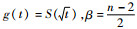
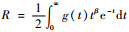
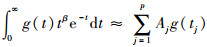 | (9) |
式中:tj为求积分点;Aj为对应的权值。求积分点可以由如下p阶切比雪夫-拉盖尔多项式[12]的解求得:
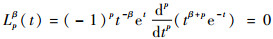 | (10) |
相应的权值可以由式(11)解得:
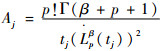 | (11) |
该准则的近似精度取决于求积分点的个数,当p=2时可以得到
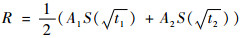 | (12) |
由式(10)、式(11)解得t1、A1、t2和A2的值为
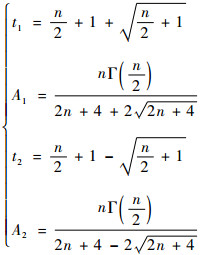 | (13) |
非线性卡尔曼滤波的核心是计算高斯加权积分
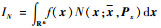
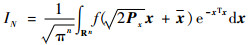 | (14) |
结合式(12)和t1、t2、A1、A2,可以得到如下计算IN的球面单形-径向容积求积分准则:
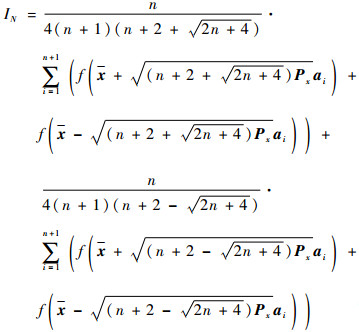 | (15) |
特别的,当式(9)中的p=1时,可以解得t1=n/2,A1=Γ(n/2),进而可推导出文献[11, 15]中的球面单形-径向容积准则。由此可见,本文提出的球面单形-径向容积求积分准则的精度要高于球面单形-径向容积准则。
用a=[a1 a2 … an+1]表示由al组成的矩阵,用[·]i表示矩阵的第i列,利用准则式(15)构造容积点
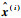
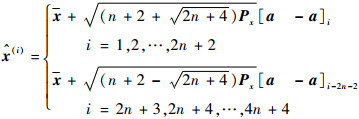 | (16) |
 | (17) |
2.2 DSSRCQKF算法 由状态方程式(2)和量测方程式(4)构成如下滤波系统方程,为了使算法研究更具有一般性,考虑状态向量xk∈Rn,量测向量zk∈Rc,同时为了使公式的表述更为简洁,在没有歧义的情况下省略下标d。
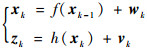 | (18) |
式中:wk和vk为不相关的零均值高斯白噪声,其协方差矩阵分别为Qk和Rk。利用统计线性误差传播方法可以得到交叉协方差矩阵Pxz的等价表达式Pxz≈Pk- HkT,从而定义伪观测矩阵
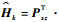
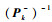
步骤1??滤波初始化。
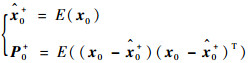 | (19) |
循环k=1, 2, …,完成以下步骤。
步骤2??时间更新。分别利用
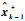
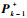
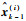
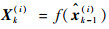 | (20) |
按照式(17)中ωi的取值加权合并Xk(i)得到先验状态估计值
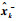
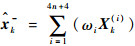 | (21) |
计算先验状态协方差矩阵Pk-:
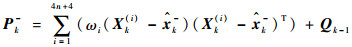 | (22) |
步骤3??量测更新。分别利用
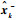
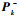
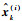
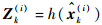 | (23) |
按照式(17)中ωi的取值加权合并Zk(i)得到量测预测值?k:
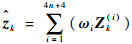 | (24) |
计算交叉协方差矩阵Pxz:
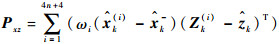 | (25) |
步骤4??与邻居星进行信息交互。向邻居星发送信息mk=(ik Ik
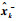
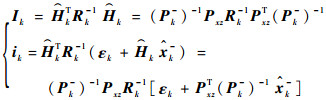 | (26) |
式中:εk=zk-?k为滤波新息;Rk为量测误差协方差矩阵。
步骤5??对接收到的信息进行融合。
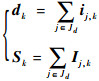 | (27) |
步骤6??状态更新。计算后验协方差矩阵Pk+:
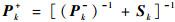 | (28) |
计算后验状态估计
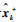
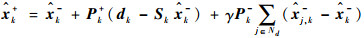 | (29) |
式中:
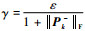
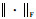
从式(18)可以看出,本文算法并没有对非线性函数的具体形式进行约束,因此DSSRCQKF算法不仅适用于本文所述的多星对合作目标的协同导航问题,同样可以应用于传感器网络目标跟踪、编队卫星协同导航和地基测控协同定轨等非线性系统协同滤波问题。
3 仿真实验 图 2为某型号卫星的地面实验模拟器,其上运行的高精度轨道预报算法经过实际飞行任务的检验,是可靠的仿真实验数据来源。仿真中考虑4颗导航星和1颗目标星,其轨道六根数见表 1。仿真时间为1 Jul 2016 12 : 00 : 00/UTC至1 Jul 2016 13 : 30 : 00/UTC,4颗导航星间的通信拓扑关系如图 3所示,假设星间测距精度为20 m。
 |
| 图 2 卫星地面实验模拟器 Fig. 2 Satellite simulator for ground experiment |
| 图选项 |
表 1 卫星轨道六根数 Table 1 Six orbital elements of satellites
| 卫星 | 半长轴/km | 偏心率 | 轨道倾角/(°) | 升交点赤经/(°) | 近地点幅角/(°) | 真近点角/(°) |
| 目标星 | 16378.1 | 0 | 27 | 35 | 30 | 10 |
| 导航星1 | 15378.1 | 0 | 45 | 60 | 0 | 0 |
| 导航星2 | 15378.1 | 0 | 10 | 60 | 15 | 20 |
| 导航星3 | 15378.1 | 0 | 38 | 60 | 20 | 0 |
| 导航星4 | 15378.1 | 0 | 70 | 60 | 30 | 0 |
表选项
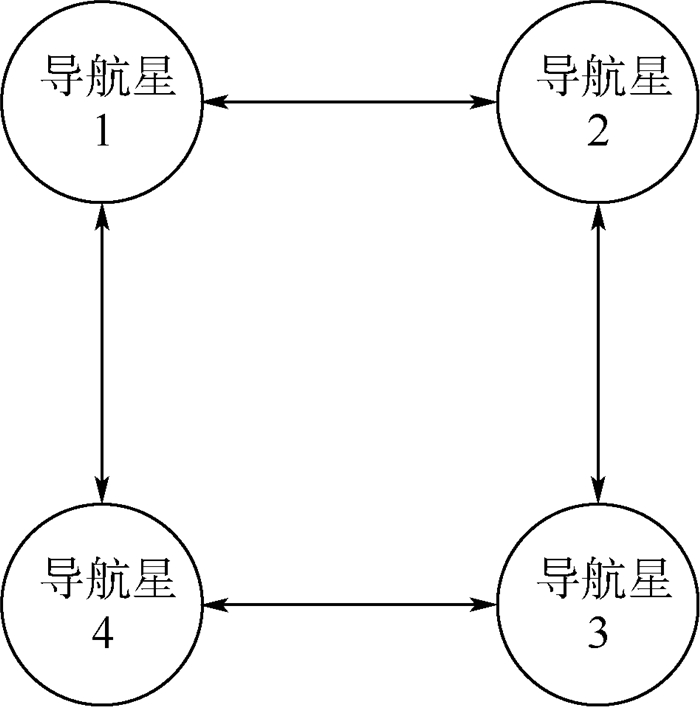 |
| 图 3 4颗导航星间的通信拓扑结构 Fig. 3 Communication topology structure among four navigation satellites |
| 图选项 |
滤波初值为
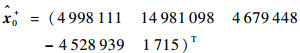 |
初始协方差矩阵为
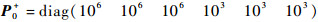 |
对比本文提出的DSSRCQKF算法与DEKF算法,参数ε取为0.01,用均方根误差(RMSE)描述导航星对目标星的实时定轨精度,运行200次Monte Carlo仿真,仿真结果如图 4~图 7所示。统计平均定轨RMSE,并分别列于表 2和表 3。从仿真结果可以看出,本文DSSRCQKF算法实时定位精度约为19 m,定速精度约为1.71 m/s,而DEKF算法定位精度约为30 m,定速精度约为1.73 m/s,从而表明本文算法具有更高的导航精度。对于多星协同导航问题,2种算法通过导航星间的分布式通信与数据融合,均可实现对目标星轨道状态的一致估计。每颗导航星的估计结果基本相同,结果间细微的差别主要由系统的非线性引起,因为在非线性卡尔曼滤波中,假设后验概率密度服从高斯分布,本质上是一种次优滤波方法,无法像线性卡尔曼滤波一样得到理论上的最优估计。而且为了将非线性卡尔曼滤波嵌入分布式滤波中而引入的伪观测矩阵同样会带来一些误差,但每颗导航星估计值间的差别在应用中是可以接受的。从导航星间的通信拓扑结构可以看出,每颗导航星仅与其邻居星通信,滤波中间数据在整个无线网络中分布式流动,从而避免了将所有数据发送到融合中心的集中式处理,提高了系统的灵活性。
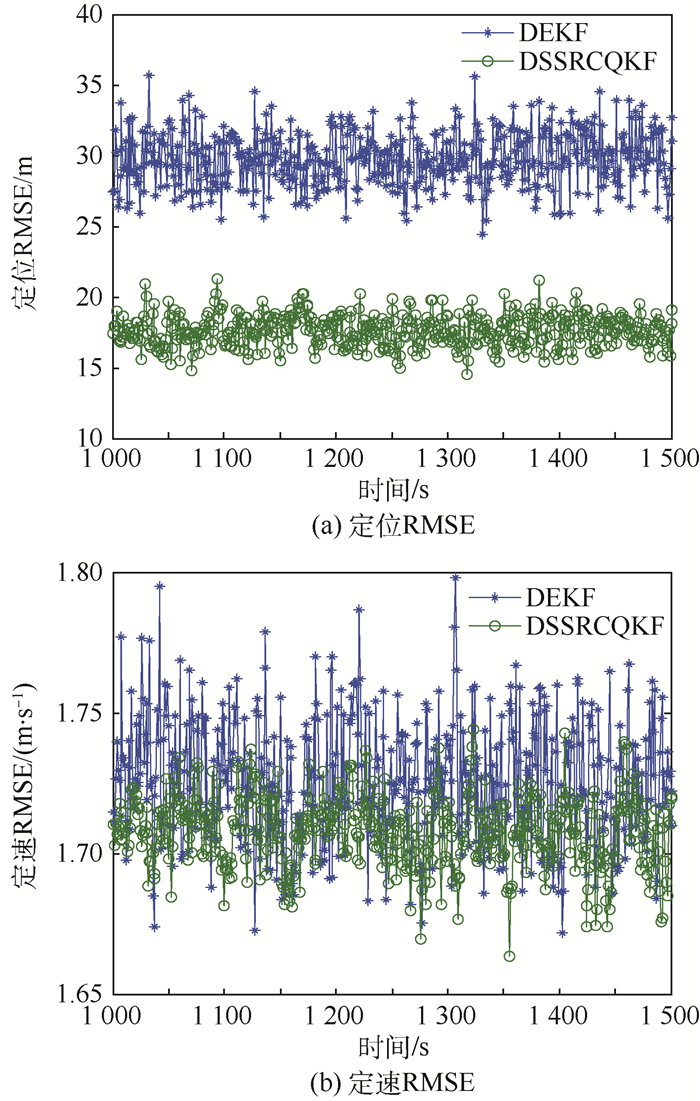 |
| 图 4 导航星1对目标星的实时定轨RMSE Fig. 4 Real-time orbit determination RMSE of navigation Satellite 1 to target satellite |
| 图选项 |
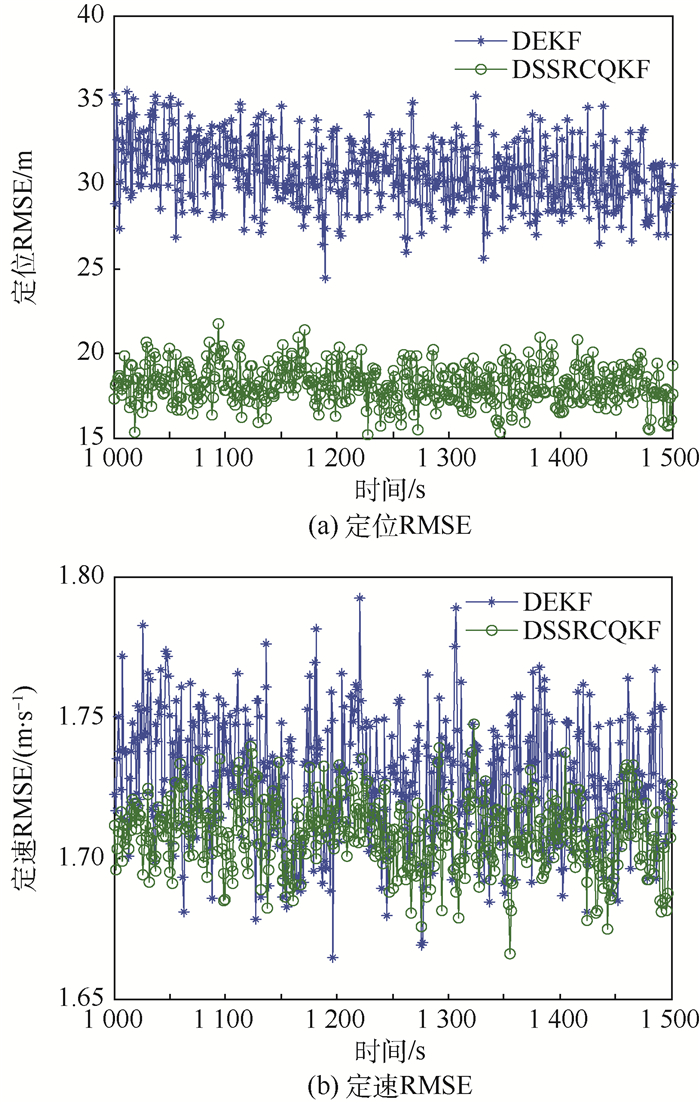 |
| 图 5 导航星2对目标星的实时定轨RMSE Fig. 5 Real-time orbit determination RMSE of navigation Satellite 2 to target satellite |
| 图选项 |
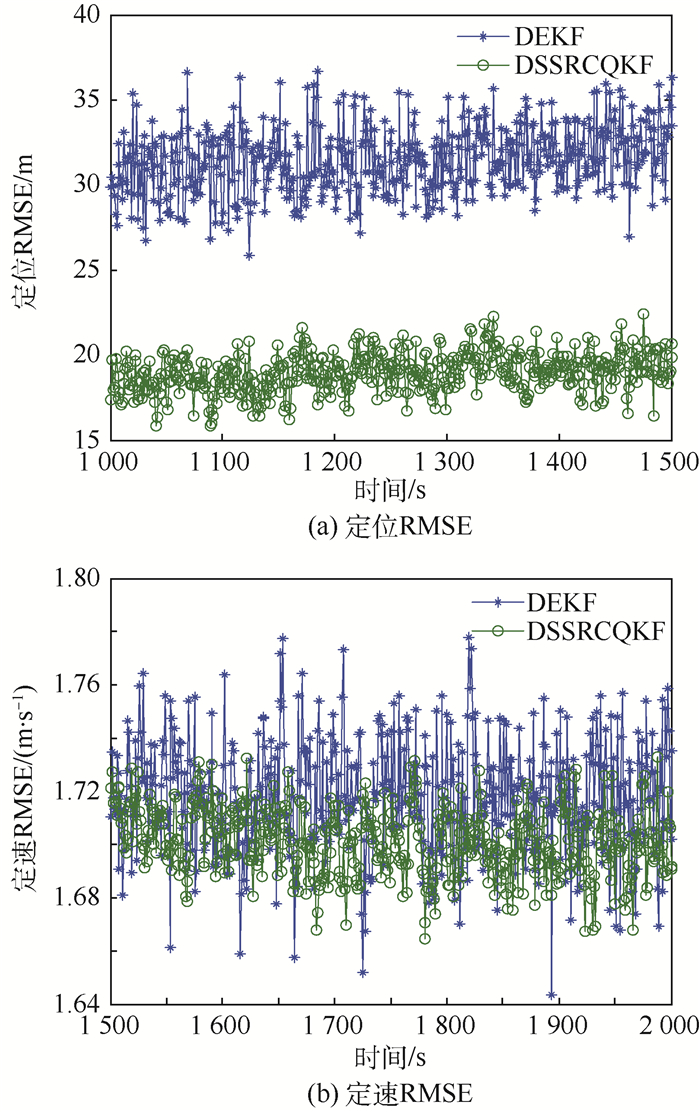 |
| 图 6 导航星3对目标星的实时定轨RMSE Fig. 6 Real-time orbit determination RMSE of navigation Satellite 3 to target satellite |
| 图选项 |
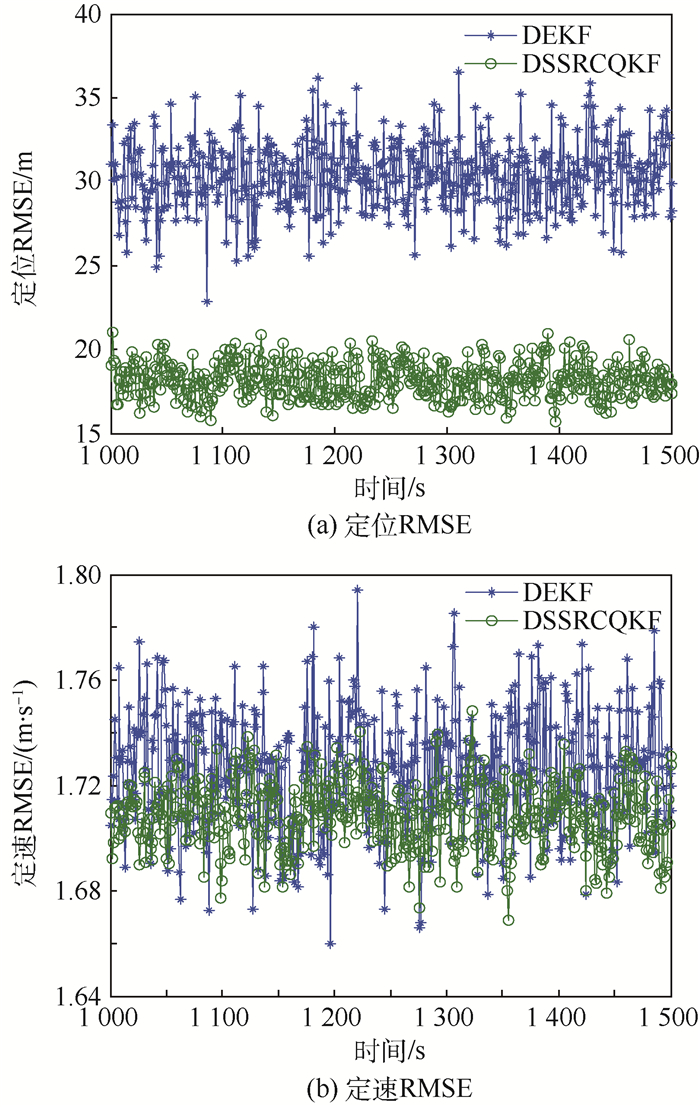 |
| 图 7 导航星4对目标星的实时定轨RMSE Fig. 7 Real-time orbit determination RMSE of navigation Satellite 4 to target satellite |
| 图选项 |
表 2 协同导航平均定位RMSE Table 2 Mean position RMSE of coordinated navigation
| 导航星 | 平均定位RMSE/m | |
| DEKF | DSSRCQKF | |
| 导航星1 | 30.775 | 18.633 |
| 导航星2 | 30.679 | 18.166 |
| 导航星3 | 31.456 | 18.969 |
| 导航星4 | 30.393 | 18.189 |
表选项
表 3 协同导航平均定速RMSE Table 3 Mean velocity RMSE of coordinated navigation
| 导航星 | 平均定速RMSE/(m·s-1) | |
| DEKF | DSSRCQKF | |
| 导航星1 | 1.726 | 1.708 |
| 导航星2 | 1.727 | 1.709 |
| 导航星3 | 1.727 | 1.709 |
| 导航星4 | 1.725 | 1.706 |
表选项
4 结论 1) 本文将球面单形准则与高斯-拉盖尔求积分准则相结合,提出一种新的球面单形-径向容积求积分准则,并将该准则嵌入DKF框架,得到一种适用于多星对空间目标协同导航的DSSRCQKF算法。该算法要求每颗导航星仅与其邻居星进行通信和数据融合,通过数据的分布式流动实现对目标星轨道状态的一致估计,从而避免了传统集中式处理中较高的通信和计算压力。
2) 仿真实验结果表明,本文DSSRCQKF算法中各导航星对目标星的实时定位精度约为19 m,定速精度约为1.71 m/s。DEKF算法中各导航星对目标星的定位精度约为30 m,定速精度约为1.73 m/s,相比之下本文算法将定位精度提高了11 m,定速精度提高了0.02 m/s,从而验证了本文算法的有效性。
3) 本文提出的DSSRCQKF算法还可以进一步应用于其他非线性系统协同滤波问题。
参考文献
| [1] | 王晓初, 尤政, 赵开春, 等. 分布式卫星系统的协同导航估计方法[J].宇航学报, 2013, 34(8): 1107–1113. WANG X C, YOU Z, ZHAO K C, et al. A cooperative navigation estimation method in distributed satellite system[J].Journal of Astronautics, 2013, 34(8): 1107–1113.(in Chinese) |
| [2] | 张艾, 李勇. 基于星间测距的编队卫星一致性导航算法[J].空间控制技术与应用, 2015, 41(3): 24–27. ZHANG A, LI Y. A consensus navigation algorithm for spacecraft formation based on distance ranging[J].Aerospace Control and Application, 2015, 41(3): 24–27.(in Chinese) |
| [3] | ZHOU Z W, FANG H T, HONG Y G. Distributed estimation for moving target based on state-consensus strategy[J].IEEE Transactions on Automatic Control, 2013, 58(8): 2097–2100. |
| [4] | OLFATI-SABER R. Distributed Kalman filtering for sensor networks[C]//Proceedings of the 46th IEEE Conference on Decision and Control. Piscataway, NJ: IEEE Press, 2007: 5492-5496. |
| [5] | BATTISTELLI G, CHISCI L. Stability of consensus extended Kalman filtering for distributed state estimation[C]//Preprints of the 19th World Congress the International Federation of Automatic Control. Amsterdam: Elsevier, 2014: 5520-5525. |
| [6] | JULIER S J, UHLMANN J K, DURRANTWHYTE H F. A new method for nonlinear transformation of means and covariances in filters and estimators[J].IEEE Transactions on Automatic Control, 2000, 45(3): 477–482.DOI:10.1109/9.847726 |
| [7] | ARASARATNAM I, HAYKIN S. Cubature Kalman filters[J].IEEE Transactions on Automatic Control, 2009, 54(6): 1254–1269.DOI:10.1109/TAC.2009.2019800 |
| [8] | ZAREI J, SHOKRI E. Convergence analysis of non-linear filtering based on cubature Kalman filter[J].IET Science, Mea-surement & Technology, 2015, 9(3): 294–305. |
| [9] | 钱华明, 黄蔚, 葛磊, 等. 基于四元数平方根容积卡尔曼滤波的姿态估计[J].北京航空航天大学学报, 2013, 39(5): 646–649. QIAN H M, HUANG W, GE L, et al. Attitude estimation based on quaternion square-root cubature Kalman filter[J].Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(5): 646–649.(in Chinese) |
| [10] | 方君, 戴邵武, 许文明, 等. 基于ST-SRCKF的超高速强机动目标跟踪算法[J].北京航空航天大学学报, 2016, 42(8): 1698–1708. FANG J, DAI S W, XU W M, et al. Highly maneuvering hypervelocity-target tracking algorithm based on ST-SRCKF[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(8): 1698–1708.(in Chinese) |
| [11] | WANG S Y, FENG J C, CHI K T. Spherical simplex-radial cubature Kalman filter[J].IEEE Signal Processing Letters, 2014, 21(1): 43–46. |
| [12] | SHOVAN B, SWATI. Cubature quadrature Kalman filter[J].IET Signal Processing, 2013, 7(7): 533–541. |
| [13] | BATTISTELLI G, CHISCI L, MUGNAI G, et al. Consensus-based linear and nonlinear filtering[J].IEEE Transactions on Automatic Control, 2015, 60(5): 1410–1415. |
| [14] | 李璟璟, 张迎春, 郑靖, 等. 基于信息融合的大椭圆轨道卫星组合导航方法[J].宇航学报, 2012, 33(9): 1234–1239. LI J J, ZHANG Y C, ZHENG J, et al. An information fusion based integrated navigation method for highly elliptical orbit satellite[J].Journal of Astronautics, 2012, 33(9): 1234–1239.(in Chinese) |
| [15] | 朱奇光, 袁梅, 王梓巍, 等. 机器人球面单径容积FastSLAM算法[J].机器人, 2015, 37(6): 709–716. ZHU Q G, YUAN M, WANG Z W, et al. A robot spherical simplex-radial cubature FastSLAM algorithm[J].Robot, 2015, 37(6): 709–716.(in Chinese) |
