自支撑臂属于充气梁的一种,其力学特性可以采用充气梁模型研究。一些****研究并提出了多种充气梁的刚度、强度和稳定性等静力学特性求解模型。如Comer和Levy[9]最早在1963年建立了充气梁的欧拉-伯努利模型;Main等[10]通过实验验证了Comer和Levy[9]模型的正确性;Liu等[11]提出了考虑压力追随效应的充气梁褶皱分析模型和相关屈曲分析模型;杜振勇[12]考虑褶皱区域对充气梁刚度的影响,提出了一种充气梁单元模型;Thomas、Bloch[13]和Elsabbagh[14]考虑褶皱、屈曲和材料非线性因素,建立了一种非线性充气梁单元模型。
柔性空间结构动力学研究也是重要的研究方向[15]。卫剑征[16]和徐彦[17]等分析了充气伸展臂、空间薄膜结构等充气展开结构的展开动力学问题;Main[18]、谭惠丰[19]和刘福寿[20]等得出充气梁的固有频率与充气压力有关;Jha和Inman[21]指出结构构型变化和充气压力会影响充气结构的振动特性。为了考虑充气压力的影响效应,****们一般采用壳或膜单元分析方法,但壳或膜单元在大型空间结构求解中会导致计算量过大。因此,合理梁单元模型的建立是非常必要的。Apedo等[22]考虑几何非线性和充气压力效应建立了充气织物梁单元模型;Thomas等[23]基于动态刚度法提出了充气梁的连续梁单元模型。这些模型主要用于单一材料构成的充气梁,而对于由2种或多种材料构成的自支撑臂结构,其梁单元模型的研究不成熟。
针对自支撑臂结构的振动模态分析问题,本文提出了一种考虑充气压力和自支撑壳离散特性的梁单元模型,并在MATLAB中实现该模型的编程;与实验结果对比验证了该模型的有效性。本文以细长充气展开自支撑臂为研究对象,研究充气压力和自支撑壳宽度等参数对结构固有频率的影响规律。
1 理论模型 1.1 自支撑臂振动微分方程 充气展开后的自支撑臂结构几何模型和横截面见图 1和图 2,自支撑臂长度为L,直径为D,自支撑壳个数为2N个,其中第i个自支撑壳与y轴的夹角为φi,自支撑臂关于xy平面对称,即第i个和第N+i个自支撑壳的尺寸和材料参数均相同。
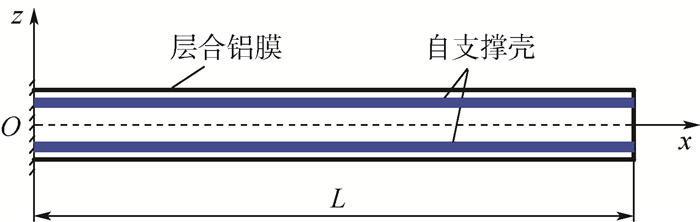 |
| 图 1 自支撑臂几何示意图 Fig. 1 Schematic of geometry of self-supporting boom |
| 图选项 |
 |
| 图 2 自支撑臂横截面示意图 Fig. 2 Schematic of cross-section of self-supporting boom |
| 图选项 |
自支撑臂结构的层合铝膜厚度为tl,等效弹性模量为El,泊松比为μl;第i个自支撑壳的弹性模量为Ei,泊松比为μi,厚度为ti,宽度为bi。基于自支撑壳对称的条件,同时考虑层合铝膜和自支撑壳的联合作用,自支撑臂的弯曲刚度可以近似表示为二者弯曲刚度的叠加:
 | (1) |
式中:E和I分别为自支撑臂的等效弹性模量和截面惯性矩;El和Es分别为层合铝膜和自支撑壳的等效弹性模量;Il和Is分别为层合铝膜和自支撑壳的截面惯性矩;ElIl和EsIs分别为层合铝膜和自支撑壳提供的弯曲刚度:
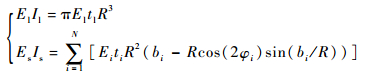 | (2) |
式中:R为自支撑臂的半径。
基于Timoshenko梁理论,假设自支撑臂振动过程中截面保持圆形,且不会出现屈曲和局部屈曲;自支撑臂的层合铝膜和自支撑壳在振动变形中厚度不变。
由于自支撑臂结构在y方向和z方向的振动形式相同,本文仅研究xy面内的二维振动。根据上述假设,得到自支撑臂的壁面上任意一点P(x, y, z)的位移(u1, v1, w1)为
 | (3) |
式中:u(x, t)和w(x, t)分别为P点所在截面中点Go的x方向和z方向位移;?(x, t)为截面转角。
通过式(3)得到自支撑臂的几何方程,即任意点P处的x方向应变εxx和z方向切应变γxz为
 | (4) |
自支撑臂的应变能可表示为
 | (5) |
式中:k为自支撑臂结构的剪切修正因子,依据文献[24]可得到圆柱薄壁梁的剪切修正因子为0.5;Gl和Al分别为层合铝膜的剪切刚度和截面面积;Gs和As分别为自支撑壳的等效剪切模量和面积;EsAs和GsAs分别为自支撑壳提供给自支撑臂的等效压缩刚度和剪切刚度。
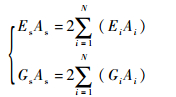 | (6) |
自支撑臂的动能为
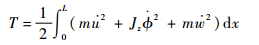 | (7) |
式中:



 | (8) |
式中:ρl和ρi分别为层合铝膜和第i个自支撑壳的密度。
哈密顿原理的变分形式为
 | (9) |
式中:δ为变分符号。
将式(5)和式(7)代入式(9)可得
 | (10) |
式中:



根据δu、δw和δ?的无关性,得到
 | (11) |
式(11)为自支撑臂的自由振动微分方程,引入形函数将位移变量进行离散,并分别代入单元的应变能和动能表达式,进而得到自支撑臂的单元刚度矩阵和单元质量矩阵,并建立自支撑臂振动特性的梁单元模型。
1.2 自支撑臂梁单元的建立 将自支撑臂离散为n个单元,第i个单元的长度为li,其节点编号为i和i+1,x方向坐标分别为xi和xi+1。
当x=xi,有u=ui, w=wi, ?=?i;当x=xi+1,有u=ui+1, w=wi+1, ?=?i+1。本文中u、w和?为独立的变量,可分别插值表示为
 | (12) |
式中:N2i-1(x)和N2i(x)为形函数,本文采用线性函数,即N2i-1=0.5(1-ξ),N2i=0.5(1+ξ),ξ=(2x-xi-xi+1)/li。
则第i个单元的应变能为
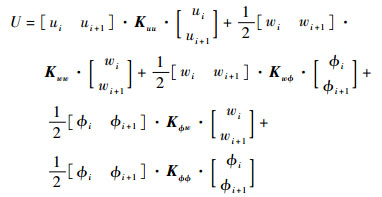 | (13) |
式中:
 | (14) |
将单元节点的位移表示为δe=[ui, wi, ?i, ui+1, wi+1, ?i+1]T,则自支撑臂的单元刚度矩阵为
 | (15) |
式中:k1=ElAl+EsAs;k2=ElIl+EsIs;k3=k(GlAl+GsAs)。
将形函数代入式(7)得到
 | (16) |
式中:质量矩阵M为
 | (17) |
自支撑臂结构在充气压力作用下,其构型会发生变化而影响抗弯刚度;同样,充气压力的预应力刚度效应也会影响结构的抗弯刚度,进而影响自支撑臂固有频率。
1) 结构构型变化效应
自支撑臂在充气压力p作用下,结构的环向张力为pR,则对应的层合铝膜处的预应力为pR/tl,自支撑壳与层合铝膜黏接处的等效预应力为pR/(tl+ti)。根据层合板理论,可近似认为层合铝膜和自支撑壳黏接处的弹性模量为
 | (18) |
通过几何关系,得到层合铝膜的环向应变为εl=pR/(Eltl),层合铝膜和自支撑壳黏接处的应变为εi=pR/[Eci(tl+ti)]。自支撑臂的截面周长改变量为
 | (19) |
根据自支撑臂的假设条件,结合式(1)和式(2)得到截面构型变化引起的刚度变化为
 | (20) |
式中:Δwi=pRwi/[Eci(tl+ti)];ΔR=Δl/(2π)。得到充气压力作用下自支撑臂的弯曲刚度为EI+Δ(EI)。
2) 预应力刚度效应
预应力下自支撑臂的振动方程的矩阵形式为
 | (21) |
式中:Q(t)为外界激振力;Kp为应力刚度矩阵,根据文献[25]可以得到,在轴向力F作用下的梁单元预应力刚度矩阵为
 | (22) |
对于自支撑臂而言,轴向力F=pA。修正后充气自支撑臂的刚度矩阵为
 | (23) |
由式(17)和式(22)可得充气压力下自支撑臂的单元刚度矩阵K′和质量矩阵M,对其进行坐标转换、组装得到结构的整体刚度和质量矩阵,组装方法见图 3,即首先将整体刚度矩阵的全部元素置零值,然后依次将每一个经过坐标转化的单元刚度矩阵组嵌入整体刚度矩阵的相应位置。在组装一个单元刚度矩阵时,分别将每一个元素krsm(根据单元的节点编号,找到与局部自由度r和s相对应的总体自由度编号I和J)累加到对应的整体刚度矩阵元素KIJ中,进而得到自支撑臂结构的整体刚度矩阵KIJ,同理得到结构整体质量矩阵MIJ。
 |
| 图 3 整体刚度矩阵或质量矩阵的组装方法 Fig. 3 Assembly method of global stiffness matrix or mass matrix |
| 图选项 |
结合上述得到的自支撑臂的整体刚度矩阵KIJ和质量矩阵MIJ,引入自支撑臂的位移边界条件,去除约束自由度相对应的刚度和质量矩阵中的行和列,生成满足位移边界条件的刚度矩阵K′IJ和质量矩阵M′IJ。最后采用MATLAB编程求解K′IJ和M′IJ的特征值和特征矩阵,进而得到自支撑臂的固有频率和振型。
相比传统梁单元模型,本文方法不仅可以考虑自支撑臂横截面变化引起的结构刚度变化效应,而且建立的结构质量矩阵比传统梁单元更加接近实际值,这是因为传统梁单元会将单元截面均匀化,使得其建立的质量矩阵无法准确反映自支撑壳的离散分布特性。本文也将进一步通过实验验证本文方法在自支撑臂固有频率方面计算的有效性。
2 自支撑臂振动模态分析 2.1 对比验证 文献[26]对L=1 m的由4根T50钢自支撑壳和层合铝膜组成的自支撑臂进行了实验测试,并得到0、10、20、30和40 kPa充气压力下自支撑臂的基频分别为17.55、17.70、17.70、17.71和17.98 Hz;其中自支撑臂的层合铝膜厚度为0.1 mm,弹性模量为12.36 GPa,泊松比为0.3,密度为1 960 kg/m3;自支撑壳的厚度为0.2 mm,宽度为15 mm,弹性模量为150 GPa,泊松比为0.3,密度为4 535 kg/m3。将自支撑臂结构离散为40个单元,并求解得到自支撑臂的固有频率,如表 1所示,与实验结果的平均偏差为8.00%;表 1中还列出了ANSYS Beam188单元计算结果,其与实验的平均误差为18.63%,验证了本文方法在自支撑臂振动特性方面的计算有效性。
表 1 自支撑臂振动模态对比 Table 1 Comparison of self-supporting boom's vibration mode
| 充气压力/kPa | 结构基频/Hz | 偏差/% | ||||
| 实验[26] | Beam188 | 本文方法 | Beam188与实验偏差 | 本文方法与实验偏差 | ||
| 0 | 17.55 | 20.23 | 18.38 | 15.27 | 4.73 | |
| 10 | 17.70 | 20.64 | 18.77 | 16.61 | 6.05 | |
| 20 | 17.70 | 21.04 | 19.16 | 18.87 | 8.25 | |
| 30 | 17.71 | 21.44 | 19.53 | 21.06 | 10.28 | |
| 40 | 17.98 | 21.82 | 19.90 | 21.36 | 10.68 | |
表选项
图 4给出了ANSYS Beam188单元模型和本文方法对自支撑臂基频的分析偏差随长细比(L/D)的变化关系。随着自支撑臂长细比的增加,二者偏差呈现非线性增加趋势;这也表明自支撑臂长细比较大时,相比Beam188单元模型,本文方法具有较高的计算精度。此外,本课题组曾对3 m自支撑臂基频进行了实验测试[27],得到0和40 kPa充气压力作用下,支撑2 kg重物的自支撑臂基频分别为0.960和0.961 Hz。通过本文方法得到2种工况下自支撑臂的基频分别为0.860和0.979 Hz,与实验值的平均偏差为6.13%,也进一步验证了本文方法的有效性。
 |
| 图 4 本文方法和ANSYS Beam188的基频求解偏差随长细比的变化曲线 Fig. 4 Variation curve of the first natural frequency solving deviation of proposed method and ANSYS Beam188 with slenderness ratios |
| 图选项 |
2.2 自支撑臂振动特性的参数影响分析 由于空间结构采用的充气展开自支撑臂一般长度较大,因此本文采用上述方法,以长为6.5 m的自支撑臂为例,研究充气压力和自支撑壳宽度等参数对结构振动模态的影响规律。本算例的自支撑臂由4个均匀分布自支撑壳和层合铝膜组成,其材料属性见表 2和表 3。
表 2 层合铝膜的材料属性 Table 2 Material properties of laminated aluminum membrane
| 参数 | 厚度/mm | 弹性模量/GPa | 泊松比 | 密度/(kg·m-3) |
| 数值 | 0.1 | 12.36 | 0.3 | 1 960 |
表选项
表 3 自支撑壳的材料属性 Table 3 Material properties of self-supporting shell
| 参数 | 宽度/mm | 厚度/mm | 弹性模量/GPa | 泊松比 | 密度/(kg·m-3) |
| 数值 | 15 | 0.2 | 150 | 0.3 | 4 535 |
表选项
通过本文方法得到自支撑臂前三阶固有频率随充气压力的变化曲线,如图 5所示。可以得到,无充气压力下自支撑壳的前五阶固有频率分别为1.68、10.53、29.48、57.72和95.33 Hz,且随着充气压力的变化较小;例如充气压力增加到40 kPa,自支撑臂的前五阶固有频率仅仅分别增加了0.81、1.14、1.03、1和1 Hz。图 6为本文方法得到的自支撑臂的前五阶固有振型,可得充气梁的振动模态主要为梁的弯曲振动。
 |
| 图 5 自支撑臂固有频率随充气压力的变化曲线 Fig. 5 Variation curves of self-supporting boom's natural frequency with internal pressure |
| 图选项 |
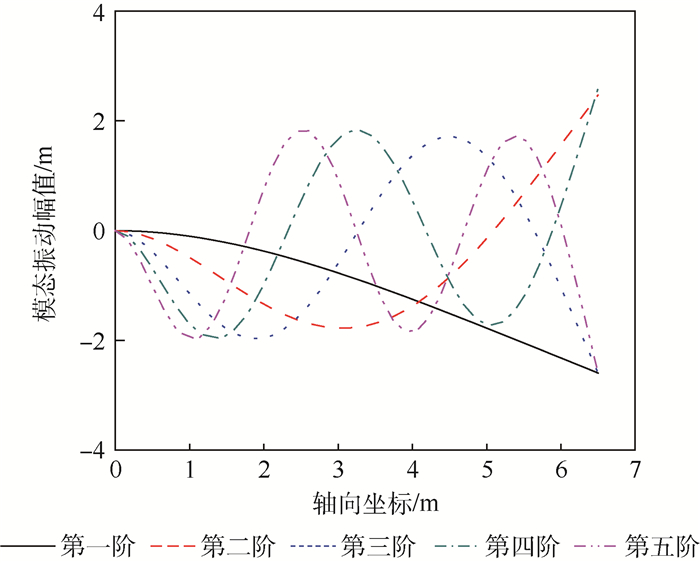 |
| 图 6 自支撑臂前五阶固有振型 Fig. 6 The first five modal shape of self-supporting boom |
| 图选项 |
充气展开自支撑臂的优点之一是可设计性高,通过自支撑壳材料和其分布的改变就可以实现自支撑臂力学特性的改变。为此,本文在保证自支撑臂的质量不变情况下,分别研究了自支撑壳宽度、个数及其分布对自支撑壳振动特性的影响规律。
首先研究自支撑壳宽度对结构固有频率的影响规律,研究中通过改变层合铝膜厚度保证自支撑臂质量不变。图 7为自支撑臂的固有频率随自支撑壳宽度的变化曲线。可以得到,随着自支撑壳宽度的增加,高阶模态频率近似于线性增加,而低阶模态频率变化较小;其中自支撑壳的宽度从5 mm增加到22 mm,结构基频仅仅增加了0.66 Hz,而第二至五阶频率分别增加了4.1、11.45、22.35和36.80 Hz。
 |
| 图 7 自支撑壳宽度对自支撑臂固有频率的影响曲线 Fig. 7 Effect curves of width of self-supporting shell on natural frequency of self-supporting boom |
| 图选项 |
在自支撑壳个数对自支撑臂振动特性的影响研究中,保证自支撑臂质量不变,即自支撑壳个数增加,自支撑壳宽度降低,其中个数为4、6、8和10个时自支撑壳的宽度分别为0.015、0.010、0.007 5和0.006 cm。图 8分析了自支撑壳个数对自支撑臂固有频率的影响规律,得到自支撑壳个数对结构固有频率没有影响。
 |
| 图 8 自支撑壳个数对自支撑臂固有频率的影响曲线 Fig. 8 Effect curves of number of self-supporting shell on natural frequency of self-supporting boom |
| 图选项 |
此外,自支撑壳的分布同样会对自支撑臂的固有频率产生明显的影响。以6个自支撑壳和层合铝膜构成的自支撑臂为例,研究自支撑壳分布对结构固有频率的影响规律。图 9为6个自支撑壳和层合铝膜构成自支撑臂的截面示意图,其中自支撑臂结构关于xOy和xOz面对称,即当φ2=90°,φ1+φ3=180°,或当φ1=0°,φ2+φ3=180°。首先对φ2=90°,φ1+φ3=180°的情况进行分析。图 10为自支撑臂固有频率随φ1的变化规律,其中低阶频率变化较小,高阶频率变化较大,例如φ1从15°增加到75°,前五阶固有频率分别增加了0.49、3.09、8.59、16.61和26.97 Hz。
 |
| 图 9 6个自支撑壳的自支撑臂截面示意图 Fig. 9 Schematic of cross-section of self-supporting boom with six self-supporting shells |
| 图选项 |
 |
| 图 10 自支撑臂固有频率随φ1的变化曲线(φ2=90°) Fig. 10 Variation curves of self-supporting boom's natural frequency with φ1(φ2=90°) |
| 图选项 |
然后对φ1=0°,φ2+φ3=180°情况进行分析,并得到自支撑臂固有频率随φ2的变化规律如图 11所示。固有频率接近于线性增长,φ2从15°增加到75°,结构固有频率分别增加了0.6、3.8、10.61、20.64和33.78 Hz。
 |
| 图 11 自支撑臂固有频率随φ2的变化曲线(φ1=0°) Fig. 11 Variation curves of self-supporting boom's natural frequency with φ2(φ1=0°) |
| 图选项 |
综上可以得到,自支撑壳的数量对结构的固有频率影响较小;其宽度和分布参数对低阶频率影响较小,对高阶频率影响较大。
3 结论 针对由层合铝膜和离散自支撑壳组成的自支撑臂,建立了其振动特性分析梁单元模型,并对其力学特性进行分析,得到如下结论:
1) 考虑充气压力的预应力和构型变化的梁单元模型计算方法与实验结果相互吻合,且计算的误差很小。
2) 当自支撑臂的长细比越大时,本文方法比Beam188单元模型具有更高的计算精度。
3) 随着充气压力的增加,自支撑臂结构的前五阶固有频率增加幅度不明显。
4) 在保证自支撑臂质量不变情况下,自支撑壳的个数对固有频率没有影响;自支撑壳宽度和其分布对低阶频率影响较小,而对高阶频率影响较大。
参考文献
| [1] | FELLINI R A, KROPP Y L. James Webb space telescope sunshield:Challenges in analysis of gossamer structures[J].Technology Review Journal, 2008, 16(1): 17–44. |
| [2] | AAROHI V. Lightweight, high-performance solar cells for high power-to-weight and deployable solar arrays: AIAA-2016-5283[R]. Reston: AIAA, 2016.https://www.researchgate.net/publication/308007414_Lightweight_High-Performance_Solar_Cells_for_High_Power-to-Weight_and_Deployable_Solar_Arrays |
| [3] | 刘龙斌, 吕明云, 肖厚地, 等. 基于压差梯度的平流层飞艇艇囊应力计算和仿真[J].北京航空航天大学学报, 2014, 40(10): 1386–1391. LIU L B, Lü M Y, XIAO H D, et al. Calculation and simulation of stratospheric airship capsule stress considering the pressure gradient[J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(10): 1386–1391.(in Chinese) |
| [4] | 卫剑征, 谭惠丰, 王伟志, 等. 充气式再入减速器研究最新进展[J].宇航学报, 2013, 34(7): 881–890. WEI J Z, TAN H F, WANG W Z, et al. New trends in inflatable re-entry aeroshell[J].Journal of Astronautics, 2013, 34(7): 881–890.(in Chinese) |
| [5] | JOSHUA B, GRANT S, JUSTIN K, et al. An investigation of three-dimensional flow over an undulating inflatable wing: AIAA-2016-0593[R]. Reston: AIAA, 2016.http://arc.aiaa.org/doi/abs/10.2514/6.2016-0593 |
| [6] | TAN D, YANG Z. Deployment simulation and comparison of inflatable antenna beam with different folded configurations[J].International Journal of Applied Electromagnetics and Mecha-nics, 2010, 33(3): 1513–1527. |
| [7] | 曹旭, 王伟志, 张宏伟, 等. 一种新型充气式重力梯度杆的研制和在轨展开试验[J].航天返回与遥感, 2014, 35(3): 20–27. CAO X, WANG W Z, ZHANG H W, et al. Development and space experiment of a new inflatable gravity gradient boom[J].Spacecraft Recovery and Remote Sensing, 2014, 35(3): 20–27.(in Chinese) |
| [8] | WEI J, TAN H, WANG W, et al. Deployable dynamic analysis and on-orbit experiment for inflatable gravity-gradient boom[J].Advances in Space Research, 2015, 55(2): 639–646.DOI:10.1016/j.asr.2014.10.024 |
| [9] | COMER R L, LEVY S. Deflections of an inflated circular-cylindrical cantilever beam[J].AIAA Journal, 1963, 1(7): 1652–1654.DOI:10.2514/3.1873 |
| [10] | MAIN A, PETERSON S W, STRAUSS A M. Load deflection behaviour of space-based inflatable beams[J].Journal of Aerospace Engineering, 1994, 7(2): 225–238.DOI:10.1061/(ASCE)0893-1321(1994)7:2(225) |
| [11] | LIU Y P, WANG C G, TAN H F. The interactive bending wrin-kling behaviour of inflated beams[J].Proceedings of the Royal Society A-Mathematical, Physical and Engineering Sciences, 2016, 472(2193): 20160504.DOI:10.1098/rspa.2016.0504 |
| [12] | 杜振勇. 充气梁弯皱特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2012. DU Z Y. Research on bending-wrinkling characteristics of inflated beams[D]. Harbin: Harbin Institute of Technology, 2012(in Chinese).http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D241186 |
| [13] | THOMAS J, BLOCH A. Non linear behaviour of an inflatable beam and limit states[J].Procedia Engineering, 2016, 155: 398–406.DOI:10.1016/j.proeng.2016.08.043 |
| [14] | ELSABBAGH A. Nonlinear finite element model for the analysis of axisymmetric inflatable beams[J].Thin-Walled Structures, 2015, 96: 307–313.DOI:10.1016/j.tws.2015.08.021 |
| [15] | 夏人伟. 自适应结构综述[J].北京航空航天大学学报, 1999, 25(6): 623–628. XIA R W. Overview of adaptive strusture[J].Journal of Beijing University of Aeronautics and Astronautics, 1999, 25(6): 623–628.(in Chinese) |
| [16] | 卫剑征, 毛丽娜, 杜星文. 空间卷曲折叠管充气控制展开动力学研究[J].工程力学, 2009, 26(1): 227–232. WEI J Z, MAO L N, DU X W. Study for inflatable control deployment dynamics of rolled booms[J].Engineering Mecha-nics, 2009, 26(1): 227–232.(in Chinese) |
| [17] | 徐彦, 关富玲. 可展开薄膜结构折叠方式和展开过程研究[J].工程力学, 2008, 25(5): 176–181. XU Y, GUAN F L. Fold methods and deployment analysis of deployable membrane structure[J].Engineering Mechanics, 2008, 25(5): 176–181.(in Chinese) |
| [18] | MAIN J A, CARLIN R A, GARCIA E, et al. Dynamic analysis of space-based inflated beam structures[J].Journal of the Acoustical Society of America, 1995, 97(2): 1035–1045.DOI:10.1121/1.412216 |
| [19] | 谭惠丰, 李云良, 毛丽娜, 等. 空间充气展开支撑管的自振特性研究[J].哈尔滨工业大学学报, 2008, 40(5): 709–713. TAN H F, LI Y L, MAO L N, et al. Free vibration characteristics of inflatable supporting tube[J].Journal of Harbin Institute of Technology, 2008, 40(5): 709–713.(in Chinese) |
| [20] | 刘福寿. 大型空间结构动力学等效建模与振动控制研究[D]. 南京: 南京航空航天大学, 2015: 49-74. LIU F S. Dynamic equivalent modeling and vibration control of large space structures[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2015: 49-74(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10287-1016751976.htm |
| [21] | JHA A, INMAN D. Importance of geometric non-linearity and follower pressure load in the dynamic analysis of a gossamer structure[J].Journal of Sound and Vibration, 2004, 278(1-2): 207–231.DOI:10.1016/j.jsv.2003.10.026 |
| [22] | APEDO K L, RONEL S, JACQUELIN E, et al. Free vibration analysis of inflatable beam made of orthotropic woven fabric[J].Thin-Walled Structures, 2014, 78: 1–15.DOI:10.1016/j.tws.2013.12.004 |
| [23] | THOMAS J C, JIANG Z, WIELGOSZ C. Continuous and finite element methods for the vibrations of inflatable beams[J].International Journal of Space Structures, 2006, 21(4): 197–222.DOI:10.1260/026635106780866033 |
| [24] | COWPER G R. The shear coefficient in Timoshenko's beam theory[J].Journal of Applied Mechanics, 1967, 33(2): 335–340. |
| [25] | PRZEMIENIECKI J S. Theory of matrix structural analysis[M].New York: McGraw-Hill, 1968: 388-391. |
| [26] | 宋博. 充气展开自支撑结构力学特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2015: 50-62. SONG B. Research of mechanical properties of inflatable self-supporting structure[D]. Harbin: Harbin Institute of Technology, 2015: 50-62(in Chinese).http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D754508 |
| [27] | WEI J Z, TAN H F, YU J X, et al. Dynamic testing and analysis of inflatable beams[J].Applied Mechanics and Materials, 2012, 226-228: 546–552.DOI:10.4028/www.scientific.net/AMM.226-228 |
