对于爬壁机器人来说，建立精确的运动学和动力学模型是保证完成所有预定目标的基础。Xu等^[1]建立了爬缆机器人的运动学和动力学模型；Provancher等^[2]建立了可切换各种表面的city-climber的动力学模型；Nam等^[3]采用拉格朗日方程推导出磁吸附柔性多体爬壁机器人的动力学模型。然而，上述建模过程是繁琐复杂的。事实上，创建沿预定轨迹移动的爬壁机器人的动力学模型也属于约束多体系统动力学建模的范畴。获得爬壁机器人精确动力学模型是实现其高品质运动控制的关键所在，进而保证爬壁机器人能够精准地沿预定轨迹运行，高精度地完成指定任务。约束多体系统传统的建模方法基于拉格朗日方程，其中拉格朗日乘子的数值解需要根据给定的初始条件求解得出^[4]。另外，还有很多其他的建模方法，如：Hamel方程，需要准速度辅助求解；Kane方程，需要一组广义伪速度辅助求解^[5]；Gibbs-Appell方程，需要伪速度和伪加速度辅助求解^[6]；Poincaré方程，需要使用一组伪速度辅助求解。值得说明的是，以上几种方程均只得到数值解。
1992年，由Udwadia和Kalaba^[7]提出的Udwadia-Kalaba方程可建立约束多体系统的解析动力学方程，该方法可以相对简单地建立完整约束和非完整约束下系统的运动方程，在不出现拉格朗日乘子的条件下，得出附加力矩的解析求法，成为分析动力学领域的一个重要突破，并凭借其在表达上的简洁性及一般性在各个领域得到了广泛应用，如卫星系统^[8]、工业机械臂^[9]、并联机械臂^[10]、柔性多体系统^[11]以及机器鱼^[12]等领域。
为此，本文基于Udwadia-Kalaba方程的建模思想，针对爬壁机器人动力学建模问题，将施加系统的预定轨迹视为系统的约束关系，并融合到系统的动力学建模过程中，从而获得爬壁机器人在预定轨迹下所需附加力矩的解析表达式及系统的解析动力学方程。然而，当初始条件与约束方程不相容时，出现了约束违约现象，采用Baumgarte稳定性方法^[13]以达到减小误差的目的，最终获得修正的爬壁机器人解析动力学模型，并通过数值仿真验证了该模型的正确性。
1 Udwadia-Kalaba方程 Udwadia-Kalaba方程建模过程需要3步^[14]：①利用拉格朗日方法建立未受约束系统的动力学方程；②描述系统所受约束的关系式；③利用Udwadia-Kalaba方程建立系统动力学方程。
1) 未受约束多体系统动力学方程
若未受约束多体系统用n维广义坐标q:=[q₁??q₂?? … ??q_n]^T∈Rⁿ描述，其动力学方程描述为

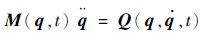(1)

式中：M(q, t)∈R^n×n为质量矩阵；Q(q, , t)∈Rⁿ为广义主动力矩阵；∈Rⁿ为广义速度；∈Rⁿ为广义加速度。
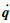
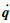
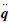
2) 约束描述
假设该系统受到p个约束作用，约束函数为

(2)

式(2)简化为

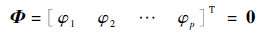(3)

假设约束式(3)具有充足的光滑度，不可积分约束对时间t求1次导数，可积分约束对时间t求2次导数，则约束方程表示为

(4)

式中：A(q, , t)∈R^p×n为约束矩阵；b(q, , t)∈R^p为p维矢量。
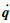
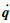
3) 约束多体系统动力学方程
由于上述约束的存在，产生了附加力矩，使得系统的动力学方程变为

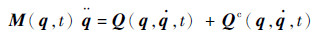(5)

式中：Q^c(q, , t)∈Rⁿ为附加力矩。
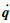
获得附加力矩的解析表达式是约束多体系统建模的重要目的，Udwadia和Kalaba^[15]给出了该问题的解：

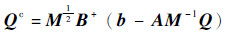(6)

式中：；上标“+”表示M-P逆。
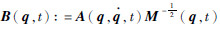
因此，约束多体系统的解析动力学方程称为Udwadia-Kalaba方程，具有如下形式：

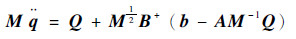(7)

按标准拉格朗日乘子形式，约束多体系统动力学方程可写为如下形式：

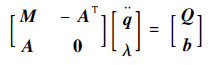(8)

式中:拉格朗日乘子λ=(AM^－1A^T)^－1(b－AM^－1Q)。
2 爬壁机器人动力学建模 本文所研究的爬壁机器人采用双腔体负压吸附方式吸附于墙壁，驱动电机采用左右两侧后置式分布，通过同步带驱动同侧的从动轮，形成四轮滑动转向机构，实现机器人的直行与转弯。为简化建模过程，作如下假设：①机器人的几何中心与质心重合；②轮子上无滑移运动；③忽略轮子的转动惯量以及轮子与墙壁之间的滑动摩擦力；④密封圈与墙壁之间的摩擦力关于机器人几何中心呈均匀对称分布。
图 1为爬壁机器人的示意图。图中：xOy为系统全局坐标系；q=[x, y, θ]^T为系统的广义坐标变量；c为质心；v为移动速度；θ为方向角；F_L和F_R分别为左、右电机产生的力；f为密封圈与墙壁之间的摩擦力；G₁为重力在v方向上的分力；J为绕质心的转动惯量；d为左、右轮距质心的距离。

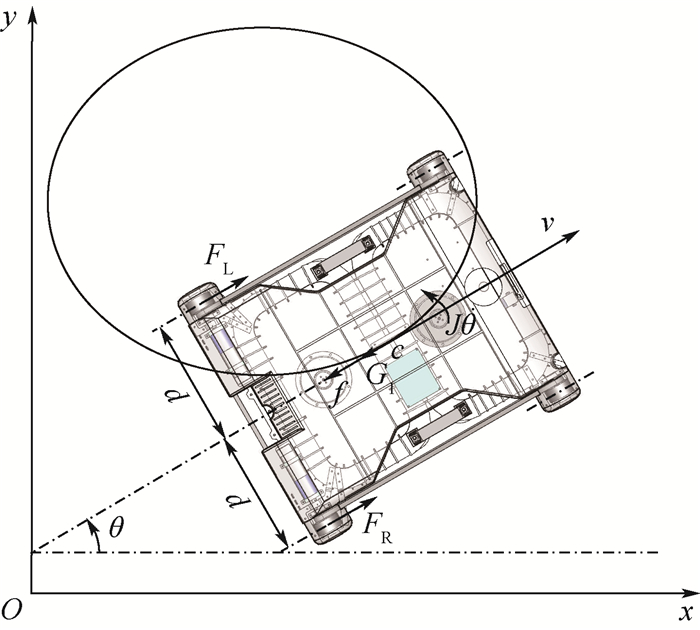图 1 爬壁机器人示意图 Fig. 1 Schematic of climbing robot

图选项

1) 动力学建模
① 根据牛顿第二定律，可得如下方程：

(9)

式中：m为爬壁机器人质量；F_R=τ_R/r，F_L=τ_L/r，τ_L和τ_R分别为左、右电机驱动力矩，r为轮子半径；G₁=mgsinθ；f=(1－k)μ_MF_S，F_S=PS，k为驱动轮压力系数，即驱动轮所受压力与整个机器人所受压力之比，μ_M为轮子与墙壁之间的摩擦系数，P为大气压与密封圈内气压的差值，S为密封圈有效吸附面积。
爬壁机器人的移动速度描述为

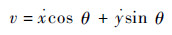(10)

对式(10)一次求导，得加速度为

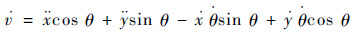(11)

式中：和分别为爬壁机器人的质心在x和y方向上的速度；和分别为爬壁机器人的质心在x和y方向上的加速度。
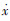
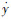
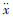
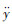
将式(11)代入式(9)，推导出如下方程：

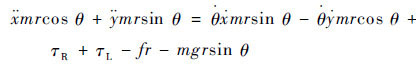(12)

② 根据力矩平衡原则，可得

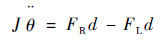(13)

或等价为

(14)

③ 爬壁机器人的固有约束表示为

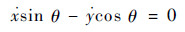(15)

对式(15)一次求导，得

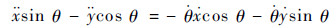(16)

至此，将式(12)、式(14)和式(16)表示为如下矩阵形式：

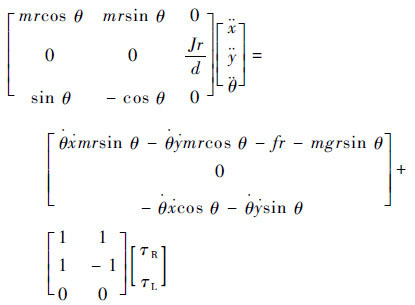(17)

式(17)可简化为

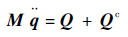(18)

式中：

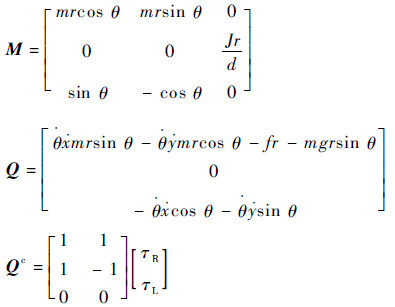2) 轨迹约束描述
爬壁机器人沿着预定轨迹移动以完成指定任务。假设轨迹约束可描述为

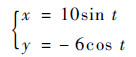(19)

对式(19)两次求导，并结合式(4)，有

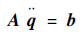(20)

式中：

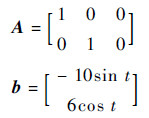3) 附加力矩解析表达式
结合式(6)，附加力矩Q^c表示为

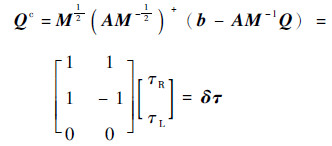(21)

式中：
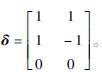
因此，可得电机驱动力矩τ为

(22)

3 数值仿真与分析 理论上，在任意时刻零阶和一阶的广义变量的初始值必须满足约束方程及其一阶导数。然而，初始条件与约束方程不相容的情况更为常见^[16]。基于此，假设初始条件为：x(0)=0，y(0)=-5.98，θ(0)=0；(0)=9.95，(0)=0，(0)=0.5。仿真参数为：m=5 kg，J=1 kg·m²，r=0.027 m，d=0.3 m，μ_M=0.8，k=0.53，P=2.5 kPa，S=0.06 m²。仿真结果如图 2~图 4所示。

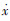
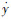
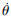
图 2 位移的数值解与理论解对比 Fig. 2 Comparison of displacements between numerical values and theoretical values

图选项

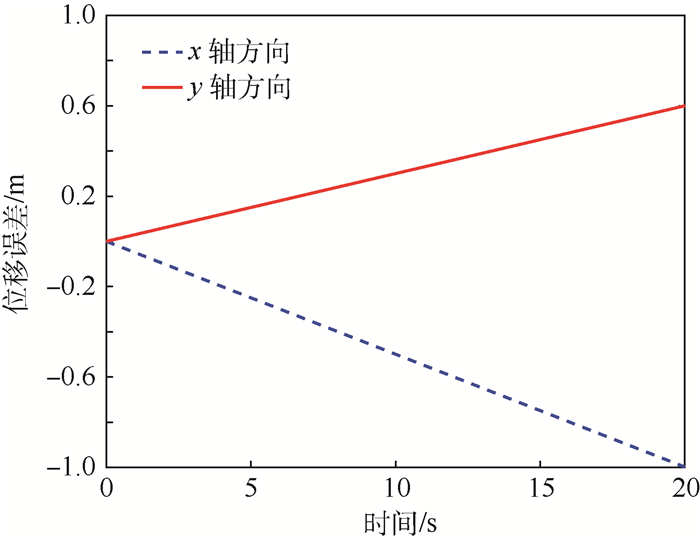图 3 位移的数值解与理论解的误差 Fig. 3 Displacement errors between numerical values and theoretical values

图选项

图 4 运行轨迹的数值解与理论解对比 Fig. 4 Comparison of trajectories between numerical values and theoretical values

图选项

图 2为x轴方向和y轴方向位移的数值解与理论解对比示意图。图 3为位移的数值解与理论解之间的误差示意图，x轴和y轴方向最大的位移误差分别达到-1.0 m和0.6 m，相比较x=10 m和y=6 m，这是不容忽视的，而且这些误差随时间递增。图 4所示的运行轨迹的数值解与理论解也有较明显的偏离。因此，有必要考虑减小误差。
4 约束违约抑制 初始条件与约束方程不相容将导致约束违约，通常使得仿真结果与实际情况相差较大，因此需要修正动力学方程。
Baumgarte约束违约稳定法利用反馈控制理论，将位移约束和速度约束引入加速度约束方程，通过约束修正得到稳定化的动力学方程。开环二阶微分约束方程，，被其稳定形式(即闭环形式)所代替：

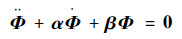(23)

式中：和βΦ可看作控制项，α=diag{α₁, α₂, …, α_p}，β=diag{β₁, β₂, …, β_p}。如果α_i>0, β_i>0，则Φ渐近趋于0。此时约束多体系统动力学方程可写为

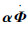
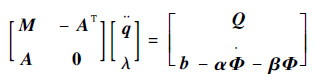(24)

则式(23)可转化为

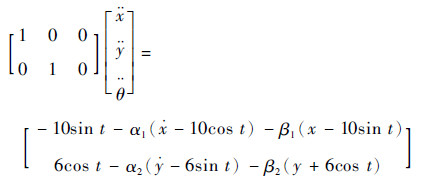(25)

初始条件与约束方程不相容的前提下，获得较为精确的系统的动力学方程，快速选择合适的Baumgarte参数成为关键问题。Baumgarte强调α和β参数可根据经验恰当选取^[13]。为简单起见，选取α₁=α₂=10, β₁=β₂=300。仿真结果如图 5~图 9所示。

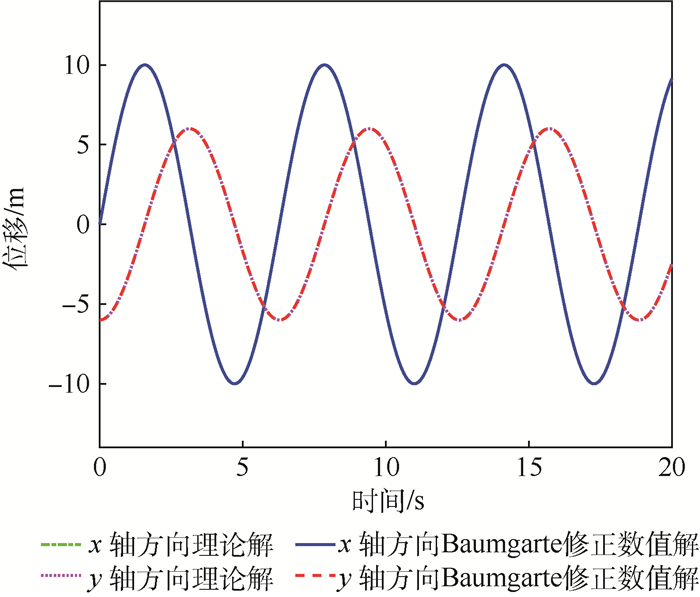图 5 位移的修正数值解和理论解对比 Fig. 5 Comparison of displacements between modified numerical values and theoretical values

图选项

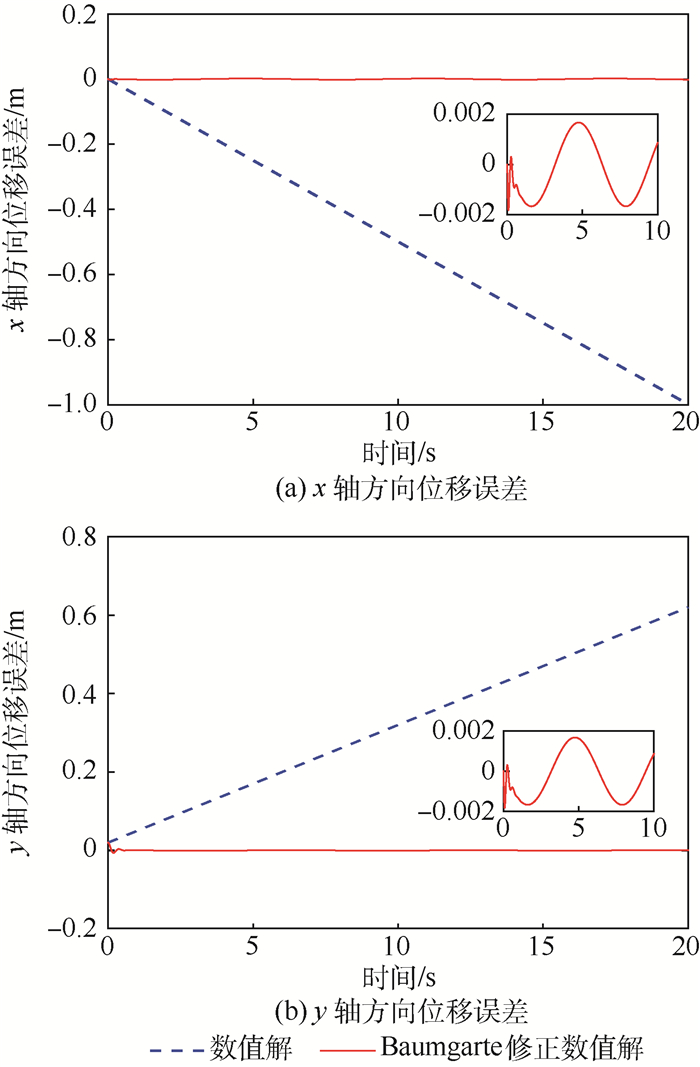图 6 位移误差的数值解与修正数值解对比 Fig. 6 Comparison of displacement errors between numerical values and modified numerical values

图选项

图 7 运行轨迹的修正数值解与理论解对比 Fig. 7 Comparison of trajectories between modified numerical values and theoretical values

图选项

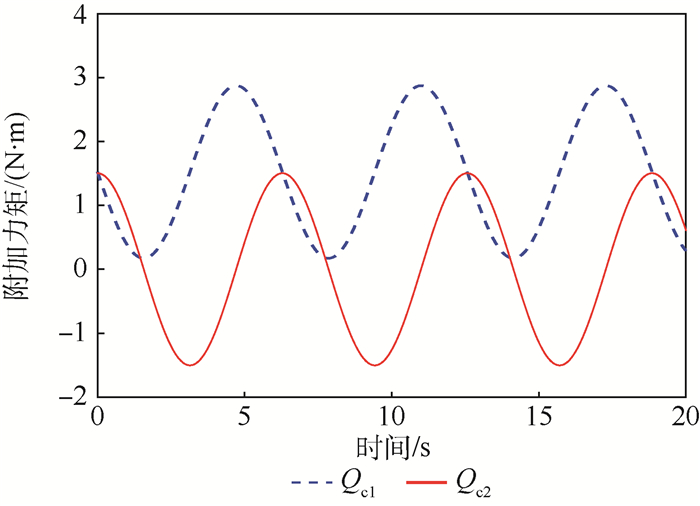图 8 附加力矩示意图 Fig. 8 Schematic of additional torques

图选项

图 9 电机驱动力矩示意图 Fig. 9 Schematic of driving torque generated by motors

图选项

图 5为x轴方向和y轴方向修正数值解与理论解的对比示意图。图 6为位移误差的数值解与修正数值解对比示意图，与图 3相比，x轴和y轴方向的位移误差的修正数值解均稳定在-0.002~0.002 m内。如图 7所示，修正后的运行轨迹的整体效果得到了很大改善。图 8为满足轨迹约束的附加力矩，图 9为电机驱动力矩示意图，图中实线和虚线分别表示左电机和右电机的驱动力矩。
5 结论 1) 应用Udwadia-Kalaba建模理论，在不引入拉格朗日乘子等额外参数的情况下，获得附加力矩的解析表达式和系统的解析动力学方程。
2) 采用Baumgarte约束违约稳定法有效地抑制约束违约，使得爬壁机器人运行轨迹能够很好地贴近系统预定的目标，具有较高精度。
3) 研究结果表明，本文建模方法可以快速、高效地建立爬壁机器人的动力学模型。
然而，摩擦力是影响爬壁机器人动力学建模效果的关键因素之一。因此，下一步工作将研究如何将摩擦力这一非线性因素融合到爬壁机器人动力学建模过程中。

参考文献

[1]	XU F, SHEN J, JIANG G P. Kinematic and dynamic analysis of a cable-climbing robot[J].International Journal of Advanced Robotic Systems, 2015, 12(7): 1–17.
[2]	PROVANCHER W R, JENSEN-SEGAL S I, FEHLBERG M A. ROCR:An energy-efficient dynamic wall-climbing robot[J].IEEE/ASME Transactions on Mechatronics, 2011, 16(5): 897–906.DOI:10.1109/TMECH.2010.2053379
[3]	NAM S, OH J, LEE G, et al. Dynamic analysis during internal transition of a compliant multi-body climbing robot with magnetic adhesion[J].Journal of Mechanical Science and Technology, 2014, 28(12): 5175–5187.DOI:10.1007/s12206-014-1141-z
[4]	BRAUN D J, GOLDFARB M. Eliminating constraint drift in the numerical simulation of constrained dynamical systems[J].Computer Methods in Applied Mechanics and Engineering, 2009, 198(37): 3151–3160.
[5]	PAN D, GAO F, MIAO Y. Dynamic research and analyses of a novel exoskeleton walking with humanoid gaits[J].Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 2014, 228(9): 1501–1511.DOI:10.1177/0954406213509611
[6]	KORAYEM M H, SHAFEI A M. A new approach for dynamic modeling of n-viscoelastic-link robotic manipulators mounted on a mobile base[J].Nonlinear Dynamics, 2015, 79(4): 2767–2786.DOI:10.1007/s11071-014-1845-8
[7]	UDWADIA F E, KALABA R E. A new perspective on constrained motion[J].Proceedings:Mathematical and Physical Sciences, 1992, 439(1906): 407–410.DOI:10.1098/rspa.1992.0158
[8]	CHO H, YU A. New approach to satellite formation-keeping:Exact solution to the full nonlinear problem[J].Journal of Aerospace Engineering, 2009, 22(4): 445–455.DOI:10.1061/(ASCE)AS.1943-5525.0000013
[9]	LIU J, LIU R. Dynamic modeling of dual-arm cooperating manipulators based on Udwadia-Kalaba equation[J].Advances in Mechanical Engineering, 2016, 8(7): 1–10.
[10]	HUANG J, CHEN Y H, ZHONG Z. Udwadia-Kalaba approach for parallel manipulator dynamics[J].Journal of Dynamic Systems, Measurement, and Control, 2013, 135(6): 1012–1030.
[11]	PENNESTRI E, VALENTINI P P, DE FALCO D. An application of the Udwadia-Kalaba dynamic formulation to flexible multibody systems[J].Journal of the Franklin Institute, 2010, 347(1): 173–194.DOI:10.1016/j.jfranklin.2009.10.014
[12]	ZHAO H, ZHEN S, CHEN Y H. Dynamic modeling and simulation of multi-body systems using the Udwadia-Kalaba theory[J].Chinese Journal of Mechanical Engineering, 2013, 26(5): 839–850.DOI:10.3901/CJME.2013.05.839
[13]	BAUMGARTE J. Stabilization of constraints and integrals of motion in dynamical systems[J].Computer Methods in Applied Mechanics and Engineering, 1972, 1(1): 1–16.DOI:10.1016/0045-7825(72)90018-7
[14]	SCHUTTE A, UDWADIA F. New approach to the modeling of complex multibody dynamical systems[J].Journal of Applied Mechanics, 2011, 78(2): 856–875.
[15]	UDWADIA F E, KALABA R E. What is the general form of the explicit equations of motion for constrained mechanical systems[J].Journal of Applied Mechanics, 2002, 69(3): 335–339.DOI:10.1115/1.1459071
[16]	CHO H, UDWADIA F E. Explicit solution to the full nonlinear problem for satellite formation-keeping[J].Acta Astronautica, 2010, 67(3): 369–387.