不确定性参数除了具有客观变量随机性外,同时还存在信息不完整、不精确性,如统计数据和专家信息等[7]。近30年来,各种不确定性分析理论出现,明确地将不完整性与随机性区分开来,如非可加集合函数,将集值与概率相结合,如Walley[8]提出的不精确概率,由概率函数组成的集合描述部分缺失概率信息。Dempster[9]在随机集的基础上提出更加具有约束性的理论—证据理论,由集值描述不完整信息,后经Shafer[10]和Smets[11]完善,形成主观非统计模式下的不确定性理论。再后来,出现了更具约束性的理论框架—可能性理论,该理论以可能性测度表征参数的不精确性,模糊集为其典型代表[12]。可能性理论也可解释为嵌套的随机集,使得不完整概率信息以连续函数表示并被分解为模糊区间的形式。
概率论作为常用的不确定性刻画与传播工具,其有效性受到许多****的质疑[7, 13-14];另外,当数据不充分、信息不完整时,单一概率无法有效刻画认知不确定性。对此,Zadeh[12]提出模糊集理论,在此基础上Yager[15]进一步提出模糊测度以刻画认知不确定性;Flage等[16]提出将概率与模糊集相结合的不确定性分析框架,并应用于故障树传播不确定性;Helton等[17]采用证据理论描述认知不确定性参数,并对参数敏感性进行了分析;Wang和Qiu[7]提出一种随机与区间数相结合的不确定性传播框架,分析稳态情形下的热传导不确定性问题。当风险模型中同时存在随机与认知不确定性时,Guyonnet等[18]提出一种概率与可能性分布相结合的混合不确定性分析框架;Tonon[19]提出基于随机集理论传播认知不确定性,对比了不同离散精度下相对误差对不确定性传播的影响。上述方法,只考虑1种或2种理论的结合来刻画传播随机与认知不确定性,并没有将异类不确定性信息建立统一的理论框架来研究混合不确定性传播问题。
离散随机集是一种广义的随机变量,离散随机集描述的是对区间的概率指配,且区间值比点值更具描述不精确性的能力。因此,随机集理论框架同时具备刻画参数的随机与认知不确定性。为此,针对上述Ferson和Ginzburg[4]提出的问题①和③,本文提出基于变步长离散随机集的风险混合不确分析方法,同时给出异类不确定性信息的统一随机集刻画框架,设计了一种变步长不确定性信息的随机焦元配置策略,对比分析了2种离散化策略,并进行讨论分析。针对不一致信息采用Dempster-Shafer(D-S)证据理论融合多源冲突信息。通过数值算例验证了本文方法的有效性和可行性。
1 不确定性刻画方法 1.1 随机集理论 随机集具有较强的不确定性信息处理能力。首先,随机集是指取值为集合的随机元,是概率论中随机变量概念的推广,因此具备描述事件的随机属性,即随机不确定性。另外,随机集的取值为集合或者区间数值,区别于概率论中的点值变量,具有描述不精确性的能力,具备描述主观知识的能力。又由于随机集不必知道概率分布中的方差、均值以及统计模型等信息,因此具备描述由于知识不完整情形下的主观不确定性,即认知不确定性能力。
在此,给出随机集的基本理论[20]:
(Ω, σΩ, PΩ)为一概率空间,设实数域内非空集合X及其幂集
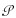
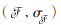
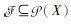

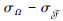
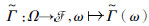
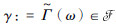



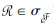




当


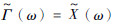

 | (1) |
 | (2) |
且有
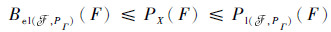 | (3) |
当F确定时,Fc为F的补,式(3)等号成立。显然,信度函数和似真函数是一双重模糊测度,满足如下关系:
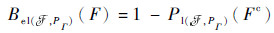 | (4) |
 | (5) |
当
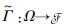

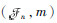
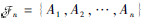
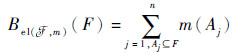 | (6) |
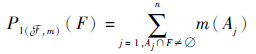 | (7) |
为处理变量之间的相互关系,引入随机关系X=?i=1dXi,随机关系(?, ρ)是定义在边缘随机集(
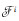
 |
映射f考虑了边缘随机集的依赖性,若(
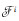
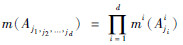
已知映射g:X→Y,随机集(

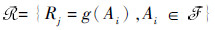 | (8) |
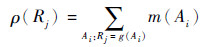 | (9) |
式中:Rj为?的焦元;Ai∈

根据文献[20]对随机集与概率包络上下界的关系,有如下关系:
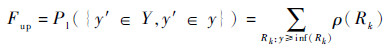 | (10) |
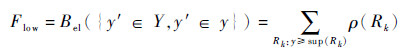 | (11) |
式中:Y为随机集(?, ρ)的辨识框架。
1.2 D-S证据理论 n个相互独立的元素命题集构成辨识框架Θ,Θ的幂集合2Θ中含有元素的个数为2N,记为[9]
 | (12) |
定义1??已知存在辨识框架Θ,则定义信度函数Bel如下:
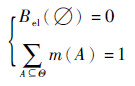 | (13) |
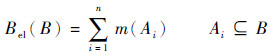 | (14) |
式中:Bel(B)为所有包含于B的元素信度之和。
定义2??已知存在辨识框架Θ,则定义似真函数Pl如下:
 | (15) |
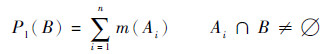 | (16) |
在概率理论框架下,事件A的概率与其补集之和等于1;在证据理论框架下,事件A的信度与其信度补集之和小于1。其次,信度函数与似真函数存在以下关系:
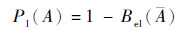 | (17) |
 | (18) |
m1与m2为相互独立的信度函数,X与Y合成新的证据焦元采用加法原则生成一个新的概率分配(BPA)[24],D-S证据合成规则为[25]:
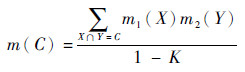 | (19) |
 | (20) |
式中:K为m1与m2的冲突系数;K=0时,m1与m2无冲突;K=1时,m1与m2完全冲突。
2 混合不确定性的随机集刻画 Dubois等[26]提出将概率分布转化为可能性分布,然后在可能性框架下进行统一处理。反之,Oussalah[27]提出将可能性分布转为概率分布的思路。但是,将概率分布转化为可能性分布将丢失信息,同理,可能性分布转化为概率分布将增加额外信息,且丢失和增加的信息无法量化与获取,因此有必要提出一种通用的不确定性信息分析框架,本文提出采用随机集理论作为混合不确定性传播理论框架,将异类不确定性信息转化为统一的随机集来刻画。
2.1 概率分布的随机集刻画 概率密度函数PDF(x), x为变量且有界表示为
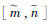
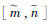
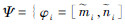
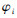
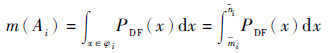 | (21) |
若x为无界参数,即x∈R,记为Ix=[-∞, +∞],则需要估计一个区间
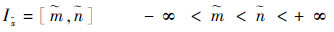 | (22) |
使得x以极高的概率包含于Ix。若记
 | (23) |
则根据实际需要确定限值δ≥0,使
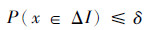 | (24) |
然后,再按以上x有界的方法将概率分布信息转化为随机集表示。
2.2 概率包络的随机集刻画 概率分布参数在不精确情形下,通常采用区间值的描述。例如已知x服从正态分布N(μ, σ2),其中μ∈[α, β], σ∈[χ, γ],则概率分布曲线变为概率包络(p-box)的形式。
设参数x的累积概率分布函数为CDF(x),其概率包络上界为CDF(x),下界为CDF(x),则可通过平均离散法(Averaging Diseretization Method, ADM)或外离散法(Outer Discretization Method, ODM)把概率包络信息转化为随机集表示[19]。
2.2.1 平均离散法 将p-box上、下界CDF(x)、CDF(x)的CDF轴值域[0, 1]离散化为n个子区间,各区间长度Mj>0(j=1, 2, …, n),且M0=0,则x的第j个焦元为区间数值
 | (25) |
BPA为
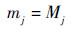 | (26) |
若n个子区间距离相等,即Mj=1/n,则相应的随机集焦元和BPA为
 | (27) |
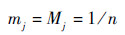 | (28) |
2.2.2 外离散法 将p-box上、下界CDF(x)、CDF(x)的值域[0, 1]离散化为n个子区间,各区间长度Mj>0(j=1, 2, …, n),且M0=0,则x的第j个焦元为
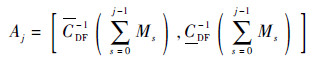 | (29) |
同理,BPA分配为
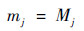 | (30) |
式中:

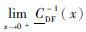
若n个子区间距离相等,即
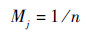 | (31) |
则离散化后的随机集焦元和BPA分配为
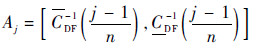 | (32) |
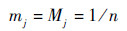 | (33) |
2.3 可能性分布的随机集刻画 Florea等[29]系统地研究了可能性分布到随机集的描述过程,并给出了对应的距离测度判据。
设u为定义在离散域Θ上的模糊集,αi为模糊隶属函数μu(θ)的象,θ?Θ,且有
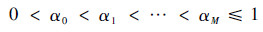 | (34) |
则模糊集u的随机集描述为(

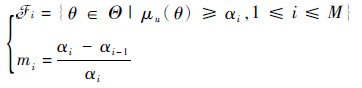 | (35) |
若u为定义在连续域Θ上的模糊集,先将Θ离散为M个嵌套焦元,再用上述离散法将μu(θ)表示为随机集描述。
2.4 区间分布的随机集刻画 针对单一区间分布信息A=[a, b],可作为独立焦元来处理,且有m(A)=1,当有n个区间分布信息时,且区间信度未知,则每一区间信息作为一个独立焦元Ai,m(Ai)=1/n。若区间信息的信度不等,通常采用D-S证据合成公式对信度区间信息进行融合。例如:对参数x,给出2组区间信息描述,如表 1所示。
表 1 参数x的证据区间信息 Table 1 Evidence interval information of parameter x
| 区间信息 | 焦元1 | 焦元2 | 焦元3 |
| 区间1 | m([0.5, 1.0])=0.3 | m([1.0, 1.4])=0.2 | m([1.2, 2.0])=0.5 |
| 区间2 | m([0.6, 1.0])=0.2 | m([0.5, 1.4])=0.4 | m([1.0, 2.0])=0.4 |
表选项
利用式(19)的D-S证据合成公式对区间信息进行合成,结果如表 2所示。
表 2 参数x的联合证据区间信息 Table 2 Combination of evidence interval information of parameter x
| 焦元A | [0.6, 1.0] | [0.5, 1.0] | [1.0, 1.4] | [1.2, 1.4] | [1.2, 2.0] |
| m(A) | 0.081 1 | 0.162 2 | 0.216 2 | 0.270 3 | 0.270 3 |
表选项
当区间信息存在高度不一致时,D-S证据合成公式存在合成悖论难题,针对这一问题,许多****做了改进,确保冲突信息的合成结果更为合理。
3 混合不确定性传播方法 3.1 离散随机集步长配置策略 文献[19]分析了基于随机集的可靠性分析方法,采用均匀离散步长将概率包络分布信息转化为随机集的处理框架,但存在截尾相对误差大的不足。为此,本文提出一种不确定性变量分布的变步长离散化方法,步长分配原则确保变量分布在截尾部分具有相对较密的离散点,不失一般性,给出具有对称特性的正态累积分布为例说明,具体步骤如下:
步骤1??正态分布的累计分布包络曲线上、下界CDF、CDF,如图 1所示,取值域1/2为分界点,设离散区间数为n。
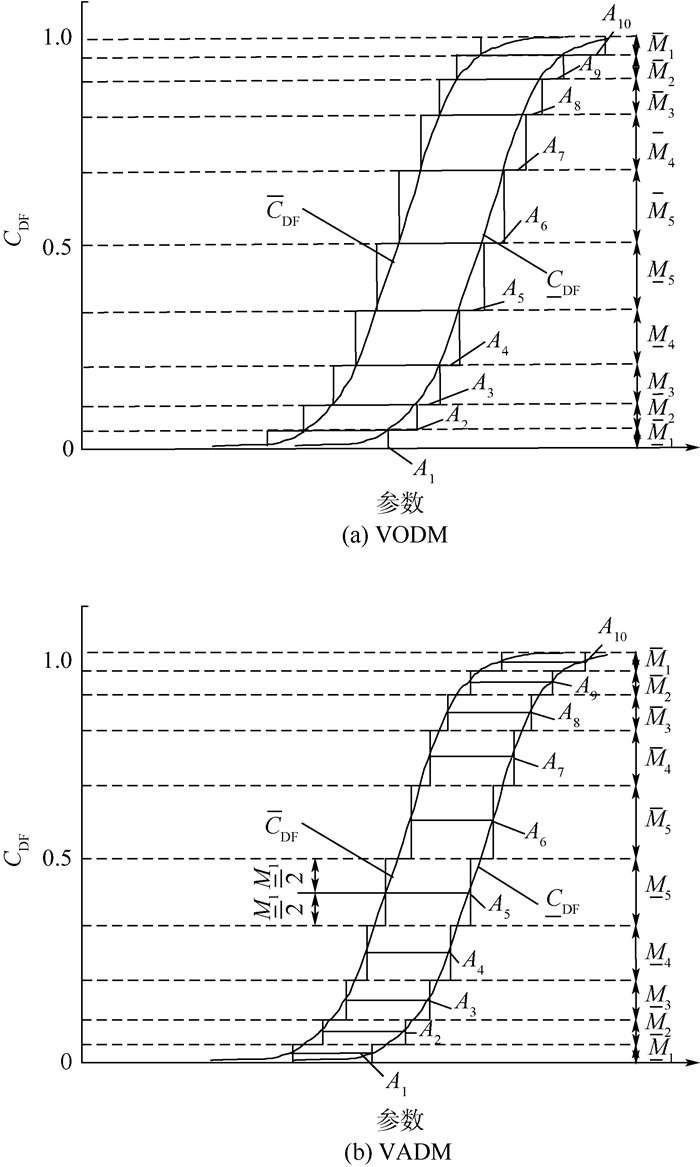 |
| 图 1 p-box的离散化方法 Fig. 1 Discretization method of p-box |
| 图选项 |
步骤2??以分界点下半部分[0, 1/2]为例,区间[CDF(0), CDF(1/2)]与[CDF(0), CDF(1/2)]各离散为n/2个区间,与坐标轴交点为 αi,0=α1 < α2 < … < αn/2=1/2。
步骤3??焦元区间Ai=[CDF-1( αi),CDF-1(αi+1)],其BPA为Mi=αi+1-αi,不失一般性,设焦元区间呈等差数列分布,且α1=d,则
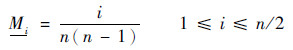 | (36) |
图 1(a)和(b)分别为p-box的变步长外离散法(VODM)与变步长平均离散法(VADM)随机集刻画,其中,n=10。
3.2 混合不确定性传播框架 工程系统风险评估中,各种类型的不完整、不精确信息通常采用不同理论框架进行刻画与处理。随机集同时具备处理随机性与不完整信息的能力,在随机集理论框架下构建风险的统一模型。设系统的风险模型为
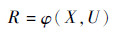 | (37) |
式中:X为确定性变量;U为不确定性变量,受不完整、不精确性的影响,既包含随机不确定性变量又包含认知不确定性变量,其描述可为随机变量、可能性变量、区间变量、证据变量等。采用基于随机集的混合不确定性刻画方法将U用随机集表示为(ζui, Mui),则
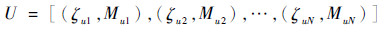 | (38) |
由于确定性变量已知,式(37)可写为
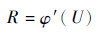 | (39) |
若不确定性变量存在不一致、冲突,在随机集描述框架下,采用D-S证据合成公式融合冲突信息。假设(

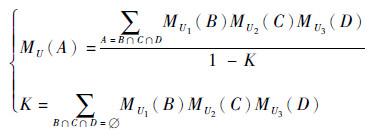 | (40) |
在此,给出基于离散变步长随机集的混合不确定性传播框架如图 2所示。
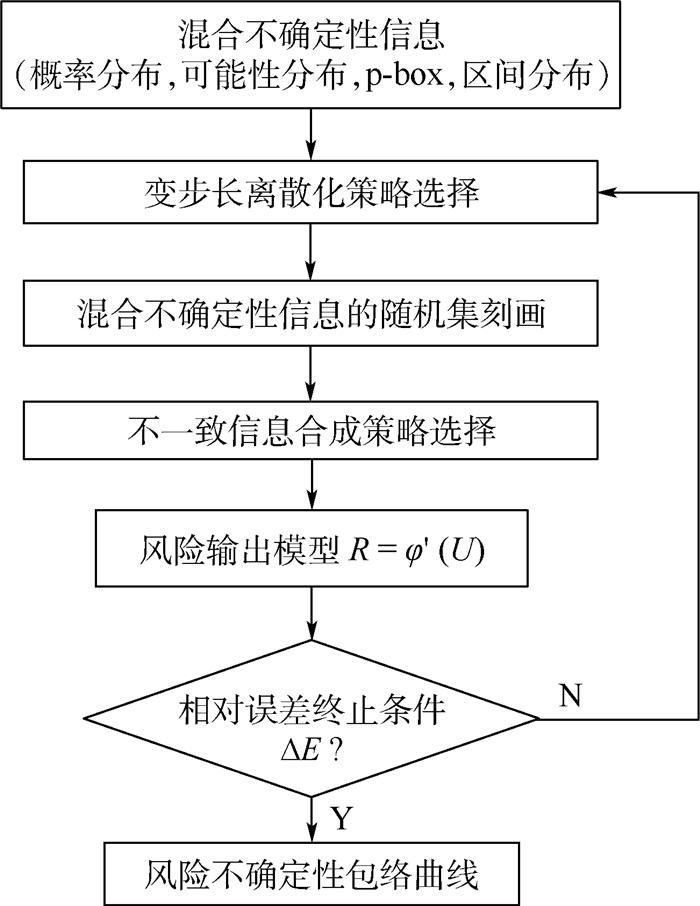 |
| 图 2 混合不确定性传播框架流程 Fig. 2 Flowchart of hybrid uncertainty propagation |
| 图选项 |
步骤1??混合不确定性信息获取,包括概率分布、可能性分布、p-box以及区间分布信息等。
步骤2??选择合理的变步长离散化策略,对步骤1获取的混合不确定性信息统一进行随机集刻画,并在随机集框架下,针对不一致冲突信息进行合成策略选择与不确定性信息融合。
步骤3??采用随机扩展原则进行混合不确定性传播,传播模型为R=
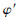
步骤4 ??判断相对误差ΔE,如果不满足要求,则重新进行不确定性信息的离散策略优化。
步骤5??若符合要求,计算风险不确定性包络曲线。
为表征风险包络曲线的不确定性度,Kolmogorov和Fomin[30]给出了定量化的计算公式:
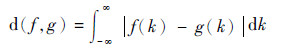 | (41) |
式中:f、g为风险包络曲线函数。
为描述改变离散策略对输出不确定性的影响,定义风险包络相对误差:
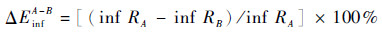 | (42) |
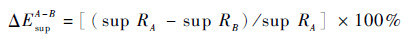 | (43) |
式中:infRA与infRB分别为离散策略A与离散策略B下输出不确定性包络下界;supRA与supRB分别为离散策略A与离散策略B下输出不确定性包络上界。
4 实例分析 4.1 质量-弹簧-阻尼系统模型 质量-弹簧-阻尼系统如图 3所示,激励为Ycos(ωt),相应函数为[31]
 | (44) |
 |
| 图 3 质量-弹簧-阻尼系统 Fig. 3 Mass-spring-damper system |
| 图选项 |
式中:m为振荡器的质量;c为阻尼系数;k为弹性系数;Y和ω分别为载荷幅度和频率。系统的稳态放大系数为
 | (45) |
其中:参数m、c、k与ω互相独立,m与k为概率分布,c为区间分布,ω为可能性分布。
各参数具体信息如下:m服从对称三角概率分布,其中mmin=10,mmod=11,mmax=12。c服从区间分布且相互独立,c1=[5,10],c2=[15,20],c3=[25,25]。k来自3个独立的三角概率分布,且三角概率分布如表 3所示。表 3中,min表示概率分布下界,mod表示概率分布众数,max表示概率分布上界。ω服从可能性分布,且有ω1=[2, 2.3],ωm=[2.5, 2.7],ωr=[3, 3.5];其中,下标l表示可能性分布下界,m表示可能性分布最大可能值,r表示可能性分布上界。
表 3 不确定性参数k Table 3 Uncertainty parameter k
| 参数 | min | mod | max |
| k1 | [100,110] | [160,170] | [210,220] |
| k2 | [90,110] | [150,180] | [210,220] |
| k3 | [80,120] | [130,180] | [200,230] |
表选项
4.2 混合不确定性信息的随机集刻画 为分析Ds的不确定性,需要将4.1节中4类不确定性参数转化为随机集描述,并计算其焦元及其BPA。
对概率分布参数m,按照2.1节方法,将[mmin, mmax]离散为n个子区间Am, i=[ai, bi],每一个子区间[ai, bi]为随机集焦元;并定义p(m)为m的概率密度函数(PDF),Fm(m)为m的累计分布函数,则焦元Am, i的BPA为
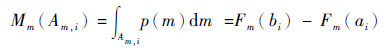 | (46) |
为对比不同离散精度对不确定性传播的影响,设离散精度n分别等于10和20,得到m的随机集焦元及其BPA如图 4(a)和(b)所示,表 4为n=10时的随机集焦元及其BPA。
 |
| 图 4 参数m的随机集刻画 Fig. 4 Random set representation of parameter m |
| 图选项 |
表 4 参数m的焦元及其BPA Table 4 Focal elements and BPA of parameter m
| 参数 | Am, i | Mm(Am, i) |
| 1 | [10, 10.2] | 0.01 |
| 2 | [10.2, 10.4] | 0.05 |
| 3 | [10.4, 10.6] | 0.11 |
| 4 | [10.6, 10.8] | 0.15 |
| 5 | [10.8, 11] | 0.17 |
| 6 | [11, 11.2] | 0.18 |
| 7 | [11.2, 11.4] | 0.16 |
| 8 | [11.4, 11.6] | 0.12 |
| 9 | [11.6, 11.8] | 0.08 |
| 10 | [11.8.12] | 0.02 |
表选项
区间参数c的随机集刻画下,焦元Ac, 1=[5,10],Ac, 2=[5,10],Ac, 3=[5,10],且区间参数相互独立,其BPA分配相等,即m(Ac, 1)=m(Ac, 1)=m(Ac, 1)=1/3。
对参数k,首先将3个参数k由概率分布离散为随机集的表示形式,每一个参数离散化后由Bel和Pl构成不确定性包络曲线,然后对参数k的包络曲线依p-box转化为随机集。参数k1按照VADM法得到随机集包络曲线如图 5(a)和(b)所示。
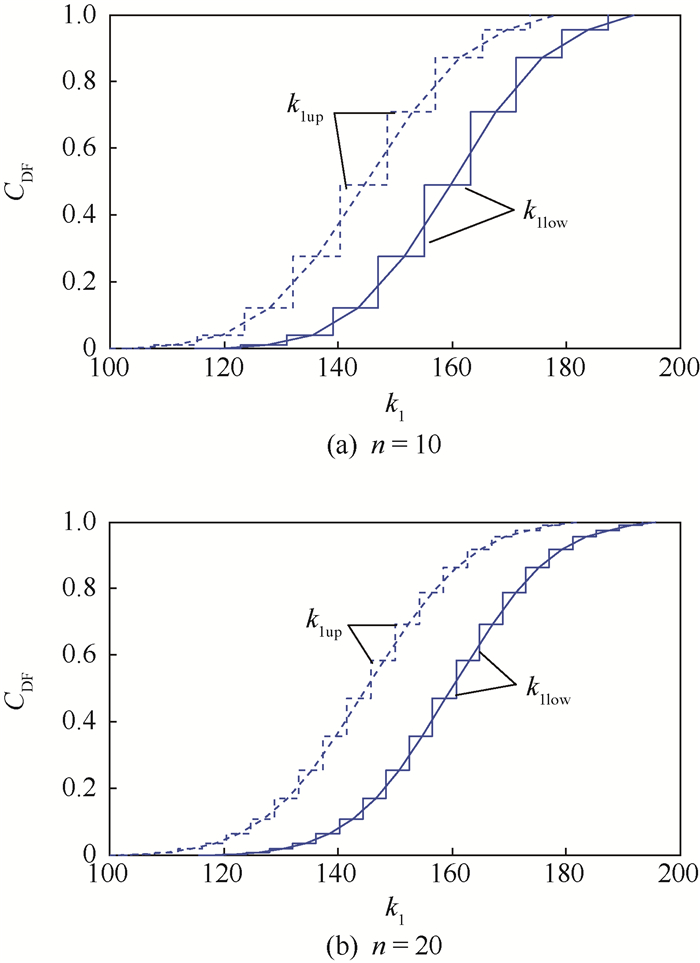 |
| 图 5 参数k1的VADM法随机集刻画 Fig. 5 Random set representation of parameter k1 based on VADM |
| 图选项 |
同理,可计算出k2和k3的随机集刻画。在此需要指出,对概率包络曲线的离散化是通过离散CDF轴实现随机集的刻画。而单一概率分布曲线通过离散目标参数坐标轴,且单一概率分布较高离散精度刻画下的随机集包含于较低离散精度刻画下的随机集,经随机扩展原则映射后其结果具有同样包含属性[19]。而概率包络的随机集离散化,随机集的包含性与离散精度无关,因此仅仅通过提高离散精度来减小不确定性的目的并不可取。
由于参数k同时具备不精确性和不一致性,在随机集描述框架下,对k1、k2和k3采用D-S证据理论进行不确定性合成,通过式(19)合成后的随机集刻画,图 6(a)和(b)给出了基于VADM法的随机集刻画,当n=10时,产生55个焦元,n=20时,产生216个焦元。
 |
| 图 6 参数k的VADM法随机集刻画 Fig. 6 Random set representation of parameterk based on VADM |
| 图选项 |
对频率参数ω,同时受不一致和不精确性影响,VODM法分别得到ω的随机集刻画如图 7(a)和(b)所示。
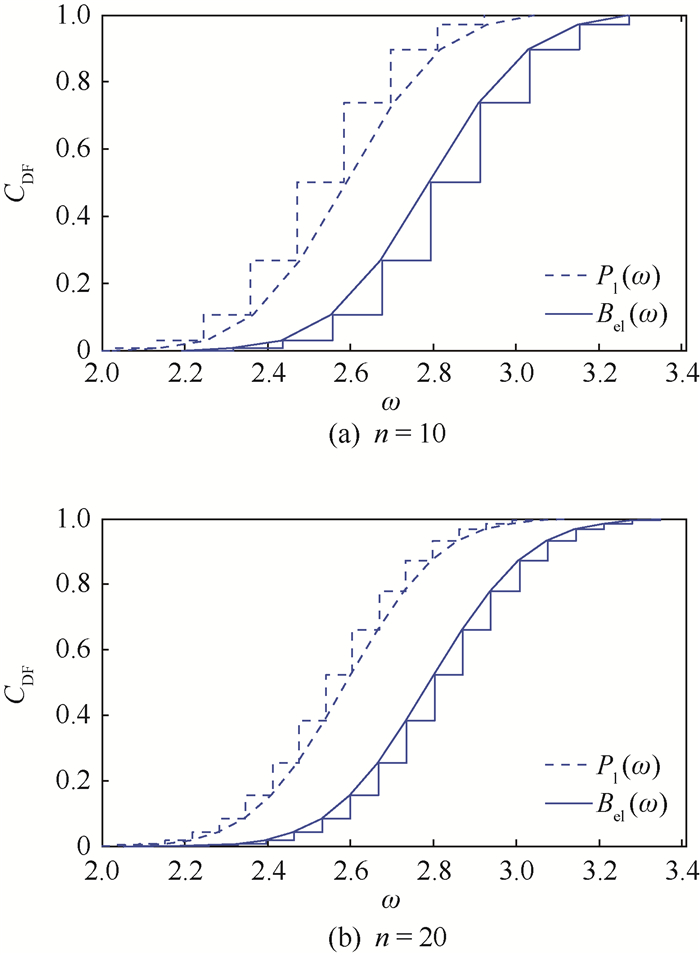 |
| 图 7 参数ω的VODM法随机集刻画 Fig. 7 Random set representation of parameter ω based on VODM |
| 图选项 |
4.3 结果分析 在此,得到4个不确定性参数的随机焦元及其BPA。分别采用均匀与变步长离散化方法,通过式(8)和式(9)、以及式(9)与随机映射得到不同离散精度、不同离散步长策略下Ds的不确定性输出包络曲线如图 8和图 9所示,以及Ds的期望μ与不确定性测度d如表 5所示。另外,为对比分析不同离散策略对输出Ds的影响,给出部分Ds包络曲线下界及其相对误差如表 6和表 7。
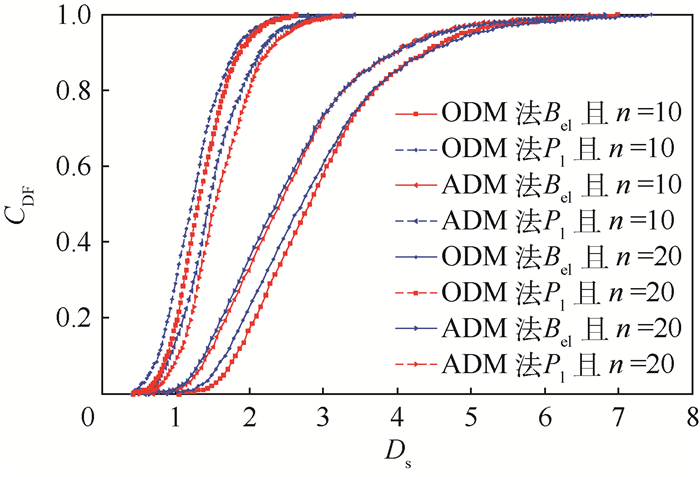 |
| 图 8 均匀步长离散策略下系统Ds响应 Fig. 8 Response of system Ds under uniform step discretization strategy |
| 图选项 |
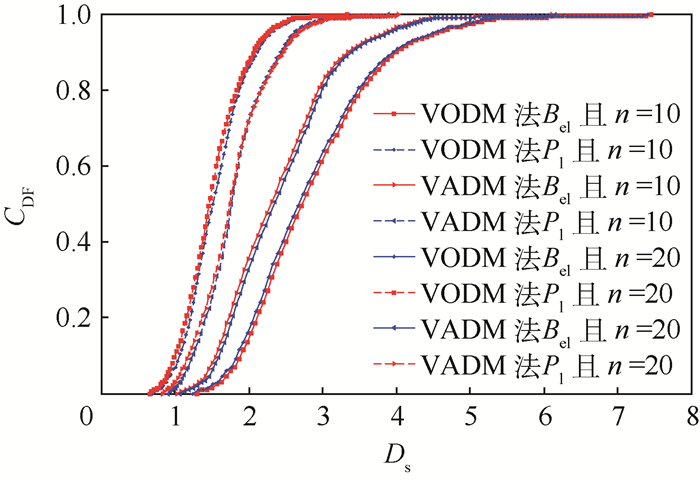 |
| 图 9 变步长离散策略下系统Ds响应 Fig. 9 Response of system Ds under variable step discretization strategy |
| 图选项 |
表 5 不同离散策略下期望μ及其不确定性测度d Table 5 Expectation μ and uncertainty measure d under different discretization strategies
| 离散策略 | μ | d |
| ODM(n=10) | [1.217 1, 2.716 9] | 2.538 |
| VODM(n=10) | [1.305 7, 2.693 4] | 2.515 |
| ADM(n=10) | [1.450 2, 2.399 6] | 2.137 |
| VADM(n=10) | [1.542 2, 2.373 2] | 2.028 |
| ODM(n=20) | [1.221 8, 2.708 5] | 2.374 |
| VODM(n=20) | [1.307 4, 2.682 1] | 2.297 |
| ADM(n=20) | [1.455 7, 2.396 2] | 2.029 |
| VADM(n=20) | [1.544 1, 2.366 8] | 1.912 |
表选项
表 6 均匀步长离散策略下Ds的下界及其相对误差ΔEA-Binf Table 6 Lowerbound of Ds and relative errors ΔEA-Binf under uniform step discretization strategy
| Ds | ODM | ADM | |||||
| n=10 | n=20 | ΔEinfA-B/% | n=10 | n=20 | ΔEinfA-B/% | ||
| 1.3 | 0.033 6 | 0.035 2 | -4.7 | 0.110 3 | 0.114 6 | -3.90 | |
| 1.5 | 0.095 4 | 0.097 8 | -2.52 | 0.140 1 | 0.143 1 | -2.14 | |
| 2 | 0.312 5 | 0.316 6 | -1.31 | 0.351 5 | 0.351 8 | -0.09 | |
| 3 | 0.665 3 | 0.669 0 | -0.56 | 0.715 4 | 0.717 8 | -0.34 | |
| 4 | 0.962 1 | 0.961 9 | 0.08 | 0.905 0 | 0.904 5 | 0.05 | |
| 5 | 0.975 5 | 0.975 2 | 0.02 | 0.975 2 | 0.975 0 | 0.01 | |
表选项
表 7 变步长离散策略下Ds的下界及其相对误差ΔEA-Binf Table 7 Lowerbound of Ds and relative errors ΔEA-Binf under variable step discretization strategy
| Ds | VODM | VADM | |||||
| n=10 | n=20 | ΔEinfA-B/% | n=10 | n=20 | ΔEinfA-B/% | ||
| 1.3 | 0.043 5 | 0.044 7 | -2.76 | 0.136 5 | 0.138 2 | -1.26 | |
| 1.5 | 0.112 3 | 0.113 3 | -0.89 | 0.157 1 | 0.158 4 | -0.83 | |
| 2 | 0.335 7 | 0.338 1 | -0.71 | 0.371 5 | 0.373 5 | -0.54 | |
| 3 | 0.622 8 | 0.626 2 | -0.55 | 0.816 3 | 0.818 7 | -0.29 | |
| 4 | 0.916 5 | 0.916 1 | 0.03 | 0.951 4 | 0.951 1 | 0.03 | |
| 5 | 0.979 4 | 0.979 0 | 0.02 | 0.987 2 | 0.987 0 | 0.01 | |
表选项
1) 对比图 8和图 9,并结合表 5数据得出,离散步长分配策略不变情况下,提高离散精度可提高随机焦元的取值精细程度,但是对不确定性测度影响较小。如采用VODM法,离散精度提高一倍时,焦元数目提高17.3倍,相对误差变化仅为0.42%。
2) 由图 8、图 9以及表 6得出,不确定性输出相对误差于包络曲线左侧截尾部分最大,其原因是在均匀步长离散化策略下,离散随机集与原包络曲线的误差造成。为减小截尾误差需通过配置更多的离散点来逐渐逼近原包络曲线,但是,随着离散点的增多,产生的计算代价呈指数增长,因此,在不增加离散点的情况下优化离散点步长策略很有必要。另外,当Ds < 4时,相对误差ΔEinfA-B为负;当Ds≥4时,相对误差ΔEinfA-B为正,得出当输入随机集的包含关系未知时,仅仅提高离散精度,并不能解决输出不确定性的包含关系。
3) 通过对比表 6和表 7,离散步长不改变情况下,通过改变离散步长分配策略,Ds输出不确定性相对误差可有效减小,其中,VODM法减小29.5%,VADM法减小23.7%。同时改变离散步长和离散步长分配策略情况下,VODM法相对误差减小33.4%,VADM法相对误差减小25.3%。
4) 由图 8和图 9可以看出,ADM法不确定性测度小于ODM法输出的不确定性测度,ODM法输出不确定性包络曲线完全包络ADM法输出不确定性包络曲线,无论是通过提高离散精度还是改变离散步长分配策略,此包络性质不变,即ODM分析法产生较保守的不确定性估计。
5 结论 定量风险评估中不确定性刻画与传播对工程系统风险决策、安全性设计具有极其重要的意义。
1) 本文针对参数信息不完整、不一致性,建立了基于随机集理论的统一不确定性传播框架,实现了异类信息统一刻画与传播。
2) 为减小截尾相对误差,提出了一种变步长随机焦元分配策略,通过对比分析,合理选择离散点与步长配置,可有效减小截尾相对误差。
3) 若要得到更加保守的评估或设计结果,可采用ODM离散化方法;若要得到更加精细化的焦元刻画以及较小不确定性测度,可采用ADM法,并通过提高离散精度与改变离散步长策略实现。
4) 通过非线性机械系统位移响应物理与现象模型算例,验证了本文所提方法的可行性与有效性,该方法可以被用于其它工程实际问题的风险与可靠性评估不确定性分析,有一定的工程应用价值。
参考文献
| [1] | GIANG P H. Decision making under uncertainty comprising complete ignorance and probability[J].International Journal of Approximate Reasoning, 2015, 62: 27–45.DOI:10.1016/j.ijar.2015.05.001 |
| [2] | SONG S, LU Z, LI W, et al. The uncertainty importance measures of the structural system in view of mixed uncertain variables[J].Fuzzy Sets & Systems, 2014, 243: 25–35. |
| [3] | HELTON J C. Uncertainty and sensitivity analysis in the presence of stochastic and subjective uncertainty[J].Journal of Statistical Computation & Simulation, 2007, 57(1): 3–76. |
| [4] | FERSON S, GINZBURG L R. Different methods are needed to propagate ignorance and variability[J].Reliability Engineering & System Safety, 1996, 54(2): 133–144. |
| [5] | BAUDRIT C. Comparing methods for joint objective and subjective uncertainty propagation with an example in risk assessment[C]//Proceedings of 4th International Symposium on Imprecise Probabilities and Their Application (ISIPTA'05), 2005: 31-40. |
| [6] | GUYONNET D, BAUDRIT C, DUBOIS D. Postprocessing the hybrid method for addressing uncertainty in risk assessments[J].Journal of Environmental Engineering, 2005, 131(12): 1750–1754.DOI:10.1061/(ASCE)0733-9372(2005)131:12(1750) |
| [7] | WANG C, QIU Z. Hybrid uncertain analysis for steady-state heat conduction with random and interval parameters[J].International Journal of Heat & Mass Transfer, 2015, 80(80): 319–328. |
| [8] | WALLEY P. Statistical reasoning with imprecise probabilities[M].London: Chapman and Hall, 1991: 12-231. |
| [9] | DEMPSTER A P. Upper and lower probabilities induced by a multi-valued mapping[J].Annals of Mathematical Statistics, 1967, 38(2): 325–339.DOI:10.1214/aoms/1177698950 |
| [10] | SHAFER G. A mathematical theory of evidence[J].Technometrics, 1978, 20(1): 1–242.DOI:10.1080/00401706.1978.10489609 |
| [11] | SMETS P. The normative representation of quantified beliefs by belief functions[J].Artificial Intelligence, 1997, 92(1-2): 229–242.DOI:10.1016/S0004-3702(96)00054-9 |
| [12] | ZADEH L A. Fuzzy sets as a basis for a theory of possibility[J].Fuzzy Sets & Systems, 1978, 1(1): 3–28. |
| [13] | BAUDRIT C, COUSO I, DUBOIS D, et al. Joint propagation of probability and possibility in risk analysis:Towards a formal framework[J].International Journal of Approximate Reasoning, 2007, 45(1): 82–105.DOI:10.1016/j.ijar.2006.07.001 |
| [14] | AVEN T. On how to define, understand and describe risk[J].Reliability Engineering & System Safety, 2010, 95(6): 623–631. |
| [15] | YAGER R R. Uncertainty representation using fuzzy measures[J].IEEE Transactions on Systems Man & Cybernetics Part B (Cybernetics), 2002, 32(1): 13–20. |
| [16] | FLAGE R, BARALDI P, ZIO E, et al. Probability and possibility-based representations of uncertainty in fault tree analysis[J].Risk Analysis, 2013, 33(1): 121–133.DOI:10.1111/risk.2013.33.issue-1 |
| [17] | HELTON J C, JOHNSON J D, OBERKAMPF W L, et al. Sensitivity analysis in conjunction with evidence theory representations of epistemic uncertainty[J].Reliability Engineering & System Safety, 2006, 91(10): 1414–1434. |
| [18] | GUYONNET D, BOURGINE B, DUBOIS D, et al. Hybrid approach for addressing uncertainty in risk assessments[J].Journal of Environmental Engineering, 2003, 129(1): 68–78.DOI:10.1061/(ASCE)0733-9372(2003)129:1(68) |
| [19] | TONON F. Using random set theory to propagate epistemic uncertainty through a mechanical system[J].Reliability Engineering & System Safety, 2004, 85(1): 169–181. |
| [20] | MOLCHANOV I. Theory of random sets[M].Berlin: Springer, 2006: 31-210. |
| [21] | BERNARDINI A. What are the random and fuzzy sets and how to use them for uncertainty modelling in engineering systems[M].Berlin: Springer, 1999: 63-125. |
| [22] | DUBOIS D, PRADE H. Random sets and fuzzy interval analysis[J].Fuzzy Sets & Systems, 1991, 42(1): 87–101. |
| [23] | ALVAREZ D A. On the calculation of the bounds of probability of events using infinite random sets[J].International Journal of Approximate Reasoning, 2006, 43(3): 241–267.DOI:10.1016/j.ijar.2006.04.005 |
| [24] | SADIQ R, NAJJARAN H, KLEINER Y. Investigating evidential reasoning for the interpretation of microbial water quality in a distribution network[J].Stochastic Environmental Research and Risk Assessment, 2006, 21(1): 63–73.DOI:10.1007/s00477-006-0044-7 |
| [25] | GRABISCH M. Dempster-Shafer and possibility theory[M].Berlin: Springer, 2016: 377-437. |
| [26] | DUBOIS D, FOULLOY L, MAURIS G, et al. Probability-possibility transformations, triangular fuzzy sets, and probabilistic inequalities[J].Reliable Computing, 2004, 10(4): 273–297.DOI:10.1023/B:REOM.0000032115.22510.b5 |
| [27] | OUSSALAH M. On the probability/possibility transformations:A comparative analysis[J].International Journal of General System, 2000, 29(5): 671–718.DOI:10.1080/03081070008960969 |
| [28] | 锁斌, 程永生, 曾超, 等. 基于证据理论的异类信息统一表示与建模[J].系统仿真学报, 2013, 25(1): 6–11. SUO B, CHENG Y S, ZENG C, et al. Unified method of describing and modeling heterogeneous information based on evidence theory[J].Journal of System Simulation, 2013, 25(1): 6–11.(in Chinese) |
| [29] | FLOREA M C, JOUSSELME A L, GRENIER D, et al. Approximation techniques for the transformation of fuzzy sets into random sets[J].Fuzzy Sets & Systems, 2008, 159(3): 270–288. |
| [30] | KOLMOGOROV A N, FOMIN S. Elements of the theory of functions and functional analysis.Vol.1, Metric and normed spaces[M].Rochester: Graylock Press, 1957: 372-389. |
| [31] | OBERKAMPF W L, HELTON J C, JOSLYN C A, et al. Challenge problems:Uncertainty in system response given uncertain parameters[J].Reliability Engineering & System Safety, 2004, 85(1): 11–19. |
