为了提高飞机的作战效能，现代高性能战斗机均采用了放宽静稳定性的设计技术^[1-3]。这类高增益闭环飞机的动态特性由本体气动参数和飞行控制系统共同决定^[4]。受到飞行控制系统的能力限制，并不是任何构型的飞机都能通过飞行控制系统设计来最终获得满意的动态特性。对于高增益闭环飞机，飞行控制系统控制飞机的过程与驾驶员人工驾驶飞机的过程是相似的。首先需要测量飞机的飞行状态并根据输入指令进行比较计算，输出控制信号给执行机构驱动操纵舵面，进而产生气动力和气动力矩来控制飞机^[2]，也即等效地改变了飞机的本体气动参数。若飞机的气动舵面操纵效能不足，不能提供相应的控制力及控制力矩，则飞机的本体气动参数取值将对闭环飞机的飞行品质产生较大影响。因此，飞机的本体气动参数取值与闭环高阶飞机飞行品质等级之间存在着一定的对应关系。为了保证采用飞控系统的高阶飞机具有良好的动态响应特性，需合理地设计并确定飞机本体气动参数的取值范围。
在开展飞机本体气动参数与闭环飞机飞行品质等级间的关系研究时，若采用常用的PID控制方法来设计飞机的控制律，飞机的本体气动参数与飞行控制律参数是互相耦合的，即每次更改飞机的本体参数都需要重新设计飞行控制律参数^[5]。而飞机本体参数与飞行控制律参数的变化都会导致闭环飞机的飞行品质发生变化。因此，无法确定闭环飞机的飞行品质变化是由飞机的本体气动参数变化还是由飞行控制系统的参数改变所导致的，也即无法开展飞机本体气动参数对闭环飞机飞行品质的影响规律研究。参考模型非线性动态逆控制律直接以闭环飞机的飞行品质为设计目标，本体气动参数直接应用于内环反馈，飞行控制系统直接计算飞机获得期望响应特性所需要的操纵力矩。因此，在本文研究中，采用模型参考动态逆方法来设计飞机的控制律，更改飞机本体气动参数时，则不需要调整已设计的飞行控制律参数^[6]，飞机本体气动参数与飞行控制律参数之间是解耦的，即可将飞机的本体气动参数视为独立的变量，方便地开展飞机本体气动参数与闭环飞机飞行品质等级间的关系研究。
在闭环飞机短周期模态飞行品质研究方面，目前多集中于时域与频域的评估方法及飞控系统的设计对短周期模态特性的影响等方面^[7-12]。文献[13]研究了控制律参数与闭环飞机飞行品质的对应关系。文献[14]开展了纵向舵面偏转速率大小对飞机短周期模态品质等级影响的相关研究。在本体气动参数对飞机飞行品质的影响研究方面，目前的研究多集中于本体气动参数对无飞行控制系统的开环飞机的飞行品质的影响。鲜有通过高增益闭环飞机飞行品质的设计要求，来确定飞机本体气动参数取值大小的研究成果报道。本文以F-16飞机为算例对象，研究了本体气动参数对闭环飞机短周期模态特性的影响关系，并建立了闭环飞机保持该模态获得一级飞行品质的本体气动参数适配集合，以供设计此类飞机时参考。
1 飞行品质评定准则与研究方法 1.1 短周期模态特性评定准则与评定方法 短周期模态是飞机纵向最重要的运动模态之一，对飞机的稳定性、操纵性以及机动性等均有较大影响。参照MIL-STD-1797A飞行品质规范^[15]，有多种评定飞机短周期模态特性的准则，包括CAP准则、等效参数准则、带宽准则、Neal-Smith准则和Chalk准则等。
其中CAP准则与等效参数准则意义类似，都是基于低阶等效系统的飞行品质评定准则，反映飞机轨迹与姿态之间的协调关系；Gibson准则没有严格的量化等级限制，只能进行飞行品质的定性评定；Neal-Smith准则采用了McRuer驾驶员模型，其模型参数具有不确定性。故本文研究时选用等效参数准则进行闭环飞机短周期模态特性的评定。
等效参数准则依据低阶等效参数ω_spT_θ2及短周期阻尼比ξ_sp、等效时间延迟τ_e等来评定飞机的短周期模态特性。其中：ω_sp和1/T_θ2分别为短周期频率和短周期轨迹响应频率，表示飞机姿态与轨迹之间的跟随关系，ω_spT_θ2表示飞机在短周期频率处的俯仰姿态响应与轨迹响应的滞后时间；ξ_sp表示飞机的阻尼特性；τ_e表示飞机在短周期频率处的俯仰姿态响应与指令的滞后时间。
为了求取闭环飞机的低阶等效参数，需采用低阶等效方法获得与高阶闭环飞机具有一致动态特性的低阶等效系统。MIL-STD-1797A^[15]在附录B中给出了一种基于频域响应特性拟合的低阶等效方法。其具体方法如下：
首先，将高阶闭环飞机的时域数据转换为频域数据，获得高阶闭环飞机的频域响应特征。
其次，建立飞机短周期模态的低阶等效模型，包括俯仰角速率对应纵向杆力或杆位移的传递函数与法向过载对应纵向杆力或杆位移的传递函数，如式(1)所示。

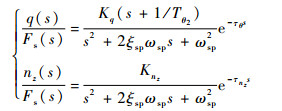(1)

式中：q为俯仰角速率；n_z为法向过载；F_s为纵向操纵位移或操纵力；K_q和K_nz为增益；τ_θ和τ_nz为短周期时间延迟。
寻求低阶等效模型中的有关参数，使式(2)的指标函数为最小。

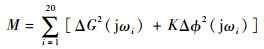(2)

式中：ω_i为给定的拟配离散点频率，可通过将0.1~10 rad/s进行20等分获得；ΔG(jω_i)为给定离散点上高阶系统与低阶系统频率特性的幅值误差，dB；Δ?(jω_i)为相应的相角误差，(°)；K为幅值误差和相角误差之间的加权系数，为了使1 dB的幅值误差与1°的相角误差在等效系统中占有相同的比重，通常选取K=0.017 5；M为失配度，用来表征低阶系统与高阶系统的近似程度，失配度越小，近似程度越高；反之，近似程度越低。
最后，对低阶等效系统的特征参数进行效果评价。若失配度M < 20，或在各离散频率处，高阶闭环飞机与低阶等效系统的相角与幅值误差满足失配包络图^[15]的要求，则该次低阶等效的结果是可信的。
至此，基于低阶等效方法获得闭环飞机的等效参数，采用等效参数准则进行评定，即可完成对闭环飞机短周期模态特性的评定。
1.2 研究方法 不适宜的本体气动参数设计会增大飞行控制系统的控制难度，使闭环飞机不能获得理想的短周期动态特性。本文建立了确定飞机本体气动参数对闭环飞机短周期模态特性影响规律的研究方法：①选取对闭环飞机短周期模态特性影响较大的气动参数；②采用参考模型非线性动态逆控制方法来设计飞行控制系统，改善闭环飞机的动态特性；③选取对飞行品质要求严格的飞行状态点；④对闭环飞机的纵向短周期模态特性进行量化等级评定；⑤修改飞机本体关键气动参数取值，并对新的闭环飞机的短周期模态特性进行评定；⑥重复步骤⑤，对比分析不同本体气动参数取值对闭环飞机短周期模态特性的影响规律。具体研究方法如图 1所示。

图 1 本体气动参数对闭环飞机短周期模态特性影响规律研究流程 Fig. 1 Process for analyzing influence rules of aerodynamic parameters on short-period mode characteristics of closed-loop aircraft

图选项

2 算例与结果分析 2.1 算例对象 选取采用了放宽静稳定性设计的F-16飞机作为研究算例，其具体数学模型参见文献[16-17]。

2.1.1 模型参考动态逆 为了解决常规飞行控制系统设计时需要针对不同本体气动参数进行调参的问题，本文选择了一种基于理想模型的模型参考动态逆控制系统^[6]，其结构如图 2所示。驾驶员输入指令通过理想参考模型生成理想跟踪指令ω_ref，与飞机状态反馈信号ω_s综合后通过PI补偿器及ω_{s, c}坐标转换生成动态逆内回路的输入指令ω_c，通过非线性动态逆内回路计算获得最终的控制变量u输入飞机，控制其运动。

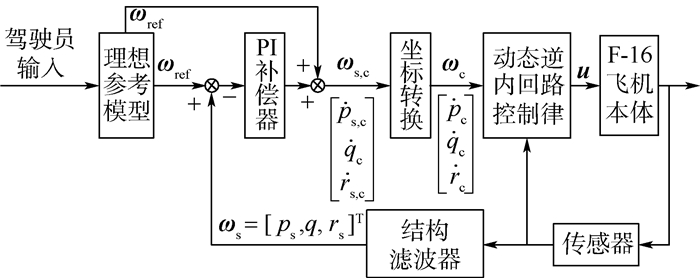图 2 模型参考动态逆结构 Fig. 2 Model reference dynamic inversion structure

图选项

图中ω_s=[p_s，q_s，r_s]^T表示三轴姿态角速率在稳定轴系上的投影，表示三轴姿态角速率变化率指令在稳定轴系上的投影，表示三轴姿态角速率变化率指令在体轴系上的投影。
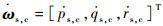
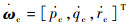
模型参考动态逆是一种基于理想参考模型的非线性动态逆控制律设计方法。通过设计表征期望的飞机动态响应特性的理想参考模型，驾驶员控制输入首先通过该理想参考模型，参考输出作为动态逆的控制输入。理论上讲，只要飞机的响应能够渐进跟踪这一参考输出，那么飞机的动态特性便与理想参考模型一致。这种控制律的控制效果已在文献[18-20]中得到了验证。
由于本文仅研究短周期模态的飞行品质问题，因此，本文仅设计了俯仰轴的理想参考模型。图 2中，俯仰轴理想参考模型的输入为杆位移指令，输出为俯仰角速率指令。参照MIL-STD-1797A^[15]中给出的等效系统短周期传递函数，理想参考模型的输入C_pitch与理想参考模型的输出q_ref之间的关系可表示为

(3)

即俯仰轴的理想参考模型。式中：K_q/T_θ2为模型稳态增益，与单位过载杆力存在对应关系，1/T_θ2与操纵期望参数CAP存在如下近似关系：

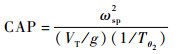(4)

式中：V_T为参考速度；g为重力加速度。
因此，确定理想参考模型中K_q、CAP、ω_sp和ξ_sp取值的大小，即可确定理想参考模型的具体形式。
模型参考动态逆控制律的设计目标是使飞机获得与理想参考模型一致的动态响应特性，且其动态逆内回路使用了本体气动参数计算控制所需的气动力矩。因此，不需要针对不同的本体气动参数进行控制律调参设计。

2.1.2 飞行状态点选取 在仿真过程中，不考虑舵面作动器时间常数与最大舵面偏转速率限制对闭环飞行短周期模态特性的影响。将舵面作动器时间常数与最大舵面偏转速率视为定值。
飞机的舵面作动器可视为一阶惯性环节，取其作动器时间常数为0.05 s，最大偏转速率为60(°)/s。飞机的本体气动参数取值大小会受到飞机的气动布局等因素限制。表 1为飞机的初始本体气动参数及取值变化范围。表中C_mq、C_mα、C_Lα和C_mδe分别为纵向阻尼导数、稳定导数、升力线斜率以及升降舵操纵导数。
表 1 飞机初始本体气动参数及变化范围 Table 1 Initial aircraft aerodynamic parameters and their variation range

气动参数	初始值	变化范围
Cmq	-3.43	-15~-0.1
Cmα	-0.12	-0.72~0.28
CLα	3.9	1.9~5.9
Cmδe	-0.65	-0.11~-0.70

表选项






由于多个飞机本体气动参数均会影响闭环飞机的短周期模态特性，在进行评定的过程中可能涉及到不同参数组合变化的问题。本文在对某一本体气动参数变化进行短周期模态特性评定时，若无特殊说明，其余的本体气动参数取值均保持不变。
此外，考虑到飞机在低速进场状态下的飞行品质较差，更容易出现由于本体参数变化导致飞行品质降级的问题。而在高空高速的飞行状态下，飞机一般都具有一级飞行品质，飞机本体参数对闭环飞机的飞行品质等级的影响不明显。因此，选取纵向典型的低速进场状态(飞行高度H=1 000 m，马赫数Ma=0.3)作为算例进行计算分析。根据F-16飞机飞行控制系统的特点，选取“3211”指令作为系统输入指令，指令形式取幅值为0.3(0-1)的纵向杆位移输入。指令持续时间为0~0.35 s。根据闭环飞机的响应，采用低阶等效拟配的方法对闭环飞机的短周期模态特性进行评定。
2.2 舵面操纵效能的影响 对不同的升降舵操纵导数(C_mδe=-0.13，-0.32，-0.65，-0.70)下闭环飞机的短周期模态特性进行评定, 评定结果如表 2所示。
表 2 不同操纵导数时评定结果对比 Table 2 Comparison of assessment results with different control derivatives

Cmδe	ωsp/(rad·s-1)	ξsp	1/Tθ2	τe/s	品质
-0.13	2.8	0.53	0.38	0.200 3级	3级
-0.32	2.9	0.46	0.40	0.107 2级	2级
-0.65	3.3	0.41	0.46	0.059 1级	1级
-0.70	3.3	0.41	0.46	0.059 1级	1级

表选项






由表 2可以看出，当操纵导数较大时，再增大操纵导数不会影响闭环飞机的飞行品质。而随着操纵导数的减小，提供控制力矩所需要的舵面偏转角度增大，舵面速率饱和的时间增大，舵机回路变成一个非线性动态环节，致使舵机输出与输入指令间存在较大的相位滞后，闭环飞机的等效时间延迟增大，进而飞机飞行品质恶化。当C_mδe减小至-0.32时，飞机短周期品质降为2级，当C_mδe减小至-0.13时，则降为3级。
2.3 不同舵面操纵效能下气动参数的影响 根据2.2节的分析，若飞机的气动舵面操纵效能足够大，则飞行控制系统能保证闭环飞机具有良好的短周期模态特性。因此，在计算过程中，不考虑气动舵面操纵效能增大的情况。
分析在升降舵操纵效能减小(C_mδe=-0.36，-0.32，-0.15)的情况下，不同稳定导数对闭环飞机短周期模态特性的影响规律, 其评定结果如表 3所示。
表 3 不同操纵导数和稳定导数时评定结果对比 Table 3 Comparison of assessment results with different control derivatives and different stability derivatives

Cmδe	Cmα	ωsp/ (rad·s-1)	ξsp	1/Tθ2	τe/s	品质
-0.36	-0.72	2.8	0.45	0.53	0.087 1级	1级
	-0.12	2.7	0.41	0.56	0.091 1级	1级
	0.28	2.7	0.38	0.57	0.102 2级	2级
-0.32	-0.72	2.7	0.48	0.53	0.096 1级	1级
	-0.12	2.7	0.40	0.57	0.107 2级	2级
	0.28	2.7	0.36	0.60	0.117 2级	2级
-0.15	-0.72	2.7	0.42	0.56	0.184 2级	2级
	-0.12	2.8	0.38	0.59	0.192 2级	2级
	0.28	2.7	0.34	0.70	0.201 3级	3级

表选项






由表 3可知，升降舵操纵效能不足时，减小飞机的静稳定裕度导致等效时间延迟增大，进而飞行品质变差。
当C_mδe减小至-0.36，稳定导数减小至0.28时闭环飞机的等效时间延迟约达到0.1 s，飞行品质由1级降为2级。C_mδe减小至-0.32，稳定导数由基准值增大至-0.72时，闭环飞机的等效时间延迟由0.107 s降至0.096 s，飞行品质由2级提高为1级。当C_mδe继续减小至-0.15时，稳定导数减小至0.28时闭环飞机的等效时间延迟约达到0.2 s，飞行品质由2级降为3级。根据表 3的评定结果，可以得到由升降舵操纵效能和稳定导数构成的闭环飞机飞行品质边界如图 3所示。

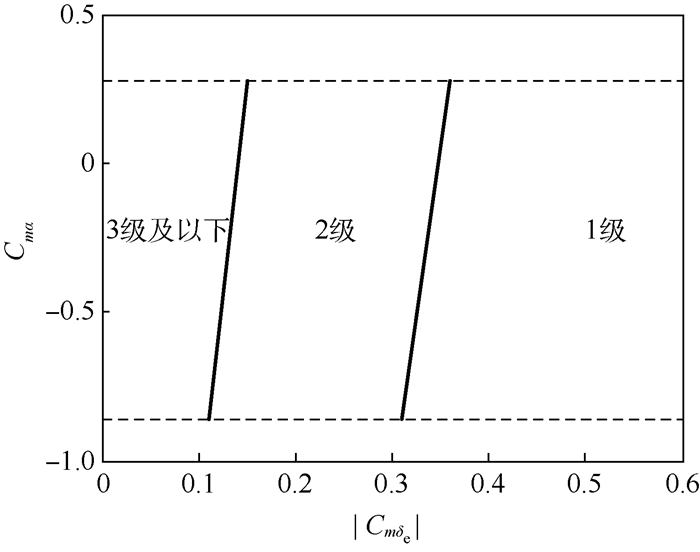图 3 升降舵操纵效能与稳定导数的飞行品质边界 Fig. 3 Flying qualities boundary elevator control efficiency and stability derivatives

图选项

图 3中，虚线为预设的稳定导数变化边界，实线为升降舵操纵效能与稳定导数共同组成的飞行品质边界。由图 3可以看出，随着升降舵操纵效能的降低，闭环飞机的飞行品质等级下降，保持良好飞行品质的稳定导数的可变化范围也相应地减小。这是因为较小的稳定导数将导致飞机本体的短周期频率减小，需要升降舵提供更大的俯仰控制力矩来改善其频率特性。而在同样的操纵效能下，提供更大的力矩导致舵面更长时间地处于速率饱和状态，等效时间延迟增大，进而飞行品质恶化。
对飞机升降舵操纵效能不足(C_mδe=-0.36, -0.32, -0.15)的情况下，不同阻尼导数对闭环飞机模态特性的影响规律进行分析，其评定结果如表 4所示。
表 4 不同操纵导数和阻尼导数的评定结果对比 Table 4 Comparison of assessment results with different control derivatives and different damping derivatives

Cmδe	Cmq	ωsp/ (rad·s-1)	ξsp	1/Tθ2	τe/s	品质
-0.36	-15	2.7	0.39	0.56	0.074 1级	1级
	-3.43	2.7	0.41	0.56	0.091 1级	1级
	-0.1	2.8	0.42	0.56	0.100 2级	2级
-0.32	-15	2.7	0.37	0.59	0.099 1级	1级
	-3.43	2.7	0.40	0.57	0.107 2级	2级
	-0.1	2.8	0.41	0.57	0.112 2级	2级
-0.15	-15	2.7	0.36	0.59	0.181 2级	2级
	-3.43	2.8	0.38	0.59	0.192 2级	2级
	-0.1	2.8	0.38	0.57	0.201 3级	3级

表选项






由表 4可知，升降舵操纵效能不足时，减小飞机的阻尼导数C_mq将导致等效时间延迟增大，飞行品质变差。
当C_mδe减小至-0.36，阻尼导数减小至-0.1时闭环飞机的等效时间延迟约达到0.1 s，飞行品质由1级降为2级。当C_mδe减小至-0.32，阻尼导数由基准值增大至-15，闭环飞机的等效时间延迟由0.107 s降至0.099 s，飞行品质由2级提高为1级。当C_mδe减小至-0.15时，阻尼导数减小至-0.1时闭环飞机的等效时间延迟约达到0.2 s，飞行品质由2级降为3级。根据表 4的评定结果，可以得到由升降舵操纵效能和阻尼导数构成的闭环飞机飞行品质边界如图 4所示。

图 4 升降舵操纵效能与阻尼导数的飞行品质边界 Fig. 4 Flying qualities boundary of elevator control efficiency and damping derivatives

图选项

图 4中，虚线为预设的阻尼导数变化边界，实线为升降舵操纵效能与阻尼导数共同组成的飞行品质边界。由图 4可知，在升降舵操纵效能不足的情况下，随着阻尼导数的减小，闭环飞机的飞行品质等级降低。这是因为较小的阻尼导数将导致飞机本体的短周期阻尼比降低，需要升降舵提供更大的俯仰控制力矩来改善其阻尼特性。而在同样的操纵效能下，提供更大的力矩导致舵面速率饱和持续时间增大，等效时间延迟增大，进而飞行品质恶化。
在飞机舵面操纵效能不足(C_mδe=-0.36，-0.32，-0.15)的情况下，分析不同升力线斜率对闭环飞机短周期模态特性的影响规律, 评定结果如表 5所示。
表 5 不同操纵导数和升力线斜率时评定结果对比 Table 5 Comparison of assessment results with different control derivatives and different lift curve slope

Cmδe	CLα	ωsp/ (rad·s-1)	ξsp	1/Tθ2	τe/s	品质
-0.36	5.9	2.7	0.39	0.65	0.074 1级	1级
	3.9	2.7	0.41	0.56	0.091 1级	1级
	1.9	2.7	0.46	0.54	0.100 2级	2级
-0.32	5.9	2.7	0.36	0.70	0.098 1级	1级
	3.9	2.7	0.40	0.57	0.107 2级	2级
	1.9	2.7	0.42	0.56	0.115 2级	2级
-0.15	5.9	2.7	0.35	0.73	0.181 2级	2级
	3.9	2.8	0.38	0.59	0.192 2级	2级
	1.9	参数剧烈振荡，拟配效果差，品质低于3级

表选项






由表 5可知，升降舵操纵效能较低时，减小飞机的升力线斜率度将导致等效时间延迟增大，飞行品质恶化。
当C_mδe减小至-0.36时，升力线斜率减小至1.9时闭环飞机的等效时间延迟达到0.1 s，飞行品质由1级降为2级。C_mδe减小至-0.32，升力线斜率由基准值增大至5.9时，闭环飞机的等效时间延迟由0.107 s降至0.098 s，飞行品质由2级提高为1级。当C_mδe减小至-0.15时，升力线斜率减小至1.9将导致闭环飞机仿真出现剧烈振荡，无法完成低阶等效拟配，飞行品质降为低于3级。根据表 5的结果，可以得到由升降舵操纵效能和升力线斜率构成的闭环飞机飞行品质边界如图 5所示。

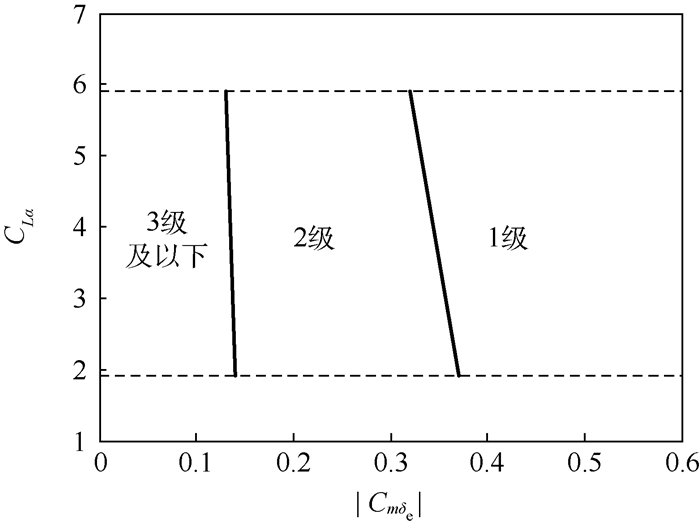图 5 升降舵操纵效能与升力线斜率的飞行品质边界 Fig. 5 Flying qualities boundary of elevator control efficiency and lift curve slope

图选项

图 5中，虚线为预设的升力线斜率变化边界，实线为升降舵操纵效能与升力线斜率共同组成的飞行品质边界。由图 5可知，在升降舵操纵效能不足的情况下，随着升力线斜率的减小，闭环飞机的飞行品质等级降低。这是因为减小升力线斜率导致飞机运动变慢，等效地降低了飞机本体的短周期振荡频率，在模型参考动态逆的作用下，升降舵需要提供更大的俯仰控制力矩来改善闭环飞机的频率特性。在同样的操纵效能下，提供更大的力矩导致舵面将更长时间的处于速率饱和状态，等效时间延迟增大，进而飞行品质恶化。
2.4 本体气动参数的适配规律 本节重点分析稳定导数、阻尼导数和升力线斜率组合变化对闭环飞机飞行品质的影响规律。经仿真计算，在升降舵操纵效能取值为C_mδe=-0.28时，满足闭环飞机1级飞行品质的飞机本体气动参数适配值集合可以用三维图形来表征，如图 6所示。

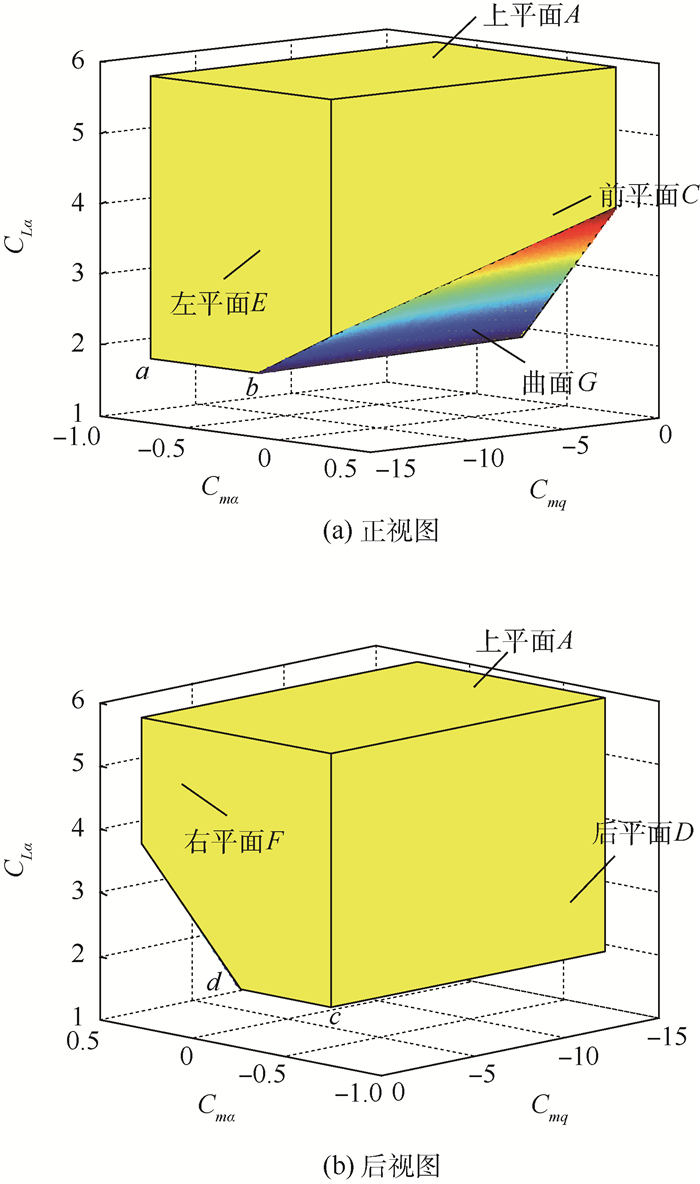图 6 满足1级品质的气动参数适配值集合 Fig. 6 Match value set of aerodynamic parameters to satisfy level 1 flying qualities

图选项

图 6中，上平面A由最大升力线斜率C_Lα=5.9时参数的集合(C_mα, C_mq)组成，平面abcd由最小升力线斜率C_Lα=1.9时的参数集合(C_mα, C_mq)组成。前平面C由阻尼导数取最大值C_mq=-15时的参数集合(C_Lα, C_mα)组成。后平面D由阻尼导数取最小值C_mq=-0.1时的参数集合(C_Lα, C_mα)组成。左平面E由稳定导数取最大值C_mα=-0.72时的参数集合(C_Lα, C_mq)组成。右平面F由稳定导数取最小值时C_mα=0.28的参数集合(C_Lα, C_mq)组成。曲面G的各边界由各本体参数取最小值时的参数集合(C_Lα, C_mq, C_mα)组成。
当飞机的本体参数位于图 6中的多边体内部时，闭环飞机的短周期模态具有1级飞行品质。本体参数越靠近深色区域，等效时间延迟越大，飞行品质越差；反之，越靠近浅色区域，等效时间延迟越小，飞行品质越好。
在适配集合中(见图 6)，取出参数C_Lα=1.9，3.9，5.9时参数C_mα和C_mq的适配区域，来分析三者的适配规律，如图 7所示。

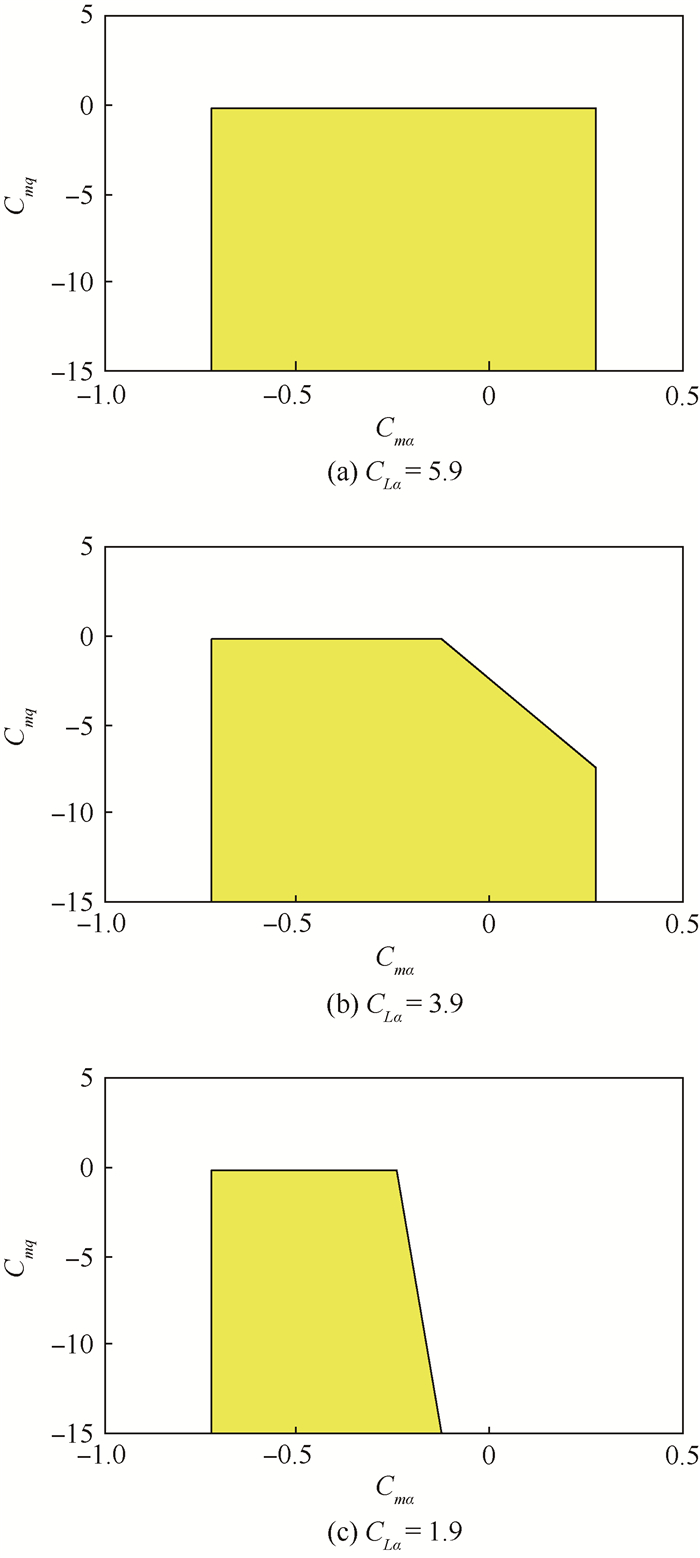图 7 阻尼导数与稳定导数的适配区域 Fig. 7 Match value area of damping derivatives and stability derivatives

图选项

图 7中的闭合区域即为闭环飞机短周期模态保持1级飞行品质的参数适配区域。当参数(C_mα, C_mq)越靠近区域的左下角，闭环飞机的等效延迟时间越小，飞行品质越好。反之，当参数越靠近区域的右上角，闭环飞机的等效时间越大，飞行品质越差。从图 7中可以看出，随着升力线斜率的减小，闭环飞机短周期模态保持1级飞行品质的参数(C_mα, C_mq)适配区域的面积逐渐缩小。当C_Lα=1.9时，参数(C_mα, C_mq)适配区域的面积最小，即为图 6的平面abcd。
对于不同的升降舵操纵效能，其本体气动参数的适配值集合大小不同。图 8为不同的升降舵操纵效能下(C_mδe=-0.28，-0.24)，闭环飞机保持1级短周期模态飞行品质的本体气动参数的适配值集合。

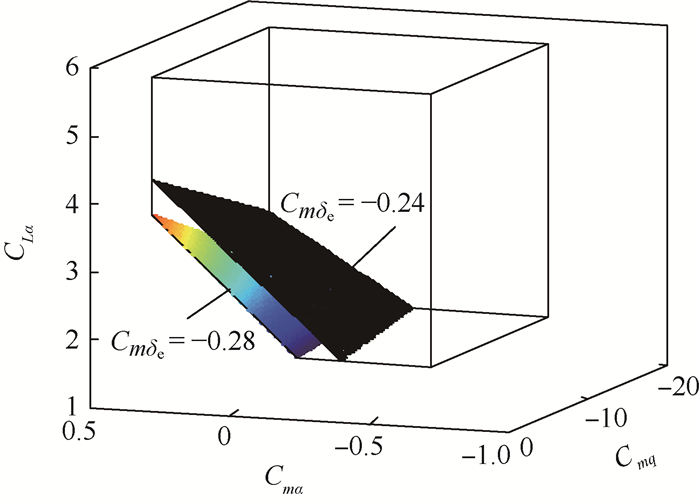图 8 不同升降舵操纵效能下的气动参数适配值集合 Fig. 8 Match value set of aerodynamic parameters with different elevator control efficiency

图选项

由图 8可知，上方的黑色曲面为C_mδe=-0.24的气动参数适配边界，下方的彩色曲面为C_mδe=-0.28的气动参数适配边界。随着升降舵操纵效能的下降，闭环飞机短周期模态具有1级品质的本体参数的适配范围缩小，曲面边界上移。这是因为随着升降舵操纵效能的减小，其等效地改变本体参数的能力也相应地下降，即改善闭环飞机短周期模态特性的能力降低。为保证闭环飞机具有1级飞行品质，飞机本体气动参数的设计要求提高，适配范围减小。
3 结论 1) 建立了本体气动参数对闭环飞机短周期模态特性影响的评定方法：采用模型参考动态逆控制方法来设计研究对象的飞行控制系统，在对短周期模态特性要求严格的飞行状态下，对不同的关键本体气动参数及参数组合下闭环飞机的飞行品质进行评定，确定本体气动参数对闭环飞机短周期模态特性的影响规律。
2) 升降舵操纵效能的大小是影响闭环飞机短周期模态特性的主要因素。若升降舵操纵效能不足时，在适当的范围内，增大飞机的俯仰稳定导数、阻尼导数和升力线斜率可减小升降舵处于速率饱和状态的持续时间，有助于改善闭环飞机的飞行品质。
3) 本文以采用模型参考动态逆控制律的F-16飞机为算例，通过对不同气动参数组合下的闭环飞机短周期模态特性进行了评估，得到了分别由升降舵操纵效能与俯仰稳定导数、俯仰阻尼导数和升力线斜率构成的飞行品质等级边界。通过仿真计算，得到了闭环飞机短周期模态达到一级飞行品质的飞机本体气动参数适配值集合。在此集合内，随着升力线斜率的减小，阻尼导数与稳定导数组成的适配区域的面积将逐渐减小。随着升降舵操纵效能的减小，闭环飞机短周期模态达到1级飞行品质的本体气动参数适配区域将逐渐缩小。

参考文献

[1]	TRAN T T, NEWMAN B.Nonlinear flight control design for longitudinal dynamics:AIAA-2015-1994[R].Reston:AIAA, 2015.
[2]	方振平, 陈万春, 张曙光. 航空飞行器飞行动力学[M].北京: 北京航空航天大学出版社, 2005: 106. FANG Z P, CHEN W C, ZHANG S G. Aircraft flight dynamics[M].Beijing: Beihang University Press, 2005: 106.(in Chinese)
[3]	JANSEN Q J M.Relaxed static stability performance assessment on conventional and unconventional aircraft configurations[D].Delft:Delft University of Technology, 2015.
[4]	NELSON R C. Flight stability and automatic control[M].New York: WCB/McGraw Hill, 1988: 72.
[5]	STEVENS B L, LEWIS F L, JOHNSON E N. Aircraft control and simulation:Dynamics, controls design, and autonomous systems[M].Hoboken: John Wiley & Sons, Inc., 2015: 192-193.
[6]	龙晋伟, 潘文俊, 王立新. 战斗机动态逆控制律对比研究[J].飞行力学, 2013, 31(4): 297–300. LONG J W, PAN W J, WANG L X. A comparison of nonlinear dynamics inversion control law designs for a fighter aircraft[J].Flight Dynamics, 2013, 31(4): 297–300.(in Chinese)
[7]	MITCHELL D G, DOMAN D B, KEY D L, et al. Evolution revolution and challenges of handling qualities[J].Journal of Guidance, Control, and Dynamics, 2004, 27(1): 12–28.DOI:10.2514/1.3252
[8]	GRATTON G. Initial airworthiness:An introduction to flying qualities evaluation[M].Berlin: Springer International Publishing, 2015: 193-199.
[9]	GERTSEN W M, SHOMBER H A. Longitudinal handing qualities criteria-An evaluation[J].Journal of Aircraft, 1967, 4(4): 371–374.DOI:10.2514/3.43851
[10]	KREKELER G.High angel of attack flying qualities criteria[C]//Proceedings of 28th AIAA, Aerospace Sciences Meeting.Reston:AIAA, 1990:1-11.
[11]	YAN Y Y, DONG W H, ZOU Q, et al.Longitudinal inner loop flight controller flight control design by using L1 adaptive control theory[C]//IEEE International Conference on Information and Automation.Piscataway, NJ:IEEE Press, 2015:2965-2970.
[12]	MANNING C, GLEASON D.Flight test results using a low order equivalent systems technique to estimate flying qualities[C]//AIAA Atmospheric Flight Mechanics Conference.Reston:AIAA, 1992:231-243.
[13]	杨宇, 陆宇平. 基于飞行品质的飞机控制增稳系统参数估计[J].航空计算技术, 2011, 41(2): 108–112. YANG Y, LU Y P. Parameter estimation for control augmentation system based on handling quality requirements[J].Aeronautical Computing Technique, 2011, 41(2): 108–112.(in Chinese)
[14]	李淼, 王立新, 黄成涛. 舵面特性对飞翼构型作战飞机短周期品质的影响[J].航空学报, 2009, 30(11): 2059–2065. LI M, WANG L X, HUANG C T. Influence of control surface characteristics on short-period mode flying qualities for flying wing aircraft[J].Acta Aeronautica et Astronautica Sinica, 2009, 30(11): 2059–2065.DOI:10.3321/j.issn:1000-6893.2009.11.008(in Chinese)
[15]	U.S.Department of Defense.Military standard:Flying qualities of piloted air planes:MIL-STD-1797A[S].Washington, D.C.:U.S.Department of Defense, 1990.
[16]	SONNEVELDT L, CHU Q P, MULDER J A. Nonlinear flight control design using constrained adaptive back stepping[J].Journal of Guidance, Control, and Dynamics, 2007, 30(2): 322–336.DOI:10.2514/1.25834
[17]	LEWIS F L, STEVENS B L. Aircraft control and simulation[M].Hoboken: John Wiley & Sons, Inc., 1992: 107-116.
[18]	SONNEVELDT L, VAN OORT E, CHU Q P, et al.Nonlinear adaptive flight control law design and handling qualities evaluation[C]//Joint 48th IEEE Conference on Decision and Control and 28th Chinese Control Conference.Piscataway, NJ:IEEE Press, 2009:7333-7338.
[19]	柳晓菁, 易建强, 赵冬斌. 基于Lyapunov稳定理论设计MRAC系统的简单方法[J].系统仿真学报, 2005, 17(8): 1933–1935. LIU X J, YI J Q, ZHAO D B. Simple scheme for MRAC system using Lyapunov theory[J].Journal of System Simulation, 2005, 17(8): 1933–1935.(in Chinese)
[20]	MILLER C J.Nonlinear dynamic inversion baseline control law:Flight-test results for the full-scale advanced system tested F/A-18 airplane:AIAA-2011-6468[R].Reston:AIAA, 2011.